Площадь поверхности конуса
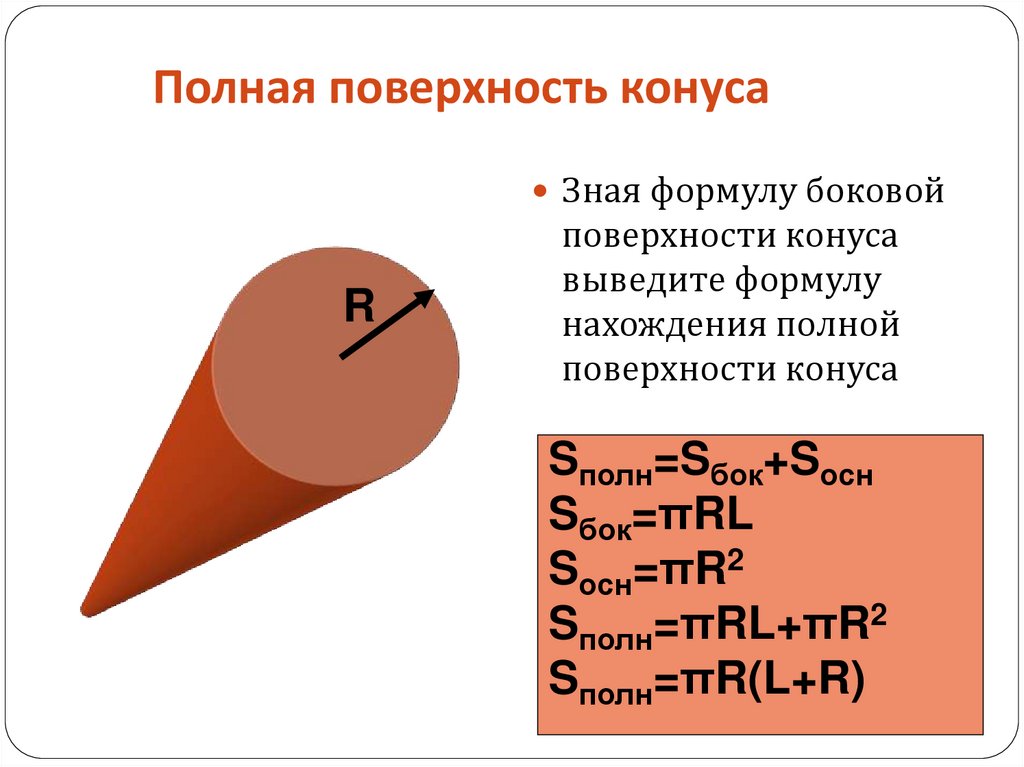
Площадь поверхности конуса (или просто поверхность конуса) равна сумме площадей основания и боковой поверхности.
Площадь боковой поверхности конуса вычисляется по формуле: S = πRl, где R — радиус основания конуса, а l — образующая конуса.
Так как площадь основания конуса равна πR2 (как площадь круга), то площадь полной поверхности конуса будет равна: πR2 + πRl = πR (R + l ).
Получение формулы площади боковой поверхности конуса можно пояснить такими рассуждениями. Пусть на чертеже изображена развёртка боковой поверхности конуса. Разделим дугу АВ на возможно большее число равных частей и все точки деления соединим с центром дуги, а соседние — друг с другом хордами.
Получим ряд равных треугольников. Площадь каждого треугольника равна ah/2 , где а — длина основания треугольника, a h — его высота.
Сумма площадей всех треугольников составит: ah/2 • n = anh/2 , где n — число треугольников.
При большом числе делений сумма площадей треугольников становится весьма близкой к площади развёртки, т. е. площади боковой поверхности конуса. Сумма оснований треугольников, т. е. an, становится весьма близкой к длине дуги АВ, т. е. к длине окружности основания конуса. Высота каждого треугольника становится весьма близкой к радиусу дуги, т. е. к образующей конуса.
Пренебрегая незначительными различиями в размерах этих величин, получаем формулу площади боковой поверхности конуса (S):
S = Cl/2, где С — длина окружности основания конуса, l — образующая конуса.
Зная, что С = 2πR, где R — радиус окружности основания конуса, получаем: S = πRl.
Примечание. В формуле S = Cl/2 поставлен знак точного, а не приближённого равенства, хотя на основании проведённого рассуждения мы могли бы это равенство считать приближённым. Но в старших классах средней школы доказывается, что равенство
S = Cl/2 точное, а не приближённое.
Теорема. Боковая поверхность конуса равна произведению длины окружности основания на половину образующей.
Впишем в конус (рис.) какую-нибудь правильную пирамиду и обозначим буквами р и l числа, выражающие длины периметра основания и апофемы этой пирамиды.
Тогда боковая поверхность её выразится произведением 1/2р • l .
Предположим теперь, что число сторон вписанного в основание многоугольника неограниченно возрастает. Тогда периметр р будет стремиться к пределу, принимаемому за длину С окружности основания, а апофема l будет иметь пределом образующую конуса (так как из ΔSAK следует, что SA — SK
1/2р• l, будет стремиться к пределу 1/2С• L. Этот предел и принимается за величину боковой поверхности конуса. Обозначив боковую поверхность конуса буквой S, можем написать:
S = 1/2С • L = С • 1/2L
Следствия.
1) Так как С = 2πR, то боковая поверхность конуса выразится формулой:
S = 1/2• 2πR • L = πRL
2) Полную поверхность конуса получим, если боковую поверхность сложим с площадью основания; поэтому, обозначая полную поверхность через Т, будем иметь:
T = πRL + πR2 = πR(L + R)
Теорема. Боковая поверхность усечённого конуса равна произведению полусуммы длин окружностей оснований на образующую.
Впишем в усечённый конус (рис.) какую-нибудь правильную усечённую пирамиду и обозначим буквами р, р1 и l числа, выражающие в одинаковых линейных единицах длины периметров нижнего и верхнего оснований и апофемы этой пирамиды.
Тогда боковая поверхность вписанной пирамиды равна 1/2 (р + р1) • l
При неограниченном возрастании числа боковых граней вписанной пирамиды периметры р и р1 стремятся к пределам, принимаемым за длины С и С1 окружностей оснований, а апофема l имеет пределом образующую L усечённого конуса. Следовательно, величина боковой поверхности вписанной пирамиды стремится при этом к пределу, равному (С + С1) L. Этот предел и принимается за величину боковой поверхности усечённого конуса. Обозначив боковую поверхность усечённого конуса буквой S, будем иметь:
Следовательно, величина боковой поверхности вписанной пирамиды стремится при этом к пределу, равному (С + С1) L. Этот предел и принимается за величину боковой поверхности усечённого конуса. Обозначив боковую поверхность усечённого конуса буквой S, будем иметь:
S = 1/2 (С + С1) L
Следствия.
1) Если R и R1 означают радиусы окружностей нижнего и верхнего оснований, то боковая поверхность усечённого конуса будет:
S = 1/2 (2πR + 2πR1) L = π (R + R1) L.
2) Если в трапеции OO1А1А (рис.), от вращения которой получается усечённый конус, проведём среднюю линию ВС, то получим:
ВС = 1/2(OA + O1A1) = 1/2 • (R + R1),
откуда
R + R1 = 2ВС.
Следовательно,
S = 2πBC• L,
т. е. боковая поверхность усечённого конуса равна произведению длины окружности среднего сечения на образующую.
е. боковая поверхность усечённого конуса равна произведению длины окружности среднего сечения на образующую.
3) Полная поверхность Т усечённого конуса выразится так:
T = π( R2 + R12 + RL + R1L)
Равна площадь боковой поверхности конуса формула. Площадь боковой и полной поверхности конуса
Тела вращения, изучаемые в школе, — это цилиндр, конус и шар.
Если в задаче на ЕГЭ по математике вам надо посчитать объем конуса или площадь сферы — считайте, что повезло.
Применяйте формулы объема и площади поверхности цилиндра, конуса и шара. Все они есть в нашей таблице. Учите наизусть. Отсюда начинается знание стереометрии.
Иногда неплохо нарисовать вид сверху. Или, как в этой задаче, — снизу.
2. Во сколько раз объем конуса, описанного около правильной четырехугольной пирамиды, больше объема конуса, вписанного в эту пирамиду?
Всё просто — рисуем вид снизу. Видим, что радиус большего круга в раз больше, чем радиус меньшего. Высоты у обоих конусов одинаковы. Следовательно, объем большего конуса будет в раза больше.
Видим, что радиус большего круга в раз больше, чем радиус меньшего. Высоты у обоих конусов одинаковы. Следовательно, объем большего конуса будет в раза больше.
Еще один важный момент. Помним, что в задачах части В вариантов ЕГЭ по математике ответ записывается в виде целого числа или конечной десятичной дроби. Поэтому никаких или у вас в ответе в части В быть не должно. Подставлять приближенное значение числа тоже не нужно! Оно обязательно должно сократиться!. Именно для этого в некоторых задачах задание формулируется, например, так: «Найдите площадь боковой поверхности цилиндра, деленную на ».
А где же еще применяются формулы объема и площади поверхности тел вращения? Конечно же, в задаче С2 (16). Мы тоже расскажем о ней.
Мы знаем, что такое конус, попробуем найти площадь его поверхности. Зачем нужно решать такую задачу? Например, нужно понять, сколько теста пойдет на изготовление вафельного рожка? Или сколько кирпичей понадобится, чтобы сложить кирпичную крышу замка?
Измерить площадь боковой поверхности конуса просто так не получится.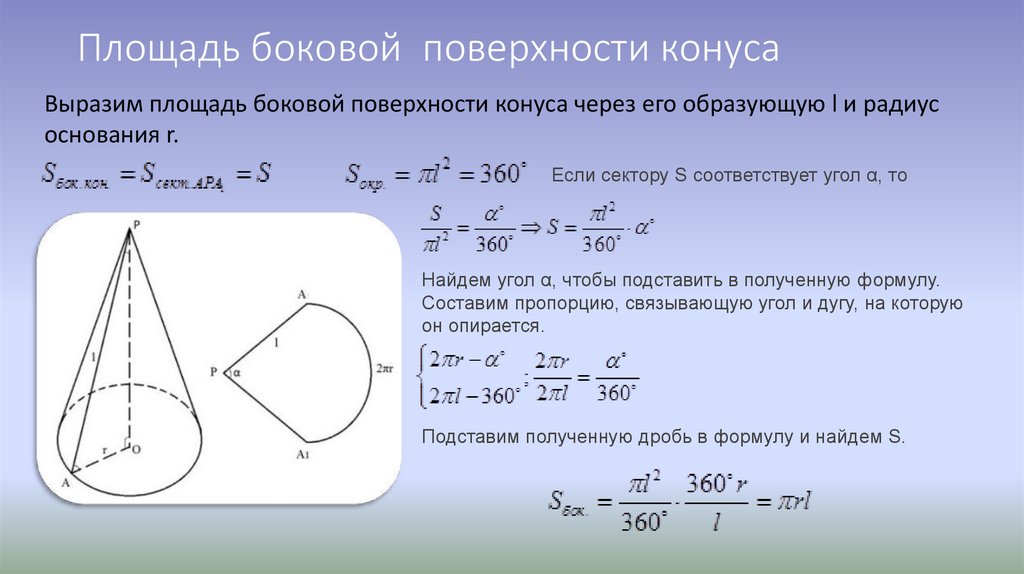 Но представим себе все тот же рожок, обмотанный тканью. Чтобы найти площадь куска ткани, нужно разрезать и разложить ее на столе. Получится плоская фигура, ее площадь мы сможем найти.
Но представим себе все тот же рожок, обмотанный тканью. Чтобы найти площадь куска ткани, нужно разрезать и разложить ее на столе. Получится плоская фигура, ее площадь мы сможем найти.
Рис. 1. Разрез конуса по образующей
Сделаем так же с конусом. «Разрежем» его боковую поверхность вдоль любой образующей, например, (см. рис. 1).
Теперь «размотаем» боковую поверхность на плоскость. Получаем сектор. Центр этого сектора — вершина конуса, радиус сектора равен образующей конуса, а длина его дуги совпадает с длиной окружности основания конуса. Такой сектор называется разверткой боковой поверхности конуса (см. рис. 2).
Рис. 2. Развертка боковой поверхности
Рис. 3. Измерение угла в радианах
Попробуем найти площадь сектора по имеющимся данным. Сперва введем обозначение: пусть угол при вершине сектора в радианах (см. рис. 3).
С углом при вершине развертки нам придется часто сталкиваться в задачах. Пока же попробуем ответить на вопрос: а не может ли этот угол получиться больше 360 градусов? То есть не получится ли так, что развертка наложится сама на себя? Конечно же, нет.
Тогда вспомним две формулы из курса планиметрии: длина дуги . Площадь сектора: .
В нашем случае роль играет образующая , а длина дуги равна длине окружности основания конуса, то есть . Имеем:
Окончательно получаем: .
Наряду с площадью боковой поверхности можно найти и площадь полной поверхности. Для этого к площади боковой поверхности надо прибавить площадь основания. Но основание — это круг радиуса , чья площадь по формуле равна .
Окончательно имеем: , где — радиус основания цилиндра, — образующая.
Решим пару задач на приведенные формулы.
Рис. 4. Искомый угол
Пример 1 .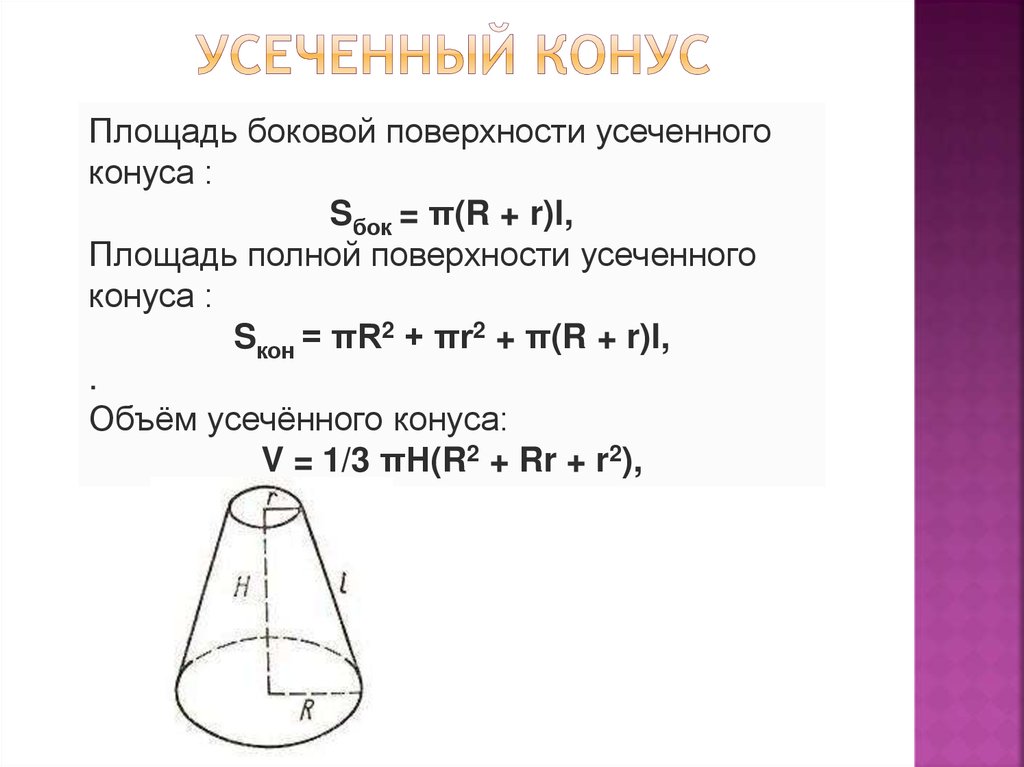 Разверткой боковой поверхности конуса является сектор с углом при вершине. Найти этот угол, если высота конуса равна 4 см, а радиус основания равен 3 см (см. рис. 4).
Разверткой боковой поверхности конуса является сектор с углом при вершине. Найти этот угол, если высота конуса равна 4 см, а радиус основания равен 3 см (см. рис. 4).
Рис. 5. Прямоугольный треугольник, образующий конус
Первым действием, по теореме Пифагора, найдем образующую: 5 см (см. рис. 5). Далее, мы знаем, что .
Пример 2 . Площадь осевого сечения конуса равна , высота равна . Найти площадь полной поверхности (см. рис. 6).
Здесь представлены задачи с конусами, условие связано с его площадью поверхности. В частности в некоторых задачах стоит вопрос об изменении площади при увеличении (уменьшении) высоты конуса или радиуса его основания. Теория для решения задач в . Рассмотрим следующие задачи:
27135. Длина окружности основания конуса равна 3, образующая равна 2. Найдите площадь боковой поверхности конуса.
Площадь боковой поверхности конуса равна:
Подставляем данные:
75697. Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в 36 раз, а радиус основания останется прежним?
Площадь боковой поверхности конуса:
Образующая увеличивается в 36 раз. Радиус остался прежним, значит длина окружности основания не изменилась.
Радиус остался прежним, значит длина окружности основания не изменилась.
Значит площадь боковой поверхности изменённого конуса будет иметь вид:
Таким образом, она увеличится в 36 раз.
*Зависимость прямолинейная, поэтому эту задачу без труда можно решить устно.
27137. Во сколько раз уменьшится площадь боковой поверхности конуса, если радиус его основания уменьшить в 1,5 раза?
Площадь боковой поверхности конуса равна:
Радиус уменьшается в 1,5 раза, то есть:
Получили, что площадь боковой поверхности уменьшилась в 1,5 раза.
27159. Высота конуса равна 6, образующая равна 10. Найдите площадь его полной поверхности, деленную на Пи.
Полная поверхность конуса:
Необходимо найти радиус:
Известна высота и образующая, по теореме Пифагора вычислим радиус:
Таким образом:
Полученный результат разделим на Пи и запишем ответ.
76299. Площадь полной поверхности конуса равна 108. Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите площадь полной поверхности отсеченного конуса.
Найдите площадь полной поверхности отсеченного конуса.
Сечение проходит через середину высоты параллельно основанию. Значит радиус основания и образующая отсеченного конуса будут в 2 раза меньше радиуса и образующей исходного конуса. Запишем чему равна площадь поверхности отсечённого конуса:
Получили, что она будет в 4 раза меньше площади поверхности исходного, то есть 108:4 = 27.
*Так как исходный и отсечённый конус являются подобными телами, то также можно было воспользоваться свойством подобия:
27167. Радиус основания конуса равен 3, высота равна 4. Найдите площадь полной поверхности конуса, деленную на Пи.
Формула полной поверхности конуса:
Радиус известен, необходимо найти образующую.
По теореме Пифагора:
Таким образом:
Результат разделим на Пи и запишем ответ.
Задача. Площадь боковой поверхности конуса в четыре раза больше площади основания. Найдите чему равен косинус угла между образующей конуса и плоскостью основания.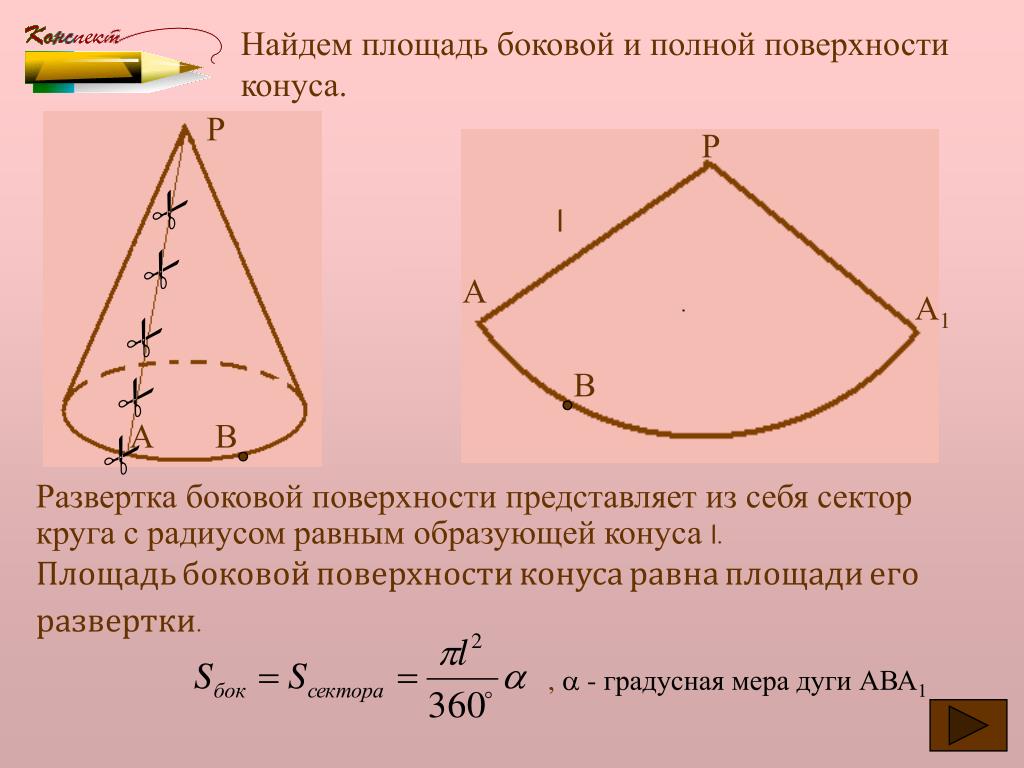
Площадь основания конуса равна:
То есть косинус будет равен:
Ответ: 0,25
Решить самостоятельно:
27136. Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в 3 раза?
27160. Площадь боковой поверхности конуса в два раза больше площади основания. Найдите угол между образующей конуса и плоскостью основания. Ответ дайте в градусах. .
27161. Площадь полной поверхности конуса равна 12. Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите площадь полной поверхности отсеченного конуса.
На этом всё. Успеха вам!
С уважением, Александр.
*Делитесь с друзьями информацией о сайте через социальные сети.
Площадь поверхности конуса (или просто поверхность конуса) равна сумме площадей основания и боковой поверхности.
Площадь боковой поверхности конуса вычисляется по формуле: S = πRl , где R — радиус основания конуса, а l — образующая конуса.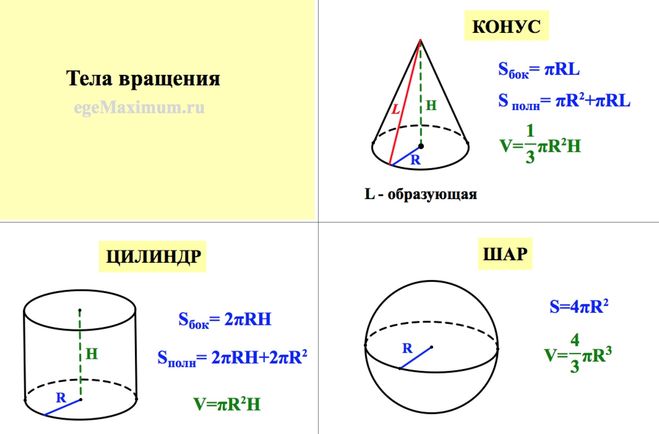
Так как площадь основания конуса равна πR 2 (как площадь круга), то площадь полной поверхности конуса будет равна: πR 2 + πRl = πR (R + l ).
Получение формулы площади боковой поверхности конуса можно пояснить такими рассуждениями. Пусть на чертеже изображена развёртка боковой поверхности конуса. Разделим дугу АВ на возможно большее число равных частей и все точки деления соединим с центром дуги, а соседние — друг с другом хордами.
Получим ряд равных треугольников. Площадь каждого треугольника равна ah / 2 , где а — длина основания треугольника, a h — его высота.
Сумма площадей всех треугольников составит: ah / 2 n = anh / 2 , где n — число треугольников.
При большом числе делений сумма площадей треугольников становится весьма близкой к площади развёртки, т. е. площади боковой поверхности конуса. Сумма оснований треугольников, т. е. an , становится весьма близкой к длине дуги АВ, т.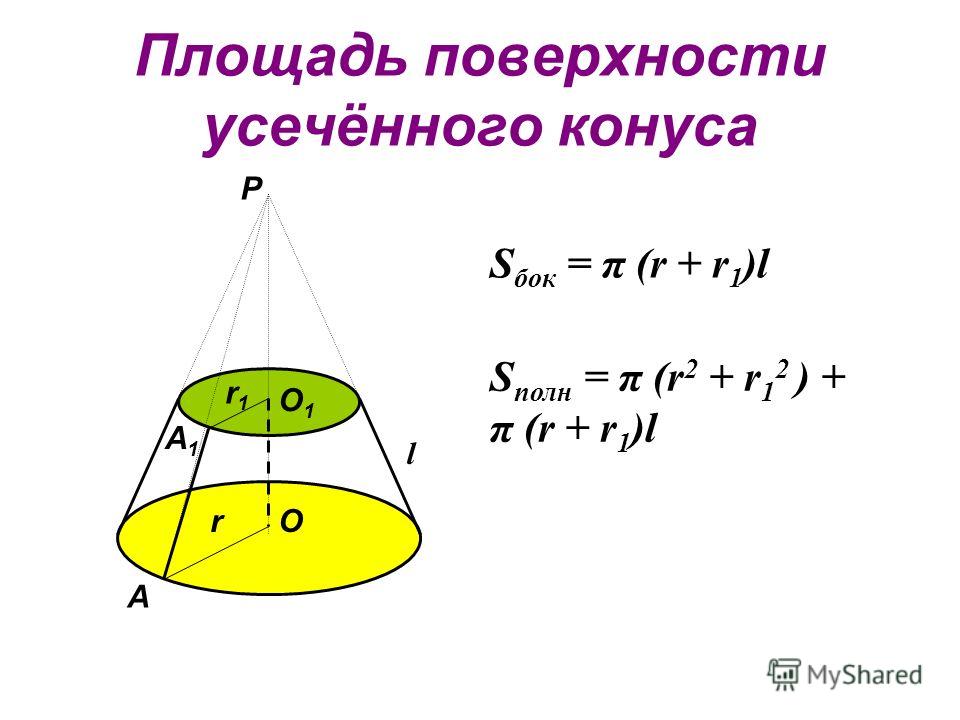 е. к длине окружности основания конуса. Высота каждого треугольника становится весьма близкой к радиусу дуги, т. е. к образующей конуса.
е. к длине окружности основания конуса. Высота каждого треугольника становится весьма близкой к радиусу дуги, т. е. к образующей конуса.
Пренебрегая незначительными различиями в размерах этих величин, получаем формулу площади боковой поверхности конуса (S):
S = Cl / 2 , где С — длина окружности основания конуса, l — образующая конуса.
Зная, что С = 2πR, где R — радиус окружности основания конуса, получаем: S = πRl .
Примечание. В формуле S = Cl / 2 поставлен знак точного, а не приближённого равенства, хотя на основании проведённого рассуждения мы могли бы это равенство считать приближённым. Но в старших классах средней школы доказывается, что равенство
S = Cl / 2 точное, а не приближённое.
Теорема. Боковая поверхность конуса равна произведению длины окружности основания на половину образующей.
Впишем в конус (рис.) какую-нибудь правильную пирамиду и обозначим буквами р и l числа, выражающие длины периметра основания и апофемы этой пирамиды.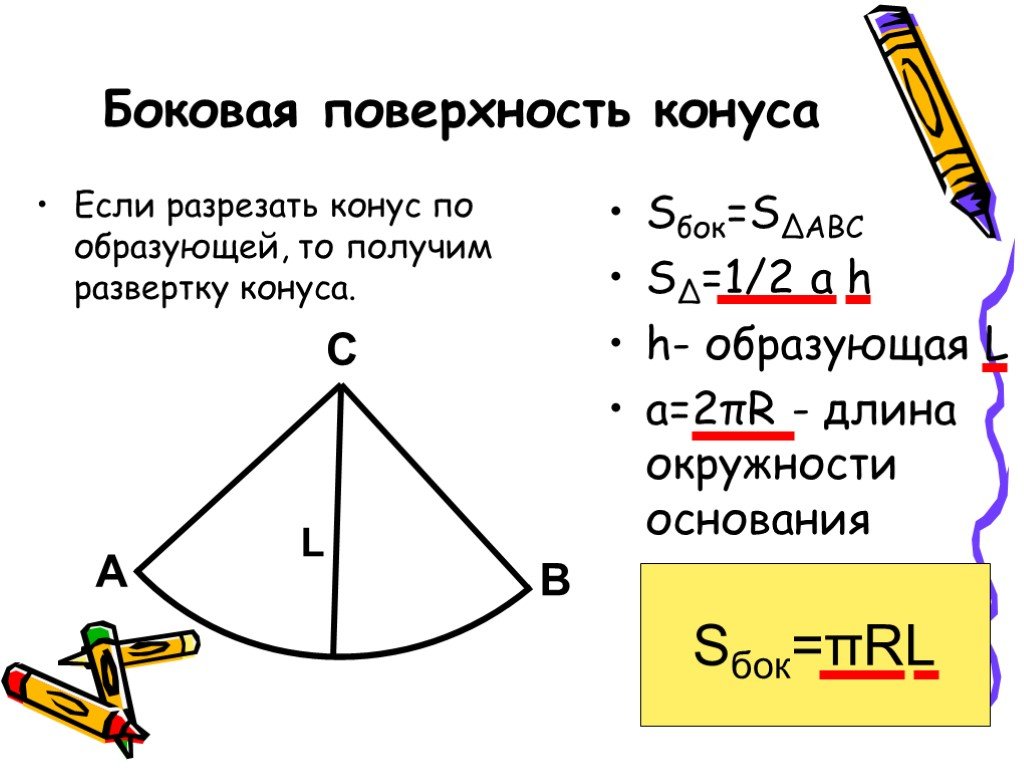
Тогда боковая поверхность её выразится произведением 1 / 2 р l .
Предположим теперь, что число сторон вписанного в основание многоугольника неограниченно возрастает. Тогда периметр р будет стремиться к пределу, принимаемому за длину С окружности основания, а апофема l будет иметь пределом образующую конуса (так как из ΔSAK следует, что SA — SK
1 / 2 р l , будет стремиться к пределу 1 / 2 С L. Этот предел и принимается за величину боковой поверхности конуса. Обозначив боковую поверхность конуса буквой S, можем написать:
S = 1 / 2 С L = С 1 / 2 L
Следствия.
1) Так как С = 2π R, то боковая поверхность конуса выразится формулой:
S = 1 / 2 2π R L = π RL
2) Полную поверхность конуса получим, если боковую поверхность сложим с площадью основания; поэтому, обозначая полную поверхность через Т, будем иметь:
T = π RL + π R 2 = π R(L + R)
Теорема.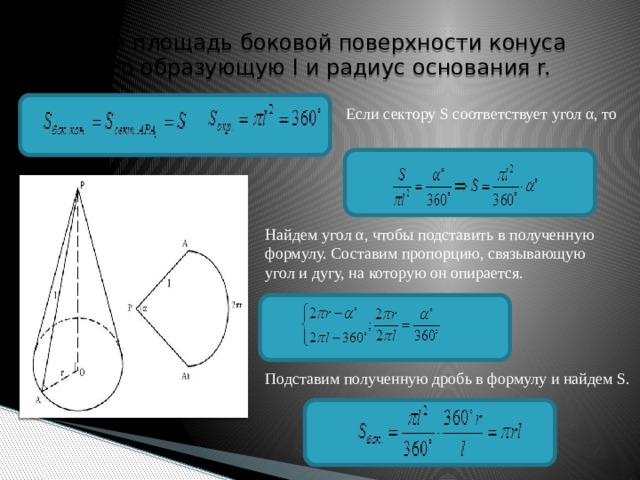 Боковая поверхность усечённого конуса равна произведению полусуммы длин окружностей оснований на образующую.
Боковая поверхность усечённого конуса равна произведению полусуммы длин окружностей оснований на образующую.
Впишем в усечённый конус (рис.) какую-нибудь правильную усечённую пирамиду и обозначим буквами р, р 1 и l числа, выражающие в одинаковых линейных единицах длины периметров нижнего и верхнего оснований и апофемы этой пирамиды.
Тогда боковая поверхность вписанной пирамиды равна 1 / 2 (р + р 1) l
При неограниченном возрастании числа боковых граней вписанной пирамиды периметры р и р 1 стремятся к пределам, принимаемым за длины С и С 1 окружностей оснований, а апофема l имеет пределом образующую L усечённого конуса. Следовательно, величина боковой поверхности вписанной пирамиды стремится при этом к пределу, равному (С + С 1) L. Этот предел и принимается за величину боковой поверхности усечённого конуса. Обозначив боковую поверхность усечённого конуса буквой S, будем иметь:
S = 1 / 2 (С + С 1) L
Следствия.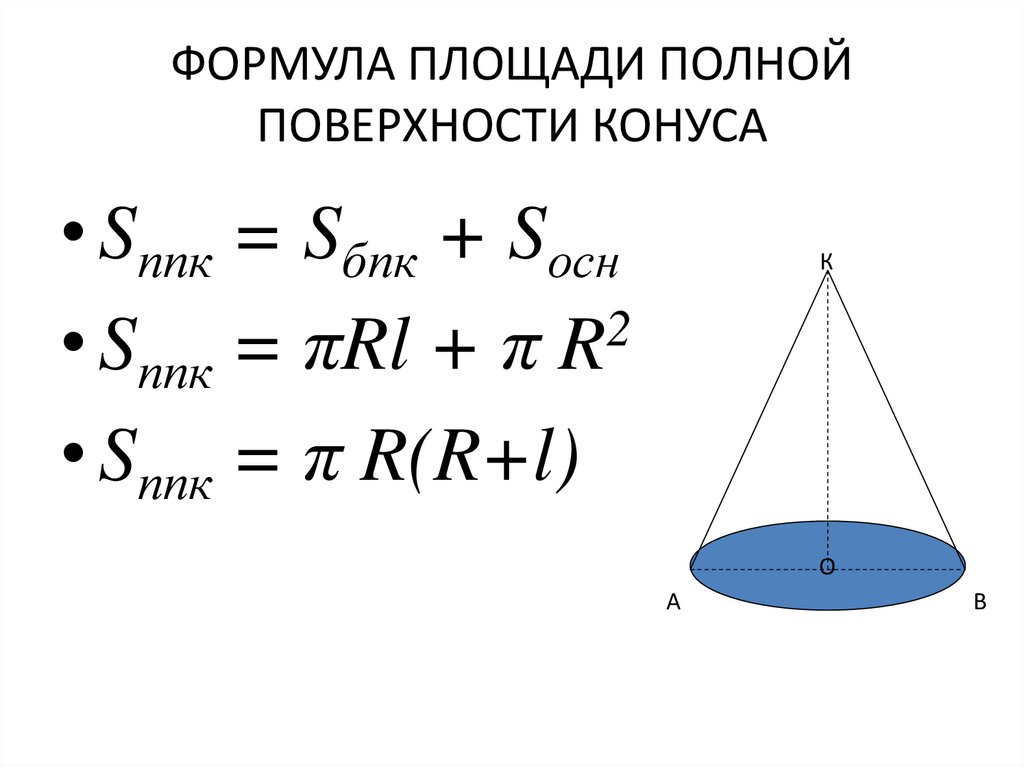
1) Если R и R 1 означают радиусы окружностей нижнего и верхнего оснований, то боковая поверхность усечённого конуса будет:
S = 1 / 2 (2π R + 2π R 1) L = π (R + R 1) L.
2) Если в трапеции OO 1 А 1 А (рис.), от вращения которой получается усечённый конус, проведём среднюю линию ВС, то получим:
ВС = 1 / 2 (OA + O 1 A 1) = 1 / 2 (R + R 1),
R + R 1 = 2ВС.
Следовательно,
S = 2π BC L,
т. е. боковая поверхность усечённого конуса равна произведению длины окружности среднего сечения на образующую.
3) Полная поверхность Т усечённого конуса выразится так:
T = π (R 2 + R 1 2 + RL + R 1 L)
Боковая площадь конуса
LearnPracticeDownload
Боковая площадь конуса определяется как площадь, покрытая криволинейной поверхностью конуса. Его также называют площадью боковой поверхности (LSA) или площадью криволинейной поверхности (CSA) конуса. Конус — это трехмерный объект, который плавно сужается от плоского круглого основания к точке, называемой вершиной.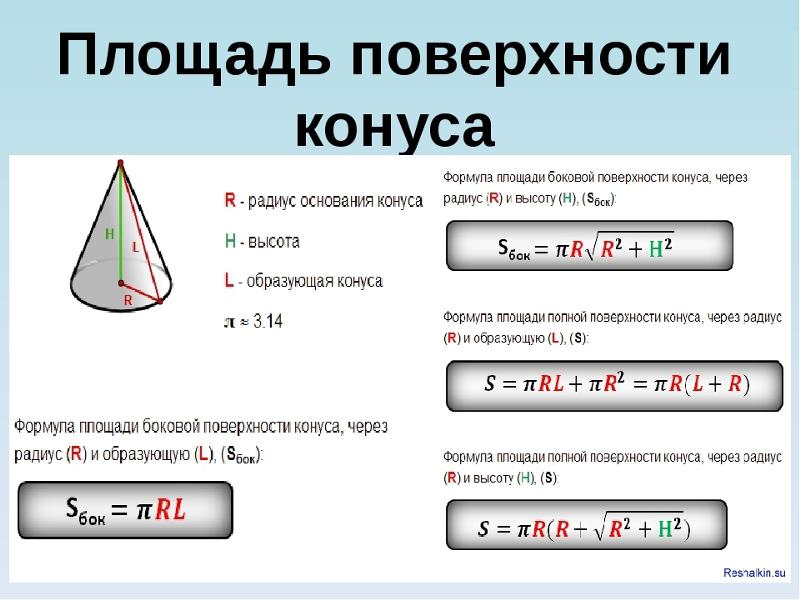 Другими словами, это форма, образованная набором отрезков, исходящих из основания, которые соединяются с общей точкой (вершиной). Эти отрезки начинаются от точек в основании и заканчиваются в вершине.
Другими словами, это форма, образованная набором отрезков, исходящих из основания, которые соединяются с общей точкой (вершиной). Эти отрезки начинаются от точек в основании и заканчиваются в вершине.
| 1. | Что такое боковая площадь конуса? |
| 2. | Формула боковой площади конуса |
| 3. | Как найти боковую площадь конуса? |
| 4. | Часто задаваемые вопросы о боковой части конуса |
Что такое боковая площадь конуса?
Площадь боковой поверхности конуса представляет собой площадь, занимаемую площадью криволинейной поверхности конуса. Поскольку конус представляет собой трехмерную форму, площадь боковой поверхности конуса также лежит в трехмерной плоскости. Когда много треугольников складываются и вращаются вокруг оси, мы получаем форму, известную как конус. Поскольку он имеет плоское основание, он имеет общую площадь поверхности, а также площадь изогнутой поверхности.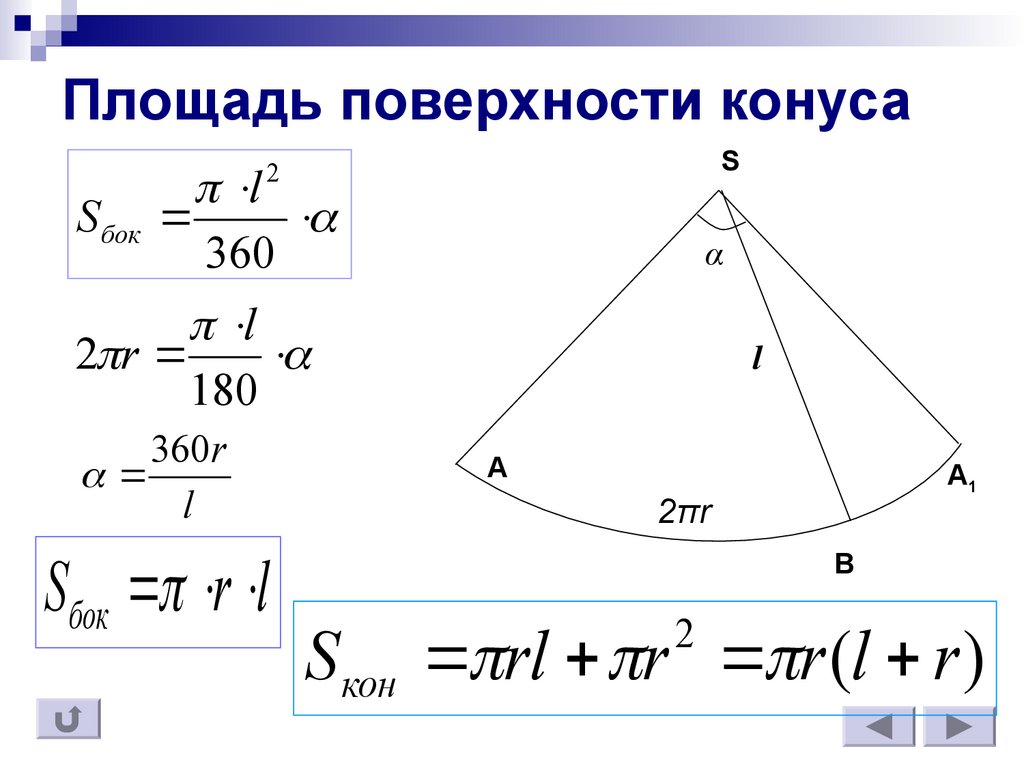 Боковая площадь конуса представлена в квадратных единицах, например, см 2 , м 2 , в 2 и др.
Боковая площадь конуса представлена в квадратных единицах, например, см 2 , м 2 , в 2 и др.
Формула боковой площади конуса
Формула площади боковой поверхности конуса: πrL, где r — радиус основания, а L — наклонная высота. Таким образом, если известны наклонная высота и радиус основания конуса, можно найти площадь его боковой поверхности (или площадь криволинейной поверхности). Мы также можем записать площадь кривизны конуса через высоту конуса, поскольку мы знаем соотношение между высотой и наклонной высотой конуса, используя теорему Пифагора. Связь между высотой и наклонной высотой конуса, заданная как L = √(h 2 + r 2 ), где h — высота конуса. Таким образом, боковая площадь конуса = πrL = πr√(h 2 + r 2 )
Как найти боковую площадь конуса?
Как мы узнали из предыдущего раздела, боковая площадь конуса равна πrL. Таким образом, мы следуем шагам, показанным ниже, чтобы найти боковую площадь конуса:
- Шаг 1: Определите радиус основания конуса и назовите его r.

- Шаг 2: Определите его высоту и назовите h.
- Шаг 3: Найдите площадь боковой поверхности конуса по формуле πrL.
- Шаг 4: Представьте окончательный ответ в квадратных единицах.
Пример: Чему равна боковая площадь конуса, имеющего радиус основания = 4 единицы и наклонную высоту = 7 единиц?
Решение: При r = 4 единицах и l = 7 единицах
Как мы знаем, боковая площадь конуса = πrL
⇒ Площадь поперечного сечения конуса = (22/7) × 4 × 7 = 88 единиц 2
Ответ: Площадь поперечного сечения конуса составляет 88 единиц 2 .
Решенные примеры на боковой поверхности конуса
Пример 1: Найдите площадь боковой поверхности конуса, имеющего радиус основания 21 единицу и высоту 20 единиц. (Используйте π = 22/7)
Решение: Учитывая, что r = 21 единица и h = 20 единиц
Таким образом, наклонная высота конуса, l = √(r 2 + h 2 ) = √(21 2 + 20 2 ) = √(441 + 400) = √841 = 29 ед.
 ⇒ Площадь боковой поверхности конуса = (22/7) × 21 × 29 = 22 × 3 × 29 = 1914 ед. 2
⇒ Площадь боковой поверхности конуса = (22/7) × 21 × 29 = 22 × 3 × 29 = 1914 ед. 2 Ответ:
Пример 2: Найдите боковую поверхность конуса высотой 15 единиц и наклонной высотой 17 единиц. (Используйте π = 3,14)
Решение: Учитывая, что h = 15 единиц и l = 17 единиц
Радиус конуса (r) = √(L 2 — h 2 ) = √(17 2 — 30 25 15 ) = √(289 — 225) = √64 = 8 единиц
Боковая площадь конуса = πrL
⇒ Площадь поперечного сечения конуса = 3,14 × 8 × 17 = 427,04 ед.
перейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Записаться на бесплатный пробный урок
Практические вопросы по боковой поверхности конуса
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о боковой части конуса
Что такое боковая площадь конуса?
Боковая площадь конуса определяется как площадь, покрываемая криволинейной поверхностью конуса.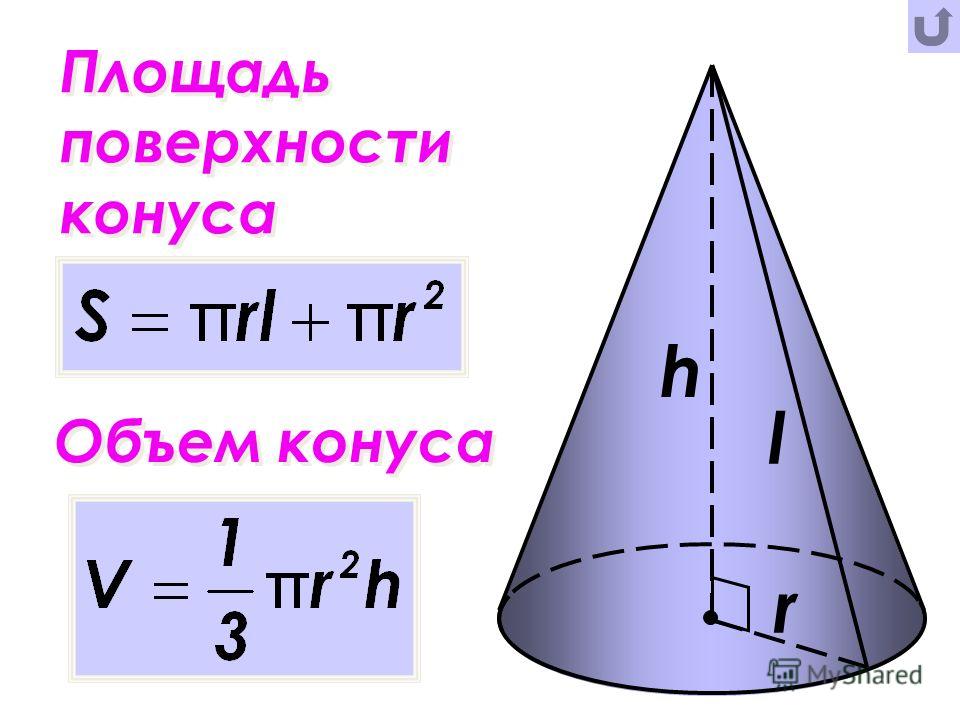 Его также обычно называют площадью боковой поверхности (LSA) или площадью криволинейной поверхности (CSA) конуса. Единица боковой площади конуса выражается в квадратных единицах, например, см 2 , m 2 , in 2 , и т.д.
Его также обычно называют площадью боковой поверхности (LSA) или площадью криволинейной поверхности (CSA) конуса. Единица боковой площади конуса выражается в квадратных единицах, например, см 2 , m 2 , in 2 , и т.д.
Какая формула площади боковой поверхности конуса?
Формула площади поперечного сечения конуса определяется как площадь поперечного сечения конуса = πrL, где «r» и «L» — радиус конуса и наклонная высота конуса. Таким образом, можно определить значение боковой площади конуса, если у нас есть значения обоих размеров конуса.
Какова формула площади поперечного сечения конуса через высоту конуса?
Мы знаем, что формула площади поперечного сечения конуса дается как площадь поперечного сечения конуса = πrL. Мы также знаем, что соотношение между наклонной высотой и высотой конуса равно L = √(h 2 + r 2 ). Таким образом, боковая площадь конуса по высоте конуса определяется как πr√(h 2 + r 2 ).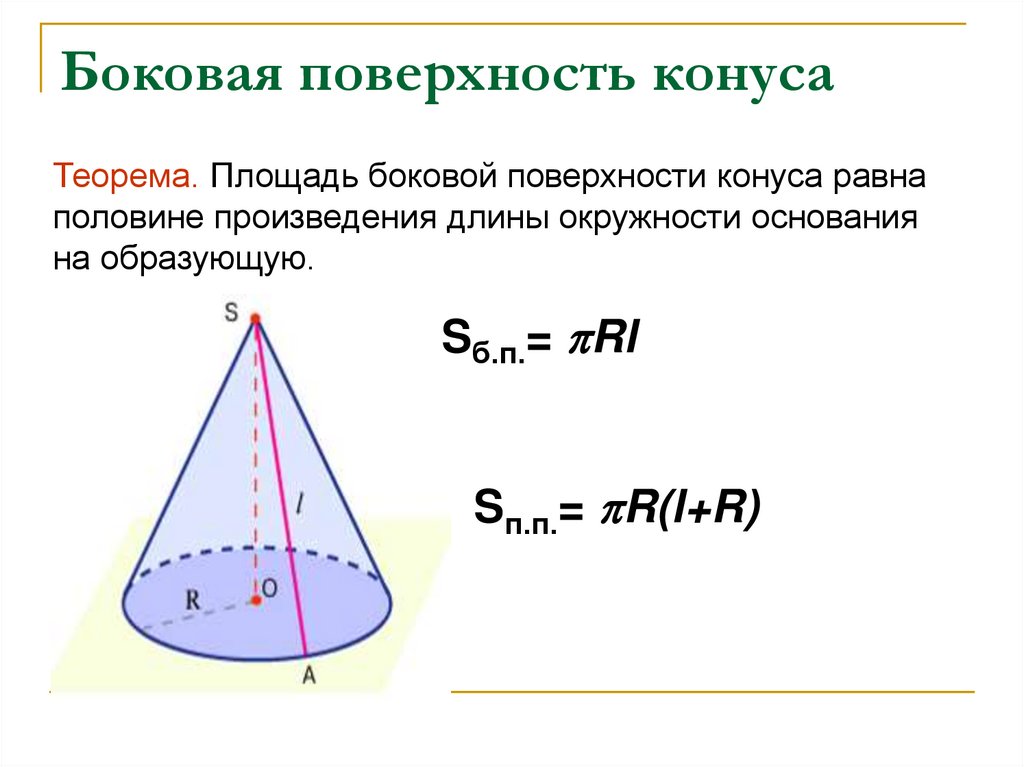
Как найти боковую площадь конуса?
Боковую площадь конуса можно определить с помощью следующих шагов:
- Шаг 1: Определите радиус основания и высоту конуса.
- Шаг 2: Определите боковую площадь конуса по формуле πrL.
- Шаг 3: После того, как значение боковой площади конуса получено, представьте окончательный ответ в квадратных единицах.
Как найти радиус конуса, если известна боковая площадь конуса?
Мы можем найти радиус конуса, если боковую площадь конуса следующие шаги:
- Шаг 1: Определите заданные размеры конуса и пусть радиус конуса равен «r»
- Шаг 2: Подставьте значения в формулу πrL и получите уравнение.
- Шаг 3: Решите уравнение для «r».
- Шаг 4: После того, как значение радиуса конуса получено, представьте окончательный ответ в единицах.

Что происходит с боковой поверхностью конуса, когда радиус конуса увеличивается вдвое?
Боковая площадь конуса удваивается, когда радиус конуса удваивается, поскольку мы подставляем «2r» вместо «r» в формулу боковой площади конуса. Таким образом, боковая площадь конуса = πrL = π(2r)L = 2(πrL), что в два раза больше первоначального значения боковой площади конуса.
Что происходит с боковой поверхностью конуса, когда наклонная высота конуса уменьшается вдвое?
Боковая площадь конуса уменьшается пополам, когда радиус конуса уменьшается вдвое, поскольку мы подставляем «(L/2)» вместо «L» в формулу боковой площади конуса. Таким образом, боковая площадь конуса = πrL = πr(L/2) = (1/2) × (πrL), что составляет половину первоначального значения боковой площади конуса.
Скачать бесплатные учебные материалы
Рабочий лист на области
Математические листы и
Визуальная учебная программа
Боковая область калькулятора конуса
, созданная Gabriela Diaz
Обзор Laciano Mino
Последний оглавления:
- Какова формула площади боковой поверхности конуса?
- В чем разница между боковой площадью и площадью поверхности?
- Как найти боковую поверхность конуса?
- Еще больше прямоугольных калькуляторов!
- Часто задаваемые вопросы
С калькулятором площади поперечного сечения конуса Omni вы сможете определить поперечное сечение правильного конуса в мгновение ока!
Возможно, вам интересно, как найти боковую площадь конуса и даже интересно, есть ли какая-либо разница между его площадью поверхности и боковой площадью, ну, вы попали в нужное место!
Если вы хотите узнать об этом и многом другом, мы приглашаем вас продолжить чтение и найти:
- Формула боковой площади конуса;
- В чем разница между боковой площадью и площадью поверхности;
- Как найти боковую поверхность конуса по его диаметру; и
- Верно ли, что боковая сторона конуса равна ровно 1/2 площади боковой поверхности цилиндра? 🤔
Какова формула площади боковой поверхности конуса?
Площадь боковой поверхности конуса определяется выражением:
A_L = π x r x √(r² + h²)
Или, с точки зрения наклона конуса:
A_L = π x r x l
Где:
-
A_L— Площадь боковой поверхности; -
r— Радиус круглого основания конуса; -
h— вертикаль высота конуса; и -
l— Наклонная высота.
В чем разница между боковой площадью и площадью поверхности?
Из приведенного выше уравнения вы могли заметить, что площадь боковой поверхности конуса не соответствует его общей площади поверхности, определяется как:
A_T = π x r x √(r² + h²) + π x r²
Эти две области состоят в том, что площадь боковой поверхности трехмерной формы является областью, которую можно увидеть при виде сбоку. Это стороны фигуры, исключая ее основание и вершину. Для частного случая конуса мы будем исключать только основание, так как у этой фигуры нет вершины.
Последнее уравнение показывает, что общая площадь поверхности включает боковую площадь π x r x √(r² + h²) и площадь круглого основания конуса π x r² _T =
2
23 Общая площадь = боковая площадь + площадь основания
A_T = π x r x (√(r² + h²) + r) Отсюда мы можем видеть, что если известна общая площадь и площадь основания конуса , мы могли бы также определить его площадь боковой поверхности как разность между ними:
A_L = Боковая площадь = Общая площадь - площадь основания
Другой вариант расчета боковой площади конуса — это его объем и радиус или объем и вертикальная высота . Это означает, что если вы знаете что-либо из этого, калькулятор площади поперечного сечения конуса сможет определить площадь поперечного сечения конуса 😉
Это означает, что если вы знаете что-либо из этого, калькулятор площади поперечного сечения конуса сможет определить площадь поперечного сечения конуса 😉
Как найти площадь поперечного сечения конуса?
Чтобы найти боковую поверхность конуса:
- Используйте формулу площади поперечного сечения конуса,
A_L = π x r x √(r² + h²) . - Чтобы использовать эту формулу, вам нужно знать радиус конуса и высоту по вертикали.
- Имея эти два известных значения, можно переходить к подстановке значений и выполнению необходимой алгебраической операции.
Например, если у нас есть конус радиусом r = 6 см и высотой h = 10 см, мы можем определить его боковую площадь:
- Используя формулу
A_L = π x r x √(r² + h²) . - Подставьте соответствующие размеры:
A_L = 3,1416 x (6 см) x √((6 см)² + (10 см)²) . - Наконец, выполните необходимые операции и получите результат:
A_L = 219,8 см² .
Еще больше прямоугольных калькуляторов!
Если вам понравился калькулятор поперечной площади конуса, и вы хотите узнать больше о геометрических свойствах прямого конуса, мы приглашаем вас посетить другие из наших связанных инструментов:
- Калькулятор правого кругового конуса;
- Вычислитель высоты конуса;
- Расчет радиуса конуса;
- Расчет высоты наклона конуса; и
- Калькулятор диаметра конуса.
Часто задаваемые вопросы
Соответствует ли площадь боковой поверхности конуса ровно 1/2 площади боковой поверхности цилиндра?
Правда. Для конуса с наклоном «h» и цилиндра высотой «h», оба с одинаковым радиусом «r», боковая площадь конуса составляет 1/2 боковой площади цилиндра:
- Формулы для боковых площадей:
A_L_конус = π x r x h и A_L_цилиндр = 2 x π x r x h . - Отсюда
2 x A_L_cone = A_L_цилиндр .
A_L = Боковая площадь = Общая площадь - площадь основания 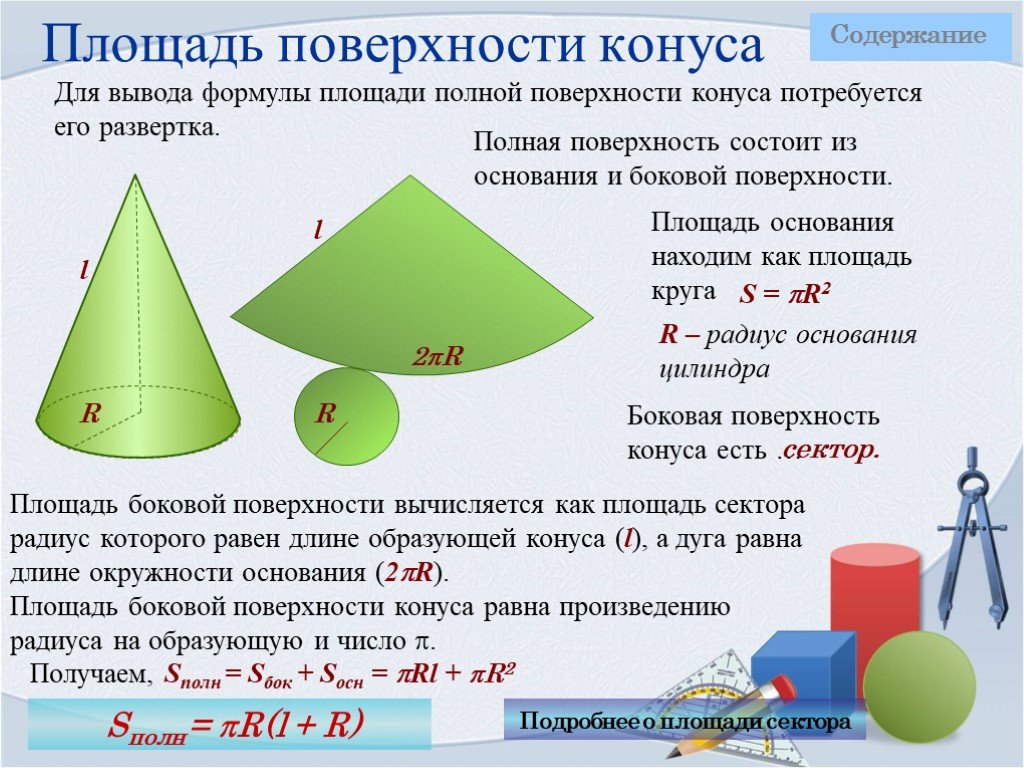 Это означает, что если вы знаете что-либо из этого, калькулятор площади поперечного сечения конуса сможет определить площадь поперечного сечения конуса 😉
Это означает, что если вы знаете что-либо из этого, калькулятор площади поперечного сечения конуса сможет определить площадь поперечного сечения конуса 😉 A_L = π x r x √(r² + h²) . A_L = π x r x √(r² + h²) . A_L = 3,1416 x (6 см) x √((6 см)² + (10 см)²) . A_L = 219,8 см² .
A_L_конус = π x r x h и A_L_цилиндр = 2 x π x r x h . 2 x A_L_cone = A_L_цилиндр .


 ⇒ Площадь боковой поверхности конуса = (22/7) × 21 × 29 = 22 × 3 × 29 = 1914 ед. 2
⇒ Площадь боковой поверхности конуса = (22/7) × 21 × 29 = 22 × 3 × 29 = 1914 ед. 2