| 4 | -2 | 4 |
| = |
10 | 2 | 12 |
1 | 2 | 2 | Вычислить определитель второго порядка всем |
1 вариант Вычислить определитель по первой строке | 2 вариант Вычислить определитель по первой строке | |
Вычислить определитель по правилу треугольника | Вычислить определитель по правилу треугольника | |
3 вариант Вычислить определитель по третьему столбцу | 4 вариант Вычислить определитель по третьему столбцу | |
Вычислить определитель по правилу треугольника | Вычислить определитель по правилу треугольника | |
5 вариант Вычислить определитель по правилу треугольника | 6 вариант Вычислить определитель по правилу треугольника | |
Вычислить определитель по второй строке | Вычислить определитель по второму столбцу | |
7 вариант Вычислить определитель по второй строке | 8 вариант Вычислить определитель по второму столбцу | |
Вычислить определитель по правилу треугольника | Вычислить определитель по правилу треугольника | Оценка уровня подготовки |
Балл (оценка) | Вербальный аналог | |
90-100 | 5 | отлично |
80-89 | 4 | хорошо |
70-79 | 3 | удовлетворительно |
менее 70 | 2 | неудовлетворительно |
Г., Задулина С.В. Под редакцией В.А. Гусева Математика. – М.: Образовательно-издательский центр «Академия», 20121.3. Вычислить определитель, предварительно выполнив элементарные преобразования.
Примеры выполнения заданий
Дано: .
Решение: Определитель
порядка выше третьего вычисляют методом
разложения по элементам какой–либо
строки (столбца) предварительно подвергнув
его элементарным преобразованиям.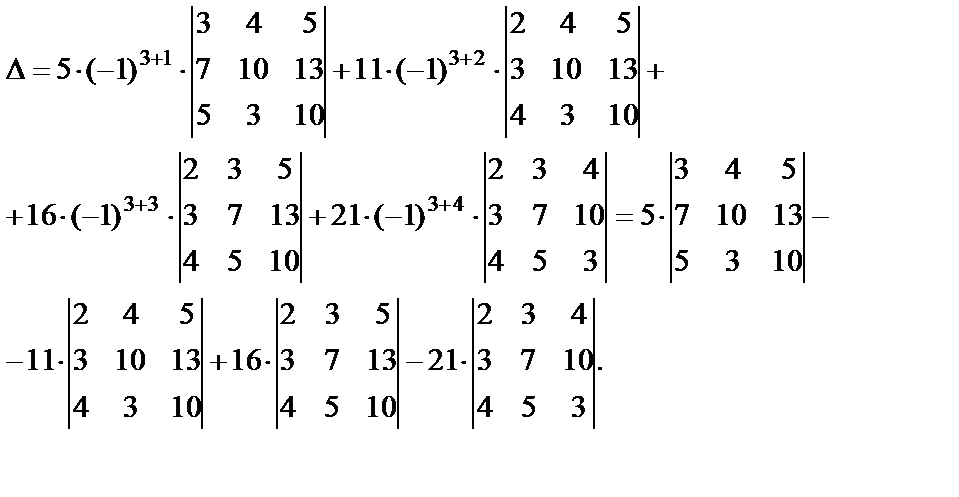
В
нашем случае преобразования удобно
делать, используя первый столбец. Умножим
первый столбец сначала на и сложим с третьим столбцом, затем первый
столбец умножим на 2 и сложим с четвертым
столбцом и, наконец, первый столбец
умножим на и сложим с пятым столбцом.
Получим:
.
Разложим этот определитель по элементам третьей строки:
.
Для вычисления полученного определителя четвертого порядка проведем с ним элементарное преобразование, для чего прибавим второй столбец к третьему. Имеем:
.
Разложим этот определитель по элементам третьего столбца и, произведя дальнейшие упрощения, вычислим заданный определитель:
.
Таким образом, элементарные преобразования определителя пятого порядка позволили свести его вычисление к вычислению простейшего определителя – второго порядка.
Для самостоятельного решения
1.
2.
3. 4.
5. 6.
7. 8.
9. 10.
11. 12.
13. 14.
15. 16.
17. 18.
19. 20. .
Дополнительные задания для самостоятельного решения
1. Расставить знаки при раскрытии определителя второго порядка и вычислить его:
2. Закончить вычисление определителя второго порядка:
3. Найти и исправить ошибку при вычислении определителя второго порядка:
а) ;
б) ;
в) ;
г) ;
д) .
4. Расставить знаки при раскрытии определителя третьего порядка:
.
5. Закончить вычисления определителя
а)
б)
6. Расставить знаки при раскрытии определителя третьего порядка:
.
7. Расставить индексы элементов при раскрытии определителя третьего порядка
.
8. Закончить вычисления определителя третьего порядка по правилу треугольника
9.
Закончить
вычисления определителя третьего
порядка по правилу треугольника и
сравнить ответ с заданием 5а
10. Найти ошибки в вычислении определителя третьего порядка:
а)
б)
в)
г)
д)
е)
11. а) Найти определитель, разложив его по элементам первой строки и сравнить с ответом в задании 7:
б) Найти определитель, разложив его по элементам первой строки и сравнить с ответом в задании 8:
в) Найти определитель, разложив его по элементам первой строки и сравнить с ответом в задании 5б:
12. Разложить определитель по элементам первого столбца
13. Вычислить определитель третьего порядка, приведя его к треугольному виду:
1 4. Вычислить определитель, используя его свойства:
2. Действия над матрицами
2.1. Сложение и вычитание матриц
Определение.
Две
матрицы равны, если они имеют одинаковую
размерность и ,
т.е. равны элементы с одинаковыми
индексами.
Равные матрицы обязательно имеют одно и то же строение: либо обе они прямоугольные типа , либо квадратные одного и того же порядка n.
Примеры выполнения заданий:
Задача 1. Определите, являются ли матрицы A и B равными:
и , если .
Ответ: Матрицы являются равными по определению.
Задача 2. Определите, являются ли матрицы D и C равными:
и .
Ответ: _____________.
Две матрицы одинаковой размерности можно суммировать: , причем результатом будет поэлементная сумма:
.
Определение. Суммой матриц A и B одинаковых размеров называется матрица ,
элементы которой равны суммам элементов
матриц A и B,
расположенных на соответствующих
местах, т.
Примеры выполнения заданий:
Задача 3. Сложить матрицы A и B, если и .
Решение:
.
Задача 4. Сложите матрицы A и B, если .
Решение:
.
Ответ: .
Для самостоятельного решения:
1. Сложите матрицы A и B, если:
а) ; б) ;
в) ; г) .
Как рассчитать определитель 4X4? Посчитайте с нашим экспертом
Мы продолжаем готовить уроки по математике. Надеюсь, это будет полезно для вас, и вам не нужно будет спрашивать наших экспертов что-то вроде «Сделай мне домашнее задание по математике, пожалуйста! Я застрял..» Это вторая часть нашего руководства, объясняющая, как вычислять определители. Нас просят вычислить определитель следующей матрицы 4 × 4:
A=\begin{pmatrix}-1 & {1} & 4 & 2 \\2 & -1 & 2 & 5 \\1 &2 & 3& 4\\3& 4& -1 & 2\end{pmatrix} 9{4+1}a_{41}M_{41}\\&=a_{11}M_{11}-a_{21}M_{21}+a_{31}M_{31}-a_{41}M_{ 41}=-1\cdot M_{11}-2 \cdot M_{21}+1\cdot M_{31}-3 \cdot M_{41} \end{aligned}
Вот видеоверсия этого руководства:
youtube.com/embed/lJkDUP4n5hI?list=UUn_YObR-sCBGWwEOdCbLzxg» frameborder=»0″ allowfullscreen=»allowfullscreen»> Чтобы найти значение \Delta , нам нужно вычислить миноры M_{11}, M_{21}, M_{31}, M_{41}. Это определители порядка 3×3:
Вычислим их таким же образом, но выбрав первую строку. Это означает, что мы устанавливаем i=1, в то время как j меняется от 1 до 3. Обратите внимание, что на этот раз верхний предел равен 3 вместо 4 для исходного определителя, потому что это определители размера 3×3. Как правило, мы можем выбрать любую строку или столбец:
\begin{выровнено} M_{11}&=\begin{vmatrix}-1&2 &5 \\2& 3 &4 \\4&-1 &2\end{vmatrix}=-1 \cdot\begin{vmatrix}3&4 \\ -1&2 \end{vmatrix}-2\cdot\begin{vmatrix}2&4 \\4&2 \end{vmatrix}+5\begin{vmatrix}2&3 \\4&-1\end{vmatrix}\\&=-1\ cdot (6+4)-2\cdot (4-16)+5\cdot(-2-12)=-10+24-70=-56\end{aligned}
Аналогично вычисляем остальные три минора:
\begin{align} M_{21}&=\begin{vmatrix}1&4&2 \\2& 3 &4 \\4&-1 &2\end{vmatrix}=1 \cdot\begin{vmatrix}3&4 \\-1&2 \ end{vmatrix}-4\cdot\begin{vmatrix}2&4 \\4&2 \end{vmatrix}+2\begin{vmatrix}2&3 \\4&-1\end{vmatrix}\\&=1\cdot (6+ 4)-4\cdot (4-16)+2\cdot (-2-12)=10+48-28=30\end{выровнено}
\begin{align} M_{31}&=\begin{vmatrix}1&4&2 \\-1& 2 &5 \\4&-1 &2\end{vmatrix}=1 \cdot\begin{vmatrix}2&5 \\-1&2 \end{vmatrix}-4\cdot\begin{vmatrix}-1&5 \\4&2 \end{vmatrix}+2\begin{vmatrix}-1&2 \\4&-1\end{vmatrix}\\&=1\cdot (4+5)-4\cdot (-2-20)+2\cdot (1-8)=9+88-14=83\end{выровнено}
M_{41}=\begin{vmatrix}1&4&2 \\-1& 2 &5 \\2&3 &4\end{vmatrix}=1\cdot (8-15)-4\cdot (-4-10)+2\cdot (-3-4)=-7+56- 14=35
Наконец, у нас есть все необходимые данные для нахождения нужного определителя.
Подставим значения в выражение для \det A:
\begin{aligned} \Delta& =-1\cdot M_{11}-2 \cdot M_{21}+1\cdot M_{31}-3 \cdot M_{41}\\&=-1\cdot (-56)-2\cdot 30+1\cdot 83-3\cdot 35=56-60+83-105=-26\end{выровнено}
Таким образом , ответ:
\det A =-26
Подводим итоги. Если вас просят вычислить определитель какой-либо матрицы, прежде всего убедитесь, что вы имеете дело с квадратной матрицей, т.е. количество строк и количество столбцов совпадают. Если это так, то можно продолжить и применить общую формулу для вычисления определителей, которая выглядит следующим образом: 9{i+j}a_{ij}M_{ij}
Здесь $n$ — размер вашей квадратной матрицы. Затем вы выбираете некоторую строку или столбец и выполняете расширение, получая, таким образом, множество меньших определителей для вычисления. Для удобства выберите строку или столбец с наименьшими значениями или лучше с нулями, если это возможно. Такой подход сэкономит ваше время и позволит быстрее выполнить домашнее задание по математике.
Больше математики в наших следующих разделах!
10 Акции
- Фейсбук
- Твиттер
- Копировать ссылку
: Детерминанты «три на три» | Нагва
В этом объяснении мы научимся вычислять детерминанты 3×3, используя разложение кофакторов (разложение Лапласа) или правило Сарруса.
Давайте сначала вспомним определение определителя 2×2.
Определение: Определитель матрицы 2 × 2
Пусть 𝐴 — матрица 2 × 2, заданная формулой 𝐴=𝑎𝑏𝑐𝑑.
Тогда определитель числа 𝐴 (обозначаемый как (det𝐴) или |𝐴|) определяется выражением det(𝐴)=|||𝑎𝑏𝑐𝑑|||=𝑎𝑑−𝑏𝑐.
По сравнению со случаем 2×2 вычисление определителей матриц 3×3 намного сложнее. В частности, не совсем ясно, как можно естественным образом распространить вышеприведенное определение на большую матрицу. Как оказалось, эти два случая на самом деле неразрывно связаны друг с другом.
Определение: Миноры
Пусть 𝐴=𝑎 — матрица порядка 𝑚×𝑚. Тогда минор элемента 𝑎 (обозначается 𝐴) является определителем матрицы (𝑚−1)×(𝑚−1), полученной после удаления строки 𝑖 и столбца 𝑗 из 𝐴.
Заметим, что хотя это определение применимо к квадратным матрицам любого размера, в этом объяснении мы будем рассматривать только матрицы порядка 3×3, а это означает, что миноры, с которыми мы будем иметь дело, всегда будут детерминантами 2×2.
Эту концепцию проще всего проиллюстрировать на примере. Предположим, что у нас есть матрица 3×3 𝐴=−23−3−4360−39.
Предположим, мы хотим найти минор элемента 𝑎, то есть 𝐴. Вычисление 𝐴 означает удаление строки 1 и столбца 2 из 𝐴 и нахождение определителя полученной матрицы.
Мы можем начать этот процесс, идентифицируя запись 𝑎 и удаляя записи, которые выровнены по горизонтали и вертикали с ней. Выделим это следующим образом:
Тогда, взяв определитель матрицы 2×2, получим 𝐴=||−4609||=(−4)×9−6×0=−36−0=−36.
Этот процесс можно повторить для любого элемента 𝐴. Например, рассмотрим минор элемента 𝑎. Как показано выше, мы можем начать с удаления 𝑎, а также строки и столбца, которым он принадлежит:
Тогда мы можем взять определитель результирующей матрицы, чтобы получить 𝐴=||3−336||=3×6−(−3)×3=18+9=27.
Прежде чем продолжить вычисление определителей 3×3, рассмотрим пример, где мы можем попрактиковаться в поиске минора матрицы.
Пример 1. Определение минора матрицы
Рассмотрим 𝐴=−65−326−899−7.
Напишите определитель, значение которого равно минору элемента 𝑎.
Ответ
Напомним, что если 𝐴 — матрица порядка 𝑚×𝑛, то минор элемента 𝑎 — определитель матрицы (𝑚−1)×(𝑛−1), полученный после удаления строки 𝑖 и столбца 𝑗 из 𝐴.
Здесь, поскольку 𝐴 — матрица 3×3, минор элемента 𝑎 (другими словами 𝐴) — это определитель матрицы 2×2, полученный удалением строки 2 и столбца 3 из 𝐴. Давайте сначала вычислим эту сокращенную матрицу, выделив элемент 𝑎 и соответствующие строки и столбцы, в которых он находится, а затем удалив их из матрицы:
Теперь, когда у нас есть матрица 2×2, мы можем найти минор 𝑎, взяв его определитель. Обратите внимание, что нам не нужно упрощать это, поскольку нас попросили написать только определитель.
Таким образом, минор числа 𝑎 равен ||−6599||.
Следующим шагом в вычислении определителей 3×3 с использованием разложения кофакторов является нахождение кофакторов матрицы. Давайте сначала определим, что такое кофакторы.
Определение: Кофакторы
Пусть 𝐴=𝑎 — матрица порядка 𝑚×𝑚. Тогда кофактор элемента 𝑎 (обозначается 𝐶) равен 𝐶=(−1)𝐴, где 𝐴 — минор элемента 𝑎.
Как видно из приведенного выше определения, кофакторы могут быть получены из миноров путем умножения на коэффициент (−1), или, другими словами, на 1 или −1, в зависимости от индекса 𝑎.
Чтобы продемонстрировать это, давайте еще раз вспомним матрицу, которую мы ранее использовали, чтобы продемонстрировать, как находить миноры:
𝐴=−23−3−4360−39.
Напомним, что мы нашли 𝐴=−36 и 𝐴=27. Используя приведенное выше определение, мы можем вычислить кофакторы 𝐶 и 𝐶, используя эти миноры. У нас есть 𝐶=(−1)𝐴=(−1)×(−36)=(−1)×(−36)=36.
Итак, в случае 𝐶, поскольку (−1)=−1, знак меняется на противоположный. Для 𝐶 имеем 𝐶=(−1)𝐴=(−1)×27=1×27=27.
Здесь, поскольку (−1)=1, имеем 𝐶=𝐴 .
Как мы видим, единственная сложность, с которой мы можем столкнуться при вычислении кофакторов, когда у нас есть миноры, заключается в том, чтобы убедиться, что мы получаем правильный знак. Один из способов сделать это — проверить, является ли 𝑖+𝑗 четным или нечетным. Это потому что ifisoddifseven𝑖+𝑗,(−1)=−1,𝑖+𝑗,(−1)=1.
Помимо прямого вычисления (−1), мы также можем обратиться к следующей матрице, которая показывает, как знаки кофакторов чередуются в шахматном порядке:
+-+-+-+-+.
Например, запись в позиции (3,2) этой матрицы показывает нам, что кофактор записи 𝑎 будет иметь коэффициент -1 по сравнению с его минором.
Определив миноры и кофакторы, мы теперь можем определить формулу для вычисления определителя матрицы 3×3.
Определение: определитель матрицы 3 × 3 (разложение на кофакторы)
Пусть 𝐴=𝑎 будет матрицей 3×3. Тогда для любого фиксированного 𝑖=1,2 или 3 определитель 𝐴 равен det(𝐴)=𝑎𝐶+𝑎𝐶+𝑎𝐶, где каждый 𝐶 является кофактором входа 𝑎. Это известно как расширение кофактора (или расширение Лапласа) по строке 𝑖. Альтернативно, для любого фиксированного 𝑗=1,2 или 3 мы имеем det(𝐴)=𝑎𝐶+𝑎𝐶+𝑎𝐶. Это расширение кофактора по столбцу 𝑗.
Заметим, что может быть полезно записать приведенные выше формулы в терминах миноров, а не кофакторов. Например, разложение софактора по строке 1 равно
det(𝐴)=𝑎𝐶+𝑎𝐶+𝑎𝐶=𝑎𝐴−𝑎𝐴+𝑎𝐴,
где мы заменили 𝐶=𝐴, 𝐶=−𝐴 и 𝐶=𝐴.
Мы также можем записать это явно как
det(𝐴)=𝑎|||𝑎𝑎𝑎𝑎|||−𝑎|||𝑎𝑎𝑎𝑎|||+𝑎|||𝑎𝑎𝑎𝑎|||.
Вместо того, чтобы заходить так далеко, чтобы вычислять кофакторы в каждой ситуации, обычно быстрее просто найти миноры и соответствующим образом чередовать знаки.
Лучше всего продемонстрировать этот процесс на примере.
Пример 2. Оценка детерминанта 3 × 3 с помощью расширения кофактора
Найдите значение ||||226-31-2-5-1-4||||.
Ответ
Пусть данная матрица равна 𝐴=𝑎. Чтобы вычислить определитель матрицы 3 × 3, мы можем использовать метод разложения кофакторов, выбирая определенную строку или столбец матрицы, вычисляя миноры для каждого элемента этой строки или столбца и чередуя знаки в соответствии с их соответствующими кофакторы.
В некоторых ситуациях может быть полезно выбрать конкретную строку или столбец, чтобы после нахождения расширения кофактора этой строки вычисления были упрощены. Однако, поскольку у нас пока нет способа идентифицировать такие случаи, мы просто выберем первую строку матрицы для простоты.
Теперь мы можем найти формулу для определителя в терминах миноров, умножая их на 1 или -1, в зависимости от соответствующих знаков в следующей матрице:
+-+-+-+-+.
Поскольку нас интересует первая строка, обратите внимание на знаки +, − и +. Затем мы можем использовать их, чтобы сформировать следующую формулу для определителя: det(𝐴)=𝑎𝐶+𝑎𝐶+𝑎𝐶=𝑎𝐴−𝑎𝐴+𝑎𝐴, где мы использовали тот факт, что
Чтобы оценить это, начнем с нахождения 𝐴, 𝐴 и 𝐴. Мы можем найти каждый минор, удалив строку и столбец, содержащие эту запись, и взяв определитель результата. Поскольку мы рассматриваем первую строку, давайте выделим ее ниже:
Мы демонстрируем этот процесс для каждой записи следующим образом:
Используя эти матрицы, теперь мы можем явно написать формулу для определителя: det(𝐴)=𝑎𝐴−𝑎𝐴+𝑎𝐴=2||1−2−1−4||−2||−3−2−5−4||+6||−31−5−1||.
Найдем определители каждой из этих матриц по очереди.
Первый из них
𝐴=||1−2−1−4||=1×(−4)−(−1)×(−2)=−4−2=−6.
Второй 𝐴=||−3−2−5−4||=(−3)×(−4)−(−5)×(−2)=12−10=2.
Наконец, третий является 𝐴=||−31−5−1||=(−3)×(−1)−(−5)×(1)=3+5=8.
Итого имеем det(𝐴)=2||1−2−1−4||−2||−3−2−5−4||+6||−31−5−1||=2×(−6) −2×2+6×8=−12−4+48=32.
Увидев процесс вычисления детерминанта 3×3 с использованием разложения кофакторов, важно понять, что этот метод работает, потому что кофакторы матрицы 3×3 являются детерминантами 2×2, которые мы знаем, как решать. Мы также отмечаем, что, хотя мы не будем пытаться сделать это в этом объяснении, расширение кофактора может быть применено к матрицам более высокого порядка, чем 3×3. Например, кофакторы матрицы 4 × 4 — это детерминанты 3 × 3, которые затем можно найти, используя расширение кофакторов рекурсивным способом. Точно так же мы можем уменьшить определители 5 × 5 до определителей 4 × 4, которые мы можем найти, используя описанный выше метод, и так далее.
Одна из основных проблем расширения кофакторов заключается в том, что оно довольно сложное, хотя с практикой его становится проще использовать. Альтернативный способ получить тот же результат — использовать правило Сарруса, которое мы сейчас объясним.
Практическое руководство. Нахождение определителей 3 × 3 с использованием правила Сарруса
Пусть 𝐴 — матрица 3 × 3, заданная формулой 𝐴=𝑎𝑎𝑎𝑎𝑎𝑎𝑎𝑎𝑎.
Чтобы найти det(𝐴), мы можем сделать следующее.
- Сначала снова напишите первый и второй столбцы 𝐴 справа от 𝐴.
- Затем выделите диагональные элементы, как показано на рисунке. Для каждой диагонали возьмите произведения элементов и сложите их:
- Теперь выделите диагонали в противоположном направлении, как показано на рисунке. Для каждой диагонали возьмите произведения элементов и вычтите их все:
- Наконец, объедините выражения из шагов 2 и 3, чтобы получить следующее выражение для определителя
det (𝐴) = 𝑎𝑎𝑎+𝑎𝑎𝑎+𝑎𝑎𝑎 — 𝑎𝑎𝑎 — 𝑎𝑎𝑎 — 𝑎𝑎𝑎.
Правило Сарруса дает нам способ вычислить определитель без необходимости сначала находить миноры или кофакторы. Следует отметить, однако, что количество вычислений, которые мы должны сделать, все еще примерно такое же, за исключением того, что этот метод может быть легче запомнить. Чтобы продемонстрировать это, давайте кратко покажем, как работает расширение кофактора по строке 1, примененное к той же самой общей матрице. У нас есть Det (𝐴) = 𝑎𝐴 — 𝑎𝐴+𝑎𝐴 = 𝑎 ||| 𝑎𝑎𝑎𝑎 ||| −𝑎 ||| 𝑎𝑎𝑎𝑎 |||+𝑎 ||| 𝑎𝑎𝑎𝑎 ||| = 𝑎 (𝑎𝑎 -𝑎𝑎) )+𝑎 (𝑎𝑎 — 𝑎𝑎) = 𝑎𝑎𝑎 — 𝑎𝑎𝑎 — 𝑎𝑎𝑎+𝑎𝑎𝑎+𝑎𝑎𝑎 — 𝑎𝑎𝑎, что является тем же результатом после небольшой перестановки условий.
Рассмотрим пример, в котором мы вычисляем определитель по правилу Сарруса.
Пример 3. Оценка определителя 3 × 3 с использованием правила Сарруса
Вычислить
||||1−9−6−8412−19||||.
Ответ
В этом вопросе нас просят оценить определитель матрицы 3×3. Один из способов сделать это — использовать правило Сарруса. Для этого начнем с перезаписи матрицы, добавив первые два столбца справа.
Теперь выделим три диагонали, идущие слева направо, возьмем их произведения и суммируем их:
Далее выделим три диагонали, идущие справа налево, возьмем их произведения и вычтем их:
Таким образом, видно, что определитель равен сумме этих двух частей: −30+−599= −629.
Мы также можем использовать расширение кофактора, чтобы проверить правильность этого значения определителя. Напомним, что если мы расширим по первой строке матрицы, формула расширения кофактора дает нам det(𝐴)=𝑎𝐴−𝑎𝐴+𝑎𝐴, где 𝐴, 𝐴 и 𝐴 — миноры 𝑎, 𝑎 и 𝑎 соответственно. Мы можем вычислить минор в каждом случае, удалив соответствующую строку и столбец для этой записи и вычислив определитель результирующей матрицы. Мы можем продемонстрировать этот процесс следующим образом:
Таким образом, используя эти явные формы миноров, определитель равен
det(𝐴)=1||41−19||−(−9)||−8129||+(−6)||−842−1||=4×9−(−1)×1+9 ((-8)×9-1×2)-6((-8)×(-1)-4×2)=37+9(-74)-6(0)=-629.
Увидев два метода вычисления определителя, мы замечаем, что оба они помогут нам прийти к одному и тому же ответу, поэтому мы должны использовать тот, который нам наиболее удобен. Для оставшихся двух примеров в этом объяснении давайте рассмотрим алгебраические задачи, связанные с определителями, где мы чередуем два метода.
Пример 4. Решение уравнения с определителем 3 × 3
Найдите набор решений ||||𝑥00−1−5𝑥021𝑥||||=−80𝑥.
Ответ
В этом вопросе нас попросили решить уравнение для 𝑥 с определителем. Наиболее естественно сначала вычислить определитель, поэтому давайте сделаем это, используя разложение на кофакторы.
Чтобы использовать расширение кофактора, мы сначала должны выбрать строку или столбец для расширения. Пусть задана матрица 𝐴=𝑎. Вспомните формулу, которая у нас есть для расширения по строке 𝑖:
det(𝐴)=𝑎𝐶+𝑎𝐶+𝑎𝐶,
где каждый 𝐶 является кофактором 𝑎. Обратите внимание, что поскольку каждому члену в уравнении соответствует соответствующая запись строки в качестве фактора, любая строка, в которой несколько записей равны нулю, является хорошим выбором для расширения кофактора.
Чтобы убедиться в этом, рассмотрим первую строку данной матрицы:
Здесь мы имеем 𝑎=𝑥, 𝑎=0 и 𝑎=0. Поскольку две записи равны нулю, формула расширения строки при 𝑖=1 упростится до det(𝐴)=𝑥𝐶+0𝐶+0𝐶=𝑥𝐶.
Напомним также, что 𝐶=(−1)𝐴=𝐴, с точки зрения минора 𝑎 как det(𝐴)=𝑥𝐴.
Следовательно, нам нужно вычислить 𝐴, только если мы расширим эту строку. Мы можем найти его, удалив из матрицы строку 1 и столбец 1 и взяв определитель результата:
Таким образом, определитель равен det(𝐴)=𝑥𝐴=𝑥||−5𝑥01𝑥||=𝑥((−5𝑥)×𝑥−1×0)=𝑥−5𝑥−0=−5𝑥.
Напомним, что мы имеем учитывая, что det(𝐴)=−80𝑥, поэтому мы имеем −80𝑥=−5𝑥.
Чтобы найти набор решений этого уравнения, мы возьмем оба члена в одну сторону и разложим их на множители: 5𝑥−80𝑥=05𝑥𝑥−16=05𝑥(𝑥−4)(𝑥+4)=0.
Мы можем видеть, что это уравнение выполняется, если 𝑥=0, 𝑥=4 или 𝑥=− 4. Таким образом, набор решений равен {0,4,−4}.
Обратите внимание, что в приведенном выше примере мы обнаружили, что вычисления были в значительной степени упрощены благодаря тому факту, что в матрице есть строка, содержащая только один ненулевой элемент. Хотя это выходит за рамки этого объяснения, мы отмечаем, что вычисления определителей можно упростить, если мы воспользуемся преимуществами таких случаев.
В качестве последнего примера давайте подойдем к задаче определителя с неизвестными переменными, используя правило Сарруса.
Пример 5. Оценка определителя, включающего переменные, с использованием заданных уравнений
Рассмотрим определитель ||||𝑥𝑧𝑦𝑦𝑥𝑧𝑧𝑦𝑥||||.
Учитывая, что 𝑥+𝑦+𝑧=−73 и 𝑥𝑦𝑧=−8, определить числовое значение определителя.
Ответ
Так как нам дан определитель с переменными значениями и сразу не видно, что данные уравнения упрощают элементы матрицы, давайте продолжим вычисление определителя по правилу Сарруса и посмотрим, получим ли мы выражение, которое можно упростить.
Чтобы использовать правило Сарруса для нахождения определителя, мы начинаем с записи первого и второго столбцов в правой части матрицы.
Теперь возьмем произведения диагональных элементов (как выделено ниже) и сложим их вместе:
Поскольку нам дали, что 𝑥+𝑦+𝑧=−73, это уже выглядит многообещающе. Затем мы берем произведения диагональных записей в противоположном направлении (как показано ниже) и вычитаем их все:
Поскольку у нас есть выражение для 𝑥𝑦𝑧, оно также упростится. Во-первых, сложение этих двух компонентов дает нам выражение для определителя: 𝑥+𝑦+𝑧−3𝑥𝑦𝑧.
Теперь мы можем использовать данные уравнения, 𝑥+𝑦+𝑧=−73 и 𝑥𝑦𝑧=−8, чтобы упростить уравнение. Объединение их вместе дает нам 𝑥+𝑦+𝑧−3𝑥𝑦𝑧=−73−3(−8)=−73+24=−49.
Таким образом, определитель равен −49.
Мы также можем проверить это с помощью метода кофакторов. Напомним, что разложение по первой строке матрицы дает нам формулу
Det (𝐴) = 𝑎𝐴 — 𝑎𝐴+𝑎𝐴 = 𝑎 ||| 𝑎𝑎𝑎𝑎 ||| −𝑎 ||| 𝑎𝑎𝑎𝑎 |||+𝑎 ||| 𝑎𝑎𝑎𝑎 ||| .
Подставив значения данной матрицы в эту формулу и вычислив определители, получим det (𝐴) = 𝑥 || 𝑥𝑧𝑦𝑥 || −𝑧 || 𝑦𝑧𝑧𝑥 ||+𝑦 || 𝑦𝑥𝑧𝑦 || = 𝑥𝑥 — 𝑦𝑧 — 𝑧 — 𝑧+𝑦𝑦 — 𝑥 — 𝑥 -𝑥𝑦𝑧 −𝑧𝑥𝑦+𝑧+𝑦−𝑦𝑥𝑧=𝑥+𝑦+𝑧−3𝑥𝑦𝑧.
Это то же самое выражение, которое мы нашли раньше. Таким образом, при использовании любого метода окончательное значение определителя равно −49.
Подытожим ключевые моменты, которые мы узнали из этого объяснения.
Ключевые точки
- Пусть 𝐴=𝑎 — матрица порядка 𝑚×𝑚. Затем минор элемента 𝑎 (обозначается 𝐴) является определителем матрицы (𝑚−1)×(𝑚−1), полученной после удаления строки 𝑖 и столбца 𝑗 из 𝐴.
- Используя приведенное выше определение миноров, кофактор элемента 𝑎 (обозначается 𝐶) равен 𝐶=(−1)𝐴.
- Из кофакторов для любого фиксированного 𝑖=1,2 или 3 определитель матрицы 3×3 𝐴 равен
det(𝐴)=𝑎𝐶+𝑎𝐶+𝑎𝐶.
Это известно как расширение кофактора 9.
