Бросают 2 кубика событие что сумма чисел больше 13 является: бросают 2 игральных кубика какова вероятность события сумма очков равна 10

Случайно бросают две игральные кости. Вероятность игральной кости

Во всех заданиях В6 на теорию вероятностей, которые представлены в Открытом банке заданий для , требуется найти вероятность какого-либо события.

Нужно знать всего лишь одну формулу , с помощью которой вычисляется вероятность :

В этой формуле р — вероятность события,

k — число событий, которые нас «устраивают», на языке теории вероятностей они называются благоприятными исходами .

n — число всех возможных событий, или число всех возможных исходов .

Очевидно, что число всех возможных событий больше, чем число благоприятных исходов, поэтом вероятность — это величина, которая меньше или равна 1.

Если вероятность события равна 1, это значит, что данное событие обязательно произойдет. Такое событие называется достоверным . Например, то, что после воскресенья будет понедельник, является, к сожалению, достоверным событием и его вероятность равна 1.

Наибольшие сложности при решении задач возникают именно с нахождением чисел k и n.

Разумеется, как при решении любых задач, при решении задач на теорию вероятностей нужно внимательно читать условие, чтобы правильно понять что дано, и что требуется найти.

Рассмотрим несколько примеров решения задач из из Открытого банка заданий для .

Пример1. В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 8 очков. Результат округлите до сотых.

Пусть на первой кости выпало одно очко, тогда на второй может выпасть 6 различных вариантов. Таким образом, поскольку у первой кости 6 различных граней, общее число различных вариантов равно 6х6=36.

Но нас устраивают не все. По условию задачи, сумма выпавших очков должна быть равна 8. Составим таблицу благоприятных исходов:

Мы видим, что число исходов, которые нас устраивают, равно 5.

Таким образом, вероятность того, что в сумме выпадет 8 очков равна 5/36=0,13(8).

Еще раз читаем вопрос задачи: требуется результат округлить до сотых.

Вспомним правило округления .

Нам нужно округлить до сотых. Если в следующем после сотых долей разряде (то есть в разряде тысячных) стоит число, которое больше или равно 5, то к числу, стоящему в разряде сотых прибавляем 1, если это число меньше 5, то число в разряде сотых оставляем без изменения.

В нашем случае в разряде тысячных стоит 8, поэтому число 3, которое стоит в разряде сотых, увеличиваем на 1.

Итак, p=5/36 ≈0,14

Ответ: 0,14

Пример 2. В чемпионате по гимнастике участвуют 20 спортсменок: 8 из России, 7 из США, остальные — из Китая. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Китая.

В этой задаче число возможных исходов равно 20 — это число всех спортсменов.

Найдем число благоприятных исходов. Оно равно числу спортсменок из Китая.

Таким образом,

Ответ: 0,25

Пример 3. В среднем из 1000 садовых насосов, поступивших в продажу, 5 подтекают. Найдите вероятность того, что один случайно выбранный для контроля насос не подтекает.

В этой задаче n=1000.

Нас интересуют насосы, которые не подтекают. Их число равно 1000-5=995. Т.е.

Задачи на вероятность игральной кости не менее популярны, чем задачи о подбрасывании монет. Условие такой задачи обычно звучит так: при бросании одной или нескольких игральных костей (2 или 3), какова вероятность того, что сумма очков будет равна 10, или число очков равно 4, или произведение числа очков, или делится на 2 произведение числа очков и так далее.

Применение формулы классической вероятности является основным методом решения задач такого типа.

Одна игральная кость, вероятность.

Достаточно просто обстоит дело с одной игральной костью. определяется по формуле: P=m/n, где m — это число благоприятствующих событию исходов, а n — число всех элементарных равновозможных исходов эксперимента с подбрасыванием кости или кубика.

Задача 1. Один раз брошена игральная кость. Какова вероятность выпадения четного числа очков?

Поскольку игральная кость собой представляет кубик (или его еще называют правильной игральной костью, на все грани кубик выпадет с одинаковой вероятностью, так как он сбалансированный), у кубика 6 граней (число очков от 1 до 6, которые обычно обозначаются точками), это значит, что в задаче общее число исходов: n=6. Событию благоприятствуют только исходы, при которых выпадает грань с четными очками 2,4 и 6, у кубика таких граней: m=3. Теперь можем определить искомую вероятность игральной кости: P=3/6=1/2=0.5.

Задача 2. Брошен один раз игральный кубик. Какова вероятность, что выпадет не менее 5 очков?

Решается такая задача по аналогии с примером, указанным выше. При бросании игрального кубика общее число равновозможных исходов равно: n=6, а удовлетворяют условие задачи (выпало не менее 5 очков, то есть выпало 5 или 6 очков) только 2 исхода, значит m=2. Далее находим нужную вероятность: P=2/6=1/3=0. 333.

Две игральные кости, вероятность.

При решении задач с бросанием 2-х игральных костей, очень удобно пользоваться специальной таблицей выпадения очков. На ней по горизонтали откладывается число очков, выпавших на первой кости, а по вертикали — число очков, которое выпало на второй кости. Заготовка имеет такой вид:

Но возникает вопрос, что же будет в пустых ячейках таблицы? Это зависит от задачи, которую потребуется решить. Если в задаче речь идет о сумме очков, тогда туда записывается сумма, а если про разность — значит записывается разность и так далее.

Задача 3. Брошены одновременно 2 игральные кости. Какова вероятность выпадения суммы менее 5 очков?

Для начала необходимо разобраться какое будет общее число исходов эксперимента. Все было очевидно при бросании одной кости 6 граней кубика — 6 исходов эксперимента. Но когда уже две кости, то возможные исходы можно представить как упорядоченные пары чисел вида (x, y), где х показывает сколько на первой кости выпало очков (от 1 до 6), а у — сколько выпало очков на второй кости (от 1 до 6).

Всего таких числовых пар будет: n=6*6=36 (в таблице исходов им как раз соответствуют 36 ячеек).

Теперь можно заполнить таблицу, для этого в каждую ячейку заносится число суммы очков, которые выпали на первой и второй кости. Заполненная таблица выглядит так:

Благодаря таблице определим число исходов, которые благоприятствуют событию » выпадет в сумме менее 5 очков». Произведем подсчет числа ячеек, значение суммы в которых будет меньше числа 5 (это 2, 3 и 4). Такие ячейки для удобства закрашиваем, их будет m=6:

Учитывая данные таблицы, вероятность игральной кости равняется: P=6/36=1/6.

Задача 4. Было брошено две игральные кости. Определить вероятность того, что произведение числа очков будет делиться на 3.

Для решения задачи составим таблицу произведений очков, которые выпали на первой и на второй кости. В ней сразу же выделим числа кратные 3:

Записываем общее число исходов эксперимента n=36 (рассуждения такие же как в предыдущей задаче) и число благоприятствующих исходов (число ячеек, которые закрашены в таблице) m=20. Вероятность события равняется: P=20/36=5/9.

Задача 5. Дважды брошена игральная кость. Какова вероятность, что на первой и второй кости разность числа очков будет равна от 2 до 5?

Чтобы определить вероятность игральной кости запишем таблицу разностей очков и выделим в ней те ячейки, значение разности в которых будет между 2 и 5:

Число благоприятствующих исходов (число ячеек, закрашенных в таблице) равно m=10, общее число равновозможных элементарных исходов будет n=36. Определит вероятность события: P=10/36=5/18.

В случае простого события и при бросании 2-х костей, требуется построить таблицу, затем в ней выделить нужные ячейки и их число поделить на 36, это и будет считаться вероятностью.

Ответ оставил Гость

С одной игральной костью дело обстоит до неприличия просто. Напомню, что вероятность находится по формуле P=m/n
P
=
m
n
, где n
n
— число всех равновозможных элементарных исходов эксперимента с подбрасыванием кубика или кости, а m
m
— число тех исходов, которые благоприятствуют событию.

Пример 1. Игральная кость брошена один раз. Какова вероятность, что выпало четное число очков?

Так как игральная кость представляет собой кубик (еще говорят, правильная игральная кость, то есть кубик сбалансированный, так что выпадает на все грани с одинаковой вероятностью), граней у кубика 6 (с числом очков от 1 до 6, обычно обозначаемых точкам), то и общее число исходов в задаче n=6

n
=
6
. Благоприятствуют событию только такие исходы, когда выпадет грань с 2, 4 или 6 очками (только четные), таких граней m=3
m
=
3
. Тогда искомая вероятность равна P=3/6=1/2=0.5
P
=
3
6
=
1
2
=
0.5
.

Пример 2. Брошен игральный кубик. Найти вероятность выпадения не менее 5 очков.

Рассуждаем также, как и в предыдущем примере. Общее число равновозможных исходов при бросании игрального кубика n=6
n
=
6
, а условию «выпало не менее 5 очков», то есть «выпало или 5, или 6 очков» удовлетворяют 2 исхода, m=2
m
=
2
. Нужная вероятность равна P=2/6=1/3=0.333
P
=
2
6
=
1
3
=
0.333
.

Даже не вижу смысла приводить еще примеры, переходим к двум игральным костям, где все интереснее и сложнее.

Две игральные кости

Когда речь идет о задачах с бросанием 2 костей, очень удобно использовать таблицу выпадения очков. По горизонтали отложим число очков, которое выпало на первой кости, по вертикали — число очков, выпавшее на второй кости. Получим такую заготовку (обычно я делаю ее в Excel, файл вы сможете скачать ниже):

таблица очков при бросании 2 игральных костей
А что же в ячейках таблицы, спросите вы? А это зависит от того, какую задачу мы будем решать. Будет задача про сумму очков — запишем туда сумму, про разность — запишем разность и так далее. Приступаем?

Пример 3. Одновременно бросают 2 игральные кости. Найти вероятность того, что в сумме выпадет менее 5 очков.

Сначала разберемся с общим числом исходов эксперимента. когда мы бросали одну кость, все было очевидно, 6 граней — 6 исходов.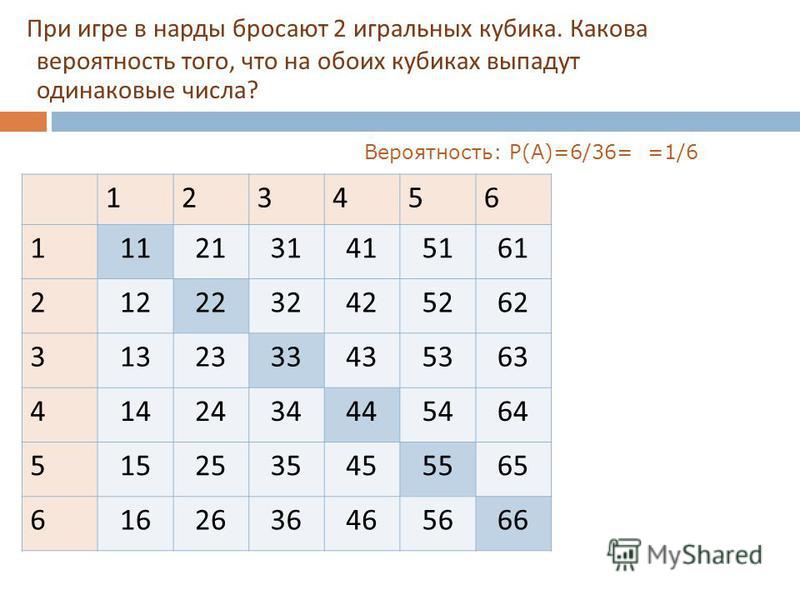 Здесь костей уже две, поэтому исходы можно представлять как упорядоченные пары чисел вида (x,y)

x
,
y
, где x
x
— сколько очков выпало на первой кости (от 1 до 6), y
y
— сколько очков выпало на второй кости (от 1 до 6). Очевидно, что всего таких пар чисел будет n=6⋅6=36
n
=
6
⋅
6
=
36
(и им соответствуют как раз 36 ячеек в таблице исходов).

Вот и пришло время заполнять таблицу. В каждую ячейку занесем сумму числа очков выпавших на первой и второй кости и получим уже вот такую картину:

таблица суммы очков при бросании 2 игральных костей
Теперь эта таблица поможем нам найти число благоприятствующих событию «в сумме выпадет менее 5 очков» исходов. Для этого подсчитаем число ячеек, в которых значение суммы будет меньше 5 (то есть 2, 3 или 4). Для наглядности закрасим эти ячейки, их будет m=6
m
=
6
:

таблица суммы очков менее 5 при бросании 2 игральных костей
Тогда вероятность равна: P=6/36=1/6
P
=
6
36
=
1
6
.

Пример 4. Брошены две игральные кости. Найти вероятность того, что произведение числа очков делится на 3.

Составляем таблицу произведений очков, выпавших на первой и второй кости. Сразу выделяем в ней те числа, которые кратны 3:

таблица произведения очков при бросании 2 игральных костей
Остается только записать, что общее число исходов n=36
n
=
36
(см. предыдущий пример, рассуждения такие же), а число благоприятствующих исходов (число закрашенных ячеек в таблице выше) m=20
m
=
20
. Тогда вероятность события будет равной P=20/36=5/9
P
=
20
36
=
5
9
.

Как видно, и этот тип задач при должной подготовке (разобрать еще пару тройку задач) решается быстро и просто. Сделаем для разнообразия еще одну задачу с другой таблицей (все таблицы можно будет скачать внизу страницы).

Пример 5. Игральную кость бросают дважды. Найти вероятность того, что разность числа очков на первой и второй кости будет от 2 до 5.

Запишем таблицу разностей очков, выделим в ней ячейки, в которых значение разности будет между 2 и 5:

таблица разности очков при бросании 2 игральных костей
Итак, что общее число равновозможных элементарных исходов n=36
n
=
36
, а число благоприятствующих исходов (число закрашенных ячеек в таблице выше) m=10
m
=
10
. Тогда вероятность события будет равной P=10/36=5/18
P
=
10
36
=
5
18
.

Итак, в случае, когда речь идет о бросании 2 костей и простом событии, нужно построить таблицу, выделить в ней нужные ячейки и поделить их число на 36, это и будет вероятностью. Помимо задач на сумму, произведение и разность числа очков, также встречаются задачи на модуль разности, наименьшее и наибольшее выпавшее число очков (подходящие таблицы вы найдете в файле Excel).

ЕГЭ Профиль №10. Теория вероятностей повышенной сложности — math200.ru

Skip to content

ЕГЭ Профиль №10. Теория вероятностей повышенной сложностиadmin2022-07-26T23:47:28+03:00

Скачать файл в формате pdf.

ЕГЭ Профиль №10. Теория вероятностей повышенной сложности

Задача 1. Симметричную монету бросают 10 раз. Во сколько раз вероятность события «выпадет ровно 5 орлов» больше вероятности события «выпадет ровно 4 орла»? Ответ ОТВЕТ: 1,2.

Задача 2. Симметричную монету бросают 17 раз. Во сколько раз вероятность события «выпадет ровно 8 орлов» больше вероятности события «выпадет ровно 7 орлов»? Ответ ОТВЕТ: 1,25.

Задача 3. В одном ресторане в г. Тамбове администратор предлагает гостям сыграть в «Шеш-беш»: гость бросает одновременно две игральные кости. Если он выбросит комбинацию 5 и 6 очков хотя бы один раз из двух попыток, то получит комплимент от ресторана: чашку кофе или десерт бесплатно. Какова вероятность получить комплимент? Результат округлите до сотых. Ответ ОТВЕТ: 0,11.

Задача 4. В одном ресторане в г. Тамбове администратор предлагает гостям сыграть в игру: гость бросает одновременно две игральные кости. Если он выбросит комбинацию которая в сумме даёт 10 очков хотя бы один раз из двух попыток, то получит комплимент от ресторана: чашку кофе или десерт бесплатно. Какова вероятность получить комплимент? Результат округлите до сотых. Ответ ОТВЕТ: 0,16.

Задача 5. Игральную кость бросили один или несколько раз. Оказалось, что сумма всех выпавших очков равна 4. Какова вероятность того, что был сделан один бросок? Ответ округлите до сотых. Ответ ОТВЕТ: 0,63.

Задача 6. Игральную кость бросили один или несколько раз. Оказалось, что сумма всех выпавших очков равна 3. Какова вероятность того, что было сделано два броска? Ответ округлите до сотых. Ответ ОТВЕТ: 0,24.

Задача 7. Игральную кость бросали до тех пор, пока сумма всех выпавших очков не превысила число 3. Какова вероятность того, что для этого потребовалось два броска? Ответ округлите до сотых. Ответ ОТВЕТ: 0,42.

Задача 8. Игральную кость бросали до тех пор, пока сумма всех выпавших очков не превысила число 8. Какова вероятность того, что для этого потребовалось два броска? Ответ округлите до сотых. Ответ ОТВЕТ: 0,28.

Задача 9. При подозрении на наличие некоторого заболевания пациента отправляют на ПЦР-тест. Если заболевание действительно есть, то тест подтверждает его в 86% случаев. Если заболевания нет, то тест выявляет отсутствие заболевания в среднем в 94% случаев. Известно, что в среднем тест оказывается положительным у 10% пациентов, направленных на тестирование. При обследовании некоторого пациента врач направил его на ПЦР-тест, который оказался положительным. Какова вероятность того, что пациент действительно имеет это заболевание? Ответ ОТВЕТ: 0,43.

Задача 10. При подозрении на наличие некоторого заболевания пациента отправляют на ПЦР-тест. Если заболевание действительно есть, то тест подтверждает его в 91% случаев. Если заболевания нет, то тест выявляет отсутствие заболевания в среднем в 93% случаев. Известно, что в среднем тест оказывается положительным у 13% пациентов, направленных на тестирование. При обследовании некоторого пациента врач направил его на ПЦР-тест, который оказался положительным. Какова вероятность того, что пациент действительно имеет это заболевание? Ответ ОТВЕТ: 0,5.

Задача 11. Стрелок в тире стреляет по мишени до тех пор, пока не поразит её. Известно, что он попадает в цель с вероятностью 0,2 при каждом отдельном выстреле. Сколько патронов нужно дать стрелку, чтобы он поразил цель с вероятностью не менее 0,6? Ответ ОТВЕТ: 5.

Задача 12. Стрелок в тире стреляет по мишени до тех пор, пока не поразит её. Известно, что он попадает в цель с вероятностью 0,7 при каждом отдельном выстреле. Сколько патронов нужно дать стрелку, чтобы он поразил цель с вероятностью не менее 0,95? Ответ ОТВЕТ: 3.

Задача 13. Стрелок стреляет по пяти одинаковым мишеням. На каждую мишень даётся не более двух выстрелов, и известно, что вероятность поразить мишень каждым отдельным выстрелом равна 0,6. Во сколько раз вероятность события «стрелок поразит ровно пять мишеней» больше вероятности события «стрелок поразит ровно четыре мишени»? Ответ ОТВЕТ: 1,05.

Задача 14. Стрелок стреляет по пяти одинаковым мишеням. На каждую мишень даётся не более двух выстрелов, и известно, что вероятность поразить мишень каждым отдельным выстрелом равна 0,5. Во сколько раз вероятность события «стрелок поразит ровно три мишени» больше вероятности события «стрелок поразит ровно две мишени»? Ответ ОТВЕТ: 3.

Задача 15. В викторине участвуют 6 команд. Все команды разной силы, и в каждой встрече выигрывает та команда, которая сильнее. В первом раунде встречаются две случайно выбранные команды. Ничья невозможна. Проигравшая команда выбывает из викторины, а победившая команда играет со следующим случайно выбранным соперником. Известно, что в первых трёх играх победила команда А. Какова вероятность того, что эта команда выиграет четвёртый раунд? Ответ ОТВЕТ: 0,8.

Задача 16. В викторине участвуют 5 команд. Все команды разной силы, и в каждой встрече выигрывает та команда, которая сильнее. В первом раунде встречаются две случайно выбранные команды. Ничья невозможна. Проигравшая команда выбывает из викторины, а победившая команда играет со следующим случайно выбранным соперником.  Известно, что в первых двух играх победила команда А. Какова вероятность того, что эта команда выиграет третий раунд? Ответ ОТВЕТ: 0,75.

Задача 17. Турнир по настольному теннису проводится по олимпийской системе: игроки случайным образом разбиваются на игровые пары; проигравший в каждой паре выбывает из турнира, а победитель выходит в следующий тур, где встречается со следующим противником, который определён жребием. Всего в турнире участвует 16 игроков, все они играют одинаково хорошо, поэтому в каждой встрече вероятность выигрыша и поражения у каждого игрока равна 0,5. Среди игроков два друга – Иван и Алексей. Какова вероятность того, что этим двоим в каком-то туре придётся сыграть друг с другом? Ответ ОТВЕТ: 0,125.

Задача 18. Турнир по настольному теннису проводится по олимпийской системе в несколько туров: если в туре участвует чётное число игроков, то они разбиваются на случайные игровые пары. Если число игроков нечётно, то с помощью жребия выбираются случайные игровые пары, а один игрок остаётся без пары и не участвует в туре. Проигравший в каждой паре (ничья невозможна) выбывает из турнира, а победители и игрок без пары, если он есть, выходят в следующий тур, который проводится по таким же правилам. Так продолжается до тех пор, пока не останутся двое, которые играют между собой финальный тур, то есть последнюю партию, которая выявляет победителя турнира. Всего в турнире участвует 20 игроков, все они играют одинаково хорошо, поэтому в каждой встрече вероятность выигрыша и поражения у каждого игрока равна 0,5. Среди игроков два друга – Иван и Алексей. Какова вероятность того, что этим двоим в каком-то туре придётся сыграть друг с другом? Ответ ОТВЕТ: 0,1.

Задача 19. Первый член последовательности целых чисел равен 0. Каждый следующий член последовательности с вероятностью \(p = 0,8\) на единицу больше предыдущего и с вероятностью \(1 — p\) на единицу меньше предыдущего. Какова вероятность того, что какой-то член этой последовательности окажется равен  \( — 1\)? Ответ ОТВЕТ: 0,25.

Задача 20. Первый член последовательности целых чисел равен 0. Каждый следующий член последовательности с вероятностью \(p = \frac{{20}}{{23}}\) на единицу больше предыдущего и с вероятностью \(1 — p\) на единицу меньше предыдущего. Какова вероятность того, что какой-то член этой последовательности окажется равен  \( — 1\)? Ответ ОТВЕТ: 0,15.

Задача 21. Первый игральный кубик обычный, а на гранях второго кубика нет чётных чисел, а нечётные числа 1, 3 и 5 встречаются по два раза. В остальном кубики одинаковые. Один случайно выбранный кубик бросают два раза. Известно, что в каком-то порядке выпали 3 и 5 очков. Какова вероятность того, что бросали второй кубик? Ответ ОТВЕТ: 0,8.

Задача 22. Первый игральный кубик обычный, а на гранях второго кубика нет нечётных чисел, а чётные числа 2, 4 и 6 встречаются по два раза. В остальном кубики одинаковые. Один случайно выбранный кубик бросают два раза. Известно, что в каком-то порядке выпали 4 и 6 очков. Какова вероятность того, что бросали первый кубик? Ответ ОТВЕТ: 0,2.

Задача 23. Маша коллекционирует принцесс из Киндер-сюрпризов. Всего в коллекции 10 различных принцесс, и они равномерно распределены, то есть в каждом очередном Киндер-сюрпризе может с равными вероятностями оказаться любая из 10 принцесс. У Маши уже есть две разные принцессы из коллекции. Какова вероятность того, что для получения следующей принцессы Маше придётся купить ещё 2 или 3 шоколадных яйца? Ответ ОТВЕТ: 0,192.

Задача 24. Маша коллекционирует принцесс из Киндер-сюрпризов. Всего в коллекции 10 различных принцесс, и они равномерно распределены, то есть в каждом очередном Киндер-сюрпризе может с равными вероятностями оказаться любая из 10 принцесс. У Маши уже есть шесть разных принцесс из коллекции. Какова вероятность того, что для получения следующей принцессы Маше придётся купить ещё 1 или 2 шоколадных яйца? Ответ ОТВЕТ: 0,64.

Задача 25. В городе 48% взрослого населения – мужчины. Пенсионеры составляют 12,6% взрослого населения, причём доля пенсионеров среди женщин равна 15%. Для социологического опроса выбран случайным образом мужчина, проживающий в этом городе. Найдите вероятность события «выбранный мужчина является пенсионером». Ответ ОТВЕТ: 0,1.

Задача 26. В городе 44% взрослого населения – мужчины. Пенсионеры составляют 14,4% взрослого населения, причём доля пенсионеров среди женщин равна 10%. Для социологического опроса выбран случайным образом мужчина, проживающий в этом городе. Найдите вероятность события «выбранный мужчина является пенсионером». Ответ ОТВЕТ: 0,2.

Реклама

Поддержать нас

Вероятность

. Вы бросаете кубик до тех пор, пока сумма всех ваших бросков не станет больше 13. Какое число вы, скорее всего, выпадете при последнем броске?

спросил 9 лет, 4 месяца назад

Изменено 9 лет, 4 месяца назад

Просмотрено 2к раз

$\begingroup$

Итак, я подумал сделать это рекурсивно: $f(x,i)$ равно вероятности выпадения большего, чем $x$, и приземления на $i$ при последнем броске. $f(0,i) = 1/6$ для $i = \{1,2,..,6\}$. $f(1,i) = 1/6 + 1/6f(0,i)$ для $i = \{2,…,6\}$ и $f(1,1) = 1/6f( 0,1)$. Наконец, мы перечисляем эту рекурсию, пока не получим $f(13,i)$ и посмотрим, для какого значения $i$ $f$ будет наибольшим.

Есть ли лучший способ приблизиться к этому или простой способ упростить этот метод?

• вероятность
• комбинаторика
• игра в кости

$\endgroup$

5

$\begingroup$

Нас не спрашивают о точных вероятностях $f(13,i)$, но очевидно, что при $n\gg 0$ имеем $f(n,i)\sim i$ (и, следовательно, $f( n,i)\приблизительно \frac i{21}$). Так что даже без вычислений разумно предположить, что $f(13,6)>f(13,i)$ для всех $i\ne 6$.

И действительно, любая последовательность бросков, которая заканчивается на $i$, превышающую 13$, может быть преобразована в последовательность бросков, которая заканчивается на $6$, превышающая 13$ (и имеющая такие же броски до этого). Поэтому $f(13,6)\ge f(13,i)$ для всех $i$. Теперь заметьте, что любая последовательность, оканчивающаяся на ровно по $13$ с $i<6$ можно превратить в последовательность, превышающую $13$ и заканчивающуюся на $6$, мы видим, что на самом деле $f(13,6)>f(13,i)$. (На этом последнем шаге мы использовали $13\ge i$ для всех $i<6$, чтобы гарантировать существование последовательности, суммирующей точно $13$ с $i$ в качестве последнего броска).

$\endgroup$

2

$\begingroup$

Ответ на вашу конкретную задачу (наиболее вероятный последний кубик) уже дан. Что касается более общей задачи (вычисление $f(n,i)$), мы видим, что 9{i-1} S(n-k)$$

, где $S(m)$ — вероятность того, что неограниченная текущая сумма игральных костей достигнет значения $m$. Теперь, конечно, эта задача уже должна быть проанализирована на фантастическом математическом сайте, который я знаю. .. дайте мне посмотреть… да, вот он. Мы видим, что $S(m)$ не имеет простой замкнутой формулы, поэтому ваш рекурсивный подход разумен. И мы также можем интуитивно видеть, что $S(m)$ должен асимпотически стремиться к константе (в частности, к 2/7), так что $f(n,i) \ приблизительно i/21$ для больших $n$.

$\endgroup$ 96+1$ имеет двойной ноль в точке $1$ и пять нулей абсолютного значения $<1$. Отсюда следует, что существуют константы $a$, $b$ с $$p_r(n)=an + b +o(1)\qquad(n\to \infty)\ .$$ Так как $0\leq p_r(n)\leq 1$ для всех $n$ обязательно $a=0$; но $b$ должен быть определен из начальных условий $\bigl(p_r(n)\bigr)_{r-5\leq n\leq r}$, которые получаются после применения $(1)$ $r$ раз .

Запуск $(1)$ на компьютере подтверждает следующую гипотезу: $$\lim_{n\to\infty} p_r(n)={r\over21}\ .$$ Эвристически это можно объяснить следующим образом: при броске $r$ сумма перескакивает через $r$ полуцелых чисел. Поскольку все броски $r\in[6]$ равновероятны и $\sum_{r=1}^6 r =21$, в среднем ${r\over21}$ всех полуцелых чисел перескакивает бросок $р$. При выборе $N\gg1$ вероятность того, что отметка в $N+{1\over2}$ будет перепрыгнута при броске $r$, равна ${r\over21}$.

Профессиональные случайные ходоки должны быть в состоянии доказать это строго.

$\endgroup$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

. 9Вероятность 0000 — бросание игральной кости до тех пор, пока сумма всех выпавших чисел не превысит 6

спросил 1 год, 9 месяцев назад

Изменено 1 год, 9 месяцев назад

Просмотрено 269 ​​раз

$\begingroup$

Я пытаюсь решить задачу, в которой мне задают функцию массы вероятности $X$, где $X$ — это количество раз, когда игральная кость бросается до тех пор, пока не выпадет сумма больше шести. Я смог сделать вывод, что возможные значения, которые может принимать $X$, составляют $2,3,4,5,6,7$ (в лучшем случае мы продолжаем получать $1$ каждый раз), однако определяя, как часто каждое из них встречается мне было нелегко сделать вывод, не нарисовав демонстрационное космическое дерево, но проблема в том, что оно быстро выходит из-под контроля (с точки зрения размера), и я не могу найти шаблон, который помог бы мне решить его быстрее, иначе .

Спасибо, хорошего дня.

• вероятность
• комбинаторика
• распределение вероятностей
• игра в кости

$\endgroup$

$\begingroup$

Пусть $P(X)$ — вероятность того, что сумма не превысит 6 после бросков $X$. Количество таких событий равно количеству положительных целых решений неравенства: $$k_1+k_2+\cdots+k_X\le6, $$ который по звездам и полосам $$ \бином 6X. $$ 9X}\binom6X.$$

Теперь заметьте, что искомая вероятность равна $$P(X-1)-P(X). $$

$\endgroup$

3

$\begingroup$

Рекурсия выполнит:

Если $f(x,n)$ — это вероятность, что вам нужно бросить $x$, пока вы не превысите $n$, тогда

• $f(0,n)=1$ для $n <0$ и $f(x,n)=1$ для $x \not=0$ и $n<0$
• $f(x,n)=\frac16(f(x-1,n-1)$ $+f(x-1,n-2)$ $+f(x-1,n-3)$ $ +f(x-1,n-4)$ $+f(x-1,n-5)$ $+f(x-1,n-6))$ для $n\ge 0$

таблица подачи

 x 0 1 2 3 4 5 6 7
н
<0 1
0 0 6/6
1 0 5/6 6/36
2 0 4/6 11/36 6/216
3 0 3/6 15/36 17/216 6/1296
4 0 2/6 18/36 32/216 23/1296 6/7776
5 0 1/6 20/36 50/216 55/1296 29/7776 6/46656
6 0 0 21/36 70/216 105/1296 84/7776 35/46656 6/279936
 

и вам нужна нижняя строка

$\endgroup$

$\begingroup$

Многие части дерева одинаковы.

No related posts.