Привести к каноническому виду матрицу онлайн: Приведение матрицы к ступенчатому виду онлайн калькулятор

Содержание

4.2. Приведение квадратичной формы к каноническому виду

Квадратичная форма однозначно определяется матрицей в выбранном ОНБ . При переходе к другому ОНБ матрица квадратичной формы будет получена с помощью преобразования подобия, т. е. , где – матрица перехода от базиса к базису .

Очевидно, результат этого преобразования зависит от матрицы . Так как матрица симметрическая, то всегда можно подобрать матрицу так, чтобы стала диагональной, причём на главной диагонали будут располагаться её собственные числа. Диагонализация произойдет в ОНБ из собственных векторов матрицы . В результате этих преобразований квадратичная форма примет вид:

, (22)

Где – собственные значения матрицы , – координаты вектора в базисе . Связь между координатами вектора в двух разных базисах выражается формулой: , где и – вектор-столбцы, составленные из координат вектора в базисах и соответственно; – матрица перехода к базису .

Рассмотренное преобразование называется Приведением квадратичной формы к каноническому виду

Любая квадратичная форма может быть приведена к каноническому виду.

Пример 18. Привести к каноническому виду квадратичную форму .

Решение. Диагонализация квадратичной формы происходит в ОНБ из собственных векторов. Если – матрица перехода к такому базису, то координаты вектора в разных базисах связаны между собой соотношением:

Где в столбцах матрицы находятся координаты векторов ОНБ из собственных векторов, соответствующих собственным значениям.

Составим матрицу квадратичной формы: , тогда характеристическое уравнение: , значит, собственные значения , . Найдём собственные векторы.

При : , откуда получаем: . Если – базисная переменная, – свободная, то, полагая , получим , следовательно, .

Аналогично, при : , откуда получаем: . Пусть – базисная переменная, – свободная. Полагая , получим , тогда .

Собственные векторы и ортогональны, т. к. , и . Тогда ОНБ составят , . Матрица перехода от ОНБ к ОНБ примет вид: .

Так как – матрица ортогонального оператора, то , что можно проверить непосредственными вычислениями:

, тогда , и .

Если – матрица перехода от одного базиса к другому, то ,

но , значит,

, т. е. .

Замечание 1. Этот результат можно было записать после нахождения собственных значений и , но необходимо вывести формулы перехода от координат к координатам : , .

Проверим правильность проведенных вычислений:

Ответ: .

Замечание 2. Приведение квадратичной формы к виду (22) может быть выполнено разными методами. Например, заданная квадратичная форма может быть представлена в таком каноническом виде:

Где . Матрица этой квадратичной формы также будет диагональной, но она не совпадает с матрицей . Это означает, что значения коэффициентов в (22) зависят от способа приведения квадратичной формы к каноническому виду. Но число ненулевых, число положительных , а, значит, и отрицательных слагаемых в квадратичной форме (22) остаётся неизменным.

Это правило называется Законом инерции квадратичной формы.

< Предыдущая		Следующая >

Метод Лагранжа и метод Гаусса

В этом и последующих пунктах существенно потребуется знание МЕТОДА ГАУССА преобразования систем линейных уравнений.

Пример. Рассмотрим матрицу квадратичной формы

из предыдущих пунктов, и, временно выходя из круга поставленных в настоящем разделе задач, побробуем применить к ней метод Гаусса приведения к треугольному виду:

Обратим внимание на два обстоятельства: диагональные элементы последней матрицы совпадают с коэффициентами канонического вида квадратичной формы, а коэффициенты замены переменных, приводящей к этому каноническому виду, совпадают с элементами строк этой матрицы, если их разделить на соответствующие диагональные элементы. Возникает подозрение , что метод Лагранжа является «замаскированной» версией метода Гаусса.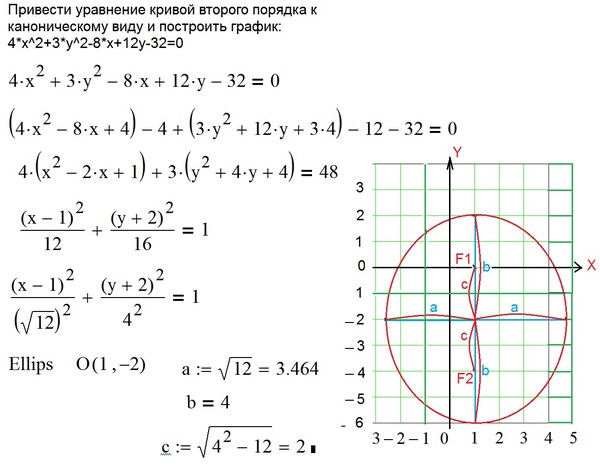

♦

Для того, чтобы выяснить аналитический смысл преобразований по методу Лагранжа найдем правило формирования коэффициентов в первом шаге приведения квадратичной формы к каноническому виду. Пусть исходная квадратичная форма записана в виде

т.е. коэффициенты при смешанных произведениях переменных записаны с выделением множителя . После выделения полного квадрата, содержащего переменные :

в правой части тождества образовалась квадратичная форма , не содержащая . Она равна

Если теперь выписать матрицу этой квадратичной формы (она имеет порядок ), то ее элементы образуются по точно такому же правилу, как и коэффициенты матрицы, получающейся из матрицы в результате первого шага метода Гаусса.

Теорема. Метод Лагранжа приведения квадратичной формы к каноническому виду эквивалентен методу Гаусса приведения матрицы к треугольному виду.

Доказательство. Действительно, первый шаг прямого хода метода исключения переменных Гаусса преобразует матрицу следующим образом:

здесь

и предполагается, что . Видим, что формула формирования элементов матрицы

точно такая же, как и матрицы квадратичной формы . Более того, поскольку матрица симметрична ( ), то и только что полученная матрица оказывается симметричной. Если , то к этой новой матрице можно снова применить ту же процедуру, и т.д., и в конце концов придем к матрице первого порядка. Собирая все промежуточные результаты в одну матрицу, получим ее в треугольном виде

при условии, что ни одно из чисел на диагонали не обратилось в нуль:

Если теперь обратиться к методу Лагранжа, то увидим, что полученная матрица как раз и определяет замену переменных

приводящую квадратичную форму к каноническому виду:

Рассмотрим некоторое линейное преобразование А с матрицей .

Это симметрическое преобразование можно записать в виде:

y₁ = a₁₁x₁ + a₁₂x₂

y₂ = a₁₂x₁ + a₂₂x₂

где у₁ и у₂ – координаты вектора в базисе .

Очевидно, что квадратичная форма может быть записана в виде

Ф(х₁, х₂) = х₁у₁ + х₂у₂.

Как видно, геометрический смысл числового значения квадратичной формы Ф в точке с координатами х₁ их₂ – скалярное произведение .

Если взять другой ортонормированный базис на плоскости, то в нем квадратичная форма Ф будет выглядеть иначе, хотя ее числовое значение в каждой геометрической точке и не изменится. Если найти такой базис, в котором квадратичная форма не будет содержать координат в первой степени, а только координаты в квадрате, то квадратичную форму можно будет привести к каноническому виду.

Если в качестве базиса взять совокупность собственных векторов линейного преобразования, то в этом базисе матрица линейного преобразования имеет вид:

При переходе к новому базису от переменных х₁ и х₂ мы переходим к переменным и . Тогда:

Тогда .

Выражение называется каноническим видом квадратичной формы. Аналогично можно привести к каноническому виду квадратичную форму с большим числом переменных.

Теория квадратичных форм используется для приведения к каноническому виду уравнений кривых и поверхностей второго порядка.

Пример. Привести к каноническому виду квадратичную форму

Ф(х₁, х

2) = 27.

Коэффициенты: а₁₁ = 27, а₁₂ = 5, а₂₂ = 3.

Составим характеристическое уравнение: ;

(27 — )(3 — ) – 25 = 0

² — 30 + 56 = 0

₁ = 2; ₂ = 28;

Пример. Привести к каноническому виду уравнение второго порядка:

17x² + 12xy + 8y² – 20 = 0.

Коэффициенты а₁₁ = 17, а₁₂ = 6, а₂₂ = 8. А =

Составим характеристическое уравнение:

(17 — )(8 — ) — 36 = 0

136 — 8 — 17 + 

2 – 36 = 0

² — 25 + 100 = 0

₁ = 5, ₂ = 20.

Итого: — каноническое уравнение эллипса.

Пример. Используя теорию квадратичных форм, привести к каноническому виду уравнение линии второго порядка. Схематично изобразить график.

Решение: Составим характеристическое уравнение квадратичной формы : при

Решив это уравнение, получим ₁= 2, ₂= 6.

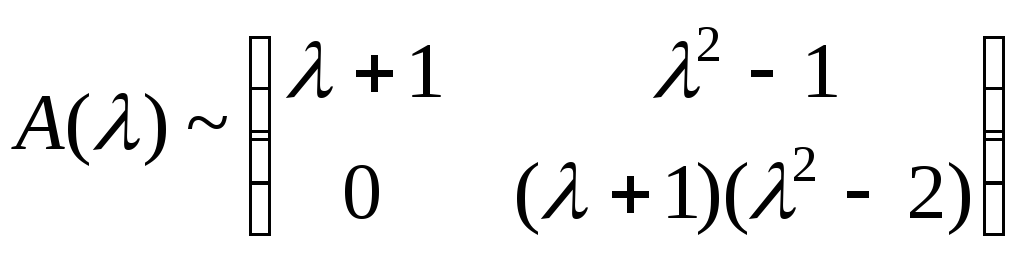
Найдем координаты собственных векторов:

полагая m₁= 1, получим n₁=

полагая m₂= 1, получим n₂=

Собственные векторы:

Находим координаты единичных векторов нового базиса.

Имеем следующее уравнение линии в новой системе координат:

Каноническое уравнение линии в новой системе координат будет иметь вид:

Решение: Составим характеристическое уравнение квадратичной формы : при

Решив это уравнение, получим ₁= 1, ₂= 11.

Найдем координаты собственных векторов:

полагая m₁= 1, получим n₁=

полагая m₂= 1, получим n₂=

Собственные векторы:

Находим координаты единичных векторов нового базиса.

Имеем следующее уравнение линии в новой системе координат:

Каноническое уравнение линии в новой системе координат будет иметь вид:

4ху + 3у² + 16 = 0

Коэффициенты: a₁₁ = 0; a₁₂ = 2; a₂₂ = 3.

Характеристическое уравнение:

Корни: ₁ = -1, ₂ = 4.

Для ₁ = -1 Для ₂ = 4

m₁ = 1; n₁ = -0,5; m₂ = 1; n₂ = 2;

= (1; -0,5) = (1; 2)

Получаем: -каноническое уравнение гиперболы.

Критерий Сильвестра определяет, является ли симметричная квадратная матрица положительно (отрицательно, неотрицательно) определённой.

Пусть квадратичная форма имеет в каком-то базисе матрицу

Тогда эта форма положительно определена, если и только если все её главные (угловые) миноры Δ_i положительны. Форма отрицательно определена, если и только если знаки Δ_i чередуются, причём Δ₁ < 0. Здесь главными минорами матрицы A называются определители вида

Для неотрицательно определённых матриц критерий действует только в одну сторону: если форма неотрицательно определена, то главные миноры неотрицательны. Обратное неверно. Например, матрица

не является неотрицательно определённой — так как, например, (Mv,v) = − 2 для v = (0,1, − 1). В то же время все её главные миноры равны 0, то есть неотрицательны.

Содержание

[убрать]

Каноническое определение и значение — Merriam-Webster

ca·не·i·cal kə-ˈnä-ni-kəl

: канона, относящегося к нему или образующего его

канонические писания

: соответствующие общему правилу или приемлемой процедуре : ортодоксальные

Его предложения были общеприняты как канонические.

: священнослужителя, являющегося каноником

: приведенный к канонической форме

каноническая матрица

канонически

kə-ˈnä-ni-k(ə-)lē

наречие

Примеры предложений

Недавние примеры в Интернете Sixty Wall слишком молод, чтобы быть канонический , несмотря на архитектурное значение Roche, и, возможно, поэтому он считается таким расходным материалом. — Обузданный , 19 сентября 2022 г. Тема книги, нацистская оккупация Киева, и ее литературные качества делают Бабий Яр равным каноническим произведениям-свидетельствам. — Джордж Пэкер, The Atlantic , 9 февраля 2023 г. Мортон теперь рассматривается как канонический пример научной недобросовестности. — Разиб Хан, Discover Magazine , 8 июня 2011 г. Нет, самая большая проблема заключается в том, что возникает множество канонических книг, особенно научной фантастики, которые — на момент публикации — смотрели в будущее, которое к настоящему времени фактически наступило. — Трэвис М. Эндрюс, Washington Post , 3 января 2023 г. Сколько новых способов найдут создатели фильма (включая Лин, которая написала сценарий вместе с новичком в сериале Дэном Мазо, заменившим его режиссером Луи Летерье и продюсером-звездой Вином Дизелем) для реткона (или ретроактивной преемственности)9. 0045 канонические знания? — Los Angeles Times , 1 января 2023 г. Если бы не подобные отчеты, каноническое повествование о COVID в Нью-Йорке могло бы быть только о страдании, стирающем краткий период трансформации и близости. — Зои Бири, The Atlantic , 23 декабря 2022 г. Эти результаты подтверждают и расширяют результаты более раннего исследования и бросают вызов почти канонических представлений о старинных итальянских скрипках. —Серьезно Наука, Discover Magazine , 28 апреля 2014 г. В Маккавейских книгах, которые не являются частью еврейской Библии, но считаются каноническими католиками и православными христианами, описываются евреи, скрывающиеся в пещерах, чтобы избежать репрессий. — Патрик Смит, NBC News , 13 декабря 2022 г. Узнать больше

Эти примеры предложений автоматически выбираются из различных онлайн-источников новостей, чтобы отразить текущее использование слова «канонический». Мнения, выраженные в примерах, не отражают точку зрения Merriam-Webster или ее редакторов. Отправьте нам отзыв.

История слов

Этимология

см. каноническую запись 1

Первое известное использование

15 век, в значении, определенном в смысле 1

Путешественник во времени

Первое известное использование канонического было в 15 веке

Посмотреть другие слова из того же века канонический

канонический

канонический возраст

Посмотреть другие записи поблизости

Процитировать эту запись «Канонический».

Словарь Merriam-Webster.com , Merriam-Webster, https://www.merriam-webster.com/dictionary/canonical. По состоянию на 26 февраля 2023 г. прилагательное

ca·не·i·cal kə-ˈnän-i-kəl

: относящийся к церковному закону или разрешенный им

: согласно общему правилу или принятой процедуре

канонически

-i-k(ə-)lē

наречие

Еще от Merriam-Webster о

canonical

Тезаурус: Все синонимы и антонимы к слову canonical

Английский: Перевод canonical для говорящих на испанском языке

Britannica English: Перевод канонического для говорящих на арабском языке

Последнее обновление: 26 фев 2023 — Обновлены примеры предложений

Подпишитесь на крупнейший словарь Америки и получите тысячи дополнительных определений и расширенный поиск без рекламы!

Merriam-Webster без сокращений

Морфеус на самом деле мертв благодаря «Матрице онлайн»

Автор Стейси Хенли

Опубликовано 9 сентября 2021 г.

Вот почему Морфеуса нет в трейлере «Матрицы», ребята

Если вы только что видели трейлер «Матрицы воскрешений», вы, вероятно, заметили, что Морфеус Лоуренса Фишберна отсутствует и, возможно, даже заменен новым персонажем. Возможно, вы не заметили, что Фишбёрн пропал, или всегда думали, что это Сэмюэл Л. Джексон в кино. Если это так, у вас могут быть некоторые нерешенные проблемы, над которыми нужно работать. Если вы заметили, вы, вероятно, немного сбиты с толку. «Почему Кэндимэн сейчас в «Матрице»?» — вопрос, который вы, возможно, задали. «Почему Яхья Абдул-Матин II в «Матрице»?» Вы могли бы сказать, если вы настоящий киноман. Дело в том, что вы можете быть немного сбиты с толку. Не бойтесь, мы вас прикроем — оказывается, Морфеуса нет в трейлере из-за «Матрицы онлайн».

The Matrix Online — это MMORPG, действие которой разворачивается в мире — как вы уже догадались — «Матрицы», запущенной в 2005 году и закрытой четыре года спустя, в 2009 году. В то время Вачовски благословили игру, которая рекламировалась как каноническая. сиквел, продолжающий трилогию, поскольку режиссеры перешли к другим проектам. В игре Морфеус умирает, а поскольку игра каноничная, значит, и в фильмах он мертв.

Связанный: Шон Мендес — ужасный выбор для сериала Life is Strange

Мы пока не знаем, кого играет Яхья Абдул-Матин II. Ходят слухи, что он может быть младшей версией Морфеуса — в конце концов, в «Матрице» реальность имеет меньшее значение. То, что Нео и Тринити повзрослели, а Морфеус постарел, имело бы логический смысл и по-прежнему соблюдало бы канон игр, если бы Морфеус появился перед его смертью, а не просто отменил его.

Однако следует подчеркнуть, насколько непостижимо дерьмовой была смерть Морфеуса. Трудно написать по-настоящему великую смерть — персонаж все равно умирает, что немного омрачает празднование — но здесь нет никаких моментов Распутина. Морфеус закладывает странную матричную бомбу и прыгает в безопасное место, пока в него стреляет вооруженный человек в маске. Пуля не попадает в цель, и Морфеус перепрыгивает через перила. Однако, когда Морфеус направляется наружу, указанный стрелок проскальзывает через вентиляционное отверстие и стреляет ему прямо в грудь — совершенно непонятно, как этот человек попал в вентиляционное отверстие, почему оно ведет наружу и как Морфеуса так легко застали врасплох. Затем мужчина снова несколько раз стреляет Морфеусу в грудь, пока тот находится на земле, затем сцена меняется на Матриксеров — вы знаете, кого я имею в виду — и Агенты спорят, причем Агенты утверждают, что они не несут ответственности за его смерть.

Фанаты «Матрицы Онлайн» — да, во множественном числе — в то время ходили слухи, что Морфеус на самом деле не мертв, и что все это было частью тщательно продуманной повествовательной уловки. Однако, поскольку серверы были отключены до того, как эта теория была подтверждена, в нынешнем виде Морфеус канонически мертв. Лана Вачовски могла бы легко сыграть Джорджа Лукаса и просто решить несколько вещей, которые когда-то были каноном, теперь таковыми не являются, но трейлер и явное отсутствие Морфеуса — кроме потенциально молодого Морфеуса — предполагают, что она поддерживает канон игры и Морфеуса.