Частные производные первого, второго и третьего порядка: понятия и примеры решений
Чтобы понять частные производные, сначала нужно разобраться с обычными. И не нужно ничего искать: в нашей отдельной статье мы уже подготовили все для того, чтобы у вас это получилось. А сейчас речь пойдет о частных производных.
Добро пожаловать на наш телеграм-канал за полезной рассылкой и актуальными студенческими новостями.
Функция двух и более переменных
Прежде чем говорить о частных производных, нужно затронуть понятие функции нескольких переменных, без которого нет смысла в частной производной. В школе мы привыкли иметь дело с функциями одной переменной:
Производными таких функций мы и считали раньше. График функции одной переменной представляет собой линию на плоскости: прямую, параболу, гиперболу и т.д.
А что, если добавить еще одну переменную? Получится такая функция:
Это – функция двух независимых переменных x и y. График такой функции представляет собой поверхность в трехмерном пространстве: шар, гиперболоид, параболоид или еще какой-нибудь сферический конь в вакууме.
Частные производные функции z по иксу и игреку соответственно записываются так:
Существуют также функции трех и более переменных. Правда, график такой функции нарисовать невозможно: для этого понадобилось бы как минимум четырехмерное пространство, которое невозможно изобразить.
Частная производная первого порядка
Запоминаем главное правило:
При вычислении частной производной по одной из переменных, вторая переменная принимается за константу. В остальном правила вычисления производной не меняются.
То есть, частная производная по сути ничем не отличается от обычной. Так что, держите перед глазами таблицу производных элементарных функций и правила вычисления обычных производных. Рассмотрим пример, чтобы стало совсем понятно. Допустим, нужно вычислить частные производные первого порядка следующей функции:
Сначала возьмем частную производную по иксу, считая игрек обычным числом:
Теперь считаем частную производную по игреку, принимая икс за константу:
Как видите, ничего сложного в этом нет, а успех с более сложными примерами – лишь дело практики.
Частная производная второго порядка
Как находится частная производная второго порядка? Так же, как и первого. Чтобы найти частные производные второго порядка, нужно просто взять производную от производной первого порядка. Вернемся к примеру выше и посчитаем частные производные второго порядка.
По иксу:
По игреку:
Частные производные третьего и высших порядков не отличаются по принципу вычисления. Систематизируем правила:
- При дифференцировании по одной независимой переменной, вторая принимается за константу.
- Производная второго порядка – это производная от производной первого порядка. Третьего порядка – производная от производной второго порядка и т.д.
Частные производные и полный дифференциал функции
Частый вопрос в практических заданиях – нахождение полного дифференциала функции. Для функции нескольких переменных полный дифференциал определяется, как главная линейная часть малого полного приращения функции относительно приращений аргументов.
Определение звучит громоздко, но с буквами все проще. Полный дифференциал первого порядка функции нескольких переменных выглядит так:
Зная, как считаются частные производные, нет никакой проблемы вычислить и полный дифференциал.
Частные производные – не такая уж и бесполезная тема. Например, дифференциальные уравнения в частных производных второго порядка широко используются для математического описания реальных физических процессов.
Здесь мы дали лишь общее, поверхностное представление о частных производных первого и второго порядка. Вас интересует эта тема или остались конкретные вопросы? Задавайте их в комментариях и обращайтесь к экспертам профессионального студенческого сервиса за квалифицированной и скорой помощью в учебе. С нами вы не останетесь один на один с проблемой!
Иван Колобков, известный также как Джони.
Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.
Частные производные. Примеры решений
На данном уроке мы познакомимся с понятием функции двух переменных, а также подробно рассмотрим наиболее распространенное задание – нахождение частных производныхпервого и второго порядка, полного дифференциала функции. Студенты-заочники, как правило, сталкиваются с частными производными на 1 курсе во 2 семестре. Причем, по моим наблюдениям, задание на нахождение частных производных практически всегда встречается на экзамене.
Для
эффективного изучения нижеизложенного
материала Вам необходимо уметь
более или менее уверенно находить
«обычные» производные функции одной
переменной. Научиться правильно
обращаться с производными можно на
уроках Как
найти производную? иПроизводная
сложной функции.
Также нам потребуется таблица производных
элементарных функций и правил
дифференцирования, удобнее всего, если
она будет под рукой в распечатанном
виде. Раздобыть справочный материал
можно на страницеМатематические
формулы и таблицы.
Начнем с самого понятия функции двух переменных, я постараюсь ограничиться минимумом теории, так как сайт имеет практическую направленность. Функция двух переменных обычно записывается как , при этом переменные , называются
Пример: – функция двух переменных.
Иногда используют запись . Также встречаются задания, где вместо буквы используется буква .
Полезно
знать геометрический смысл функций.
Функции одной переменной соответствует
определенная линия на плоскости,
например, –
всем знакомая школьная парабола. Любая
функция двух переменных с
геометрической точки зрения представляет
собой поверхность в трехмерном
пространстве (плоскости, цилиндры,
шары, параболоиды и т.
д.). Но, собственно,
это уже аналитическая геометрия, а у
нас на повестке дня математический
анализ, который никогда
не давал списывать мой вузовский
преподаватель является
моим «коньком».
Переходим к вопросу нахождения частных производных первого и второго порядков. Должен сообщить хорошую новость для тех, кто выпил несколько чашек кофе и настроился на невообразимо трудный материал: частные производные – это почти то же самое, что и «обычные» производные функции одной переменной.
Для частных производных справедливы все правила дифференцирования и таблица производных элементарных функций. Есть только пара небольших отличий, с которыми мы познакомимся прямо сейчас.
Пример 1
Найти частные производные первого и второго порядка функции
Сначала найдем частные производные первого порядка. Их две.
Обозначения: или – частная производная по «икс» или – частная производная по «игрек»
Начнем
с .
Когда
мы находим частную производную по
«икс», то переменная считается
константой (постоянным числом).
Решаем. На данном уроке я буду приводить полное решение сразу, а комментарии давать ниже.
Комментарии к выполненным действиям:
(1) Первое, что мы делаем при нахождении частной производной – заключаем всю функцию в скобки под штрих с подстрочным индексом.
Внимание, важно! Подстрочные индексы НЕ ТЕРЯЕМ по ходу решения. В данном случае, если Вы где-нибудь нарисуете «штрих» без , то преподаватель, как минимум, может поставить рядом с заданием (сразу откусить часть балла за невнимательность).
Далее данный шаг комментироваться не будет, все сделанные замечания справедливы для любого примера по рассматриваемой теме.
(2)
Используем правила дифференцирования , .
Для простого примера, как этот, оба
правила вполне можно применить на одном
шаге. Обратите внимание на первое
слагаемое: так как считается
константой, а любую константу можно
вынести за знак производной,
то мы
выносим за скобки.
(3) Используем табличные производные и .
(4) Упрощаем, или, как я люблю говорить, «причесываем» ответ.
Теперь . Когда мы находим частную производную по «игрек», то переменная считается константой (постоянным числом).
(1) Используем те же правила дифференцирования , . В первом слагаемом выносим константу за знак производной, во втором слагаемом ничего вынести нельзя поскольку – уже константа.
(2) Используем таблицу производным элементарных функций. Мысленно поменяем в таблице все «иксы» на «игреки». То есть данная таблица рАвно справедлива и для (да и вообще почти для любой буквы).
Итак, частные производные первого порядка найдены
Подведем итог, чем же отличается нахождение частных производных от нахождения «обычных» производных функции одной переменной:
1)
Когда мы находим частную
производную , переменная считается
константой.
2) Когда мы находим частную производную , переменная считается константой.
Частные производные
Частная производная — это производная, в которой некоторые переменные остаются постоянными. Как в этом примере:
Пример: функция для поверхности, которая зависит от двух переменных
x и y
Когда мы находим наклон в направлении x (при фиксированном частичном y ), мы нашли a производная.
Или мы можем найти наклон в y направление (при сохранении фиксированного x ).
Давайте сначала подумаем о функции одной переменной (x):
f(x) = x 2
Мы можем найти его производную, используя степенное правило:
f’(x) = 2x
А как насчет функции двух переменных (x и y):
f(x, y) = x 2 + y 3
Мы можем найти его частичную производную по отношению к x , когда мы рассматриваем y как константу (представьте, что y — это число вроде 7 или что-то в этом роде):
f’ х = 2х + 0 = 2х
Объяснение:
- производная от x 2 (относительно x) равна 2x
- мы рассматриваем y как константу , поэтому y 3 также является константой (представьте, что y=7, тогда 7 3 =343 также является константой), а производная константы равна 0
Чтобы найти частную производную по y , мы рассматриваем
f’ г = 0 + 3г 2 = 3г 2
Объяснение:
- мы теперь рассматриваем x как константу , поэтому x 2 также является константой, а производная константы равна 0
- производная от y 3 (по y) равна 3y 2
Вот и все.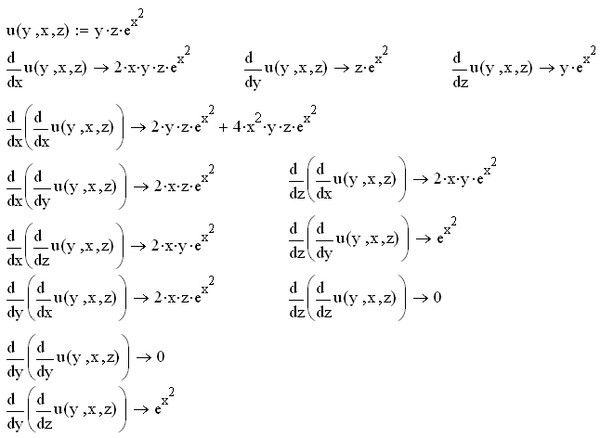
Просто не забудьте рассматривать все остальные переменные, как если бы они были константами .
Хранение переменной константы
Итак, на что похоже «удержание переменной константой»?
Пример: объем цилиндра V = π r
2 hМы можем записать это в многомерной форме как
f(r, h) = π r 2 h
Для частной производной по r мы считаем h постоянным , а r изменяется:
f’ r = π (2r) h = 2πrh
(производная от 7 3 r по отношению к r равно 2r, а π и h — константы)
Здесь сказано, что «поскольку изменяется только радиус (минимально), объем изменяется на 2πrh»
Это похоже на то, как мы добавляем скин с окружностью окружности (2πr) и высота h.
для частичной производной по отношению к H мы держим R Constant :
F ‘ H = π R 2 (1) = πr 2
(π и r 2
(π и r 2
(1).
являются константами, а производная h по h равна 1)
В нем говорится, что «поскольку изменяется только высота (минимально), объем изменяется на πr 2 »
Это похоже на то, как мы складываем самый тонкий диск сверху с площадью круга πr 2 .
Давайте посмотрим на другой пример.
Пример: площадь поверхности квадратной призмы.
Поверхность включает верхнюю и нижнюю части площадью x 2 каждая и 4 стороны площадью xy каждая: ‘ x = 4x + 4y
f’ y = 0 + 4x = 4x
Три или более переменных
У нас может быть 3 или более переменных. Просто найдите частную производную каждой переменной по очереди, обрабатывая все остальные переменные как константы .
Пример: Объем куба с вырезанной из него квадратной призмой.
F (x, y, z) = z 3 — x 2 y
F ‘ x = 0 — 2xy = −2xy
F’ y = 0 — x 27 27 = −x 2
f’ z = 3z 2 − 0 = 3z 2
Когда есть много x и y, это может привести к путанице, поэтому умственный трюк состоит в том, чтобы заменить «постоянные» переменные буквами, такими как «c» или «k», которые выглядят как как константы.