Производная от x 2 1: Найти производную y’ = f'(x) = x^2-1 (х в квадрате минус 1)

alexxlab / / Разное

Производная функции — Математика — Уроки

Тема: Производная функции.

Цель: Ввести понятия «производная функции», научить обучающихся находить производную функции в точке по определению.

Определения: Производная функции в точке, производная функции, дифференцирование.

Ход урока:

  1. Организационный момент.

Добиться дисциплины в классе. Проверить готовность учеников к уроку, мобилизовать внимание.

  1. Актуализация знаний.

  2. Введение нового материала.

Пусть функция y=f(x) определена на промежутке [a;b]. Точка x [a;b]. В точке x функция y=f(x) имеет значение f(x).Точка (x+∆x)[a;b]. В точке (x+∆x) функция y=f(x) имеет значение f(x+∆x). Разность (x+∆х – x) — приращение аргумента. Обозначается ∆x.

Р азность f(x+∆x) – f(x)— приращение функции. Обозначается ∆ y, т.е.

∆y = f(x+∆x) – f(x).

Составим отношение

.

Если ∆x 0, то

.

Этот предел называется производной функции y=f(x) в точке x.

Определение: Производной функции y=f(x) в точке x называется предел отношения функции к приращению аргумента, если приращение аргумента стремится к нулю. Обозначают производную : f'(x) или или . Обычно, если данная функция обозначена буквой у, то ее про­изводная может быть обозначена у’, читать: «производная функции у» или , читать: «производная функции у по х». Если данная функция обозначена символом f(x), то ее производная может быть обозначена f ‘(х), читать: «производная функции f(x)».

Определение: Операция нахождения производной называется дифференцированием.

Функция y=f(x), которая имеет производную в точке x, называется дифференцируемой в этой точке. Функция y=f(x), которая имеет производную в каждой точке некоторого промежутка, называется дифференцируемой на этом промежутке.

Общее правило дифференцирования (нахождения про­изводной) следующее:

1) найти приращение ∆y функции, т. е. разность значений функции при значениях аргумента х+ ∆x и x;

2) найти отношение ∆y/∆x, для этого полученное выше равенство разделить на ∆x;

3) найти предел отношения ∆y/∆x при ∆x →0.

Еще Софья Ковалевская говорила : “Математик должен быть поэтом в душе”. Приведу стихотворение (из учительского фольклора) о производной с использованием таблицы алгоритмического поиска производной.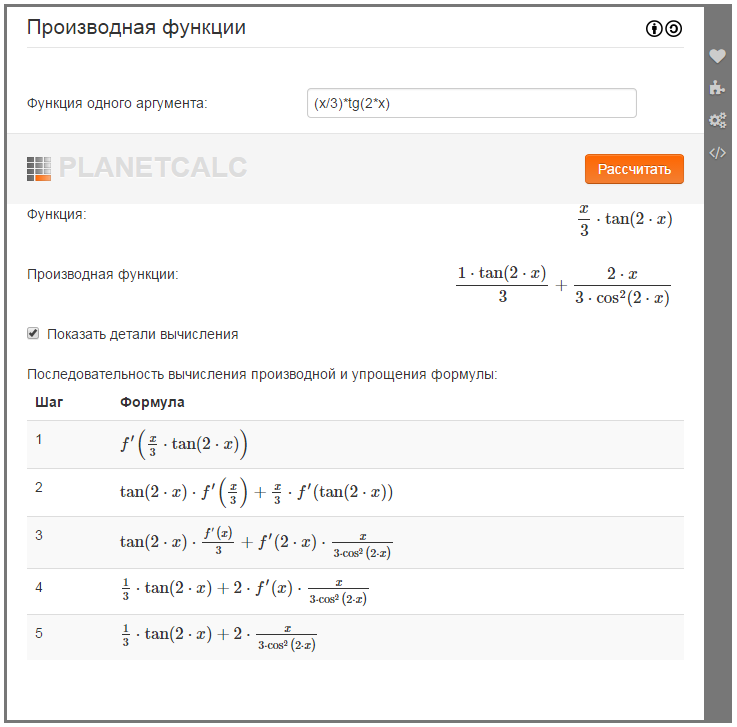

Пример 1. (Учитель на доске, ученики записывают в тетрадь) Найти производную функции у = х3 + 1 в любой точке x.

Решение. 1) ∆y = (x + ∆x)3 + 1 — (х3 + 1).

По выполнении действий:

∆y = Зx2∆x+Зx∆x 2+∆x 3;

2) ∆y/∆x=3x2 + Зx∆x+∆x 2;

3) у‘= lim(3x2+3x∆x+∆x 2 )= 3x2+3x0+0 = 3x2.

∆x→0

Пример 2. (учитель с классом) Найти производную функции .

Решение: Составим отношение:

Значит, .

Пример 3. (Учитель с классом) Найти производную функции f(x)=x

Решение:

(x)’=1

Пример 4. (Учитель с классом) Найти производную функции f(x)=5x+7.

Решение: Составим отношение:

. Но

Значит, (5x+7)’=5.

Пример 5. (Ученики выполняют самостоятельно в тетрадях) Найти производную функции f(x)=ax+b.

Решение: Составим отношение:

(ax+b)’=a.

Замечание: Заметим, что производная линейной функции у= kx+b есть величина постоянная, равная k.

Пример 6. (Один ученик у доски, остальные – в тетрадях) Найти производную функции f(x)=C (Const)

Решение:

Таким образом, (C)’=0

  1. Решение упражнений

  1. Вычислите ∆y/∆x в точке х0, если: а) у=2х2, х0 = 1, ∆x равно 0,5; 0,1; 0,01; б) у=х2, х0 = 1, ∆x равно 0,5; 0,1; 0,01.

  2. К какому числу стремится отношение ∆y/∆x при ∆x→0, если

а) ∆y/∆x =8 х0 +4 ∆ х, х0 равно 2; -1;

б) ∆y/∆x =3 х02+3 х0∆ х +(∆ х) 2, х0 равно 1; -21;

в) ∆y/∆x = -2 х0 + ∆ х, х0 равно 1; 3?

  1. Пользуясь определением производной, найдите значения производной функции у, если:

а) у = х2 — 3х в точках -1; 2;

б) у=2х3 в точках 0; 1;

в) у =4 — х2 в точках 3;0.

Учитель с учениками обсуждают полученные результаты.

  1. Домашнее задание.

1. Пользуясь определением производной, найти значения производной функции у в точке, если:

  1. у = х2 — 3х +7 в точках -3; 4; 7;

  2. у = х2 — 9х — 18 в точках -1;2;

  3. у =4 – 6х + х2 в точках -2; 2;

  4. у=2х3— 29х — 18 в точках -1; 3;

  5. у=2х3 +4х2 — 11х — 13 в точках 0;1;

  6. у=-3х3 -42х2 -24х — 1 в точках 1; 4,

  7. , в точке 1.

2. Пользуясь определением производной, найти производную функции у, если:

  1. ,

  2. ,

  3. у = 5 − 6x ,

  4. у= 4 − 7x,

  5. ,

  6. ,

  7. у = 2х2 — 13х +3,

  8. у=-3x2-13x,

  9. у=7x2+3x,

  10. у =4 – 5х + 2х2,

  11. у = 3х2 — 2х – 8,

  12. у=х3— 9х – 4,

  13. у=3х3 — 4х2 — 8х – 4,

  14. у =-2х3 -4х2 -4х,

  15. у = ,

  16. у = ,

  1. Подведение итогов урока.

Вопросы:

1) Что называется приращением аргумента?

2) Что называется приращение функции?

3) Что называется производной функции y = f(x) в точке x?

4) Как называется операция нахождение производной?

5) Какая функция называется дифференцируемой в точке?

6) Какая функция называется дифференцируемой на отрезке?

Отметить учащихся, активно работавших на уроке.

Производная. 11-й класс

Цели урока:

обучающие – повторение и закрепление теоретического материала, т.е. актуализация опорных знаний и отработка умений находить производную функции, исследовать функцию с помощью производной; владение геометрическим и физическим смыслом производной; применение производной при выполнении заданий ЕГЭ;

развивающие –

  1. формирование компетентности в сфере самостоятельной познавательной деятельности на основе расширения представлений о производной, умения ориентироваться в информационном пространстве, развитие умения составлять задачи и задачи, обратные к ним;
  2. вовлечение учащихся в коммуникативную, практическую деятельность как фактор личностного развития;
  3. научить детей работать в нестандартной ситуации;

воспитательные – воспитание уважения к мнению других, умение слушать.

I. ОРГАНИЗАЦИОННЫЙ МОМЕНТ.

Число. Тема. Цели.

Вы умеете находить производные функций и решать задачи на применение производных.

Сегодня вы будете работать в нестандартной ситуации, познакомитесь с заданиями по теме: «Производная», которые предлагались на ЕГЭ.

Понятие производной является одним из основных математических понятий. Производная широко используется при решении ряда задач математики, физики и других наук, в особенности при изучении скорости разных процессов.

Основной вопрос: Виды задач, встречающиеся на применение производной.

Ребята в группах провели исследовательскую работу по отбору задач из КИМов ЕГЭ и на этом уроке представят нам свои проекты.

Ребята, нужно слушать внимательно, записывать в тетрадь, т.к. будет самостоятельная работа, где встретятся похожие задачи.

II. АКТУАЛИЗАЦИЯ ЗНАНИЙ УЧАЩИХСЯ.

1. Геометрический смысл производной.

Повторение теории.

Практическая часть:

  • Устная работа. Слайды 3-4.
  1. Найдите угловой коэффициент касательной к графику функции y= 2x+eх в его точке с абсциссой xo=0.
    Ответ: 3.
  2. Найдите тангенс угла наклона касательной к графику функции y=7x-5sinx в точке с абсциссой xo=π/2.
    Ответ: 7.
  • Письменная работа. Слайды 5-8.

  1. Найдите т. xo, если тангенс угла наклона касательной, проведенной к графику функции y=3x2-7x+5 в точке с абсциссой xo, равен 2.
    Решение. Так как тангенс угла наклона касательной к графику функции в точке с абсциссой x

    o равен значению производной функции в точке xo, то tgα=y‘ (xo)=2. Найдем производную y‘=6x-7 и решим уравнение
    6 xo-7=2
    xo=1,5.
    Ответ: 1,5.

  2. Пусть касательная к графику функции y= f(x), проведенная в т. М(-2;-9) параллельна прямой 28x-4y+420=0. Найдите значение производной f ‘(-2).
    Решение. Значение производной f ‘ (-2) это угловой коэффициент касательной к графику функции y= f(x) в т. М(-2;-9). Так как эта касательная параллельна прямой 28x-4y+420=0, то их угловые коэффициенты равны.
    Найдём угловой коэффициент прямой:
    28x-4y+420=0,
    4y=28x=420,
    y=7x+105.
    k=7=kкас = f ‘

    (-2).
    Ответ: 7.

  3. В8. На рисунке изображен график производной функции y=f (x).
    1) К графику функции y=f(x) в точке с абсциссой xo =-4 проведена касательная. Найдите ее угловой коэффициент.
    Ответ: -2.
    2) К графику функции проведены все касательные параллельные прямой y=x-5,(или совпадающие с ней). Найдите число этих касательных.
    Ответ: 3.
    3) Найдите число касательных к графику функции y=f(x), которые наклонены под углом 45° к положительному направлению оси абсцисс.
    Ответ: 3.
    4) Найдите наибольшую из абсцисс точек, в которых касательные к графику функции параллельны оси абсцисс [прямой у=6].
    Ответ: 4.

2. Физический смысл производной.

Повторение теории.

Практическая часть:

  • Устная работа. Слайд 3.

Найдите момент остановки тела, движущегося по закону s(t)= t²-6t-16

Ответ: 3

  • Письменная работа. Слайды 4-8.

  1. Точка движется по координатной прямой согласно закону x(t)= t²+t+2, где x(t) – координата точки в момент времени t (время измеряется в секундах, расстояние в метрах). В какой момент времени скорость точки будет равна 5 м/с?
    Решение: Скорость точки в момент времени t есть производная от координаты по времени.
    Т.к. v(t) = x'(t) = 2t+1 и v = 5 м/с, то
    2t +1= 5
    t=2
    Ответ: 2.

  2. При торможении маховик за t секунд поворачивается на угол φ(t)= 6t — t² радиан. Найдите угловую скорость ω вращения маховика в момент времени t=1 с.(φ(t) – угол в радианах, ω(t) – скорость в рад/с., t – время в секундах).

    Решение:
    ω(t) = φ'(t),
    ω(t) = 6 – 2t,
    t = 1 c,
    ω(1) = 6 – 2 × 1 = 4 рад/с.
    Ответ:4.

  3. При движении тела по прямой его скорость v'(t) (в м/с) изменяется по закону v(t)=15+8t-3t² (t – время движения тела в секундах). Каким будет ускорение тела (в м/с²) через 1 секунду после начала движения тела?
    Решение:
    v(t)=15+8t-3t²,
    a(t)=v'(t),
    a(t)=8-6t,
    t=1,
    a(1)=2 м/с².
    Ответ: 2.

  4. Заряд, проходящий через поперечное сечение проводника, вычисляется по формулеq(t)=2t2-5t. Найти силу тока при t=5c.
    Решение:
    i(t)=q'(t),

    i(t)=4t-5,
    t=    5,
    i(5)=15 А.
    Ответ: 15.

  5. При движении тела по прямой расстояние s(t) от начальной точки М изменяется по закону s(t)=t4 -4t3 -12t +8 (t – время в секундах). Каким будет ускорение тела (в м/с2) через 3 секунды?
    Решение.
    a(t)=v ‘(t)=s»(t).
    Найдем
    v(t)=    s‘(t)=(t4-4t3-12t +8)’ =4t3-12t2-12.
    a(t)=v ‘(t)= s»(t)= (4t3-12t2-12)’ =12t2-24t,
    a(3)=12×32-24×3=108-72=36м/с2.
    Ответ. 36.

3. Монотонность функции. Экстремумы

Повторение теории.

Слайды 1-4

Практическая часть:

Устная работа. Слайды 6-7.

  • Функция у =f (х) определена на промежутке (-4; 13). График производной у = f ‘(x) изображен на рисунке.
  1. Найдите число критических точек функции у = f (x).
  2. Укажите число точек максимума функции у = f (х).
  3. Найдите число промежутков убывания.
  4. Найдите длину промежутка возрастания функции.

Письменная работа. Слайды 8-10.

  • На рисунке изображен график производной функции y=f(x), определенной на интервале (-9;8).
  1. В какой точке отрезка[-8;-4] функция f(x) принимает наименьшее значение?
  2. В какой точке отрезка[0;6] функция f(x) принимает наибольшее значение?
  3. Найдите промежутки возрастания функции. В ответе укажите сумму целых точек, входящих в эти промежутки.
  4. Определите количество целых точек, в которых производная функции положительна.


Рисунок 1.

  • Найдите число точек экстремума разностей функций у = f (х) и у = 5х — 6, используя график производной у = f ‘ (x) (на рис.1).

Решение: Найдем точки экстремума функции g (x) = f (x)-5x+6.

Поскольку производная g’ (x) = f ‘(x) – 5 существует при всех х из (-8;13), то в точке экстремума xo выполняется g’ (xo) =0.

График функции g'(x) =f ’(x) – 5 получается из графика функции у = f ‘ (x) параллельным переносом вдоль оси у на 5 единиц вниз и пересекает ось абсцисс в двух точках:

х=2, х=6 (рис.2). Производная в этих точках g ‘ (x) =f ‘ (x) – 5 равна нулю и при переходе через каждую из них меняет знак.

Следовательно, в этих двух точках функция g (x) имеет экстремумы.

Ответ: 2

 
Рисунок 2.

Вывод. Ребята проработали достаточно много материала, отобрали и рассмотрели задачи на применение производной, в особенности задачи на использование графика производной функции. Нужно обратить внимание на то, что задан график не только функции, но и её производной.

На партах лежат листы с демонстрационным вариантом ЕГЭ. Найдите задания, при решении которых применяется производная. Вы запишите эти задания и выполните дома.

III.УСТНАЯ РАБОТА.

Задание 1. Найти производную функции y= 7x+4/x в точке

х0=-1.

Ответ: 3.

Задание 2. Изменив формулировку данной задачи, составьте задачи на нахождение производной.

  1. Найдите f ’(-1), если f(x)=7x+4/x.
  2. Найдите скорость изменения функции f(x)=7x+4/x в точке х0=-1.
  3. Найти угловой коэффициент касательной к графику функции f(x)= 7x+4/x в точке х0=-1.
  4. Найти тангенс угла наклона касательной к графику функции f(x)= 7x+4/x в точке х0=-1.

Задание 3. Составьте задачи, обратные составленным.

  1. Найти х0, если значение производной функции у=7х+4/х в точке х0 равно 3.
  2. Найти абсциссу точки графика функции f(x)=7x+4/x
    , в которой скорость изменения функции равна 3.
  3. Найти абсциссу точки графика функции f(x)=7x+4/x, в которой, угловой коэффициент касательной равен 3.

Вывод. При изменении фабулы задачи схема решения одна и та же. При выполнении этих заданий надо владеть геометрическим и физическим смыслом производной.

IV. ПЕРВИЧНОЕ ЗАКРЕПЛЕНИЕ ЗНАНИЙ.

Самостоятельная работа (листы с текстом с/р. на партах).

Вариант 1. [Вариант 2]. 

А1.Найдите производную функции y=lnx+sin2x [y= ex+ cos2x].

1) 2sin2x; 2) 1/x-2cos2x; 3) 1/x+2cos2x; 4) 1/x+ cos2x. [1) 1 -cos2x; 2) ex+sin2x; 3) ex-2sin2x; 4) ex+2sin2x. ]

В1. Найдите угловой коэффициент касательной, проведенной к графику функции f(x)=3x-4ex [f(x)=7x – 5lnx] в его точке с абсциссой х0=0 [х0=1].

В2.Найдите угловой коэффициент касательной, проведённой к графику функции y=f(x) в точке с абсциссой х0= -3 [х0=4],если на рисунке изображён график производной этой функции.

 

В3.Функция у = f(x) определена на промежутке (-4,5;5) [ (-4,5;4) ]. На рисунке изображён график её производной.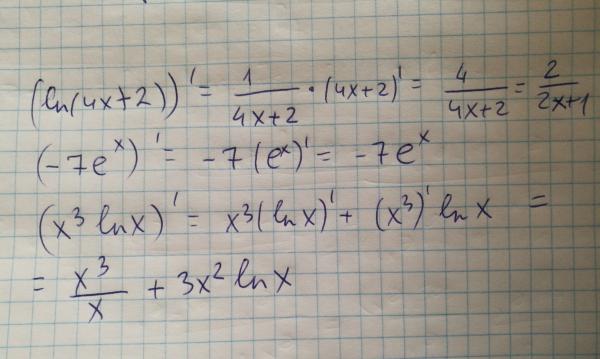 Найдите число точек минимума [максимума] функции у=f(x).

 

В4. Найдите наибольшую [наименьшую] из абсцисс точек, в которых тангенс угла наклона касательных равен -1 [1], используя график производной из задания В2.

С*. Составьте задачу, используя график производной функции у = f(x) (из зад. В2).

Время выполнения – 10 мин.

Критерий оценивания:

  • 5-6 заданий – «5» НА ДОСКЕ.
  • 4 задания – «4»
  • 3 задания – «3».

Взаимопроверка.

     А1       В1       В2       В3       В4   
№1 3 -1 1 2 4
№2 3 2 -1 1 -3

Вывод. «5» – , «4» – , «3» –

V. ЗАДАНИЕ из ЕГЭ

Найти точки минимума функции .

Решение:

f (x) = 3x4 + 7x3– 18x2 + 5–log 0,2 (x³+8).
D (f): x > -2.

Преобразуем показатель степени: -log0,2(x³+8)=-log5(x³+8)/log50,2=log5(x³+8), тогда степень равна 5–log 0,2 (x³+8)=5log5(x³+8) =(x³+8).

Функция примет вид:

f (x) = 3x4 + 7x³– 18x² + x³ + 8
f (x) = 3x4 + 8x³ — 18x² + 8
f ‘(x) = 12x³ + 24x² — 36x
f ‘(x) = 0, 12x³ + 24x² — 36x = 0
x³ + 2x² — 3x = 0
x(x² + 2x – 3) = 0
x = 0 или x² + 2x – 3 = 0
x1=-4; x2=1.


x=1 – точка минимума

Ответ: 1.

VI.

ИТОГ УРОКА.

Рефлексия

О чём мы говорили на этом уроке? Какие умения нужны при решении задач на применение производной?

(Умение находить производную функции, владение геометрическим и физическим смыслом производной (Баз.), умение исследовать функцию с помощью производной (Повыш.)).

На следующем уроке продолжим работу по вопросу: Виды задач на применение производной, рассмотрим решение задач на нахождение производной.

2+3x-4)}
  • Решение: Каково наименьшее расстояние между кораблями?
  • Решение: Когда два корабля окажутся ближе всего друг к другу?

    • Другие вопросы в: Дифференциальное исчисление (ПРЕДЕЛЫ И ПРОИЗВОДНЫЕ)

    Также вопросы в: Дифференциальное исчисление (МАКСИМА-МИНИМУМ И ВРЕМЕННЫЕ КОЭФФИЦИЕНТЫ)

    Онлайн-вопросы и ответы в Дифференциальное исчисление (ПРЕДЕЛЫ И ПРОИЗВОДНЫЕ)

    MCQ Дифференциальное исчисление (ЛИМИТЫ И ПРОИЗВОДНЫЕ)

    Онлайн-вопросы и ответы по дифференциальному исчислению (МАКСИМА-МИНИМУМ И ВРЕМЕННЫЕ КОЭФФИЦИЕНТЫ)

    MCQ по дифференциальному исчислению (МАКСИМА-МИНИМУМ И ВРЕМЕННЫЕ КОЭФФИЦИЕНТЫ)

    Пред.

    AlleBilderVideosNewsMapsShoppingBücher

    suchoptionen

    [PDF] ap исчисление bc глава 2 обзор

    www.ebnet.org › Домен › ГЛАВА 2 ТЕСТ ОБЗОР – ОТВЕТЫ

    Чтобы пройти ТЕСТ по главе 2, вы должны быть знакомы с . … АП ИСЧИСЛЕНИЕ до н.э. ГЛАВА 2 ОБЗОР. 2. Уравнение положения движущейся частицы …

    [PDF] AP Calculus Chapter 2 Test — Math KSU

    www.math.ksu.edu › ~dbski › calculus › chapt2_test

    AP Calculus Chapter 2 Test . Название: Период: Часть I. Вопросы с несколькими вариантами ответов (по 5 баллов за каждый). 1. График функции f дан справа.

    Исчисление Ap глава 2 | Викторина по исчислению — Викторина

    quizizz.com › admin › викторина › ap-calculus-chapter-2

    Сыграйте в эту игру, чтобы просмотреть исчисление. d/dx (sin 3 (4x -6 )) = ? … В. Какова производная от кроватки(х)?. варианты ответов. сек2(х). -сек2(х). csc2 (х). -csc2(х).

    High Speed ​​Review on Limit Solutions to Chapter 2 Test Calculus . ..

    www.youtube.com › смотреть

    27.08.2014 · High Speed ​​Review on Limit Solutions to Chapter 2 Test Calculus AP AB BC … 4,1 тыс. просмотров 8 …
    Дауэр: 39:26
    Прислан: 27.08.2014

    Исчисление Глава 2 Практический тест — YouTube

    www.youtube.com › смотреть

    22.02.2020 · Практический тест по Главе 2 Производные правилаhttp://mshavrot.pbworks.com/ w/file/fetch/138689319 …
    Дата: 37:41
    Прислан: 22.02.2020

    AP Calc BC Тестовые карточки для главы 2 — Quizlet

    quizlet.com › ap-calc-2bc-chapter-2 -тестовые-флеш-карты

    |x-x₀| < δ → |f(x)-L| < ε, чтобы найти δ через ε. - если такой ответ существует, то предел доказан по определению.

    Ap-исчисление Глава 2 Тестовые ответы

    diecyberversicherung.de › ap-calculus-chapter-2-test…

    Ap-Исчисление Глава 2 Тестовые ответыПрямая x = 2 является вертикальной асимптотой f(x) = 1/(х — 2)3. AP Calculus AB Chapter 6 Test (Practice) Multiple Choice .

    No related posts.

    Добавить комментарий

    Ваш адрес email не будет опубликован. Обязательные поля помечены *