Определение функции область определения: § Область определения функции

9 класс. Алгебра. Определение числовой функции. Способы задания функций. — Область определения иррациональных функций.

Комментарии преподавателя

Функция с квадратным корнем  определена только при тех значениях «икс», когдаподкоренное выражение неотрицательно: . Если корень расположился в знаменателе , то условие очевидным образом ужесточается: . 

Пример 5

Найти область определения функции 

Решение: подкоренное выражение должно быть неотрицательным:

Прежде чем продолжить решение, напомню основные правила работы с  неравенствами, известные ещё со школы.

 Итак, для неравенства равносильны следующие преобразования:

1) Слагаемые можно переносить из части в часть со сменой знака.

2) Обе части неравенства можно умножить на положительное число.

3) Если обе части неравенства умножить на отрицательное число, то необходимо сменитьзнак самого неравенства. Например, если было «больше», то станет «меньше»; если было «меньше либо равно», то станет «больше либо равно».

В неравенстве  перенесём «тройку» в правую часть со сменой знака (правило №1):

Умножим обе части неравенства на –1 (правило №3):

Умножим обе части неравенства на  (правило №2):

Ответ: область определения: 

Ответ также можно записать эквивалентной фразой: «функция определена при ».
Геометрически область определения изображается штриховкой соответствующих интервалов на оси абсцисс. В данном случае:

Ещё раз напоминаю геометрический смысл области определения – график функции  существует только на заштрихованном участке и отсутствует при .

В большинстве случаев годится чисто аналитическое нахождение области определения, но когда функция сложная, следует чертить ось  и делать пометки.

Пример 6

Найти область определения функции 

Это пример для самостоятельного решения.

Когда под квадратным корнем находится квадратный двучлен или трёхчлен, ситуация немного усложняется, и сейчас мы подробно разберём технику решения:

Пример 7

Найти область определения функции 

Решение: подкоренное выражение должно быть строго положительным, то есть нам необходимо решить неравенство . На первом шаге пытаемся разложить квадратный трёхчлен на множители:

Дискриминант положителен, ищем корни:

Таким образом, парабола  пересекает ось абсцисс в двух точках, а это значит, что часть параболы расположена ниже оси (неравенство ), а часть параболы – выше оси (нужное нам неравенство ).

Поскольку коэффициент , то ветви параболы смотрят вверх. Из вышесказанного следует, что на интервалах  выполнено неравенство  (ветки параболы уходят вверх на бесконечность), а вершина параболы расположена на промежутке  ниже оси абсцисс, что соответствует неравенству :

 

Обратите внимание, что сами точки  выколоты (не входят в решение), поскольку неравенство у нас строгое.

Ответ: область определения: 

Вообще, многие неравенства (в том числе рассмотренное) решаются универсальнымметодом интервалов, известным опять же из школьной программы. Но в случаях квадратных дву- и трёхчленов, на мой взгляд, гораздо удобнее и быстрее проанализировать расположение параболы относительно оси . 

Источник конспекта: http://www.mathprofi.ru/oblast_opredeleniya.html

Источник видео: http://www.youtube.com/watch?v=6aqZHIHeMeQ

Файлы

Нет дополнительных материалов для этого занятия.

Область определения функции

График функции f(x) = √x, область определения которой — все неотрицательные числа

Область определения  — множество, на котором задаётся функция. В каждой точке этого множества значение функции должно быть определено.

Содержание

• 1 Определение
• 2 Примеры
  • 2.1 Числовые функции
    • 2. 1.1 Тождественное отображение
    • 2.1.2 Гармоническая функция
    • 2.1.3 Дробно-рациональные функции
  • 2.2 Мера
  • 2.3 Функционал
• 3 См. также
• 4 Примечания
• 5 Литература

Определение

Если на множестве X{\displaystyle X} задана функция, которая отображает множество X{\displaystyle X} в другое множество, то множество X{\displaystyle X} называется областью определения или областью задания функции.

Более формально, если задана функция f{\displaystyle f}, которая отображает множество X{\displaystyle X} в Y{\displaystyle Y}, то есть: f:X→Y{\displaystyle f\colon X\to Y}, то множество X{\displaystyle X} называется областью определения^[1] или

областью задания^[2] функции f{\displaystyle f} и обозначается D(f){\displaystyle D(f)} или domf{\displaystyle \mathrm {dom} \,f} (от англ. domain — «область»).

Иногда рассматриваются и функции, определённые на подмножестве D{\displaystyle D} некоторого множества X{\displaystyle X}. В этом случае множество X{\displaystyle X} называется областью отправления функции f{\displaystyle f}^[3].

Примеры

Наиболее наглядные примеры областей определения доставляют числовые функции. Мера и функционал также доставляют важные в приложениях виды областей определения.

Числовые функции

Числовые функции — это функции, относящиеся к следующим двум классам:

• вещественнозначные функции вещественного переменного — это функции вида f:R→R{\displaystyle f\colon \mathbb {R} \to \mathbb {R} };
• а также комплекснозначные функции комплексного переменного вида f:C→C{\displaystyle f\colon \mathbb {C} \to \mathbb {C} },

где R{\displaystyle \mathbb {R} } и C{\displaystyle \mathbb {C} } — множества вещественных и комплексных чисел соответственно.

Тождественное отображение

Область определения функции f(x)=x{\displaystyle f(x)=x} совпадает с областью отправления (R{\displaystyle \mathbb {R} } или C{\displaystyle \mathbb {C} }). {2}-4\neq 0}. Таким образом domf{\displaystyle \mathrm {dom} \,f} является множеством всех действительных (или комплексных) чисел кроме 2 и −2.

Мера

Если каждая точка области определения функции — это некоторое множество, например, подмножество заданного множества, то говорят, задана функция множества.

Мера — пример такой функции, где в качестве области определения функции (меры) выступает некоторая совокупность подмножеств заданного множества, являющееся, например, кольцом или полукольцом множеств.

Например, определённый интеграл представляет собой функцию ориентированного промежутка.

Функционал

Пусть F={f∣f:X→R}{\displaystyle \mathbb {F} =\{f\mid f\colon X\to \mathbb {R} \}} — семейство отображений из множества X{\displaystyle X} в множество R{\displaystyle \mathbb {R} }. Тогда можно определить отображение вида F:F→R{\displaystyle F\colon \mathbb {F} \to \mathbb {R} }. Такое отображение называется функционалом.

Если, например, фиксировать некоторую точку x0∈ X{\displaystyle x_{0}\in ~X}, то можно определить функцию F(f)=f(x0){\displaystyle F(f)=f(x_{0})}, которая принимает в «точке» f{\displaystyle f} то же значение, что и сама функция f{\displaystyle f} в точке x0{\displaystyle x_{0}}.

См. также

• Область значений функции

Примечания

1. ↑
   В. А. Садовничий. Теория операторов. — М.: Дрофа, 2001. — С. 10. — 381 с. — ISBN 5-71-074297-X.
2. ↑ В. А. Ильин, В. А. Садовничий, Бл. Х. Сендов. Глава 3. Теория пределов // Математический анализ / Под ред. А. Н. Тихонова. — 3-е изд., перераб. и доп. — М.: Проспект, 2006. — Т. 1. — С. 105—121. — 672 с. — ISBN 5-482-00445-7.
3. ↑ В. А. Зорич. Глава I. Некоторые общематематические понятия и обозначения. § 3. Функция // Математический анализ. Часть I. — четвертое, исправленное. — М.: МЦНМО, 2002. — С.  12—14. — 664 с. — ISBN 5-94057-056-9.

Литература

• Функция, математический энциклопедический словарь. — Гл. ред. Ю. В. Прохоров. — М.: «Большая российская энциклопедия», 1995.
• Клейн Ф. Общее понятие функции. В кн.: Элементарная математика с точки зрения высшей. Т.1. М.-Л., 1933
• И. А. Лавров, Л. Л. Максимова. Часть I. Теория множеств // Задачи по теории множеств, математической логике и теории алгоритмов. — 3-е изд.. — М.: Физматлит, 1995. — С. 13—21. — 256 с. — ISBN 5-02-014844-X.
• А. Н. Колмогоров, С. В. Фомин. Глава 1.. Элементы теории множеств // Элементы теории функций и функционального анализа. — 3-е изд.. — М.: Наука, 1972. — С. 14—18. — 256 с.
• Дж. Л. Келли. Глава 0. Предварительные сведения // Общая топология. — 2-е изд.. — М.: Наука, 1981. — С. 19—27. — 423 с.
• В. А. Зорич. Глава I. Некоторые общематематические понятия и обозначения. § 3. Функция // Математический анализ, часть I. — М.: Наука, 1981. — С. 23—36. — 544 с.
• Г. Е. Шилов. Глава 2. Элементы теории множеств. § 2.8. Общее понятие функции. График // Математический анализ (функции одного переменного). — М.: Наука, 1969. — С. 65—69. — 528 с.
• А. Н. Колмогоров. Что такое функция // «Квант» : науч.-поп. физ.-мат. журн. — М.: «Наука», 1970. — № 1. — С. 27—36. — ISSN 0130-2221.

Что такое область видимости в JavaScript. Объяснение поведения Var… | by RayRay

Объяснение поведения Var, Const, Let, функций, объектов и классов в области видимости.

Фото Paweł Czerwiński на Unsplash

Для новичков в коде и разработчиков, которые только начинают разработку JavaScript, Scope в JavaScript может быть очень сложной темой для понимания.

В этом посте я хочу превратить эту сложную тему в очень простую для понимания концепцию, чтобы каждый мог понять, как она работает и что с ней можно делать.

Область действия — очень важная концепция для понимания. Если вы овладеете этой концепцией в своей голове, вам будет намного проще создавать удивительные вещи с помощью JavaScript.

Если вы относитесь к тому типу людей, которым нравятся презентации, то я рекомендую один из моих слайдов, которые я сделал пару лет назад: Презентация основ JavaScript

Для разработчиков, для которых английский язык является родным, это не проблема. . Но для тех, кто английский не родной язык, это не так очевидно.

Мне нравится приведенное ниже определение, которое делает его таким ясным.

масштаб, дальность, досягаемость, орбита, компас, амбит (существительное)
Область, в которой что-то действует или действует, или имеет силу или контроль: «дальность действия сверхзвукового реактивного самолета». Источник : Definitions.net

Это правильно!

Я бы определил это как область, которая может быть скрыта снаружи, но видна изнутри .

В JavaScript есть 2 типа области видимости. Глобальная область и локальные области.

1. Глобальная область видимости : все вещи, объявленные в глобальной области видимости, общедоступны.
2. Локальная область : вся информация, объявленная в локальной области, доступна только в этой области.

Давайте рассмотрим оба типа прицелов. Узнайте, что вы можете и не можете сделать с этим, и как вы можете его использовать.

1. Var
2. Function
3. Class
4. Const & Let

Photo by NASA on Unsplash

Наиболее важной, но критической областью является « глобальная область ». Любая другая область может достигать всего, что определено в глобальной области.

В браузере у нас есть объект window , а в NodeJS у нас есть объект global . В этом посте, когда я говорю « global scope », я имею в виду их обоих.

Одна вещь, которую вы должны помнить о глобальной области видимости, заключается в том, что вам не нужно хранить в ней слишком много информации. Рекомендуется хранить информацию в ваших локальных областях.

1.1 Var

Когда вы определяете var в глобальной области видимости, она общедоступна в глобальном объекте.

Переменная , которую вы храните в глобальной или любой другой области, может быть перезаписана. Рекомендуется использовать let или const вместо var . Потому что var не имеет поведения для «блочной области».

1.2 Функция

При определении функции в глобальном масштабе он общедоступен в глобальном объекте.

1.4 Класс

Когда вы определяете класс , он общедоступен, но не привязан к глобальному объекту.

Существует большая разница в том, что привязано к глобальному объекту, а что нет, но все же доступно в глобальной области видимости.

1.3 Const & Let

Когда вы определяете переменную let или const , она общедоступна, но не привязана к глобальному объекту.

1. Var
2. Function
3. Const & Let
4. Class

Photo by Benjamin Davies on Unsplash

When you define function , if or class , basiclly everything between a {} than inside a размах создается. Это то, что мы называем локальной областью действия.

Все, что объявлено внутри локальной области, доступно только внутри. Другая область или даже глобальная область не может достичь этого.

При определении var в локальной области он доступен только внутри этой области. Таким образом, var — это то, что мы называем функцией с областью действия . Если вы попытаетесь добраться до него за пределами этой области, вы получите сообщение об ошибке undefined .

Поскольку у нас есть let и const , я рекомендую больше не использовать var , потому что это имеет некоторые побочные эффекты. Я объясню это лучше в этом посте.

Нажмите на консоль, чтобы увидеть результаты 😉

В этом примере кода мы видим, что если var определена в глобальной области видимости, она видна для любой другой области. Когда мы определяем var внутри функции, мы можем видеть ее только внутри этой функции. Вне функции он показывает, что это undefined .

Но внутри нашей функции мы можем перезаписать глобальную переменную var .

Нажмите на консоль, чтобы увидеть результаты 😉

Как видите, после того, как мы определили переменную globalScope , значение такое же, как мы определили «GlobalScope». После того, как мы манипулируем этим внутри нашей функции, после него появляется смайлик 👏.

Это приведет к непредсказуемому поведению приложения в вашем здании. Вы определенно закончите с ошибкой.

Функция сама по себе называется функцией , функция , присоединенная к объекту или классу , называется метод .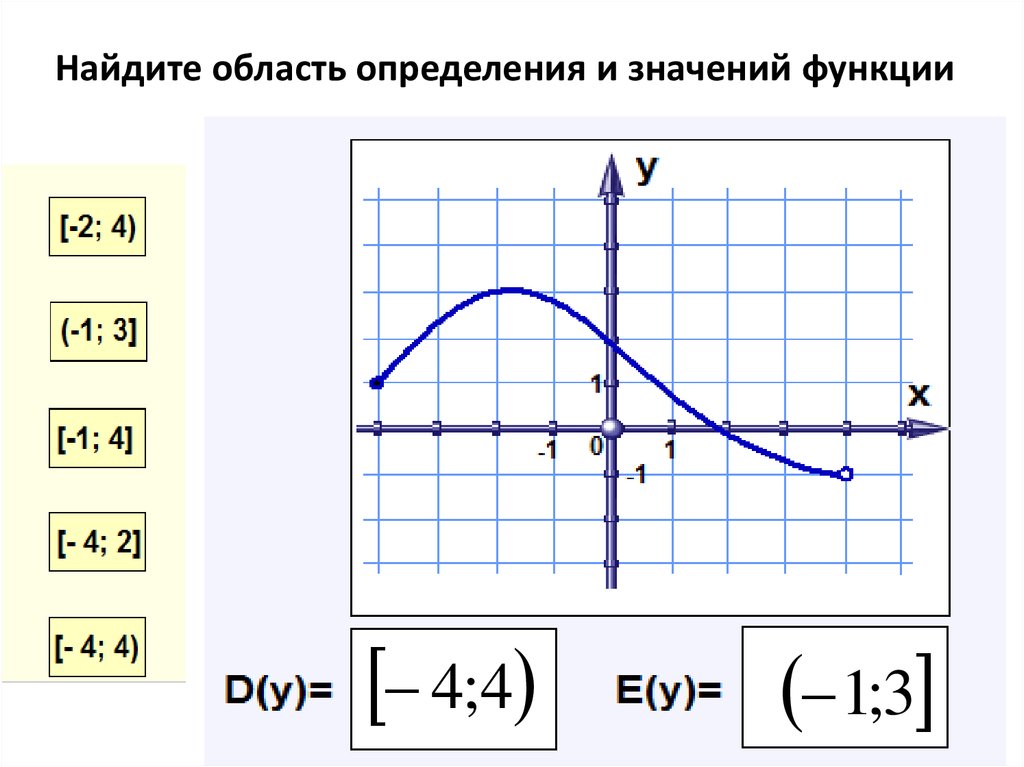 Функция , определенная в функции, является обычной функцией, но скрыта от внешней области.

Когда вы определяете функцию в глобальной области, она общедоступна в глобальном объекте.

2.2.2 Методы внутри объекта

Когда вы определяете метод или свойство в объекте , он привязывается к этой области, но по-прежнему доступен через этот объект. Если вы определяете переменные в этом методе, они остаются скрытыми.

С класс работает аналогично объекту .

В будущем это изменится для класса после введения частных полей в классах. В настоящее время это поддерживается только в браузерах Chrome и Opera, а также в инструментах Babel и TypeScript (v3.8).

Нажмите на консоль, чтобы увидеть результаты 😉

Как видите, мы можем перезаписать переменную globalScope из Object . Мы также можем изменить значение свойства name из globalScope.

Хотя эти вещи не защищены, переменные внутри наших методов не могут быть изменены и не видны из глобальной области видимости.

2.2.3 Функция в функции

С функцией внутри функции

Нажмите на консоль, чтобы увидеть результаты 😉

Переменные const и let имеют блочную область видимости. Где var привязан к области функция , const и let находятся между каждым {} .

Переменные const и let могут быть защищены функцией , оператором if , циклом for (или любым другим циклом). Вне его сферы до него нельзя добраться.

2.3.1 Let

Если вы хотите перезаписать информацию в той же области, вы должны объявить переменную let , потому что информация может быть изменена. 9Переменная 0068 let не может быть переобъявлена.

2.

3.2 Const

Информация, которая должна быть одинаковой во время выполнения вашего JavaScript, может найти свое место в переменной const . Константная переменная не может быть перезаписана или повторно объявлена.

Если переменная const имеет Объект или Массив , у вас есть возможность добавлять и удалять свойства. Но если вы храните в нем значения одного типа, он остается прежним.

Функция сама по себе называется функцией , функция , присоединенная к объекту или классу , называется методом . Функция , определенная в функции, является обычной функцией, но скрыта от внешней области.

2.4.1 Методы внутри класса

В этом примере вы можете видеть, что переменные, объявленные в методе, недоступны снаружи. Переменная globalScope доступна во всех локальных областях. Свойства и методы доступны вне класса при создании новый экземпляр.

Внутри нашего класса мы можем изменить переменную globalScope . Вне нашего класса мы можем изменить наше свойство name . Но это будет только в том случае. Если бы мы создали еще один экземпляр, имя было бы таким, как определено в классе .

Надеюсь, вы лучше понимаете область видимости в JavaScript, а также знаете, что с ней делать и как реализовать это в собственном коде! Если нет, пишите вопросы в комментариях! С удовольствием помогу разобраться!

Привет, я Рэй , голландский 🇳🇱 разработчик JavaScript, и мне нравится делиться своими знаниями, которые я получил, работая разработчиком с 2009 года. Я пишу рассказы о JavaScript, TypeScript, Angular и обо всем, что связано с жизнью разработчика. .

Вы можете подписаться на меня в Twitter и Instagram или подписаться на мою рассылку, которую я отправляю, когда публикую новую историю.

Happy Coding 🚀

Создавайте быстрые формы на основе JSON на Angular с помощью NGX Formly

Формы могут быть кошмаром — давайте сделаем их лучше

medium. com

Вам не нужен JavaScript Framework

Иногда React, Angular или Vue.js могут быть излишними

medium.com

2 способа устранения дублирования в массивах и объектах JavaScript

Знаете ли вы, как бороться с дублированием?

medium.com

7 шагов по докеризации приложения Angular 9 с помощью Nginx

Настройка Angular 9приложение в среде Docker и разверните его в кратчайшие сроки

medium.com

Scope in Python | Область действия переменной, время жизни

Использование функции определяет концепцию области действия в Python .

Если мы определяем переменную внутри функции или передаем значение параметру функции, значение этой переменной действительно доступно только внутри этой функции. Это называется размахом.

Другими словами, область действия — это область программы, в которой мы можем получить доступ к определенному идентификатору или переменной.

Это называется областью действия переменной или просто областью действия переменной.

Переменные, объявленные внутри программы, могут быть доступны не во всех местах этой программы. Это зависит от того, где мы объявили переменную в программе.

Большинство переменных, которые мы определяем в Python, являются локальными по отношению к их собственной функции или классу. Рассмотрим следующий пример кода ниже.

Пример 1:

 # Программа Python демонстрирует локальную область действия переменной.
определение локальной области видимости():
    имя = 'Джон'
    print(name) # Доступно.
# Основная программа.
print(name) # Недоступно, так как имя переменной здесь не определено.
localScope() # вызывающая функция.
 

 Выход:
      print(name) # Недоступно, так как имя переменной здесь не определено.
      NameError: имя «имя» не определено
 

В приведенном выше примере имя переменной, определенное внутри функции, будет доступно во всей этой функции. Таким образом, мы легко получили доступ и напечатали значение имени переменной в консоли.

Но когда мы обращались из основной программы, которая вызывает функцию, мы получили NameError. Это связано с тем, что переменная, определенная внутри функции, имеет локальную область видимости и видна только внутри функции, а не вне ее.

Область действия и время существования переменной в Python

---

Область действия переменной — это область программы, в которой переменная видна или доступна. Время жизни переменной — это время, в течение которого переменная существует в памяти. Существование и доступность зависят от объявления переменной в программе.

Например, время жизни переменной, объявленной внутри функции, равно продолжительности существования функции. Когда выполнение тела функции завершено, переменная, определенная внутри функции, будет уничтожена.

Типы области видимости переменных в Python

---

В Python существует два основных типа области видимости переменных . Это:

• Глобальная область действия
• Локальная область действия

Давайте разберемся с каждым типом области видимости переменных на примерах.

Глобальная область видимости в Python

---

Когда мы определяем переменную внутри основной программы, но вне тела функции, она имеет глобальную область видимости. Переменная, объявленная в основном теле программы или файла, является глобальной переменной.

В глобальной области глобальная переменная будет видна во всей программе или файле, а также внутри любого файла, который импортирует этот файл. Мы можем легко получить доступ к переменной, определенной в глобальной области видимости, из всех видов функций и блоков.

Давайте возьмем несколько важных примеров программ, основанных на глобальной области видимости в Python.

Пример 2: 

Давайте напишем программу на Python, в которой мы определим глобальную переменную и будем обращаться к ней как внутри функции, так и из основного тела программы.

 # Объявление глобальной переменной в глобальной области видимости.
х = 50
# Объявить простую функцию, которая печатает значение x.
защита showMe():
    print('Значение x из локальной области видимости = ',x) # вызов переменной x внутри функции.
# Основная программа.
showMe() # вызывающая функция.
print('Значение x из глобальной области видимости = ',x)
 

 Выход:
      Значение x из локальной области видимости = 50
      Значение x из глобальной области видимости = 50
 

В этом примере переменная x является глобальной. Мы получили к нему доступ как внутри функции, так и снаружи функции, потому что она имеет глобальную область видимости.

Локальная область действия

---

Переменная, определенная или созданная внутри тела функции или блока, имеет локальную область действия. Мы можем получить к нему доступ только внутри объявленной функции или блока, а не снаружи этой функции или блока.

По завершении выполнения тела функции или блока Python удаляет локальную переменную из памяти. Другими словами, локальная переменная существует в памяти, пока выполняется функция.

Рассмотрим следующий пример кода ниже, в котором мы определим локальную переменную внутри функции и получим доступ к ней внутри функции и снаружи функции.

Пример 3:

 def my_funct():
    msg = 'Доброе утро!' # локальная переменная с локальной областью видимости.
    print(msg) # доступ к локальной переменной изнутри функции.
моя_функция()
print(msg) # доступ к локальной переменной извне функции.
 

 Выход:
       Доброе утро!
       print(msg) # доступ к локальной переменной извне функции.
       NameError: имя «msg» не определено
 

Как видно из вывода, когда мы вызывали локальную переменную извне функции или основной программы, мы получили ошибку, потому что Python уничтожил локальную переменную после выполнения функции. То есть локальная переменная не существует вне функции.

---

Когда мы определяем переменную внутри функции, она никак не связана с другой переменной с таким же именем, используемой вне функции.

Однако переменная, определенная вне функции, будет прочитана внутри функции только в том случае, если функция не изменяет значение. Приведем пример.

Пример 4:

 # Создание переменной города и установка Нью-Йорка.
city ​​= 'Нью-Йорк' # глобальная область видимости.
защита showMe():
    city ​​= 'Dhanbad' # локальная область внутри функции.
    print('Город:',город)
# Вызов функции
Покажите мне()
print('City:',city) # доступ к глобальной переменной из глобальной области видимости.
 

 Выход:
      Город: Дханбад
      Город: Нью-Йорк
 

В приведенном выше программном коде мы сначала присвоили городу значение «Нью-Йорк», а затем вывели значение города на консоль после вызова функции.

Далее мы создали функцию с именем showMe(). Внутри функции showMe() мы определили переменную с тем же именем, что и у глобальной переменной, но со значением изменения.

Когда мы обращаемся к этой переменной, Python выводит на консоль значение изменения, а не значение глобальной переменной, потому что оно никак не связано с другой переменной с таким же именем, используемой вне функции.