Внеклассный урок — Простейшие тригонометрические уравнения: обобщения, таблицы значений x, примеры
Простейшие тригонометрические уравнения: обобщения, таблицы значений x, примеры
Уравнение sin x = a
Условия:
1) | a | ≤ 1
2) при | a | > 1 уравнение sin x = a не имеет решения среди действительных чисел.
Формула решения уравнения sin x = a:
x = (-1)n · arcsin α + πn где n – любое целое число (n ∈ Z). |
Частные случаи, когда уравнение sin x = а имеет более простое решение:
| |
|
|
|
|
|
|
Остальные значения x в уравнении sin x = а:
| | |
1 | π | 5π |
1 | π | 5π |
√2 | π | 3π |
√2 | π | 3π |
√3 | π | 2π |
√3 | π | 2π |
Уравнение cos x = a
Условия:
1) | a | ≤ 1
2) при | a | > 1 уравнение sin x = a не имеет решения среди действительных чисел.
Формула решения уравнения cos x = a:
x = ± arccos α + 2πk где k – любое целое число (k ∈ Z). |
Частные случаи, когда уравнение cos x = а имеет более простое решение:
| |
| π |
| |
| |
Остальные значения x в уравнении cos x = а:
|
| |
1 | π | π |
1 | 2π | 2π |
√2 | π | π |
√2 | 3π | 3π |
√3 | π | π |
√3 | 5π | 5π |
Уравнения tg x = a и ctg x = a.
Формула решения уравнения tg x = a:
x = arctg a + πk где a – любое действительное число (a ∈ R), k – любое целое число (k ∈ Z). |
Формула решения уравнения ctg x = a:
x = arcctg a + πk где a – любое действительное число (a ∈ R), k – любое целое число (k ∈ Z). |
Значения x в уравнениях tg x = а и ctg x = а:
|
| |
| | |
√3 | | π |
√3 | | π |
| | π |
| | π |
| √3 | π |
| √3 | π |
| | π |
Примеры.
1) Решим уравнение
√2
sin 3x = ——
2
Решение.
Для простоты заменим переменную 3x обобщенной переменной t. Итак:
3x = t .
Тогда наше уравнение принимает привычный вид:
√2
sin t = ——
2
Применяем формулу:
√2
t = (–1)n arcsin —— + πn
2
Находим значение арксинуса:
√2 π
arcsin —— = —
2 4
Подставляем это значение арксинуса:
π
t = (–1)n — + πn
4
Теперь вместо t вновь подставляем переменную 3x:
π
3x = (–1)n — + πn
4
Находим значение переменной, применяя правило деления дробей:
π π 1 πn π πn
x = (–1)n — : 3 + πn : 3 = (–1)n — ∙ — + —— = (–1)n —— + ——
4 4 3 3 12 3
Ответ:
π πn
x = (–1)n —— + ——
12 3
2) Решим уравнение
1
cos 2x = – —
2
Решение.
Напомним: решать пример будем по формуле
x = ± arccos a + 2πn.
Для простоты можем заменить 2x на t. Тогда наша формула примет вид t = ± arccos a + 2πn. Но в данном случае можем обойтись и без этого.
Итак, вычисляем значение арккосинуса:
1 2π
2x = ± arccos (– —) + 2πn = ± —— + 2πn
2 3
Находим значение x, применяя правило деления дробей:
2π 2π 1 2π π
x = ± —— : 2 + 2πn : 2 = ± —— ∙ — + πn = ± —— + πn = ± — + πn
3 3 2 6 3
Ответ:
π
x = ± — + πn
3
3) Решим уравнение
π √3
tg (4x – —) = ——
6 3
Решение.
Напомним: здесь мы применяем формулу
x = arctg a + πn.
Чтобы не запутаться при следующем шаге, заменим в формуле переменную x на переменную t:
t = arctg a + πn.
Далее отмечаем, что:
π
t = (4x – —).
6
Тогда наше уравнение принимает следующий вид:
π √3
4x – — = arctg —— + πn.
6 3
Находим значение арктангенса:
√3 π
arctg —— = —
3 6
Подставляем значение арктангенса в нашу формулу:
π π
4x – — = — + πn.
6 6
Находим значение 4x:
π π 2π π
4x = — + — + πn = —— + πn = — + πn
6 6 6 3
Осталось найти значение x, применяя правило деления дробей:
π π 1 πn π πn
x = — : 4 + πn : 4 = — ∙ — + —— = —— + ——
3 3 4 4 12 4
Ответ:
π πn
x = —— + ——, n ∈ Z
12 4
Частные случаи формул приведения и чётности или нечётности триг.
функций в упрощении выражений12+
4 месяца назад
Математика от Баканчиковой253 подписчика
Тригонометрия 8-11 класс. Как не допускать ошибок при упрощении тригонометрических выражений, применяя формулы приведения, свойства чётности, нечетности и периодичности тригонометрических функций? Сегодня мы ответим на этот вопрос. Если Вы не видели наши предыдущие уроки по теме: «Тригонометрические функции в алгебре», то обязательно посмотрите их, тогда этот урок будет Вам очень понятен. Мы покажем Вам два варианта применения формул приведения для упрощения выражений с тригонометрическими функциями, угол поворота которых находится в четверной координатной четверти. Поясним Вам, чем они отличаются. Обратим Ваше внимание на то, что в формулах приведения можно работать не только с острым углом. Но в этом случае формулы приведения нужно применять дважды. Разберём частные случаи чётности и нечётности тригонометрических функций в формулах приведения, незнание которых приводит к появлению ошибок при упрощении выражений.
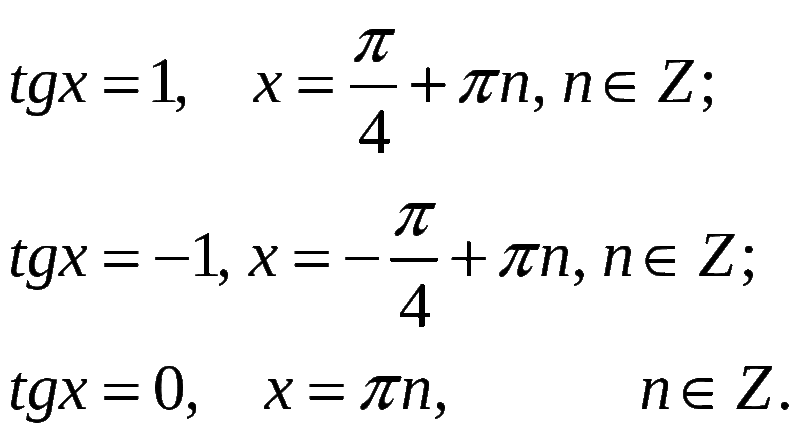17:36 Частные случаи чётности и нечётности тригонометрических функций при возведении их в степень.
17:40 Упростить выражение: 1) sin² (-α + π).
18:14 Упростить выражение: 2) sin³ (-α — π).
19:19 Упростить выражение: 3) sin² (-π + α).
20:13 Упростить выражение: 4) sin³ (-π + α).
21:13 Упростить выражение: 5) cos³ (-π + α).
22:52 На следующем уроке …
Если Вы впервые на нашем канале или не смотрели наши предыдущие уроки, то рекомендуем Вам посмотреть следующие видео:
Чётность, нечётность, периодичность и формулы приведения тригонометрических функций в упрощении выражений. Тригонометрия 8-11 класса. https://rutube.ru/video/51744cd6ca50799674225efa06f6b658/
Чётность и нечётность тригонометрических функций. Тригонометрия 8-11 класса. https://rutube.ru/video/862e199545ac877d9adb674ac6115cbc/
Чётность функции. Определение чётной функции. Является ли чётной функция. Свойства функции. Алгебра 7-11 класс. https://rutube.ru/video/00526d89c84dd14af604458fc65bca66/
Нечётность функции. Определение нечётной функции.
Особые случаи для тригонометрических корней
Решение: Первое уравнение можно записать как 2 sin [1 / 2] (x + y) cos [1 / 2] (x − y) = 2 sin [1 / 2] ( x + y) cos [1 / 2] (x + y)∴ Либо sin [1 / 2] (x + y) = 0, либо sin [1 / 2] x = 0, либо sin [1 / 2] y = 0 Таким образом, , x + y = −1, x − y = −1.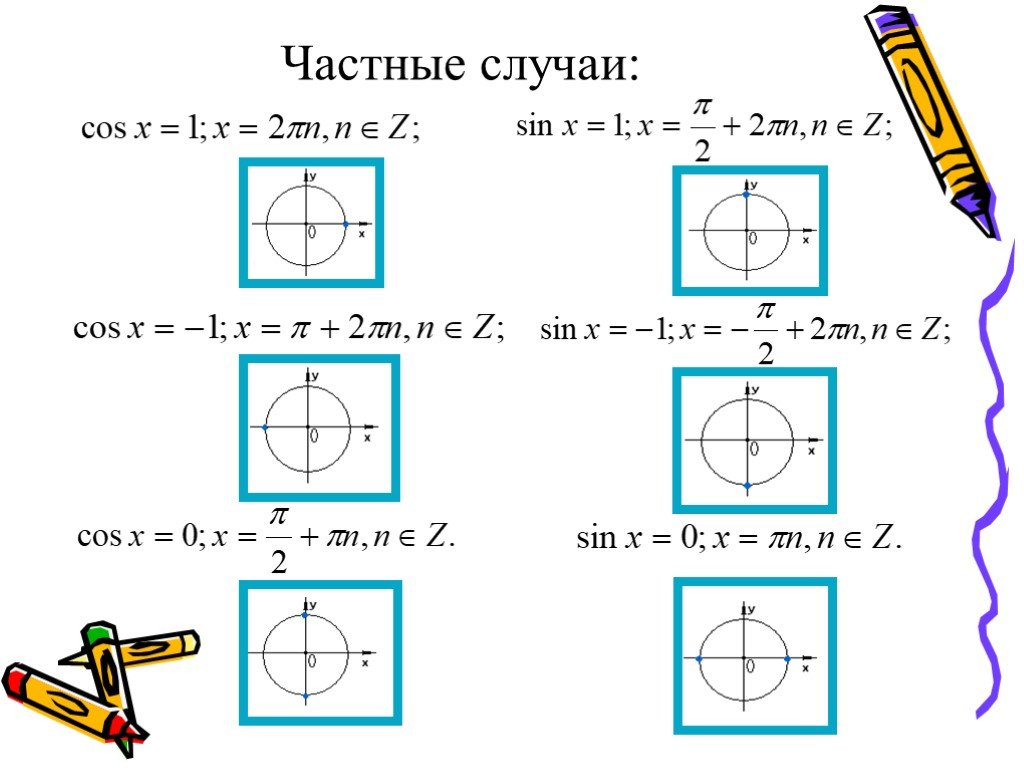
Когда x + y = 0, мы должны отклонить x + y = 1 и проверить с вариантами или x + y = −1 и решить его с помощью x − y = 1 или x — y = -1, что дает (1 / 2, -1 / 2) или (-1 / 2, 1 / 2) как возможное решение. Опять же, решая с x = 0, мы получаем (0, ±1) и решая с y = 0, мы получаем (± 1, 0) как другое решение. Таким образом, у нас есть шесть пар решений для −4, −3, −2, −1, 0, 1, 2, 3 и y.Пример 2: Общее решение sin x − 3 sin 2x + sin 3x = cos x − 3 cos 2x + cos 3x равно __________.
Решение:
sin x − 3 sin 2x + sin 3x = cos x − 3 cos 2x + cos 3x 2cosx — 3) — cos2x (2cosx — 3) = 0
⇒ (sin2x — cos2x) (2cosx — 3) = 0
⇒ sin2x = cos2x
⇒ 2x = 2nπ ± (π / 2 — 2x) 9000 т. е. x = [nπ/2] + [π/8]
Пример 3: Найдите решение следующего уравнения так, чтобы 0 ≤ x < 2π, 2sin 2 (x) − sin (x) + 3 = 4
Решение:
2 sin 2 (x) − sinx − 1 = 0
Далее мы факторизуем.
(2 sin (x) + 1) (sin (x) − 1) = 0
Приравняйте каждый множитель к нулю и решите.
2 sin (x) + 1 = 0 или sin (x) − 1 = 0
sin (x) = −1 / 2 sin (x) = 1
Определите углы, удовлетворяющие каждому решению за один оборот.
Углы 7π/6 и 11π/6 удовлетворяют первому, а π/2 удовлетворяют второму.
Пример 4: Решите следующее уравнение для 0 ≤ x < 2π, sin 2x = cos 2x
Решение:
Пусть u = 2x.
Теперь уравнение принимает следующий вид:
sin u = cos u
Функции синуса и косинуса равны при следующих углах.
и = π/4; 5π/4; 9π/4; 13π / 4
Эти углы делятся на 2 так, чтобы они находились в пределах диапазона.
2x = π/4; 2х = 5π/4; 2х = 9π/4; 2x = 13π / 4
Разделение каждого ответа на 2 дает
x = π / 8; 5π/8; 9π/8; 13π / 8
Пример 5: Решите уравнение для 0 ≤ x < 2π, 3 тангенс 2 x = 1
Решение:
3 тангенс 2 9103;
Разделите обе стороны на 3
tan 2 x = 1 / 3
Извлеките квадратный корень из обеих сторон.
тангенс х = ± 1 / √3
Это можно записать в виде двух отдельных уравнений
tan x = 1 / √3 и tan x = −1 / √3
Возьмем арктангенс
x = π / 6; 7π/6 и х = 5π/6; 11π / 6
Пример 6: Если cos θ + cos 7θ + cos 3θ + cos 5θ = 0, то каково значение θ?
Решение:
Объединение θ и 7θ, 3θ и 5θ, мы получаем
2 cos 4θ (cos 3θ + cos θ) = 0
4 cos 4θ cos 2os = 0
4 [(1 / 2 3 ) sinθ] (sin2 3 θ) = 0; sin 8θ = 0.
Следовательно, θ = nπ / 8
Читайте также: Обратные тригонометрические функции в математике
Сколько тригонометрических функций?
В математике 6 являются важной тригонометрической функцией. это синус, косинус, тангенс, косеканс, секанс, котангенс.
Чем полезна функция тригонометрии?
Тригонометрические функции очень полезны для изучения треугольника. Он используется в океанографии для расчета высоты приливов и отливов в океанах.
В. Что такое частный случай тригонометрии?
Ответ: Если любое уравнение тригонометрии не имеет точных корней. угол зависит от двух случаев, таких как
- интервал задан, тогда угол, удовлетворяющий уравнению в данном интервале
- интервал не задан, то общее решение может быть рассчитано для любого угла.
Вопрос Видео: Нахождение значений тригонометрических функций специальных углов
Стенограмма видео
Найдите точное значение греха 30 градусов.
Теперь вы, возможно, привыкли пользоваться калькулятором или компьютером при работе с
тригонометрические функции. Это связано с тем, что для большинства значений угла sin, cos и tan оцениваются как число с
много десятичных разрядов. Однако в некоторых случаях sin, cos и tan оцениваются как целое число или число.
что можно записать в виде дроби. Обычные случаи, с которыми вы можете столкнуться, относятся к нулю градусов, 30 градусам, 45 градусам.
Глядя на наш вопрос, мы видим, что у нас действительно есть один из этих случаев. Хотя тригонометрические функции тесно связаны с прямоугольными треугольниками, в В этом случае мы начнем с рассмотрения равностороннего треугольника. Мы знаем, что в любом равностороннем треугольнике все углы равны 60 градусов, а все стороны равны. Мы могли бы выбрать любую длину стороны для этого треугольника и получить правильный ответ. Тем не менее, мы собираемся выбрать два, чтобы упростить задачу позже.
Первое, что мы собираемся сделать с нашим треугольником, это разрезать его пополам линией.
перпендикулярно основанию. Теперь мы можем отбросить одну из половин нашего треугольника. При этом у нас остается новый прямоугольный треугольник. Поскольку и верхний угол, и основание были разделены пополам, мы знаем, что они равны половине
их первоначальных значений. Это оставляет нам верхний угол 30 градусов и основание 1.
Обозначим стороны нашего нового треугольника как 𝑎, 𝑏 и 𝑐.
Чтобы получить полную информацию об этом треугольнике, нам нужно найти длину стороны 𝑎, и мы можно сделать это с помощью теоремы Пифагора. Теорема утверждает, что для любого прямоугольного треугольника квадрат гипотенузы равен сумме квадратов двух других сторон.
Давайте подставим значения, которые у нас есть для 𝑏 и 𝑐. Возводя наши числа в квадрат, мы видим, что 𝑎 в квадрате плюс один равняется четырем. Вычитая единицу с обеих сторон, мы видим, что 𝑎 в квадрате равно трем. Наконец, извлекая квадратный корень из обеих частей, мы видим, что 𝑎 равно квадратный корень из трех.
Стоит отметить, что на самом деле у этого уравнения есть два решения. Можно сказать, что 𝑎 равно положительному квадратному корню из трех или отрицательному
квадратный корень из трех. В нашем случае 𝑎 — это длина, поэтому нас интересуют только положительные значения.
решение.
Теперь, когда мы нашли ответ, у нас есть завершенный прямоугольный треугольник. Треугольник может помочь нам решить такую задачу, используя тригонометрические тождество для синуса. Тождество говорит нам, что для любого прямоугольного треугольника грех угла 𝜃 равен равна длине стороны, противоположной этому углу, деленной на длину гипотенуза.
Из нашего треугольника видно, что угол действительно равен 30 градусам. Таким образом, мы можем написать, что грех в 30 градусов равен длине его противоположной стороны. сторона — это 𝑏 — разделить на длину гипотенузы — это 𝑐. Поскольку у нас есть эти значения, мы можем заменить 𝑏 единицей и 𝑐 двумя, что дает нам, что грех в 30 градусов равен одному больше двух или половине.
Теперь вам может быть интересно, почему мы нашли значение длины стороны 𝑎, поскольку это не было
участвует в расчете sin 30 градусов. Причина в том, что этот треугольник очень полезен при расчете некоторых
другие точные тригонометрические соотношения.