Градиент функции онлайн калькулятор: Градиент функции онлайн

Содержание

Оператор Гамильтона (набла) в Вольфрам Альфа

Ирландская юбилейная монета 10 евро.
К 200-летию со дня рождения ирландского
физика, астронома и математика У. Р. Гамильтона.

Характерной особенностью системы Вольфрам Альфа является то, что ее запросы не являются строго регламентированными. В большинстве случаев Вольфрам Альфа отлично понимает запросы на выполнение различных математических преобразований и операций, составленные на «естественном» английском языке. Это значит, что математические запросы к системе Вольфрам Альфа можно задавать разными способами. Довольно часто пользователю достаточно иметь лишь самое общее представление о той математической операции, которую он хочет выполнить. Если Вы сумеете сообщить системе Вольфрам Альфа при помощи простейших английских слов и выражений о том, что именно Вам нужно, то немедленно получите желаемый результат.

Это в равной степени касается как простых арифметических действий, так и самых сложных математических операций, например, таких, как применение дифференциальных операторов Гамильтона и Лапласа.

Оператор Гамильтона — это векторный дифференциальный оператор, компоненты которого являются частными производными по координатам. Название этого оператора связано с именем ирландского физика, астронома и математика Уильяма Гамильтона (Sir William Rowan Hamilton). Для записи оператора Гамильтона используется специальный символ «набла» (перевернутый треугольник), форма которого напоминает древнегреческий музыкальный инструмент «набла». Поэтому его другое название — оператор набла.

Оператор набла удобно рассматривать, как символический вектор, компонентами которого являются частные производные по координатам. Таким образом, применяя оператор набла достаточно следовать простым правилам, по которым выполняются различные операции над векторами.

Результат действия оператора набла зависит от того, к какому математическому объекту и как именно он применяется.

(3z)}

Калькуляторы на основе оператора Гамильтона

Кроме того, для удобства пользователей в Вольфрам Альфа имеются калькуляторы градиента, дивергенции и ротора, который выводятся по запросам:

grad calculator

divergence calculator

curl calculator или rot calculator

Вычисление поверхностного интеграла первого рода / Поверхностный интеграл / 3dstroyproekt.ru

Определение единичного вектора нормали к поверхности. Выражения для элемента площади поверхности

Предположим, что поверхность $\sigma $ задаётся неявным уравнением $\Phi (x,y,z)=0 (\Phi (x,y,z)$ — непрерывно дифференцируемая функция и взаимно однозначно проецируется в область $D_ { xy } $ на плоскости $\mathbf { \textit { Oxy } } $.

Из теории функций нескольких переменных известно, что градиент функции ортогонален поверхности уровня этой функции, проходящей через точку, в которой найден градиент. Рассматривая уравнение $\Phi (x,y,z)=0$ как уравнение поверхности уровня функции трёх переменных $\Phi (x,y,z)$, получаем, что в каждой точке поверхности $\sigma grad\Phi (x,y,z)$ ортогонален $\sigma $, т. 4 } { 3 } . $

Односторонние и двусторонние поверхности. Ориентация поверхности

Вычисление криволинейного интеграла первого рода. Плоский случай

Определение двойного интеграла

Выражение площади плоской области через криволинейный интеграл

Вычисление площадей плоских областей

Свойства криволинейного интеграла второго рода

Нормальные формы

Класс $L$. Теорема о замкнyтости класса $L$

Механические и физические приложения поверхностного интеграла первого рода

Свойства двойного интеграла

Критерий полноты {формулировка}. Лемма о немонотонной функции

Формула Грина

Теорема о полныx системаx в Pk

Вычисление объёмов

Огравление $\Rightarrow $

23 сентября 2016, 12:08 проектирование км, кмд, кж Поверхностный интеграл 0 10738 0

Калькулятор градиента | Математические онлайн-калькуляторы

Этот калькулятор находит градиент (наклон) прямой линии. Калькулятор градиента вычисляет градиент (наклон) прямой линии и предоставляет уравнение градиента и обработанные расчеты градиента для каждого расчета градиента. Обозначение для градиента m. Вас также может заинтересовать наш Калькулятор уклона.

4.NTIIZ4.NTIIZ4.NTIIZ4.NONTIGALIGINAT

Калькулятор градиента
Калькулятор градиента Точность (десятичные разряды)01234567891011112131415
1 ^ST Горизонтальная координата (x ₁)
1 ^ST Вертикальная координата (Y ₁)
2 ^{NO HORESTIRIIZ}
2 ^и Вертикальная координата (Y ₂)
Восстание (вертикальная высота) (V) M
пробег (горизонтальная высота) (ч) M
Грагент (M) (M) (M) (M) (M) (M) (M) (M) (M) (M) (M) (M) (M) г) °

G =
G = .

0014 horizontal coordinate (x ₁ )

Gradient Calculator Results (detailed calculations and formula below)
Gradient Description

The Gradient Rise is m
The Gradient Run is m
Градиент °
Рост градиента расчет
v = y ₂ — y ₁ v = — v =
The slope of a Gradient calculation
h = x ₂ — x ₁ h = — h =
Gradient calculation
g = V / H G = / G =
1 ^st vertical coordinate (y ₁ )
2 ^nd horizontal coordinate (x ₂ )
2 ^ND Вертикальная координата (Y ₂)
Восстание (вертикальная высота) (V) M
RUN (горизонтальная высота) (H) M
Gradient (M) (G) °

Мы надеемся, что калькулятор градиента помог вам понять и рассчитать свойства градиента. Если у вас есть время, пожалуйста, оцените калькулятор градиента, так как обратная связь всегда приветствуется.

★ ★ ★ ★ ★ [ 18 Votes ]

About the Gradient Calculator

The Gradient calculator allows you to calculate any component of a Gradient, vertical/horizontal coordinates, rise, run и/или Градиент, введя известные величины Градиента.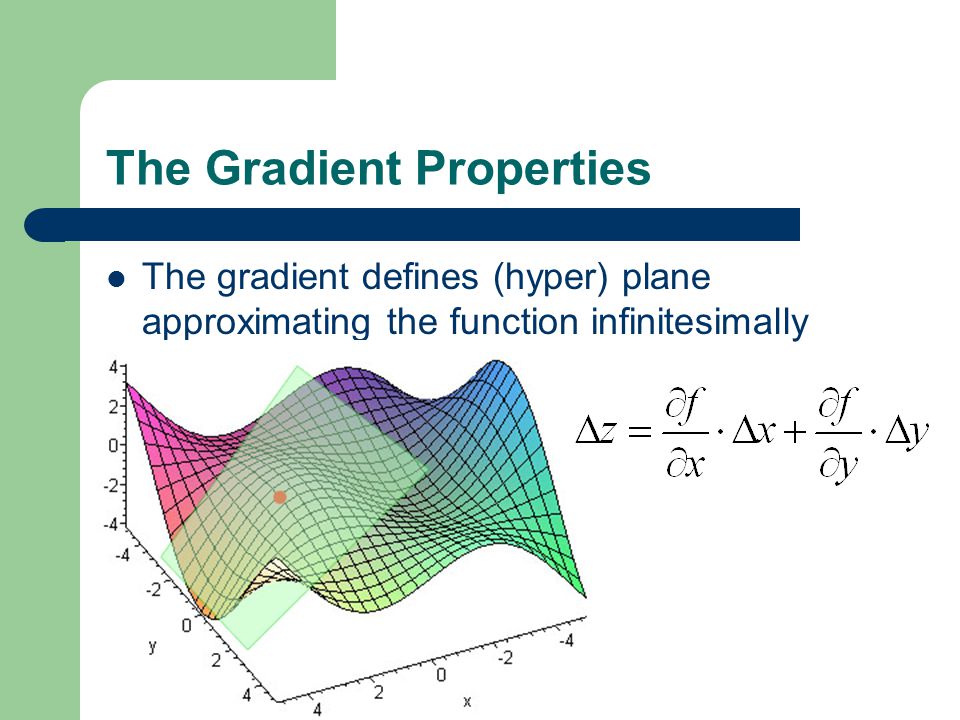 Вы можете рассчитать недостающие координаты в градиенте, подъем градиента, прогон градиента и любую математическую величину, связанную с расчетами градиента.

Свойства градиента

Линия с уклоном слева направо имеет положительный градиент

Линия с наклоном вниз слева направо имеет отрицательный градиент

Градиент вертикальной линии не определен

Градиент горизонтальной линии 0

Обозначение уклона м

Вас также может заинтересовать наш Калькулятор уклона.

Уравнения градиента

Калькулятор градиента включает следующие формулы

Уравнение для расчета повышения градиента

Восстание = Y ₂ — Y ₁

Уравнение для расчета наклона градиента

пробег = x ₂ — x ₁9

9015 2 — x _{16399999 9015 9015. Расчет градиента на основе уклона и подъема Градиент = подъем / пробег
Уравнение градиента Свойства и значения
x0273
x ₂ : Вторая горизонтальная координата, влияет на подъем и уклон
y ₁ : Первая вертикальная координата, влияет на подъем и уклон
y ₂ : Вторая вертикальная координата, влияет на подъем и уклон Градиент
Подъем: высота по вертикали, влияет на y2 и градиент
Прогон: высота по горизонтали, влияет на x2 и градиент
Градиент: размер градиента, влияет на подъем и y2
Калькулятор градиента с шагами — определение
Компания CalCon разработала калькулятор градиента, инструмент для расчета градиента.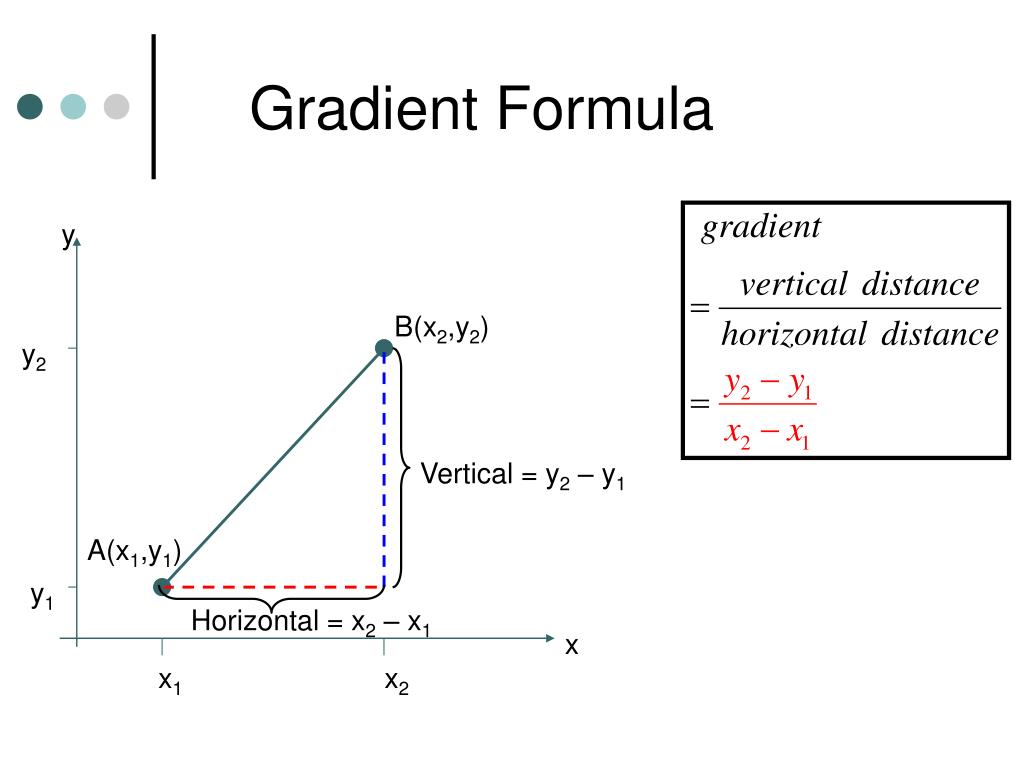 Вы знаете, что такое градиент? Звучит интересно, не так ли? С помощью этого калькулятора вы узнаете, как вычислить уклон линии, проходящей через два места, что такое свойства градиента, как рассчитать уклон посреди леса и многое другое.
Кроме того, в этой статье кратко рассказывается о том, какие градиенты у нас есть, как рассчитать градиент по специальной формуле и как рассчитать его шаг за шагом. Позже мы сделаем несколько примеров для практики.
Пока вы здесь, ознакомьтесь с другими нашими математическими калькуляторами, такими как Калькулятор сферических координат и Калькулятор касательной.
Градиент (наклон) в математике – Определение
Наклон ( м ) кривой – это еще один термин для градиента. Например, тангенс угла равен наклону или градиенту плоскости, наклоненной под этим углом. Кроме того, чем острее линия в том месте, где градиент графика выше. Отрицательный градиент указывает на нисходящий уклон. Более того, мы можем определить градиент геометрически для любых двух точек на линии ( x1,y1 ), ( x2,y2 ).
Более того, градиент — это переменная, которая помогает понять изменчивость одной величины по отношению к другой. Более того, градиент функции f(x) определяется с помощью ее первой производной:
\frac{d}{dx} {f}{(x)}

Подводя итог предыдущим предложениям, мы имеем:
m=\tan\theta=\frac{{y2}-{y1}}{{x2}-{x1}}
Мы используем «вертикальный сдвиг» для « горизонтальное смещение» между (любыми) двумя уникальными точками на линии для вычисления наклона. Иногда мы можем записать отношение как делитель («подъем над пробегом»). Он также дает одно и то же значение для каждых двух разных точек на одной линии. «Подъем» падающей линии отрицателен. Дорожный инспектор может нарисовать линию, или она может появиться на схеме, изображающей дорогу.
Расширенная математика определяет градиент линии в точке как градиент касательной линии в этой точке. Когда линия представлена последовательностью точек на схеме или списком координат точек, ее можно определить между любыми двумя указанными точками.
Всякий раз, когда мы представляем линию как непрерывную функцию, такую как алгебраическая формула, дифференциальное исчисление дает правила, которые дают уравнение для части кривой.
Математики обычно используют простые дроби для выражения градиента. Также они измеряют его как пропорцию или десятичное значение.
Свойства градиента
Ниже приведен список характеристик градиента, который поможет вам понять ориентацию линии:
Значение градиента может быть потенциально положительным или отрицательным.
Градиент оси X равен 0, поскольку наклон горизонтальной линии равен нулю.
Градиент оси Y не определен, так как наклон вертикальной линии не определен.
Наклон кривой в каждой точке кривой равен наклону ее касательной в определенной точке.
Две параллельные линии имеют одинаковый уклон. m1=m2
И, наконец, произведение градиентов двух перпендикулярных линий равно -1.
Types of Gradient
There are six types of gradient:
Ruling gradient
Limiting gradient
Exceptional gradient
Minimum gradient
Average gradient
Floating gradient
Gradient Formula
To compute gradient или уклон, отношение подъема (изменение по вертикали) к длине (изменение по горизонтали) должно быть рассчитано между двумя точками на линии.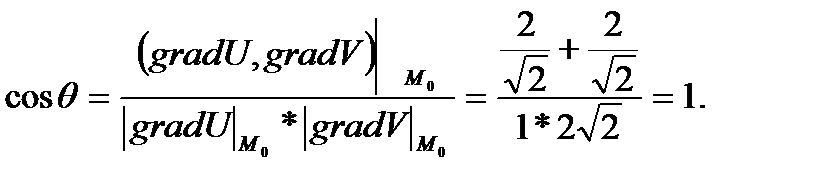 Поэтому вы можете сделать это с помощью этой формулы:
m=\frac{rise}{run}=\frac{{y2}-{y1}}{{x2}-{x1}}
Расчет градиента (наклона) – шаг за шагом
Вам нужны две точки от линии, чтобы определить ее наклон: ( x1, y1 ) и ( x2, y2 ). Формула для расчета наклона между двумя точками:
наклон=\frac{{y2}-{y1}}{{x2}-{x1}}
Но если у вас нет уравнения для прямой линии, есть три части для расчета ее наклона:
Во-первых, определите две точки: начальную точку и пункт назначения.
Определение наличия положительного или отрицательного градиента.
Градиент можно выразить в процентах. Резкое изменение появляется вверху, тогда как горизонтальное изменение появляется внизу. Его можно записать так:
\frac{rise(y)}{run(x)}
Градиент линии
Мы выбираем два места на линии, чтобы определить наклон прямой линии. Во-первых, мы делаем расчет на основе этих двух точек: разница высот (координаты y), деленная на разницу ширины (координаты x). Кроме того, если решение является положительным числом, линия идет вверх. Если ответ отрицательный, линия идет вниз.
Кроме того, градиент линии указывает на то, насколько крута прямая линия. Градиент обозначается символом м в данной формуле горизонтального пути,
y=m\cdot x + c
Градиенты могут быть положительными или отрицательными, но мы всегда наблюдаем их по часовой стрелке.
Диаграмма наклона (наклона)
На нормальном графике оси x – и y перпендикулярны и дают четыре прямых угла. Наклон графика только с x и y линий всегда составляют 90 градусов. Это связано с тем, что мы определяем наклон как положительное сечение оси x (два вертикальных квадранта графика), пока оно не достигнет линии. Поскольку ось y — единственная другая линия на графике, наклон охватывает весь правый верхний квадрант, что составляет 90 градусов. Любая горизонтальная линия имеет подъем 0, а любая вертикальная линия имеет подъем 90.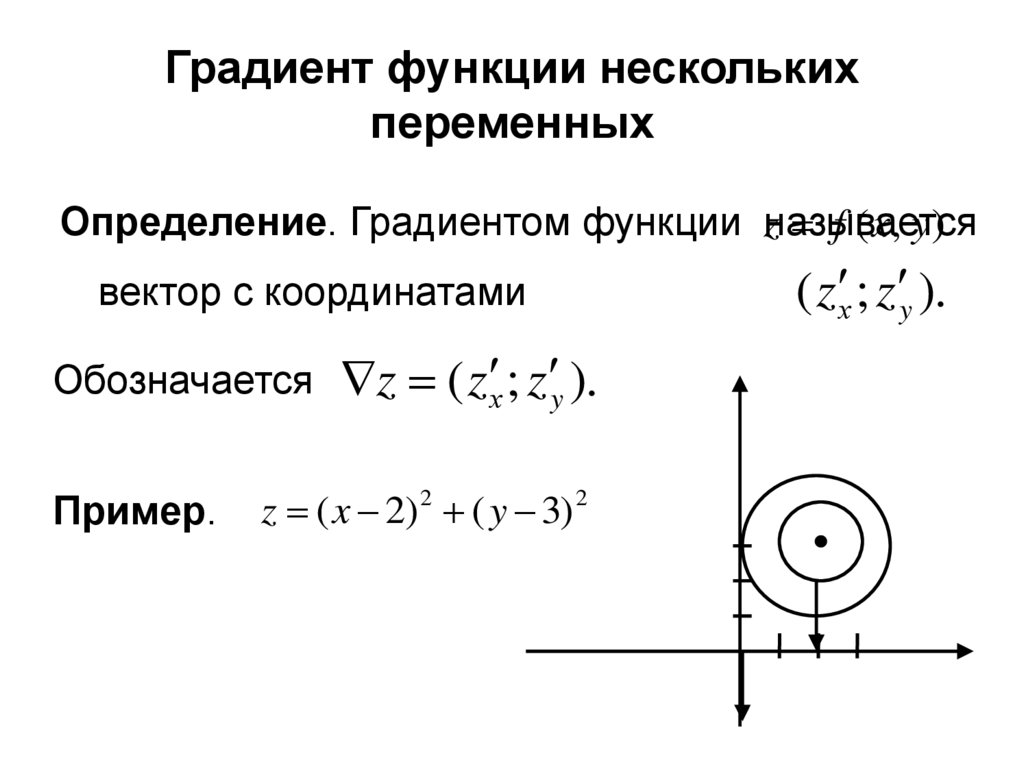 Ничего не стоит то, что горизонтальные линии отражают 9ось 0304 x , а вертикальные линии отражают ось y .
Вектор градиента
Мы можем рассматривать «направление и скорость наибольшего увеличения» как вектор градиента. Всякий раз, когда путь наклона – это путь, по которому функция быстрее всего возрастает от 90 304 p 90 305 , а величина наклона – это скорость роста в этом направлении, наибольшая абсолютная производная по направлению, если наклон функции отличен от нуля в точка p .
Кроме того, если и только если точка неподвижна, градиент является нулевым вектором (где производная равна нулю). В результате градиент важен в теории оптимизации, в которой использование градиентного восхождения приводит к максимизации функции.
Slope Conversion Table
Horizontal to Vertical slope ratio 1/4 1/2 3/4 1 1-1/4 1-1/2 1 -3/4 2 2-1/2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
Percent slope 400 200 133 100 80 67 57 50 44 33 25 20 16. 7 14.3 12.5 11.1 10.0 9.1 8.3 7.7 7.1 6.7 6.3 5.9 5.6
Degrees slope 76.0 63.4 53.1 45.0 38.7 33.7 29.7 26.6 24.0 18.4 14.0 11.3 9.5 8. 1 7.1 6.3 5,7 5,2 4,8 4,4 4,1 3,8 3,6 3,4 3,2
дюйма на ногу 486 486 486 486 486 486 486 486 486 486 486 486 486 486 486 486 486 486 486 486 486 486 486 486 486 486 486 486 486 486 486 486 486 486 486 486 486 486 486 486 486 486 486 486 486 486 486 486 486 486
.0436 24 16 12 9.6 8 6.9 6 5.3 4 3 2. 4 2.0 1.7 1.5 1.3 1.2 1.1 1,0 0,92 0,86 0,80 0,75 0,71 0,67
15.0304 x1, y1
) и ( x2, y2 ). Во-первых, давайте представим, что мы хотим найти наклон линии, проходящей через набор точек (5, 2) и (3, 7).
Введите параметры первой точки как x1 и y1 в калькулятор.
Теперь сделайте то же самое с параметрами второй точки. Просто переключитесь на x2 и y2 .
И последнее, но не менее важное: калькулятор рассчитает уравнение наклона и рассчитает его автоматически.
\frac{{7}-{2}}{{3}-{5}}=-2,5
Калькулятор градиента – практические примеры
Соединенное Королевство использует коэффициенты для описания крутизны на дорожных знаках. В этом случае дорожный знак отображает соотношение 1:3. Первое значение относится к изменению расстояния по вертикали, а второе значение относится к пройденному расстоянию по горизонтали. По сравнению с полностью ровной дорогой соотношение 1:3 указывает на то, что на каждые три единицы, пройденные по горизонтали, дорога поднимается на одну единицу выше. В заключение мы выражаем это как наклон 1/3 в математическом классе.
Часто задаваемые вопросы
Что означает градиент в математике?
Математики используют градиент в качестве дифференциального оператора в математике для трехмерной вектор-функции, чтобы получить вектор с тремя компонентами, которые также являются дробными производными функции относительно ее трех параметров.
Как рассчитать градиент на топографической карте?

При расчете уклона на топографической карте важно понимать, что термины «градиент» и «уклон» эквивалентны. Это связано с тем, что структура земли проявляется в сдвиге градиента, который происходит внутри определенного места на карте. В результате геологи и экологи могут установить, влияет ли уклон обозначенной территории на окружающие территории. Кроме того, эрозия является прекрасным примером того, почему важно понимать наклон конкретных мест.
Как рассчитать градиент потока?
Градиент русла ручья называется градиентом ручья. Это вертикальное падение потока на горизонтальном расстоянии. Мы можем использовать следующее уравнение для его вычисления: Gradient=\frac{изменение высоты}{расстояние}
Обычно мы представляем его в футах на милю или метрах на километр. Уклоны потока часто сильнее в верховьях (где поток начинается) и ниже в устье (где он впадает в какой-либо другой водоем) (например, в океан).
Как рассчитывается градиент в географии?
Используйте вертикальные данные для расчета разницы высот между точками, затем используйте масштаб на карте для измерения горизонтального расстояния от точки A до B.
No related posts.}