Тест синергия математика: Тесты по математике (Синергия) — Помощь студентам

Дискретная математика — бесплатные ответы на тест Синергия ☛ Helpstudent24.ru

Если на множестве всех треугольников на плоскости рассматривается отношение
подобия, то данное отношение является отношением …

• толерантности
• порядка
  
• эквивалентности+

Матрица смежности для графа

1
2
3+

Полный неориентированный граф с числом вершин n=4 …
обладает эйлеровым циклом
не обладает эйлеровым циклом+
может обладать эйлеровым циклом — это зависит от числа дуг

Полный неориентированный граф с числом вершин, равным n, имеет …ребер

1
2+
3
4

Если на множестве М задано отношение А «х знаком с у», тогда на основе данного соотношения нельзя разбить множество М на непересекающиеся классы, потому что
отношение А …
нерефлексивно
несимметрично
нетранзитивно+
не антирефлексивно

Пустое множество θ … подмножеством некоторого множества
будет собственным
будет несобственным+
не будет никаким
не всегда является

Количество «нулевых» значений таблицы истинности формулы XYZvXYZvXYZ составляет…

0
5+
3

Отношение «х — победитель у» является …
антирефлексивным
симметричным
транзитивным
антисимметричным+

Если на множестве М задано отношение А «х знаком с у», тогда на основе данного соотношения нельзя разбить множество М на непересекающиеся классы, потому что
отношение А …
нерефлексивно
несимметрично
нетранзитивно+
не антирефлексивно

Бинарное отношение, заданное на множестве натуральных чисел соотношением X =
Y(mod3) (остатки отделения на 3 равны), является отношением …
толерантности
порядка
эквивалентности+

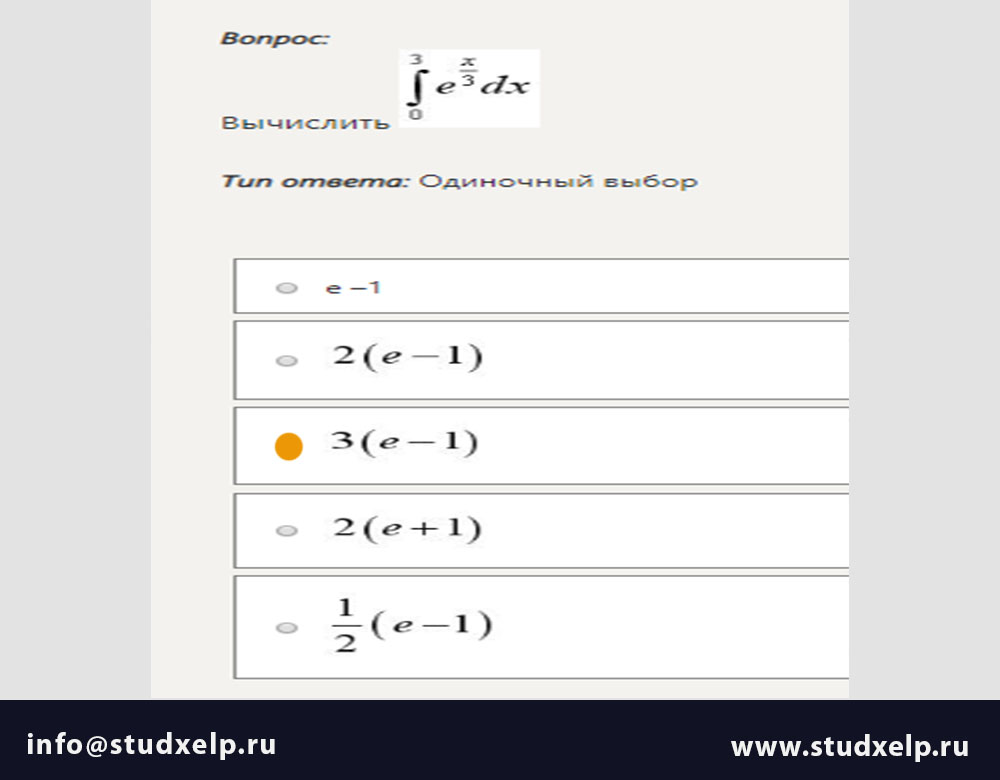
Значение X, определяемое уравнением

1+
2
3

Высказывание «Если а — четное число, b — нечетное число, то их произведение делится на 2» в символической… форме имеет вид «…»

1
2
3+
4

Если выразите конъюнкцию АvВ через импликацию и отрицание, получим:

1+
2
3

Если заданы два нечетких отношения R1 и R2 :

, то результат операции пересечения равен

1
2
3
4+

Конечное множество, состоящее из n элементов, имеет …
1 несобственное подмножество+
2 несобственных подмножества
n несобственных подмножеств
n2 несобственных подмножеств

Граф … обладает эйлеровым циклом

G1
G2
G3+
G4

Отношение |x-y|<1 , заданное на множестве действительных чисел, является отношением . толерантности порядка эквивалентности

• отношением
• толерантности
• порядка
  
• эквивалентности+

Решите уравнение

1
2
3
4+

Хроматическое число графа равно

6
3+
2
1

Если из высказывания S1 следует S2 и, наоборот, из S2 следует S1 , то высказывания
S1 и S2 … эквивалентными
являются+
не являются
могут являться, а могут и не являться

Дистрибутивные законы булевой алгебры и алгебры действительных чисел …
совпадают+
не совпадают
совпадают в частном случае

Если даны два высказывания — S1 («Если треугольники равны, то равны их
стороны») и S2 («Стороны треугольников равны тогда и только тогда, когда равны
треугольники»), — то можно утверждать, что …
из S1 следует S2
из S2 следует S1+
ни одно из высказываний не следует из другого

Если заданы два нечетких множества – А=1 |x1 +0,3 |x2 +0,1|хз И В = 0,7 |x1 +0 |x2 +0,5 |хз , то результат операции пересечения равен
1 AnB = l|x1 + 0. 3|x2+0.1|х3
2 AnB =l|x1+0,3|х2+0,5|х3
3 AnB = 057|X1 + 0|х2 + 0.1|х3
4 AnB =0,7|x1 + 0|х2 + 0.5|х3
1
2
3+
4

Решите уравнение

1
2
3
4+

Решите уравнение

1
2+
3
4

Решите уравнение

1
2
3+
4

Логической функции f (0,0,0) = f(0,0,l) = f (1,0,0) = 1
соответствует формула алгебры высказываний

1
2
3+

Отношение ««быть старше»: «х старше у»» является …

• рефлексивным
• симметричным
  
• транзитивным+
  
• антисимметричным

Пусть А=1.В = 1. С = 1. К = (А —>В)лС л(А <->С) тогда

К=-1
К=1+
К=0

Пусть … тогда …

Выражение S=(A→B)Λ(B→С)->(A→C)… высказыванием

является тождественно истинным+
является тождественно ложным
является переменным
не является

Если А — множество всех книг во всех библиотеках России, а В — множество всех книг в библиотеке МГУ по различным отделам науки и искусства, тогда А\В есть множество …

• всех книг в библиотеках России без книг по различным отделам науки и искусства в МГУ+
• книг по искусству в библиотеке МГУ
• всех книг в российских библиотеках
• книг в библиотеке МГУ по искусству и науке, кроме математических

Выражение S = (ABvB)<->B .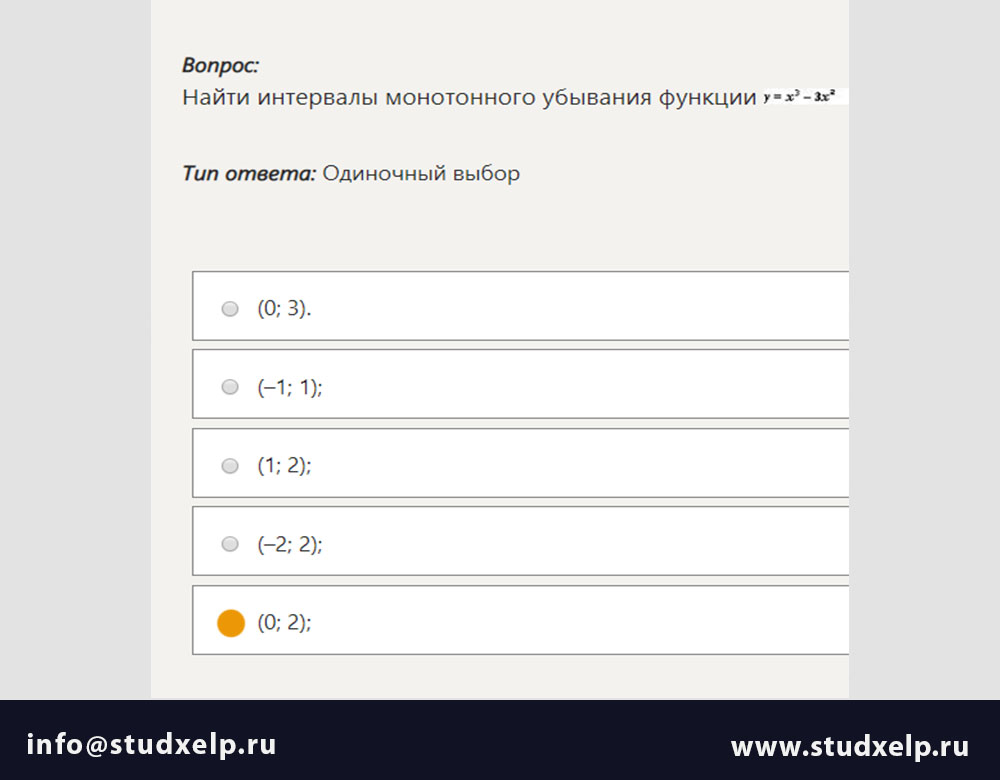 .. высказыванием

• является тождественно истинным
• является тождественно ложным+
• является переменным
• не является

Если отношение А на множестве М рефлексивно, симметрично и транзитивно, то разбить множество М на непересекающиеся классы …

• можно+
• нельзя
• можно, но не всегда
• можно только в том случае, если А — отношение порядка

Количество «единичных» значений таблицы истинности формулы (Xv YvZXXv YvZXXv Y vZ)

0
5+
3

Граф … содержит эйлерову цепь, соединяющую две различные вершины

G1
G2
G3
G4+

Преобразовывая формулу S-AnBuCnBuA
1 (An(BuC)nB)uA
2 (AnB)u(Cn(BuA))
3 AH(BU(COB)UA)
4 (AnB)u(CnBM
, нужно производить операции в следующем порядке:

1
2
3
4+

Если заданы два нечетких отношения R1 и R2 :

то результат операции, дополнения R1 равен

1
2+
3

Если заданы два нечетких множества — A = 1| Xl +0,3 |x2+0,l|x3 и B = 0,7|Xl +0|х2
+0,5|x3 , то результат операции

1
2
3+
4

Высказывание «Произведение целых чисел а и b не делится на 2 в том и только в том случае, если а или b

1 С<->АлВ 2 C<->AvB 3 А АВ —> С 4 А лВ vC нечетное» в символической форме имеет вид

1
2+
3
4

Высказывание «Неверно, что первым пришел Петр или Павел» может быть интерпретировано как сложное
1 AvBl
2 AvB
3 АлВ
4 АлВ
высказывание и записано формулой «…»

1
2+
3
4

Полный неориентированный граф с числом вершин п = 5 …
обладает эйлеровым циклом+
не обладает эйлеровым циклом
может обладать эйлеровым циклом — это зависит от числа дуг
может обладать эйлеровым циклом — это зависит от количества вершин с нулевыми
степенями

Если отношение А на множестве M рефлексивно, симметрично и транзитивно, то
разбить множество M на непересекающиеся классы…
можно+
нельзя
можно, но не всегда
можно только в том случае, если А — отношение порядка

Можем решить этот и любой другой тест Синергия. Для заказ необходимо обратиться к менеджеру. Все контакты указаны на сайте, можете выбрать любой удобный.

Другие тесты Синергии:

• Макроэкономическое планирование и прогнозирование
• Маркетинг
• Маркетинговые исследования
• Методы и средства проектирования информационных систем и технологий
• Муниципальное управление и местное самоуправление
• Муниципальное право

Ответы на тест Вступительный Математика Синергия Вариант 1

Выбери предмет

Технические

Авиационная и ракетно-космическая техника

Автоматизация технологических процессов

Автоматика и управление

Архитектура и строительство

Базы данных

Военное дело

Высшая математика

Геометрия

Гидравлика

Детали машин

Железнодорожный транспорт

Инженерные сети и оборудование

Информатика

Информационная безопасность

Информационные технологии

Материаловедение

Машиностроение

Металлургия

Метрология

Механика

Микропроцессорная техника

Начертательная геометрия

Пожарная безопасность

Приборостроение и оптотехника

Программирование

Процессы и аппараты

Сварка и сварочное производство

Сопротивление материалов

Текстильная промышленность

Теоретическая механика

Теория вероятностей

Теория игр

Теория машин и механизмов

Теплоэнергетика и теплотехника

Технологические машины и оборудование

Технология продовольственных продуктов и товаров

Транспортные средства

Физика

Черчение

Электроника, электротехника, радиотехника

Энергетическое машиностроение

Ядерные физика и технологии

Другое

Естественные

Агрохимия и агропочвоведение

Астрономия

Безопасность жизнедеятельности

Биология

Ветеринария

Водные биоресурсы и аквакультура

География

Геодезия

Геология

Естествознание

Землеустройство и кадастр

Медицина

Нефтегазовое дело

Садоводство

Фармация

Химия

Хирургия

Экология

Гуманитарные

Актерское мастерство

Английский язык

Библиотечно-информационная деятельность

Дизайн

Документоведение и архивоведение

Журналистика

Искусство

История

Китайский язык

Конфликтология

Краеведение

Криминалистика

Кулинария

Культурология

Литература

Логика

Международные отношения

Музыка

Немецкий язык

Парикмахерское искусство

Педагогика

Политология

Право и юриспруденция

Психология

Режиссура

Реклама и PR

Религия

Русский язык

Связи с общественностью

Социальная работа

Социология

Физическая культура

Философия

Французский язык

Этика

Языки (переводы)

Языкознание и филология

Экономические

Анализ хозяйственной деятельности

Антикризисное управление

Банковское дело

Бизнес-планирование

Бухгалтерский учет и аудит

Внешнеэкономическая деятельность

Гостиничное дело

Государственное и муниципальное управление

Деньги

Инвестиции

Инновационный менеджмент

Кредит

Логистика

Маркетинг

Менеджмент

Менеджмент организации

Микро-, макроэкономика

Налоги

Организационное развитие

Производственный маркетинг и менеджмент

Рынок ценных бумаг

Стандартизация

Статистика

Стратегический менеджмент

Страхование

Таможенное дело

Теория управления

Товароведение

Торговое дело

Туризм

Управление качеством

Управление персоналом

Управление проектами

Финансовый менеджмент

Финансы

Ценообразование и оценка бизнеса

Эконометрика

Экономика

Экономика предприятия

Экономика труда

Экономическая теория

Экономический анализ

EVIEWS

SPSS

STATA

Синергия Арифметика – Метафорическая математика

Опубликовано 28 января 2020 г. 28 января 2020 г. автором Meta

Арифметика  (от греческого arithmos , «число» и tike [techne] , «искусство») – обычно определяется как изучение чисел и манипулирование ими с помощью процессов сложения, вычитания, умножения и разделение.

Синергия (образовано от греческого слова синергос «работаем вместе») — это концепция, согласно которой целое больше, чем сумма частей.

Синергия Арифметика — парадоксальный принцип.

Некоторые базовые уравнения, не поддающиеся арифметическим соглашениям, включают 1 + 1 = 1 или

1 + 1 = 3 в зависимости от контекста. На первый взгляд, эти уравнения являются неточными расчетами, но есть определенные исключения из обычного подсчета, когда эти утверждения верны.

Одна капля дождя, добавленная к другой капле дождя, объединяется в одну каплю дождя. И наоборот, мужчина и женщина объединяются, чтобы создать семейную единицу из трех или более человек. Слияние двух компаний потенциально может использовать их объединенные активы для достижения гораздо более высоких результатов, чем каждая из них могла бы достичь в одиночку, а группы людей, объединенных общей целью, могут разрабатывать и внедрять решения, которые приносят огромные результаты, и в этом случае можно даже представить, как 1 + 1 = ∞ .

Математика переплетается с наукой, и обе области постоянно стремятся понимать, доказывать и объяснять фундаментальные законы Вселенной, которые управляют наше существование. Многие общепринятые истины, которые мы с легкостью принимаем в настоящее время, были не так давно считалось абсурдом. Наше знакомство с идеями влияет на наше когнитивное понимание и частота воздействия имеют тенденцию подтверждать то, что мы верим в будь настоящим.

Исторический Контекст

Рассмотрим понятие отрицательных чисел. До 18 ^го века европейские математики отказался принимать отрицательные числа и назвал эту идею «абсурдной» и «бессмысленной». хотя ученые в Индии и Китае уже использовали отрицательные числа на века. Такие настроения сохранялись и в 19 веке, когда подобные было оказано сопротивление идеям мнимых и иррациональных чисел как а также понятие бесконечности – все они общеприняты и часто используется в областях физики, химии, биологии и финансов сегодня.

Во второй половине 20

-го -го века концепции 1 + 1 = 3 и 1 + 1 = 1 стали все более распространенными для описания определенного поведения в областях экономики, бизнеса и социальных наук. , хотя до недавнего времени синергетические выражения игнорировались как не основанные на истинной математике.

В то время как традиционная арифметика широко использовалась и признавалась на протяжении тысячелетий, лидеры мысли в наше время все чаще ставят вопросы, касающиеся более широкого круга парадоксов, присущих традиционной школе арифметической мысли. Исследователи и математики Марк Бургин и Гюнтер Мейснер официально представили несколько формул, которые подтверждают достоверность синергетической арифметики в некоторых ситуациях. Всем любителям математики и исследований я предлагаю прочитать их статью о синергетической арифметике в экономике в журнале Applied Mathematics за 2017 год.

Заключение их исследования говорится: «Хотя в течение длительного времени эти [Synergy Арифметические] выражения считались математически бессмысленными, покажем что они математически правильны в какой-то недиофантовой арифметике или в предарифметика. Поэтому эти выражения одобрены и разрешены математические законы и способны отражать явления в экономике и физика».

Вот так поскольку я собираюсь рассматривать эту идею с точки зрения традиционных математических доказательств, но я только начинаю обосновывать преимущества применения Synergy Арифметика в моей жизни. Я намереваюсь более подробно изучить различные социальные примеры. глубины, а также в ходе математического проекта 2020 года.

Хотя в начале декабря 2019 года у меня не было ни названия, ни четкого объяснения этому парадоксу, идея метафорической математики родилась из наблюдения возможности того, что вычитание умножает изобилие .

Когда я начал глубже погружаться в то, как математика может быть использована для описания драматических результатов, которые я испытал в своей жизни, я стал все более и более очарован парадоксами. Кажется, это уравнение может подпадать под определение синергии, так как -1 + 1 = 1 900 10 или больше, а не ноль.

На всей территории 2020, я буду исследовать и представлять свои выводы, стремясь доказать, как операция вычитания может быть использована для получения положительных и даже драматических результатов. результаты в жизни отдельных людей, сообществ и бизнеса – независимо от того, мы рассматриваем индивидуального предпринимателя или сотрудника крупной корпорации. Синергия кажется ключевым драйвером.

Кови 6 ^th Привычка

Основные моменты Стивена Кови Синергия как 6-я ^-я -я привычка и венчающее достижение предыдущих 5 основополагающих привычек высокоэффективных людей. Он также тесно связывает синергию с экологией, которая описывает, как вся природа взаимосвязана и синергична.

Потенциал синергии заключается в способности оценить различия.

Такое мышление чрезвычайно ценно в отношениях, где заложен потенциал сотрудничества. Когда ты сможешь распознать что два человека могут иметь противоположные взгляды или методы, но оба могут быть правильными подходами для достижения той же конечной цели вы получаете более высокий уровень перспективы. Этот может допускать оркестровку нескольких людей и частей, каждый из которых вносит свой вклад свои уникальные силы и таланты в создание искусной симфонии, громкость реверберирует громче и дальше, чем любой отдельный инструмент когда-либо мог самостоятельно.

Синергия процветает в условиях свободы. Слишком много правил и ожидания подавляют потенциал творчества, а творчество ключевой компонент синергетического сотрудничества с другими. Сила Командная работа заключается в том, что каждый член вносит свой уникальный набор сильных сторон и точки зрения, заполняя пробелы в знаниях и навыках, которые могут помешать единственный член от достижения цели.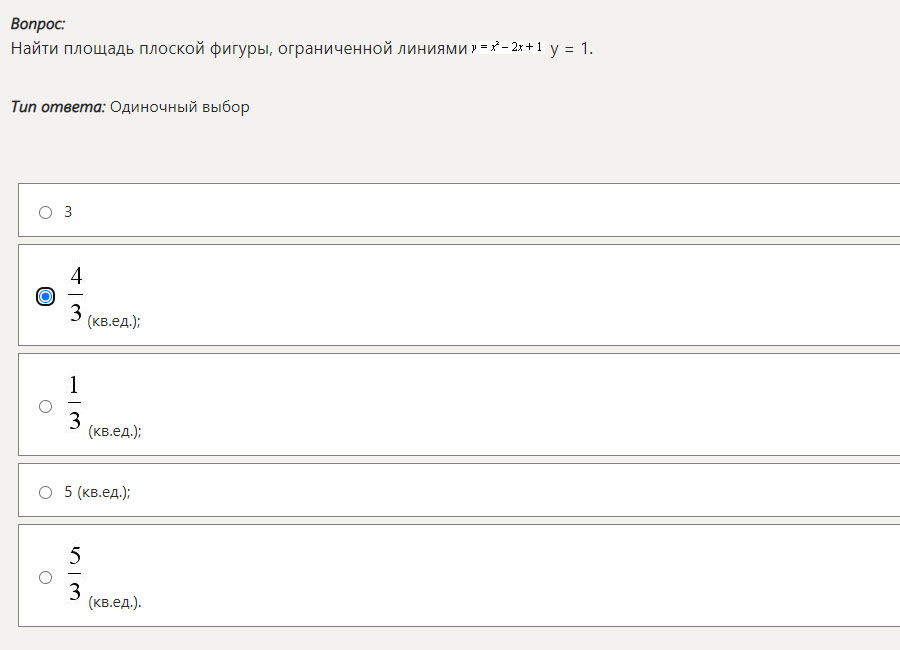

Будучи открытым для разных точек зрения признавая и ценя различия, вы можете создать атмосферу, которая культивирует сотрудничество и творческие альтернативы.

Цели «выиграл/выиграл» — это активаторы синергии.

Не путайте компромисс с синергией, которая является высшим цель Win/Win.

Компромисс — это низшая форма Win/Win: 1 + 1 = 1 ½ . При компромиссе целое меньше суммы частей. В идеале цель должна быть синергетической Win/Win: 1 + 1 = 3 . Компромисс не является синонимом синергии.

Выигрыш/Выигрыш также может применяться к личному выбору и является ключевым к наращиванию импульса в арифметике привычек. На самом деле, Think Win/Win — еще одна 7 взаимосвязанных привычек Кови. Это смена парадигмы с бесконечным потенциал. Какие положительные привычки вы можете сложить вместе, чтобы противодействовать слабым тенденции и поддержка следуют за желаемыми изменениями поведения, таким образом увеличить вероятность большего общего результата?

Если вы сможете переориентировать свое внимание на положительные преимущества по сравнению с трудностями внедрения новой привычки и применить научно обоснованные методы, такие как сложение привычек от эксперта по привычкам, такого как Джеймс Клир, ваша мотивация и выполнение могут значительно принести пользу и привести к положительным результатам. изменить эти соединения с течением времени.

Ищите синергию. Результаты вас удивят.

SynergyPrep Inc.

• Что такое общее ядро?
• Как оценивается Common Core?
• Почему Common Core важен?
• Что такого особенного в нашей программе Common Core?

Что такое общее ядро?

Common Core — это набор образовательных стандартов которые были представлены в 2010 году, в которых подробно описывается, что К-12 студенты в Соединенных Штатах должны знать в Искусство английского языка (ELA) и Математика.

Ежегодно в апреле и мае штат Нью-Йорк проводит экзамен Common Core для учащихся 3-8 классов, чтобы проверить свои понимание стандартов Common Core, которые они учились в течение года.

Как оценивается Common Core?

Экзамены ELA и Mathematics Common Core оцениваются по шкале от 1 до 4.

1 — самый низкий балл возможный, а 4 — самый высокий. Обычно хороший результат по Common Core колеблется между a 3 и 4. Принимая во внимание, что плохой результат находится в диапазоне между 1 и 2.

В пределах этих масштабированных оценок есть диапазоны, которые различают успеваемость учащегося на основе его балла по шкале. Ты возможно, слышал, как кто-то сказал до «Мой сын получил четыре балла по математике Common Core. экзамен» или «Моя дочь получила низкие три на ее экзамен ELA Common Core» .

Пожалуйста, смотрите диаграмму ниже для более подробной информации.

Марка	Уровень 1 штата Нью-Йорк (низкий)	Уровень 1 штата Нью-Йорк (высокий)	Уровень 2 штата Нью-Йорк (низкий)	Уровень штата Нью-Йорк 2 (высокий)	Уровень 3 штата Нью-Йорк (низкий)	Уровень 3 штата Нью-Йорк (высокий)	Уровень штата Нью-Йорк 4 (низкий)	Уровень 4 штата Нью-Йорк (высокий)
3	530 — 555	556 — 582	583 — 591	592 — 601	602 — 614	615 — 628	629 — 642	643 — 655
4	532 — 556	557 — 583	584 — 592	593 — 602	603 — 609	610 — 618	619 — 635	636 — 654
5	509 — 550	551 — 593	594 — 600	601 — 608	609 — 614	615 — 621	622 — 640	641 — 661
6	514 — 550	551 — 589	590 — 594	595 — 601	602 — 606	607 — 613	614 — 634	635 — 657
7	511 — 54	550 — 590	591 — 597	598 — 606	607 — 613	614 — 622	623 — 637	638 — 654
8	507 — 544	545 — 583	584 — 592	592 — 602	603 — 608	609 — 616	617 — 633	634 — 651

Почему Common Core важен?

Common Core преподается в школах по всей стране. штаты которых приняли учебную программу. Всего девять штатов в настоящее время не преподают Common Core в своих школах потому что они никогда не были приняты или были приняты ранее но позже отменили.

Хотя большинство штатов приняли учебную программу, штаты такие как Нью-Йорк начали менять стандарты чтобы удовлетворить их потребности. В последнее время штат Нью-Йорк пересмотрел знания ELA и математики в Учебная программа Common Core и выпущен новый набор стандартов называется Обучение следующего поколения Стандарты.

Так почему же Common Core так важен? Есть несколько причины, по которым Common Core важен, но вот основные:

• Common Core был создан с целью обучение критическому мышлению, решению проблем и аналитические навыки. Их преподают студентам с мысль о том, что они будут использовать их позже в жизни когда в средней школе и колледже
• Результаты общего экзамена штата определят, будет ли или не учащийся будет переведен в следующий класс
  • С оценкой или ниже 2 или ниже существует большая вероятность того, что студент останется позади. Однако студенческое продвижение в конечном итоге будет определен их учителем и их общая успеваемость в школе
• Общие баллы экзамена штата могут определить, не студент принят в конкретную программу например, одаренные и талантливые (G&T) или магнитный класс или школа. Например, студент с высоким ELA и по математике на свои 5 ^-й класс Обыкновенный Базовый экзамен может получить приглашение на поступление экзамен для школ кампуса колледжа Хантер, одного из самые престижные и отборные школы Нью-Йорка Город

Что такого особенного в нашей программе Common Core?

Программа Common Core Synergy Prep специализируется на подготовка 5 ^-й и 6 ^-й грейдеров для экзаменов NYS Common Core ELA и Math, которые проводятся в марте и апреле. Экзамен оценивает понимание учащимися стандартов, которым их учат в течение года.

Наша задача — сделать учебный план легким для понимания. понятным и доступным для учащихся. Мы сделайте это, проводя 2,5-часовые сеансы чтения и математика, обеспечивая краткий, легкий для понимания урок планы и еженедельные классные и домашние задания, чтобы укрепить наши учения.

Наши занятия проходят в личном кабинете, с 1 по 6, инструктор к коэффициентам учащихся. Это делается для того, чтобы каждый студент получает как можно больше внимания и поэтому преподаватели могут удовлетворить каждого студента с различными стили обучения.

Если вы зарегистрируетесь в нашей программе Common Core, вы получите другие функции, которые включены. Эти функции включают в себя:

• Программное обеспечение для оценки
• • С нашим программным обеспечением для выставления оценок учащиеся получают мгновенная обратная связь, когда они отправляют свои задания. Студентам будет предоставлена ​​их собственная информация для входа чтобы родители могли проверять успеваемость учеников на протяжении всего программу и посмотреть, представляют ли студенты свои задания вовремя.
  • Помощь с домашним заданием Через Дискорд
  • • Когда учащиеся зарегистрируются в нашей программе, они также получите специальный доступ к нашему каналу Discord, где они могут отправить билеты, чтобы получить помощь с домашним заданием, будь то для заданий Synergy Prep или задания, данные из школы.
    • Бесплатные дополнительные сеансы
    • Мы заботимся об академической успеваемости студента как внутри и снаружи Synergy Prep. Чтобы убедиться, что студенты получают всю необходимую им помощь, мы предоставляем бесплатно дополнительные занятия для повышения успеваемости учащихся. Просто попросите наставника студента или одного из наших менеджеров о дополнительной помощи, и мы посмотрим, как мы можем разместить вас.
    • Индивидуальные работы на основе студенческих работ Слабые стороны
    • В отличие от многих наших конкурентов, которые берут на себя «один размер подходит всем» подход к распределению работы студенты, Synergy Prep может настроить нашу работу чтобы удовлетворить потребности ученика.

      No related posts.