Монета брошена 2 раза найти вероятность того что герб выпадет 2 раз: Монета брошена 2 раза найти вероятность того что герб выпадет хотя бы 1 раз

монета брошена 2 раза, найти вероятность, что хотя бы один раз появится «герб» (в книге дается ответ- 3/4). поясните! — Спрашивалка

монета брошена 2 раза, найти вероятность, что хотя бы один раз появится «герб» (в книге дается ответ- 3/4). поясните! — Спрашивалка

ЮК

Юля Климова

Это предмет теория вероятности. решается по формулам, а не удачей и положением во вселенной. =))))

• ответ
• раз
• книга
• монета
• вероятность
• герб

Иришка Голованова

4 раза кинешь 1 раз герб выйдет=)

Ле

Леночка

Ответ получается без тервера:
вероятность, что не выпадет герб после 1 броска — 50%
вероятность, что не выпадет герб после 2 бросков — 25%
и так далее. 100

Вероятность, что выпадет герб + вероятность, что не выпадет герб = 100%

Очевидно, вероятность, что выпадет герб = 100% — вероятность, что не выпадет.
То есть получаем 100% — 25% = 75% = 3/4

Это строгое рассуждение, которое легко подкреплять утверждениями из тервера.

ОШ

Ольга Шебестюк

Существует на самом деле 1 вариант. ибо вселенная при каждом подбрасывании монеты разделяется на 2, поэтому в той всленной где это проиошло возможен уже 1 из 4 вариантов, и так далее, в итоге их бесконечное множество, твоя книга врёт

Константин Зенкин

ну слушай здесь надо расписать но проще объяснить так что всего 4 варианта положения монетки из них герб а 3 раза от суда и ответ 3\4 вот так ну если надо полное подробное объяснениние то зайди на сайт ГДЗ там все есть

ВЧ

Виктория Ч

Идем от обратного так быстрее вероятность того что герб не выпадет 1/2*1/2=1/4 вероятность того что хоть что то выпадет 1 вероятность того что хоть раз выпадет герб 1-1/4

Похожие вопросы

4)Монету бросают пять раз. Найти вероятность того, что «герб» выпадет: а) менее двух раз; б) не менее двух раз.

Помогите с задачей Монета подбрасывается в три раза . Найти вероятность того что хотя бы в 2 раза появится орел .

Теория вероятности. Монету бросают семь раз. Найти вероятность того, что герб выпадет три раза.

Задача! Монета подброшена 3 раза. Найти вероятность того, что герб появится 2 раза. Не по формулам Бернулли нужно решить

Монету подбрасывают шесть раз. Найти вероятность того, что «герб» выпадет не более двух раз. Помогите пожалуйста

игральная кость бросается два раза. Найти вероятность событий. 1)хотя бы на одной кости появится цифра 4.

Монета бросается 5 раз. Найти вероятность того, что герб поя- вится: а) 1 раз; б) 2 раза; в) 3 раза.

Монету подбросили 8 раз. Найти вероятность того, что герб появится ровно 2 раза.

Два игрока бросают монету по 4 раза каждый. Выигрывает тот, кто выбросит больше гербов. Найти вероятность победы первого

Вероятность события А=2/3. Вероятность того, что при 4 испытаниях событие А появится 2 раза, принадлежит промежутку…

tv_ms_1 — Стр 5

P(A)= Pk(a)*P(k) + Pl(a)*P(l) + Pm(a)*P(m) = 0.7*0.5 + 0.8*0.3 + 0.9*0.2 = 0.77

А вероятность что больной страдал именно заболеванием К равно:

Pa(K) = (Pk(a)*P(k))/P(A)= (0.5*0.7)/0.77 = 5/11

#102

Изделие проверяется на стандартность одним из двух товароведов . Вероятность того, что изделие попадет к первому товароведу , равна 0,55, а ко второму – 0,45. Вероятность того, что стандартное изделие будет признано стандартным первым товароведом , равно 0,9, а вторым – 0,98. Стандартное изделие при проверке было признано стандартным. Найти вероятность того , что это изделие проверил второй товаровед.

Решение: Обозначим через А – изделие признана стандартной. — вероятность того, что изделие попало к первому товароведу. — ко второму. P() = 0,55 , P() = 0,45.

Условная вероятность того что изделие будет признано стандартным первым товароведом равна (A) = 0,9, вторым — (A) = 0,98.

Вероятность того, что изделие будет признано стандартным по формуле полной вероятности равна

P(A)= P() (A) + P() (A) = 0,55 * 0,9 + 0,45 * 0,98 = 0,936

Искомая вероятность того, что изделие проверил второй товаровед, по формуле Бейеса равна

()= P() * (A) / P(A)= 0,45*0,98 / 0,936 = 0,47.

#103

Событие А может появится при условии появления одного из несовместимых событий В1, В2,…, Вn, образующих полную группу событий. После появления события А были переоценены вероятности гипотез, то есть были найдены условные вероятности РА(Вi) (i=1,2,…,n). Доказать, что сумма РА(Вi) (i=1,2,…,n) равна 1.

Решение:

По формуле Бейеса:

i=1n∑РА(Вi)= i=1n∑Р(Вi)* РВi(А)/Р(А)=Р(А)/Р(А)=1

Что и требовалось доказать.

#104

Условие:

Событие может появиться при условии появления одного из несовместных событий (гипотез) , образующих полную группу событий. После появления события были переоценены вероятности этих гипотез, т. е. были найдены условные вероятности этих гипотез, причем оказалось, что . Чему равна условная вероятность гипотезы ?

Решение:

Так как события образуют полную группу, и появится при условии появления лишь одного из них, то верно . Так как имеем , то:

#105

Имеются три партии деталей по 20 деталей в каждой. Число стандартных деталей в первой, второй и третьей партиях соответственно равно 20, 15, 10. Из наудачу выбранной партии наудачу извлечена деталь, оказавшаяся стандартной. Деталь возвращают в партию

и вторично из той же партии наудачу извлекают деталь, которая также оказывается стандартной. Найти вероятность того, что детали были извлечены из третьей партии.

Решение:

Обозначим через А событие – в каждом из двух испытаний была извлечена стандартная деталь. Можно предположить, что B1 – детали извлекались из первой партии; B2 – детали извлекались из второй партии; В3 – детали извлекались из третей партии.

Детали извлекались на удачу, поэтому вероятности предположений одинаковы:

P(B1) = P(B2) = P(B3) =

Вероятность того, что из первой партии будут последовательно извлечены две стандартные детали; поэтому

Условная вероятность т. е вероятность того, что из второй партии будут извлечены две стандартные детали:

Найдем условную вероятность т.е вероятность того, что из третей партии будут последовательно извлечены две стандартные детали:

Искомая вероятность того, что обе извлеченные детали стандартные взяты из третей партии, по формуле Бейеса равна

Ответ:

#106

Условие:

Батарея из трех орудий произвела залп, причем два снаряда попали в цель. Найти вероятность того, что первое орудие дало попадание, если вероятности попадания в цель первым, вторым и третьим орудиями соответственно равны , , .

Решение:

Обозначим через A событие- два орудия попали в цель. Сделаем два предположения: — орудие не попало в цель.

По условию , следовательно

Найдем условную вероятность , т.е. вероятность того, что в цель попало 2 снаряда, причем один из них послан первым орудием и, следовательно, второй — либо вторым орудием, либо третьим. Эти два события несовместны, поэтому применима теорема сложения:

.

Найдем условную вероятность , т.е. вероятность того, что в цель попало два снаряда, причем первое орудие дало промах. Другими словами найдем вероятность того, что второе и третье орудие попали в цель. Эти два события независимы, поэтому применима теорема умножения:

Искомая вероятность того, что первое орудие дало попадание, по формуле Бейеса равна:

.

Ответ:

#107

Три стрелка произвели залп, причем две пули поразили мишень. Найти вероятность того, что третий стрелок поразил мишень, если вероятности попадания в мишень первым, вторым и третьим стрелками соответственно равны 0,6, 0,5 и 0,4.

Решение. Обозначим через А событие – две пули поразили мишень. Сделаем два предположения (гипотезы): В1 – третий стрелок поразил мишень; В2 – третий стрелок не попал в мишень.

По условию, Р(В1) = 0,4; следовательно (событие В2 противоположно событию В1),

Р(В2) = 1 – 0,4 = 0,6.

Найдем условную вероятность РВ1(А), т.е. вероятность того, что мишень поразили две пули, причем одна из них принадлежит третьему стрелку и, следовательно, вторая – либо первому стрелку (при этом второй не попал), либо второму стрелку (при этом первый не попал).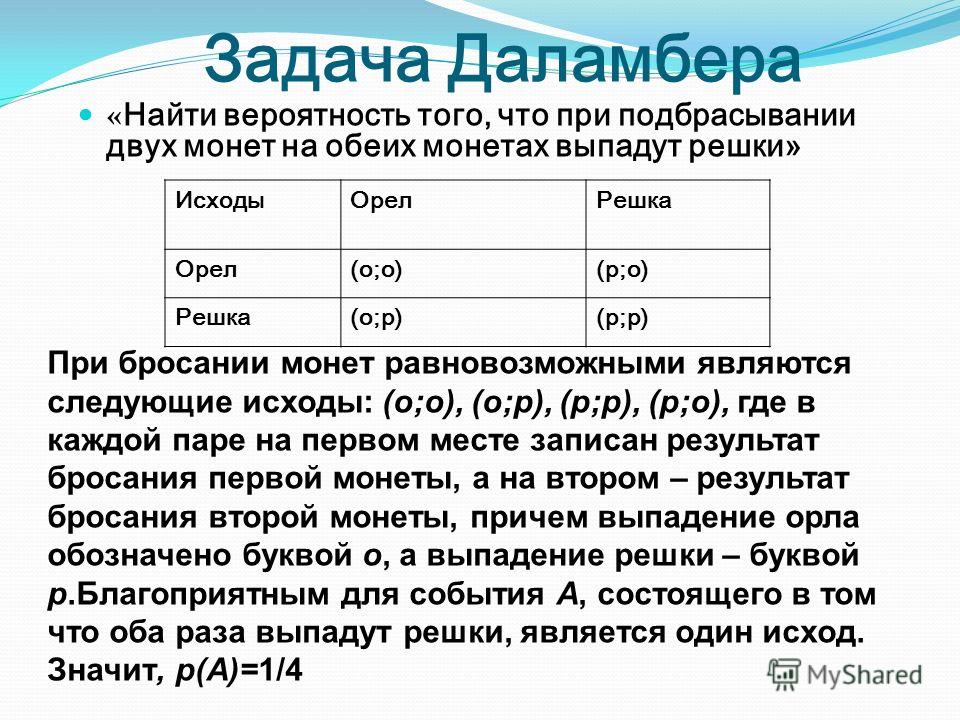 Эти два события несовместны, поэтому применима теорема сложения:

РВ1(А) = p1∙q2 + p2∙q1 = 0,6∙0,5 + 0,5∙0,4 = 0,5.

Найдем условную вероятность РВ2(А), т.е. вероятность того, что мишень поразили две пули, причем третий стрелок промахнулся. Другими словами, найдем вероятность того, что первый и второй стрелки поразили мишень. Эти два события независимы, поэтому применима теорема умножения:

РВ2(А) = p1∙p2 = 0,6∙0,5 = 0,3.

Искомая вероятность того, что третий стрелок поразил мишень, по формуле Бейеса равна

РА(В1) = Р(В1)∙РВ1(А)/[ Р(В1)∙РВ1(А) + Р(В2)∙РВ2(А)] = 0,4∙0,5/( 0,4∙0,5 + 0,6∙0,3 ) = 10/19.

Ответ: 10/19.

#108

Два из трех независимо работающих элементов вычислительного устройства отказали. Найти вероятность того, что отказали первый и второй элементы, если вероятности отказа первого, второго и третьего элементов соответственно равны 0,2; 0,4 и 0,3.

Решение. Обозначим через А событие – отказали два элемента. Можно сделать следующие предположения (гипотезы):

В1 — отказали первый и второй элементы, а третий элемент исправен, причем (поскольку элементы работают независимо, применима теорема умножения)

Р(В1) = p1∙p2∙q3 = 0,2∙0,4∙0,7 = 0,056;

В2 — отказали первый и третий элементы, а второй элемент исправен, причем

Р(В2) = p1∙p3∙q2 = 0,2∙0,3∙0,6 = 0,036;

В3 — отказали второй и третий элементы, а первый — исправен, причем

Р(В3) = p2∙p3∙q1 = 0,4∙0,3∙0,8 = 0,096;

В4 — отказал только один элемент; В5 — отказали все три элемента; В6 — ни один из элементов не отказал.

Вероятности последних трех гипотез не вычислены, так как при этих гипотезах событие А (отказали два элемента) невозможно и значит условные вероятности РВ4(А), РВ5(А) и РВ6(А) равны нулю, следовательно, равны нулю и произведения Р(В4)∙РВ4(А), Р(В5)∙РВ5(А) и Р(В6)∙РВ6(А) при любых значениях вероятностей гипотез В4, В5 и В6.

Поскольку при гипотезах В1, В2 и В3 событие А достоверно, то соответствующие условные вероятности равны единице:

РВ1(А) = РВ2(А) = РВ3(А) = 1.

По формуле полной вероятности, вероятность того, что отказали два элемента, равна

Р(А) = Р(В1)∙РВ1(А) + Р(В2)∙РВ2(А) + Р(В3)∙РВ3(А) + Р(В4)∙РВ4(А) + Р(В5)∙РВ5(А) + Р(В6)∙РВ6(А) = 0,056 + 0,036 + 0,096 = 0,188.

По формуле Бейеса, искомая вероятность того, что отказали первый и второй элементы,

РА(В1) = Р(В1)∙РВ1(А)/ Р(А) = 0,056/0,188 = 0,3.

Ответ: 0,3.

#109

Две из четырех независимо работающих ламп прибора отказали. Найти вероятность того, что отказали первая и вторая лампы, если вероятности отказа первой, второй, третьей и четвертой ламп соответственно равны 0,1, 0,2, 0,3 и 0,4.

Решение. Обозначим через А событие – отказали две лампы. Можно сделать следующие предположения (гипотезы):

В1 — отказали первая и вторая лампы, а третья и четвертая лампы исправны, причем (поскольку лампы работают независимо, применима теорема умножения)

Р(В1) = p1∙p2∙q3∙q4 = 0,1∙0,2∙0,7∙0,6 = 0,0084;

В2 — отказали первая и третья лампы, а вторая и четвертая исправны, причем

Р(В2) = p1∙q2∙p3 ∙q4 = 0,1∙0,8∙0,3∙0,6 = 0,0144;

В3 — отказали первая и четвертая лампы, а вторая и третья — исправны, причем

Р(В3) = p1∙q2∙q3∙p4 = 0,1∙0,8∙0,7∙0,4 = 0,0224;

В4 — отказали вторая и третья лампы, а первая и четвертая — исправны, причем

Р(В4) = q1∙p2∙p3∙q4 = 0,9∙0,2∙0,3∙0,6 = 0,0324;

В5 — отказали вторая и четвертая лампы, а первая и третья — исправны, причем

Р(В5) = q1∙p2∙q3∙p4 = 0,9∙0,2∙0,7∙0,4 = 0,0504;

В6 — отказали третья и четвертая лампы, а первая и вторая — исправны, причем

Р(В6) = q1∙q2∙p3∙p4 = 0,9∙0,8∙0,3∙0,4 = 0,0864;

В7 – отказала только одна лампа; В8 — отказали три лампы; В9 — отказали все четыре лампы и В10 – все лампы остались исправны.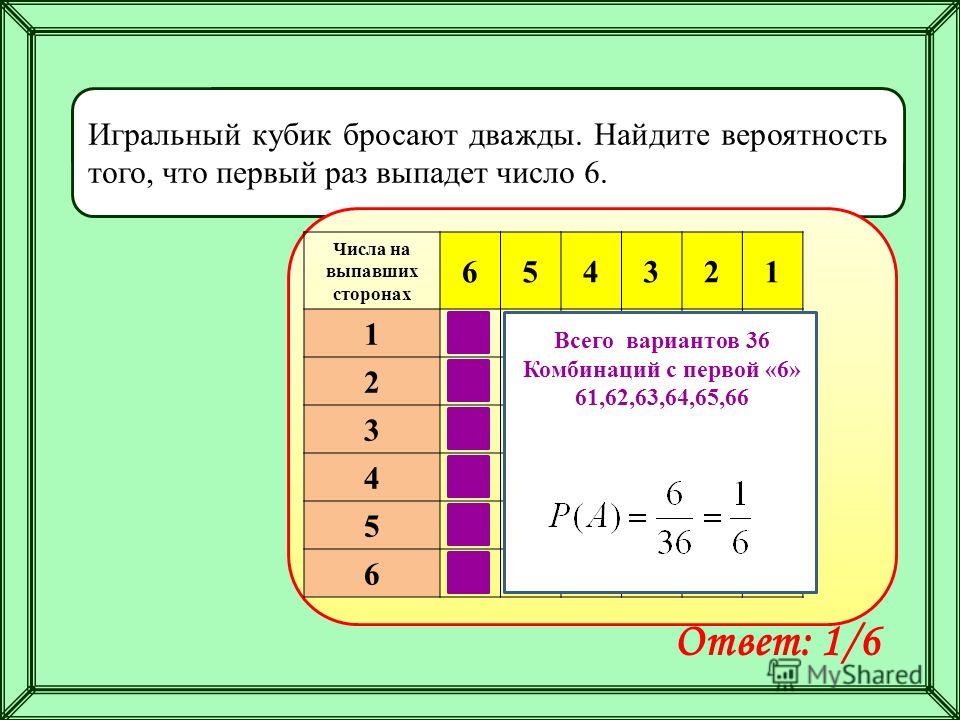

Вероятности последних четырех гипотез не вычислены, так как при этих гипотезах событие А (отказали две лампы) невозможно и значит условные вероятности РВ7(А), РВ8(А), РВ9(А) и РВ10(А) равны нулю, следовательно, равны нулю и произведения Р(В7)∙РВ7(А), Р(В8)∙РВ8(А), Р(В9)∙РВ9(А) и Р(В10)∙РВ10(А) при любых значениях вероятностей гипотез В7, В8, В9 и В10.

Поскольку при гипотезах В1 – В6 событие А достоверно, то соответствующие условные вероятности равны единице:

РВ1(А) = РВ2(А) = РВ3(А) = РВ4(А) = РВ5(А) = РВ6(А) = 1.

По формуле полной вероятности, вероятность того, что отказали две лампы, равна

Р(А) = Р(В1)∙РВ1(А) + Р(В2)∙РВ2(А) + Р(В3)∙РВ3(А) + Р(В4)∙РВ4(А) + Р(В5)∙РВ5(А) + Р(В6)∙РВ6(А) + Р(В7)∙РВ7(А) + Р(В8)∙РВ8(А) + Р(В9)∙РВ9(А) + Р(В10)∙РВ10(А) = 0,0084 + 0,0144 + 0,0224 + 0,0324 + 0,0504 + 0,0864 = 0,2144.

По формуле Бейеса, искомая вероятность того, что отказали первая и вторая лампы, равна

РА(В1) = Р(В1)∙РВ1(А)/ Р(А) = 0,0084/0,2144 ~ 0,039.

Ответ: 0,039.

#110

Два равносильных шахматиста играют в шахматы. Что вероятнее: выиграть две партии из четырех или три из шести (ничьи во внимание не принимаются)?

Решение.

Играют равносильные шахматисты, поэтому вероятность выигрыша p=1/2; следовательно, вероятность проигрыша q также равна 1/2. Так как во всех партиях вероятность выигрыша постоянна и безразлично, в какой последовательности будут выиграны партии, то применима формула Бернулли.

Найдем вероятность того, что две партии из четырех будут выиграны:

Найдем вероятность того, что выиграны три партии из шести:

Так как P4(2)>P6(3), то вероятнее выиграть две партии из четырех, чем три из шести.

#111

Два равносильных противника играют в шахматы. Что вероятнее: а) Выиграть одну партию из двух или две партии из четырех? б)выиграть не менее двух партий из четырех или не менее трех партий из пяти? Ничьи во внимание не принимаються.

Решение:

Играют равносильные шахматисты, поэтому вероятность выигрыша ; следовательно, вероятность проигрыша . Так как во всех партиях вероятность выигрыша постоянна и безразлично, в какой последовательности будут выигранв партии, то применима формула Бернулли.

А) Найдем вероятность того, что две партии из четырех будут выиграны:

Найдем вероятность того, что одна партия из двух будет выиграна:

Б) Найдем вероятность выиграть не менее двух партий из четырех:

Найдем вероятность выиграть не менее трех партий из пяти:

#112

Условие задачи:

Монету бросают пять раз. Найти вероятность того, что “герб” выпадет: а)мене двух раз; б)не менее двух раз.

Решение задачи:

При бросании монеты вероятность выпадения герба и решки, равновероятны, поэтому вероятность выпадения герба равна ; следовательно вероятность выпадения решки ; Так как при бросании вероятность постоянна, то применима формула Бернулли.

А) Найдем вероятность того, что герб выпадет менее двух раз:

;

.

.

Б) Найдем вероятность того, что герб выпадет не менее двух раз:

;

Ответ: a) ; б)

#113

а) Найти вероятность того, что событие А появится не менее трёх раз в четырёх независимых испытаниях, если вероятность появления события А в одном испытании равна 0,4;

б) Событие В появится в случае, если событие А наступит не менее четырёх раз. Найти вероятность наступления события В, если будет произведено 5 независимых испытаний, в каждом из которых вероятность появления события А равна 0,8.

Решение

а)Так как вероятность появления события А во всех испытаниях одинакова и все испытания независимы, то применяем формулу Бернулли. Так как вероятность появления события А в одном испытании равна 0,4, т.е. р = 0,4, то вероятность не появления события А в одном испытании равна

q = 1- 0,4 = 0,6.

Найдём вероятность того, что событие А появится ровно 3 раза в четырёх независимых испытаниях и найдём вероятность того, что событие А появится ровно 4 раза в четырёх независимых испытаниях и просуммируем их:

б) Так как вероятность появления события А во всех испытаниях одинакова и все испытания независимы, то применяем формулу Бернулли.

р = 0,8 q = 0,2

Найдём вероятности того, что событие А появится ровно 4 раза и 5 раз в пяти независимых испытаниях и просуммируем:

Ответ: а) 0,1792 б) 0,73728

#114

Задание: Устройство состоит из трех независимо работающих основных элементов. Устройство отказывает, если откажет хотя бы один элемент. Вероятность отказа каждого элемента за время t равна 0,1. Найти вероятность безотказной работы устройства за время t, если: а) работают только основные элементы; б) включен один резервный элемент; в) включены два резервных элемента. Предполагается, что резервные элементы работают в том же режиме, что и основные, вероятность отказа каждого резервного элемента также равна 0,1 и устрой- устройство отказывает, если работает менее трех элементов.

Решение: По условию , следовательно вероятность стабильной работы каждого элемента . Так как безразлично какой из элементов откажет и вероятности отказа всех элементов равны, применима формула Бернулли.

а) Найдём вероятность того, что будут работать все 3 элемента:

б) Найдём вероятность того, что устройство будет работать при одном дополнительном элементе на протяжении времени t. :

в) Найдём вероятность того, что устройство будет работать при двух дополнительных элементах на протяжении времени t. :

#115

В семье пять детей. Найти вероятность того, что среди этих детей: а) два мальчика; б) не более двух мальчиков в) более двух мальчиков г) не менее двух и не более трёх мальчиков.

Вероятность рождения мальчиков принять равной 0.51

Решение: По условию =0.51 следовательно вероятность = 0.49 и применима формула Бернулли.

а) Найдём вероятность того, что в семье 2 мальчика:

0.62

б) Найдём вероятность того, что в семье не более двух мальчиков:

в) Найдём вероятность того, что в семье более двух мальчиков:

г) найдём вероятность того, что в семье не менее двух и не более трёх мальчиков:

116……

#117

На отрезок АВ длины а наудачу брошено пять точек. Найти вероятность того, что две точки будут находиться от точки А на расстоянии, меньшем x, а три — на расстоянии, большем x. Предполагается, что вероятность попадания точки на отрезок пропорциональна длине отрезка и не зависит от его расположения.

Решение: т.к. p = xa — вероятность того, что точка будет находиться на расстоянии меньшем чем x, следовательно, q = 1 – p=1- xa= a-xa. По формуле Бернулли имеем: Pnk= Cnkpkqn-k. P52= C52xa2a-xa3.

#118

Отрезок разделен на четыре равные части. На отрезок наудачу брошено восемь точек. Найти вероятность того, что на каждую из четырех частей отрезка попадет по две точки. Предполагается, что вероятность попадания точки на отрезок пропорциональна длине отрезка и не зависит от его расположения.

Решение:

Вероятность того, что точка попадет в нужный отрезок равна р=1/4.

q=3/4

Искомая вероятность равна

Р= С82 С62 С42 С22*(1/4)8

#119

Найти вероятность того, что событие A наступит ровно 70 раз в 243 испытаниях, если вероятность появления этого события в каждом испытании равна 0,25.

Решение: По условию, n=243; k=70; p=0,25; q=0,75. Т.к. n=243 – достаточно большое число, воспользуемся локальной теоремой Лапласа:

Найдем значение x: . По таблице найдем

Тогда искомая вероятность

Ответ: .

#120

Найти вероятность того, что событие А наступит 1400 раз в 2400 испытаниях, если вероятность появления этого события в каждом испытании равна 0,6.

Решение: По условию, n=2400; k=1400; p=0,6; q=0,4. Так как n=2400 – достаточно большое число, воспользуемся локальной теоремой Лапласа:

Найдем значение x: .

Так как четная функция, то = .

По таблице найдем

Тогда искомая вероятность

Ответ: 0,0041.

#121

Вероятность поражения мишени при одном выстреле равна 0,8. Найти вероятность того, что при 100 выстрелах мишень будет поражена ровно 75 раз.

Решение.

Так как n велико, воспользуемся локальной теоремой Лапласа:

(k)=φ(x).

Вычислим x:

X===-1,25.

Функция φ(x) четная, поэтому φ(-1,25)= φ(1,25)=0,1826.

Искомая вероятность

.

#122

Вероятность рождения мальчика равна 0,51. =е~лг*/’2—четная, поэтому ф(—1,67)=ф( 1,67).

По таблице приложения 1 найдем ф( 1,67) = 0,0989.

Искомая вероятность

Я24оо A400) = 1/24-0,0989=0,0041.

#123

Монета брошена 2N раз (N велико!). Найти вероятность того, что «герб» выпадет ровно N раз.

Решение. n=2N, k=N, p=0,5, q=0,5. Для нахождения вероятности выпадения «герба» ровно N раз воспользуемся локальной теоремой Лапласа :

(N)=φ(x)* 1/;

φ(x)=1/;

x=(k-pn)/;

x=0; φ(x)≈0,3989; (N)≈0.5641/

#124

Монета брошена 2N раз. Найти вероятность того, что «герб» выпадет на 2m раз больше, чем надпись.

РЕШЕНИЕ.

Т.к. исход каждого испытания не зависит от предыдущих исходов и возможных исходов два («герб» или надпись), то вероятность выпадения «герба» в каждом испытании равна . Всего проведено n=2N испытаний, а «герб» выпал на 2m раза больше, чем надпись, значит обозначим количество выпадений «герба» за t, получим уравнение: . Очевидно, что количество исходов, в которых выпал «герб», равно .

По локальной теореме Лапласа вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна p, событие наступит ровно k раз, равна:

Подставим значения:

#125

Условие:

Вероятность появления события в каждом из независимых испытаний постоянна и равна . Найти вероятность того, что событие появится: а) не менее раз и не более раз; б) не менее раз; в) не более раз.

Решение:

Воспользуемся интегральной теоремой Лапласа: , где – функция Лапласа,

Подбрасывание монеты | Вероятность | Формула | Калькулятор | Примеры

У монеты всегда есть две стороны: орел и решка.

Вы когда-нибудь принимали важное решение, подбрасывая монетку?

В американском футболе капитан каждой команды выбирает сторону монеты, а затем судья подбрасывает монету.

Капитан, который правильно предсказывает жеребьевку, решает, какие ворота будет защищать его команда.

Давайте посмотрим, как это работает и какова вероятность каждой стороны медали.

План урока

1.	Что вы подразумеваете под вероятностью подбрасывания монеты?
2.	Решенные примеры
3.	Важные примечания
4.	Интерактивные вопросы
5.	Сложные вопросы

Какие возможные события могут произойти при подбрасывании монеты?

У каждой монеты две стороны: Орел и Решка

Мы обозначаем Орел как H и Решка как Решка.

При подбрасывании монеты выпадает либо орёл, либо решка.

Набор всех возможных результатов случайного эксперимента известен как его выборочное пространство . Таким образом, если ваш случайный эксперимент заключается в подбрасывании монеты, то выборочное пространство равно {Орел, Решка} или, более кратко, { H ,  T }.

Если монета честная , что означает, что ни один исход не является особенно предпочтительным, или все исходы равновероятны , то мы знаем, что для большого количества бросков количество орлов и число число хвостов должно быть примерно равным. То есть количество орлов должно составлять примерно 1/2 от общего количества бросков, как и количество решек. Это числовое значение 1/2 можно использовать как мера вероятности или вероятность .

---

Что вы подразумеваете под вероятностью подбрасывания монеты?

Подбрасывание монеты Вероятность – это вероятность того, что каждая сторона монеты выпадет.

Подбрасывание монеты имеет два возможных исхода: Орел или Решка. Вы не знаете, какой результат вы получите при конкретном подбрасывании, но вы знаете, что это будет либо орел, либо решка (мы исключаем возможность того, что монета упадет ребром!).

Сравните это с научным экспериментом. Например, если ваш эксперимент заключается в падении предмета, вы точно знаете результат: предмет упадет на землю. Однако подбрасывание монеты — это случайный эксперимент , так как вы знаете набор результатов, но не знаете точный результат для конкретного выполнения случайного эксперимента.

Общая формула для определения вероятности:0003

При подбрасывании монеты возможны только два исхода.

Таким образом, используя формулу вероятности

При подбрасывании монеты вероятность выпадения орла равна:

P(орел) = P(H) = 1/2 получить решку:

P(хвост) = P(T) = 1/2

Попробуйте подбросить монету ниже, нажав кнопку «Подбросить монету», и проверьте свои результаты.

Нажмите кнопку «Сброс», чтобы начать заново.

---

Как предсказать выпадение орла или решки?

• Если монета честная (беспристрастная), то есть ни один исход не является особо предпочтительным, то мы не можем предсказать орел или решку. Оба результата с одинаковой вероятностью появятся.
• Если монета нечестная (пристрастная), то есть исход предпочтительнее, то мы можем предсказать исход, выбрав сторону с большей вероятностью.
  • Если вероятность выпадения орла больше 1/2, то мы можем предсказать, что следующим результатом будет орел.
  • Если вероятность выпадения решки больше 1/2, то мы можем предсказать, что следующим результатом будет решка.

Предположим, вы подбрасываете монету 100 раз. Какой из следующих результатов более вероятен, чем  ?

Результат-1:  Вы получаете 95 орлов и 5 решек

Результат-2:  Вы получаете 48 орлов и 52 решки чтобы выпасть больше, чем другая сторона, вы ожидаете, что при большом количестве бросков орел и решка должны выпасть примерно одинаковое количество раз. Это означает, что из двух приведенных выше результатов Результат-2 кажется более вероятным, поскольку количество орлов примерно равно количеству решек, что согласуется с тем фактом, что ни орел, ни решка не являются предпочтительными результатами.

С другой стороны, в Результате-1 количество орлов намного больше, чем количество решек. Ясно, что такой результат крайне смещен в сторону орла, что маловероятно, учитывая, что орел и решка являются одинаково предпочтительными исходами. Заметьте, мы не говорим, что Результат-1 невозможен. Мы только говорим, что это маловероятно или маловероятно . Другими словами, вероятность  Результата-1 намного ниже, чем вероятность  Результата-2.

Изучение вероятности позволяет нам количественно оценить вероятность. Это позволяет нам ответить на такие вопросы, как: Насколько вероятно, что  является Результатом-2? Насколько маловероятен  Результат-1? И так далее.

Однако подбрасывание монеты является случайным экспериментом , так как вы знаете набор результатов, но не знаете точный результат для конкретного выполнения случайного эксперимента.

 

---

Решенные примеры

Пример 1

 

 

Монету подбрасывают определенное количество раз. Относительная частота выпадения голов составляет 0,75. Можно ли сказать, что монета смещена в сторону орла?

Решение

Нет, мы не можем, потому что эксперимент (подбрасывание монеты) мог быть повторен очень небольшое количество раз, и, таким образом, относительное возникновение в таком сценарии не дает истинной вероятности.

Пример 2

 

 

Монета-А подбрасывается 200 раз, и относительная вероятность выпадения решки составляет 0,47. Монета-B подбрасывается неизвестное количество раз, но известно, что относительная вероятность выпадения орла составляет 0,50. Какая монета честнее?

Решение

Невозможно прокомментировать справедливость монеты-Б, поскольку неизвестно, сколько раз она была подброшена. С другой стороны, Coin-A кажется справедливой, поскольку относительное появление решки при большом количестве подбрасываний составляет почти 1/2.

Монета-А

Пример 3

 

 

При двойном подбрасывании монеты какова вероятность того, что выпадет только одна решка?

Решение:

При двукратном подбрасывании монеты возможные исходы {HH, TT, HT, TH}

Таким образом, общее количество исходов равно 4

Выпадение только одной решки включает {HT, TH}

Следовательно, число благоприятных исходов равно 2

Следовательно, вероятность выпадения ровно одной решки равна 2/4 = 1/2

 

Важные примечания

• Относительное появление 2 7 7 90 90 90 71 2 исхода 900 используется для обозначения отношения количества раз, когда был получен конкретный результат, к общему количеству раз, когда был проведен случайный эксперимент.
• При подбрасывании монеты вероятность каждого исхода равна 1/2
• P(голова) + P(хвост) = 1

Интерактивные вопросы  

Вот несколько упражнений для практики.

Выберите/введите свой ответ и нажмите кнопку «Проверить ответ», чтобы увидеть результат.

 

 

 

 

 

 

Задающие вопросы

• Если решка выпадет при первых четырех бросках, то какова вероятность того, что голова выпадет при пятом броске?
• Если монету бросают три раза подряд, какова вероятность того, что выпадет хотя бы один орел и хотя бы одна решка?

Подведем итоги 

Мы надеемся, что вам понравилось изучение подбрасывания монеты с помощью симуляций и практических вопросов. Теперь вы сможете легко решать задачи по математике «Подбрасывание монеты» с помощью нескольких математических примеров, которые вы узнали сегодня.

О Cuemath  

В Cuemath команда экспертов по математике стремится сделать обучение интересным для наших любимых читателей, студентов!

Благодаря интерактивному и увлекательному подходу «обучение-преподавание-обучение» учителя изучают тему со всех сторон.

Будь то рабочие листы, онлайн-классы, сеансы сомнений или любая другая форма отношений, это логическое мышление и разумный подход к обучению, в которые мы в Cuemath верим.

---

Часто задаваемые вопросы (FAQ)

1. Может ли монета упасть на бок?

Монета может упасть на бок, если она упадет на предмет, такой как коробка, обувь и т. д.

Маловероятно, что монета упадет на бок на плоскую поверхность, но нельзя сказать, что это невозможно.

2. Является ли подбрасывание монеты хорошим способом принять решение?

Принятие решений путем подбрасывания монеты помогает человеку сделать выбор, когда он застрял между двумя вариантами, потому что каждый исход имеет равную вероятность.

3. Как предсказать подбрасывание монеты?

Подбрасывание монеты — это случайный эксперимент, поскольку вы знаете набор результатов, но не знаете точный результат конкретного выполнения случайного эксперимента.

Следовательно, мы не можем предсказать бросок монеты, если монета честная.

4. Действительно ли подбрасывание монеты происходит случайно?

Подбрасывание монеты считается случайным событием.

Согласно Ньютону, если человек переворачивается определенным образом с определенной скоростью, то результат можно определить.

5. Какова вероятность выпадения пяти решек подряд?

При пятикратном подбрасывании монеты число возможных исходов равно 2 ⁵

Следовательно, вероятность выпадения пяти орлов подряд равна 1/2 ⁵

6. Является ли подбрасывание монеты простой случайной выборкой?

Простая случайная выборка берет небольшую часть большого набора данных для представления данных.

Подбрасывание монеты является случайным экспериментом, и каждый исход имеет одинаковую вероятность.

Таким образом, подбрасывание монеты представляет собой простую случайную выборку.

7. Действительно ли подбрасывание монетки 50/50?

При подбрасывании монеты все исходы имеют одинаковую вероятность и возможны два исхода.

Следовательно, подбрасывание монеты 50/50.

8. При подбрасывании монеты что честнее: поймать монету или дать ей упасть?

При подбрасывании монеты более справедливо дать ей упасть, чем поймать ее, потому что сила рук может подбросить ее.

9. Каковы шансы выпадения трех решек подряд?

При трехкратном подбрасывании монеты число возможных исходов равно 2 ³

Следовательно, вероятность выпадения пяти орлов подряд равна 1/2 ³

Вероятность выпадения орла при первом подбрасывании предстоящий?

спросил 5 лет, 3 месяца назад

Изменено 1 год, 5 месяцев назад

Просмотрено 26 тысяч раз

$\begingroup$

Какова вероятность выпадения орла при втором броске, если при первом броске выпал орел. (Пытаюсь немного освежить мою вероятность). Я видел, как это проанализировано следующим образом:

• HH 1/4
• НТ 1/4
• ТН 1/4
• ТТ 1/4

Итак, поскольку мы получили информацию (Голова при первом переворачивании), то TT исчезает и остается с:

• HH 1/3
• НТ 1/3
• ТН 1/3

Таким образом, мы можем сказать, что HH теперь имеет вероятность 1/3. Не следует ли нам также избавиться от TH, поскольку мы знаем, что первый бросок — это решка? Итак, теперь у нас есть:

• ЧЧ 1/2
• НТ 1/2

• вероятность
• теория вероятностей
• байесовская теория
• байесовская теория

$\endgroup$

6

$\begingroup$

Да, верно. Вы также можете использовать концепцию, называемую независимостью; если два подбрасывания монеты независимы, то знание того, что первый выпал орлом, совсем не меняет вероятность выпадения орла во втором.

$\endgroup$

2

$\begingroup$

Если мы дадим информацию, что «первая монета была орлом», то из HH, HT, TH, TT будет удалено , TT, и TH. Остаются только HH и HT, так что вероятность того, что второй бросок также выпадет орлом, равна 1/2.

$\endgroup$

3

$\begingroup$

два события не связаны между собой, исход второго (как уже упоминалось) не зависит от первого. Таким образом, вероятность того, что второй выпадет орлом, равна 1/2.

Вероятность того, что оба выпадут решками, равна 1/4.

Если вы сделали 49 подбрасываний, и все они выпали орлом, то вероятность следующего выпадения орла по-прежнему равна 1/2.

$\endgroup$

12

$\begingroup$

В общем, для двух событий $A, B$ $$ P(A\mid B)=\frac{P(A\cap B)}{P(B)}. $$ Пусть $A$ будет событием выпадения орла при втором подбрасывании, а $B$ — событием выпадения орла при первом броске. Затем $$ P(A\mid B)=\frac{1/4}{1/2}=1/2. $$ Числитель объясняется тем, что из четырех возможных последовательностей двух бросков (все равновероятных) мы хотим $HH$.

$\endgroup$

$\begingroup$

Если монета честная, то результаты первого и второго бросков независимы, поэтому есть ровно две возможности для второго броска: H и T. Вероятность выпадения H равна 1/2. Не забывайте, что монета могла быть подброшена тысячи раз до того, о ком мы заботимся. Ни один из них не влияет на результат; в последнем из этих предварительных бросков нет ничего особенного.

$\endgroup$

$\begingroup$

Что смущает в данном случае нашу интуицию, так это различие между вероятностями событий в будущем и событий, которые уже произошли (прошлое). Если все подбрасывания монеты лежат в будущем, вероятность прямой последовательности H уменьшается, чем больше подбрасываний монеты мы планируем сделать. Таким образом, только для одного броска вероятность H равна 1/2, для двух бросков (HH) она равна 1/4 и т. д., так что, например. для 10 бросков последовательность HHHHHHHHHH имеет вероятность около 0,001. (Математически это P(AB) = P(A) * P(B) для независимых событий A и B.) 9number_of_tosses участников). Причина, по которой вероятность прямой последовательности Н так мала при большом количестве подбрасываний, заключается в том, что она сравнивается со всеми последовательностями, где одна или несколько Т появляются в любом месте последовательности (а не только одна в конце).

No related posts.