Корень из 2 в степень корень из 2: Ничего не найдено для Ru Ege Materialy Matematika Korni I Stepeni %23Stepen S Tselym Pokazatelem

Вычисление целочисленного квадратного корня / Хабр

paluke

30 сен 2019 в 20:16

Время на прочтение 2 мин

Количество просмотров

11K

Математика *

Возникла нужда проверить, является ли целое число квадратом, и если да, то вычислить корень. Причем хочется сделать это в целочисленной арифметике. Понятно, что можно реализовать метод Ньютона в целых числах, но он требует деления на каждом шаге. А нельзя ли по другому? Найти квадратный корень по модулю степени двойки, и проверить, а не будет ли он обычным квадратным корнем.

Можно ограничиться нечетными числами: для четного числа, если количество нулевых младших разрядов нечетно, то корня нет, а если четно, то можно сдвинуть число вправо, посчитать корень от нечетного, и сдвинуть обратно влево на половину от первоначального количества нулевых бит.

Для нечетного N и 2^k, k > 3, если N ≡ 1 mod 8, то есть 4 разных корня по модулю 2^k, а иначе корней нет. Нам нужен наименьший из этих четырех корней x. При этом другие три корня это 2^k — x, 2^k-1 + x и 2^k — 2^k-1 — x

Хочется что-то подобное вычислению обратного по модулю 2^k — удваивая количество верных бит за итерацию.

Пусть у нас уже есть корень x₀ из N по модулю 2^k: N — x₀² = 2^ka
И мы хотим найти x₁ = x₀ + 2^k-1y, такое чтобы в N — x₁² было больше младших нулевых бит.
N — (x₀ + 2^k-1y)² = 2^ka — 2^kx₀ * y — 2^2k-2y²
Поделим на 2^k: a — x₀ * y — 2^k-2y²
И приравняем к 0 по модулю 2

k-2: y = a * x₀^-1 mod 2^k-2
Получилии x₁ = x₀ + 2^k-1a * (x₀^-1 mod 2^k-2)
И окончательно x₁ = x₀ + (N — x₀²)/2 * (x₀^-1 mod 2^k-2)

Из k бит на следующей итерации получится 2(k-1) бит.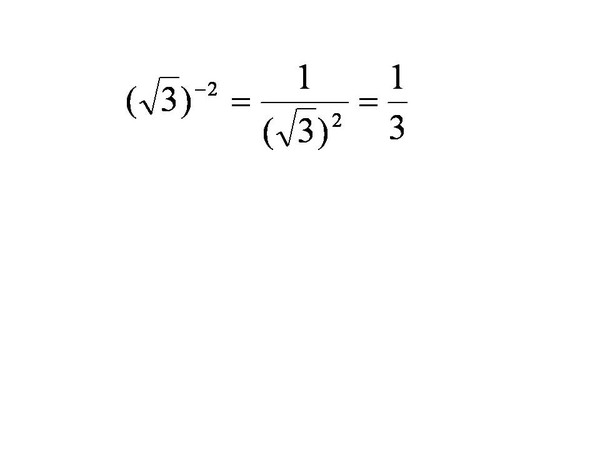 Параллельно считаем на каждой итерации обратное к корню.

Тестовый код:

uint8_t sqr16(uint16_t n) {
  if (n % 8 != 1) return 0;
  uint16_t sqr = (n + 1) / 2;  //4 bit
  uint16_t inv = 2 - sqr;
  sqr += inv * (n-sqr*sqr)/2;   //6 bit
  inv *= 2 - sqr * inv;
  sqr += inv * (n-sqr*sqr)/2;  //10 bit
  //inv *= 2 - sqr * inv;
  if (sqr & 256)
    sqr = 0u - sqr;
  sqr = (uint8_t)sqr; // lowest root
  if (n == sqr*sqr) return sqr;
  return 0;
}

Добавив пару итераций, получим корень из uint_64

Теги:

• теория чисел
• квадратный корень

Хабы:

• Математика

Всего голосов 29: ↑24 и ↓5 +19

Комментарии 13

@paluke

Пользователь

Комментарии Комментарии 13

3-8 9 Оценить квадратный корень из 12 10 Оценить квадратный корень из 20 11 Оценить квадратный корень из 50 94 18 Оценить квадратный корень из 45 19 Оценить квадратный корень из 32 20 Оценить квадратный корень из 18 92

Чему равен квадратный корень из \\[2\\] в степени \\[2\\] ?

Последняя обновленная дата: 19 февраля 2023 г.

•

Всего просмотров: 206,4K

•

Просмотры сегодня: 3,93K

. Веркция

.

.

. довольно легко решить, если мы четко понимаем ключевые понятия, лежащие в основе данного вопроса. В таких задачах в первую очередь необходимо теоретическую постановку задачи преобразовать в математическую форму, а затем решить ее в соответствии с нашим требованием. Чтобы эффективно решить эту проблему, нам нужно иметь четкое представление о таких главах, как сурды и квадратные корни чисел. В этой конкретной задаче нам нужно найти квадратный корень из заданного числа. Общее представление квадратного корня любого числа ‘n’ имеет форму \[\sqrt{n}\] . Здесь, согласно постановке задачи, заданное число описывается как \[2\] в степени \[2\] , что математически представляется как \[{{2}^{2}}\].