Формулы ромба, формулы для расчета площади и периметра ромба
Содержание:
- Формулы площади ромба:
- Формула периметра ромба:
Ромб — это четырёхугольник, у которого все стороны равны. Ромб можно рассматривать как частный случай параллелограмма, у которого или две смежные стороны равны, или диагонали взаимно перпендикулярны, или диагональ делит угол пополам. Ромб с прямыми углами называется квадратом.
Формулы площади ромба:
Площадь геометрической фигуры — часть поверхности, ограниченная замкнутым контуром данной фигуры. Величина площади ромба выражается числом заключающихся в него квадратных единиц.
1) Площадь ромба равна произведению длины его стороны на высоту (a, h).
2) Площадь ромба равна половине произведения его диагоналей.
S — площадь ромба
a — длина основания ромба
h — длина высоты ромба
d1 — длина 1-ой диагонали
d2 — длина 2-ой диагонали
См. также: Программа для расчета площади ромба.
также: Программа для расчета площади ромба.
Формула периметра ромба:
Периметр геометрической фигуры — суммарная длина границ плоской геометрической фигуры. Периметр имеет ту же размерность величин, что и длина.
1) Периметр ромба равен сумме 4-х длин его сторон или произведению длины любой его стороны на четыре (так как у ромба длины всех сторон равны).
P — периметр ромба
a — длина стороны ромба
Здесь вы найдете ответы.
Что понимается под высотой ромба?
Высота ромба представляет собой перпендикуляр, который опущен из одного из его углов на сторону, противоположную данному углу.
Высота ромба, опущенная из одного его угла, делит противолежащую сторону пополам. Как найти величины углов этого ромба?
Обозначим имеющийся ромб как ABCD. Из его угла В проведем высоту ВН, после
чего получим треугольник АВН с прямым углом. Известно, что длина всех
сторон ромба одинаковая, а длина АН равна половине длины АВ.
Учитывая то, что сумма всех углов треугольника равна 180 градусом, можно найти неизвестную величину третьего угла треугольника:
BAH=180-30-90=60 градусов.
Так, угол АВС равен:
ABC=180-60=120 градусов.
Как найти высоту ромба, если единственной величиной, которая известна, является длина одной его стороны?
Известна формула площади (S) ромба, которая представляет собой произведение длины его стороны (а) на высоту (h), проведенную к ней:
S = a*h.
Есть возможность выразить высоту из приведенной выше формулы. Она будет равна отношению площади ромба к длине его стороны:
h = S/a.
Имеется треугольник с прямым углом и катетами длиной 3 см. и 4 см. Его
площадь аналогична площади ромба со стороной 5 см. Как найти высоту ромба?
Как найти высоту ромба?
Площадь (S) треугольника с прямым углом рассчитывается путем деления пополам произведения длин его катетов. В данном случае она будет равна:
SΔ = 4*3/2 = 6 см.кв.
Площадь ромба определяется умножением длины его стороны на высоту, проведенную к ней. Если принять высоту за х, и учесть, что площадь ромба равна площади прямоугольного треугольника (6 см.кв.), то:
S = 5*x = 6 см.кв.
Отсюда можно найти значение х:
х = 6/5 = 1,2 см.
Ответ: высота ромба составляет 1,2 см.
Как найти высоту ромба при условии, что длины его диагоналей равны 6 см. и 8 см.?
Диагонали, проведенные в ромбе, делят эту фигуру на четыре треугольника,
которые являются равными. Длины катетов этих треугольников составляют 3
см. и 4 см. Такой вывод можно сделать на основании того, что в точке
пересечения диагоналей они делятся пополам. Гипотенуза (с) треугольников
представляет собой сторону ромба. Ее длина равна:
Гипотенуза (с) треугольников
представляет собой сторону ромба. Ее длина равна:
с = √(9+16) = √25 = 5 см.
Следовательно, сторона ромба также равна 5 см.
Площадь ромба высчитывается как произведение длин его диагоналей, деленное пополам:
S = d1*d2/2 = 6*8/2 = 24 см. кв.
Известна также другая формула, используемая для вычисления площади ромба, в которой длина его стороны (а) умножается на высоту(h):
S = a*h
h = S/a = 24/5 = 4,8 см.
Ответ: Высота ромба составляет 4,8 см.
Как найти высоту ромба при условии, что его диагонали равны d1 и d2, а длина стороны – а?
Высоту ромба можно рассчитать, если его диагонали (d1 и d2)и сторона (а) – известные величинами. В этом случае для определения неизвестной высоты следует пользоваться приведенной ниже формулой:
h = (d1 * d2)/a
Площадь ромба составляет 60 см. кв., а его периметр равен 48 см. Как найти
высоту ромба в конкретном случае?
кв., а его периметр равен 48 см. Как найти
высоту ромба в конкретном случае?
Периметр (Р) ромба равен сумме длин всех его сторон (а) и вычисляется по следующей формуле:
Р = а+а+а+а
В данном случае периметр ромба равен 48 см., это значит, что:
а+а+а+а = 48 см.
Находим значение а:
а = 48/4 = 12 см.
Площадь ромба (S) является произведением длины его стороны (а) и высоты (h), проведенной к этой стороне:
S = а*h
В задании сказано, что площадь ромба – 60 см.кв. Значит:
а*h=60
Находим неизвестную высоту:
h=60/а=60/12=5 см.
Ответ: Высота ромба – 5 см.
Как найти высоту ромба, зная о том, что его площадь составляет 48 см.кв., а периметр – 32 см.?
Согласно формуле расчета периметра (Р) ромба, он равен сумме длин всех его сторон (а) (Р=а+а+а+а). Известно, что все стороны ромба имеет одинаковую длину. Из этого следует, что длина одной стороны будет равна ¼ части его периметра:
а = Р/4 = 32/4 = 8 см.
Площадь (S) ромба можно высчитать путем умножения длины его стороны (а) на высоту (h), проведенную к ней:
S = а* h
В конкретном случае:
48 = 8* h
Отсюда можем найти высоту (h), разделив площадь на длину стороны ромба:
H = 48/8 = 6 см.
Ответ: Высота ромба составляет 6 см.
Отношение длин диагоналей ромба выглядит как 10/24. Его периметр равен 52 см. Как найти высоту ромба в данном случае?
Периметр (Р) ромба равен сумме длин всех его сторон (а), длины которых равны. Это значит:
Р = 4*а
По условию задачи:
52 = 4*а
Следовательно:
а = 52/13 = 13 см.
Предположим, что длина одной из диагоналей ромба равна 10х, тогда длина второй его диагонали будет выглядеть как 24х. Отношение их длин можно записать в следующем виде:
10х:24х=10:24
Доказано, что диагонали ромба взаимно перпендикулярны и в точке
пересечения они делятся пополам, при этом образуя четыре равных
треугольника с прямым углом.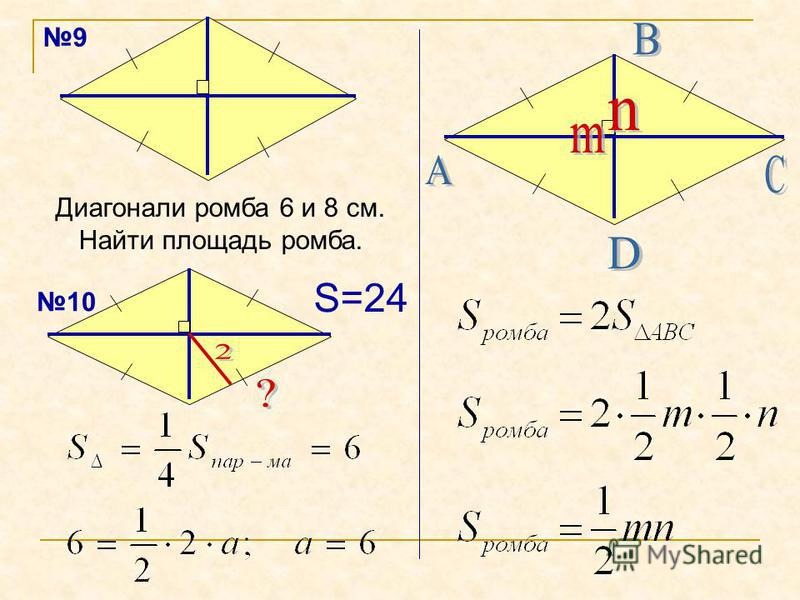
Теорема Пифагора гласит, что сумма длин его катетов, возведенных во вторую степень, равна длине гипотенузы, которая также возведена в квадрат:
с2 = а2 + b2
Для данной задачи это равенство записывается так:
(5х)²+(12х)²=13²
Отсюда видно, что:
169х²=169; следовательно, х2 = 1. Значит х тоже будет равен 1.
Длина диаметра, обозначенного как 10х, равна 10 см. (10*1), а длина второго диаметра, который обозначен как 24х, равна 24 см. (24*1).
Площадь (S) ромба рассчитывается как:
S = d₁*d₂/2 или a·h
Из этого можно составить следующее уравнение:
d₁*d₂=2a*h
Выражаем h и получаем:
h= d₁*d₂/2*а=10·24:26=240/26=120/13 см.
Какая формула используется с целью вычисления высоты ромба?
Ромб имеет четыре высоты. Все они имеют равные длины. Вывод об этом можно
сделать, рассмотрев все треугольные фигуры, элементами которых являются
эти высоты.
Предположим, что нам известна площадь (S) ромба и длина его стороны (а). В этом случае высота ромба будет равна отношению его площади к длине высоты: h = S/a.
Если же по условию задачи известны длины диагоналей ромба d1 и d2, а также его сторона а, то высоту можно рассчитать так: h = (d1*d2 )/a.
В случае, когда известна длина стороны (а) ромба и угол А, находящийся между смежными сторонами, то для расчета высоты ромба используется следующая формула:
h = a*a*sin A /a = a*sin A.
Существуют также и другие варианты вычисления длины высоты ромба на
основании того, какие величины будут известны по условию задания. Однако
ключевыми параметрами, используя которые можно вычислить высоту ромба,
являются диагонали, длина любой его стороны и угол, образованный между
смежными сторонами.
В каком виде записываются формулы, используемые для определения площади ромба?
Площадь ромба можно рассчитать одним из трех способов:
1. S = a² sin a, в которой α — образованный двумя сторонами угол, a — сторона.
2. S = ah, или Длина стороны ромба, умноженная на его высоту.
3. S = (d1*d2)/2, в которой d1 и d2 – длины диагоналей фигуры.
На сторону ромба опущена высота, которая на 1,7 см. меньше ее длины. Периметр фигуры составляет 32 см. Как в данном случае вычислить площадь ромба?
Зная, чему равен периметр ромба, можно вычислить длину его стороны:
Р/4 = 8 см.
Известно, что высота данной фигуры меньше ее стороны на 1,7 см. Теперь можем определить длину высоты:
h = 8-1,7 = 6,3 см.
Площадь ромба можно найти, умножив его сторону на высоту, которая на нее опущена:
8 * 6,3 = 50,4 см².кв.
Ответ: S = 50,4 см.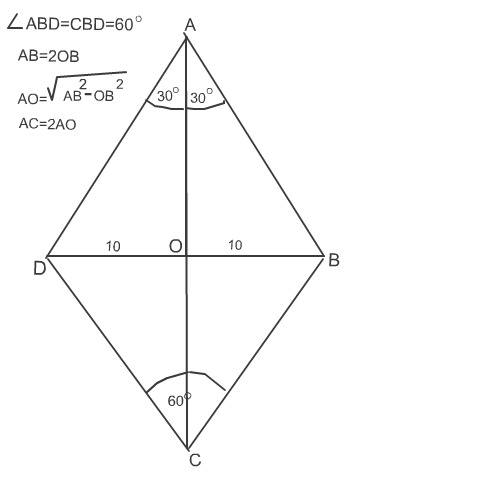 кв.
кв.
Известно, что диагонали ромба относятся как 4/3, а его сторона составляет 10 см. Как найти площадь ромба?
Если длины диагоналей фигуры относятся как 4/3, то их половины будут относиться также:
(4d)²+(3d)²=10² = 16d²+9d² = 100
Отсюда:
25d²=100
d =2,
Значит:
d¹/2 = 4d = 8 см.
d²/2 = 3d = 6 см.
Теперь можно найти площадь:
S= 2*d¹/2*d²/2=2*8*6 = 96 см.кв.
Ответ: S ромба = 96 см.кв.
Как записывается формула расчета площади ромба через длины его диагоналей d1 и d2?
Площадь ромба можно описать как сумму площадей 2-х треугольных фигур, основанием которых является одна диагональ, а вторая диагональ ромба представляет собой сумму длин высот этих фигур. Диагонали ромба при пересечении образуют угол в 90 градусов. На основании этого можно найти площадь ромба следующим образом:
S = ½ d1*d2.
Как записать формулу вычисления площади ромба через диагонали?
Известно, что, пересекаясь, диагонали ромба образуют угол в 90 градусов и
в точке пересечения делятся пополам.
Для расчета площади ромба через диагонали нужно перемножить их длины, а затем разделить полученное число на два:
S = ½ d1*d2.
Для примера можно рассмотреть ромб, одна диагональ которого равна 5 см., а вторая – 4 см. Тогда его площадь будет равна:
S=1/2*5*4=10 см. кв.
Как выглядит формула для определения площади ромба?
S ромба возможно вычислить, перемножив длину одной из его сторон (а) и высоту (h). Формула записывается так:
S=a*h.
См. также: Программа для расчета периметра ромба.
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Как узнать периметр ромба зная его диагонали.
Ромб – геометрическая фигура, у которой все четыре стороны ровны. Не стоит путать ромб с параллелограммом, у которого параллельные стороны равны. Еще одной характерной особенностью ромба является то, что противоположные углы в нем тоже равны, а в точке пересечения диагоналей образуется прямой угол.
Еще одной характерной особенностью ромба является то, что противоположные углы в нем тоже равны, а в точке пересечения диагоналей образуется прямой угол.
Как найти периметр ромба? Для этого достаточно знать всего лишь одну величину – длину стороны. Так как периметр представляет собой длину замкнутого контура, то эта величина для нашей фигуры будет равна произведению стороны на 4, ведь у этой фигуры четыре одинаковых стороны. В геометрии не всегда решения задач настолько простые. Довольно часто по условиям задания длина стороны неизвестная. Как найти периметр фигуры, если нет этой величины? Если дана диагональ, то периметр можно найти, используя теорему Пифагора. Пусть одна диагональ будет 8 см, а другая 4 см. В таком случае их половины будут 4 и 2 см соответственно. Это катеты прямоугольного треугольника, а его гипотенуза – сторона ромба, которую нам необходимо вычислить.
По теореме Пифагора гипотенуза — это квадратный корень из суммы квадратов катетов, то есть сторона l 2 =4 2 +2 2 =20. Извлеките квадратный корень из полученного результата, и получите сторону ромба или гипотенузу прямоугольного треугольника, образованного диагоналями ромба. В нашем случае сторона ромба 4,5 см, соответственно периметр будет 4,5*4=18 см.
Извлеките квадратный корень из полученного результата, и получите сторону ромба или гипотенузу прямоугольного треугольника, образованного диагоналями ромба. В нашем случае сторона ромба 4,5 см, соответственно периметр будет 4,5*4=18 см.
В задачах по геометрии иногда известны значения не двух диагоналей, а лишь одной. В таком случае дается еще один из углов ромба. Если угол ромба равен 60 градусов, а длина одной из диагоналей равна 10 см, то можно рассчитать длину стороны ромба по формуле, используя теорему Пифагора. Соответственно, угол прямого треугольника, образованного диагоналями, будет равен 60/2=30 градусов. Тогда длина катета равна 10/2=5 см. Чтобы найти длину гипотенузы, воспользуемся формулой:
Lгипотенузы=Lкатета*cos(α)
В нашем случае длина гипотенузы равна 5*cos30=5*0,87= 4,35 см. Тогда периметр искомой фигуры равен 4,35*4=17,4 см. Воспользуйтесь инженерным калькулятором для расчетов или специальной таблицей со школьного курса геометрии, где указаны синусы и косинусы основных углов.
Можно рассчитать периметр, зная площадь фигуры и ее диагональ. В таком случае мы сможем рассчитать длину второй диагонали и найти сторону ромба по теореме Пифагора. Площадь фигуры равна S=(d1+d2)/2. Тогда d2=2S/d1. Если площадь искомой фигуры 18 см, а одна из диагоналей 8 см, тогда длина второй диагонали равна 2*18/8=4,5 см. По теореме Пифагора находим гипотенузу, квадрат которой равен сумме квадратов половин диагоналей. Получаем, что квадрат гипотенузы 4 2 +2,25 2 =16+5=21. Извлекаем квадратный корень и получаем 4,6 см. Тогда периметр фигуры можно рассчитать по формуле 4,6*4=18,4 см.
Как видите, рассчитать периметр ромба достаточно просто, необходимо знать самые простые теоремы и аксиомы геометрии. За основу взята теорема Пифагора, а также формулы определения длины гипотенузы по углам прямоугольного треугольника. Если трудно разобраться с углами, нарисуйте треугольник и обозначьте его углы.
Инструкция
Рассмотрите любой квадрат. Вспомните его свойства. У него 4 стороны, причем все они одинаковы по длине и расположены по отношению друг к другу под прямым углом. Обозначьте сторону квадрата как а, а периметр — как р.
Вспомните его свойства. У него 4 стороны, причем все они одинаковы по длине и расположены по отношению друг к другу под прямым углом. Обозначьте сторону квадрата как а, а периметр — как р.
Вспомните, как найти размер части любого объекта, если эти части равны, а количество их вам известно. Это можно сделать, разделив целое на количество частей. Представьте периметр как целый объект, тогда каждая сторона будет его частью. Всего этих частей четыре. То есть размер стороны можно найти, разделив периметр на 4. Выразить это можно формулой a=p/4.
Точно таким же образом, зная периметр, можно найти размер стороны любого правильного многоугольника. Для пятиугольника справедлива формула а=р/5, для шестиугольника — а=р/6 и т. д.
Подумайте, у какого еще многоугольника 4 стороны, и при том они равны между собой. Это ромб, частным случаем которого многие математики считают квадрат. У ромба углы, принадлежащие одной стороне, не равны между собой, но для вычисления периметра это не играет никакой роли. Сторону любого ромба можно найти точно так же, как и сторону квадрата , то есть разделив периметр на 4.
Сторону любого ромба можно найти точно так же, как и сторону квадрата , то есть разделив периметр на 4.
Зная периметр квадрата , можно найти еще несколько размеров, важных для этой геометрической фигуры. Сделайте дополнительное построение, вписав в квадрат окружность. Проведите диаметр так, чтобы он соединил точки касания окружности с противолежащими сторонами квадрата . Диаметр равен стороне этой геометрической фигуры. А это значит, что и его можно найти точно тем же способом, то есть разделив периметр на 4. Выразить это можно формулой d=p/4.
В задачах очень часто требуется не диаметр окружности, а ее радиус. Найти его можно, разделив диаметр на 2. А если попытаться выразить радиус через периметр, получится формула r=d/2=(p:4)/2=р/8.
Через периметр можно выразить и радиус описанной окружности. Постройте ее и проведите радиус, который пересечет окружность в одной из вершин квадрата . Из центра окружности проведите перпендикуляр к одной из сторон данного угла. 2.
2.
Часто в геометрических задачах требуется найти длину стороны квадрата, если известны другие его параметры — такие, как площадь, диагональ или периметр.
Вам понадобится
- Калькулятор
Инструкция
Найти длину стороны квадрата.
Решение:
a=√9=3
Ответ:
Сторона квадрата равняется 3 метрам.
В том случае, когда известен периметр квадрата, для определения длины стороны нужно числовое значение периметра разделить на четыре (так как квадрат имеет четыре стороны одинаковой длины):
a=P/4, где:
a — длина стороны квадрата;
P — периметр квадрата.
Единицей измерения стороны квадрата будет являться та же самая линейная единица измерения длины как и у периметра. Например, если периметр квадрата задан в сантиметрах, то длина его стороны также получится в сантиметрах.
Пример:
Периметр квадрата составляет 20 метров.
Найти длину стороны квадрата.
Решение:
a=20/4=5
Ответ:
Длина стороны квадрата равняется 5 метрам. 2), где:
2), где:
a — длина стороны квадрата;
d — длина диагонали квадрата.
Единицей измерения стороны квадрата будет являться единица измерения длины та же самая, что и у диагонали. Например, если диагональ квадрата измерена в сантиметрах, то и длина его стороны получится в сантиметрах.
Пример:
Диагональ квадрата равняется 10 метров.
Найти длину стороны квадрата.
Решение:
a=10/√2, или приблизительно: 7,071
Ответ:
Длина стороны квадрата равняется 10/√2, или примерно 1,071 метра.
Источники:
- стороны квадрата
Ромб — это параллелограмм, у которого все стороны равны. Кроме равенства сторон, ромб обладает другими свойствами. В частности, известно, что диагонали ромба пересекаются под прямым углом и точкой пересечения каждая из них делится пополам.
Инструкция
Периметр ромба можно вычислить, зная длину его стороны. В этом случае по определению периметр ромба равен сумме длин его сторон, а значит равен 4a, где a — длина стороны ромба .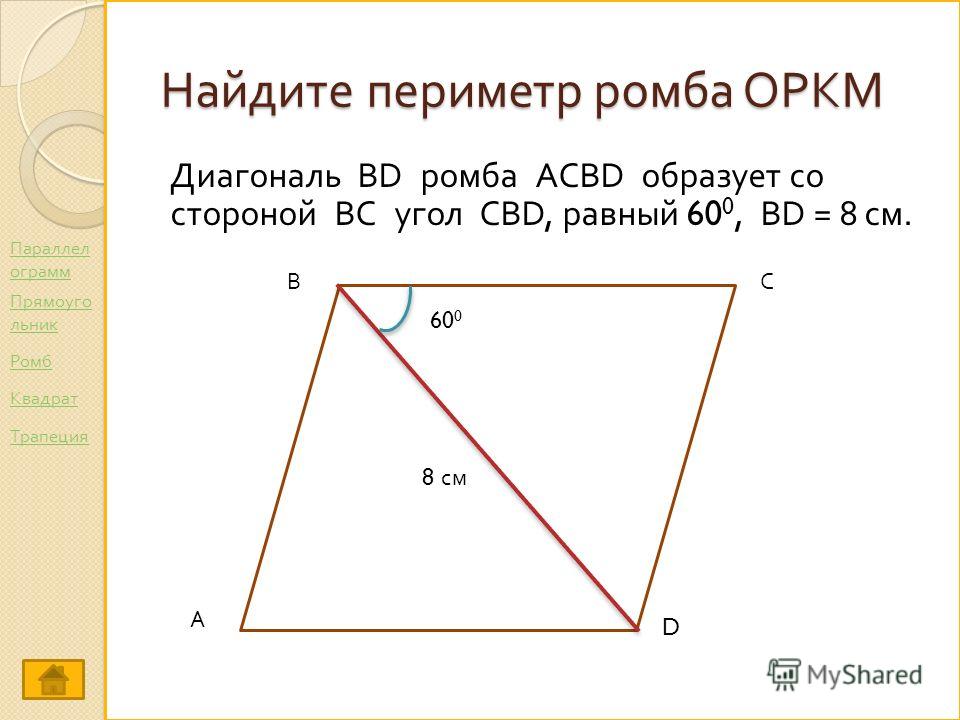
Если известны площадь ромба и соотношение между диагоналями, то задача нахождения периметра ромба несколько усложняется. Пусть дана площадь ромба S и соотношение диагоналей AС/BD = k. Площадь ромба можно выразить через произведение диагоналей: S = AC*BD/2. Треугольник AOB является прямоугольным, так как диагонали ромба пересекаются под углом 90°. Сторону ромба AB по теореме Пифагора можно найти из следующего выражения: AB² = AO² + OB². Так как ромб — частный случай параллелограмма, а в параллелограмме диагонали делятся пополам точкой пересечения, то AO = AC/2, а OB = BD/2. Тогда AB² = (AC² + BD²)/4. По условию AC = k*BD, тогда 4*AB² = (1 + k²)*BD².
Выразим BD² через площадь:
S = k*BD*BD/2 = k*BD²/2
BD² = 2*S/k
Тогда 4*AB² = (1 + k²)*2S/k. Отсюда AB равно корню квадратному из S(1 + k²)/2k. А периметр ромба по-прежнему равен 4*AB.
Источники:
- найди периметр ромба если площадь а угол
Квадрат – красивая и простая плоская геометрическая фигура. Это прямоугольник с равными сторонами. Как же найти периметр квадрата , если известна длина его стороны?
Это прямоугольник с равными сторонами. Как же найти периметр квадрата , если известна длина его стороны?
Инструкция
Прежде всего, стоит вспомнить, что периметр есть ни что иное как сумма длин сторон геометрической фигуры. Рассматриваемый нами квадрат имеет четыре стороны. Более того, по определению квадрата , все эти стороны равны между собой.
Из этих предпосылок вытекает простая формула для нахождения периметр а квадрата – периметр квадрата равен длине стороны квадрата , умноженной на четыре:
Р = 4а, где а – длина стороны квадрата .
Видео по теме
Периметр – это суммарная длина сторон геометрической фигуры. Но если возникнет необходимость быстро рассчитать периметр чего-либо (например, во время ремонта или строительства), не каждый сможет это сделать с легкостью. Вспомним основные правила для вычисления периметра.
Задание 2. Периметр ромба | Уроки математики и физики для школьников и родителей
Прежде чем приступить к решению примеров и задач, обязательно ознакомьтесь с теоретической частью урока
или
посмотритеВИДЕОУРОК youtube.com/embed/XxqzZyzeGTk» youtube-src-id=»XxqzZyzeGTk»>
1. Диагонали ромба 14 см и 48 см. Вычислите периметр ромба.
а) 200 см;
б) 100 см;
в) 50 см;
г) 75 см.
2. В равносторонний треугольник вписан ромб, периметр которого равен 16 см. Найдите периметр треугольника.
а) 16 см;
б) 32 см;
в) 24 см;
г) 22 см.
3. Один из углов ромба в 5 раз больше другого. Найдите расстояние от
вершины острого угла ромба до прямой, на которой лежит противоположная сторона
ромба, если его периметр равен 56 см.
а) 7 см;
б) 5 см;
в) 14 см;
г) 12 см.
4. Диагонали ромба равны 10 см и 24 см. Найдите периметр ромба.
а) 68 см;
б)
104 см;
в) 136 см;
г) 52 см.
5. Диагонали ромба образуют со стороною углы, пропорциональные числам 1 и 5. Найдите периметр ромба, если расстояние между его параллельными сторонами равно 8 см.
а) 68 см;
б) 58 см;
в) 64 см;
г) 62 см.
6. Диагональ ромба АВСD разделили на 6 равных частей и через точки деления провели
прямые, параллельные другой диагонали. Найдите периметр ромба, если длина
одного из полученных на стороне АВ отрезков
равна 2,5 см.
Диагональ ромба АВСD разделили на 6 равных частей и через точки деления провели
прямые, параллельные другой диагонали. Найдите периметр ромба, если длина
одного из полученных на стороне АВ отрезков
равна 2,5 см.
а) 45 см;
б) 30 см;
в) 15 см;
г) 60 см.
7. Найдите периметр ромба, меньшая диагональ которого равна 6 см, а острый угол – 60°.
а) 36 см;
б) 18 см;
в) 12 см;
г) 24 см.
8. Найдите периметр ромба АВСD, если его диагонали равны соответственно
АС = 6м и ВD = 8м.
а) 32 см;
б) 20 см;
в) 18 см;
г) 24 см.
9. Найдите периметр ромба, если его диагонали
равны соответственно
12см и 16см.
а) 40 см;
б) 48 см;
в) 32 см;
г) 34 см.
10. В равносторонний треугольник ABC вписан ромб AMNP. Найдите периметр ромба, если периметр четырёхугольника AMNC равен 60 см.
а) 45 см;
б) 36 см;
в) 48 см;
г) 60 см.
11. Периметр ромба
равен 16 см, а высота, опущенная из
вершины тупого угла, делит сторону ромба пополам. Найдите углы ромба.
Найдите углы ромба.
а) 60°, 120°, 60°, 120°;
б) 30°, 150°, 30°, 150°;
в) 40°, 140°, 40°, 140°;
г) 80°, 100°, 80°, 100°.
12. Один из углов ромба равен 60°. Перпендикуляр, опущенный из точки пересечения его диагоналей на большую сторону, равен 5/3√͞͞͞͞͞3 см. Найдите периметр ромба.
а) 32 см;
б) 40 см;
в) 44 см;
г) 36 см.
Найдите площадь ромба если его диагонали 8см и 12см: Найдите площадь ромба,если его диагонали равны 8 см и 12 см — ЭкоДом: Дом своими руками
Вариант 1 | ВАРИАНТ 2 |
1. | 1. Периметр квадрата равен 36 см. Чему равна его площадь? |
2. В прямоугольнике АВСD сторона АВ равна 12см. Расстояние от точки пересечения диагоналей до этой стороны равно 8 см. Найдите площадь треугольника АВС. | 2. В прямоугольнике АВСD сторона ВС равна 18см. Расстояние от точки пересечения диагоналей до этой стороны равно 7см. Найдите площадь треугольника ВСD. |
3. Высота ВD треугольника АВС равна 8см и делит сторону АС на отрезки, равные 5 см и 6 см. Найдите площадь треугольника. | 3. Высота ВD треугольника АВС делит сторону АС на отрезки, равные 7см и 4см. Площадь треугольника равна 55 см2 . Найдите длину ВD. |
4. Стороны параллелограмма равны 10 см и 6 см, а угол между ними равен 150°. Чему равна площадь этого параллелограмма? | 4. Стороны параллелограмма равны 12 см и 8 см, а угол между ними равен 30°. |
5. Чему равна площадь ромба, диагонали которого равны 8 см и 6 см? | 5. Чему равна площадь ромба, диагонали которого равны 6 см и 13 см? |
6. Две стороны треугольника равны 12 см и 9 см, а угол между ними 30°. Чему равна площадь треугольника? | 6. Найдите площадь треугольника, две стороны которого равны 6 см и 8 см, а угол между ними 30°. |
7. В прямоугольной трапеции основания равны 5 см и 9 см, а меньшая боковая сторона равна 4 см. Чему равна площадь трапеции? | 7. В прямоугольной трапеции основания равны 6 см и 10 см, а меньшая боковая сторона 5 см. Чему равна площадь трапеции? |
8. Найдите сторону квадрата, площадь которого равна площади прямоугольника со сторонами 13 и 52. | 8. Найдите сторону квадрата, площадь которого равна площади прямоугольника со сторонами 0,5 и 2. |
9. Найдите площадь ромба, если его стороны равны 5, а один из углов равен 150°. | 9. Найдите площадь ромба, если его стороны равны 6, а один из углов равен 150o. |
10. Найдите площадь прямоугольника, если его периметр равен 52, а отношение соседних сторон равно 3 : 10. | 10. Найдите периметр прямоугольника, если его площадь равна 624, а отношение соседних сторон равно 4 : 39. |
11. Площадь ромба равна 507. Одна из его диагоналей в 6 раз больше другой. Найдите меньшую диагональ. | 11. Площадь ромба равна 48. Одна из его диагоналей в 6 раз больше другой. Найдите меньшую диагональ. |
№ 2 | |
Вариант 2 | ВАРИАНТ 1 |
1. | 1. Периметр квадрата равен 160 см. Найдите площадь квадрата. |
2. Два катета прямоугольного треугольника равны 4 и 9. Найдите площадь этого треугольника. | 2. Два катета прямоугольного треугольника равны 4 и 10. Найдите площадь этого треугольника. |
3. Чему равна площадь ромба, диагонали которого равны 7 см и 6 см? | 3. Найдите площадь ромба, если его диагонали равны 14 и 6. |
4. Найдите площадь прямоугольника, если его периметр равен 60, а отношение соседних сторон равно 4:11. | 4. Найдите площадь прямоугольника, если его периметр равен 102, а отношение соседних сторон равно 2:15. |
5. Найдите площадь ромба, если его стороны равны 8, а один из углов равен 150°. | 5. |
6. В прямоугольной трапеции основания равны 5 см и 9 см, а меньшая боковая сторона равна 4 см. Чему равна площадь трапеции? | 6. В прямоугольной трапеции основания равны 6 см и 10 см, а меньшая боковая сторона 5 см. Чему равна площадь трапеции? |
7. Периметр ромба равен 116, а один из углов равен 30°. Найдите площадь ромба. | 7. Стороны параллелограмма равны 10 см и 8 см, а угол между ними равен 30°. Чему равна площадь этого параллелограмма? |
8. Стороны параллелограмма равны 9 и 15. Высота, опущенная на первую сторону, равна 10. Найдите высоту, опущенную на вторую сторону параллелограмма. | 8. Стороны параллелограмма равны 20 и 110. Высота, опущенная на первую сторону, равна 66. Найдите высоту, опущенную на вторую сторону параллелограмма. |
9. Площадь параллелограмма ABCD равна 12. Точка E — середина стороны АВ. Найдите площадь трапеции EBCD. | 9. Площадь параллелограмма ABCD равна 56. Точка E — середина стороны CD. Найдите площадь трапеции AECB. |
Вариант 1. 1. Найдите площадь прямоугольного треугольника, если его катеты равны 12 см и 18 см 2. Найдите площадь ромба, если его диагонали равны 14 см и 22 см. 3. Чему равна площадь квадрата со стороной 13 см? 4. Смежные стороны прямоугольника равны 15м и 20 м. Найдите его площадь. 5. В треугольнике известны длины двух сторон: 18 дм и 16 дм. Высота, проведенная к большей стороне, равна 9 дм. Чему равна высота, проведенная к меньшей стороне? 6. Смежные стороны параллелограмма равны 12см и 10см, а высота, проведенная к меньшей стороне, равна 18см. 7. Найдите площадь трапеции с основаниями 22 см и 38 см и высотой 20 см. | Вариант 2 1. Найдите площадь квадрата со стороной 16 дм. 2. Найдите площадь треугольника, если известно, что одна сторона равна 20 см, а высота, проведенная к ней, равна 18 см. 3. Чему равна площадь трапеции, если известно, что её основания равны 26 см и 24 см, а высота равна 15 см. 4. Чему равна площадь прямоугольного треугольника с катетами 15см и 22 см? 5. Чему равна площадь ромба с диагоналями 24 м и 18 м? 6. Чему равна площадь прямоугольника со сторонами 18 м и 12 м? 7. Смежные стороны параллелограмма равны 16см и 20 см. Найдите меньшую высоту, если большая равна 14 см. |
Вариант 3. 1. Найдите площадь прямоугольного треугольника, если его катеты равны 16 м и 20 м 2. Найдите площадь ромба, если его диагонали равны 16 см и 24 см. 3. Чему равна площадь квадрата со стороной 17 см? 4. 5. В треугольнике известны длины двух сторон: 20см и 18 см. Высота, проведенная к большей стороне, равна 12 см. Чему равна высота, проведенная к меньшей стороне? 6. Смежные стороны параллелограмма равны 18см и 10см, а высота, проведенная к большей стороне, равна 18см. Найдите площадь параллелограмма. 7. Найдите площадь трапеции с основаниями 22 см и 38 см и высотой 20 см. | Вариант 4. 1. Найдите площадь квадрата со стороной 19 дм. 2. Найдите площадь треугольника, если известно, что одна сторона равна 30 см, а высота, проведенная к ней, равна 16 см. 3. Чему равна площадь равнобедренной трапеции, если известно, что её основания равны 28 см и 22 см, боковая сторона – 5 см, а высота равна 4 см. 4. Чему равна площадь прямоугольного треугольника с катетами 16см и 18 см? 5. Чему равна площадь ромба с диагоналями 32 м и 22 м? 6. Чему равна площадь прямоугольника со сторонами 15 м и 21 м? 7. |
Вариант 1. 1. Найдите площадь прямоугольного треугольника, если его катеты равны 12 и 18 см 2. Найдите площадь ромба, если его диагонали равны 14 см и 22 см. 3. Чему равна площадь квадрата со стороной 13 см? 4. Смежные стороны прямоугольника равны 15м и 20 м. Найдите его площадь. 5. В треугольнике известны длины двух сторон: 18 дм и 16 см. Высота, проведенная к большей стороне, равна 7 дм. Чему равна высота, проведенная к меньшей стороне? 6. Смежные стороны параллелограмма равны 12см и 10см, а высота, проведенная к меньшей стороне, равна 18см. Найдите площадь параллелограмма. 7. Найдите площадь трапеции с основаниями 22 см и 38 см и высотой 20 см. | Вариант 2 1. Найдите площадь квадрата со стороной 16 дм. 2. Найдите площадь треугольника, если известно, что одна сторона равна 20 см, а высота, проведенная к ней, равна 18 см. 3. Чему равна площадь трапеции, если известно, что её основания равны 26 см и 24 см, а высота равна 15 см. 4. Чему равна площадь прямоугольного треугольника с катетами 15см и 22 см? 5. Чему равна площадь ромба с диагоналями 24 м и 18 м? 6. Чему равна площадь прямоугольника со сторонами 18 м и 12 м? 7. Смежные стороны параллелограмма равны 16см и 20 см. Найдите меньшую высоту, если большая равна 14 см. |
Вариант 3. 1. Найдите площадь прямоугольного треугольника, если его катеты равны 16 м и 20 м 2. Найдите площадь ромба, если его диагонали равны 16 см и 24 см. 3. Чему равна площадь квадрата со стороной 17 см? 4. Смежные стороны прямоугольника равны 18 дм и 30 дм. Найдите его площадь. 5. В треугольнике известны длины двух сторон: 20см и 18 см. Высота, проведенная к большей стороне, равна 12 см. Чему равна высота, проведенная к меньшей стороне? 6. Смежные стороны параллелограмма равны 18см и 10см, а высота, проведенная к большей стороне, равна 18см. 7. Найдите площадь трапеции с основаниями 22 см и 38 см и высотой 20 см. | Вариант 4. 1. Найдите площадь квадрата со стороной 19 дм. 2. Найдите площадь треугольника, если известно, что одна сторона равна 30 см, а высота, проведенная к ней, равна 16 см. 3. Чему равна площадь равнобедренной трапеции, если известно, что её основания равны 28 см и 22 см, боковая сторона – 5 см, а высота равна 4 см. 4. Чему равна площадь прямоугольного треугольника с катетами 16см и 18 см? 5. Чему равна площадь ромба с диагоналями 32 м и 22 м? 6. Чему равна площадь прямоугольника со сторонами 15 м и 21 м? 7. Смежные стороны параллелограмма равны 16см и 20 см. Найдите большую высоту, если меньшая равна 8 см. |
Вариант 1. 1. Найдите площадь прямоугольного треугольника, если его катеты равны 12 и 18 см 2. Найдите площадь ромба, если его диагонали равны 14 см и 22 см. 3. Чему равна площадь квадрата со стороной 13 см? 4. Смежные стороны прямоугольника равны 15м и 20 м. Найдите его площадь. 5. В треугольнике известны длины двух сторон: 18 дм и 16 см. Высота, проведенная к большей стороне, равна 7 дм. Чему равна высота, проведенная к меньшей стороне? 6. Смежные стороны параллелограмма равны 12см и 10см, а высота, проведенная к меньшей стороне, равна 18см. Найдите площадь параллелограмма. 7. Найдите площадь трапеции с основаниями 22 см и 38 см и высотой 20 см. | Вариант 2 1. Найдите площадь квадрата со стороной 16 дм. 2. Найдите площадь треугольника, если известно, что одна сторона равна 20 см, а высота, проведенная к ней, равна 18 см. 3. Чему равна площадь трапеции, если известно, что её основания равны 26 см и 24 см, а высота равна 15 см. 4. Чему равна площадь прямоугольного треугольника с катетами 15см и 22 см? 5. Чему равна площадь ромба с диагоналями 24 м и 18 м? 6. 7. Смежные стороны параллелограмма равны 16см и 20 см. Найдите меньшую высоту, если большая равна 14 см. |
Персональный сайт учителя Низамутдиновой З.И.
Ромб
I вариант
Часть А
1. Установите истинность или ложность следующего высказывания:
Если в ромбе ABCD угол B равен 150°, то угол D равен 30°.
а) да;
б) нет;
в) не знаю.
2. Периметр ромба 8 см, а длина перпендикуляра, опущенного из вершины тупого угла на противоположную сторону, равна 1 см. Вычислить углы ромба.
а) 60° и 120°;
б)30° и 150°;
в) 80° и 100°.
3. Найдите периметр ромба ABCD, если ∟B =60°, AC=20 см.
а) 40 см;
б) 20 см;
в) 80 см.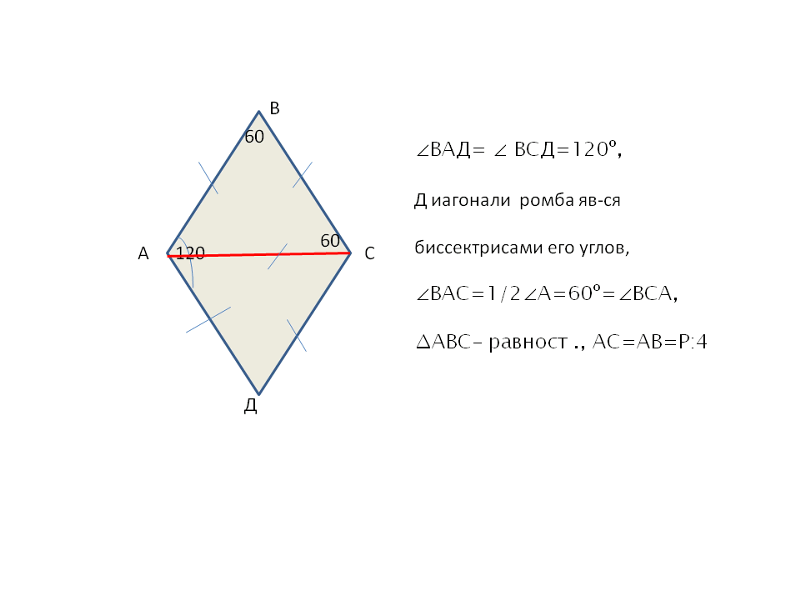
Часть В
4. Найдите сторону ромба, если его площадь равна 8√2 см², а угол равен 45°.
5. Найдите меньшую диагональ ромба, если его периметр равен 20 см, а один из углов 120°.
6. На сторонах AB и AD ромба ABCD взяты две точки M и N так, что прямые MC и NC делят ромб на три равновеликие части. Найти длину отрезка MN, если |BD|=d.
Часть C
7. В ромбе ABCD со стороной a угол при вершине A равен 120°. Точки E и F на сторонах BC и AD соответственно, отрезок EF и диагональ ромба AC пересекаются в точке M. Площади четырехугольников BEFA и ECDFотносятся, как 1:2. Найти длину отрезка EM, если|AM|:|MC|=1:3.
8. Найти площадь ромба ABCD, если радиусы окружностей, описанных около треугольников ABC и ABD, равны R и r.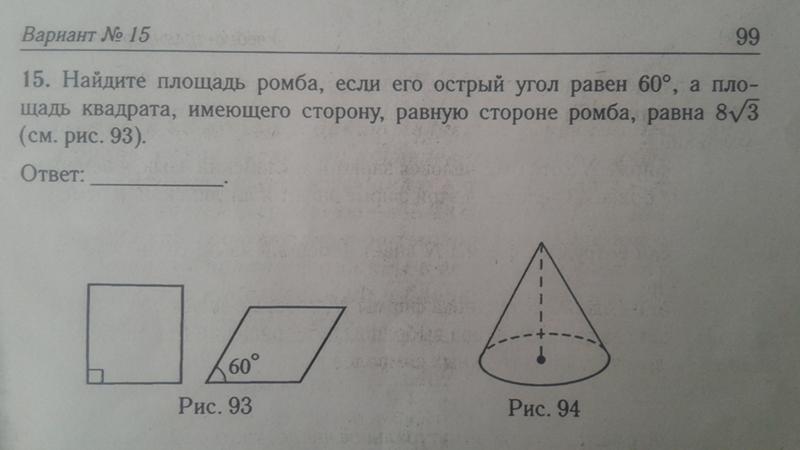
9. Найти углы ромба, если площадь вписанного в него круга вдвое меньше площади ромба.
II вариант
Часть А
1. Установите истинность или ложность следующего высказывания:
В ромбе ABCD стороны AB и BC равны и параллельны.
а) да;
б) нет;
в) не знаю.
2. Расстояния от точки пересечения диагоналей ромба до его вершин 8 см и 6 см. Какова длина каждой диагонали?
а) 6 см и 8 см;
б) 3 см и 4 см;
в) 12 см и 16 см.
3. Найдите меньшую диагональ ромба, если его периметр равен 20 см, а один из углов 120°.
а) 5 см;
б) 20 см;
в) 10 см.
Часть В
4. Найдите периметр ромба ABCD, если ∟B=60°, AC=20 см.
5. Определить острый угол ромба. в котором длина стороны есть среднее геометрическое длин диагоналей.
6. Площадь ромба S, сумма длин его диагоналей равна m. Найти сторону ромба.
Найти сторону ромба.
Часть C
7. Диагонали четырехугольника разбивают его на четыре треугольника равного периметра. Доказать, что данный четырехугольник — ромб.
8. В ромбе ABCD AP —биссектриса треугольника CAD, ∟BAD = 2ά, PD = a. Найдите площадь ромба.
9. В ромб с высотой h и острым углом ά вписана окружность. Найти радиус наибольшей из двух возможных окружностей, каждая из которых касается данной окружности и двух сторон ромба.
Сканави. Планиметрия. Задачи 101 – 150 с ответами и решениями
Сканави М. И.
Задачи по планиметрии с ответами и решениями
перейти к содержанию
Группа А. Задачи 101 — 150 (с ответами и решениями)
В прямоугольный треугольник с катетами а и b вписан квадрат, имеющий с треугольником общий прямой угол. Найти периметр квадрата. Ответ: Решение
В правильный треугольник вписан квадрат, сторона которого равна m.
 Найти сторону треугольника. Ответ: Решение
Найти сторону треугольника. Ответ: РешениеНайти площадь квадрата, вписанного в правильный треугольник со стороной а. Ответ: Решение
Сторона правильного треугольника, вписанного в окружность, равна а. Вычислить площадь квадрата, вписанного в ту же окружность. Ответ: Решение
На сторонах квадрата вне его построены правильные треугольники, и их вершины последовательно соединены. Определить отношение периметра полученного четырехугольника к периметру данного квадрата. Ответ: Решение
В квадрате, сторона которого а, середины двух смежных сторон соединены между собой и с противоположной вершиной квадрата. Найти площадь полученного треугольника. Ответ: Решение
В равнобедренный треугольник вписан квадрат единичной площади, одна сторона которого лежит на основании треугольника. Найти площадь треугольника, если известно, что центры масс треугольника и квадрата совпадают (центр масс треугольника лежит на пересечении его медиан).
 Ответ: 9/4 Решение
Ответ: 9/4 Решение- Площадь равнобедренного треугольника равна 1/3 площади квадрата, построенного на основании данного треугольника. Длины боковых сторон треугольника короче длины его основания на 1 см. Найти длины сторон и высоты треугольника, проведенной к основанию. Ответ: 4; 6 Решение
- Найти площадь правильного треугольника, вписанного в квадрат со стороной а при условии, что одна из вершин треугольника совпадает с вершиной квадрата. Ответ: Решение
- На сторонах равнобедренного прямоугольного треугольника с гипотенузой с вне этого треугольника построены квадраты. Центры этих квадратов соединены между собой. Найти площадь полученного треугольника. Ответ: Решение
- В квадрате со стороной а середины двух смежных сторон соединены между собой и с противоположной вершиной квадрата. Определить площадь внутреннего треугольника. Ответ: Решение
- В квадрат вписан другой квадрат, вершины которого лежат на сторонах первого, а стороны составляют со сторонами первого квадрата углы в 60°.
 Какую часть площади данного квадрата составляет площадь вписанного? Ответ: Решение
Какую часть площади данного квадрата составляет площадь вписанного? Ответ: Решение - Дан квадрат, две вершины которого лежат на окружности радиуса R, две другие — на касательной к этой окружности. Найти длину диагонали квадрата. Ответ: Решение
- Около квадрата со стороной а описана окружность. В один из образовавшихся сегментов вписан квадрат. Определить площадь этого квадрата. Ответ: Решение
- В сегмент, дуга которого равна 60°, вписан квадрат. Вычислить площадь квадрата, если радиус круга равен . Ответ: 1 Решение
- Сторона квадрата, вписанного в окружность, отсекает сегмент, площадь которого равна см2. Найти площадь квадрата. Ответ: 16 Решение
- Площадь прямоугольника равна 9 см2, а величина одного из углов, образованного диагоналями, равна 120°. Найти стороны прямоугольника. Ответ: Решение
- В круг радиуса R вписан прямоугольник, площадь которого вдвое меньше площади круга. Определить стороны прямоугольника.
 Ответ: Решение
Ответ: Решение - В прямоугольнике проведены биссектрисы двух углов, прилежащих к большей стороне. Определить, на какие части делится площадь прямоугольника этими биссектрисами, если стороны прямоугольника равны 2 и 4 м. Ответ: 2,2; 4 Решение
- В прямоугольный треугольник с углом 60° вписан ромб со стороной, равной 6 см, так, что угол в 60° у них общий и все вершины ромба лежат на сторонах треугольника. Найти стороны треугольника. Ответ: Решение
- В треугольник вписан ромб так, что один угол у них общий, а противоположная вершина делит сторону треугольника в отношении 2 : 3. Диагонали ромба равны n и m. Найти стороны треугольника, содержащие стороны ромба. Ответ: Решение
- Сумма длин диагоналей ромба равна m, а его площадь равна S. Найти сторону ромба. Ответ: Решение
- В ромб с острым углом 30° вписан круг, площадь которого равна Q. Найти площадь ромба. Ответ: Решение
- Периметр ромба равен 2 м, длины его диагоналей относятся как 3 : 4.
 Найти площадь ромба. Ответ: 0,24 Решение
Найти площадь ромба. Ответ: 0,24 Решение - Определить сторону ромба, зная, что площадь его равна S, а длины диагоналей относятся как m : n. Ответ: Решение
- Периметр ромба равен 2р, а длины диагоналей относятся как m : n. Вычислить площадь ромба. Ответ: Решение
- Высота ромба равна 12 см, а одна из его диагоналей равна 15 см. Найти площадь ромба. Ответ: 150 Решение
- Высота ромба, проведенная из вершины тупого угла, делит его сторону на отрезки длиной m и n (m считать от вершины острого угла). Определить диагонали ромба. Ответ: Решение
- Ромб, у которого сторона равна меньшей диагонали, равновелик кругу радиуса R. Определить сторону ромба. Ответ: Решение
В ромб с острым углом 30° вписан круг, а в круг — квадрат. Найти отношение площади ромба к площади квадрата. Ответ: 4 Решение
- В пересечение двух равных кругов вписан ромб с диагоналями 12 и 6 см. Найти радиус окружностей. Ответ: 7,5 Решение
- В ромб, который делится своей диагональю на два равносторонних треугольника, вписана окружность радиуса 2.
 Найти сторону ромба. Ответ: Решение
Найти сторону ромба. Ответ: Решение - Доказать, что если в четырехугольнике диагонали лежат на биссектрисах его углов, то такой четырехугольник есть ромб.
- На сторонах ромба как на диаметрах описаны полуокружности, обращенные внутрь ромба. Определить площадь полученной розетки, если диагонали ромба равны а и b. Ответ: Решение
- Периметр параллелограмма равен 90 см, а острый угол содержит 60°. Диагональ параллелограмма делит его тупой угол на части в отношении 1:3. Найти стороны параллелограмма. Ответ: 15; 30 Решение
- Величина одного из углов параллелограмма равна 60°, а меньшая диагональ см. Длина перпендикуляра, проведенного из точки пересечения диагоналей к большей стороне, равна см. Найти длины сторон и большей диагонали параллелограмма. Ответ: Решение
- Перпендикуляр, проведенный из вершины параллелограмма к его диагонали, делит эту диагональ на отрезки длиной 6 и 15 см. Разность длин сторон параллелограмма равна 7 см. Найти длины сторон параллелограмма и его диагоналей.
 Ответ: 10, 17, 21, Решение
Ответ: 10, 17, 21, Решение - В параллелограмме с периметром 32 см проведены диагонали. Разность между периметрами двух смежных треугольников равна 8 см. Найти длины сторон параллелограмма. Ответ: 4; 12 Решение
- В параллелограмме ABCD высота, проведенная из вершины В тупого угла на сторону DA, делит ее в отношении 5 : 3, считая от вершины D. Найти отношение AC : BD, если AD : AB = 2. Ответ: 2:1 Решение
- Через точки R и E, принадлежащие сторонам АВ и AD параллелограмма ABCD и такие, что AR = 2 АВ /3, АЕ = AD/3, проведена прямая. Найти отношение площади параллелограмма к площади полученного треугольника. Ответ: 9 Решение
- Доказать, что в параллелограмме ABCD расстояния от любой точки диагонали АС до прямых ВС и CD обратно пропорциональны длинам этих сторон.
- Доказать, что если через вершины четырехугольника провести прямые, параллельные его диагоналям, то площадь параллелограмма, определяемою этими прямыми, в 2 раза больше площади данного четырехугольника.

- Две окружности радиуса R с центрами О1 и О2 касаются друг друга. Их пересекает прямая в точках А, В, С и D так, что АВ = ВС = CD. Найти площадь четырехугольника O1ADO2. Ответ: Решение
- В точках пересечения двух окружностей с радиусами 4 и 8 см касательные к ним взаимно перпендикулярны. Вычислить площадь фигуры О1АВО2, где АВ — общая касательная к окружностям, а О1 и О2 — их центры. Ответ: Решение
- Большее основание трапеции имеет длину 24 см. Найти длину ее меньшего основания, если известно, что расстояние между серединами диагоналей трапеции равно 4 см. Ответ: 16 Решение
- Один из углов трапеции равен 30°, а прямые, содержащие боковые стороны трапеции, пересекаются под прямым углом. Найти длину меньшей боковой стороны трапеции, если ее средняя линия равна 10 см, а одно из оснований 8 см. Ответ: 2 Решение
- Вычислить площадь трапеции, параллельные стороны которой содержат 16 и 44 см, а непараллельные — 17 и 25 см.
 Ответ: 450 Решение
Ответ: 450 Решение - Длины параллельных сторон трапеции равны 25 и 4 см, а длины непараллельных сторон — 20 и 13 см. Найти высоту трапеции. Ответ: 12 Решение
- Основания трапеции равны а и b, углы при большем основании равны и . Найти площадь трапеции. Ответ: Решение
- Вычислить площадь трапеции ABCD (AD параллельно BC), если длины ее оснований относятся как 5 : 3 и площадь треугольника ADM равна 50 см2, где М — точка пересечения прямых АВ и CD. Ответ: 32 Решение
Метки Сканави. Смотреть запись.
Как найти периметр ромба
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает одно
или несколько ваших авторских прав, сообщите нам об этом, отправив письменное уведомление («Уведомление о нарушении»), содержащее
в
информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как
в виде
ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатов), если вы существенно
искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится
на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Площадь и периметр ромба
Площадь и периметр ромба
Ромб — это двухмерный четырехугольник с четырьмя эквивалентными сторонами и четырьмя внутренними углами, которые не обязательно равны 90 градусам. Сумма длин всех четырех сторон ромба составляет периметр ромба. Квадрат также является разновидностью ромба, потому что он выполняет все условия, которыми обладает ромб.
Квадрат также является разновидностью ромба, потому что он выполняет все условия, которыми обладает ромб.
В ромбе:
• Все четыре стороны одинаковой длины
• Противоположные стороны параллельны.
• Высота — это расстояние под прямым углом к двум противоположным сторонам.
• Диагонали делят друг друга пополам под углом 90 градусов.
Площадь ромба
Площадь ромба можно охарактеризовать как меру пространства, заключенного ромбом на плоской поверхности или в двухмерном пространстве.Ромб — это четырехугольник с четырьмя равными сторонами, в котором две пары противоположных сторон параллельны. Он также известен как симметричный четырехугольник, потому что все его четыре стороны эквивалентны.
Как найти Площадь Ромба?
Есть разные методы расчета площади ромба. Есть три различные формулы для определения площади ромба:
- Использование базы и высоты
- Использование диагоналей
- Использование тригонометрии
Площадь формулы ромба
Существуют различные формулы для определения площади ромба:
Различные формулы для определения площади ромба | |
Основание и высота | А = с × в |
Диагонали | A = ½ × d 1 × d 2 |
Тригонометрия | A = b 2 × Sin (x) |
Где,
- s по длине с любой стороны
- h на высоте ромба
- d 1 à длина диагонали 1
- d 2 à длина диагонали 2
- x любой внутренний угол ромба
Площадь ромба с основанием (с любой стороны ромба) и высотой
Сначала мы найдем основание (сторону ромба) и высоту перпендикуляра ромба. Затем умножим основание и высоту.
Затем умножим основание и высоту.
Пример 1: Найдите площадь ромба, если его основание 9 см, а высота 6 см.
Решение:
Дан,
База, b = 9 см
Высота, h = 6 см
Площадь, A = b × h
= 9 × 6 см 2
Площадь ромба = 54 см 2
Площадь ромба с диагоналями
Предположим, ромб PQRS, имеющий две диагонали, т.е.е. d1 = PR & d2 = QS.
Сначала мы найдем длину d1. Это расстояние между P и R. Диагонали ромба пересекаются друг с другом под прямым углом, образуя 4 прямоугольных треугольника в центре ромба. Во-вторых, мы найдем длину d2, которая является расстоянием между Q и S. Затем умножим обе диагонали, d1 и d2. Наконец, разделите результат на 2.
Пример 2: Найдите площадь ромба, диагонали которого составляют 10 см и 12 см в длину.
Решение:
Дан,
Диагональ 1, d 1 = 10 см
Диагональ 2, d 2 = 12 см
Площадь ромба = (d 1 × d 2 ) / 2
= (10 × 12) / 2
= 120/2
= 60 см 2
Таким образом, Площадь ромба 60 см 2 .
Площадь ромба по тригонометрии
В этом случае, сначала мы должны возвести в квадрат длину любой из сторон, а затем умножить ее на синус любых внутренних углов.
Пример 3 Определите площадь ромба, если длина его стороны равна 4 см, а угол А равен 30 градусам.
Решение:
Дан,
Сторона, a = 4 см
Угол A = 30 градусов
квадрат со стороной a = 4 × 4 = 16 см 2
Площадь, A = s 2 × sin (30)
А = 16 × 1/2
Площадь ромба = 8 см 2
Формула периметра ромба
Периметр любой геометрической формы — это общее расстояние, пройденное вокруг границы, которое может быть определено алгебраической суммой длин каждой стороны.У ромба все четыре стороны имеют одинаковую длину; таким образом, периметр становится в четыре раза больше длины стороны.
Периметр ромба = 4 x сторона
Похожие видео:
Решенные задачи по формуле площади ромба и периметра
Вопрос 1: Найдите периметр ромба со стороной 6 см?
Решение:
Дано,
a = 6 см
Периметр ромба = 4 ×
Периметр ромба = 4 × 6
Периметр ромба = 24 см
Вопрос 2: Найдите площадь ромба, каждая сторона которого равна 10 см, а одна из диагоналей равна 12 см.
Решение:
ABCD — ромб, в котором AB = BC = CD = DA = 10 см
Диагональ AC = 12 см (где O — средняя точка пересечения диагонали)
Следовательно, АО = 6 см
In ∆ AOD,
AD 2 = AO 2 + OD 2
⇒ 10 2 = 6 2 + OD 2
⇒ 100-36 = OD 2
⇒ 64 = OD 2
⇒ OD = 8
Следовательно, BD = 2 × OD
= 2 × 8
= 16 см
Сейчас, площадь ромба
= ½ × d 1 × d 2
= ½ × 12 × 16
Площадь ромба = 96 см 2
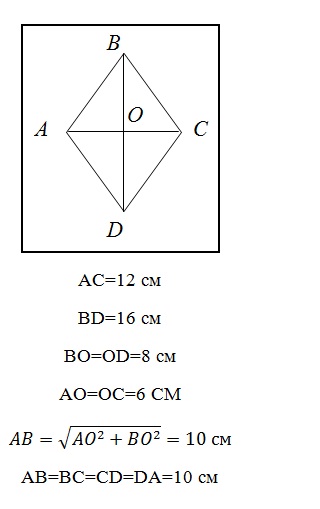
Вопрос 3: Длина диагоналей ромба составляет 20 и 48 метров.Найдите периметр ромба.
Решение: Применение теоремы Пифагора к треугольнику BOC
BC 2 = 10 2 + 24 2
BC2 = 100 + 576 м
BC2 = 676 = 26 м
Периметр ромба = 4 x сторона
= 4 x 26 м = 104 м
Вопрос 4: Найдите длину диагонали ромба, если его площадь равна 100 см 2 , а длина одной диагонали равна 20 см.
Решение:
Дано: Площадь ромба = 100 см 2 и Допустим, d 1 = 20 см.
Площадь ромба, A = (d 1 x d 2 ) / 2,
100 = (20 x d 2 ) / 2
100 = 10 x d 2
или 10 = d 2
Важные разделы:
Как рассчитать периметр и площадь ромба (с примерами)
Люди в Индии знают ромб как समचतुर्भुज (именно так ромб называется на хинди). Давайте перейдем к делу.
О ромбе: что такое ромб?
Ромб — это четырехугольник (у него всегда четыре стороны).Все стороны ромба равны по длине (всегда будут иметь одинаковую длину для всех четырех сторон).
Ромб также называют Бриллиантом (так как Бриллиантовая масть игральной карты похожа)
Некоторые примеры ромбов
Площадь ромба: по какой формуле рассчитывать?
Давайте изучим формулы вместе с решенными примерами.
Если известны обе диагонали ( p и q ) — p и q также известны как d 1 и d 2 :
Площадь ромба = (p x q) / 2
Также можно записать как; A = (d 1 x d 2 ) / 2 или 1/2 x d1 x d2 (все будет одинаково)
Пример 1
Вопрос: Найдите площадь ромба, где HM = 15 см и RO = 8 см
Тот же вопрос, но другим способом: найдите площадь данного ромба, где одна из диагоналей равна 8 см, а другая — 15 см.
Решение:
d 1 = 15 см (можно также написать: p = 15 см)
d 2 = 8 см (можно также написать как q = 8 см)
Итак, A = (d 1 x d 2 ) / 2 (вы также можете записать как: A = (p x q) / 2)
(15 см x 8 см) / 2
120 см 2 /2
60 см 2
Итак, Площадь ромба = 60см 2
Пример 2
Как найти одну из недостающих диагоналей ромба
Определение площади ромба Если вам известна только одна диагональ (p или q) и длина каждой стороны :
Когда знаешь только одну диагональ и длину сторон.
Вопрос: Найдите площадь ромба, когда AD = 10 см и AC = 12 см.
Решение:
Поскольку AD = 10 см, это означает, что длина всех сторон будет одинаковой (10 см).
Это означает, что a = 10 см
и мы уже знаем ac = 12 см
итак, p = 12см (это одна из диагоналей)
Формула и решение:
Итак, мы уже знали одну из диагоналей, а теперь получили другую, так что теперь мы можем легко вычислить площадь ромба.
q = 16см
р = 12 см
Площадь ромба = (p x q) / 2
(16 см x 12 см) / 2
192 см 2 /2
96 см 2
так Площадь ромба = 96 см 2
Периметр ромба: по какой формуле вычислить?
Пример
Определение периметра ромба Зная длину сторон
Вопрос: Найдите периметр ромба, длина всех сторон которого составляет 15 см.
Решение:
Как мы уже говорили в предыдущих примерах, длина всех сторон ромба всегда одинакова. Поэтому, даже если в вопросе говорится о длине одной стороны, вы должны предполагать одинаковую длину всех сторон.
Итак, a = 15см
Формула Периметра Ромба = 4a
= 4 x 15 см
= 60 см
, поэтому площадь ромба составляет 60 см.
Длина сторон (а) ромба: по какой формуле рассчитывать?
Пример 1
Определение длины сторон (a) ромба, зная периметр
Совет: значение всех 4 сторон ромба всегда одинаково.
Вопрос: Периметр ромба составляет 54 см. Найдите значение его сторон (длину).
Ответ:
a = P / 4
а = 54/4
a = 13,5 см
Таким образом, ширина со всех сторон составляет 13,5 см.
Пример 2
Определение длины всех 4 сторон (а) ромба, если известен периметр
Совет: значение всех 4 сторон ромба всегда одинаково.
Вопрос: Значение одной диагонали ромба составляет 6 м, а значение другой диагонали — 8 м. Найдите значение его сторон.
Ответ:
Мы уже знаем из вопроса:
p = 6 м
q = 8 м
a =?
Нам нужно найти значение a .
Итак, мы нашли значение всех 4 сторон, и оно равно 5.
Итак, а = 5
Пустой ромб ABCD, который вы можете загрузить, щелкнув изображение, если он вам нужен для каких-либо целей
Есть еще проблемы? Не волнуйтесь! Прокомментируйте свой вопрос, и мы ответим, как только сможем.
Площадь ромба Формула
Готовитесь ли вы к школьным экзаменам или к вступительным экзаменам, математика и геометрия играет ключевую роль. Ромб — неотъемлемая часть раздела «Геометрия». Вы можете ожидать один или два вопроса от этой части ромба. Итак, давайте подробно разберемся с этой концепцией. Вы можете найти некоторые идеи ромба в своем учебнике, а также в Интернете. Но для того, чтобы ясно понять это, недостаточно.Вы можете посетить веб-сайт Веданту и найти формулу «Площадь ромба», так прекрасно объясненную нашими опытными учителями. Концепции вместе с примерами Веданту заинтересуют студентов, чтобы они получили знания о части ромба. Что такое ромб?
Что такое ромб?
Ромб — это особый тип параллелограмма, все стороны которого равны. Углы между сторонами ромба не обязательно должны быть прямым, и в этом он отличается от квадрата, у которого все углы — прямые.Таким образом, ромб с прямыми углами становится квадратным.
Углы между сторонами ромба не обязательно должны быть прямым, и в этом он отличается от квадрата, у которого все углы — прямые.Таким образом, ромб с прямыми углами становится квадратным.
Как рассчитать площадь ромба?
Площадь ромба можно вычислить тремя способами. Использование диагоналей, основание и высота, а также тригонометрия.
Формула периметра ромба — Ромб имеет:
Все стороны равной длины.
Противоположные стороны параллельны.
Высота — это расстояние под прямым углом между двумя параллельными сторонами.
Диагонали ромба делят друг друга пополам под углом 90 градусов.
Формула периметра ромба дается как p = 4 × a, где «a» — длина стороны ромба.
Диагональ ромба Формула:
Площадь ромба можно рассчитать с помощью диагоналей, как указано A = ½ × d 1 × d 2 .
Где,
A = Площадь ромба.
d 1 = Длина диагонали 1.
d 2 = Длина диагонали 2.
Площадь и периметр ромба могут быть вычислены, если у нас есть значение, равное одному из этих двух, т.е. если площадь задана, мы можем вычислить периметр и наоборот. .
Как найти площадь ромба?
Площадь ромба может быть получена тремя способами:
Используя диагонали — A = ½ × d 1 × d 2 .
Использование базы и высоты — A = b × h.
Использование тригонометрии — A = b 2 × Sin (a).
Где
d 1 = Длина диагонали 1.
d 2 = Длина диагонали 2.

b = Длина с любой стороны.
h = Высота ромба.
a = Измерение внутреннего угла.
Веданту — лучшее руководство к экзамену
В настоящее время Веданту — одна из лучших онлайн-репетиторских услуг в Индии. Плата за обучение охватывает практически все области образования.Веданту — продукт четырех страстных людей, которые хотели заниматься чем-то отличным от традиционного образа жизни. Они выбрали тренерскую работу. Все закончили ИИТ; они обладали хорошими знаниями и использовали их для обучения детей рабочих на одном заводе. Команда RDX (Research Develop and Explore), поскольку Vedantu создает технологии в образовании, чтобы оказать разрушительное положительное влияние, создать больше «учителей по выбору», чтобы сделать качественное образование более доступным и доступным. Веданту имеет преимущество перед другими с точки зрения — высших учителей элитной группы, которые считают это вопросом гордости и ответственности.
Веданту имеет преимущество перед другими с точки зрения — высших учителей элитной группы, которые считают это вопросом гордости и ответственности.
Решения NCERT класса 8 — Глава 11 Измерение — Упражнение 11.2
Вопрос 1. Форма верхней поверхности стола представляет собой трапецию. Найдите его площадь, если его параллельные стороны равны 1 м и 1,2 м, а расстояние по перпендикуляру между ними равно 0,8 м.
Решение:
Одна параллельная сторона трапеции (a) = 1 м
И вторая сторона (b) = 1,2 м и
высота (h) = 0,8 м
Площадь верха поверхность стола = (½) × (a + b) h
= (½) × (1 + 1.2) 0,8
= (½) × 2,2 × 0,8
= 0,88
Площадь верхней поверхности стола 0,88 м 2 .
Вопрос 2. Площадь трапеции составляет 34 см 2 , длина одной из параллельных сторон — 10 см, а высота — 4 см. Найдите длину другой параллельной стороны.
Решение:
Пусть длина другой параллельной стороны равна b.
Длина одной параллельной стороны, a = 10 см
высота, (h) = 4 см и
Площадь трапеции составляет 34 см2
Формула для, Площадь трапеции = (1/2) × (a + b) h
34 = ½ (10 + b) × 4
34 = 2 × (10 + b)
После упрощения, b = 7
Следовательно, другая необходимая параллельная сторона равна 7 см.
Вопрос 3. Длина ограждения поля трапециевидной формы ABCD составляет 120 м. Если BC = 48 м, CD = 17 м и AD = 40 м, найдите площадь этого поля. Сторона AB перпендикулярна параллельным сторонам AD и BC.
Решение:
Дано: BC = 48 м, CD = 17 м,
AD = 40 м и периметр = 120 м
∵ Периметр трапеции ABCD
= AB + BC + CD + DA
120 = AB + 48 + 17 + 40
120 = AB = 105
AB = 120 — 105 = 15 м
Итак, площадь поля = (½) × (BC + AD) × AB
= (½) × (48 + 40) × 15
= (½) × 88 × 15
= 660
Следовательно, площадь поля ABCD составляет 660 м 2
Вопрос 4. Диагональ поля четырехугольной формы составляет 24 м, а перпендикуляры, падающие на него из оставшихся противоположных вершин, составляют 8 м и 13 м. Найдите площадь поля.
Диагональ поля четырехугольной формы составляет 24 м, а перпендикуляры, падающие на него из оставшихся противоположных вершин, составляют 8 м и 13 м. Найдите площадь поля.
Решение:
Рассмотрим, h3 = 13 м, h4 = 8 м и AC = 24 м
Площадь четырехугольника ABCD = Площадь треугольника ABC + Площадь треугольника ADC
= ½ (bh3 ) + ½ (bh4)
= ½ × b (h3 + h4) = (½) × 24 × (13 + 8)
= (½) × 24 × 21 = 252
Следовательно, требуемая площадь поля составляет 252 м 2
Вопрос 5.Диагонали ромба 7,5 см и 12 см. Найдите его область.
Решение:
Дано: d1 = 7,5 см и d2 = 12 см
Мы знаем, что Площадь ромба = (½) × d1 × d2 = (½) × 7,5 × 12 = 45
Следовательно, площадь ромба составляет 45 см 2 .
Вопрос 6. Найдите площадь ромба со стороной 5 см и высотой 4,8 см. Если одна из диагоналей 8 см, найдите длину другой диагонали.
Если одна из диагоналей 8 см, найдите длину другой диагонали.
Решение:
Поскольку ромб — это еще и разновидность параллелограмма.
Формула для площади ромба = основание × высота
Подставляя значения, получаем
Площадь ромба = 6 × 4 = 24
Площадь ромба составляет 24 см2
Также формула для площади ромба = (½) × d1d2
После подстановки значений получаем
24 = (½) × 8 × d2
d2 = 6
Следовательно, длина другой диагонали равна 6 см.
Вопрос 7. Пол здания состоит из 3000 плиток, которые имеют форму ромба , а каждая из его диагоналей составляет 45 см и 30 см в длину. Найдите общую стоимость полировки пола, если стоимость 1 м 2 составляет рупий. 4.
Решение:
Длина одной диагонали, d1 = 45 см и d2 = 30 см
∵ Площадь одной плитки = (½) d1d2 = (½) × 45 × 30 = 675
Площадь одной плитки 675 см 2
Площадь 3000 плиток
= 675 × 3000
= 2025000 см 2
= 2025000/10000
= 202.
50 м2 [∵ 1м2 = 10000 см2]
∵ Стоимость полировки пола на квадратный метр = 4
Стоимость полировки пола на 202,50 кв.м = 4 × 202,50 = 810
Отсюда общая стоимость полировки пола этаж рупий. 810.
Вопрос 8. Мохан хочет купить поле трапециевидной формы . Его сторона вдоль реки параллельна дороге и вдвое больше ее. Если площадь этого поля составляет 10500 м 2 , а расстояние по перпендикуляру между двумя параллельными сторонами равно 100 м, найдите длину стороны вдоль реки.
Решение:
Перпендикулярное расстояние (h) = 100 м (дано)
Площадь поля в форме трапеции = 10500 м2 (дано)
Пусть сторона дороги будет ‘x’ m и сторона вдоль реки = 2x м
Площадь трапециевидного поля = (½) × (a + b) × h
10500 = (½) × (x + 2x) × 100
10500 = 3x × 50
После упрощения получаем x = 70, что означает, что сторона реки составляет 70 м.
Следовательно, сторона вдоль реки = 2x = 2 (70) = 140 м.
Вопрос 9. Верхняя поверхность приподнятой платформы имеет форму правильного восьмиугольника, как показано на рисунке. Найдите площадь восьмиугольной поверхности.
Решение:
Восьмиугольник с восемью равными сторонами по 5 м каждая. (дано)
Разделите восьмиугольник, как показано на рисунке ниже, на 2 трапеции с параллельными и перпендикулярными сторонами 11 м и 4 м соответственно, а третья — прямоугольник длиной и шириной 11 м и 5 м соответственно.
Итак, площадь двух трапеций = 2 [(½) × (a + b) × h]
= 2 × (½) × (11 + 5) × 4
= 4 × 16 = 64
Площадь двух трапеций составляет 64 м 2
Также, Площадь прямоугольника = длина × ширина
= 11 × 5 = 55
Площадь прямоугольника составляет 55 м 2
Общая площадь восьмиугольника = 64 + 55
= 119 м 2
Вопрос 10. Существует парк пятиугольной формы, как показано на рисунке.
Существует парк пятиугольной формы, как показано на рисунке.
Для нахождения своего района Джиоти и Кавита разделили его двумя разными способами. Найдите территорию этого парка обоими способами. Вы можете предложить какой-нибудь другой способ найти его район?
Решение:
Первый способ: По диаграмме Джоти,
Площадь пятиугольника = Площадь трапеции ABCP + Площадь трапеции AEDP
= (½) (AP + BC) × CP + (1 / 2) × (ED + AP) × DP
= (½) (30 + 15) × CP + (1/2) × (15 + 30) × DP
= (½) × (30 + 15) × (CP + DP)
= (½) × 45 × CD
= (1/2) × 45 × 15
= 337.5 м2
Площадь пятиугольника 337,5 м 2
Второй способ: По диаграмме Кавиты
Здесь перпендикуляр AM к BE.
AM = 30-15 = 15 м
Площадь пятиугольника = Площадь треугольника ABE + Площадь квадрата BCDE (на рисунке выше)
= (½) × 15 × 15 + (15 × 15)
= 112,5 + 225,0
= 337,5
Следовательно, общая площадь парка в форме пятиугольника = 337,5 м2
Вопрос 11. Диаграмма соседней рамы имеет внешние размеры = 24 см × 28 см и внутренние размеры 16 см × 20 см.Найдите площадь каждой секции рамы, если ширина каждой секции или то же самое.
Диаграмма соседней рамы имеет внешние размеры = 24 см × 28 см и внутренние размеры 16 см × 20 см.Найдите площадь каждой секции рамы, если ширина каждой секции или то же самое.
Решение:
Разделите данный рисунок на 4 части, как показано ниже:
Здесь две из приведенных фигур (I) и (II) имеют одинаковые размеры.
А также фигуры (III) и (IV) аналогичны по размерам.
Площадь рисунка (I) = Площадь трапеции
= (½) × (a + b) × h
= (½) × (28 + 20) × 4
= (½) × 48 × 4 = 96
Площадь фигуры (I) = 96 см 2
Также, Площадь фигуры (II) = 96 см 2
Теперь, Площадь фигуры (III) = Площадь трапеции
= (½) × (a + b) × h
= (½) × (24 + 16) 4
= (½) × 40 × 4 = 80
Площадь рисунка (III) равна 80 см 2
Также, Площадь рисунка (IV) = 80 см 2
Периметр и площадь плоских фигур
Найдите периметр и площадь квадрата, если нам известна длина его диагонали d = 4. 2 мес.
2 мес.
Найдите площадь прямоугольника ABCD , где длина стороны | AB | = a = 8,2 см и диагональ d = 2 a .
Длины сторон прямоугольного сада находятся в соотношении 1: 2. Длина линии, соединяющей центры соседних сторон сада, составляет 20 м. Рассчитайте периметр и площадь сада.
Прямоугольный сад имеет длину 57 м и ширину 42 м.Подсчитайте, на сколько метров 2 уменьшится площадь сада, если декоративный забор шириной 60 см будет посажен внутри его периметра.
Периметр параллелограмма 2,8 метра. Длина одной из его сторон равна одной седьмой части всего периметра. Найдите длины сторон параллелограмма.
Один из внутренних углов ромба составляет 120 °, а длина более короткой диагонали составляет 3,4 метра.Найдите периметр ромба.
Найдите длину диагонали AC ромба ABCD , если ее периметр P = 112 дм, а вторая диагональ BD имеет длину 36 дм.
В равнобедренной трапеции ABCD мы знаем: AB || CD , | CD | = c = 8 см, высота h = 7 см, | ∠ CAB | = 35 °. Найдите площадь трапеции.
Найдите площадь трапеции.
Трапеция ABCD имеет длину основания a = 120 мм, c = 86 мм и площадь A = 2,575 мм 2 . Найдите высоту трапеции.
Рассмотрим равнобедренную трапецию PQRS . Базы | PQ | = 120 мм, | RS | = 62 мм и плечо s = 48 мм. Найдите высоту трапеции, длину диагонали и площадь трапеции.
Площадка прямоугольной трапециевидной формы имеет длину основания 92 м и 76 м и длину вертикального плеча 6,3 м. Найдите площадь участка и длину ограждения, необходимую для ограждения участка.
Периметр равнобедренного треугольника 474 м. Основание треугольника на 48 м длиннее плеча. Найдите длину сторон и площадь треугольника.
Прямоугольный треугольник ABC имеет ноги a = 5 см, b = 8 см.Треугольник A’B’C ‘ похож на треугольник ABC и в 2,5 раза меньше. Вычислите, какой процент площади треугольника ABC занимает площадь треугольника A’B’C ‘.
Прямоугольный равнобедренный треугольник площадью 32 см 2 . Каков его периметр?
Равносторонний треугольник имеет периметр 36 дм. Какая у него площадь?
Треугольник ABC имеет длину стороны a = 14 см, b = 20 см, c = 7.5 см. Найдите размер внутренних углов и площадь треугольника.
Найдите периметр, площадь и размер оставшихся углов треугольника ABC , когда: a = 8,4, β = 105 ° 35 ‘и медиана стороны a равна м a = 12,5.
Найдите длину всех сторон и размер всех внутренних углов треугольника ABC , если мы знаем: A = 501.9; α = 15 ° 28 ‘и β = 45 °.
Параллелограмм ABCD имеет площадь 40 см 2 , | AB | = 8,5 см и | BC | = 5,65 см. Найдите длину его диагоналей.
Найдите площадь правильного шестиугольника, если нам известен радиус вписанной в него окружности ρ = 4 см.
В правильном шестиграннике ABCDEF диагональ AC имеет длину 12 см.Найдите длину стороны шестиугольника ABCDEF и определите его площадь.
Найдите периметр круга, если его площадь составляет 706,5 см 2 .
Найдите площадь круга, если его периметр 94,2 дм.
Квадрат на картинке имеет длину 8 см. Найдите площадь цветной части круга.
На рисунке два и еще два полукруга идентичны.Радиус одного полукруга вдвое больше радиуса другого полукруга. Найдите площадь цветного узора, если | AB | = 12 см.
Вас также может заинтересовать:
Как найти высоту ромба
Параллелограмм — это плоская форма с противоположными сторонами, которые параллельны и равны по длине.Ромб — это параллелограмм с четырьмя равными (совпадающими) сторонами, например ромб. Квадраты и прямоугольники также являются разновидностями параллелограммов. Вы можете рассчитать высоту ромба, если знаете другие значения, такие как площадь, основание или диагонали.
TL; DR (слишком длинный; не читал)
Чтобы найти высоту ромба, используйте формулу высота = площадь ÷ основание. Если вы знаете диагонали ромба, но не знаете его площадь, используйте формулу площадь = (d1 x d2) ÷ 2, а затем примените площадь к первой формуле.
Свойства ромба
Независимо от размера ромба всегда применяются определенные правила. Все его стороны равны, его противоположные углы равны, а его две диагонали перпендикулярны (то есть они делят друг друга пополам под углом 90 градусов). Высота ромба (также называемая его высотой) — это кратчайшее перпендикулярное расстояние от его основания до противоположной стороны. Основание ромба может быть любой из четырех сторон, в зависимости от того, как он расположен.
Определение высоты по площади и основанию
Формула высоты ромба: высота = площадь ÷ основание.Например, если вы знаете, что площадь ромба составляет 64 см2, а основание — 8 см, вы получите 64 ÷ 8 = 8. Высота ромба 8 см. Помните, что основание — это одна из сторон, и они равны по длине, поэтому, если вы знаете длину одной из сторон, вы знаете длину их всех.
Высота ромба 8 см. Помните, что основание — это одна из сторон, и они равны по длине, поэтому, если вы знаете длину одной из сторон, вы знаете длину их всех.
Эта же формула применяется независимо от размера ромба или единиц измерения. Например, у вас есть ромб площадью 1000 дюймов и основанием 20 дюймов. Выполните 1000 ÷ 20 = 50.Высота ромба 50 дюймов.
Выберите правильный ответ А)СУММА УГЛОВ ПАРАЛЛЕЛОГРАММА РАВНА а) 1800
Геометрия, 24.04.2020 11:03, Alesja4788
5. ПЛОЩАДЬ ПАРАЛЛЕЛОГРАММА, СО СТОРОНОЙ 10СМ И
ВЫСОТОЙ, ПРОВЕДЕННОЙ К ЭТОЙ СТОРОНЕ, РАВНОЙ 15СМ
РАВНА:
а) 75СМ2
б) 300СМ2
в) 150СМ2
5. ГИПОТЕНУЗА ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА С
КАТЕТАМИ 6СМ И 8СМ РАВНА:
а) 48СМ б) 24СМ в)10СМ
6. ГИПОТЕНУЗА ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА С
КАТЕТАМИ 5СМ И 12СМ РАВНА:
а) 13СМ б) 17СМ в)30СМ
6.Установить верные утверждения, обведя кружком номер правильного
ответа:
А)
1) Около любой трапеции можно описать окружность.
2) Диагонали ромба взаимно перпендикулярны.
3)Если основания трапеции 5 и 15, то средняя линия этой трапеции равна 10.
Б)
1) Диагонали ромба точкой пересечения делятся пополам.
2) Если основания трапеции 4 и 6, то средняя линия этой трапеции равна 10.
3) Все вписанные углы, опирающиеся на одну и ту же дугу окружности,
равны.
7.ДОПОЛНИТЬ
А)
1) СИНУСОМ ОСТРОГО УГЛА ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА
НАЗЫВАЕТСЯ ОТНОШЕНИЕ_ КАТЕТА К ГИПОТЕНУЗЕ.
2) ЦЕНТРАЛЬНЫЙ УГОЛ ИЗМЕРЯЕТСЯ _, НА КОТОРУЮ
ОН ОПИРАЕТСЯ.
3) ОКРУЖНОСТЬ НАЗЫВАЕТСЯ ВПИСАННОЙ В ТРЕУГОЛЬНИК, ЕСЛИ
ОНА_ СТОРОН ТРЕУГОЛЬНИКА.
б)
1) КОСИНУСОМ ОСТРОГО УГЛА ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА
НАЗЫВАЕТСЯ ОТНОШЕНИЕ _КАТЕТА К
ГИПОТЕНУЗЕ.
2) ВПИСАННЫЙ УГОЛ ИЗМЕРЯЕТСЯ _ _, НА
КОТОРУЮ ОН ОПИРАЕТСЯ.
3) ОКРУЖНОСТЬ НАЗЫВАЕТСЯ ОПИСАННОЙ ВОКРУГ
ТРЕУГОЛЬНИКА, ЕСЛИ ВЕРШИНЫ ТРЕУГОЛЬНИКА_
НА ОКРУЖНОСТИ.
2 часть
Решите задачи
1.Найдите площадь трапеции, изображённой на рисунке.
2.
Боковая сторона трапеции равна 5, а один из прилегающих к ней углов равен
30°. Найдите площадь трапеции, если её основания равны 3 и 9.
3.
В равнобедренной трапеции основания равны 3 и 9, а один из углов между
боковой стороной и основанием равен 45°. Найдите площадь трапеции.
4.
Основания равнобедренной трапеции равны 5 и 17, а ее боковые стороны
равны 10. Найдите площадь трапеции.
5.
Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 65° и 50°. Найдите меньший угол параллелограмма.
6.
Разность углов, прилежащих к одной стороне параллелограмма, равна 40°.
Найдите меньший угол параллелограмма. ответ дайте в градусах.
7.
Один угол параллелограмма в два раза больше другого. Найдите меньший
угол. ответ дайте в градусах.
8.
Биссектриса угла A параллелограмма ABCD пересекает сторону BC в точке
K. Найдите периметр параллелограмма, если BK = 7, CK = 12.
Посмотреть ответы
Другие вопросы по: Геометрия
Опубликовано: 04. 03.2019 08:00
03.2019 08:00
в Математика
Ответов: 2
Загвоздка с одним интересным квадратом 19 ? ? ? 23 10 ? 7 27…
Опубликовано: 04.03.2019 12:10
в Математика
Ответов: 3
Сейчас отец в 7 раз старше сына, а через 10 лет он будет втрое старше сына. сколько лет отцу и сколько лет сыну?…
Опубликовано: 07.03.2019 22:40
в Математика
Ответов: 3
Кусок золотой ткани квадратной формы разрезали на полоски шириной по 2см и соединили их (стык в стык). какой длины получилась золотая лента, если сторона куска ткани была 20 см? н…
Опубликовано: 08.03.2019 11:20
в Математика
Ответов: 3
Вычисли и найди значение неизвестного уравнения х+14=20+14…
Опубликовано: 09.03.2019 16:20
в Математика
Ответов: 2
Площадь кухни 9 кв. метров , что составляет одну восьмую часть всей квартиры. найди площадь квартиры….
найди площадь квартиры….
Опубликовано: 03.03.2019 09:36
в Математика
Ответов: 2
Вклассе 30 учеников, из которых 8 отличников и два отстающих. вероятность решить предложенную для отличника 0,9, для отстающего-0,3. наудачу вызванный ученик решил . какова вероят…
Знаешь правильный ответ?
Выберите правильный ответ А)СУММА УГЛОВ ПАРАЛЛЕЛОГРАММА РАВНА а) 1800 б)3600 в) 5400 б)СУММА УГЛОВ Р…
Популярные вопросы
Опубликовано: 02.03.2019 23:50
в Математика
Ответов: 1
Запиши парами уравнения с равными корнями. 2000-х=520х2 2000-х=520/2 (2000-х)/2=520 (2000-х)х2=520…
Опубликовано: 03.03.2019 04:10
в Математика
Ответов: 1
Катя придумала 5 примеров на сложение и 4 примера на вычитание. поставь вопрос так чтобы решалась вычитанием…
Опубликовано: 04.03.2019 01:10
в Математика
Ответов: 3
Выбрав удобный порядок действий, вычислить: а) 4/7*(-9,27)-4/7*(-2,27) ; б) 3/8*(-7/16)*(-2 целых 2/3)*(-1 целая 1/7). …
…
Опубликовано: 04.03.2019 05:20
в Математика
Ответов: 3
Впарк «а» деревьев. из них 40% березы, а 2/3 остальных тополя. сколько тополей в парк?…
Опубликовано: 06.03.2019 21:20
в Математика
Ответов: 2
Возле школы растут только березы и сосны. березы составляют 2/3 всех деревьев. сколько деревьев возле школы если берез 42 штуки?…
Опубликовано: 08.03.2019 01:20
в Математика
Ответов: 3
Маса 30 ящиків печева така сама, як маса 25 ящиків цкерок. яка маса одного ящика печева якщо маса ящика цукерок 12 кг….
Опубликовано: 09.03.2019 12:30
в Математика
Ответов: 2
Из одной той же точки шоссе в противоположных направлениях выехали два велосипедиста ,один со скорость 12км/ч, а другой со скоростью 14км/ч. первый велосипедист выехал на час раньш…
Опубликовано: 10. 03.2019 14:30
03.2019 14:30
в Математика
Ответов: 2
Как обозначают отрезок, соединяющий точки c и d?…
Опубликовано: 03.03.2019 13:16
в Математика
Ответов: 1
Реши , записав столбиком в конструкторе 338 деталей. 3 ребёнка взяли одинаковое количество. сколько деталей осталось?…
Опубликовано: 03.03.2019 15:16
в Математика
Ответов: 1
Мишко, віталик та олег вирішили купити одну книжку. мишкові не вистачило на покупку 15 грн., віталікові 37 грн., а олегові – 26 грн. склавши гроші (а вони були у кожного з хлопців)…
Больше вопросов по предмету: Геометрия Случайные вопросы
Периметр ромба – объяснение и примеры
Периметр ромба – это общая длина, измеренная по его границам.
Все стороны ромба равны друг другу . Если длина любой отдельной стороны равна $x$, как показано на рисунке выше, то периметр равен
Периметр $=4x$
Мы получаем периметр ромба как , складывая значения всех его сторон . Эта тема поможет вам понять свойства ромба и как вычислить его периметр.
Эта тема поможет вам понять свойства ромба и как вычислить его периметр.
Прежде чем мы перейдем к теме, вы должны знать разницу между ромбом, квадратом и параллелограммом, поскольку все они являются четырехугольниками (то есть четырехсторонними геометрическими фигурами) и имеют некоторые общие черты. Различия между ними представлены в таблице ниже .
Параллелограмм | квадрат | Rhombus |
| Опные с сандами Parallegram Ants Ants Ants Ants Ant Ant Ant Ante Ars Art Ante Ars Ante | ||
| Апения | ||
| Опные | ||
| Опенные | ||
| .o$ каждый, превращая его в квадрат. | ||
| Диагонали параллелограмма делят друг друга пополам. | Диагонали квадрата равны по длине. | Диагонали ромба делят пополам и равны по длине. |
Каждый параллелограмм не является ромбом. | Каждый ромб является параллелограммом. | |
| Все четыре стороны квадрата перпендикулярны друг другу. | Стороны ромба не обязательно перпендикулярны. |
Что такое периметр ромба?
Периметр ромба равен , а общее расстояние вокруг его границ . Ромб — это плоская геометрическая фигура с четырьмя сторонами, и если мы добавим длины всех четырех сторон, это даст нам периметр ромба.
Все стороны ромба равны, как у квадрата, а периметр вычисляется как , умножая 4 на длину одной стороны .
Обратите внимание, что в отличие от квадрата четыре угла ромба 9{о}$.
Периметр равен линейной мере , поэтому единицы измерения периметра совпадают с единицами длины каждой стороны, т. е. сантиметры, метры, дюймы, футы и т. д.
Как найти периметр a Ромб
Периметр ромба определяется как сумма всех сторон ромба . Если мы сложим все стороны, это даст нам периметр ромба. Этот метод применим только в том случае, если нам дана длина любой стороны ромба.
Если мы сложим все стороны, это даст нам периметр ромба. Этот метод применим только в том случае, если нам дана длина любой стороны ромба.
Иногда нам дают диагонали ромба и просят найти его периметр. Таким образом, заданные данные определяют, какой метод следует использовать для вычисления периметра ромба.
Периметр ромба с использованием метода сторон
Этот метод используется, когда нам известна длина любой стороны ромба . Как говорилось ранее, все стороны ромба равны. Следовательно, если одна сторона ромба равна «х», то мы можем вычислить периметр ромба, умножив «х» на 4.
Периметр ромба с использованием диагонального метода
Этот метод используется, когда нам даны длины диагоналей ромба с и отсутствуют данные о длинах сторон ромба. Однако мы знаем, что диагонали ромба делят друг друга пополам под прямым углом, поэтому, когда мы рисуем диагонали ромба, мы получаем четыре конгруэнтных прямоугольных треугольника, как показано на рисунке ниже.
Чтобы вычислить периметр с помощью этого метода, действуем по шагам, указанным ниже:
- Сначала запишем измерения диагоналей ромба.
- Затем примените теорему Пифагора, чтобы получить значение любой стороны ромба.
- Наконец, умножьте вычисленное на шаге 2 значение на «4».
Формула периметра ромба
Мы можем вывести формулу периметра ромба на , умножив длину любой из сторон на «4» . Мы знаем, что все стороны ромба равны, и мы можем записать формулу периметра ромба как:
Периметр ромба $= x + x + x + x$
Периметр ромба $= 4\times x$
Периметр ромба при данных двух диагоналях
Выведем формулу периметра ромба, когда нам обеспечена длина диагоналей . Рассмотрим это изображение ромба с доступными значениями обеих диагоналей.
Мы можем взять любой из четырех треугольников для решения формулы . Возьмем треугольник ABP. Мы знаем, что диагонали ромба делят друг друга пополам на расстоянии 9 долларов.{2})}$
Мы знаем, что диагонали ромба делят друг друга пополам на расстоянии 9 долларов.{2})}$
Примечание : Вы также можете использовать приведенную выше формулу для расчета периметра ромба, если вам предоставлена длина одной диагонали вместе с площадью ромба. Формула площади ромба $= \dfrac{диагональ\hspace{1мм} 1\кратная диагонали \hspace{1мм} 2}{2}$. Таким образом, мы можем вычислить длину второй диагонали , используя формулу площади, а затем использовать приведенную выше формулу периметра для вычисления периметра ромба.
Применение периметра ромба в реальной жизни
Слово «периметр» представляет собой комбинацию двух греческих слов: «пери», что означает окружение или границы поверхности или объекта, и «метр», что означает измерение поверхности или объекта, поэтому периметр означает общее измерение. границ данной поверхности .
Обладая этой информацией, мы можем использовать периметр ромба во многих реальных приложениях. Различные примеры приведены ниже:
Различные примеры приведены ниже:
- Например, мы можем использовать периметр ромба для расчета расстояния от пятна питчера до нападающего в бейсболе, если все поле имеет форму ромба.
- Формула периметра также полезна при проектировании столов и шкафов в форме ромба.
- Он также полезен при строительстве ромбовидных офисов и помещений.
Пример 1:
Если длина одной стороны ромба равна 11 см, какова будет длина остальных сторон?
Решение:Мы знаем, что все стороны ромба равны по длине , поэтому длина остальных трех сторон также равна 11 см каждая.
Пример 2:
Вычислите периметр ромба для фигуры, приведенной ниже.
Решение:Нам дана длина одной стороны ромба, и мы знаем, что все стороны равны по длине .
Периметр ромба $= 4\x 8$
Периметр ромба $= 32 см$
Пример 3:
Если периметр ромба равен 80 см, какова длина всех его сторон ромб?
Решение: Дан периметр ромба. Мы можем вычислить длину каждой стороны ромба на , используя формулу периметра :
Мы можем вычислить длину каждой стороны ромба на , используя формулу периметра :
Периметр ромба $= 4\times сторона$
$ 80 = 4\times сторона$
Сторона $= \frac{ 80}{4}$
Сторона $= \frac{80}{4}$
Сторона $= 20 см$
Все стороны ромба равны 20 см.
Пример 4:
Если длина диагоналей ромба равна 9{2})}$
Периметр ромба $= 2 \times \sqrt{64 + 256}$
Периметр ромба $= 2 \times \sqrt{320}$
Периметр ромба $= 2 \times 17.89$
Периметр ромба $= 35.78 см $ ок.
Практические вопросы- Если одна сторона ромба равна $20 см$, какова длина остальных сторон и периметр ромба?
- Если периметр ромба $100 см$, какова длина сторон ромба? 9{2}$, а длина одной из диагоналей $4 см$. Чему будет равен периметр ромба?
1. Мы знаем, что все стороны ромба равны по длине . Если длина одной стороны ромба равна 20 см, то и длина остальных трех сторон будет такой же, т. е. 20 см.
е. 20 см.
Периметр ромба $= 4\х сторона$
Периметр ромба $= 4\х 20$
Периметр ромба $= 80 см$
2. Дан периметр ромба. Мы можем вычислить длину каждой стороны ромба на , используя формулу периметра :
Периметр ромба $= 4\times сторона$
$ 100 = 4\times сторона$
Сторона $= \frac{ 100}{4}$
Сторона $= 25 см$
Мы знаем, что все стороны ромба равны по длине, поэтому все стороны ромба имеют длину $25 см$.
3. Даны длины двух диагоналей ромба. Пусть «а» и «b» будут двумя диагоналями. Тогда мы можем вычислить периметр и площадь ромба на 9{2})}$
Периметр ромба $= 2 \times \sqrt{81 + 144}$
Периметр ромба $= 2 \times \sqrt{225}$
Периметр ромба $= 2 \times 15$
Периметр ромба $= 30 см $ ок.
4. Пусть диагональ «а» $= 4 см$ и надо найти «b»
Площадь ромба $ = \dfrac{a\times b}{2}$
$36 = \dfrac{4 \times b}{2}$
$72 = 4 \times b$
$ b = \dfrac{72}{4}$
$ b = 18 см $ 9{2})}$
Периметр ромба $= 2 \times \sqrt{16 + 324}$
Периметр ромба $= 2 \times \sqrt{340}$
Периметр ромба $= 2 \times 18,44$
Периметр ромба $= 36,88 см $ ок.
Изображения/Математические чертежи создаются с помощью GeoGebra.
Как найти периметр ромба
Все ресурсы по промежуточной геометрии
8 Диагностические тесты 250 практических тестов Вопрос дня Карточки Учитесь по концепции
← Предыдущая 1 2 3 4 Следующая →
Справка по промежуточной геометрии » Плоская геометрия » Четырехугольники » ромбы » Как найти периметр ромба
Дан ромб с длинами диагоналей 12см и 16см, найдите периметр.
Возможные ответы:
Правильный ответ:
Пояснение:
Ромб – это параллелограмм, у которого все стороны равны. Квадрат – это ромб, у которого все углы равны, как и все стороны. И квадраты, и ромбы имеют перпендикулярные диагональные биссектрисы, которые делят каждую диагональ на 2 равные части, а также разбивают четырехугольник на 4 равных прямоугольных треугольника.
При этом мы знаем, что теорема Пифагора отлично сработает в этой ситуации, используя половину каждой диагонали в качестве двух катетов прямоугольного треугольника.
где — гипотенуза.
—>
Мы находим гипотенузу равной 10 см. Поскольку гипотенуза каждого треугольника является стороной ромба, мы нашли то, что нужно для нахождения периметра.
Каждая сторона одинакова, поэтому мы складываем все 4 стороны, чтобы найти периметр.
Сообщить об ошибке
Диагонали ромба имеют длины и единицы. Каков его периметр?
Возможные ответы:
Правильный ответ:
Пояснение:
Начнем с картинки.
Мы должны помнить несколько вещей. Во-первых, все четыре стороны ромба конгруэнтны, а это означает, что если мы найдем одну сторону, мы можем просто умножить ее на четыре, чтобы найти периметр. Во-вторых, диагонали ромба являются перпендикулярными биссектрисами друг друга, что дает нам четыре прямоугольных треугольника и делит каждую диагональ пополам. Таким образом, у нас есть четыре конгруэнтных прямоугольных треугольника. Используя теорему Пифагора для любого из них, мы получим длину наших сторон.
Во-вторых, диагонали ромба являются перпендикулярными биссектрисами друг друга, что дает нам четыре прямоугольных треугольника и делит каждую диагональ пополам. Таким образом, у нас есть четыре конгруэнтных прямоугольных треугольника. Используя теорему Пифагора для любого из них, мы получим длину наших сторон.
При длине стороны 17 периметр легко получить.
Наш периметр 68 единиц.
Сообщить об ошибке
Ромб имеет площадь квадратных единиц и высоту . Найдите периметр ромба.
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы решить эту задачу, используйте данную информацию, чтобы работать в обратном порядке, чтобы найти длину стороны ромба:
Затем применим формулу периметра:
, где сторона ромба.
Сообщить об ошибке
Ромб имеет площадь в квадратных единицах и высоту . Найдите периметр ромба.
Найдите периметр ромба.
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы решить эту задачу, используйте данную информацию, чтобы найти длину стороны ромба в обратном направлении: 9
Периметр=
Сообщить об ошибке Найдите периметр ромба.
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти периметр, примените формулу: , где
Сообщить об ошибке
Площадь ромба составляет квадратные единицы, а высота равна . Найдите периметр ромба.
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы решить эту задачу, используйте данную информацию, чтобы найти длину стороны ромба в обратном порядке: имеет длину стороны , найдите периметр ромба.
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти периметр этого ромба, примените формулу: , где
Сообщить об ошибке
Площадь ромба составляет квадратные единицы, а высота . Найдите периметр ромба.
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы решить эту задачу, используйте данную информацию, чтобы найти длину стороны ромба в обратном направлении:
, где
Сообщить об ошибке
Длина стороны ромба равна футу, какова длина периметра (в дюймах).
Возможные ответы:
дюйма
футов
дюйма
дюйма
дюйма
Правильный ответ:
дюйма
Объяснение:
Чтобы найти периметр, сначала преобразуйте футы в эквивалентное количество дюймов. Так как, и , равно дюймам.
Так как, и , равно дюймам.
Затем применим формулу , где равна длине одной стороны ромба.
Поскольку,
Решение:
Сообщить об ошибке
Найдите периметр ромба, длина стороны которого равна .
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти периметр этого ромба, сначала преобразуйте смешанное число в неправильную дробь:
Тогда применим формулу: , где равно одной стороне ромба.
Так как решение:
Сообщить об ошибке
← Назад 1 2 3 4 Далее →
Уведомление об авторских правах 250 практических тестов Вопрос дня Карточки Learn by Concept
Формула периметра ромба — объяснение, площадь, примеры решений и часто задаваемые вопросы
Хотите знать, как найти периметр ромба? Как и у любого многоугольника, периметр ромба — это общее расстояние вокруг внешней стороны, которое можно просто рассчитать, сложив длины каждой стороны. В случае ромба все четыре стороны имеют одинаковую длину, поэтому периметр в четыре раза больше длины стороны. Или по формуле: Периметр ромба = 4 а = 4 × сторона. Здесь «а» представляет каждую сторону ромба.
В случае ромба все четыре стороны имеют одинаковую длину, поэтому периметр в четыре раза больше длины стороны. Или по формуле: Периметр ромба = 4 а = 4 × сторона. Здесь «а» представляет каждую сторону ромба.
О периметре ромба Формула
Ромб — двумерная (2D) геометрическая фигура, состоящая из четырех равных сторон. У ромба все стороны равны, а противоположные углы равны по измерению. Давайте теперь поговорим о формуле ромба, т.е. площади и периметра ромба.
Периметр ромба
Периметр равен сумме длин всех четырех сторон. У ромба все стороны равны.
Таким образом, Периметр ромба = 4 × сторона
Итак, P = 4s
Где
S = длина стороны ромба
Площадь ромба Формула
Площадь ромба — это количество квадратных единиц внутри многоугольника. Площадь ромба можно определить двумя способами:
i) Умножение основания и высоты ромба — уникальный вид параллелограмма.
Площадь ромба = b × h
В котором
B = основание ромба
H = высота ромба
ii) Путем определения произведения диагоналей и деления произведения на 2.
Формула площади ромба = \[\frac {1}{2}\] × d1 × d2
В котором
d 1 × d 2 = диагональ ромба
Вывод площади ромба
Пусть MNOP — ромб, основание которого MN = b, PN ⊥ MO, PN — диагональ ромба = d 1 , MO — диагональ ромба = d 2 , а высота от О до MN равна OZ, т. е. h.
= 2 × \[\frac {1}{2}\] MN × OP кв.ед.
= 2 × \[\frac {1}{2}\] b × h кв. единиц
= основание × высота кв. единиц
= 4 × \[\frac {1}{2}\] × MZ × ZN кв.ед.
= 4 × \[\frac {1}{2}\] × d 2 × \[\frac {1}{2}\] d 1 кв. ед.
ед.
Таким образом,
= 4 × \[\frac {1}{8}\] d 1 × d 2 квадратных единиц
= \[\frac {1}{2}\] × d 1 × d 2
Следовательно, площадь ромба
}{\frac
{\frac 2}\] (произведение диагоналей) кв.ед.
Интересные факты
Ромб состоит из вписанной окружности
У ромба все стороны равны, как у прямоугольника все углы равны.
У ромба противоположные углы равны друг другу, а у прямоугольника противоположные стороны равны.
Нахождение периметра ромба, когда известны только диагонали
Во многих вопросах вы увидите, что длина сторон ромба не дана. Вместо этого вопрос предоставит вам длину его диагоналей. Вы можете использовать диагонали, чтобы найти сторону ромба и вычислить его периметр. Вот как это можно сделать:
Вместо этого вопрос предоставит вам длину его диагоналей. Вы можете использовать диагонали, чтобы найти сторону ромба и вычислить его периметр. Вот как это можно сделать:
Рассмотрим ромб PQRS с диагоналями a и b и центром O.
Выберите треугольник, скажем POS. Поскольку диагонали ромба делят друг друга пополам под прямым углом, длина OP будет равна \[\frac {a}{2}\], а OS будет равна \[\frac {b}{2}\]. 92)} \].
Решенные примеры
1. Найдите площадь ромба MNOP, каждая сторона которого равна 15 см, а одна из его диагоналей равна 18 см.
ANS:
Дано:- MNOP- это ромб, в котором Mn = NO = OP = PM = 15 см
MO = 18 см
Таким ,
МП 2 = МЗ 2 + ЗП 2
⇒ 152 = 92 + ZP 2
⇒ 225 = 81 + ZP 2
⇒ 144 = ZP 2
⇒ ZP = 12
Hence, NP = 2 P
= 2 × 12
= 24 см
Сейчас, чтобы узнать площадь роба, мы применим формулу, т. е.
е.
= \ [\ frac {1,
=. {2}\] × d 1 × d 2
= \[\frac {1}{2}\] × 18 × 24
= 216 см 2
2. Найдите периметр ромба MNOP, диагонали которого равны 20 см и 24 см соответственно?
ANS:
Дано: D 1 = 20 см
D 2 = 24 CM
MZ = \ [\ FRAC {20} {2} \] = 100714
. NZ= \[\frac {24}{20}\]= 12 см
∠MZP = 90°
Применяя теперь теорему Пифагора, мы знаем, что
MN 2 = MZ 2 + NZ 2
MN = \[\sqrt {(100+144)} \]
= 15. 62 cm
62 cm
Since, MN = NO = OP = MP,
Следовательно, периметр MNOP = 15,62 × 4 = 62,48 см.
Свойства ромба
Определить ромб не так уж сложно. Есть некоторые свойства ромба, которые помогут вам определить, является ли данная фигура ромбом или нет. Если фигура удовлетворяет следующим условиям, то это ромб:
Все стороны ромба равны.
Противоположные стороны ромба параллельны друг другу.
Все противоположные углы ромба будут равны.
Диагонали ромба делят друг друга пополам под углом 90 градусов, то есть под прямым углом.
При сложении любых двух смежных углов ромба сумма должна быть равна 180 градусам.

Проверка формулы периметра ромба – объяснение, площадь, примеры решений и часто задаваемые вопросы
Формула периметра ромба — одна из важнейших математических формул. Он подпадает под измерение, которое является важной главой математики. Вы должны иметь четкое представление о формуле периметра ромба — объяснение, площадь, решенные примеры и часто задаваемые вопросы, чтобы обеспечить хороший результат в финале. Зная периметр и площадь ромба, вы сможете решить любой вопрос, связанный с этим понятием. Вот почему вам следует тщательно практиковать и пересматривать формулу периметра ромба — объяснение, площадь, решенные примеры и часто задаваемые вопросы. Вот несколько советов по изменению:
Во-первых, изучите формулу периметра ромба — объяснение, площадь, примеры решения и часто задаваемые вопросы, чтобы четко понять тему.
Тщательно прочитайте объяснения периметра и площади ромба в учебнике.

Практикуйте как можно больше вопросов, связанных с периметром и площадью ромба, чтобы стать более опытным в решении задач измерения.
Используйте разные справочники и выбирайте важные вопросы на основе периметра и площади ромба, чтобы понять различные типы вопросов, которые могут появиться на вашем выпускном экзамене по математике.
Посетите платформу электронного обучения Vedantu через наш веб-сайт или мобильное приложение, чтобы изучить формулу периметра ромба — объяснение, площадь, решенные примеры и часто задаваемые вопросы. Каждое объяснение и вопрос, предоставленные Vedantu, курируются одними из лучших экспертов в предметной области, чтобы обеспечить точность и высокое качество.
Просмотрите решенные примеры из учебника или справочника, чтобы узнать, как решать различные виды задач на основе площади и периметра ромба.

После того, как вы решите все вопросы учебника, найдите вопросы из контрольных работ предыдущего года и образцы заданий, чтобы понять схему и уровень сложности экзамена.
Что это такое?, площадь, периметр, факты и примеры
Ромб представляет собой параллелограмм с четырьмя конгруэнтными сторонами (стороны равной длины). Квадрат – это частный случай ромба. Следовательно, ромб – это четырехугольник с четырьмя равными сторонами. Таким образом, определяя ромб, мы можем сказать, что:
Ромб — это тип четырехугольника, в котором обе пары противоположных сторон параллельны, все стороны имеют одинаковую длину, а все противоположные углы равны. Он также известен как ромб. Любая сторона ромба может быть Выбранный в качестве основания ромба перпендикуляр, опущенный на эту сторону из противоположной вершины, известен как его высота или высота
Свойства ромба:
- Ромб имеет две пары параллельных сторон
- Противоположные углы ромба равны.

- У ромба четыре равные стороны. Это означает, что все его стороны равны.
- Диагонали ромба делят друг друга пополам
- Диагонали ромба перпендикулярны друг другу
Поймем каждое из вышеперечисленных свойств через ромб ABCD.
Свойства ромба
Давайте разберем каждое из вышеуказанных свойств через изображенный ниже ромб ABCD.
- Ромб ABCD имеет две пары параллельных сторон, а именно (AB и CD) и (AD и BC)
- У ромба ABCD все стороны равны, т.е. AB = CD = AD = BC
- У ромба ABCD противоположные углы равны, т. е. ∠A = ∠C и ∠B = ∠D.
- Диагонали ромба делят друг друга пополам, т.е. AP = PC и BP = PD
- Диагонали ромба ABCD перпендикулярны друг другу, т.е. АС ⟂ BD.
Ромб – это параллелограмм, у которого все стороны равны. Некоторые свойства ромба:
- Все стороны ромба равны.
- Поскольку все стороны ромба равны, он также известен как равносторонний четырехугольник .

- Диагонали ромба делятся пополам под прямым углом.
- Помимо сторон, площадь ромба можно вычислить и по его диагоналям.
Площадь ромба с учетом его сторон
Поскольку ромб является параллелограммом, все стороны которого равны, формула площади параллелограмма также применима для вычисления площади ромба.
Отсюда
Площадь ромба = основание x высота
Пример :
Пусть у нас есть ромб, высота которого 7 см, а периметр ромба 180 см.
Решение
Дано, что
Высота ромба = 7 см
Периметр ромба = 180 см.
Нам нужно найти площадь ромба. Для этого нужно сначала найти сторону ромба.
Теперь вспомните, что периметр замкнутой формы равен сумме всех ее сторон. Так как ромб является четырехугольником, у которого все стороны равны, то можно сказать, что если ромб имеет сторону «а», то
а + а + а + а = 180 см
4а = 180 см
а = 45 см
Отсюда сторона (основание) ромба = 45 см
Теперь, чтобы вычислить площадь ромба, мы знаем, что
Площадь ромба = Основание х Высота
Следовательно,
Площадь = (45 х 7) см 2 = 315 см 2
Площадь ромба по его диагоналям
Мы также можем вычислить площадь ромба, если знаем его диагонали. Формула для вычисления площади ромба, когда мы знаем его диагонали, задается следующим образом:
Формула для вычисления площади ромба, когда мы знаем его диагонали, задается следующим образом:
Площадь ромба = $\frac{1}{2}$ x (Произведение диагоналей)
Если d 1 и d 2 две диагонали ромба, тогда
Площадь ромба = $\frac{1}{2}$ x (d 1 x d 2 )
Пример
Если две диагонали ромба равны 9 см и 12 см соответственно, найдите площадь ромба. ромб.
Решение
Мы знаем, что нам даны диагонали, площадь ромба = $\frac{1}{2}$ x (d 1 x d 2 )
Здесь две диагонали 9см и 12см.
Итак, пусть
D1 = 9 см и d2 = 12 см.
Площадь ромба = $\frac{1}{2}$ x (d 1 x d 2 ) = $\frac{1}{2}$ x (9 x 12) см 2 = 54 см 2
Отсюда площадь ромба = 54 см 2
Периметр замкнутой фигуры равен сумме всех ее сторон. Мы знаем, что ромб — это разновидность четырехугольника, у которого все стороны равны. Следовательно, периметр ромба будет полной мерой его границы. Итак, как найти периметр ромба? Давайте узнаем.
Мы знаем, что ромб — это разновидность четырехугольника, у которого все стороны равны. Следовательно, периметр ромба будет полной мерой его границы. Итак, как найти периметр ромба? Давайте узнаем.
Периметр ромба по сторонам
Периметр ромба очень просто найти, если известны размеры его сторон. Чтобы найти периметр, нужно найти сумму всех его сторон. Поскольку у ромба 4 стороны,
Отсюда
Периметр ромба = 4 x Сторона
Разберем это на примере.
Предположим, у нас есть ромб, каждая сторона которого равна 4 см. Каков будет его периметр?
Мы узнали, что периметр ромба равен сумме его четырех сторон. Кроме того, у ромба все четыре стороны равны. У нас есть формула для нахождения периметра ромба:
Периметр ромба = 4 x сторона
Здесь сторона = 4 см
Следовательно, периметр ромба = 4 x 4 = 16 см
Итак, мы теперь знаем, как найти периметр ромба, используя его стороны. А что, если вместо сторон нам известны диагонали ромба? Можем ли мы все же найти его периметр? Давайте узнаем.
Периметр ромба по диагоналям
Мы научились находить периметр ромба, зная его стороны. Но когда мы знаем диагонали вместо сторон, мы используем теорему Пифагора, чтобы узнать стороны. Давайте посмотрим, как.
Следующие свойства ромба используются для нахождения значения сторон:
- Ромб разделен на 4 конгруэнтных прямоугольных треугольника двумя диагоналями.
- Диагонали делят друг друга пополам под прямым углом.
Предположим, у нас есть следующий ромб, где диагональ AC = a и диагональ BD = b
Теперь рассмотрим треугольник APD. Используя теорему Пифагора, мы можем сказать, что
AP 2 + PB 2 9{2}}$
= $2\times\sqrt{36+64}$
= $2\times\sqrt{100}$
= $2 \times 10 = 20$ см
Следовательно, периметр данный ромб = 20 см
- Термин «ромб» был получен из греческого слова «ромб (ῥόμβος)», что означает что-то, что вращается, и этот термин в конечном итоге был получен из греческого глагола «rhembō (ῥέμβω)», который значит крутиться по кругу.

- Ромб можно найти в самых разных вещах вокруг нас, таких как воздушный змей, окна автомобиля, серьги в форме ромба, конструкция здания, зеркала и даже участок бейсбольного поля.
- Квадраты-ромбы. Это просто ромб, у которого все углы прямые. Хотя наиболее распространенным термином, используемым для описания этой формы в геометрии, является «ромб», вы также можете услышать, что форма называется ромбом или ромбом. Множественное число для некоторых из них — ромбы или ромбы.
Пример 1
Сторона ромба равна 6,5 см, а высота 4 см. Найдите его площадь
Решение
Нам известно, что сторона ромба равна 6,5 см, а его высота равна 4 см.
Теперь мы знаем, что если нам известны сторона ромба и его высота, то площадь ромба рассчитывается по формуле:
Площадь ромба = основание x высота
Подставляя данные значения в Приведенная выше формула, которую мы получаем,
Площадь ромба = (6,5 x 4) CM 2 = 26 см 2
Следовательно, площадь ромба = 26 см 2
Пример 2 Площадь ромба 72см 2 . Решение Нам известно, что площадь ромба равна 72 см 2 , а его периметр равен 32 см. Сейчас, Периметр ромба = 32см. Это означает, что сумма его четырех сторон = 32 см. Пусть одна из сторон ромба равна а. Тогда 4a = 32 см ⇒ a = $\frac{32}{4}$ = 8 см Итак, теперь мы знаем, что сторона ромба равна 8 см. Кроме того, нам известно, что площадь ромба равна 72 см 2 Мы также знаем формулу для вычисления площади ромба, которая равна Площадь ромба = основание x высота Подставляя значения площади и стороны (основания) в приведенном выше уравнении имеем 72 = 8 x Высота ⇒ Высота = $\frac{72}{8}$ см = 9 см Отсюда высота (высота ) ромба 9 см Пример 3 Если сторона квадрата равна 4 м и он преобразован в ромб, большая диагональ которого равна 6 м; найти другую диагональ и площадь ромба. Решение Нам известно, что сторона квадрата превращается в ромб. Пусть ABCD — квадрат, который превратился в ромб. Теперь у нас есть АВ = 4 м. Также известно, что длина большой диагонали равна 6 м. Следовательно, Пусть AC — большая диагональ, а BD — малая диагональ ромба. Нам дали это, AC = 6 м Мы знаем, что диагонали ромба делятся пополам под прямым углом. Пусть диагонали AC и BD пересекают друг друга под прямым углом в точке O. Следовательно, мы можем сказать, что OA = $\frac{1}{2}$ x AC = 3 м и ∠AOB = 90 o Используя теорему Pythagoras, мы будем иметь AB 2 = OA 2 + OB 2 ⇒ 4 2 = 3 2 Найдите его высоту, если его периметр равен 32 см.
Найдите его высоту, если его периметр равен 32 см.
 0905 2 = 16 – 9
0905 2 = 16 – 9⇒ OB 2 = 7
⇒ OB = $\sqrt{7}$ m
Теперь мы знаем, что диагональ BD = 2 x OB.
Следовательно,
BD = 2 x $\sqrt{7}$ m =2$\sqrt{7}$ m
Отсюда другая диагональ ромба = $2\sqrt{7}$ m
Теперь нам нужно найти площадь ромба.
Мы знаем, что можем найти площадь ромба, если знаем значения его диагоналей, формула для которых равна
Площадь ромба = $\frac{1}{2}$ x (Произведение диагоналей)
Диагонали ромба равны 6 м и $2\sqrt{7}$ м соответственно. Следовательно,
Площадь ромба = $\frac{1}{2}\times (6\times 2\sqrt{7})$
Площадь ромба = $6\sqrt{7}$ м 2
Отсюда площадь данного ромба = $6\sqrt{7}$ м 2
Пример 4
Одна из диагоналей ромба равна одной из его сторон. Найдите углы ромба.
Решение
Нам известно, что диагонали ромба равны одной из его сторон. Нам нужно найти углы ромба.
Нам нужно найти углы ромба.
Пусть ABCD ромб такой, что его диагонали BD равны сторонам.
Это означает, что стороны AB = BC = CD = AD = BD
Также можно сказать, что
DABD и DBCD равносторонние. Это означает, что
∠A = ∠C = 60° ……………………………….. (1)
Теперь угол, образованный при A, и угол, образованный при B, являются смежными углами. Поэтому можно сказать, что
∠A + ∠B = 180° ………………………………….. (2)
Подставив значение РA из уравнения (1) в уравнение (2), получим,
60° + ∠B = 180°
∠B = 180° – 60°
∠B = 120° Следовательно, ∠A = 60° = ∠C и ∠B = ∠D = 120°
Следовательно, четыре угла ромба равны ∠A = ∠C = 60° = и ∠B = ∠D = 120°
Пример 5
Если площадь ромба 48 кв. см, а одна из его диагоналей 6 см, то найдите его высоту
Решение
Пусть ABCD — заданный ромб, диагональ AC = 6 см.
Теперь площадь ромба ABCD = 48 кв. см
см
Теперь мы знаем, что
Площадь ромба = $\frac{1}{2}$ x (Произведение диагоналей)
⇒ Площадь ромб = $\frac{1}{2}$ x 6 x BD
⇒ 48 = $\frac{1}{2}$ x 6 x BD
⇒ BD = 16 см
Поскольку диагонали а ромбы делят друг друга пополам под прямым углом, поэтому
OA = $\frac{1}{2}AC$ = 3 см и OB = $\frac{1}{2}BD$ = 8 см
Кроме того, треугольник OAB является прямым углом. Таким образом, используя теорему Pythagoras, мы имеем
AB 2 = OA 2 + OB 2
⇒ AB 2 = 3 2 + 8 2 = 3 2 + 8 2 = 3 2 + 8 2 . 9. 9 2
⇒ AB 2 = 73
⇒ AB = $\sqrt{73}$ см
Теперь площадь ромба ABCD = 48 см 2
Это означает, что База x Высота = 48 см 2
⇒ AB x Высота = 48
⇒ Высота x $\sqrt{73}$ = 48
⇒ Высота = $\frac{48}{\sqrt{ 73}}$ см
Следовательно, высота данного ромба = $\frac{48}{\sqrt{73}}$ см
- Квадрат, прямоугольник и ромб являются параллелограммами.

- Квадрат — это прямоугольник, а также ромб.
- Параллелограмм является трапецией, а не ромбом
- Воздушный змей не является параллелограммом
- Трапеция не является параллелограммом или ромбом (поскольку в трапеции параллельна только одна пара противоположных сторон, и мы требуем, чтобы обе пары были параллельны в параллелограмме).
- Прямоугольник или ромб не является квадратом
- Ромб имеет две пары параллельных сторон
- Противоположные углы в ромбе равны
- У ромба четыре равные стороны Это означает, что все его стороны равны
- Диагонали ромба разделить друг друга пополам 9{2}}$
Нахождение площади треугольников и четырехугольников Рабочие листы по математике для 6-го класса
Определение треугольников, четырехугольников, пятиугольников, шестиугольников и кубов Рабочие листы по математике для 2-го класса
Просмотреть все рабочие листы
поиск и сбор информации на этом сайте. Если вы сочтете это полезным в своем исследовании, используйте приведенный ниже инструмент, чтобы правильно указать ссылку Helping with Math в качестве источника. Мы ценим вашу поддержку!
Если вы сочтете это полезным в своем исследовании, используйте приведенный ниже инструмент, чтобы правильно указать ссылку Helping with Math в качестве источника. Мы ценим вашу поддержку!
Калькулятор площади ромба | Шаги, чтобы найти площадь ромба
Площадь ромба Калькулятор: Вы хотите понять концепцию площади ромба? Вы достигли правильного места. Эта страница содержит полезную информацию о площади ромба. Студенты могут узнать полные детали, такие как формулы площади ромба, как рассчитать площадь ромба, что подразумевается под ромбом и некоторые примеры вопросов. Наш удобный калькулятор дает точные и мгновенные результаты после того, как вы введете входные данные.
Выбрать Площадь ромба Площадь ромба
- Площадь ромба, если известны сторона и высота
- Площадь ромба по диагоналям
- Площадь ромба, если даны сторона и любой угол
Сторона (а) сммкминмийдфтмм
Высота (ч) сммкминмийдфтмм
Примеры расчетов площади ромба (сторона и высота)
Диагональ (е) сммкминмийдфтмм
Диагональ (f) сммкминмийдфтмм
Вот несколько примеров расчета площади ромба (диагонали)
Сторона (а) cmmkminmiydftmm
Угол α градусы радиан
Вот несколько примеров расчета площади ромба (сторона под любым углом)
Воспользуйтесь преимуществами этого простого в использовании инструмента Калькулятор площади ромба, чтобы получить площадь ромба за считанные секунды. Вы должны выбрать любой вариант из стороны и высоты, диагонали, стороны и любого варианта угла в зависимости от ваших требований. Введите значения в соответствующие поля ввода калькулятора и нажмите кнопку расчета, чтобы легко проверить площадь ромба.
Вы должны выбрать любой вариант из стороны и высоты, диагонали, стороны и любого варианта угла в зависимости от ваших требований. Введите значения в соответствующие поля ввода калькулятора и нажмите кнопку расчета, чтобы легко проверить площадь ромба.
Здесь перечислены наиболее часто используемые формулы для расчета площади ромба. Студентам рекомендуется знать, когда использовать эти формулы, чтобы получить точный результат.
1. Если известны длина стороны ромба и высота, то воспользуйтесь этой формулой.
Площадь ромба = a x h
Где
a длина стороны ромба
h высота ромба
2. Если у вас есть длины двух диагоналей, то используйте приведенная ниже формула.
Площадь = ½ × e × f
Где,
e, f — длины диагоналей ромба.
3. Если известна длина стороны, угол ромба, то
Площадь ромба = a² x sin(α)
Где,
a – длина стороны ромба
α – угол между любыми стороны ромба.
Ниже приведены некоторые шаги, которые помогут вам решить вопросы области ромба, зная любое его значение. Посмотрите на них и следуйте, когда вы не можете решить вопросы.
Посмотрите на них и следуйте, когда вы не можете решить вопросы.
1. Когда у вас есть сторона, высота
- Получите необходимые данные, такие как длина стороны и высота ромба из ваших вопросов.
- Умножьте эти значения, чтобы найти результат, т. е. площадь.
2. При длине диагоналей
- Запишите длину большой и малой диагоналей ромба из вопроса.
- Умножьте диагональные значения.
- Разделите произведение диагоналей на 2, чтобы получить площадь.
3. Если у вас есть длина стороны и угол
- Получите длину стороны и угол между сторонами ромба из вопроса.
- Возведите в квадрат длину стороны и найдите тригонометрический синус угла.
- Умножьте эти два значения, чтобы найти площадь ромба.

Пример 1: Вычислите площадь ромба, диагонали которого равны 10 см и 8 см?
Решение:
Учитывая, что
Диагонали ромба e = 10 см, f = 8 см 10 × 8
= ½ × 80
= 40
∴ Площадь ромба, диагонали которого равны 10 см и 8 см, равна 40 см².
Пример 2: Вычислить площадь ромба, если длина его стороны 14 см, а один из углов А равен 40 градусов?
Решение:
Учитывая, что
Длина стороны ромба a = 14 см
Угол = 40 градусов
Площадь ромба = a² x sin(α)
Подставим формулу .
Площадь = 14² x sin(40°)
= 14 x 14 x 0,64279
= 125,98
∴ Площадь ромба со стороной 14 см и углом 40 градусов равна 125,98 см².
Пример 3: Найдите площадь ромба, если его основание 7 см, а высота 5 см?
Решение:
Учитывая, что
Длина основания A = 7 см
Высота H = 5 см
Площадь ромба = A X H
= 7 x 5
= 35
∴. 35 см².
35 см².
Areavolumecalculator.com — это инструмент для геометрического калькулятора, с помощью которого вы изучите, попрактикуетесь и откроете для себя площадь нескольких фигур, площадь поверхности, периметр, объем и т. д.
1. Что такое ромб?
Ромб – это четырехугольник, у которого противоположные стороны параллельны и имеют одинаковую длину. Кроме того, противоположные углы ромба измеряют одинаковую величину, а его диагонали перпендикулярны друг другу.
2. Как измерить площадь ромба?
Простые методы используют диагонали, используют основание и высоту и используют тригонометрию. Площадь ромба можно определить как половину произведения диагоналей или произведение длины основания на высоту. Вы должны возвести в квадрат базовую длину и применить синусоидальную функцию угла, чтобы получить значение площади.
3. По какой формуле найти периметр ромба?
Периметр ромба p = 4a. где а — длина стороны ромба.
4. Одна из диагоналей ромба на 3 см больше другой. Найдите длину диагоналей, если его площадь 14 см².
e = x, f = x+3
площадь = ½ × e × f = ½ × x x (x+3)
14 = (x² + 3x) / 2
x² + 2x = 28
x² + 2x — 28 = 0
(x + 7) (x — 4) = 0
Итак, e = 4 см, f = 7 см
Калькулятор площади и периметра
Решатель геометрических задач — ромб
Решатель геометрических задач
Ромб
Они дают дорожки, некоторые проблемы могут быть решены автоматически, числовые значения не имеют значения в различных примерах.
Дорожка 1
Сторона ромба 20 см. Вычислите периметр.
Дорожка 2
Диагонали ромба 20 см и 40 см. Вычислите периметр и площадь.
Дорожка 3
Периметр ромба 100 см. Вычислите длину стороны.
Дорожка 4
Два равносторонних треугольника имеют общую сторону и образуют ромб. Вычислите периметр ромба, зная, что периметр каждого треугольника равен 45 см.
Вычислите периметр ромба, зная, что периметр каждого треугольника равен 45 см.
Дорожка 5
Диагональ ромба 80 см, а другая диагональ в два раза больше первой. Вычислите площадь ромба.
Дорожка 6
Сумма диагоналей ромба 200 см; вторая диагональ в три раза больше первой. Вычислите площадь ромба.
Путь 7
Ромб имеет периметр 100 м; имеет высоту 10 м. Вычислите площадь ромба.
Дорожка 8
Вычислите площадь ромба, зная, что диагональ на 4 см меньше другой в три раза, а их сумма равна 28 см.
Дорожка 9
Ромб и прямоугольник имеют одинаковый периметр. Сторона ромба равна 30 см, а основание прямоугольника 40 см. Вычислите меру высоты прямоугольника.
Дорожка 10
Ромб имеет вершины в середине сторон прямоугольника, площадь которого равна 1000 см. Зная, что диагонали ромба равны друг другу по 2/5, вычислить их размер.
Дорожка 11
Прямоугольник эквивалентен квадрату с периметром 40 см. Учитывая, что высота прямоугольника равна 1/4 основания, вычисляет площадь ромба прямоугольника, изопериметрически конгруэнтного высоте, равной 3/5 стороны квадрата, а периметр равностороннего треугольника равен ромбу.
Дорожка 12
Вычислите меру гипотенузы каждого из четырех треугольников, в которых ромб разделен диагоналями, зная, что сумма диагоналей, имеющих длину 14 м, равна 3/4 другой.
Дорожка 13
В сумме диагоналей ромба размером 150 см и а составляет 1/2 другой. Вычислите: меру стороны квадрата, эквивалентную ромбу, периметру прямоугольника, эквивалентному одной пятой части ромба, зная, что его размер составляет 4/5 другой, меру трех высот разнонаправленной треугольник, равный 6/25 ромба, стороны которого соответственно равны 30 см, 40 см и 50 см
Дорожка 14
Ромб: сумма диагоналей 130 см, разница 30 см. область? периметр?
область? периметр?
Дорожка 15
Сумма диагоналей ромба 130 см, разница 30 см. Вычисляет площадь и периметр.
Дорожка 16
Диагонали ромба 48 см и 14 см. Чему равна площадь прямоугольника, эквивалентного гулу?
Дорожка 17
Прямоугольник имеет основание 20 см и высоту 30 см. Чему равна площадь ромба, равная 3/5 прямоугольника?
Дорожка 18
Площадь ромба 900 см, диагональ 30 см. Вычислить меру диагонали.
Дорожка 19
Площадь ромба 900 см, диагональ 30 см. Определяет площадь квадрата, длина стороны которого равна другой диагонали ромба.
Дорожка 20
Периметр прямоугольника 160 см, а основание 50 см. Найдите площади прямоугольника и ромба, равные 3/4 площади прямоугольника.
Дорожка 21
В ромбе длина диагонали 96 см, а длина другой составляет 7/24 первой. Найдите площадь квадрата, периметр которого равен периметру ромба.
Найдите площадь квадрата, периметр которого равен периметру ромба.
Дорожка 22
Вычислите периметр ромба площадью 1344 см, зная, что диагональ равна 28 см.
Дорожка 23
В ромбе диагонали составляют 3/5 диагонали другой, площадь ромба 750 см. Вычисляет длину диагоналей и периметр ромба.
Дорожка 24
Периметр ромба 120 см, а длина диагонали 48 см. Вычислите площадь ромба.
Дорожка 25
Ромб и квадрат эквивалентны. Зная, что сторона квадрата равна 18,33 см, вычислить периметр ромба, высота которого по длинной стороне 13,44 см.
Дорожка 26
В ромбе апофема равна 6 см, а каждая сторона равна 25/12 диаметра вписанной окружности. Вычислите периметр прямоугольника, основание которого совпадает со стороной ромба, равной высоте и высоте ромба.
Путь 27
Квадрат со стороной 50 дм эквивалентен грохоту ; найти диагонали ромба, зная, что половина другой.
Дорожка 28
Сторона ромба равна 30 см, а относительная высота равна 4/5 стороны. Вычислите высоту ромба, периметр и площадь.
Дорожка 29
Отношение площадей двух подобных ромбов равно 9/16. Зная, что диагонали первого равны 48 см и 14 см, вычислить периметр второго ромба.
Дорожка 30
Нарисуйте ромб, указав его основание АВ, и отследите его высоту.
Дорожка 31
Ромб имеет площадь 864 квадратных сантиметра и высоту стороны 28,8 см. Вычислите периметр и диагонали.
Дорожка 32
Периметр ромба 200 см, периметр квадрата 120 см, шум эквивалентен 10/9 квадрата. Вычислите высоту ромба.
Дорожка 33
Площадь ромба равна 864 см, а диагональ равна 4/3 другого. Вычислите площадь параллелограмма, основание и высота которого соответственно равны 25/24 и 15/24 наибольшей диагонали ромба, периметр квадрата равен 16/15 параллелограмма.
Дорожка 34
Прямоугольник имеет площадь 1500 см и основание 50 см. Вычисляет площадь и периметр ромба, полученного при соединении середины сторон прямоугольника.
Дорожка 35
Нижняя диагональ ромба на 12 см меньше большей и их отношение 3 к 4. Определить периметр и площадь ромба.
Дорожка 36
Диагонали ромба равны квадрату 20 м и 40 м, они делят квадрат на четыре треугольника, а пол квадрата должен быть попеременно окрашен в красный и черный цвета. Чему равна площадь черных треугольников?
Трек 37
Вычислите площадь ромба, периметр которого равен 100 см, а диагональ равна 6/5 стороны.
Дорожка 38
Ромб эквивалентен прямоугольнику с периметром 100 м и основанием 20 м. Вычисляет размер диагонали ромба, зная, что другая равна 30 м.
Дорожка 39
Вычислите сторону ромба, диагонали которого равны 30 см и 40 см соответственно.
Направляющая 40
Сумма оснований трапеции 80см, основание 5/3 другого, высота 2/3 меньшего основания. Вычислите размер каждой диагонали ромба, эквивалентного трапеции, зная, что диагональ равна 25/16 другой.
Дорожка 41
Ромб с диагональю 96 см равен удвоенному равнобедренному треугольнику с периметром 128 см и основанием 28 см. Определяет периметр ромба.
Трек 42
Правая призма имеет основание для грохота с диагональю 20 см. Зная, что размер боковой поверхности 3120 см, а общий 4080 см, вычисляем измерение высоты и объема призмы.
Дорожка 43
Диагонали ромба 48 см и 20 см, рассчитайте длину радиуса вписанной окружности
Дорожка 44
Сумма и разность мер диагоналей равны соответственно 34 м и 14 м, рассчитайте диаметр окружности, эквивалентной грохоту.
Дорожка 45
Площадь ромба 480 см, а сторона 26 см. Вычислите диагональ и периметр.
Вычислите диагональ и периметр.
Дорожка 46
Ромб имеет площадь 480 квадратных сантиметров и периметр 104 см. Вычислите диаметр окружности, вписанной в ромб.
Дорожка 47
Зная, что сумма диагоналей ромба равна 68 см и что на 8 см больше, чем в два раза, вычисляет площадь ромба.
Дорожка 48
Ромб имеет площадь 480 квадратных сантиметров и периметр 104 см. Вычислите площадь круга, радиус которого равен диагонали ромба.
Дорожка 49
Ромб имеет площадь 480 квадратных сантиметров и периметр 104 см. Вычислите площадь круга, радиус которого меньше диагонали ромба
Дорожка 50
Периметр ромба равен 104 см. Вычислите площадь круга, радиус которого равен стороне ромба.
Дорожка 51
Диагонали ромба 48 см и 36 см. Рассчитаем:
сторона ромба;
радиус окружности, вписанной в ромб;
длина хорды, зная, что PQ удалена от центра O на 8,64 см;
— центральный угол, опирающийся на хорду PQ;
длина дуги, опирающейся на хорду PQ.
Дорожка 52
Диагонали ромба 48 см и 36 см. Рассчитать:
сторона ромба;
радиус окружности, вписанной в ромб;
длина хорды PQ;
— центральный угол, опирающийся на хорду PQ;
длина дуги, опирающейся на хорду PQ;
длина хорды PS
центральный угол, опирающийся на хорду PS.
Путь 53
Сторона ромба 30 м, а высота 28,8 м. Вычислите площадь ромба.
Дорожка 54
Площадь ромба 864 см, а сторона 30 см. Вычислите высоту.
Дорожка 55
Сторона ромба 30 см, а диагональ 48 см. Вычислите другую диагональ.
Дорожка 56
Периметр правильного пятиугольника равен 94,71 см. Вычислите периметр ромба, равного 7/5 пятиугольника и имеющего высоту 28,8 см.
Дорожка 57
Периметр правильного шестиугольника равен 92,475 см. Вычислите периметр ромба, конгруэнтного шестиугольнику 7/5 и имеющего высоту 28,8 см.
Трек 58
Периметр правильного семиугольника равен 91,221757 см. Вычислите периметр ромба, конгруэнтного 7/5 дельеттагоно и имеющего высоту 28,8 см.
Трек 59
Периметр правильного восьмиугольника равен 90,448 см. Вычислите периметр ромба, конгруэнтного восьмиугольнику 7/5 и имеющего высоту 28,8 см.
След 60
Периметр обычного эннагоно составляет 89,923 см. Вычислите периметр ромба, конгруэнтного 7/5 дель Эннагоно и имеющего высоту 28,8 см.
Дорожка 61
Периметр правильного десятиугольника равен 89,56 см. Вычислите периметр ромба, равного 7/5 десятиугольника и имеющего высоту 28,8 см.
След 62
Периметр обычного эндекагоно равен 89,2
см. Вычислите периметр ромба, конгруэнтного 7/5 дель Эндекагоно и имеющего высоту 28,8 см.
Трек 63
Периметр правильного двенадцатиугольника равен 89,09.

 Площадь квадрата равна 36 см2. Чему равен его периметр?
Площадь квадрата равна 36 см2. Чему равен его периметр? Чему равна площадь этого параллелограмма?
Чему равна площадь этого параллелограмма?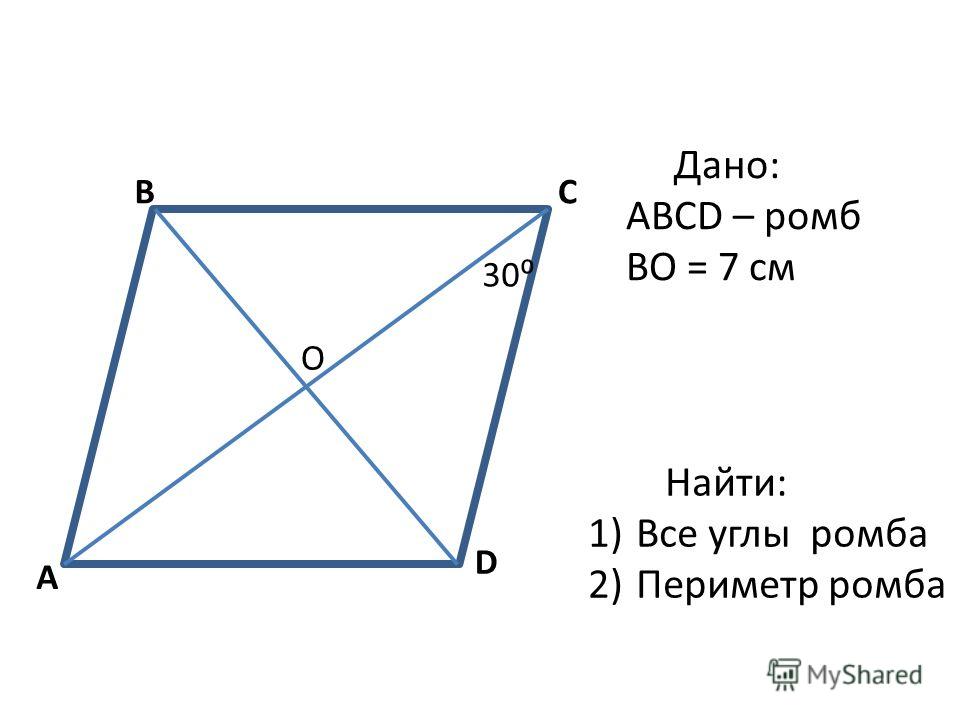
 Площадь квадрата равна 81 см2. Чему равен его периметр?
Площадь квадрата равна 81 см2. Чему равен его периметр?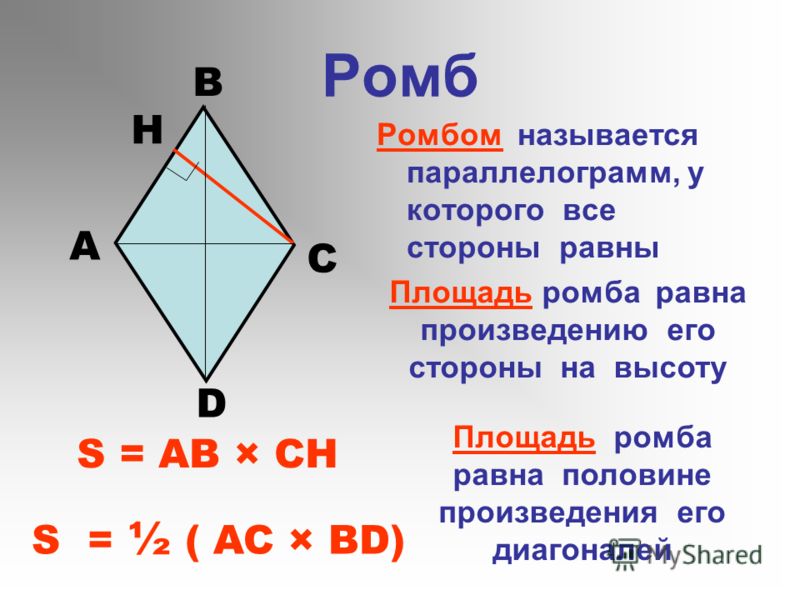 Площадь ромба равна 54, а периметр равен 36. Найдите высоту ромба.
Площадь ромба равна 54, а периметр равен 36. Найдите высоту ромба.
 Найдите площадь параллелограмма.
Найдите площадь параллелограмма. Смежные стороны прямоугольника равны 18 дм и 30 дм. Найдите его площадь.
Смежные стороны прямоугольника равны 18 дм и 30 дм. Найдите его площадь. Смежные стороны параллелограмма равны 16см и 20 см. Найдите большую высоту, если меньшая равна 8 см.
Смежные стороны параллелограмма равны 16см и 20 см. Найдите большую высоту, если меньшая равна 8 см.
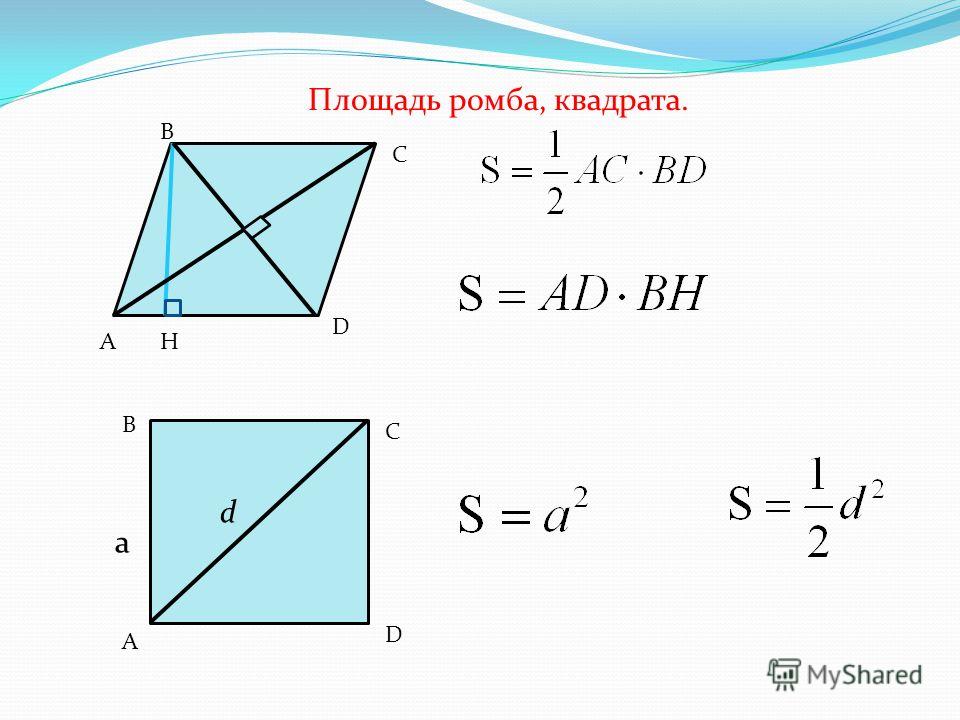 Найдите площадь параллелограмма.
Найдите площадь параллелограмма.
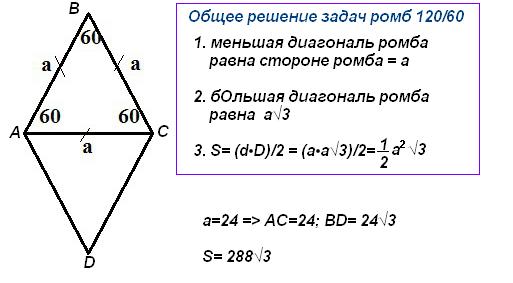 Чему равна площадь прямоугольника со сторонами 18 м и 12 м?
Чему равна площадь прямоугольника со сторонами 18 м и 12 м?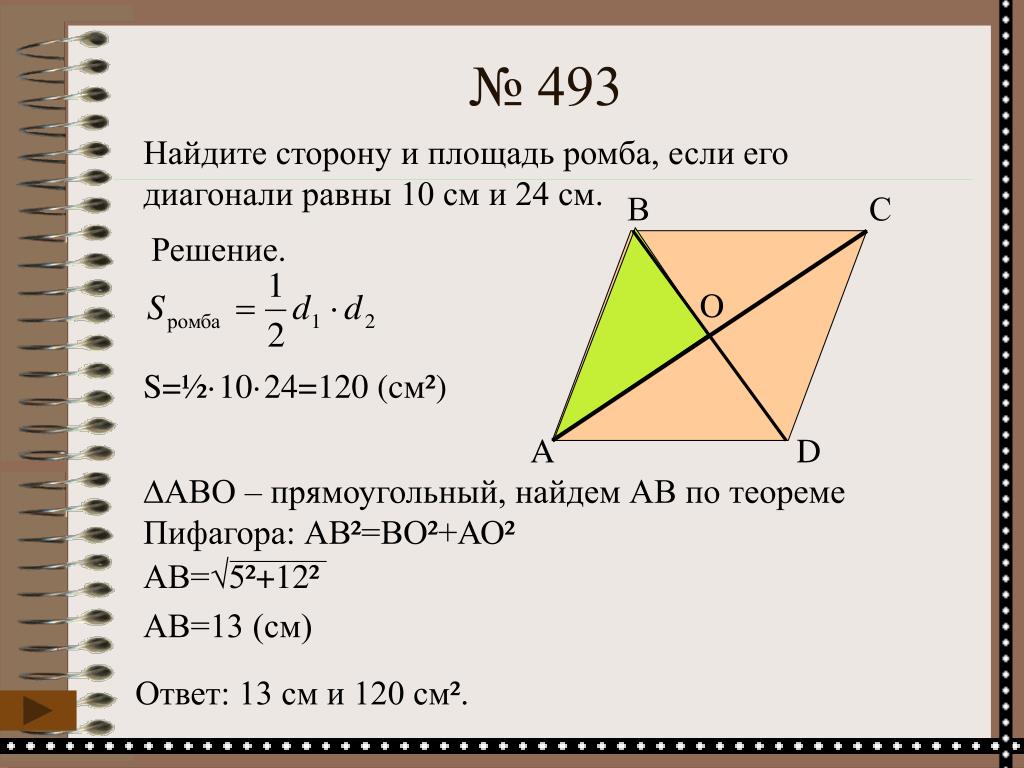 Найти сторону треугольника. Ответ: Решение
Найти сторону треугольника. Ответ: Решение Ответ: 9/4 Решение
Ответ: 9/4 Решение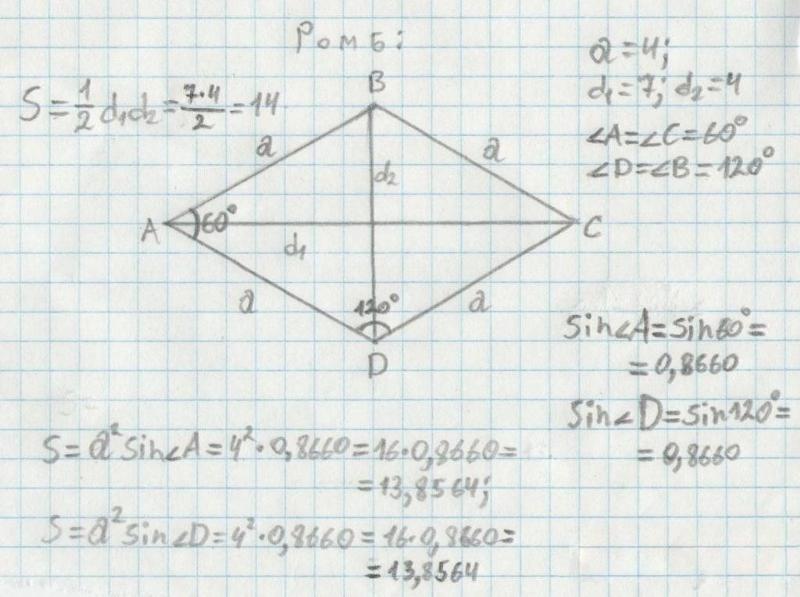 Какую часть площади данного квадрата составляет площадь вписанного? Ответ: Решение
Какую часть площади данного квадрата составляет площадь вписанного? Ответ: Решение