Лучший ответ по мнению автора | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||
Другие ответы
| ||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика
| Похожие вопросы |
Решено
основание прямой призмы ромб с острым углом 60градусов. боковое ребро призмы 10см а площадь боковой поверхности 240см в квадрате найдите площадь…
боковое ребро призмы 10см а площадь боковой поверхности 240см в квадрате найдите площадь…
Решено
В прямоугольном треугольнике ABC катет AC=24, а высота CH, опущенная на гипотенузу, равна 615. Найдите sin∠ABC.
Решено
высота над землёй подброшенного вверх мяча меняется по закону h(t)=1.8+13t-5t2 h высота т время в секундах прошедшее с момента броска. сколько секунд мяч будет находиться на высоте не менее 9м?
Решено
Углы при одном из оснований трапеции равны 23 и 67 градусов, а отрезки, соединяющие середины противоположных сторон, равны 15 и 8. Найти основания трапеции.
Решено
поезд двигался равномерно со скоростья 57 км/ч ,проезжает мимо пешехода,идущего параллельно путям со скоростью 3 км/ч навстречу поезду,за 18 секунд…
Пользуйтесь нашим приложением
Геометрия 7-9 класс.
 Длина окружности. Длина дуги — math200.ru Skip to content
Длина окружности. Длина дуги — math200.ru Skip to contentГеометрия 7-9 класс. Длина окружности. Длина дугиadmin2022-12-27T22:47:04+03:00
Скачать файл в формате pdf.
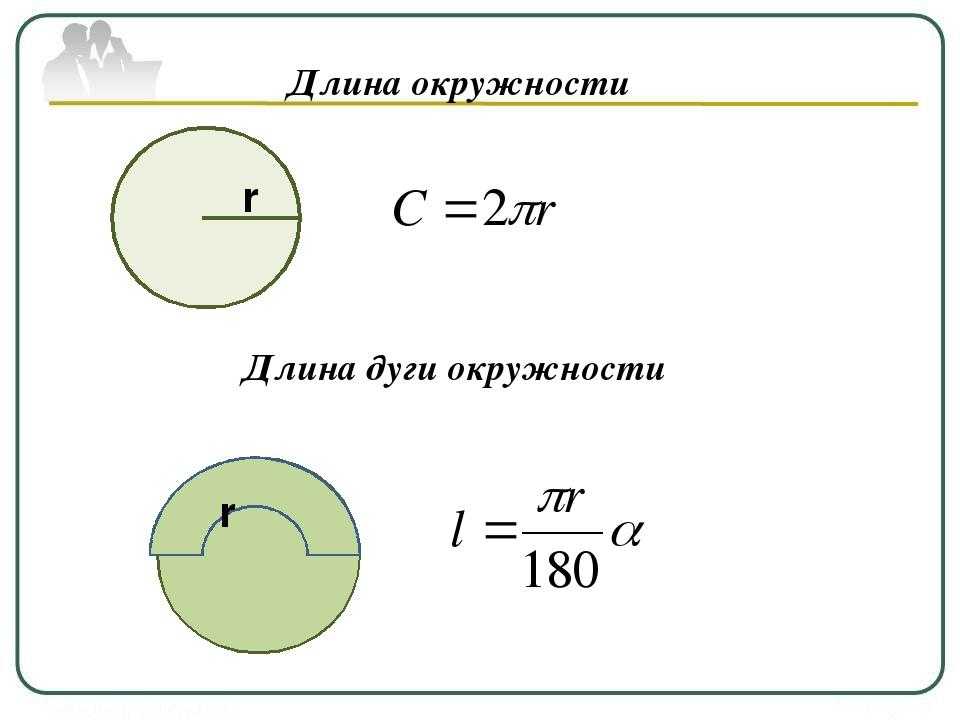
Геометрия 7-9 класс. Длина окружности. Длина дуги
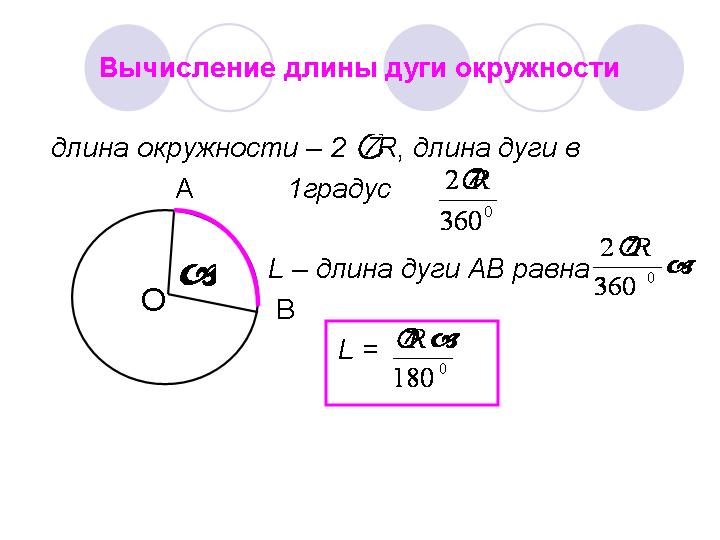
Длина окружности радиуса R равна \(L = 2\pi R.\)
Длина дуги \({L_{AB}} = 2\,\pi {\kern 1pt} R\frac{\alpha }{{360}}\).
| Задача 1. Найдите длину окружности, радиус которой равен \(\frac{8}{{\rm{\pi }}}.\) Ответ ОТВЕТ: 16. | |
| Задача 2. Найдите радиус окружности, если её длина равна \(24{\rm{\pi }}.\) Ответ ОТВЕТ: 12. | |
| Задача 3. Длины двух окружностей, имеющих общий центр, равны \(50\pi \) и \(30\pi .\) Найдите ширину кольца x. Ответ ОТВЕТ: 10. | |
| Задача 4. Длины двух окружностей, имеющих общий центр, равны \(20{\rm{\pi }}\) и \(12{\rm{\pi }}.\) Найдите длину хорды Ответ ОТВЕТ: 16. | |
| Задача 5. Найдите длину окружности вписанной в квадрат, сторона которого равна \(\frac{6}{{\rm{\pi }}}.\) Ответ ОТВЕТ: 6. | |
| Задача 6. Найдите площадь квадрата, если длина окружности, описанной около его, равна \(8{\rm{\pi }}.\) Ответ ОТВЕТ: 32. | |
| Задача 7. Найдите длину окружности, описанной около прямоугольника, стороны которого равна \(\frac{3}{{\rm{\pi }}}\) и \(\frac{4}{{\rm{\pi }}}.\) Ответ ОТВЕТ: 5. | |
Задача 8. Найдите длину окружности, описанной около правильного шестиугольника, площадь которого равна \(\frac{{24\sqrt 3 }}{{{{\rm{\pi }}^2}}}. \circ }.\) \circ }.\)Ответ ОТВЕТ: 27. | |
| Задача 11. Длина окружности равна длине дуги. Найдите R. Ответ ОТВЕТ: 18. | |
| Задача 12. Длина окружности равна длине дуги. Найдите r. Ответ ОТВЕТ: 4. | |
| Задача 13. В равнобедренном треугольнике ABC основание АС = 12, а высота BH = 8. Найдите длину окружности описанной около треугольника АВС. Ответ ОТВЕТ: \(12,5{\rm{\pi }}.\) | |
| Задача 14. В равнобедренном треугольнике ABC боковые стороны АВ = ВС = 25, а высота BH = 20. Найдите длину окружности вписанной в треугольник АВС. Ответ ОТВЕТ: \(15{\rm{\pi }}.\) | |
Задача 15. Найдите длину окружности, описанной около равнобедренной трапеции ABCD основания которой AD = 16 и ВС = 12, если высота трапеции равна 14. \circ }.\) \circ }.\)Ответ ОТВЕТ: \({\rm{8\pi }}\left( {\sqrt 3 — 1} \right).\) | |
Реклама
Поддержать нас
Вычисление длины дуги
Все математические ресурсы GMAT
22 Диагностические тесты 693 практических теста Вопрос дня Карточки Learn by Concept
Помощь по математике GMAT » Проблемные вопросы » Геометрия » Круги » Сектора » Вычисление длины дуги
Примечание: Рисунок выполнен НЕ в масштабе
См. рисунок выше.
Что такое ?
Возможные ответы:
Правильный ответ:
Объяснение:
Градусная мера – это половина градусной меры дуги, которую она пересекает, то есть .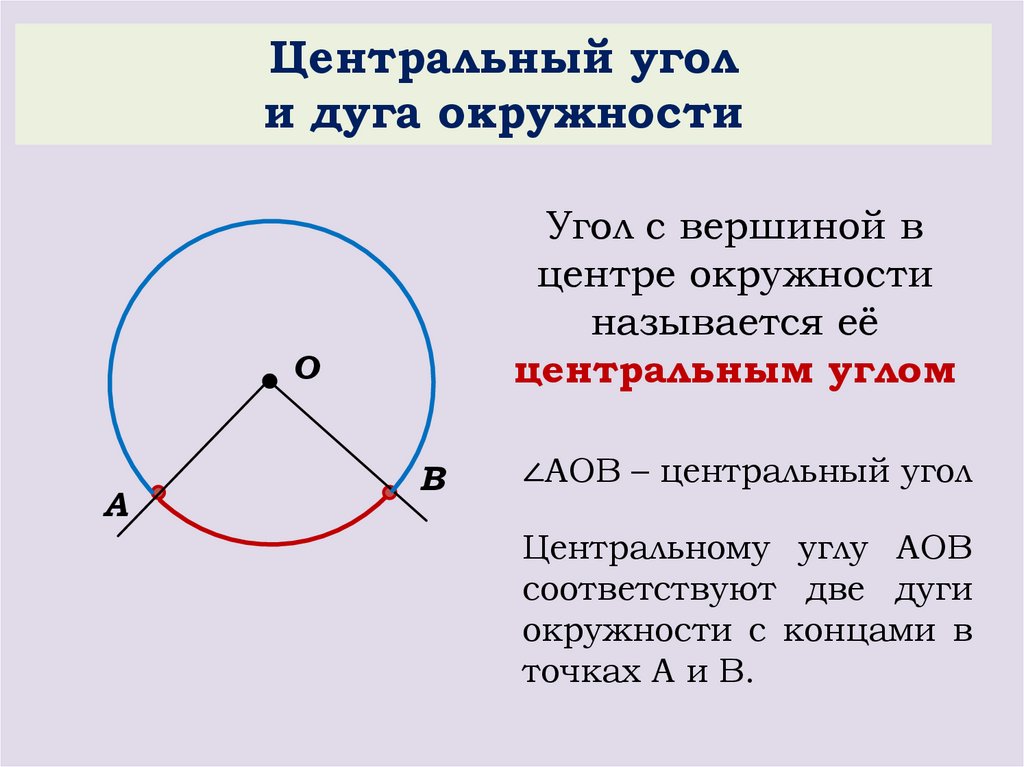 Мы можем использовать размеры двух заданных больших дуг, чтобы найти , а затем взять половину этого:0005
Мы можем использовать размеры двух заданных больших дуг, чтобы найти , а затем взять половину этого:0005
Гигантские часы имеют минутную стрелку длиной восемь футов. Сейчас 14:40. На какое расстояние в дюймах продвинулся кончик минутной стрелки между полуднем и сегодняшним днем?
Возможные ответы:
Правильный ответ:
Пояснение:
Между полуднем и 14:40 прошло два часа сорок минут или, что то же самое, два и две трети часа. Это означает, что минутная стрелка сделала оборотов.
За один оборот кончик восьмифутовой минутной стрелки перемещается на футы или дюймы.
После оборотов кончик минутной стрелки переместился на дюймы.
Сообщить об ошибке
На рисунке ниже отрезок прямой проходит через центр окружности и имеет длину . Точки , и находятся на окружности. Сектор покрывает всю площадь круга. Ответьте на следующие вопросы относительно этой формы.
Ответьте на следующие вопросы относительно этой формы.
Какова длина дуги, образованной углом ?
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти длину дуги, нам нужно найти полную длину окружности, а затем долю окружности, которая нас интересует. Наша формула длины окружности:
диаметр.
В этой задаче наш диаметр равен длине , то есть нашей общей окружности:
Теперь, чтобы найти интересующую нас часть окружности, нам нужно понять, что угол составляет градусы. Мы знаем это, потому что это сделано по прямой линии. Вооружившись этими знаниями, мы можем безопасно рассчитать длину нашей дуги, используя следующую формулу:
Сообщить об ошибке
Рассмотрите окружность :
(Рисунок не в масштабе.)
Предположим . Какова мера дуги в метрах?
Какова мера дуги в метрах?
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти длину дуги, умножьте общую длину окружности на долю общей окружности, которая определяет дугу с длиной, которую вы решаете.
В этом случае, чтобы найти полную длину окружности:
Чтобы найти интересующую нас дробь, сделайте дробь с количеством градусов в в числителе и общим количеством градусов в круге в знаменателе:
Умножьте и упростите:
Сообщить об ошибке
Какова длина дуги для сектора с центральным углом , если радиус окружности ?
Возможные ответы:
Правильный ответ:
Объяснение:
Используя формулу для длины дуги, мы можем подставить данные угол и радиус, чтобы вычислить длину дуги, которая опирается на центральный угол сектора.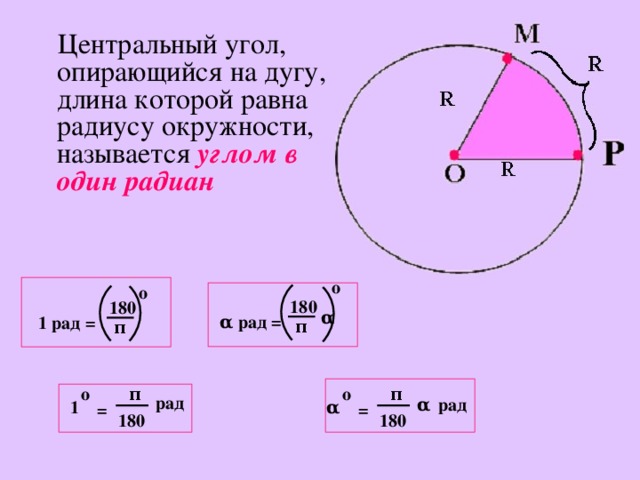 Однако угол должен быть в радианах, поэтому мы обязательно преобразуем градусы соответствующим образом, умножив заданный угол на :
Однако угол должен быть в радианах, поэтому мы обязательно преобразуем градусы соответствующим образом, умножив заданный угол на :
Сообщить об ошибке
Измерение дуги окружности. Хорда дуги имеет длину. Укажите длину дуги .
Возможные ответы:
Правильный ответ:
Объяснение:
Посмотрите на рисунок ниже, на котором показаны рассматриваемая дуга и хорда.
Если мы расширим фигуру, чтобы изобразить круг как составную часть четырех четвертей окружностей, каждая из которых представляет собой дугу, мы увидим, что это также сторона вписанного квадрата. Диагональ этого квадрата, умноженная на эту длину стороны, или
,
— диаметр этого круга. Длина окружности умножается на диаметр, или
.
Поскольку дуга составляет одну четвертую окружности, длина дуги равна
Сообщить об ошибке
Уведомление об авторских правах 693 практических теста Вопрос дня Карточки Learn by Concept
Видео с вопросами: Определение длины малой дуги в окружности по ее центральному углу и радиусу окружности
Стенограмма видео
Зная, что 𝐴𝑀 равно 11 сантиметрам, найдите длину дуги 𝐴𝐵𝐶, округленную до ближайшего целого числа.
Во-первых, давайте разберемся с обозначениями, использованными в вопросе. Я прочитал это 𝐴𝐵𝐶 с циркумфлексом или шляпой над ним как дугу 𝐴𝐵𝐶, что означает часть окружности круга, соединяющую 𝐴 с 𝐵 и 𝐶. Это длина дуги, которую я отметил оранжевым цветом. Теперь дуга всегда опирается на угол в центре окружности. Это угол, образованный радиусами, соединяющими две конечные точки дуги с центром окружности, и часто обозначается греческой буквой 𝜃.
Напомним, что длину окружности можно найти по формуле два 𝜋𝑟 или 𝜋𝑑, где 𝑟 обозначает радиус окружности, а 𝑑 обозначает диаметр. Чтобы найти длину дуги, мы берем эту полную окружность круга, две 𝜋𝑟, и умножаем ее на 𝜃 на 360, что является долей полной окружности круга, которую представляет эта длина дуги. Итак, чтобы вычислить длину дуги 𝐴𝐵𝐶, нам нужно знать две вещи: радиус окружности и угол 𝜃, образуемый этой дугой в центре.
Нам дано в вопросе, что длина 𝐴𝑀 равна 11 сантиметрам. А 𝐴𝑀 — это радиус окружности, потому что он соединяет центр 𝑀 с точкой на окружности 𝐴.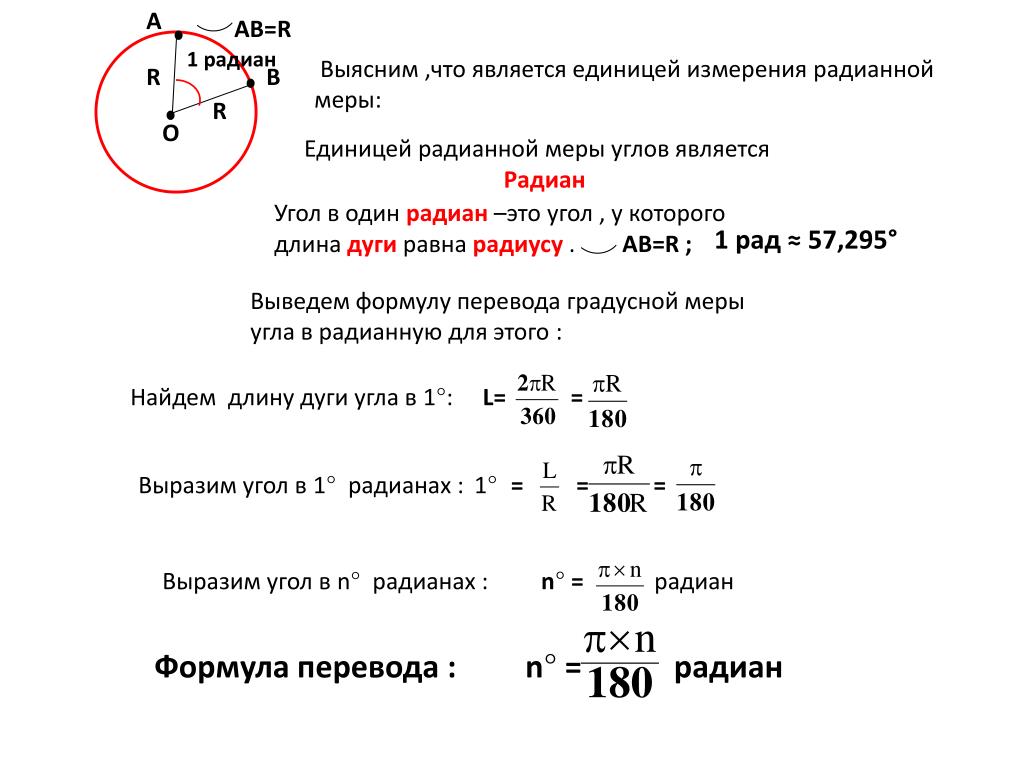 Итак, мы нашли радиус окружности. Рассмотрим угол 𝜃. Глядя на треугольник 𝐴𝐶𝑀, мы видим, что нам дан один угол в этом треугольнике, угол 42 градуса. Теперь линия 𝑀𝐶 также является радиусом окружности. Он соединяет центр 𝑀 с точкой 𝐶 на окружности. А значит, он тоже равен 11 сантиметрам, а это значит, что треугольник 𝐴𝐶𝑀 равнобедренный с линией 𝐴𝐶 в основании.
Итак, мы нашли радиус окружности. Рассмотрим угол 𝜃. Глядя на треугольник 𝐴𝐶𝑀, мы видим, что нам дан один угол в этом треугольнике, угол 42 градуса. Теперь линия 𝑀𝐶 также является радиусом окружности. Он соединяет центр 𝑀 с точкой 𝐶 на окружности. А значит, он тоже равен 11 сантиметрам, а это значит, что треугольник 𝐴𝐶𝑀 равнобедренный с линией 𝐴𝐶 в основании.
Равнобедренные треугольники имеют два равных угла. Значит, угол 𝐴𝐶𝑀 равен углу 𝐶𝐴𝑀. Они оба равны 42 градусам. Мы могли бы выразить это рассуждение, написав, что треугольник равнобедренный, потому что он образован двумя радиусами. Мы также знаем, что сумма углов любого треугольника равна 180 градусам. Таким образом, мы можем вычислить третий угол в этом треугольнике, угол 𝜃, вычитая два угла в 42 градуса из 180 градусов. Два лота по 42 равны 84. И если вычесть из этой формы 180, получится 9.6. Итак, мы нашли угол, образуемый этой дугой в центре окружности.
Теперь мы можем подставить значения 𝜃 и 𝑟 в нашу формулу длины дуги.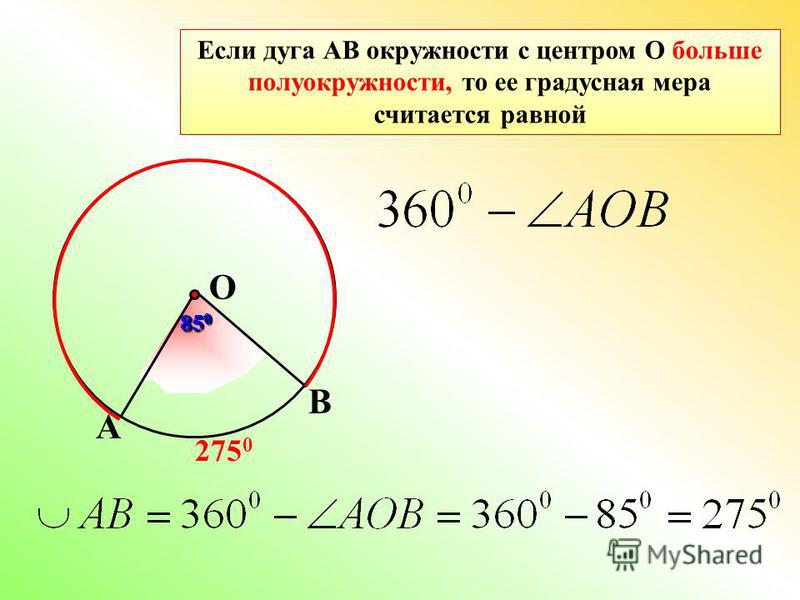

 03.15
03.15