Сложение и вычитание Н.Ч Виленкин математика 5 класс № 188 Чему равна координата – Рамблер/класс
Сложение и вычитание Н.Ч Виленкин математика 5 класс № 188 Чему равна координата – Рамблер/классИнтересные вопросы
Школа
Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?
Новости
Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?
Школа
Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?
Школа
Когда в 2018 году намечено проведение основного периода ЕГЭ?
Новости
Будет ли как-то улучшаться система проверки и организации итоговых сочинений?
Вузы
Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?
Здравствуйте, кто может подсказать решение задачки?
188
Начертите координатный луч и отметьте на нём точку С(6), от-

Чему равна координата точки D?
ответы
Здравствуй
ваш ответ
Можно ввести 4000 cимволов
отправить
дежурный
Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения
похожие темы
3 класс
Репетитор
Химия
Алгебра
похожие вопросы 5
Координатная прямая. Математика 5 класс.Зубарева И.И.Параграф 10, задание 191
Укажите начало отсчёта и координаты точек А, В, С, (Подробнее…)
ГДЗЗубарева И.И.Математика5 класс
Помогите выбрать утверждения. Математика базовый уровень ЕГЭ — 2017. Вар.№1. Зад.№18. Под руководством Ященко И.В.
Здравствуйте! Перед волейбольным турниром измерили рост игроков волейбольной команды города N. Оказалось, что рост каждого из (Подробнее…)
ЕГЭЭкзаменыМатематикаЯщенко И. В.
В.
11. Выпишите слово, в котором на месте пропуска пишется буква Е. Русский язык ЕГЭ-2017 Цыбулько И. П. ГДЗ. Вариант 12.
11.
Выпишите слово, в котором на месте пропуска пишется буква Е.
произнос., шь (Подробнее…)
ГДЗЕГЭРусский языкЦыбулько И.П.
16. Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)… Цыбулько И. П. Русский язык ЕГЭ-2017 ГДЗ. Вариант 13.
16.
Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)
в предложении должна(-ы) стоять запятая(-ые). (Подробнее…)
ГДЗЕГЭРусский языкЦыбулько И.П.
ЕГЭ-2017 Цыбулько И. П. Русский язык ГДЗ. Вариант 13. 18. Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)…
18.
Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)
в предложении должна(-ы) стоять запятая(-ые). (Подробнее…)
ГДЗЕГЭРусский языкЦыбулько И. П.
П.
Координатная плоскость — что это, определение и ответ
Координатная плоскость – это прямоугольная система координат, состоящая из двух взаимно перпендикулярных осей, имеющих направление, начало отсчета и единичные отрезки.
ОПРЕДЕЛЕНИЕ КООРДИНАТЫ ТОЧКИ:
Любая точка на этой плоскости имеет свои координаты в соответствии с координатами осей. Рассмотрим координатную плоскость, на которой отмечены несколько точек:
Найдем координаты каждой из этих точек.
Чтобы найти координаты точки, нужно:
1. Провести перпендикуляры от точки к каждой координатной оси.
2. Перпендикуляр, упавший на ось Ох, попадет на координату x данной точки, а перпендикуляр, упавший на ось Оу, попадет на координату y данной точки.
Например:
Координата точки А на оси Ох равна 4, а на оси ОУ равна 3. Координаты записывают так:
\(А(4;3)\)
Координата на оси Ох называется абсциссой.
Координата на оси Оу называется ординатой.
Сначала записывают координату оси абсцисс, потом координату оси ординат.
Найдем координаты других точек:
Таким образом:
\({A\left( 4;3 \right) }{B\left( –2;1 \right) }{C\left( –6;–2 \right) }{D\left( 3;–4 \right)}\)
КООРДИНАТНЫЕ ЧЕТВЕРТИ:
Координаты могут быть как положительными, так и отрицательными, в зависимости от того, с какой стороны от начала координат находится точка. Мы видим, что каждая из представленных точек имеет разные знаки для абсцисс и ординат. Все потому, что они находятся в разных четвертях координатной плоскости, которые образуют координатные оси. На каждой из этих четвертей координаты x и y имеют определенные знаки:
Первой четвертью является четверть, где и абсцисса, и ордината принимают положительные значения. В этой четверти находилась точка А.
Дальше четверти нумеруются против часовой стрелки.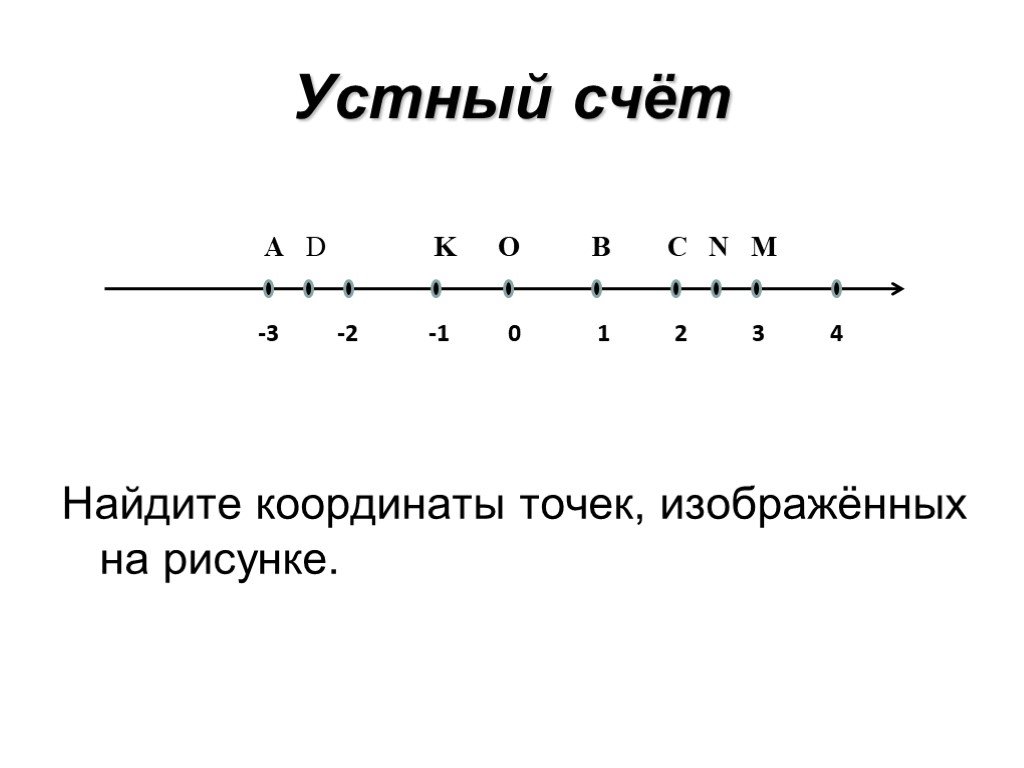 Таким образом точка В находилась во второй четверти и имела отрицательную абсциссу и положительную ординату, точка С имела только отрицательные координаты, а точка D имела положительную абсциссу и отрицательную ординату.
Таким образом точка В находилась во второй четверти и имела отрицательную абсциссу и положительную ординату, точка С имела только отрицательные координаты, а точка D имела положительную абсциссу и отрицательную ординату.
СИММЕТРИЯ:
Виды симметрии:
Относительно оси Ох (ордината меняет знак на противоположный).
Относительно оси Оу (абсцисса меняет знак на противоположный).
Относительно начала координат (абсцисса и ордината меняют знаки на противоположные).
Суть симметрии:
Рассмотрим каждый вид симметрии подробнее.
На плоскости можно симметрично отражать любые построение. Представим всю координатную плоскость, как сгибаемый лист бумаги, и отметим на нем точку M(3; 5):
1. Согнем наш лист по линии оси Ох. Получим, что наша точка отпечатается на другой стороне от этой оси. Получим новую точку М1 с координатами (3; –5).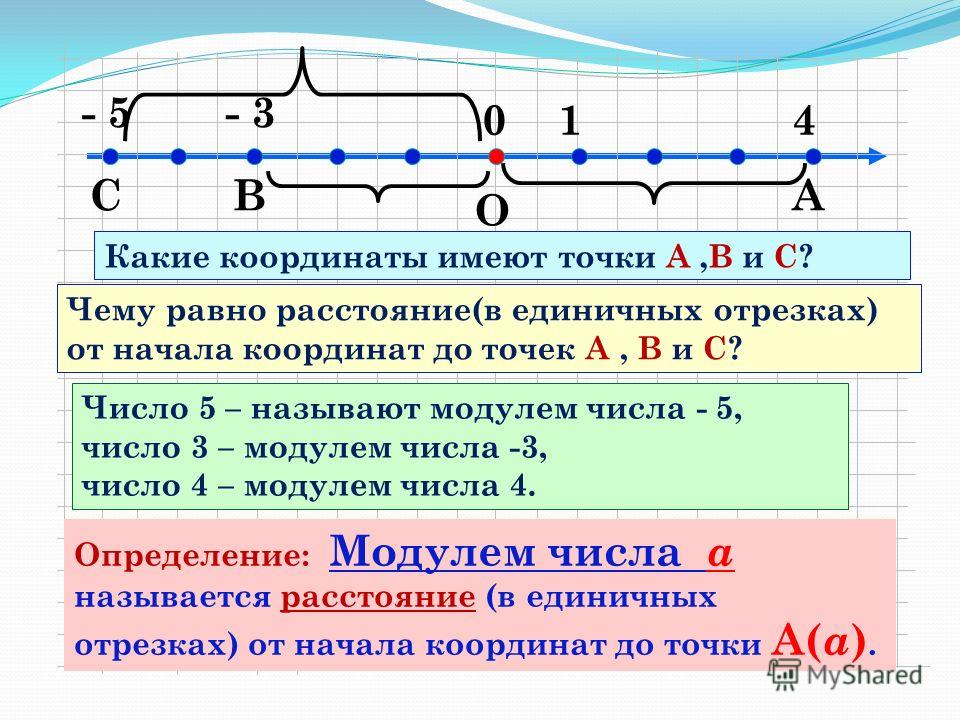 Эта точка будет симметрична данной относительно оси Ox:
Эта точка будет симметрична данной относительно оси Ox:
2. Согнем наш лист по линии оси Оу. Тогда наша точка «отпечатается» на другой стороне от этой оси и попадет в точку М2(–3; 5). Эта точка будет симметрична данной относительно оси Оу:
3. Если мы согнем лист сначала относительно оси Ох, а потом еще и по оси Оу (неважно в каком порядке), то наша точка попадет в точку, M3(–3; –5). Эта точка будет симметрична данной относительно начала координат:
ПОСТРОЕНИЕ ТОЧКИ НА КООРДИНАТНОЙ ПЛОСКОСТИ ПО КООРДИНАТАМ:
Мы можем как узнать координаты точек на плоскости, так и сами их задавать.
Чтобы отметить на координатной плоскости точку с конкретными координатами, нужно:
1. Провести через абсциссу точки прямую, перпендикулярную оси Ох.
2. Провести через ординату точки прямую, перпендикулярную оси Оу.
3. Точка пересечения этих прямых и будет являться точкой с заданными координатами. Отметить эту точку.
Отметить эту точку.
Например:
Построим точку на координатной плоскости по координатам: \(N\left( –1;5 \right)\)
Точка N имеет координаты \((–1;\ 5)\).
1. На оси Ох отметим координату –1 и проведем через нее перпендикуляр к этой оси.
2. На оси Оу отметим координату 5 и проведем через нее перпендикуляр к этой оси.
3. На пересечении этих прямых отметим точку \(N(–1;\ 5\)):
Прямые, которые мы провели в первом и втором пункте можно записать в виде формул:
\({x = \ –1 }{y = 5}\)
Такие формулы описывают, в каких точках прямые пересекают оси под прямым углом.
ОПИСАНИЕ УЧАСТКОВ ПЛОСКОСТИ:
Задавать на плоскости можно не только координаты точек и прямых, но и выделять некоторые площади. Например, разбиение координатной плоскости на четверти задается неравенствами.
Рассмотрим несколько случаев выделения частей плоскости.
Пример №1:
Выделите область, которая включает в себя множество точек так, что: \(x > 2\)
Это выражение описывает множество точек на плоскости, абсциссы которых больше 2.
Чтобы выделить это множество на плоскости, проведем прямую \(x\ = \ 2\):
2. Таким образом эта прямая поделила всю координатную плоскости на две полуплоскости: одна находится справа от прямой, вторая слева.
— Если мы отметим любую точку слева от прямой \(x = 2\), то увидим, что абсцисса этой точки будет меньше, чем 2.
— Если мы отметим любую точку справа от прямой \(x = 2\), то увидим, что абсцисса этой точки будет больше, чем 2.
3. Нам подходит второй вариант, значит множество точек, для которых неравенство \(x > 2\) верное – красная полуплоскость:
Пример №2:
Выделите область, которая включает в себя множество точек так, что: \(–1 < y < 3\)
Здесь нам так же заданы определённые точки, но уже с ограничением ординаты. Нужно выделить область, все точки на которой будут иметь ординату больше, чем –1 и меньше, чем 3. Алгоритм построение такой же, как в примере №1, только у нас появилась вторая прямая.
Нужно выделить область, все точки на которой будут иметь ординату больше, чем –1 и меньше, чем 3. Алгоритм построение такой же, как в примере №1, только у нас появилась вторая прямая.
1. Проведем прямые \(y = \ –1\) и \(y = 3\):
2. У нас появилось три полуплоскости. Проанализируем каждые из них:
— Если поставить точку выше прямой \(y = 3,\) её ордината будет больше 3.
— Если поставить точку ниже прямой \(y = \ –1\), её ордината будет меньше –1.
— Если поставить точку между прямыми \(y = \ –1\ \)и \(y = 3\), её ордината будет больше –1 и меньше 3.
3. Нам подходит область между прямыми, где \(–1 < y < 3\):
Точки и координаты
Каждой точке в пространстве можно присвоить три числа относительно начальной точки. Эти три числа позволяют нам отличить любую точку от любой другой точки в пространстве. К счастью для вас, мы имеем здесь дело не с тремя измерениями, а только с двумя.
- Координаты точки: Каждой точке на числовой прямой присвоен номер.
 Точно так же каждой точке на плоскости ставится в соответствие пара чисел.
Точно так же каждой точке на плоскости ставится в соответствие пара чисел.
- Ось x и ось Y: Для определения точек на плоскости используются две перпендикулярные линии: горизонтальная линия, называемая осью x , и вертикальная линия, называемая осью y .
- Происхождение: Точка пересечения оси x и оси y .
- Координатная плоскость: — ось x , ось y и все точки на плоскости, которые они определяют.
- Упорядоченные пары: Каждая точка на координатной плоскости называется парой чисел, порядок которых важен; эти числа записываются в круглых скобках и разделяются запятой.
- x -координата : Число слева от запятой в упорядоченной паре — это x -координата точки и указывает величину перемещения по оси x от начала координат.

- y -координата : Число справа от запятой в упорядоченной паре представляет собой y -координату точки и указывает величину перемещения перпендикулярно оси x . Движение выше оси x , если число положительное, и ниже оси x , если число отрицательное.
Примечание. Координаты [упорядоченная пара] для начала координат (0, 0).
x 9Ось 0015 и ось и делят координатную плоскость на четыре области, называемые квадрантами . (См. рис. 1.) Верхний правый квадрант — это квадрант 1; верхний левый квадрант — это квадрант II; нижний левый квадрант — это квадрант III; а нижний правый квадрант — это квадрант IV. Обратите внимание на следующее:
Рисунок 1 Оси координат делят плоскость на четыре квадранта.
- В квадранте I x всегда положительно и y всегда положительный.

- В квадранте II x всегда отрицательно, а y всегда положительно.
- В квадранте III x всегда отрицательно, а y всегда отрицательно.
- В квадранте IV x всегда положительно, а y всегда отрицательно.
Точка, связанная с упорядоченной парой действительных чисел, называется графом упорядоченной пары.
Пример 1: Определите точки A, B, C, D, E, и F на координатном графике на рисунке .
Рисунок 2 Нахождение координат конкретных точек на плоскости.
Пример 2: Прямоугольник ABCD имеет следующие координаты: A (−5,2), B (8,2) и C (8, −4). Найдите координаты D.
Для решения этой задачи полезен график. См. рисунок . Координаты D должен быть (−5,−4) .
Рисунок 3 Нахождение координат четвертой вершины прямоугольника.
Пример 3: . Используйте рисунок 3, чтобы найти следующие расстояния: (a) от A до B (обозначается AB ) и (b) от B до C 9001 5 (называется BC ).
Что такое координаты в математике? Определение, примеры, факты
Координаты: введение
Координаты — это упорядоченные пары точек, которые помогают нам найти любую точку в 2D-плоскости или 3D-пространстве. Возможно, вы видели, как сетки используются в математике. Что это за сетки? Эти сетки помогают нам построить любую точку, используя ее координаты. Итак, что такое координаты в математике? Давайте посмотрим, что означают координаты в математике.
Координаты точки на 2D-плоскости, также известные как декартовы координаты, представляют собой два числа или иногда комбинацию буквы и цифры, которые сообщают нам точное местоположение определенной точки на сетке. Здесь сетка известна как координатная плоскость.
Здесь сетка известна как координатная плоскость.
Координатная плоскость имеет четыре квадранта и две оси: ось X является горизонтальной осью, а ось Y является вертикальной осью.
Родственные игры
Что такое координаты в математике?
Давайте разберемся с определением координат в математике.
Координаты — это пара чисел, которые используются для определения положения точки или фигуры в двухмерной плоскости.
Мы определяем положение точки на двумерной плоскости с помощью двух чисел, называемых координатой x и координатой y. Координата x всегда идет первой в упорядоченной паре, за которой следует координата y, и она определяет, где находится точка в левом-правом или горизонтальном направлении, а координата y определяет положение точки по вертикали, вверх-вниз. направление вниз.
Ordered Pair
Итак, как вы пишете координаты? Декартовы координаты точки обычно записываются в круглых скобках и разделяются запятыми, например (x, y). Обратите внимание, что порядок имеет значение при записи координат точки.
Обратите внимание, что порядок имеет значение при записи координат точки.
Координаты записываются в виде «упорядоченной пары», как показано ниже. Буква P — это просто название точки и используется, чтобы отличить ее от других.
Давайте посмотрим на примеры координат.
Пример 1: Точка, в которой пересекаются обе оси, называется исходной точкой.
Координаты начала координат записываются как O(0, 0).
Пример 2: На рисунке ниже координаты точки А (3,4). Это означает, что точка находится на расстоянии 3 единицы по оси x и 4 единицы вверх.
Пример 3: Координаты точки по оси X и оси Y.
Для точки, лежащей на оси X, координата y равна 0. Для точки на оси Y координата x равна 0.
Типы координат
У нас есть два основных типа систем координат, перечисленных ниже.
- Декартова система координат
Декартова система координат помогает однозначно представить точку в n-мерной координатной плоскости.
- Полярная система координат
В полярной системе координат началом считается точка отсчета, называемая полюсом. Положение каждой точки определяется расстоянием от полюса, а угол берется от опорного направления.
Здесь мы выражаем координаты точки как $(r, θ)$. Проще говоря, у нас есть два параметра — угол и радиус.
Координата r — это длина отрезка прямой от точки (x, y) до начала координат, а координата θ — это угол между отрезком прямой и положительной осью x. 92$ и $tan \theta = \frac{y}{x}$
Координаты на плоскости (2D)
Двумерная координатная плоскость образована пересечением осей x и y. Две оси пересекаются в точке O (0, 0), называемой началом координат.
Две оси пересекаются в точке O (0, 0), называемой началом координат.
Координаты указывают положение точки в 2D-координатной плоскости относительно начала координат. Координата x точки — это ее перпендикулярное расстояние от оси y, измеренное вдоль оси x. Y-координата точки — это ее перпендикулярное расстояние от оси x, измеренное вдоль оси y.
Координаты записываются в виде упорядоченной пары чисел P(x, y), где P — название точки, x — положение по горизонтали, а y — положение по вертикали.
Например, точка P(3, 5) представлена как
Квадранты в 2D-плоскости
На 2D-плоскости в основном имеется 4 квадранта, образованных из-за пересечения осей x и y. Иногда их называют римскими цифрами: I, II, III и IV.
Вы можете задаться вопросом, меняются ли правила координат в зависимости от квадрантов или как они записываются в разных квадрантах. Давай выясним.
Квадрант 1: это верхний правый квадрант.
Здесь обе координаты имеют положительные значения. Например, P(3, 5), U(8, 4).
Например, P(3, 5), U(8, 4).
Квадрант 2:
Здесь координата x имеет отрицательные значения, а координата y имеет положительные значения. Например, P$(-3, 5)$, U$(-8, 4)$.
Квадрант 3:
Здесь обе координаты имеют отрицательные значения. Например, P$(-3,-5)$, U$(-8,-4)$.
Квадрант 4:
Здесь координата x имеет положительные значения, а координата y имеет отрицательные значения. Например, P$(3, -5)$, U$(-8, 4)$.
Координата в пространстве (3D)
Трехмерная система координат может использоваться для определения положения точки в трехмерном пространстве. Трехмерная координатная плоскость образована пересечением трех осей, а именно оси x, оси y и оси z, которые перпендикулярны друг другу в начале координат.
Ось Z можно визуализировать как продолжение двумерной координатной плоскости. Учитывая, что оси x и y являются горизонтальной и вертикальной осями на странице, ось z можно визуализировать как выходящую из страницы или проходящую через страницу, создавая третье измерение.
Положение точки в 3D-координатной плоскости очень похоже на положение точки в 2D-координатной плоскости с добавленной координатой z: (x, y, z).
Как читать и наносить координаты
Координаты всегда записываются в квадратных скобках, причем два числа разделяются запятой (,). Координаты представляют собой упорядоченные пары чисел. Первое число указывает точку на оси X (также известную как абсцисса), а второе — точку на оси Y (также известную как ордината).
Давайте разберемся, как нанести точку на координатную плоскость на примере.
Пример: Постройте $(2,3), (3,-2)$ и $(-3,1)$
Сначала отметьте координату x или горизонтальное расстояние вдоль оси x, а затем отметьте расстояние по вертикали с использованием координаты y.
Факты
Координаты имеют важное значение на картах. Часто карты используют букву в качестве одной из координат для определения местоположения точки и используют цифру для другой точки. Координаты на карте указаны ниже.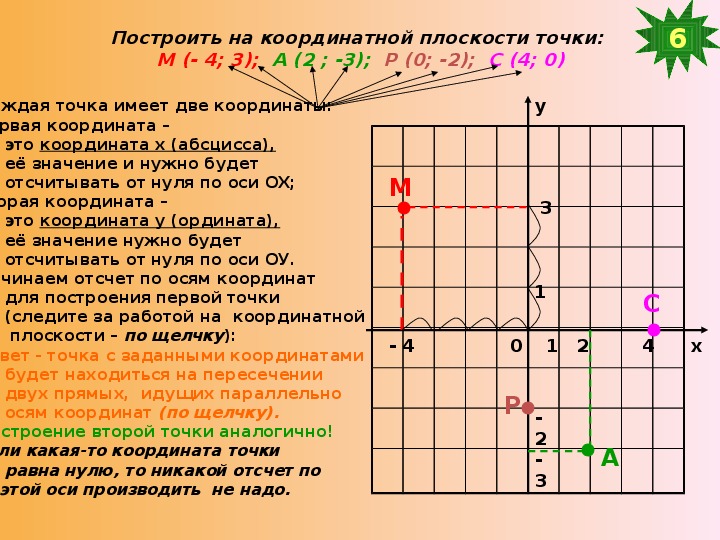
- Координата x точки также известна как «абсцисса». Произносится как «аб-сисс-ах» (буква «с» не произносится). Чаще всего используется термин «координата x».
- Координата Y также называется «ординатой». Вы можете произнести это как «ORD-inet». Термин «координата Y» является предпочтительным.
Заключение
В этой статье мы узнали о координатах точки, их представлении, построении точки на декартовой плоскости вместе с двумя типами координат.
Решенные примеры
1. Нанесите заданную точку на график: P(2, 5).
Решение:
Поскольку оба значения x и y положительны, точка лежит в 1-м квадранте.
Точка находится на 2 единицы вправо от начала координат по оси X и на 5 единиц вверх.
Заданную точку на графике можно изобразить как-
2. Нанести данную точку на график: P $(-3,4)$ .
Решение:
Поскольку значение x положительное, а y отрицательное, точка лежит в третьем квадранте. Данную точку на графике можно изобразить как:
Данную точку на графике можно изобразить как:
3. Нанесите данную точку на график: P $(3, -2)$ и определите, в каком квадранте она находится.
Решение:
Поскольку оба значения x и y отрицательны, точка находится в 3-м квадранте. Данную точку на графике можно изобразить как:
4. Найдите соответствующие декартовы координаты, если полярные координаты точки равны 9\circ$
$x = 2 (\frac{\sqrt{3}}{2})$ и $y = 2 (\frac{1}{2})$
$x = \sqrt{3} $ и $y = 1$
Декартовы координаты равны $(\sqrt{3},1)$.
5. Нанесите данную точку на график: P(4, 4)
Решение:
Поскольку оба значения x и y положительны, точка лежит в 1-м квадранте. Данную точку на графике можно изобразить следующим образом:
Практические задачи
1
Определите квадрант, в котором находится точка P$(-5, -5)$.
I
II
III
IV
Правильный ответ: III
Поскольку оба значения x и y отрицательны, точка лежит в 3-м квадранте.
2
Что такое «ордината» в (5, 8)?
5
8
13
Правильный ответ: 8
Координата Y известна как ордината. В упорядоченной паре $(5, 8) 5$ — это абсцисса, а 8 — это ордината.
3
Какая из следующих точек лежит на оси Y? $(0, 4), (0, 2)$ и $(0,-3)$.
$(0, -3)$
$(0, 4)$
Все
Нет
Правильный ответ: Все
Координата x всех точек равна 0. Итак, все точки лежат по оси Y.
4
Точки $(-1, 0), (2, 0)$ и $(5, 0)$ лежат на $ \underline{}$ .
ось x
ось y
обе оси
линия x $=$ y
Правильный ответ: ось x
Координата y всех точек равна 0. Итак, все точки лежат на оси x.
Итак, все точки лежат на оси x.
5
Точки $(7, 8), (3, 6)$ и $(8, 2)$ лежат в квадранте$\underline{}$.
I
II
III
IV
Правильный ответ: I
Точки $(7, 8), (3, 6)$ и $(8, 2)$ имеют положительные координаты. Итак, точки лежат в первом квадранте.
Часто задаваемые вопросы
Что такое формула расстояния?
Формула расстояния используется для расчета расстояния между двумя точками.
Пусть это две точки A и B с координатами (x 1 , y 1 ) и (x 2 , y 2 ) соответственно.
Таким образом, расстояние между двумя точками определяется как:
Кто изобрел декартову плоскость?
Рене Декарт впервые опубликовал систему координат в семнадцатом веке.
Что такое широта и долгота в координатах?
Координаты представлены в виде упорядоченной пары двух чисел.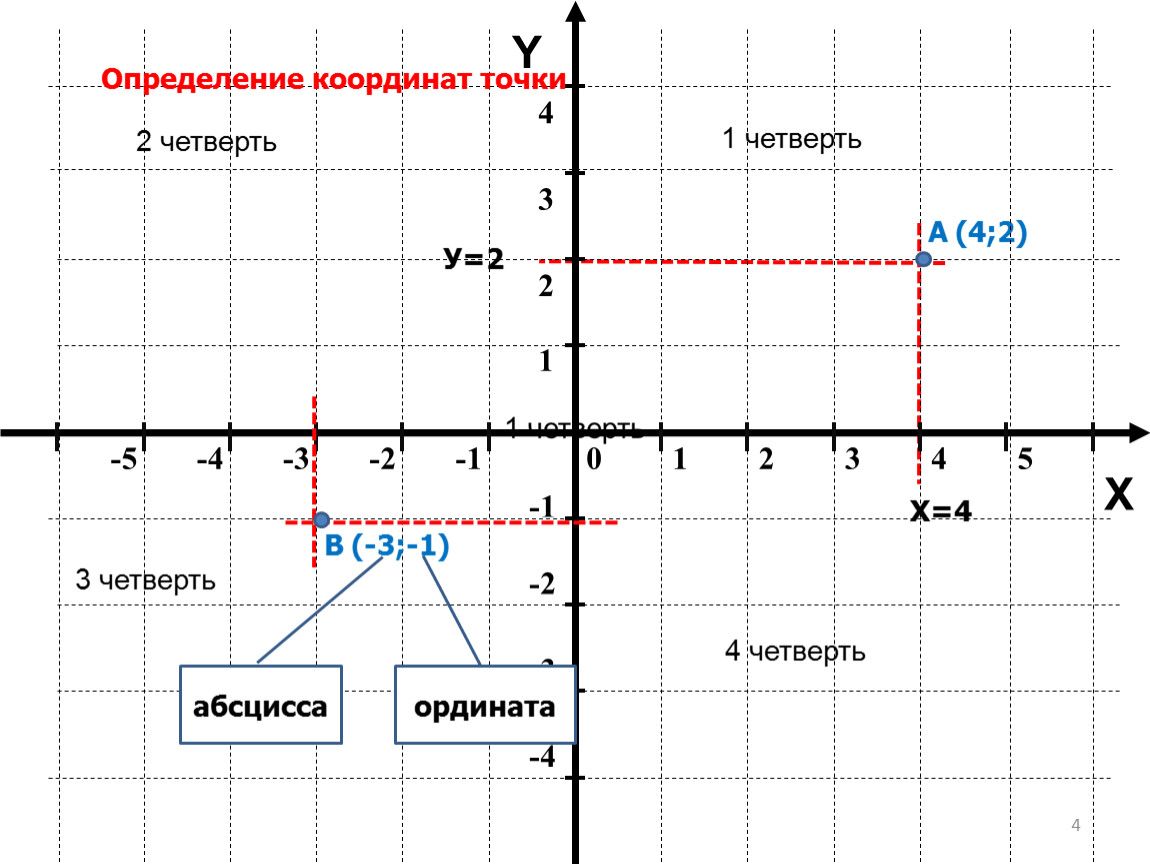

 Точно так же каждой точке на плоскости ставится в соответствие пара чисел.
Точно так же каждой точке на плоскости ставится в соответствие пара чисел.