Чему равна площадь треугольника формула: Площадь треугольника

Как найти площадь треугольника — Лайфхакер

6 февраля 2020 Ликбез Образование

Вспоминаем геометрию: формулы для произвольных, прямоугольных, равнобедренных и равносторонних фигур.

Как найти площадь любого треугольника

Посчитать площадь треугольника можно разными способами. Выбирайте формулу в зависимости от известных вам величин.

Зная сторону и высоту

1. Умножьте сторону треугольника на высоту, проведённую к этой стороне.
2. Поделите результат на два.

• S — искомая площадь треугольника.
• a — сторона треугольника.
• h — высота треугольника. Это перпендикуляр, опущенный на сторону или её продолжение из противоположной вершины.

Зная две стороны и угол между ними

1. Посчитайте произведение двух известных сторон треугольника.
2. Найдите синус угла между выбранными сторонами.
3. Перемножьте полученные числа.
4. Поделите результат на два.

• S — искомая площадь треугольника.
• a и b — стороны треугольника.
• α — угол между сторонами a и b.

Сейчас читают 🔥

• 9 традиций, от которых давно стоит отказаться

Зная три стороны (формула Герона)

1. Посчитайте разности полупериметра треугольника и каждой из его сторон.
2. Найдите произведение полученных чисел.
3. Умножьте результат на полупериметр.
4. Найдите корень из полученного числа.

• S — искомая площадь треугольника.
• a, b, c — стороны треугольника.
• p — полупериметр (равен половине от суммы всех сторон треугольника).

Зная три стороны и радиус описанной окружности

1. Найдите произведение всех сторон треугольника.
2. Поделите результат на четыре радиуса окружности, описанной вокруг прямоугольника.

• S — искомая площадь треугольника.
• R — радиус описанной окружности.
• a, b, c — стороны треугольника.

Зная радиус вписанной окружности и полупериметр

Умножьте радиус окружности, вписанной в треугольник, на полупериметр.

• S — искомая площадь треугольника.
• r — радиус вписанной окружности.
• p — полупериметр треугольника (равен половине от суммы всех сторон).

Как найти площадь прямоугольного треугольника

1. Посчитайте произведение катетов треугольника.
2. Поделите результат на два.

• S — искомая площадь треугольника.
• a, b — катеты треугольника, то есть стороны, которые пересекаются под прямым углом.

Как найти площадь равнобедренного треугольника

1. Умножьте основание на высоту треугольника.
2. Поделите результат на два.

• S — искомая площадь треугольника.
• a — основание треугольника. Это та сторона, которая не равняется двум другим. Напомним, в равнобедренном треугольнике две из трёх сторон имеют одинаковую длину.
• h — высота треугольника. Это перпендикуляр, опущенный на основание из противоположной вершины.

Как найти площадь равностороннего треугольника

1. Умножьте квадрат стороны треугольника на корень из трёх.
2. Поделите результат на четыре.

• S — искомая площадь треугольника.
• a — сторона треугольника. Напомним, в равностороннем треугольнике все стороны имеют одинаковую длину.

Читайте также 🧠👨🏻‍🎓✍🏻

• 7 причин полюбить математику
• ТЕСТ: Помните ли вы геометрию?
• 10 хитрых головоломок со спичками для тренировки воображения
• Интересные математические факты для тех, кто хочет больше узнать о мире вокруг
• ТЕСТ: Сможете ли вы решить простые математические примеры?

Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия

Справочник по математике

Геометрия (Планиметрия)

Площади

Формулы для площади треугольника

Вывод формул для площади произвольного треугольника

Вывод формул для площади равностороннего (правильного) треугольника

Вывод формул для площади прямоугольного треугольника

Формулы для площади треугольника

      Формулы, позволяющие находить площадь треугольника, удобно представить в виде следующей таблицы.

Фигура	Рисунок	Формула площади	Обозначения
Произвольный треугольник		Посмотреть вывод формулы	a – любая сторона, ha – высота, опущенная на эту сторону
		Посмотреть вывод формулы	a и b – две любые стороны, С – угол между ними
		. Посмотреть вывод формулы Герона	a, b, c – стороны, p – полупериметр Формулу называют «Формула Герона»
		Посмотреть вывод формулы	a – любая сторона, B, С – прилежащие к ней углы
		Посмотреть вывод формулы	a, b, c – стороны, r – радиус вписанной окружности, p – полупериметр
		Посмотреть вывод формулы	a, b, c  – стороны, R – радиус описанной окружности
		S = 2R2 sin A sin B sin C Посмотреть вывод формулы	A, B, С – углы, R – радиус описанной окружности
Равносторонний (правильный) треугольник		Посмотреть вывод формулы	a – сторона
		Посмотреть вывод формулы	h – высота
		Посмотреть вывод формулы	r – радиус вписанной окружности
		Посмотреть вывод формулы	R – радиус описанной окружности
Прямоугольный треугольник		Посмотреть вывод формулы	a и b – катеты
		Посмотреть вывод формулы	a – катет, φ – прилежащий острый угол
		Посмотреть вывод формулы	a – катет, φ – противолежащий острый угол
		Посмотреть вывод формулы	c – гипотенуза, φ – любой из острых углов

Произвольный треугольник
	где a – любая сторона, ha – высота, опущенная на эту сторону Посмотреть вывод формулы
	где a и b – две любые стороны, С – угол между ними Посмотреть вывод формулы
	. где a, b, c – стороны, p – полупериметр Формулу называют «Формула Герона» Посмотреть вывод формулы Герона
	где a – любая сторона, B, С – прилежащие к ней углы Посмотреть вывод формулы
	где a, b, c – стороны, r – радиус вписанной окружности, p – полупериметр Посмотреть вывод формулы
	где a, b, c  – стороны, R – радиус описанной окружности Посмотреть вывод формулы
	S = 2R2 sin A sin B sin C где A, B, С – углы, R – радиус описанной окружности Посмотреть вывод формулы
Равносторонний (правильный) треугольник
	где a – сторона Посмотреть вывод формулы
	где h – высота Посмотреть вывод формулы
	где r – радиус вписанной окружности Посмотреть вывод формулы
	где R – радиус описанной окружности Посмотреть вывод формулы
Прямоугольный треугольник
	где a и b – катеты Посмотреть вывод формулы
	где a – катет, φ – прилежащий острый угол Посмотреть вывод формулы
	где a – катет, φ – противолежащий острый угол Посмотреть вывод формулы
	где c – гипотенуза, φ – любой из острых углов Посмотреть вывод формулы

Произвольный треугольник

где a – любая сторона, ha – высота, опущенная на эту сторону Посмотреть вывод формулы

где a и b – две любые стороны, С – угол между ними Посмотреть вывод формулы

. где a, b, c – стороны, p – полупериметр Формулу называют «Формула Герона» Посмотреть вывод формулы Герона

где a – любая сторона, B, С – прилежащие к ней углы Посмотреть вывод формулы

где a, b, c – стороны, r – радиус вписанной окружности, p – полупериметр Посмотреть вывод формулы

где a, b, c  – стороны, R – радиус описанной окружности Посмотреть вывод формулы

S = 2R2 sin A sin B sin C где A, B, С – углы, R – радиус описанной окружности Посмотреть вывод формулы

Равносторонний (правильный) треугольник

где a – сторона Посмотреть вывод формулы

где h – высота Посмотреть вывод формулы

где r – радиус вписанной окружности Посмотреть вывод формулы

где R – радиус описанной окружности Посмотреть вывод формулы

Прямоугольный треугольник

где a и b – катеты Посмотреть вывод формулы

где a – катет, φ – прилежащий острый угол Посмотреть вывод формулы

где a – катет, φ – противолежащий острый угол Посмотреть вывод формулы

где c – гипотенуза, φ – любой из острых углов Посмотреть вывод формулы

Вывод формул для площади произвольного треугольника

      Утверждение 1.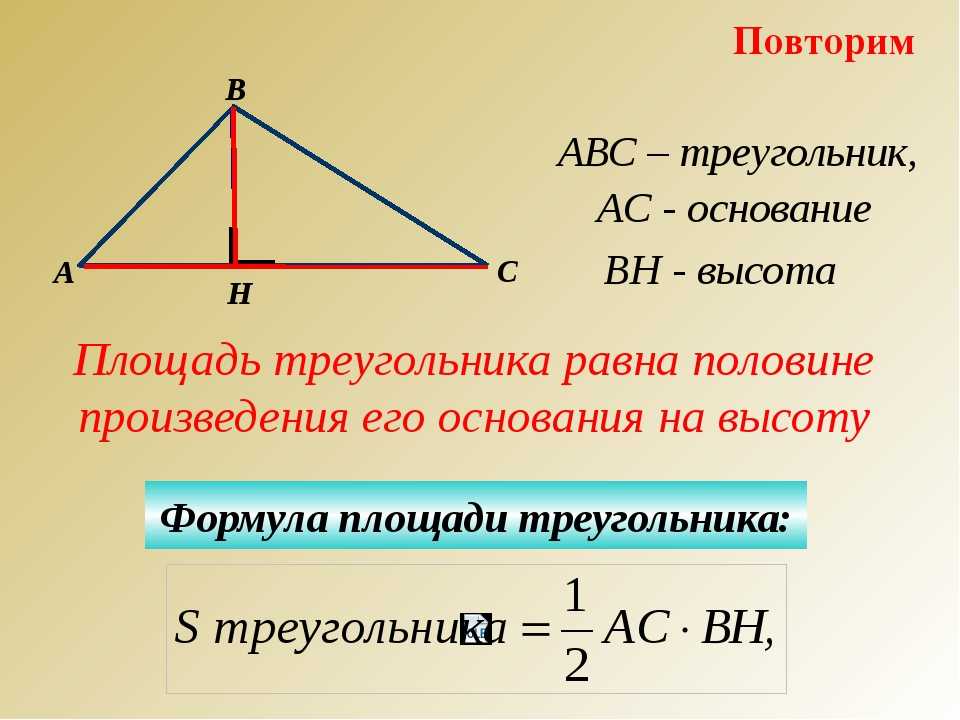

Площадь треугольника можно найти по формуле

где a – любая сторона треугольника, а h_a – высота, опущенная на эту сторону.

      Доказательство.

Рис. 1

Достроив треугольник ABC до параллелограммапараллелограмма ABDC (рис. 1), получим

что и требовалось доказать.

      Утверждение 2. Площадь треугольника можно найти по формуле

где a и b – две любые стороны треугольника, а С – угол между ними.

      Доказательство.

Рис. 2

Поскольку

h_a = b sin C ,

то, в силу утверждения 1, справедлива формула

что и требовалось доказать.

      Утверждение 3. Площадь треугольника можно найти по формуле

где a – любая сторона треугольника, а B, С – прилежащие к ней углы.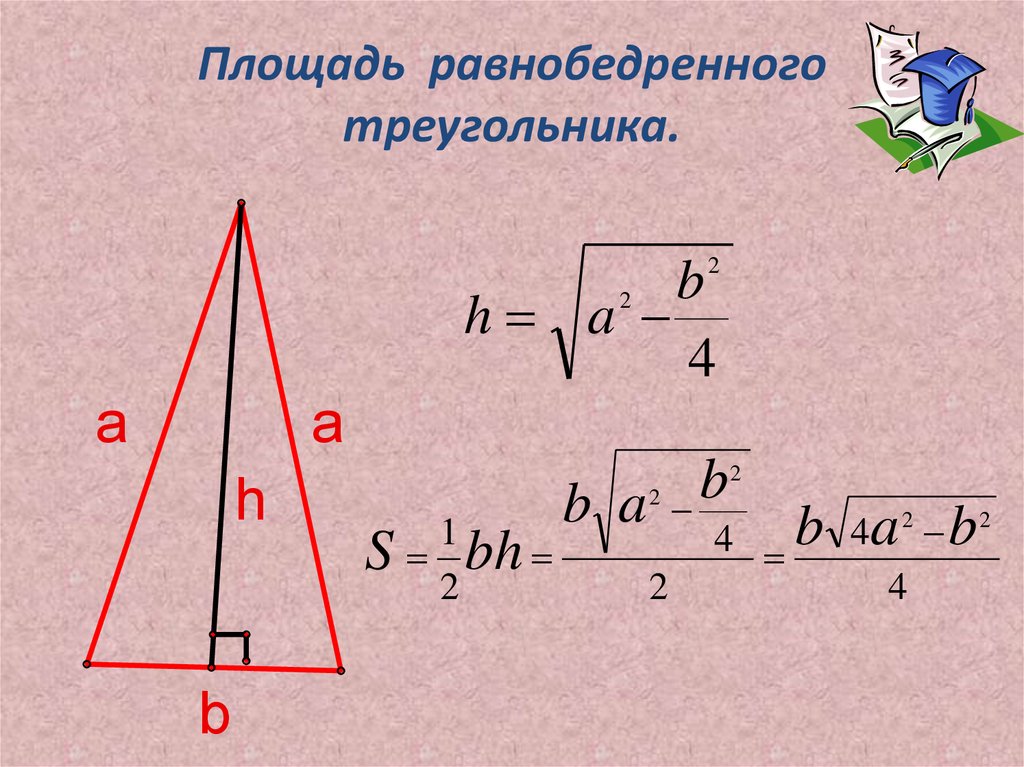

      Замечание. Докажем утверждение 3 в случае остроугольного треугольника. Доказательство в случаях прямоугольного и тупоугольного треугольников требует лишь незначительных изменений, совершить которые мы предоставляем читателю в качестве самостоятельного упражнения.

      Доказательство.

Рис. 3

Поскольку (рис.3)

x = h_actg C ,       y = h_actg B ,

то

a = x + y =
= h_actg C +

h_actg B =
= h_a( ctg C + ctg B) .

      Следовательно,

      Поэтому

что и требовалось доказать.

      Утверждение 4. Площадь треугольника можно найти по формуле

где a, b, c – стороны треугольника, а r – радиус вписанной окружности.

      Доказательство.

Рис. 4

Соединив центр O вписанной окружности с вершинами треугольника (рис.4), получим

что и требовалось доказать.

      Утверждение 5. Площадь треугольника можно найти по формуле

где a, b, c – стороны треугольника, а R – радиус описанной окружности.

      Доказательство.

Рис. 5

В силу теоремы синусов справедливо равенство

.

      Следовательно,

      Поэтому

что и требовалось доказать.

      Утверждение 6. Площадь треугольника можно найти по формуле:

S = 2R² sin A sin B sin C ,

где A, B, С – углы треугольника, а R – радиус описанной окружности.

      Доказательство.

Рис. 6

В силу теоремы синусов справедливо равенство

.

      Поэтому

a = 2R sin A ,    
b = 2R sin B ,    
c = 2R  sin C ,

      В силу утверждения 5

что и требовалось доказать.

Вывод формул для площади равностороннего треугольника

      Утверждение 7.

1. Если a – сторона равностороннего треугольника, то его площадь

2. Если h – высота равностороннего треугольника, то его площадь

3. Если r – радиус вписанной в равносторонний треугольник окружности, то его площадь

4. Если R – радиус описанной около равностороннего треугольника окружности, то его площадь

      Доказательство.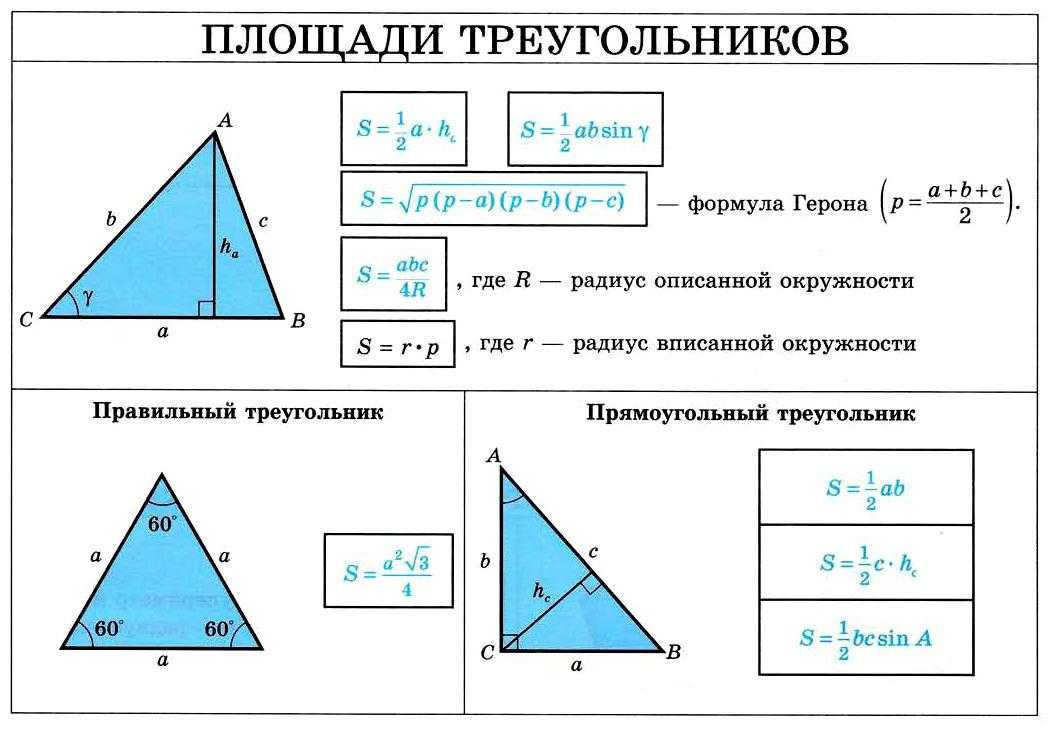

1. Рассмотрим рисунок 7.

Рис. 7

В силу утверждения 2

2. Рассмотрим рисунок 8.

Рис. 8

Поскольку

то

3. Рассмотрим рисунок 9.

Рис. 9

Поскольку у равностороннего треугольника центр вписанной окружности совпадает с точкой пересечения медиан, высот и биссектрис, то выполнено равенство   h = 3r.  Следовательно,

4. Рассмотрим рисунок 10.

Рис. 10

Поскольку у равностороннего треугольника центр описанной окружности совпадает с точкой пересечения медиан, высот и биссектрис, то выполнено равенство Следовательно,

      Доказательство утверждения 7 завершено.

Вывод формул для площади прямоугольного треугольника

      Утверждение 8.

1. Если a и b – катеты прямоугольного треугольника, то его площадь

2. Если a – катет прямоугольного треугольника, а φ – прилежащий к этому катету острый угол, то площадь прямоугольного треугольника

3. Если a – катет прямоугольного треугольника, а φ – противолежащий этому катету острый угол, то площадь прямоугольного треугольника

4. Если c – гипотенуза прямоугольного треугольника, а φ – острый угол, то площадь прямоугольного треугольника

      Доказательство.

1. Рассмотрим рисунок 11.

Рис. 11

В силу утверждения 2

2. Рассмотрим рисунок 12.

Рис. 12

Поскольку

b = a tg φ ,

то

3. Рассмотрим рисунок 13.

Рис. 13

Поскольку

b = a ctg φ ,

то

4. Рассмотрим рисунок 14.

Рис. 14

Поскольку

a = c cos φ ,    
b = c sin φ ,

то

      Доказательство утверждения 8 завершено.

      На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.

Площадь треугольников

Есть несколько способов найти площадь треугольника.

q8zqh4VR6KY

Знание базы и высоты

Когда мы знаем основание и высоту, это легко.

Это просто половина b умноженная на час

Площадь = 1 2 шв

(подробнее на странице треугольников)

Самое главное, чтобы основание и высота были под прямым углом. Поиграй здесь:

Пример: Какова площадь этого треугольника?

(Примечание: 12 — высота , а не длина левой стороны)

Высота = h = 12

Основание = b = 20

Площадь = 9 ½ 4 h 20 × 12 = 120

627 723, 3132, 3133

Знание трех сторон

Существует также формула для нахождения площади любого треугольника, если известны длины всех трех его сторон.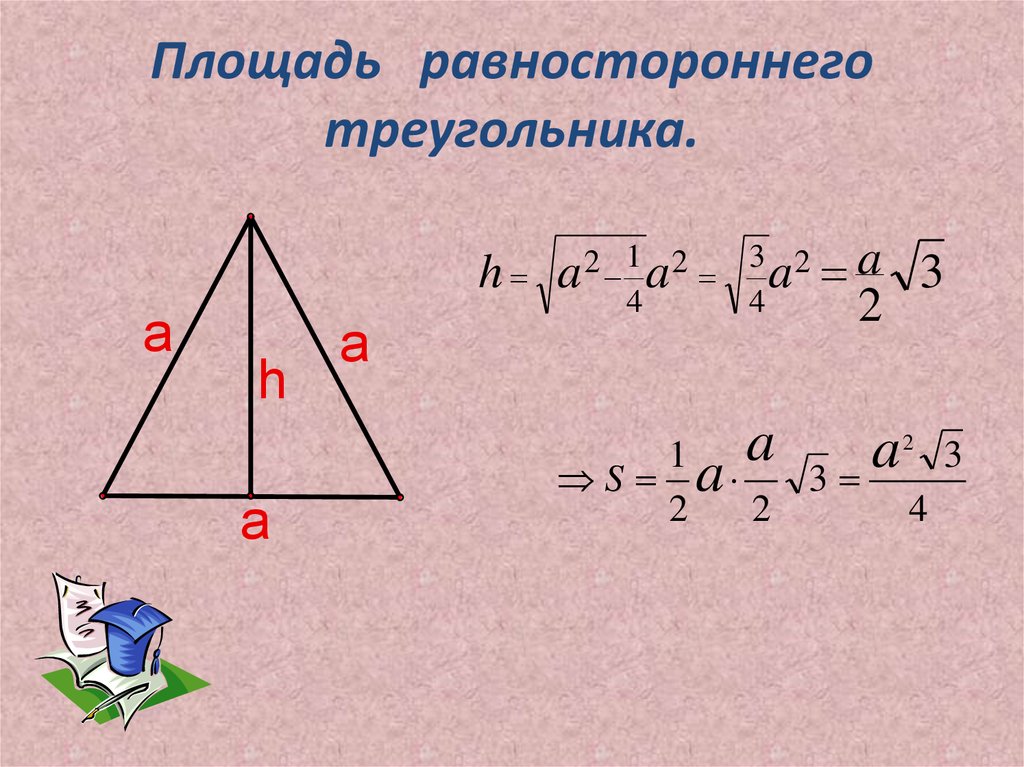

Это можно найти на странице Формулы Герона.

Знание двух сторон и угла между ними

Когда мы знаем две стороны и угол между ними (SAS), мы можем использовать другую формулу (фактически три эквивалентные формулы).

В зависимости от того, какие стороны и углы мы знаем, формулу можно записать тремя способами:

Площадь = 1 2 абсин С

Площадь = 1 2 до н.э. sin A

Площадь = 1 2 casin B

Это действительно одна и та же формула, только стороны и угол изменены.

Пример: Найдите площадь этого треугольника:

Прежде всего мы должны решить, что мы знаем.

Нам известен угол C = 25º, стороны a = 7 и b = 10.

Итак, приступим:

Площадь = (½)ab sin C

Подставим известные нам значения:½ × 7 × 10 × sin(25º)

Поработайте с калькулятором: 35 × 0,4226. ..

Площадь =   14,8 с точностью до одного десятичного знака

Как запомнить

Просто подумайте «abc»: Площадь = ½ a b sin C

Также хорошо помнить, что угол всегда равен между двумя известными сторонами , который называется «включенный угол».

Как это работает?

Начнем с этой формулы:

Площадь = ½ × основание × высота

Мы знаем, что основание равно c , и можем вычислить высоту:

высота b × sin A

Получаем:

Площадь = ½ × (c) × (b × sin A)

Что можно упростить до:

Площадь = 1 2 до н.э. sin A

Изменив метки на треугольнике, мы также можем получить:

• Площадь = ½ абс. C
• Площадь = ½ корпуса B

Еще один пример:

Пример: Найдите, сколько земли

Фермер Ригби владеет треугольным участком земли.

Длина забора АВ 150 м. Длина ограждения БЦ 231 м.

Угол между ограждением AB и ограждением BC равен 123º.

Сколько земли принадлежит фермеру Ригби?

 

Прежде всего мы должны решить, какие длины и углы нам известны:

• AB = c = 150 м,
• до н.э. = а = 231 м,
• и угол B = 123º

Итак, мы используем:

Площадь = 1 2 ca sin B

Подставим известные нам значения: × 0,838… м ²

 Площадь =14 530 м ²

 

У фермера Ригби 14 530 м ²

4 земли

 

259, 1520, 1521, 1522,260, 1523, 2344, 2345, 3940, 3941

2.4: Площадь треугольника

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

3257

• Майкл Коррал
• Колледж Скулкрафт

Из курса элементарной геометрии вы узнали, что площадь треугольника равна половине произведения основания на высоту. Теперь мы будем использовать это в сочетании с некоторой тригонометрией, чтобы вывести больше формул для площади при заданных частях треугольника.

Вариант 1: Две стороны и прилежащий угол.

Предположим, что у нас есть треугольник \(\triangle\,ABC\), в котором угол \(A\) может быть острым, прямым или тупым, как на рис. 2.4.1. Предположим, что \(A\), \(b\) и \(c\) известны. 9\circ — A) =b\;\sin\;A \) на рис. 2.4.1(c)). Таким образом, мы получаем следующую формулу:

\[\fbox{\(\text{Area} ~=~ K ~=~ \tfrac{1}{2}\,bc\;\sin\;A\)}\ label{2.23} \]

Приведенная выше формула для площади \(\треугольника\,ABC\) выражена в известных частях \(A\), \(b\) и \(c\). Аналогичные рассуждения для углов \(B \) и \(C \) дают нам:

\[ \begin{align}\text{Area} ~&=~ K =~ \tfrac{1}{2}\, ac\;\sin\;B \\
\text{Area} ~&=~ K =~ \tfrac{1}{2}\,ab\;\sin\;C\label{2.25} \end{align } \] 9\circ}\\
K ~&=~ 21.58
\end{align*} \]

Случай 3: Три стороны.

Предположим, что у нас есть треугольник \(\треугольник\,ABC \), в котором известны все три стороны. Тогда Формула Герона дает нам площадь:

Формула Герона

Для треугольника \(\треугольник\,ABC\) со сторонами \(a\), \(b\) и \(c\), пусть \(s = \frac{1}{2}\,(a+b+c) \) (т.е. \(2s = a+b+c \) — периметр треугольника). Тогда площадь \(K\) треугольника равна 92 ~=~ s\,(s-a)\,(s-b)\,(s-c) ~, \nonumber \]
поэтому при извлечении квадратных корней мы получаем
\[\nonumber K ~=~ \sqrt{s\,( s-a)\,(s-b)\,(s-c)} ~~.\quad \textbf{QED} \nonumber \]

Пример 2.15

Найдите площадь треугольника \(\triangle\,ABC \) по данному \ (а=5\), \(b=4\) и \(с = 7\).

Решение

Используя формулу Герона с \(s = \frac{1}{2}\,(a+b+c) = \frac{1}{2}\,(5+4+7) = 8 \), площадь \(K \) определяется как:
\[ \begin{align*}
K ~&=~ \sqrt{s\,(s-a)\,(s-b)\,(s-c) }\\
&=~ \sqrt{8\,(8-5)\,(8-4)\,(8-7)} ~=~ \sqrt{96} \quad\Стрелка вправо\quad \boxed{K ~= ~ 4\,\sqrt{6}
~\приблизительно 9. 8} ~.
\end{align*} \]

Формула Герона полезна в теоретических целях (например, при выводе других формул). Однако он не подходит для использования в калькуляторе, демонстрируя так называемую численную нестабильность для «экстремальных» треугольников, как в следующем примере.

Пример 2.16

,ABC \) задано \(a=1000000\), \(b=999999,9999979 \) и \(c = 0,0000029 \).

Решение:

Чтобы использовать формулу Герона, нам нужно вычислить \(s = \frac{1}{2}\,(a+b+c) \). Обратите внимание, что фактическое значение \(a+b+c \) равно \(2000000,0000008 \), что имеет \(14 \) цифр. Большинство калькуляторов могут хранить \(12\)-\(14\) цифр внутри (даже если они отображают меньше), и, следовательно, могут округлять это значение \(a+b+c\) до \(2000000\). Когда мы затем разделим это округленное значение для \(a+b+c\) на \(2\), чтобы получить \(s\), некоторые калькуляторы (например, TI-83 Plus) дадут округленное вниз значение \( 1000000 \).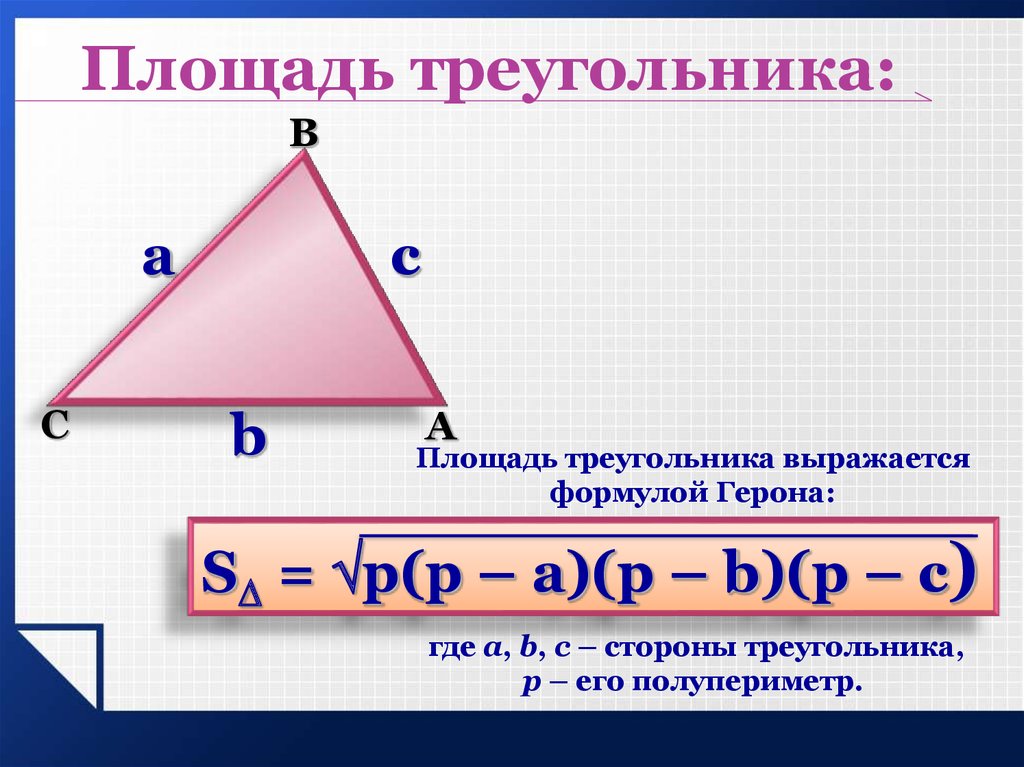

Это проблема, потому что \(a=1000000 \), поэтому мы получим \(s-a=0 \), в результате чего формула Герона даст нам площадь треугольника \(0 \)! И это действительно неправильный ответ, который возвращает TI-83 Plus. Другие калькуляторы могут дать другой неточный ответ, в зависимости от того, как они хранят значения внутри. Фактическая площадь — с точностью до \(15\) знаков после запятой — равна \(K = 0,99999999999895 \), то есть в основном равна \(1 \).

Приведенный выше пример показывает, как проблематичная арифметика с плавающей запятой может быть. К счастью, есть лучшая формула для площади треугольника, когда известны три стороны:

Для треугольника \(\треугольник\,ABC\) со сторонами \(a \ge b \ge c \) площадь равна :

\[ \text{Площадь} ~=~ K ~=~ \tfrac{1}{4}\,\sqrt{(a + (b+c))\,(c — (a-b))\,(c + (a-b))\,(a + (b-c))}\label{2.33} \]

Чтобы использовать эту формулу, отсортируйте названия сторон так, чтобы \(a \ge b \ge c \). Затем выполните операции внутри квадратного корня в точном порядке, в котором они появляются в формуле, включая использование круглых скобок . Затем извлеките квадратный корень и разделите на \(4\). Для треугольника в примере 2.16 приведенная выше формула дает точное значение \(K = 1 \) на том же калькуляторе TI-83 Plus, который не смог использовать формулу Герона. Что удивительно в этой формуле, так это то, что это просто переписанная формула Герона! Использование круглых скобок — это то, что заставляет соблюдать правильный порядок операций для числовой стабильности.

Другая формула площади треугольника для трех его сторон приведена ниже:

Для треугольника \(\треугольник\,ABC \) со сторонами \(a \ge b \ge c \) площадь равна: 92} \]

---

Эта страница под названием 2.4: Площадь треугольника распространяется в соответствии с лицензией GNU Free Documentation License 1.3 и была создана, изменена и/или курирована Майклом Корралом с помощью исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts. ; подробная история редактирования доступна по запросу.

No related posts.