Подобные треугольники. Отношение площадей подобных треугольников 8 класс онлайн-подготовка на Ростелеком Лицей |
Подобные треугольники. Отношение площадей подобных треугольников.
При сравнении двух величин возникает вопрос: во сколько раз одна больше другой?
Например, во сколько раз собака пробежит быстрее некоторое расстояние, чем это же расстояние проползёт жук? Или какую часть всех деревьев парка составляют дубы?
Ответ в таких случаях дается в виде частного двух чисел, которое называют отношением. Отношение показывает, во сколько раз первое число больше второго, или какую часть первое число составляет от второго.
Отношением отрезков АВ и СD называется отношение их длин, т. е. ABCD (или AB:CD).
На рисунке отрезки AB и CD пропорциональны отрезкам A1B1 и C1D1, если AB:A1B1 = CD:C1D1.
В геометрии фигуры одинаковой формы называют подобными. Любые два квадрата и любые два круга являются подобными.
Любые два квадрата и любые два круга являются подобными.
А какие два треугольника называют подобными? Возьмём два треугольника ABC и A1B1C1, у которых угол А равен углу A1, угол B равен углу B1, а угол C равен углу C1.
Тогда стороны AB и A1B1, BC и B1C1, AC и A1C1 называются сходственными. И если эти сходственные стороны пропорциональны, то есть AB:A1B1 = BC:B1C1 = AC:A1C1, то треугольники ABC и A1B1C1 являются подобными. Подобие треугольников обозначается следующим образом ⊿ABC∼⊿A1B1C1.
Подобными называются треугольники, у которых углы соответственно равны, а сходственные стороны пропорциональны.
Отношение сходственных сторон называют коэффициентом подобия.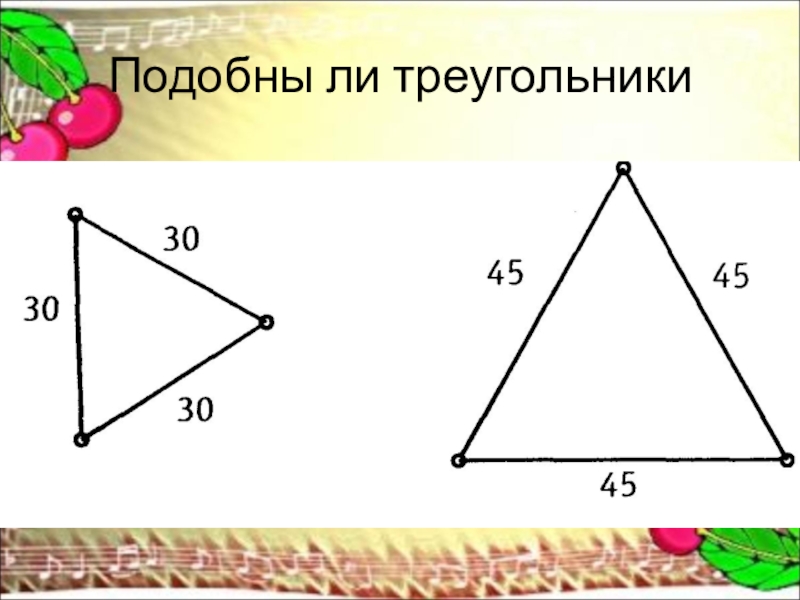 Если стороны треугольника ABC в два раза больше сторон треугольника A1B1C1, то отношение сходственных сторон равно 2, то есть коэффициент подобия равен 2.
Если стороны треугольника ABC в два раза больше сторон треугольника A1B1C1, то отношение сходственных сторон равно 2, то есть коэффициент подобия равен 2.
Подобие треугольников можно установить, проверив только некоторые из равенств:
AB:A1B1 = BC:B1C1 = AC:A1C1 = 2, то есть k=2.
Теорема. Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
Дано: ⊿ABC∼⊿A1B1C1, k — коэффициент подобия.
Найти: отношение площадей ABC и A1B1C1
Решение:
Обозначим SABC= S, SA1B1C1 = S1.
∠A = ∠A1, значит, SS1=AB∙ACA1B1∙A1C1 (площади треугольников, имеющих равный угол, относятся как произведения сторон, содержащих этот угол).
ABA1B1=k
ACA1C1=k
Следовательно, SS1=k2.
Задача. Площади подобных треугольников АВС и А1В1С1 равны соответственно 20 см2 и 5 см2. Сторона А1В1 = 2 см. Найдите сходственную ей сторону АВ треугольника АВС.
Выше мы доказали, что отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
SS1=k2, значит, 205=k2, следовательно k=2.
k=ABA1B1=2, значит, AB=2∙A1B1=2∙4=8 см.
Ответ: 8 см.
Подобные треугольники | это… Что такое Подобные треугольники?
ТолкованиеПеревод
- Подобные треугольники
Подобные треугольники — треугольники, у которых углы соответственно равны, а стороны одного пропорциональны сходственным сторонам другого.
Содержание
- 1 Признаки подобия треугольников
- 1.
 1 Первый признак
1 Первый признак - 1.2 Второй признак
- 1.3 Третий признак
- 1.4 Признаки подобия прямоугольных треугольников
- 1.
- 2 Свойства подобных треугольников
- 3 Подобие в прямоугольном трегольнике
- 4 Связанные определения
- 5 Литература
- 6 См. также
- 7 Ссылки
Признаки подобия треугольников
Признаки подобия треугольников — геометрические признаки, позволяющие установить, что два треугольника являются подобными без использования всех элементов.
Первый признак
Если два угла одного треугольника соответственно равны двум углам другого, то треугольники подобны.
Дано: ∆ABC и ∆A1B1C1, ∠A=∠A1, ∠B=∠B1.Доказать: ∆ABC ∆A1B1C1.
Доказательство
Второй признак
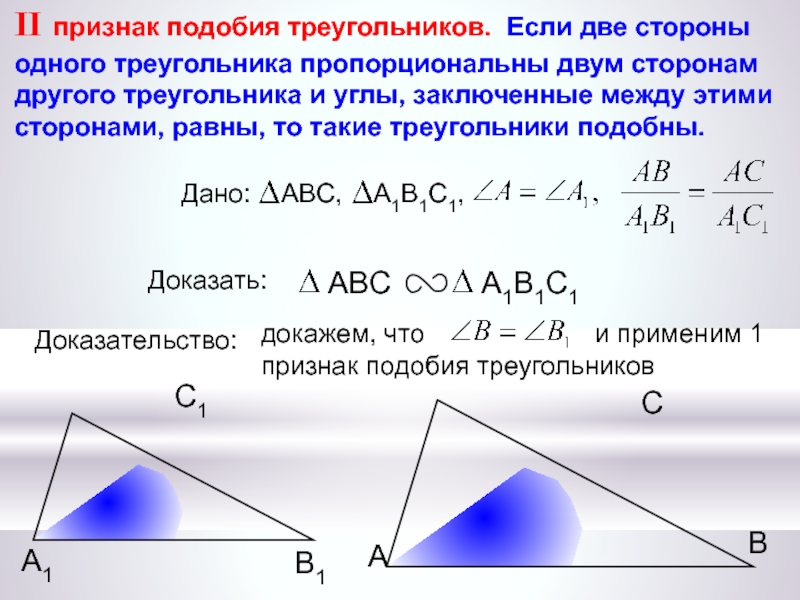
Если две стороны одного треугольника пропорциональны двум сторонам другого и углы между этими сторонами равны, то треугольники подобны.

Дано: ∆ABC и ∆A1B1C1, ∠A=∠A1, = .Доказать: ∆ABC ∆A1B1C1.
Доказательство
Третий признак
Если три стороны одного треугольника пропорциональны трем сходственным сторонам другого, то треугольники подобны.
Дано: ∆ABC и ∆A1B1C1, = = .Доказать: ∆ABC ∆A1B1C1.
Доказательство
Признаки подобия прямоугольных треугольников
- По острому углу — см. первый признак;
- По двум катетам — см. второй признак;
- По катету и гипотенузе — см. второй признак.
Свойства подобных треугольников
- Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
- Отношение периметров и длин биссектрис, медиан, высот и серединных перпендикуляров равно коэффициенту подобия.

Треугольники, на которые высота, опущенная из прямого угла, делит прямоугольный треугольник, подобны всему треугольнику по первому признаку, а значит:
- Высота прямоугольного треугольника, опущенная на гипотенузу, равна среднему геометрическому проекций катетов на гипотенузу,
- Катет равен среднему геометрическому гипотенузы и проекции этого катета на гипотенузу.
Связанные определения
- Коэффициент подобия — число k, равное отношению сходственных сторон подобных треугольников.
- Сходственные стороны подобных треугольников — стороны, лежащие напротив равных углов.
Литература
- Геометрия 7-9/Л. С. Атанасян и др. — 12-е изд. — М.: Просвещение, 2002. — 384 c.: ил.
См. также
- Подобие
- Среднее геометрическое
- Треугольник
Ссылки
- Подобие треугольников
- Признаки подобия из учебника за восьмой класс
- Признаки подобия через преобразования
- 1 Признаки подобия треугольников
Wikimedia Foundation. 2010.
2010.
Игры ⚽ Поможем написать реферат
- Подобные фигуры
- Поднять тремя пальцами
Полезное
Свойства подобных треугольников — обзор алгебры (видео)
TranscriptFAQsPractice
Привет, и добро пожаловать в этот обзор подобных треугольников! Сегодня мы собираемся изучить, как идентифицировать подобные треугольники и как мы можем использовать эти знания для решения очень популярной задачи геометрии.
Определение подобных треугольников
Начнем с простого определения. Подобные треугольники – это треугольники, имеющие одинаковую форму. Значит, у них будут одинаковые три углы . Но вот в чем загвоздка — похожие треугольники не обязательно должны быть одинакового размера! Поэтому, если вы возьмете копию треугольника и увеличите ее в два раза, она все равно будет похожа на исходный треугольник.
Метод «угол-угол-угол»
Обратите внимание, что два треугольника имеют одинаковую форму и пропорции. Это потому, что у них одинаковые углы, что делает их похожими треугольниками. Это Angle-Angle-Angle , или AAA, метод определения сходства. Следует отметить, что каждый раз, когда вы расширяете треугольник, вы получаете два подобных треугольника.
Это потому, что у них одинаковые углы, что делает их похожими треугольниками. Это Angle-Angle-Angle , или AAA, метод определения сходства. Следует отметить, что каждый раз, когда вы расширяете треугольник, вы получаете два подобных треугольника.
Поскольку мы знаем, что эти два треугольника подобны треугольникам, мы можем выразить это в математической записи следующим образом: \(△ABC\) ~ \(△A’B’C’\)
Хорошо, но что, если бы мы не Не начать с расширения и не знать всех углов? Есть ли другой способ определить, подобны ли два треугольника?
Метод стороны-стороны-стороны
Давайте рассмотрим пример, где мы знаем только длины сторон двух треугольников:
Эти два треугольника кажутся одной и той же формы, но помните, что в геометрии мы можем’ всегда доверяем своим глазам. Нам нужно доказать, что они имеют одинаковую форму, и мы можем сделать это, проверив, пропорциональны ли их стороны друг другу. Мы настраиваем наши пропорции, устанавливая отношения или дроби соответствующих сторон и устанавливая их равными друг другу, например: (△DEF\) — знаменатели. Это сработало бы так же хорошо, если бы мы поменяли его местами.
Это сработало бы так же хорошо, если бы мы поменяли его местами.
Очень важно отметить пропорции, чтобы убедиться, что мы поместили все числа на свои места.
Итак, что эта пропорция делает для нас? Что ж, нам нужно проверить, правда ли это. В этом случае мы можем сделать это, приведя каждую из этих дробей к их простейшей форме. Мы видим, что 3 идет вверху и внизу \(\frac{6}{9}\), поэтому мы можем уменьшить его до 2 вместо 3. Четыре входит в \(\frac{8}{12}\) и 5 переходит в \(\frac{10}{15}\). Когда мы уменьшаем эти две дроби, мы также получаем \(\frac{2}{3}\). В сокращенном виде наша пропорция выглядит так:
Это доказательство того, что все наши стороны пропорциональны. Если все стороны пропорциональны, то мы знаем, что наши треугольники пропорциональны. Это Side-Side-Side , или SSS, метод доказательства сходства. Итак, теперь мы можем сказать, что \(△ABC\) ~ \(△DEF\).
Вместо уменьшения мы могли бы также проверить, пропорциональны ли отношения, преобразовав каждое отношение в десятичное число, разделив верхнее значение каждого из них на нижнее. В этом случае \(\frac{6}{9}\), \(\frac{8}{12}\) и \(\frac{10}{15}\) дали бы нам одно и то же десятичное число значение, которое составляет 0,66666666.
В этом случае \(\frac{6}{9}\), \(\frac{8}{12}\) и \(\frac{10}{15}\) дали бы нам одно и то же десятичное число значение, которое составляет 0,66666666.
Итак, теперь мы знаем, что если все углы равны или если все стороны пропорциональны, наши треугольники подобны.
Метод Сторона-Угол-Сторона
Существует еще один метод доказательства сходства, называемый Сторона-Угол-Сторона , или SAS. Здесь мы знаем, что два треугольника имеют один угол, который имеет одинаковую меру, и что две стороны, исходящие из этого угла, пропорциональны.
Давайте посмотрим на наши последние два треугольника, но вместо того, чтобы знать все три стороны, мы знаем только два набора соответствующих сторон вместе с углом между ними, например:
Мы видим, что угол между двумя измеренными сторонами помечен квадратом, что, как мы знаем, означает, что это прямой угол и, следовательно, 90 градусов. Поскольку этот угол одинаков в обоих треугольниках, нам просто нужно проверить, пропорциональны ли две соседние стороны, например:
Повторное сокращение дробей дает 2 на 3, поэтому стороны пропорциональны.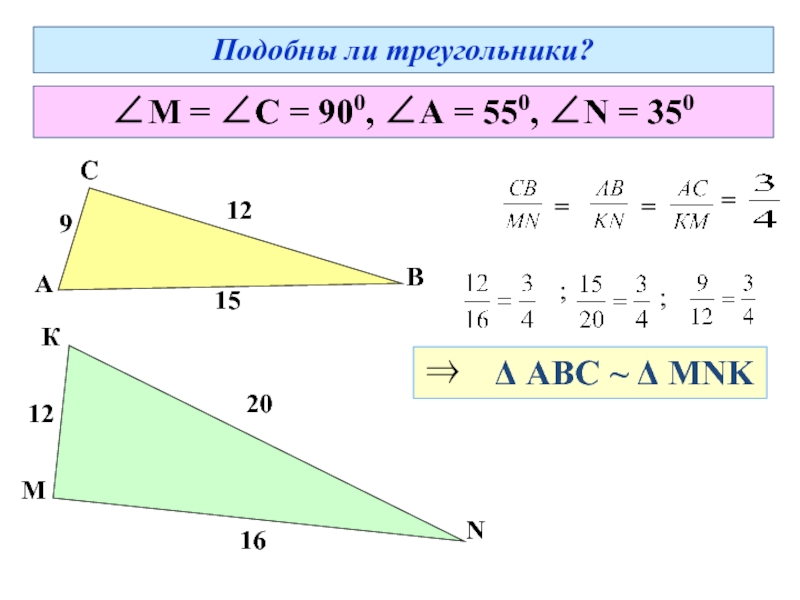 Поскольку угол между этими сторонами один и тот же, или конгруэнтны , этот треугольник подобен.
Поскольку угол между этими сторонами один и тот же, или конгруэнтны , этот треугольник подобен.
Высота дерева Задача
Итак, что мы можем сделать с этой способностью распознавать похожие треугольники? Возможно, вы уже видели это раньше, но вот классическая задача о высоте дерева:
Вот что мы знаем. Дерево и флагшток стоят прямо перпендикулярно земле. Каждый из них отбрасывает тень от одного и того же источника света — солнца. Лучи, исходящие от солнца, представляют собой прямые линии, падающие на предметы под углом. Земля плоская и может считаться плоской, а это значит, что любые две точки на ней можно соединить прямой линией. Это означает, что я могу нарисовать два треугольника поверх этого рисунка, например:
Теперь давайте сохраним наши треугольники, но избавимся от красивого пейзажа.
Далее давайте пометим все точки, чтобы мы могли ссылаться на них. Неважно, какую букву мы используем для каждой точки.
Мы также знаем, что угол B и угол D являются прямыми углами, так как флагшток и дерево направлены вертикально вверх, перпендикулярно земле, поэтому мы также пометим это:
Поскольку мы знаем, что угол A один и тот же для обоих треугольников и что углы B и D оба прямые и, следовательно, конгруэнтны, это означает, что углы C и E также конгруэнтны.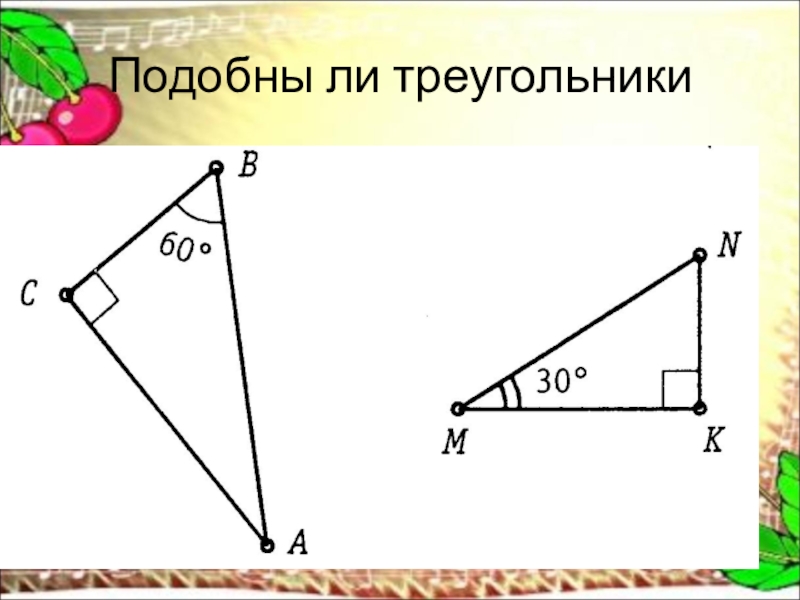 Почему? Потому что сумма внутренних углов треугольника должна составлять 180°. Итак, если A равно 30°, а B и D равны 90°, то C и E будут равны 60°.
Почему? Потому что сумма внутренних углов треугольника должна составлять 180°. Итак, если A равно 30°, а B и D равны 90°, то C и E будут равны 60°.
Теперь мы знаем, что это подобные треугольники, используя метод ААА для доказательства сходства.
Теперь мы можем перейти к самой интересной части и использовать эти треугольники, чтобы найти высоту дерева. Во-первых, нам нужно провести некоторые измерения. Нам нужно измерить флагшток, длину тени флагштока и длину тени дерева. К счастью, все это легко сделать. Стандартный флажок для гольфа имеет высоту 7 футов. Очевидно, что тени лежат на земле, поэтому мы можем измерить их длинной рулеткой. Затем мы можем добавить их к нашим треугольникам.
Так как стороны подобных треугольников всегда пропорциональны, мы можем установить пропорцию со всеми строками и столбцами, помеченными:
Мы не знаем ни одной из диагональных сторон, но они нам не нужны для этого типа проблемы. Мы знаем наземные стороны обоих треугольников и знаем высоту \(△ABC\). Мы можем поместить переменную для высоты дерева, которая равна \(\overline{DE}\) в нашем треугольнике. Теперь мы просто используем перекрестные произведения для решения:
Мы можем поместить переменную для высоты дерева, которая равна \(\overline{DE}\) в нашем треугольнике. Теперь мы просто используем перекрестные произведения для решения:
Взятие перекрестных произведений приводит к уравнению \(9x=45\cdot 7\) или \(9x=315\) после умножения 45 и 7. Разделив обе части на 9, мы получим \(x=35\). Итак, наше дерево 35 футов в высоту!
Обзор
Хорошо, теперь, когда мы все рассмотрели, давайте кратко подытожим:
Подобные треугольники — это треугольники, имеющие одинаковую форму. Есть три способа доказать, что два треугольника подобны. Метод подобия ААА – это когда пропорции всех трех углов треугольников одинаковы. Метод SSS – это когда все три стороны треугольников имеют одинаковую длину. И, наконец, метод SAS заключается в том, что два треугольника имеют один угол одинаковой меры, а две стороны, выходящие из этого угла, пропорциональны.
Надеюсь, отзыв был полезен! Спасибо за просмотр и удачной учебы!
Часто задаваемые вопросы
Q
Что такое подобные треугольники?
A
Подобные треугольники — это треугольники, соответствующие углы которых равны, а соответствующие стороны пропорциональны, но не обязательно равны.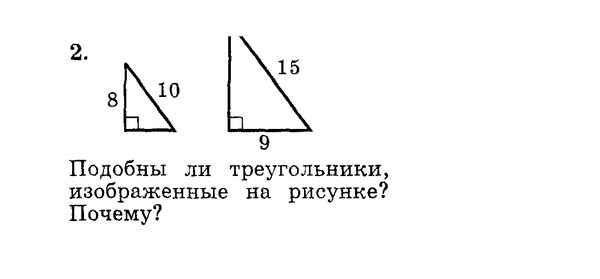
пр.
Q
Все ли прямоугольные треугольники подобны?
A
Нет, не все прямоугольные треугольники подобны. Чтобы треугольники были подобны, они должны иметь одинаковые величины углов. Все прямоугольные треугольники имеют один прямой угол, но два других угла могут быть любой комбинацией мер, которые в сумме дают 9.0°.
пр. ⊿ABC не похож на ⊿DEF.
Q
Все ли равносторонние треугольники подобны?
A
Да, все равносторонние треугольники подобны, потому что все они имеют одинаковые углы.
Q
Все равнобедренные треугольники подобны?
A
Нет, не все равнобедренные треугольники подобны. Чтобы треугольники были подобны, они должны иметь одинаковые величины углов. Не все равнобедренные треугольники имеют одинаковые величины углов.
пр. ⊿ABC не похож на ⊿DEF
Практические вопросы
Вопрос №1:
Какое из следующих утверждений неверно относительно подобных треугольников?
У них одинаковая форма
У них одинаковые углы
У них одинаковый размер
У них одинаковые пропорции
Показать ответ
Ответ:
Правильный ответ: они одного размера. . Подобные треугольники — это треугольники, которые имеют одинаковую форму, одинаковые величины углов и пропорциональны друг другу. Подобные треугольники не имеют одинакового размера. Если треугольники одинакового размера, то они равны.
. Подобные треугольники — это треугольники, которые имеют одинаковую форму, одинаковые величины углов и пропорциональны друг другу. Подобные треугольники не имеют одинакового размера. Если треугольники одинакового размера, то они равны.
Скрыть ответ
Вопрос №2:
△ ABC похож на △ DEF . Найдите х.
12
18
3
6
Показать ответ
Ответ:
Правильный ответ 1 2. Поскольку треугольники подобны, их стороны пропорциональны. \(\overline{BC}\) пропорционально \(\overline{EF}\) и \(\overline{AC}\) пропорционально \(\overline{DF}\). Составьте пропорцию.
\(\frac{6}{x}=\frac{7}{14}\)
Перемножить крест-накрест и найти x. А BC похож на △ ДЕФ . Найдите х.
81°
31°
46°
56°
Показать ответ
Ответ:
Правильный ответ: 46°.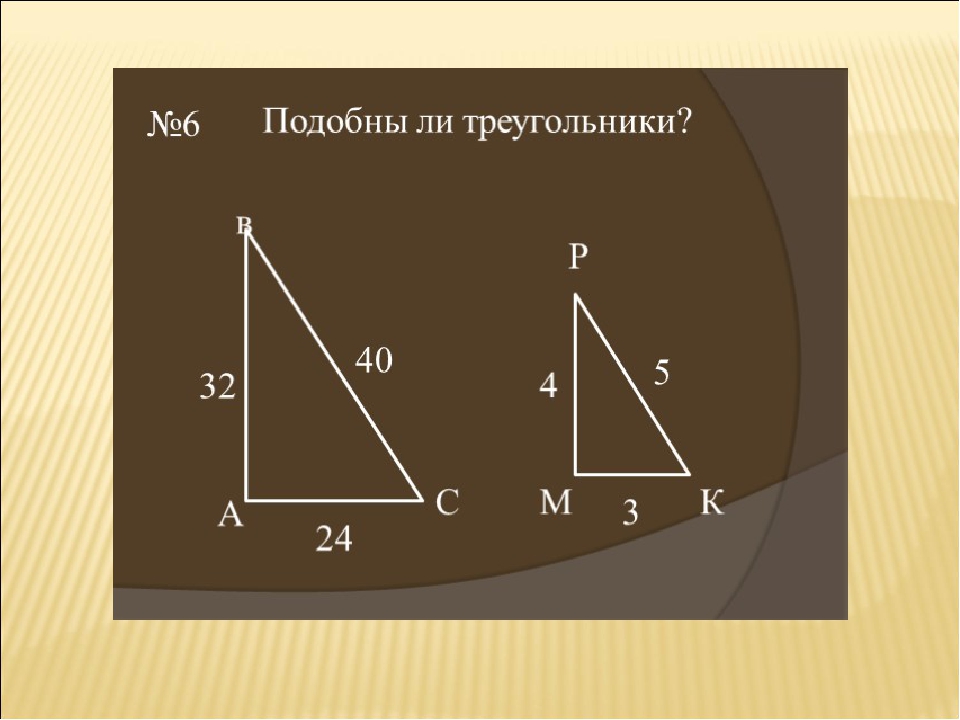 Подобные треугольники имеют конгруэнтные меры углов. Поскольку ∠B = 46°, ∠E также должно быть 46°.
Подобные треугольники имеют конгруэнтные меры углов. Поскольку ∠B = 46°, ∠E также должно быть 46°.
Скрыть ответ
Вопрос №4:
Эти два треугольника подобны?
Да
Нет
Иногда
нельзя определить с помощью данной информации
Показать ответ
Ответ:
Правильный ответ — да. Подобные треугольники должны иметь конгруэнтные меры углов. Поскольку в каждом треугольнике известны два угла, и они одинаковы, их можно определить как подобные треугольники, поскольку третьи углы также должны быть одинаковыми. У всех треугольников внутренние углы в сумме составляют 180°, поэтому третий угол в обоих этих треугольниках должен быть равен \(180°-93°-47°=30°\).
Скрыть ответ
Вопрос №5:
△ ABC похож на △ DEF . Найдите х.
Найдите х.
58.53
52.27
47.19
43.62
Показать ответ
Ответ: 900 03
Правильный ответ: 43,62. Поскольку треугольники подобны, их стороны пропорциональны. \(\overline{AB}\) пропорционально \(\overline{DE}\) и \(\overline{BC}\) пропорционально \(\overline{EF}\). Составьте пропорцию.
\(\frac{13}{27}=\frac{21}{x}\)
Крест умножить и найти x.
\(13x=21\times27\)
\(13x=567\)
\(x≈43,62\)
Скрыть ответ
Вернуться к видео по геометрии
398538523787239422891859604785
Калькулятор подобных треугольников
Этот калькулятор подобных треугольников поможет вам найти подобный треугольник путем масштабирования известного треугольника . Вы также можете использовать этот калькулятор, чтобы найти недостающую длину подобного треугольника!
Пролистайте эту статью, пока мы обсуждаем законы подобных треугольников и изучаем некоторые основы:
- Что такое подобные треугольники?
- Нахождение подобных треугольников: как определить, подобны ли два треугольника?
- Как найти недостающую сторону подобного треугольника?
- Как найти площадь подобного треугольника?
Что такое подобные треугольники?
Два треугольника подобны , если их соответствующих сторон находятся в одном и том же отношении , что означает, что один треугольник является версией другого треугольника в масштабе .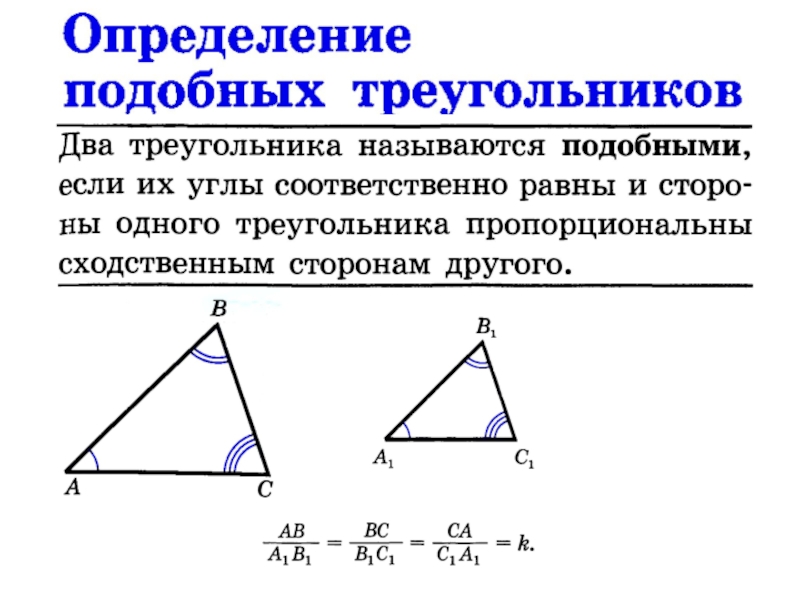 Естественно, что соответственных углов подобных треугольников равны . Например, рассмотрим следующие два треугольника:
Естественно, что соответственных углов подобных треугольников равны . Например, рассмотрим следующие два треугольника:
Обратите внимание, что соответствующие стороны пропорциональны:
DEAB=EFBC=DFAC=2\frac{\text{DE}}{\text{AB}} = \frac{\text{EF}}{\text{BC }} =\frac{\text{DF}}{\text{AC}} = 2ABDE=BCEF=ACDF=2
Следовательно, мы можем сказать △ABC\triangle \text{ABC}△ABC ∼\sim∼ △DEF\triangle \text{DEF}△DEF. Здесь символ ∼\sim∼ указывает на то, что треугольники подобны.
Мы называем долю сходства масштабным коэффициентом (k)(k)(k). В приведенном выше примере коэффициент масштабирования k=2k = 2k=2. Если вам нужна помощь в поиске коэффициентов, воспользуйтесь нашим калькулятором коэффициентов.
Нахождение подобных треугольников: закон подобных треугольников
Мы знаем, что два треугольника подобны, если верно одно из следующих утверждений:
- соответствующих сторон треугольника находятся в пропорции ; или
-

Отсюда мы можем вывести специальные правила для определения того, подобны ли любые два треугольника:
- Сторона-сторона-сторона (SSS) : Если все три соответствующие стороны двух треугольников находятся в пропорции , они подобны. Это правило является самым простым и требует, чтобы вы знали все стороны треугольников.
Мы можем выразить это, используя аналогичную формулу треугольника:
DEAB=EFBC=DFAC=k\qquad \frac{\text{DE}}{\text{AB}} = \frac{\text{EF}}{\ text{BC}} =\frac{\text{DF}}{\text{AC}} = kABDE=BCEF=ACDF=k
где kkk — масштабный коэффициент .
- Side-Angle-Side (SAS): При наличии две соответствующие стороны двух треугольников пропорциональны и их углов равны , тогда треугольники подобны.
 Мы можем использовать это правило всякий раз, когда нам известны только две стороны каждого треугольника и прилежащие к ним углы.
Мы можем использовать это правило всякий раз, когда нам известны только две стороны каждого треугольника и прилежащие к ним углы.
Треугольники на изображении выше подобны, если:
DEAB=DFAC=k,и∠BAC=∠EDF\qquad \begin{align*} &\frac{\text{DE}}{\text{AB}} = \frac{\text{DF}}{\text{AC}} = k, \text{and}\\\\ & \угол\текст{BAC} = \угол\текст{EDF} \end{align*}ABDE=ACDF=k,and∠BAC=∠EDF
Это правило удобно в случаях, как на изображении ниже, где треугольники имеют общий угол:
Треугольники △ABC\треугольник \text{ABC}△ABC и △PBQ\треугольник \text{PBQ}△PBQ имеют общий угол . В таких случаях проще проверить критерий SAS.- Угол-Сторона-Угол (ASA) : Если любые два соответствующих угла двух треугольников равны и соответствующие стороны между ними пропорциональны, треугольники подобны.

Треугольники на изображении выше похожи, если:
∠BAC=∠EDF,∠ABC=∠DEF и DEAB=k\qquad \begin{align*} & \угол\текст{BAC} = \угол\текст{EDF}, \\ & \angle\text{ABC} = \angle\text{DEF}, \text{ и}\\\\ &\frac{\text{DE}}{\text{AB}} = k \end{align*}∠BAC=∠EDF,∠ABC=∠DEF, andABDE=k
Вы можете найти третий угол , если вы знаете любые два угла в треугольнике с помощью нашего калькулятора углов треугольника. Мы знаем, что если любые два соответствующих угла в треугольниках равны, треугольники подобны, а это означает, что в правиле конгруэнтности ASA нам не нужно знать сторону, пока известны углы. Однако без сторон мы не можем определить масштабный коэффициент ккк.
💡 Нужно найти площадь треугольника? У нас есть калькулятор площади треугольника, который поможет вам в этом.
Как найти недостающую сторону подобного треугольника?
Чтобы найти отсутствующую сторону треугольника , используя соответствующую сторону подобного треугольника , выполните следующие действия:
- Найдите масштабный коэффициент 7 подобных треугольников, взяв отношение любой известной стороны большего треугольника к соответствующей стороне меньшего.

- Определите , является ли треугольник с отсутствующей стороной на меньше или на больше .
- Если треугольник на меньше , разделите соответствующей стороны большего треугольника на
k, чтобы получить недостающую сторону . В противном случае умножьте соответствующую сторону в меньшем треугольнике наk, чтобы найти недостающую сторону .
Например, рассмотрим следующие два подобных треугольника.
Два подобных треугольника △ABC\треугольник \text{ABC}△ABC и △DEF\треугольник \text{DEF}△DEF, где сторона AC\text{AC}AC неизвестна.Чтобы найти недостающую сторону, мы сначала вычисляем их масштабный коэффициент .
k=DEAB=84=2k = \frac{\text{DE}}{\text{AB}} = \frac{8}{4} = 2k=ABDE=48=2
Далее используйте соотношение масштабного коэффициента между отсутствующей стороной AC и соответствующей стороной DF :
DFAC=k=2AC=DF2=62AC=3\begin{align*} \frac{\text{DF}}{\text{AC}} &= k=2\\[1em] \text{AC} &= \frac{\text{DF}}{2} = \frac{6}{2}\\[1em] \текст{АС} &= 3 \end{align*}ACDFACAC=k=2=2DF=26=3
🙋 Вы также можете сравнить два прямоугольных треугольника и увидеть их сходство, используя наш Калькулятор проверки сходства прямоугольных треугольников.
Как найти площадь подобного треугольника?
Чтобы найти площадь треугольника A1 из площади подобного ему треугольника A2 , выполните следующие действия:
- Найдите масштабный коэффициент треугольники, взяв соотношение из любых известных 9Сторона 0010 большего треугольника и соответствующая ей сторона меньшего треугольника.
- Определите , является ли треугольник с неизвестной площадью на меньше или на больше .
- Если треугольник меньше, разделите A2 на квадрат масштабного коэффициента k , чтобы получить A1 = A2/k 2 . В противном случае умножьте A2 на k 2 , чтобы получить A1 = A2 × k 2 .
Как пользоваться этим калькулятором подобных треугольников
Теперь, когда вы узнали, как найти длину подобного треугольника, формулу для подобных треугольников и многое другое, вы можете быстро понять, как работает этот калькулятор подобных треугольников.
Чтобы проверить, подобны ли два известных треугольника, используйте этот калькулятор следующим образом:
- Выберите проверьте сходство в поле
Введите. - Выберите критерий сходства, который вы хотите использовать. Вы можете выбрать между Side-Side-Side, Side-Angle-Side и Angle-Side-Angle .
- Введите размеры двух треугольников. Калькулятор оценит, похожи они или нет.
Чтобы использовать этот калькулятор для вычисления стороны или периметра подобных треугольников, выполните следующие действия:
- Выберите Найдите недостающую сторону в поле
Введите. - Введите известные размеры, площадь, периметр и масштабный коэффициент треугольников. Калькулятор подобных треугольников найдет неизвестные значения.


 1 Первый признак
1 Первый признак
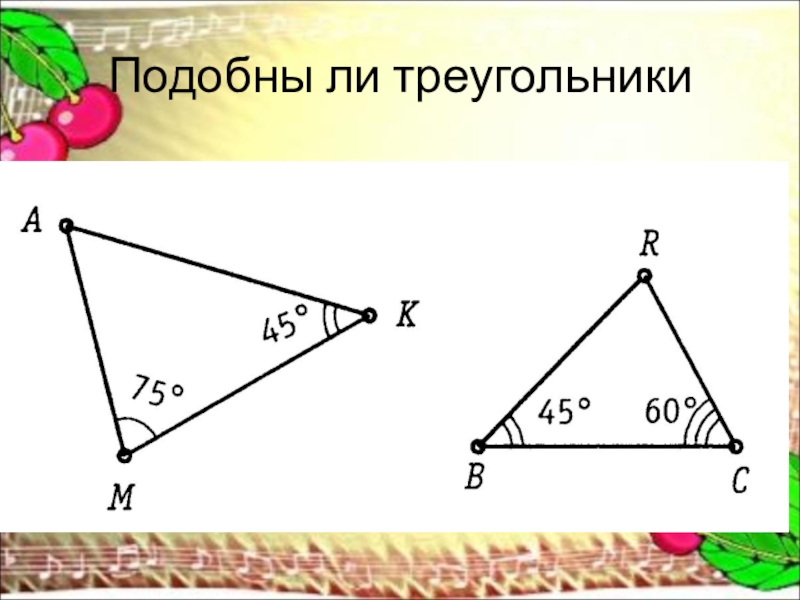
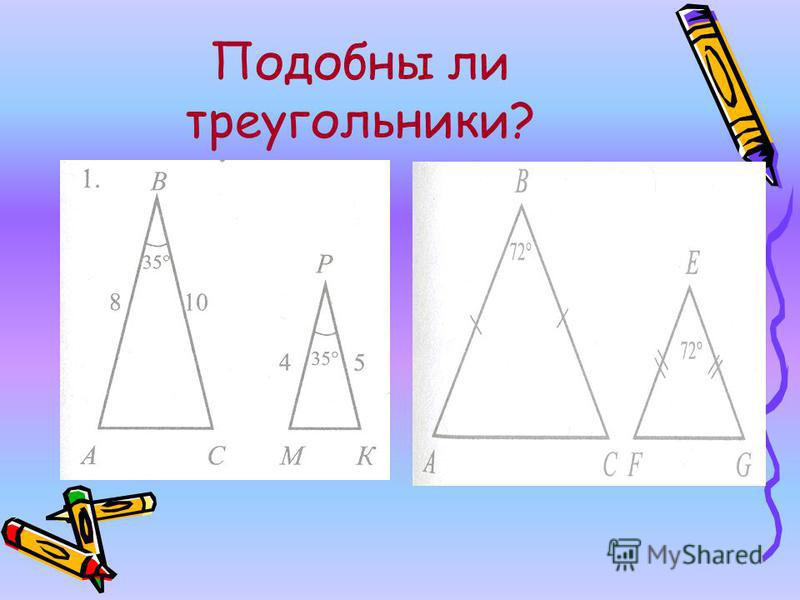
 Мы можем использовать это правило всякий раз, когда нам известны только две стороны каждого треугольника и прилежащие к ним углы.
Мы можем использовать это правило всякий раз, когда нам известны только две стороны каждого треугольника и прилежащие к ним углы.