Четность и нечетность функции онлайн калькулятор: Четность и нечетность функции | Онлайн калькулятор

2*arctgh(x)*arcctgh(x)

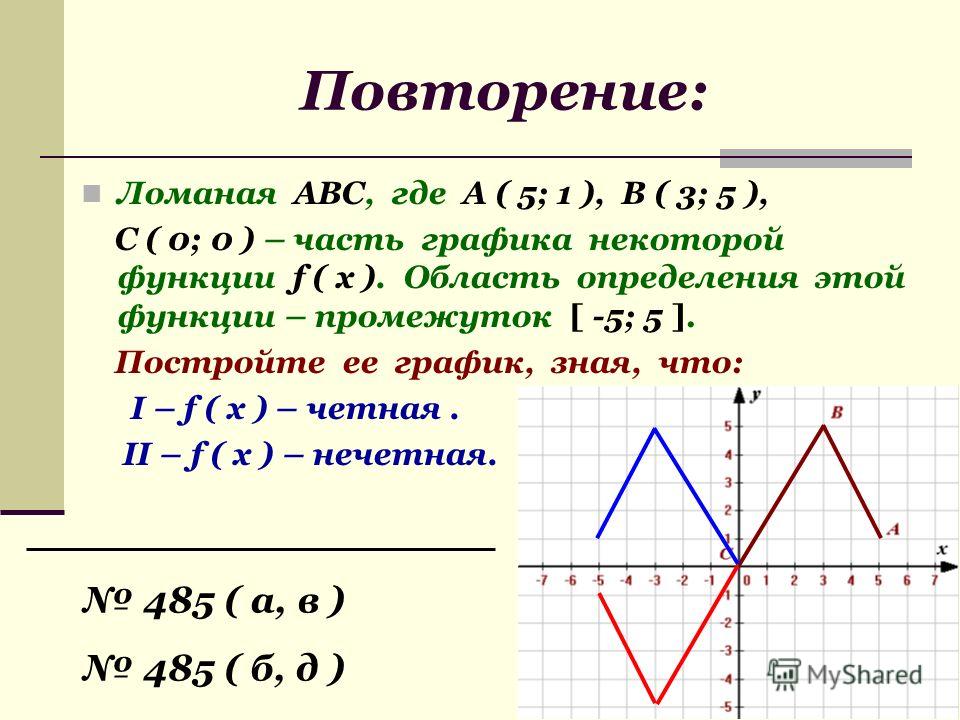
Что исследует?

Для периодических функций идет исследование графика функции только на промежутке периода

Наш калькулятор позволяет исследовать график функции. Но пока что нет возможности находить область определения функции

Что умеет находить этот калькулятор:

• Область определения функции: Да. Умеет определять только точки, в которых знаменатель функции обращается в нуль, но в остальных случаях:
• Умеет определять точки пересечения графика функции с осями координат: Да
• Экстремумы функции: интервалы (отрезки) возрастания и убывания функции: Да
• Точки перегибов графика функции: перегибы: интервалы выпуклости, вогнутости (впуклости): Да
• Вертикальные асимптоты : Да (это завязано с областью определения функции, на точки, где знаменатель функции обращается в нуль)
• Горизонтальные асимптоты графика функции: Да
• Наклонные асимптоты графика функции: Да
• Четность и нечетность функции: Да
• Минимум и максимум функции: Да

Правила ввода выражений и функций

Выражения могут состоять из функций (обозначения даны в алфавитном порядке):

absolute(x)

Абсолютное значение x
(модуль x или |x|)

arccos(x)

Функция — арккосинус от x

arccosh(x)

Арккосинус гиперболический от x

arcsin(x)

Арксинус от x

arcsinh(x)

Арксинус гиперболический от x

arctg(x)

Функция — арктангенс от x

arctgh(x)

Арктангенс гиперболический от x

exp(x)

Функция — экспонента от x (что и e^x)

log(x) or ln(x)

Натуральный логарифм от x
(Чтобы получить log7(x), надо ввести log(x)/log(7) (или, например для log10(x)=log(x)/log(10))

sin(x)

Функция — Синус от x

cos(x)

Функция — Косинус от x

sinh(x)

Функция — Синус гиперболический от x

cosh(x)

Функция — Косинус гиперболический от x

sqrt(x)

Функция — квадратный корень из x

sqr(x) или x^2

Функция — Квадрат x

ctg(x)

Функция — Котангенс от x

arcctg(x)

Функция — Арккотангенс от x

arcctgh(x)

Функция — Гиперболический арккотангенс от x

tg(x)

Функция — Тангенс от x

tgh(x)

Функция — Тангенс гиперболический от x

cbrt(x)

Функция — кубический корень из x

gamma(x)

Гамма-функция

LambertW(x)

Функция Ламберта

x! или factorial(x)

Факториал от x

DiracDelta(x)

Дельта-функция Дирака

Heaviside(x)

Функция Хевисайда

Интегральные функции:

Si(x)

Интегральный синус от x

Ci(x)

Интегральный косинус от x

Shi(x)

Интегральный гиперболический синус от x

Chi(x)

Интегральный гиперболический косинус от x

В выражениях можно применять следующие операции:

Действительные числа

вводить в виде 7. 3

— возведение в степень

x + 7

— сложение

x — 6

— вычитание

15/7

— дробь

Другие функции:

asec(x)

Функция — арксеканс от x

acsc(x)

Функция — арккосеканс от x

sec(x)

Функция — секанс от x

csc(x)

Функция — косеканс от x

floor(x)

Функция — округление x в меньшую сторону (пример floor(4.5)==4.0)

ceiling(x)

Функция — округление x в большую сторону (пример ceiling(4.5)==5.0)

sign(x)

Функция — Знак x

erf(x)

Функция ошибок (или интеграл вероятности)

laplace(x)

Функция Лапласа

asech(x)

Функция — гиперболический арксеканс от x

csch(x)

Функция — гиперболический косеканс от x

sech(x)

Функция — гиперболический секанс от x

acsch(x)

Функция — гиперболический арккосеканс от x

Постоянные:

pi

Число «Пи», которое примерно равно ~3. 14159..

e

Число e — основание натурального логарифма, примерно равно ~2,7183..

i

Комплексная единица

oo

Символ бесконечности — знак для бесконечности

×

Где учитесь?

Для правильного составления решения, укажите:

(не выбрано)9 класс10 класс11 класс1-й курс2-й курс3-й курс4-й курсдругое

Четность и нечетность тригонометрических функций

• Главная
• Справочник
• Тригонометрия
• Четность и нечетность тригонометрических функций

• Синус
• Косинус
• Тангенс
• Котангенс

Четной называется функция, которая не меняет своего значения при изменении знака независимой переменной (график такой функции симметричен относительно оси ординат):

Нечетной называется функция, которая меняет свое значение при изменении знака независимой переменной (график такой функции симметричен относительно начала координат):

Индифферентной называется функция, которая не обладает симметрией.

Синус

— нечетная функция

Косинус

— четная функция

Тангенс

— нечетная функция

Котангенс

— нечетная функция

В вашем браузере отключен Javascript.
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!

Тригонометрия Математика Тригонометрия Формулы Теория 28897

Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!

• Значения тригонометрических функций

  Значения тригонометрических функций для основных углов: 0, 30, 45, 60, 90, 120, 180, 270 и 360 градусов

  Тригонометрия Математика Тригонометрия Формулы Теория

• Меры углов

  Для измерения углов используются градусы или радианы.

  Тригонометрия Математика Тригонометрия Формулы Теория

• Соотношения между тригонометрическими функциями

  Знак тригонометрической функции в левой части должен совпадать со знаком правой части.

  Тригонометрия Математика Тригонометрия Формулы Теория

• Периодичность тригонометрических функций

  Тригонометрические функции sin(x) и cos(x) являются периодическими, с наименьшим периодом равным 2*π. Тригонометрические функции tg(x) и ctg(x) являются периодическими, с наименьшим периодом равным π.

  Тригонометрия Математика Тригонометрия Формулы Теория

• Тригонометрические функции суммы и разности углов

  Тригонометрические функции суммы и разности углов

  Тригонометрия Математика Тригонометрия Формулы Геометрия Теория

• Тригонометрические функции двойного, половинного и тройного аргументов

  Тригонометрические функции двойного, половинного и тройного аргументов

  Тригонометрия Математика Тригонометрия Формулы Геометрия Теория

• Соотношения между обратными тригонометрическими функциями

  Тригонометрия Математика Тригонометрия Формулы Теория

• Свойства обратных тригонометрических функций

  Названия обратных тригонометрических функций образуются следующим образом: приставка «арк-» (от латинского arc — дуга) + соответствующие им названия тригонометрических функций.

  Тригонометрия Математика Тригонометрия Формулы Теория

• Конвертер текста в цифровой код

  Онлайн калькулятор преобразует символы в их цифровые коды.

  Работа с текстом Калькулятор Расчёт Конвертер Преобразовать Текст

• Таблица перевода сухопутных миль в километры (mi в км)

  1 сухопутная миля (США и Британия) = 1,60934 км

  Размеры и расстояния Теория Расстояния

• Калькулятор идеального веса

  Калькуляторы веса и калорий Калькулятор Расчёт

• Сложение и вычитание векторов

  Суммой двух векторов a и b называется третий вектор c, проведенный из начала a к концу b, если начало вектора b совпадает с концом вектора a. Разностью двух векторов a и b называется вектор c при условии: c = a − b, если c + b =a.

  Вектора Формулы Геометрия Алгебра Теория Обозначения

• Как перевести число из десятичной системы в двоичную

  Основы Расчёт Справочник Информатика Программирование

• Треугольник Паскаля

  Числа Калькулятор Расчёт Математика Формулы

• Латинский алфавит

  В «современном» латинском алфавите 26 букв.

  Литература 1 класс Литература Алфавит Азбука

• Солько весит ведро?

  Ведро́ — сосуд для хранения жидких и сыпучих материалов и транспортировки их на небольшие расстояния.

  Масса и вес Масса Теория Единицы измерения

Калькулятор четных и нечетных чисел

Узнать, является ли число четным или нечетным , очень просто. Вам просто нужно разделить на два, но если вы хотите сохранить его, наш калькулятор выдаст вам результат автоматически.

Его работа очень проста. Все, что вам нужно сделать, это ввести число, которое вы хотите узнать, является ли оно нечетным или четным , и нажать кнопку расчета, чтобы узнать результат.

Разделы статей

• Как узнать, четное число или нечетное?
• Ноль нечетный или четный?
• 1 четная или нечетная
• Когда функция четная или нечетная
• Нечетные числа от 1 до 1000

Как узнать, четное или нечетное число?

Чтобы узнать, четное или нечетное число, достаточно разделить его на два .

Если остаток от этого деления равен нулю, то есть деление точное, то вы имеете дело с четным числом. В противном случае это четное число.

Примеры:

• Число 4: 4/2 = 2, это четное число.
• Число 5: 5/2 = 2,5, это нечетное число.

Понятно, что выяснить, является число нечетным или четным, довольно легко, и большинство людей уже знают это, просто взглянув на последнюю цифру числа и без необходимости делать деление между двумя.

Еще один трюк , чтобы узнать, будет ли число нечетным или четным, заключается в следующем:

• Пара x Пара = Пара
• Нечетное х четное = четное
• Нечетное x Четное = Четное
• Нечетное x Нечетное = Четное

В зависимости от чисел, участвующих в умножении, мы получим четный результат, если присутствует любая из вышеперечисленных комбинаций. Во всех остальных случаях мы получим нечетный результат.

Ноль нечетный или четный?

Число ноль считается четным , потому что оно является целым числом, кратным числу 2, т. е. ноль, умноженный на два, равно нулю.

Из-за этого число ноль разделяет все свойства, приписываемые четным числам.

1 нечетная или четная

Еще одно частое сомнение заключается в том, является ли 1 нечетной или четной. Предвидим, что единица нечетная , но для проверки делим на 2 и видим, что деление не точное, следовательно, нечетное.

1 / 2 = 0,5

Если у вас есть сомнения по поводу какого-либо другого числа, вы можете сделать вышеуказанную проверку или воспользоваться нашим онлайн-калькулятором нечетных/четных чисел , чтобы узнать наверняка.

Когда функция четная или нечетная

Если вы выполняете упражнения с функциями, у вас также может возникнуть вопрос , когда функция четная или нечетная .

Представленная четная функция

Функция является четной, когда она удовлетворяет этим двум предпосылкам:

• f(x) = f(-x)
• x и -x принадлежат домену функции

Например, четные функции — это абсолютное значение, x ² cos(x). Рекомендуем нарисовать их самостоятельно на осях координат, чтобы проверить выполнение следующих условий. условия для того, чтобы функция была четной .

Когда вы это сделаете, вы увидите, что четные функции имеют симметрию относительно оси Y .

График нечетной функции

Функция является нечетной, если соответствует следующему:

• f(-x) = -f(x)

При представлении на осях координат

нечетные функции имеют обратную симметрию относительно начала координат и поэтому проходят через точку (0,0).

Типичными примерами нечетных функций являются x, x ³ , синус (x) или гиперболический синус.

Нечетные числа от 1 до 1000

В заключение мы оставляем вам таблицу со всеми нечетными числами от 1 до 1000 . Без сомнения, вам будет очень полезно его распечатать, чтобы дети могли узнать, когда число четное или нечетное.

60138 601380139 30138 839 30138 899

1	101	201	301	401	501	701	801	901
3	103	203	303	403	503	603	703	803	903
5	105	205	305	405	505	605	705	805	905
7	107	207	307	407	507	607	707	807	907
9	109	209	309	409	509	609	709	809	909
11	111	211	311	411	511	611	711	811	911
13	113	213	313	413	513	613	713		813	9
15	115	215	315	415	515	615	715	815	915
17	117	217	317	417	517	617	717	817	917
19	119	219	319	419	519	619	719	819	919
21	121	221	321	421	521	621	721	821	921
23	123	223	323	423	523	623	723	823	923
25	125	225	325	425	725	625	725	625	725	625	725	625	725	625	725	625	725	.
27	127	227	327	427	727	627	727	627	727	627	727	627	727	627	727	627	727	627	727	.
29	129	229	329	429	529	629	729	829	929
31	131	231	331	431	731	631	731	631	731	631	731	631	731	631	731	.
33	133	233	333	433	7339	633	73339	633	733339	633	733339	633	733339	633	733339	633	733	633	733	.
35	135	235	335	435	535	635	735	835	935
37	137	237	337	437	537	637	737	837	937
39	139	239	339	439	539	9139 39 391	939
41	141	241	341	441	741	641	741	641	741	641	741	641	741	641	741	641	741	641	741	.
43	143	243	343	443	543	643	743	843	943
45	145	245	345	445	545	645	745	845	945
47	147	247	347	447	747	647	747	647	747	647	747	647	747	647	747	647	747	647	747	.
49	149	249	349	449	749	649	749	649	749	649	749	649	749	649	749	.
51	151	251	351	451	551	651	751	851	951
53	153	253	353	453	753	653	753	653	753	653	753	653	753	653	753	653	753	653	753	.
55	155	255	355	455	555	655	755	855	955
57	157	257	357	457	757	657	757	657	757	657	757	657	757	657	757	657	757	.
59	159	259	359	459	559	659	759	859	959
61	161	261	361	461	561	661	761	861	961
63	163	263	363	463	563	663	763	863	963
65	165	265	365	465	565	665	765	865	965
67	167	267	367	467	567	667	767	867	967
69	169	269	369	469	569	669	769	869	969
71	171	271	371	471	771	671	771	671	771	671	771	671	771	671	771	671	771	.
73	173	273	373	473	573	673	773	893 9013
75	175	275	375	475	575	675	775	875	975
77	177	277	377	477	577	677	77777799999999999999999999999999999999999999999999999999979Н.	977
79	179	279	379	479	579	679	779	879	979
81	181	281	381	481	781	681	781	681	781	681	781	681	781	681	781	681	781	.
83	183	283	383	483	583	683	783	883	983
85	185	285	385	485	585	685	785	885	985
87	187	287	387	487	587	687	787	887	987
89	189	289	389	489	589	689	789	889	989
91	191	291	391	491	591	691	791	891	991
93	193	293	393	493	593	693	793	893	993
95	195	295	395	495	595	695	795	895	995
97	197	297	397	497	597	697	797	897	997
99	199	299	399	499	599	699 391	999

Nacho

Ingeniero de Telecomunicaciones dedicado al mundo de Internet. En Esta веб-те Ayudo hacer cálculos у преобразования sencillas дие кон-эль-Пасо-де-лос-Años се-нос-ха olvidado Cómo себе Hace. Si tienes dudas, déjame un commentario y te ayudaré. Si quieres mejorar tu proyecto online o necesitas asesoramiento, напишите мне сообщение.

• Градусы в радианы
• Апофема
• Калькулятор антилогарифмов
• Division calculator
• Exponent calculator
• Exponential Function Calculator
• Logarithm Calculator
• Neperian logarithm calculator
• Prime Number Calculator
• Odd or even calculator
• Exponent calculator
• Cube root calculator
• Calculator for n-th root числа
• Калькулятор квадратных уравнений
• Онлайн-калькулятор факториала
• Калькулятор гипотенузы
• Калькулятор наибольшего общего делителя
• Калькулятор наименьшего общего кратного
• Калькулятор умножения
• Онлайн-калькулятор

Четные и нечетные функции: определение, проверка, интегрирование

Определения вычислений >

Содержание:

• Что такое четные и нечетные функции?
• Свойства нечетных и четных функций
• Проверка четных и нечетных функций
• Интеграция четных и нечетных функций

Четные и нечетные функции имеют особые симметрии относительно начала координат или оси Y.

• Функция четная, если она симметрична относительно вертикальной оси y; если это так, f (-x) = f (x) для каждого x в области.
• Функция нечетна, если она симметрична относительно начала координат. В этом случае f(-x) = -f(x) для каждого x в области.

Примеры четных и нечетных функций

Парабола f(x) = x ² равна пример четной функции . Как вы можете видеть на изображении ниже, он симметричен относительно вертикальной оси Y.

Функция f(x) = x ³ , с другой стороны, является примером нечетной функции . Он симметричен относительно начала координат.

Поскольку определения четного и нечетного не являются взаимоисключающими, можно иметь функцию, которая одновременно является четной и нечетной. Для такой функции истинны как f(-x) = f(x), так и f(-x)=-f(x). Подставляя эти уравнения друг в друга, мы находим, что для этих функций f (x) = -f (x). Есть только один способ, который может быть верным: если f(x) = 0.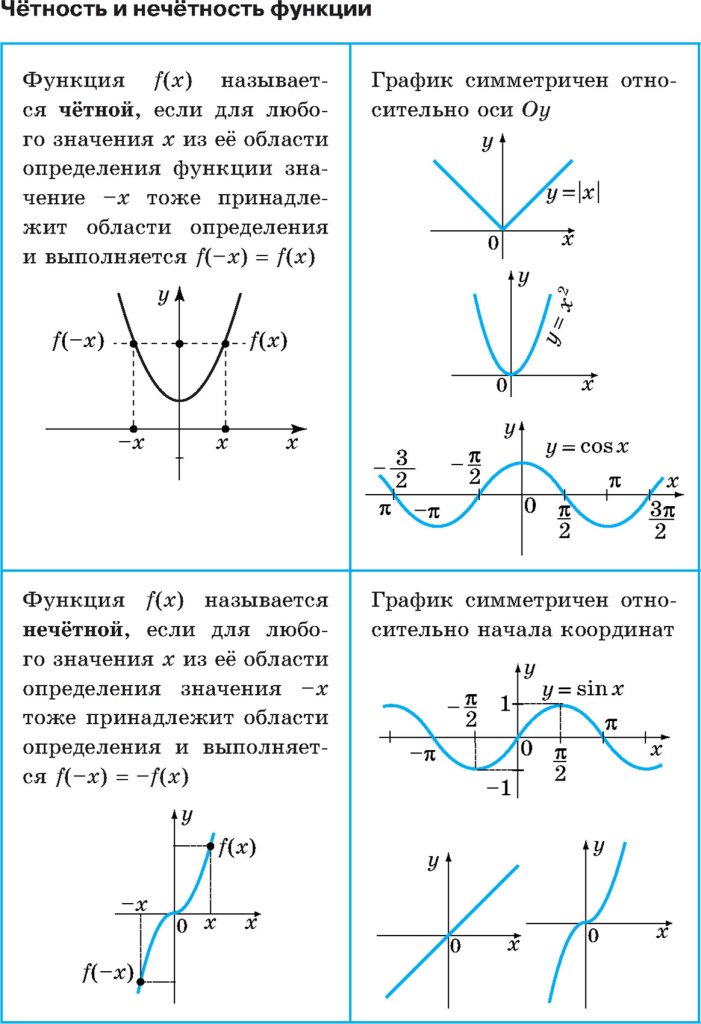 Таким образом, функция f(x) = 0 — единственная функция, которая одновременно является четной и нечетной.

Вот некоторые основные свойства нечетных и четных функций, которые стоит запомнить:

• Сумма двух нечетных функций нечетна, а сумма двух четных функций четна (обратите внимание, что это , а не то же самое, что и правило для четных и нечетных целых чисел)
• Сумма четной и нечетной функций не является ни четной, ни нечетной, если только одна из них или обе не равны нулю.
• Разность двух четных функций четна; точно так же разность двух нечетных функций нечетна.
• Произведение двух четных функций является еще одной четной функцией, и произведение двух нечетных функций также является четной функцией.
• Произведение четной функции на нечетную является нечетной функцией.

Этот простой тест показывает:

Функция y – f(x) равна четному , если f(-x) = f(x)
Функция y – f(x) равна нечетному , если f(-x) = f(x)

Пример вопроса №1: Является ли функция f(x) = x ³ – x нечетной или четной?

Решение:
Шаг 1: Замените любой «x» в функции на «-x»:
f(-x) = (-x) ³ – (-x)

Шаг 2: Решите с помощью алгебры. Цель состоит в том, чтобы получить функцию в форме, которая является либо исходной функцией, x ³ – x, либо ее отрицательной -(x ³ – x),

• f(-x) = (-x ) ³ – (-х) =
• = -х ³ + х

Результат, -x ³ + x, является отрицательным значением функции, поэтому эта функция нечетная.

Пример вопроса № 2: Является ли функция f(x) = 2 + cos(x) нечетной или четной?

Решение:
Шаг 1: Замените любой «x» в функции на «-x»:
f(-x) = 2 + cos(-x)

Шаг 2: Решите с помощью алгебры. Цель состоит в том, чтобы получить функцию в форме, которая является либо исходной функцией, x ³ – x или его минус -(x ³ – x),

• f(-x) = 2 + cos(x)*

Результат: 2 + cos(x) — исходная функция, значит, это четная функция.
Одно из тригонометрических тождеств для отрицаний утверждает, что -cos(x) = cos(x).

Теорема «Интегрирование четных и нечетных функций» — это способ нахождения интегралов для нечетных и четных функций. Это метод, облегчающий нахождение некоторых сложных определенных интегралов. Чтобы использовать его, вы должны вычислять функцию на интервале, который либо симметричен относительно начала координат, либо симметричен относительно оси Y [1].

Чтобы использовать эту теорему для упрощения нахождения определенного интеграла:

1. Ваш закрытый интервал должен быть в форме [-a, a]. Другими словами, ваш интервал должен иметь такое же число «а», как [-3, 3] или [-π, π].
2. У вас должна быть четная или нечетная функция. Если вы не уверены, используйте тест на четные и нечетные функции для проверки, прежде чем продолжить.

Интегрирование четных и нечетных функций: четный пример

1. Четные функции Правило:

Пример вопроса: Найдите следующий интеграл:

Мы можем умножить выделенную площадь на 2, чтобы получить площадь всей области, потому что функция симметрична относительно оси Y.
Шаг 1: Перепишите интеграл, чтобы покрыть положительную половину области (показанной на изображении выше). В этом примере вместо интегрирования от -1 до 1 мы интегрируем от 0 до 1:

Шаг 2: Решите интеграл (использовал калькулятор Symbolab):
Решая интеграл, получаем 8/7 &приблизительно; 1.14285.

Шаг 3: Умножьте решение из шага 2 на 2:
8/7 * 2 = 16/7 &приблизительно; 2.28571.

Вот и все!

2. Нечетные функции Пример определенного интеграла

Это простейший определенный интеграл, который вы когда-либо вычисляли (на самом деле, вам даже не нужно выполнять никаких вычислений… читайте дальше!).
Формула:

Эта часть теоремы проще, чем для четных функций. В нем просто говорится, что , если ваша функция симметрична относительно начала координат для интервала [-a, a], определенный интеграл будет равен нулю.
График нечетной функции. Две синие области идентичны по площади, но противоположны по знаку, поэтому компенсируют друг друга,

Ссылки

Набор академических навыков Университета Ньюкасла. Нечетные и четные функции. Получено с https://internal.ncl.ac.uk/ask/numeracy-maths-statistics/core-mathematics/pure-maths/functions/odd-and-even-functions.html 10 августа 2019 г.
Смит, Кен В. Элементарные функции. Часть 1: Лекция 1.4a, Симметрии функций. Получено с https://www.shsu.edu/~kws006/Precalculus/1.4_Function_Symmetries_files/1.4%20FunctionSymmetries%20slides%204to1.pdf 10 августа 2019 г.
Сиктар, Джошуа. Алгебраический анализ функций: четные и нечетные функции. Получено с https://opencurriculum.org/5507/even-and-odd-functions/ 10 августа 2019 г.
Maplesoft. Основные функции и отношения: математические приложения. Четные и нечетные функции. Онлайн-справка Maplesoft. Получено с https://www.maplesoft.com/support/help/Maple/view.aspx?path=MathApps%2FEvenAndOddFunctions 10 августа 2019 г.