Приведение к каноническому виду уравнения: Приведение кривой второго порядка к каноническому виду онлайн

Приведение уравнения второго порядка к каноническому виду

В главе «Поверхности второго порядка», где рассматривались поверхности второго порядка, было выписано их общее уравнение (13.1), а дальше для каждой поверхности использовалась своя прямоугольная декартова система координат, в которой уравнение поверхности имело канонический вид. В этом разделе мы выясним, как по общему уравнению найти такую систему координат. Результаты этого раздела используются и для приведения общего уравнения кривой второго порядка к каноническому виду. Достаточно будет во всех рассуждениях отбросить третью координату.

Пусть в пространстве задана прямоугольная декартова система координат . Рассмотрим общее уравнение поверхности второго порядка, коэффициенты в котором обозначены специальным образом

(19.7)

где  — числа, причем хотя бы одно из чисел отлично от нуля.

Выделим квадратичную часть выражения, стоящего в уравнении слева,

Такое выражение называется квадратичной формой от трех переменных. Составим матрицу

Эта матрица называется матрицей квадратичной формы . Она является симметричной, то есть , или, другими словами, . Следует обратить внимание на то, как эта матрица составлена. На диагонали у нее стоят коэффициенты при квадратах переменных, а в остальных местах — половины коэффициентов при произведениях переменных.

Исходная система координат является прямоугольной, поэтому скалярное произведение векторов с координатными столбцами , задается формулой . Сформулируем две теоремы, позволяющие пользоваться приведенным ниже алгоритмом.

        Теорема 19.4   Если матрица  — симметричная, то ее собственные числа являются вещественными числами и существует ортонормированный базис из собственных векторов.     

Пусть — матрица квадратичной формы . По сформулированной теореме у нее существует ортонормированный базис из собственных векторов. Обозначим их , , , и пусть эти векторы имеют координаты

Базис i, j, k назовем старым, а базис  — новым. Тогда матрица перехода 19.1.4.а будет иметь вид

Выберем новую систему координат так, что начало координат не изменяется, а новые базисные векторы , , задают направления новых координатных осей , , (рис. 19.8).

Рис.19.8.Система координат

Тогда координаты точки являются координатами ее радиус-вектора и, следовательно, при замене базиса меняются по формуле (18.1)

(19.8)

        Теорема 19.5   Пусть собственные векторы , , матрицы квадратичной формы , образующие ортонормированный базис, соответствуют собственным числам , , . Тогда в системе координат квадратичная форма принимает вид

    

Если мы из равенства (19.8) выпишем выражение , , через новые переменные , , и подставим в уравнение (19.7), то обнаружим, что квадратичная его часть и линейная часть преобразуются независимо друг от друга. В результате уравнение в системе координат имеет вид

(19.9)

Хотя бы одно из чисел , , отлично от нуля, иначе матрица была бы нулевой.

Рассмотрим три случая.

1. Пусть все собственные числа , , отличны от нуля. В уравнении (19.9) выделим полные квадраты

Выполним параллельный перенос системы координат , взяв за новое начало системы координат точку (см. формулы (13.21)). Тогда в новой системе координат уравнение запишется в виде

Здесь возможны следующие варианты.

1. Пусть . Перенесем в правую часть и поделим обе части на , получим

1. Если числа , , отрицательны, то ни одна точка пространства не удовлетворяет этому уравнению. Говорят, что оно определяет мнимый эллипсоид.

2. Если числа , , положительны, то уравнение является каноническим уравнением эллипсоида.

3. Если одно из чисел , , отрицательно, а остальные положительны, то (после переименования осей) получим каноническое уравнение однополостного гиперболоида.

4. Если одно из чисел , , положительно, остальные отрицательны, то (после переименования осей) получим каноническое уравнение двуполостного гиперболоида.

1. Пусть .

   1. Если все числа , , положительны, то только начало координат удовлетворяет этому уравнению. Поверхность выродилась в точку.

   2. Если одно из чисел , , отрицательно, а два положительны, то (после переименования осей) получим каноническое уравнение конуса.

Если же два числа отрицательны или все три отрицательны, то, умножив обе части уравнения на , получим случай 2 или случай 1.

2. Пусть одно из чисел , , равно нулю, а два других отличны от нуля. Допустим, что . Тогда в уравнении (19.9) выделим полные квадраты по переменным ,

1. Пусть . Преобразуем уравнение к виду

Поделим обе части уравнения на и выполним параллельный перенос осей координат, взяв за новое начало координат точку . Получим уравнение

1. Если числа и положительны, то это — каноническое уравнение эллиптического параболоида.

2. Если , , получим каноническое уравнение гиперболического параболоида.

Если числа и отрицательны или , , то сменим направление у оси на противоположное и получим либо случай 1, либо случай 2.

2. Пусть . Тогда поверхность является цилиндрической, образующие которой параллельны оси , а направляющей служит кривая на плоскости с уравнением

Анализ поверхностей с таким уравнением предоставляем читателю.

3. Пусть только одно из чисел , , отлично от нуля. Допустим, что . Тогда в уравнении (19.9) выделим полный квадрат по переменному

1. Пусть хотя бы одно из чисел , отлично от нуля. Тогда на плоскости возьмем две перпендикулярные прямые и . Возьмем новую систему координат, у которой начало будет в точке , ось направлена по оси , ось направлена вдоль второй прямой, а ось направлена вдоль первой прямой.

   Тогда уравнение примет вид

Это — уравнение цилиндрической поверхности, образующие которой параллельны оси , а направляющей служит кривая на плоскости с уравнением

Анализ возможных поверхностей оставляем читателю.

2. Пусть . Тогда уравнение принимает вид

1. Если число справа положительно, то уравнение определяет две плоскости

2. Если число справа равно нулю, то уравнение определяет одну плоскость

3. Если число справа отрицательно, то ни одна точка пространства уравнению не удовлетворяет.

Итак, получен алгоритм, позволяющий установить, какая поверхность задается уравнением второго порядка и каково ее положение в пространстве.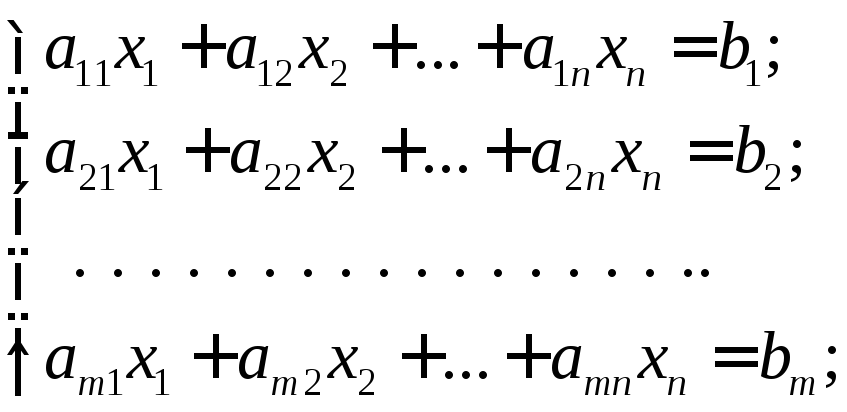

        Пример 19.11   Приведите уравнение поверхности

к каноническому виду.

Решение. Квадратичная форма имеет вид

Выписываем ее матрицу

Находим ее собственные числа. Для этого запишем характеристическое уравнение

После вычисления определителя получим

Подбором находим один корень . Преобразуем уравнение, выделяя множитель

или

откуда

Находим два других корня характеристического уравнения и .

Находим собственные векторы. Для собственного числа для координат собственного вектора получим систему уравнений

Решая ее находим, что фундаментальная система решений содержит только одно решение, и в качестве собственного вектора можно взять . Для собственного числа для координат собственного вектора получим систему уравнений

Отсюда находим собственный вектор .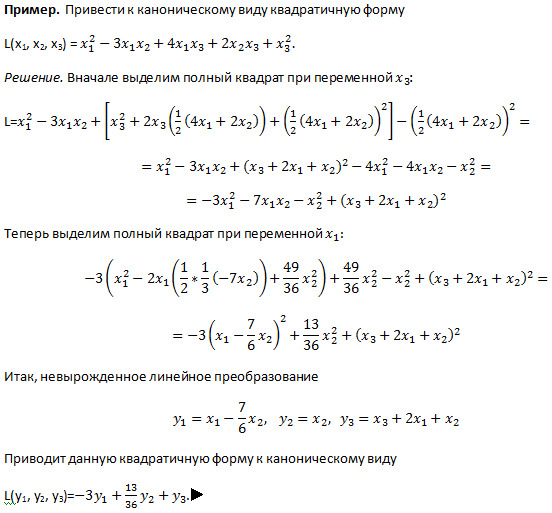 Для собственного числа для координат собственного вектора получим систему уравнений

Отсюда находим собственный вектор .

Легко проверить, что , то есть собственные векторы попарно ортогональны. Их длины равны соответственно , , . Поэтому векторы нового ортонормированного базиса будут иметь координаты

Матрица перехода имеет вид

Старые координаты связаны с новыми уравнением , то есть

(19.10)

Подставим эти выражения в исходное уравнение. Квадратичная форма примет вид, в котором произведения переменных будут отсутствовать, а коэффициентами при квадратах будут служить собственные числа

Приводим подобные члены

Выделим полные квадраты

или

Выполняем параллельный перенос осей координат

Новое начало системы координат имеет координаты

В исходной системе координат точка в соответствии с формулами (19. 10) имеет координаты

Рис.19.9.Система координат

В новой системе координат (рис. 19.9) уравнение принимает канонический вид

Это уравнение является каноническим уравнением однополостного гиперболоида. Его центр находится в точке , две вещественные оси параллельны векторам , , вещественные полуоси равны , . Мнимая ось параллельна вектору , мнимая полуось равна . Изображение гиперболоида приведено на рисунке 19.10.

Рис.19.10.Изображение гиперболоида

Приведение уравнений линий и поверхностей второго порядка к каноническому виду

Математика \ Аналитическая геометрия и линейная алгебра

Страницы работы

11 страниц (Word-файл)

Посмотреть все страницы

Скачать файл

Содержание работы

§. 5. Приведение уравнений линий и поверхностей

второго порядка к каноническому виду

Известно, что для любой квадратичной формы на конечном действительном евклидовом пространстве в этом пространстве существует ортонормированный базис, в котором рассматриваемая квадратичная форма имеет канонический вид. Используя этот факт, любую линию или поверхность второго порядка можно привести к каноническому виду по следующему плану.

1.  Для квадратичной части уравнения (т. е. квадратичной формы) находим канонический вид и ортогональное преобразование переменных, приводящее квадратичную форму к этому каноническому виду.

2.  Подставляем выражение старых переменных через новые в исходное уравнение. При этом квадратичная часть переходит в известный нам канонический вид, в котором коэффициенты при квадратах совпадают с собственными значениями ее матрицы, свободный член не меняется, линейная часть преобразуется непосредственно.

3.  Получили уравнение, не содержащее произведений переменных. С помощью преобразования параллельного переноса избавляемся от лишних слагаемых первых степеней и тем самым окончательно приводим уравнение к каноническому виду.

Если линия или поверхность второго порядка имеет центр симметрии, то решение задачи можно существенно упростить, поменяв местами 1-й и третий пункты, а второй тогда совсем исчезает.

Для того чтобы точка  была центром симметрии поверхности второго порядка , необходимо и достаточно, чтобы координаты этой точки удовлетворяли системе линейных уравнений

                                          (5. 3)

Если с помощью параллельного переноса поместить начало координат в центр симметрии поверхности второго порядка, то при этом: квадратичная часть ее уравнения не изменится; слагаемые первой степени пропадут; свободный член нового уравнения можно найти по формуле

.                                      (5. 4)

Аналогичные утверждения справедливы и для линий второго порядка (подробно обоснование см., например, в []).

Пример 1. Определить вид линии второго порядка, приведя ее уравнение к каноническому виду, и нарисовать эту линию, если ее уравнение имеет вид

.                              (5.5)

►В первую очередь проверим, имеет ли эта линия центр симметрии. Составляем систему линейных уравнений (5.3)

из которой находим: . Поместим с помощью параллельного переноса начало координат в точку  (если в задаче используются несколько систем координат, то обязательно надо указывать, в какой именно из них вы даете координаты точки). По формуле (5.4) (подставляем координаты  в левую часть (5.5)) находим . После преобразования параллельного переноса уравнение линии примет вид .

Теперь приведем к каноническому виду квадратичную часть уравнения  (т. е. квадратичную форму) с помощью ортогонального преобразования переменных. Для этого записываем матрицу этой квадратичной формы и находим ее собственные значения:

,   ,   .

Для нахождения первого собственного вектора решаем систему линейных уравнений с матрицей  при : , . Чтобы найти второй собственный вектор нет необходимости решать вторую систему. Достаточно вспомнить, что он ортогонален вектору  в силу симметричности матрицы А и что его координаты можно получить, как и в аналитической геометрии, переставив местами координаты вектора  и в одной из них поменяв знак. Итак, . Применим ортогональное преобразование, в результате которого оси новой системы координат будут направлены по собственным векторам. После этого уравнение примет вид (коэффициенты при квадратах совпадают с найденными собственными значениями) , или , которое задает гиперболу с полуосями 1 и 3 и осью  в качестве действительной.

Приступаем к рисованию. На одном рисунке изображаем и старую систему координат, и новую. Намечаем новое начало координат – точку . От этой точки откладываем собственные векторы  и , которые задают направление новых осей. В полученной системе координат рисуем полученную гиперболу (рис.5.1). ◄

Замечания. 1. При таком способе решения нет необходимости выписывать ни преобразование параллельного переноса, ни ортогональное преобразование, т. к. мы и без непосредственной подстановки их в уравнение знаем, как оно преобразуется. Нет необходимости даже собственные векторы нормировать: ортогональное преобразование не нужно, а векторы с целочисленными координатами легче рисовать. Именно поэтому задачу приведения линии второго порядка к каноническому виду в том случае, когда эта линия имеет центр симметрии, сложной не назовешь.

Похожие материалы

Информация о работе

Скачать файл

уравнений в частных производных — Приведение квадратичной формы к канонической форме

Задавать вопрос

спросил 6 лет, 11 месяцев назад

Изменено 4 года, 6 месяцев назад

Просмотрено 879 раз

92\\\\ &\xi = x-\frac{1}{2}y\\ &\эта = у \end{align}

Теперь я могу определить функцию $u$ следующим образом:

$$ и (х, у) = и (\ х (х, у), \ эта (х, у)) $$

Теперь мне нужно также вывести $u_x$ и $u_y$:

\begin{align} u_x &= u_\xi \cdot \xi_x + u_\eta \cdot \eta_x = u_\xi\\ u_y &= u_\xi \cdot \xi_y + u_\eta \cdot \eta_y = -\frac{1}{2}u_\xi + u_\eta \end{align}

Итак, моя каноническая форма выглядит так: \начать{выравнивать} q &= u_{\xi\xi} — \frac{9}{4}u_{\eta\eta} + u_\xi — \frac{1}{2}u_\xi + u_\eta\\ &= \underline{\underline{u_{\xi\xi} — \frac{9{4}u_{\eta\eta} + \frac{1}{2}u_\xi + u_\eta}} \end{align}

Правильно ли мое решение или это ошибка?

• дифференциальные-уравнения в частных производных
• доказательство-проверка
• квадратичные формы

$\endgroup$

$\begingroup$

Приводим УЧП второго порядка с постоянными коэффициентами к каноническому виду

$ u_{xx} — u_{xy} — 2 u_{yy} + u_x + u_y = 0$

Квадратичная форма:

92$

Получаем преобразование

$\xi=x,\quad\eta=\frac{x}{3}+\frac{2y}{3}$

и каноническую форму УЧП:

$u_ {\xi\xi}-u_{\eta\eta}+u_\xi+u_\eta=0$

см. :

Владимиров В.С. Сборник задач на уравнения математической физики, Springer, 1986

В нашем случае $$B=\begin{pmatrix}1 & \frac{1}{3}\\ 0 & \frac{2}{3}\end{pmatrix}$$

$\endgroup$

$\begingroup$ 92$$ где v = (х, у) Надеюсь поможет

$\endgroup$

1

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

Приведение к каноническому виду полиномиальной матрицы третьего порядка с одним характеристическим корнем с помощью полускалярно-эквивалентных преобразований корня относительно преобразования полускалярной эквивалентности устанавливаются специальные треугольные формы. Доказаны теоремы их единственности. Это дает основание рассматривать такие канонические формы.

1. Введение

В [1] доказано, что матрица полного ранга с помощью преобразования: где и может быть приведена к нижнему треугольному виду с инвариантными множителями на главной диагонали. Поддиагональные элементы в матрице такого вида определяются неоднозначно. Матрицы, связанные преобразованием (1), называются полускалярно эквивалентными [1]. В [2] указанная треугольная форма для полиномиальных матриц с одним характеристическим корнем несколько упрощена. Полученная матрица упрощенной треугольной формы называется уменьшенный . В [2] установлены инварианты редуцированной матрицы. В частности, доказана инвариантность расположения нулевых поддиагональных элементов. В [3] редуцированная матрица, если под ее главной диагональю находятся нулевые элементы, с помощью преобразований вида (1) (т. е. с помощью полускалярно эквивалентных преобразований ) приводится к таким матрицам, которые однозначно определено. Это дает основание считать полученные матрицы каноническими для выбранного класса матриц. В этой статье вводятся канонические формы редуцированных матриц со всеми ненулевыми поддиагональными элементами.

2. Предыдущая информация

Вот некоторые определения и обозначения, которые будут использоваться в этой статье и известны из [2, 3]. Это относится к определениям младшей степени , младшего члена, младшего коэффициента , -мономиала, -коэффициента полинома и других. Например, моном и его степень – соответственно младший член и младшая степень многочлена , а – младший коэффициент этого многочлена. Мономиал и его коэффициент являются, соответственно, -мономом и -коэффициентом многочлена .

Пусть все корни характеристического полинома (= характеристические корни) матрицы равны между собой; т. е. матрица имеет только один (без учета кратности) характеристический корень. Без ограничения общности считаем, что единственный характеристический корень равен нулю, а первый инвариантный множитель матрицы равен единице. При таких предположениях в [2] доказано, что с помощью полускалярно эквивалентных преобразований матрица приводится к матрице вида, удовлетворяющего следующим условиям: (1), , , .(2), , если .( 3) и -мономиальный в отсутствует, если .(4)Младшие коэффициенты в и являются единицами.

Матрица вида (2) с условиями (1)–(4) в [2] называется приведенной матрицей. Далее рассмотрим ситуацию, когда два последних инвариантных множителя матрицы не совпадают, т. е. . Случай рассмотрен в [4]. Обозначение означает, что матрицы и полускалярно эквивалентны. Следует отметить, что задача классификации относительно полускалярной эквивалентности матриц второго порядка решена в статье [5]. Таким образом, в данной статье обсуждаются другие ситуации, отличные от [4, 5]. В [2] доказано, что в случае можно выбрать левую матрицу преобразования при переходе от к редуцированной матрице нижнетреугольной формы. Затем мы применим к матрице полускалярно эквивалентные преобразования, чтобы получить редуцированную матрицу вида (3) с предопределенными свойствами. Покажем, что по заданной приведенной матрице вида (2) и матрице можно найти матрицу и правую матрицу преобразования так, что . Методом неопределенных коэффициентов для заданных элементов и матриц и соответственно с конгруэнтностью находим , . Обозначим такие элементы через :

Здесь . Формируем матрицу и рассматриваем сравнение с неизвестным. Поскольку свободный член матричного многочлена является единичной матрицей, мы можем использовать метод неопределенных коэффициентов, чтобы решить это сравнение и найти , . Мы можем это проверить. В дополнение к сказанному обозначим также

. По указанному выше , а из сравнений (5) и (7) построим и матрицу вида (3) соответственно. Мы можем убедиться в равенстве. Это означает, что оно обратимо и его обращенная матрица вместе с матрицей сводится к . Если матрица (4) при переходе от к имеет один из следующих видов: то будем говорить, что к матрице применяются преобразования типа I, преобразования типа II или преобразования типа III соответственно. Мы будем использовать следующие обозначения для матриц вида (2) и вида (3):

3. Основные результаты

Теорема 1. Пусть в редуцированной матрице вида (2) имеем , , , , , , , . Тогда матрица полускалярно эквивалентна редуцированной матрице вида (3), элементы которой удовлетворяют одному из следующих условий: (1) -моном отсутствует в , если и . (2) — и -мономы отсутствуют при и . (3) Если и , то в первом из полиномов , , удовлетворяющем условию , -моном отсутствует, а в первом из этих многочленов, удовлетворяющем условию , -моном отсутствует.

Матрица определена однозначно.

Доказательство. Существование. (1)Если , то искомая матрица. В противном случае через и обозначим соответственно нижний коэффициент и -коэффициент полинома и применим к преобразованиям типа III. В левой матрице преобразования (см. (9)) положим . Элементы , , полученной таким образом матрицы удовлетворяют сравнению:   Во-первых, из (11) и (12) получаем, что нижние члены в совпадают с нижними членами в соответственно. Далее отметим, что младшие члены в и совпадают, младшие степени двух последних сложений в левой части (13) превышают и выполняется неравенство. Поэтому, сравнивая -коэффициенты в обеих частях (13), получаем нуль для такого -коэффициента в . Итак, искомая матрица имеется. (2)Если в матрице есть , то все доказано — эта матрица искомая. В противном случае применим к нему преобразование, упомянутое в разделе 1. Чтобы показать отсутствие -монома в , нужно учесть, что (см. (11)). Поэтому в (13) имеем . Остальные рассуждения те же, что и в п. 1. Чтобы не вводить новых обозначений, далее будем считать, что в элементе исходной матрицы нет -монома. Если , то все доказано — матрица искомая. В противном случае к применяем преобразование типа II. В то же время в левой матрице преобразования (см. (9)), положим , где и – соответственно нижний коэффициент и -коэффициент полинома . Полученные таким образом элементы редуцированной матрицы удовлетворяют соотношению ). Запишем (16) следующим образом: Из (14) имеем . Поскольку и , то, сравнивая -коэффициенты в обеих частях (17), находим, что не содержит -моном. А так как , то в , как и в , нет -монома. (3) Предположим, что в матрице выполнены условия и . (1) Если и , то все доказано — матрица искомая. (2) Пусть и . Так как , то (как и ) инвариантно (см. предложение 6 [2]). Применим преобразование, указанное в разделе 1. В результате получим матрицу вида (3). Его элементы удовлетворяют сравнениям (11)–(13). Так как , то из (11) имеем . Из (12) видно, что . Теперь мы можем представить (13) как Из последнего сравнения имеем . Следовательно, — редуцированная матрица. Если учесть , то, сравнивая -коэффициенты в оба момента времени (19), придем к выводу, что в , -монома нет. Если , то все доказано — матрица искомая. В противном случае делаем еще один шаг. Чтобы не вводить новых обозначений, будем считать, что элемент матрицы не содержит -моном. Применим к преобразованиям типа I. В левой матрице преобразования (см. (9)) положим , где и – соответственно нижний коэффициент и коэффициент полинома . Элементы , полученной матрицы удовлетворяют сравнению:  Из (20) имеем , а из (21) следует . Тогда из (22) получаем где мы можем получить . Сравнивая коэффициенты в обеих частях (23), заключаем, что в многочлене нет монома степени. В то же время в , как и в , нет -монома. (3) Теперь предположим, что в матрице имеем и . Применим к преобразованиям типа I. В левой матрице преобразования (см. (9)), положим , где и – соответственно нижний коэффициент многочлена и -коэффициент многочлена . В результате получаем матрицу вида (3), элементы которой удовлетворяют сравнениям (20)–(22). Из (20) имеем, что и -моном в отсутствует. Из (21), и из (22) имеем . Из (20)–(22) также следует, что нижние коэффициенты при и , совпадают. То есть это редуцированная матрица. Если , то все уже доказано. Тогда – искомая матрица. В противном случае, чтобы не вводить новых обозначений, будем считать -коэффициент в элементе матрицы нулевым. Обозначим через и соответственно нижний полиномиальный коэффициент полинома и -коэффициент полинома . Проведем над матрицей преобразование типа III. Для этого подставим в левую матрицу преобразования (см. (9)). Элементы полученной матрицы удовлетворяют сравнениям (11)–(13). Из (21) получаем, что , нижний коэффициент полинома равен , а его — и -коэффициенты равны нулю. Из (12) видно, что нижний коэффициент при , как и при , равен . Следовательно, матрица обладает необходимыми свойствами. (4) Пусть и . Можно считать, что -коэффициент в матрице равен нулю. Если это не так, то к применим преобразование типа I, описанное в разделе 3. Если , то к применим преобразование типа III, описанное в разделе 3. Тогда результирующая матрица будет нуль-коэффициентной и останется нулевой коэффициент полинома в позиции . Если , то от матрицы с помощью преобразований типа III, указанных в п. 1, переходим к избыточной матрице , в которой -мономиал полинома отсутствует. Тогда -фактор in также останется равным нулю. Это доказывает первую часть теоремы (существование).

3.1. Единственность матрицы в теореме 1

(1)Пусть для приводимых матриц вида (2) и (3) выполнено условие 1 теоремы и, кроме того, имеем . Тогда левая преобразующая матрица в равенстве может быть выбрана в виде (9) (см. следствие 1 и замечание 1 [2]), а элементы и , , этих матриц удовлетворяют сравнению Имеем . Если , то из (24) следует. В противном случае в (24) имеем т.к. -мономы в и отсутствуют. В любом случае .(2) Предположим, что редуцированные матрицы , форм (2) и (3) удовлетворяют условию 2 теорем и . Тогда в левой преобразующей матрице (4) при переходе от к имеем (см. следствие 1 и замечание 1 [2]) и элементы и матриц и удовлетворяем сравнениям: Из (25) можно записать Из (25) имеем . Легко видеть, что Если , то из (26) имеем ; отсюда следует . Так как , то из (26) следует, откуда . Из (25) с учетом получаем откуда . Итак, у нас есть . Если , то из (25) получаем . Если , то с учетом и из (25) и (26) имеем , , и . Поэтому совпадают. Если , то из (26) получаем . Значит, и в этом случае матрицы совпадают. (3) Предположим, что редуцированные матрицы вида (2) и (3) удовлетворяют условию 3 теорем и . Тогда для элементов этих матриц можно написать сравнения:

Если , то и из (28) получаем . Тогда (28) примет вид

Очевидно, . Если , то из (29) следует, поскольку .

Тогда из (28) получаем так как

Если , то из (29) следует . Если к тому же , то из (29) следует и все доказано. Если , то все равно из (28) и (29) имеем и соответственно.

Если , то из (28) получаем . Если дополнительно , ​​то из (28) также следует и все доказано. Если , то и снова из (28) переходим к (29). Отсюда следует, что если . А если , то сразу из (28) и (29) имеем и соответственно. Теорема доказана.

Предположим, что в редуцированных матрицах вида (2) и (3) имеем . Сохраним обозначения, данные в теореме:

Определим многочлены:

Из коэффициентов каждого из многочленов , и , составим соответственно столбцы , и высоты . На первое место в этих столбцах ставим -коэффициенты, а ниже в порядке возрастания степеней — остальные их коэффициенты до степеней включительно. Обозначим через , и , столбцы высоты , построенные из коэффициентов многочленов , и , соответственно. На первое место в каждом из этих столбцов мы ставим -коэффициенты. Ниже мы помещаем остальные их коэффициенты (включая нулевой) до степени . Аналогично из коэффициентов многочленов , , , и , составим столбцы , , , и высоты . Здесь мы также ставим на первое место -коэффициенты, а затем в порядке возрастания степеней ставим все остальные коэффициенты. На последних местах будут -коэффициенты. Для по сформированным столбцам построим матрицы следующего вида:

По полной аналогии для строим матрицы следующего вида:

Очевидно, что в этих матрицах каждая строка состоит из мономиальных коэффициентов одной и той же степени.

Теорема 2. Пусть в редуцированной матрице вида (2) имеем , , и , . Тогда , где в редуцированной матрице вида (3) все элементы отличны от нуля, полиномиальная не содержит -мономиальную, если , и полиномиальная не содержит -мономиальную, если .

Кроме того, выполняется одно из следующих условий: (1) В , — моном отсутствует, если и . (2) В , — и -мономы отсутствуют, если и . (3) В , — и — мономы отсутствуют, если и .(4) В первом столбце матрицы (35) коэффициентами полиномов являются нулевые элементы, соответствующие максимальной системе первых линейно независимых строк подматрицы , если и .

Матрица определена однозначно .

Доказательство. Существование. Позволять .
Применим преобразование типа II с левой матрицей преобразования вида (9). При этом положим , где — младший коэффициент и — -коэффициент в . Элементы , , полученной редуцированной матрицы удовлетворяют сравнениям (14)–(16). Запишем (16) в видегде . Сравнивая -коэффициенты в обеих частях последнего сравнения, имеем, что не содержит -моном. Предположим далее, что элемент матрицы не содержит -мономиала (если ).
Пусть . Обозначим через и соответственно младший и -коэффициенты полинома . Применим к преобразованиям типа I с левой матрицей преобразования вида (9), положив .
Элементы , , полученной приведенной матрицы удовлетворяют сравнениям (20)–(22) (с указанным здесь ). Из (21) и (22) получаем Если сравнить -коэффициенты в обеих частях последнего сравнения, то придем к выводу, что не содержит -моном: (1)Пусть в элементе матрицы нет монома степени , а в многочлене нет монома степени . Обозначим через и соответственно нижний коэффициент при и -коэффициент при . С помощью преобразования типа III переходим от к редуцированной матрице . В левой матрице преобразования (см. (9)) ставим . Элементы полученной матрицы удовлетворяют сравнениям (11)–(13) (с указанным здесь). Из (11) получаем, что в элементе отсутствует -моном. Запишем (13) в виде где . Так как , то, как видно из последнего сравнения, в , как и в , нет -монома. Также в , как и в , нет -мономиала. Это видно из сравнения, которое записывается на основании (12) и (13), поскольку . Это доказывает существование матрицы с условием (1), указанным в теореме. (2) Предположим, что условия , , выполнены в матрице , а -мономиал отсутствует в многочлене . Обозначим через и соответственно нижний коэффициент при и -коэффициент при . Сделаем надматричное преобразование типа II. Для этого подставим в левую матрицу преобразования (см. (9)). Получим редуцированную матрицу, элементы которой удовлетворяют сравнениям вида (14)–(16) (с указанными здесь). Учитывая, что нижние коэффициенты у и совпадают, то из (15) находим, что -моном в отсутствует. Из (15) и (16) имеем . Отсюда следует, что в , как и в , нет мономов степени . Далее рассмотрим отсутствие -монома в элементе матрицы . Обозначим через и соответственно нижний коэффициент при и -коэффициент при . Над матрицей проведем преобразование типа III. Здесь мы подставляем левую матрицу преобразования (см. (9)). Элементы полученной редуцированной матрицы удовлетворяют сравнениям вида (11)–(13) (с указанными здесь). Из (12) видно, что -мономиал отсутствует в . Также -коэффициент in останется нулевым, т.к. Как видно из (40), в , как и в , -моном отсутствует, так как . Существование искомой матрицы с условием (2) доказано. (3) Пусть для и в нет монома степени . На первом шаге применим к матричному преобразованию типа I с левой преобразующей матрицей (см. (9)), в котором , где и – соответственно нижний коэффициент при и -коэффициент при . В результате получаем редуцированную матрицу вида (3), элементы которой удовлетворяют условиям вида (20)–(22) (с выбранными здесь). Из (20) видно, что в -моном отсутствует. Из (20) и (22) можно записать как где . Из последнего сравнения видно, что -моном отсутствует как в . Пусть уже в не содержит -мономиал. Обозначим через и соответственно нижний коэффициент в и -коэффициент в и пусть . На втором шаге с помощью преобразования типа III с заданной слева преобразующей матрицей (см. (9)), перейдем от к некоторой редуцированной матрице вида (3). Для элементов матрицы выполняются условия (11)–(13) (при заданном здесь ). Из (11) следует, что в нет -монома. Кроме того, не содержит -мономиал. На основании (11) и (13) можно записать сравнение вида (41), в котором . Это показывает, что при , по сравнению с , нулевой коэффициент при -мономе сохраняется. Это доказывает существование для матрицы полускалярно эквивалентной приведенной матрицы с условием 3. (4) Предположим, что в приведенной матрице выполняются условия , , . Если в (33), то искомая матрица есть и все уже доказано. В противном случае на первом шаге фиксируем в матрице первую ненулевую строку и соответствующую строку в . Пусть состоит из -коэффициентов и является -й строкой в ​​. Найдем произвольное решение уравнения. Применим к нему полускалярно эквивалентное преобразование с левой преобразующей матрицей вида (4). При этом в положим , , и . Элементы , , полученной редуцированной матрицы вида (3) удовлетворяют сравнению: В зависимости от того, какой из матриц , , или (см. (34)) принадлежит строка, рассмотрим соответственно сравнение (43). Сравнивая -коэффициенты в обеих частях этого сравнения, заключаем, что -й элемент первого столбца матрицы (35) равен нулю.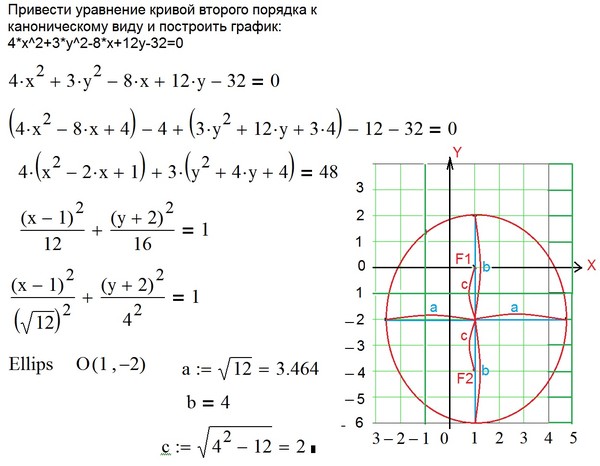 Кроме того, все строки в , предшествующие -й, совпадают с соответствующими строками матрицы .
Если , то все уже доказано. Матрица искомая. В противном случае считаем, что -й элемент первого столбца матрицы равен нулю. На втором шаге фиксируем в первой линейно независимую от строки , а также соответствующую ей строку в и степени мономов, коэффициенты которых образуют эти строки. Также пусть будет -я строка в .
Найдем некоторое решение уравнения. Применим к полускалярно эквивалентному преобразованию с левой преобразующей матрицей вида (4), полагая , , и . Получим редуцированную матрицу вида (3).
Снова, как и на предыдущем шаге, рассмотрим одно из сравнений (43) в зависимости от того, какая из матриц , , или (см. (34)) содержит строку . В обеих частях этого сравнения сравниваем коэффициенты при -мономах и заключаем, что -й элемент первого столбца матрицы (34) равен нулю. Также из этого и предыдущего сравнений получаем, что каждая строка, предшествующая -й в , совпадает с соответствующей строкой в ​​. Если , то все уже доказано. Тогда искомая матрица. В противном случае, чтобы не вводить новых обозначений, будем считать, что первый столбец матрицы имеет нулевой -й и -й элементы. В матрице фиксируем -ю строку, первую линейно независимую от , (). Пусть это будет линия. Ему соответствует . Также пусть будет показатель степени, соответствующий этим строкам. Находим (единственное) решение уравнения. Применим к полускалярно эквивалентному преобразованию с левой матрицей преобразования вида (4), полагая , , и . Получаем матрицу. Приведенные выше соображения показывают, что это искомая матрица.

3.2. Единственность матрицы в теореме 2

Предположим, что для редуцированных матриц вида (2) и (3) имеем . Предположим также, что элементы , этих матриц не содержат -мономов, если , а в многочленах , , нет -мономов, если . Покажем сначала, что матрица при переходе от к может быть выбрана в форме если или в форме если.

Действительно, элементы матриц , удовлетворяют сравнению

Если сравнить коэффициенты при мономерах степени в обеих частях этого сравнения, получим . Также из эквивалентности легко получить конгруэнтность

Если сравнить коэффициенты мономеров степени в обеих частях последнего сравнения, то придем к :(1) В случае , матрица перехода из в имеет вид (46) и (47) одновременно. Следовательно, у нас есть . Элементы в удовлетворяют (11). Отсюда получаем . По этой причине матрицы 1 и 2 совпадают. (2) Так как , то матрица перехода от к имеет вид (47), а элементы , в удовлетворяют (25). В , , нет — и -мономов, поэтому из (25) получаем . Итак, .(3)Если , то матрица перехода от к имеет вид (46). Элементы в удовлетворяют сравнению (28). Отсюда имеем , так как в , как и в , нет -и -мономов. Следовательно, в этом случае совпадают. (4) Предположим, что матрица удовлетворяет условию 4, т. е. в элементе первого столбца, соответствующего максимальной системе первых линейно независимых строк подматрицы, равны нулю. Предположим, что матрица также обладает тем же свойством и, кроме того, выполнено условие. Тогда элементы , , , этих матриц удовлетворяют сравнениям (43). Если в имеем , то

Поэтому, как видно из (43), , .

Если в , имеем , и – номер первой ненулевой строки в , то первые элементы первого столбца матрицы совпадают с соответствующими элементами матрицы ; более того, -е элементы равны нулю. Поэтому в первые строки совпадают с соответствующими строками матрицы . Кроме того, из сравнений (43) имеем Если следующая за строкой в ​​(или в ) линейно зависит от , то

Тогда из (43) получаем, что первые элементы в первом столбце матрицы совпадают с соответствующими элементами в . Если и линейно независимы, то (51) по-прежнему выполняется, так как в этом случае -е элементы в первых столбцах матриц и равны нулю. Тогда ая строка совпадает с соответствующей строкой матрицы . Мы думаем об этой строке так же, как это было сделано выше со строкой. Пусть — первая линейно независимая от строки и — ее номер в . Тогда эта строка совпадает с -той строкой в ​​, а первые элементы первого столбца в совпадают с соответствующими элементами в , причем th элементы равны нулю. Тогда из (43) имеем . Если -я строка в , то соответствующая -я строка в тоже . Если линейно зависит от системы , , то и -е элементы в первых столбцах матриц , совпадают. В противном случае эти элементы также совпадают, потому что они равны нулю. Продолжая наши рассуждения, покажем, что при , первые столбцы совпадают, или на некоторых шагах получим . В каждом случае, . Теорема доказана.

Пример 1. Матрицы , , и полускалярно эквивалентны. В этом случае – редуцированная и – каноническая матрица для .

4. Заключение

Матрицы , существование которых установлено в теоремах 1 и 2, можно считать каноническими в классе полускалярно эквивалентных матриц. Способ их построения следует из доказательства первых частей этих теорем. На этом завершается исследование полускалярной эквивалентности полиномиальных матриц третьего порядка с одним характеристическим корнем, начатое в предыдущих работах автора.

Результаты, полученные в данной статье, а также результаты цитируемых здесь работ применимы к изучению одновременного подобия наборов числовых матриц. В этом контексте следует отметить работы [6–9]. Эти результаты также полезны при решении матричных уравнений типа Сильвестра над кольцами многочленов. Такие уравнения часто возникают в прикладных задачах.

Доступность данных

Данные предыдущих исследований использовались для поддержки этого исследования. Они цитируются в соответствующих местах в тексте в качестве ссылок.

Конфликт интересов

Автор заявляет об отсутствии конфликта интересов.

Литература

1. Казимирский П. С., Петрычкович В. М. Об эквивалентности полиномиальных матриц // . Теоретические и прикладные проблемы алгебры и дифференциальных уравнений. . С. 61–66.

   Посмотреть по адресу:

   Google Scholar

2. Шаваровский Б. З. Приведенная треугольная форма полиномиальных матриц размера 3 на 3 с одним характеристическим корнем и ее инварианты, Математический журнал , том. 2018, ID статьи 3127984, 2018.

   Посмотреть по адресу:

   Google Scholar

3. Шаваровский Б. З. Каноническая форма редуцированной матрицы 3 на 3 с одним характеристическим корнем и с некоторыми нулевыми поддиагональными элементами. Математика , вып. 2019, ID статьи 7646132, 2019.

   Посмотреть по адресу:

   Google Scholar

4. Шаваровский Б.З. О некоторых «ручных» и «диких» аспектах проблемы полускалярной эквивалентности полиномиальных матриц, Математические заметки , том. 76, нет. 1-2, 2004.

   Посмотреть по адресу:

   Сайт издателя | Google Scholar. 2017, ID статьи 6701078, 2017.

   Посмотреть по адресу:

   Google Scholar

5. Ю. А. Дрозд, Прирученные и дикие матричные задачи , Springer, New York, NY, USA, 1980.

6. Белицкий Г., Бондаренко В. М., Липянский Р., Плахотник В. В., Сергейчук В. В. Проблемы классификации пар форм и локальных алгебр с нулевым радикалом куба дикие, Линейная алгебра и ее приложения , том. 402, pp. 135–142, 2005.

   Просмотр по адресу:

   Google Scholar

7. Футорный В., Хорн Р. А., Сергейчук В. В. Каноническая форма для неуничижительных матриц при унитарном подобии // Линейная алгебра. Его приложения , том. 435, нет. 4, стр. 830–841, 2011.

   Посмотреть по адресу:

   Сайт издателя | Google Scholar

8. С. Фридланд, «Одновременное сходство матриц», Успехи математики , том. 50, нет. 3, стр. 189–265, 1983.

   Посмотреть по адресу:

   Сайт издателя | Google Scholar

Copyright

Copyright © 2020 Б.