Калькулятор онлайн комплексные числа в показательной форме: Комплексные числа онлайн

Калькулятор комплексных чисел

Калькулятор комплексных чисел

Далее приводится более подробное описание возможностей версии 2.30d и предлагается к скачиванию 3 версии программы.

Принцип двух аргументов и результата

Если в обычном калькуляторе для проведения некоей операции с двумя числами (например, сложение или х в степени у) на дисплее в любой момент времени можно видеть только первое число, второе или результат, то в ComplexCalc видим все 3 одновременно. В верхней части окна вводим первое комплексное число либо в алгебраической, либо в показательной форме, в средней — второе, нажимаем на кнопку нужной алгебраической операции («+», «-«, «*», «/», «х^у» или корень у-ной степени от х) и в нижней части окна получаем результат. Первое комплексное число в терминологии программы при этом называется Аргумент 1, второе — Аргумент 2, а результат тат и носит название

Результат. Чтобы использовать Результат в дальнейших вычислениях его можно напрямик скопировать в Аргумент 1 и Аргумент 2 с помощью кнопок «Копировать в 1» и «Копировать в 2».

Если нужно получить некую операцию над одним комплексным числом (например cos, sin, ln, x²), достоточно поместить это число в Аргумент 1 или Аргумент 2, а затем нажать кнопку нужной операции справа от нашего числа. Требуемый ответ опять получим в поле Результат.

Работа с ячейками памяти

Производится посредством вызова окна «Чтение/запись в память», которое вызывается при каждом нажатии кнопок «В память / из памяти» или  «В память». В окне можно записывать в выбранные ячейки памяти загруженное в верхней части окна комплексное число, считывать комплексное число, хранящееся в одной из ячеек, переименовывать ячейки из названий типа «Переменная 12» в более осмысленные, заполнять ячейки памяти

«Страшным нулем», то есть обнулять хранящиеся в них значения при сбросе имени ячейки в «Переменная XX». Также здесь можно сохранить содержимое ячеек памяти во внутренний формат файла *.rcv (Record of Complex Values) или текстовый файл, загрузить из файла *.rcv или текстового файла сохраненное ранее содержимое ячеек или очистить содержимое памяти.

В качестве передаваемого из главного окна в окно «Чтение/запись в память» значения может выступать Аргумент 1, Аргумент 2 и Результат. Извлечь содержимое ячейки памяти можно только в Аргумент 1 или Аргумент 2. 2 кнопки «В память / из памяти» подразумевают работу с

Аргумент 1 или Аргумент 2 соответственно, а кнопка «В память» — с Результат, поэтому, если окно «Чтение/запись в память» вызывалось посредством нажатия кнопки «В память», то кнопки «Извлечь» будут неактивны.

Настройки программы

Программа позволяет настроить цвета своего интерфейса, использование градусов или радиан при вычислениях и отображении комплексных чисел, количество именованных ячеек памяти для хранения комплексных чисел, с которыми сможет работать пользователь посредством вызова окна «Запись/чтение из памяти» (по умолчанию 20 ячеек, максимально 40). Флажок «Сохранять/загружать содержимое ячеек при выходе из программы/запуске её» отвечает за автоматическое сохранение рабочей среды пользователя , чтобы при последующем запуске пользователю в окне «Запись/чтение из памяти» были предоставлены те переменные, с которыми он завершил работу. Сами настройки программы сохраняются всегда в файле «[папка программы]\complexcalc.ini» независимо от состояния флажка.

Выбор значения многозначной функции

Теория комплексного переменного предусматривает, что некоторые функции комплексных чисел могут иметь ограниченное количество значений (например, корень n-й степени, где n — натуральное число принимает n различных значений, каждое из которых отличается от предыдущего на угол 360/n градусов) или бесконечное множество значений (например, общая функция логарифм Ln, общая функция нахождения аргумента Arg, обобщенная степень комплексного числа, корень обобщенной степени комплексного числа).

В случае вызова подобных функций программа предоставляет пользователю окно «Выбор значения многозначной функций», в котором ему предоставляется на выбор одно из n возможных значений функции, если функция имеет количество значений n не больше 210 и одно из 210 значений, если функция принимает больше 210 значений или бесконечное их множество. Значение функции, возвращаемое по кнопке «0» является основным (например, основное значение натурального логарифма ln для Ln, основное значение угла arg для Arg).

Для нахождения корня квадратного, который, как известно, имеет два комлексных значения предусмотрено 2 кнопки прямо в главном окне Калькулятора. Кнопка с индексом 1 возвращает значение угла в показательной форме, полученное делением угла аргумента на два, а кнопка с индексом 2 —  полученное делением угла аргумента на два с последующим поворотом на 180 градусов.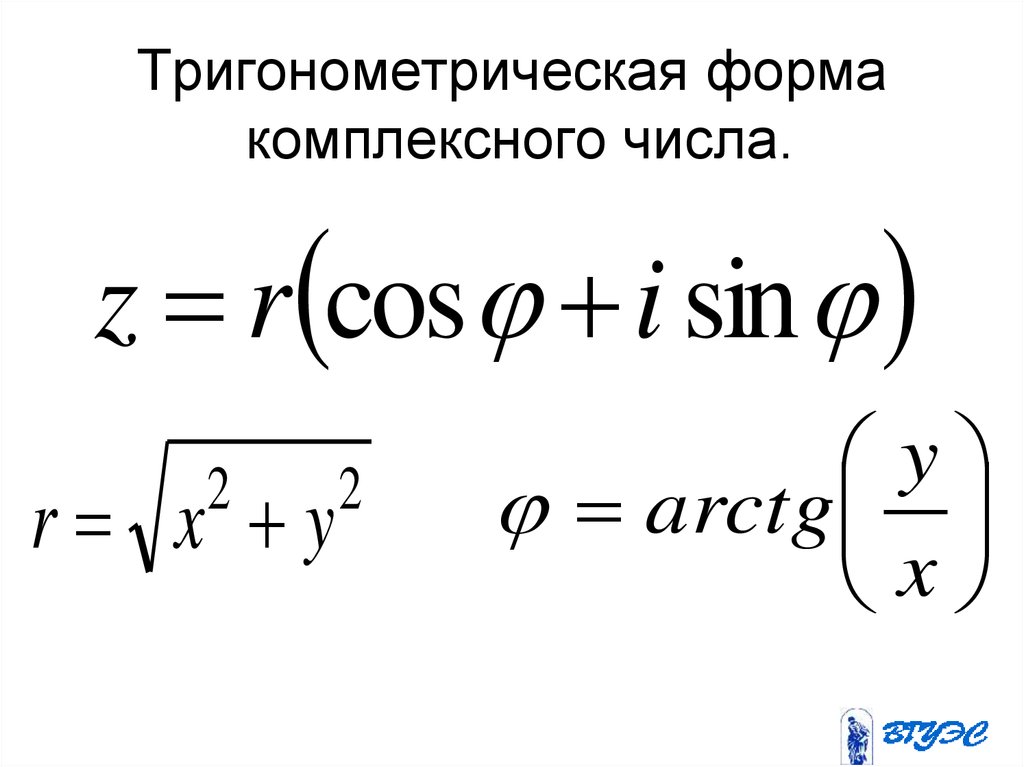

Более подробные сведения о возможностях различных версий Калькулятора можно посмотреть в Истории версий.

---

Среди 16 выпущенных Щербой С.В. версий Калькулятора комплексных чисел Вашему вниманию предлагается 2.30d как наиболее функциональная и доработанная, 1.3f как наиболее доработанная и стабильная среди первых версий, не перегруженных дополнительной функциональностью, 1.0 как самая первая, предоставляющая только самые базовые возможности.

Версия 2.30d

Версия, объединяющая в себе все описанные на этой странице возможности. Тщательно отработана на предмет наличия ошибок. Рекомендуется и использованию.

Примечание: Единственная найденная и неисправленная на сегодня недоработка в ней заключается в возникновении ошибки обращения к памяти по нулевому адресу (Сообщение «Access violation at address . .. Read of address 00000000″) при попытке дать переменной имя, начинающееся с цифры или служебного символа. Тем не менее программа продолжает работать и значение переменной в этой ячейке сохраняется.

Скачать complexcalcsetup.exe 294 кБ. (FreeWare)

Версия 1.3f

Базовые возможности только по операциям сложения, вычитания, умножения, деления. Позволяет сохранять промежуточные результаты вычислений в именованных ячейках памяти (только 10 штук!). Невозможно сохранение содержимого ячеек памяти на диск. Доступны расширенные возможности перемещения по окну и управления с помощью клавиатуры.

Примечание: при установке в окне авторские права содержится текст «Правом на бесплатное пользование программой обладают все преподаватели этого университета. Студенты обладают этим правом только при личном согласии автора программы. » На самом деле с выходом версии 2.30 программа стала FreeWare и новый текст лицензионного соглашения «7. Данная лицензия снимает ограничения на платное использование предыдущих версий программы «Калькулятор комплексных чисел». Теперь их можно использовать и распространять согласно новой лицензии» дает право на бесплатное пользование программой. Текст нового лицензионного соглашения можно прочитать по этой ссылке.

Скачать complexcalcsetup.exe 227 кБ. (FreeWare)

Версия 1.0

Базовые возможности только по операциям сложения, вычитания, умножения, деления. Не создана возможность сохранять промежуточные результаты вычислений в ячейках памяти, недоступны расширенные возможности перемещения по окну и управление с помощью клавиатуры. Переносит значение Результата в Аргумент 1 или Аргумент 2 можно только вручную с помощью буфера. Отображаемые числа всегда содержат 8 знаков после запятой, если число целое — они заполняются нулями, что затрудняет чтение.

Примечание: программа на сегодняшний день является FreeWare так же, как и версия 1.3f (см примечание к версии 1.3f).

Скачать complexcalcsetup.exe 220 кБ. (FreeWare)

---

Вернуться к Программы для математических вычислений
Вернуться на главную

 

Портал тоэ — калькуляторы. Возведение комплексных чисел в степень Комплексные числа со степенями примеры с решением

Использование калькулятора

Для вычисления выражения необходимо ввести строку для вычисления. При вводе чисел, разделителем целой и дробной части является точка. Можно использовать скобки. Операциями над комплексными числами являются умножение (*), деление (/), сложение (+), вычитание (-), возведение в степень (^) и другие. {i1{,}25\pi}}\]

В калькуляторе возможно использование констант, математических функций, дополнительных операций и более сложных выражений, ознакомиться с этими возможностями вы можете на странице общих правил использования калькуляторов на этом сайте.

Сайт находится в разработке, некоторые страницы могут быть недоступны.

Новости

07.07.2016
Добавлен калькулятор для решения систем нелинейных алгебраических уравнений: .

30.06.2016
На сайте реализован адаптивный дизайн, страницы адекватно отображаются как на больших мониторах, так и на мобильных устройствах.

Спонсор

РГРОнлайн.ru – мгновенное решение работ по электротехнике онлайн.

Начнем с любимого квадрата.

Пример 9

Возвести в квадрат комплексное число

Здесь можно пойти двумя путями, первый способ это переписать степень как произведение множителей и перемножить числа по правилу умножения многочленов.

Второй способ состоит в применение известной школьной формулы сокращенного умножения :

Для комплексного числа легко вывести свою формулу сокращенного умножения:

Аналогичную формулу можно вывести для квадрата разности, а также для куба сумма и куба разности. Но эти формулы более актуальны длязадач комплексного анализа. Что делать, если комплексное число нужно возвести, скажем, в 5-ую, 10-ую или 100-ую степень? Ясно, что в алгебраической форме проделать такой трюк практически невозможно, действительно, подумайте, как вы будете решать пример вроде?

И здесь на помощь приходит тригонометрическая форма комплексного числа и, так называемая, формула Муавра : Если комплексное число представлено в тригонометрической форме , то при его возведении в натуральную степеньсправедлива формула:

Просто до безобразия.

Пример 10

Дано комплексное число , найти.

Что нужно сделать? Сначала нужно представить данное число в тригонометрической форме. Внимательные читатели заметили, что в Примере 8 мы это уже сделали:

Тогда, по формуле Муавра:

Упаси боже, не нужно считать на калькуляторе , а вот угол в большинстве случае следует упростить. Как упростить? Образно говоря, нужно избавиться от лишних оборотов. Один оборот составляетрадиан или 360 градусов. Выясним сколько у нас оборотов в аргументе. Для удобства делаем дробь правильной:, после чего становится хорошо видно, что можно убавить один оборот:. Надеюсь всем понятно, чтои– это один и тот же угол.

Таким образом, окончательный ответ запишется так:

Отдельная разновидность задачи возведения в степень – это возведение в степень чисто мнимых чисел.

Пример 12

Возвести в степень комплексные числа ,,

Здесь тоже всё просто, главное, помнить знаменитое равенство.

Если мнимая единица возводится в четную степень, то техника решения такова:

Если мнимая единица возводится в нечетную степень, то «отщипываем» одно «и», получая четную степень:

Если есть минус (или любой действительный коэффициент), то его необходимо предварительно отделить:

Извлечение корней из комплексных чисел. Квадратное уравнение с комплексными корнями

Рассмотрим пример:

Нельзя извлечь корень? Если речь идет о действительных числах, то действительно нельзя. В комплексных числах извлечь корень – можно! А точнее, два корня:

Действительно ли найденные корни являются решением уравнения ? Выполним проверку:

Что и требовалось проверить.

Часто используется сокращенная запись, оба корня записывают в одну строчку под «одной гребёнкой»: .

Такие корни также называют сопряженными комплексными корнями .

Как извлекать квадратные корни из отрицательных чисел, думаю, всем понятно: ,,,,и т.д. Во всех случаях получаетсядва сопряженных комплексных корня.

Пример 13

Решить квадратное уравнение

Вычислим дискриминант:

Дискриминант отрицателен, и в действительных числах уравнение решения не имеет. Но корень можно извлечь в комплексных числах!

По известным школьным формулам получаем два корня: – сопряженные комплексные корни

Таким образом, уравнение имеет два сопряженных комплексных корня:,

Теперь вы сможете решить любое квадратное уравнение!

И вообще, любое уравнение с многочленом «энной» степени имеет ровнокорней, часть из которых может быть комплексными.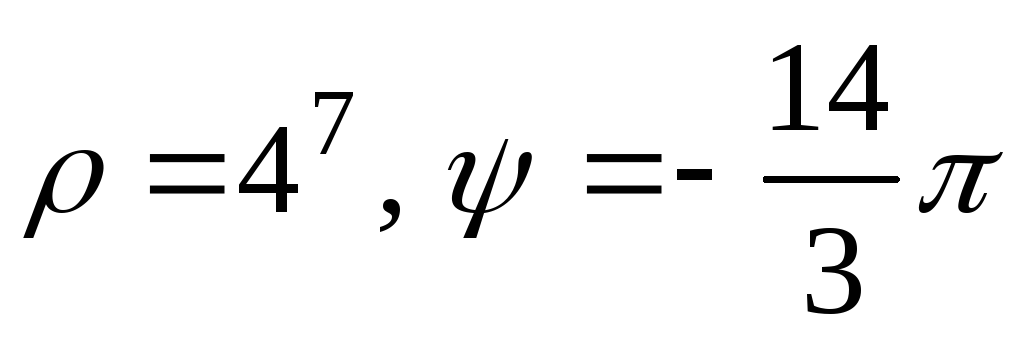

Простой пример для самостоятельного решения:

Пример 14

Найти корни уравнения и разложить квадратный двучлен на множители.

Разложение на множители осуществляется опять же по стандартной школьной формуле.

Начнем с любимого квадрата.

Пример 9

Возвести в квадрат комплексное число

Здесь можно пойти двумя путями, первый способ это переписать степень как произведение множителей и перемножить числа по правилу умножения многочленов.

Второй способ состоит в применение известной школьной формулы сокращенного умножения :

Для комплексного числа легко вывести свою формулу сокращенного умножения:

Аналогичную формулу можно вывести для квадрата разности, а также для куба сумма и куба разности. Но эти формулы более актуальны длязадач комплексного анализа. Что делать, если комплексное число нужно возвести, скажем, в 5-ую, 10-ую или 100-ую степень? Ясно, что в алгебраической форме проделать такой трюк практически невозможно, действительно, подумайте, как вы будете решать пример вроде?

И здесь на помощь приходит тригонометрическая форма комплексного числа и, так называемая, формула Муавра : Если комплексное число представлено в тригонометрической форме , то при его возведении в натуральную степеньсправедлива формула:

Просто до безобразия.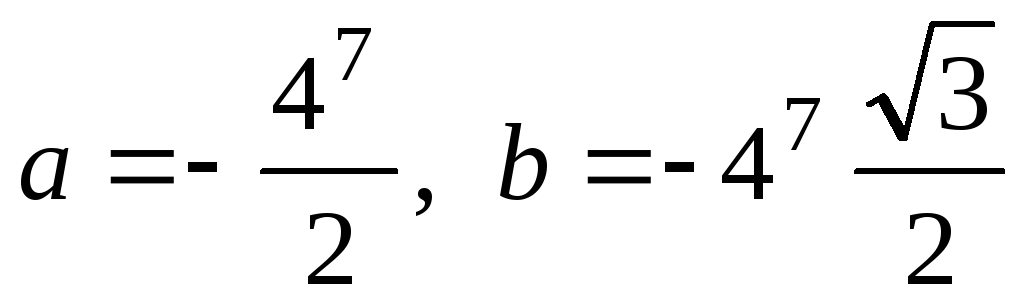

Пример 10

Дано комплексное число , найти.

Что нужно сделать? Сначала нужно представить данное число в тригонометрической форме. Внимательные читатели заметили, что в Примере 8 мы это уже сделали:

Тогда, по формуле Муавра:

Упаси боже, не нужно считать на калькуляторе , а вот угол в большинстве случае следует упростить. Как упростить? Образно говоря, нужно избавиться от лишних оборотов. Один оборот составляетрадиан или 360 градусов. Выясним сколько у нас оборотов в аргументе. Для удобства делаем дробь правильной:, после чего становится хорошо видно, что можно убавить один оборот:. Надеюсь всем понятно, чтои– это один и тот же угол.

Таким образом, окончательный ответ запишется так:

Отдельная разновидность задачи возведения в степень – это возведение в степень чисто мнимых чисел.

Пример 12

Возвести в степень комплексные числа ,,

Здесь тоже всё просто, главное, помнить знаменитое равенство.

Если мнимая единица возводится в четную степень, то техника решения такова:

Если мнимая единица возводится в нечетную степень, то «отщипываем» одно «и», получая четную степень:

Если есть минус (или любой действительный коэффициент), то его необходимо предварительно отделить:

Извлечение корней из комплексных чисел.

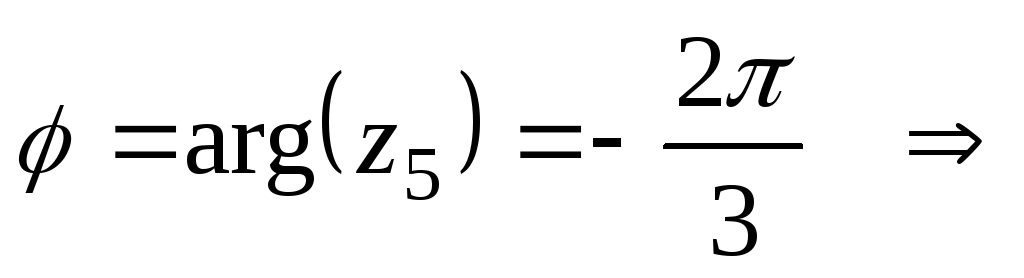Квадратное уравнение с комплексными корнями

Рассмотрим пример:

Нельзя извлечь корень? Если речь идет о действительных числах, то действительно нельзя. В комплексных числах извлечь корень – можно! А точнее, два корня:

Действительно ли найденные корни являются решением уравнения ? Выполним проверку:

Что и требовалось проверить.

Часто используется сокращенная запись, оба корня записывают в одну строчку под «одной гребёнкой»: .

Такие корни также называют сопряженными комплексными корнями .

Как извлекать квадратные корни из отрицательных чисел, думаю, всем понятно: ,,,,и т.д. Во всех случаях получаетсядва сопряженных комплексных корня.

Экспоненциальная форма комплексных чисел: Пример

Еще один день в нашей сложной жизни. Вы уже немного знаете о комплексных числах, а также о их полярной форме. Зачем тогда нужна другая форма комплексных чисел? Что ж, вам придется пойти и спросить об этом Эйлера (он, вероятно, ухмыляется нам сверху). {2}}\).

Это можно записать более компактно; в экспоненциальной форме. Но откуда взялась экспоненциальная форма? Ответ: Формула Эйлера .

Формула Эйлера

Неудивительно, что здесь, как и почти в любой другой области математики, мы встречаемся с Леонардом Эйлером. Существует очень элегантное уравнение, которое объединяет экспоненциальные функции, комплексные числа и тригонометрические функции в одной формуле. Она известна как Формула Эйлера 9.{i\theta}\), комплексное число будет исходить из начала координат и наклоняться под углом \(\theta\) к положительной оси \(x-\).

Рис. 1: Комплексное число на плоскости Аргана

Экспоненциальная форма — это очень краткий способ записи комплексных чисел, а также очень полезный, поскольку он отображает аргумент и модуль комплексного числа.

В отношении комплексных чисел в этой форме важно отметить, что комплексное число вида \(z=a+ib\) может быть записано не единицей, а 92} \\ \следовательно r&=5\sqrt{3} \end{aligned}$$

Теперь нам нужно вычислить главный аргумент \(z\):

$$\begin{aligned} \tan \theta &=\frac{b}{a} \\ \tan \theta &=\frac{\sqrt{3}}{1} \\ \tan \theta &=\sqrt{3} \\ \следовательно \ theta &=\frac{\pi}{3}\end{aligned}$$

Обратите внимание, что мы не учли \(\frac{5\sqrt{3}}{2}\), так как это отменит в конце концов.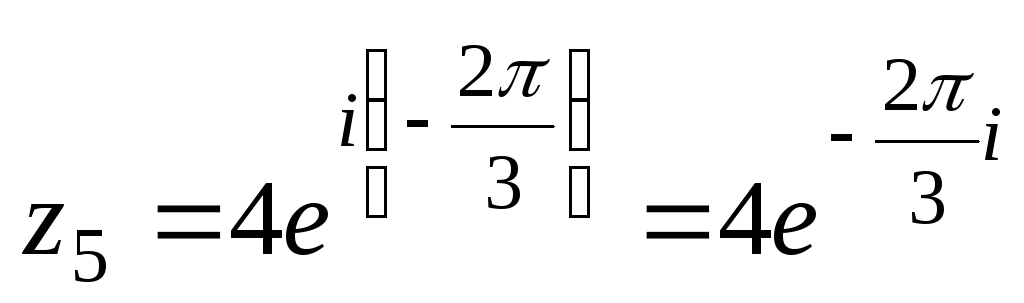 {i \theta}\): 9{i\theta}=\cos\theta+i\sin\theta\).

Exponential form calculator

• Expression
• Equation
• Inequality
• Contact us

• Simplify
• Factor
• Expand
• GCF
• LCM

• Solve
• Graph
• System

• Решение
• График
• Система

• Математический решатель на вашем сайте

Наших пользователей:

Знаете, в качестве пошаговой программы для обучения алгебре я рекомендую Algebrator каждому ученику, родителю, репетитору, учителю и члену правления, которому я могу!
Маргарет Томас, Нью-Йорк

Ваш новый релиз стал намного более интуитивным! Ваша команда быстро отреагировала. Отличная работа! Я буду рекомендовать новую версию другим студентам.
Генри Баркер, Алабама

Слава Алгебратору! Моя дочь Сара получала пятерки в своем табеле успеваемости благодаря этому выдающемуся программному обеспечению. У нее больше нет проблем с домашним заданием по алгебре. Попользовавшись программой несколько недель, мы попрощались с ее требовательным наставником. Спасибо!
Саманта Джордан, Невада

---

Студенты, борющиеся со всевозможными задачами по алгебре, узнают, что наше программное обеспечение может спасти им жизнь. Вот поисковые фразы, которые сегодняшние поисковики использовали, чтобы найти наш сайт. Сможете ли вы найти среди них свою?

Поисковые фразы, использованные 18 января 2015 г.:

• алгебра 2 ответа
• решатель excel без линейных уравнений
• расчет среднего геометрического по t1-83 плюс
• неравенство в формулировке gcse
• значение уравнения Matlab
• java примеры генератора случайных строк
• найти число игра в java
• программы, которые учитывают уравнения
• НОД формула
• графический вывод в режиме emacs cacl
• дистрибутивные свойства предалгебры
• примера соотношения в нашей повседневной жизни
• mcdougal littell наука о жизни раздел 2. 1 чтение учебного пособия ответы
• математика бесплатно рабочий лист +13 лет
• рабочие листы для умножения и деления дробей
• Калькулятор решения рациональных уравнений
• бесплатно Рабочий лист уравнения с 1 переменной
• Рабочий лист умножения рациональных выражений
• решать производные онлайн
• образец максимума урок математики
• Полное руководство идиота по алгебре скачать бесплатно
• Бесплатный решатель алгебраических выражений
• тест на гениальность по математике в средней школе с классной книгой E
• рабочие листы на сложение и вычитание до 15
• наш класс будет делать работу по алгебре 1 Книга Макдугал Литтел
• куда мне пойти, чтобы решить задачу по алгебре?
• фольга куб функция
• разница между перестановкой и комбинацией
• факторизация уравнения 4-го корня
• Калькулятор упрощения рациональных выражений
• Решатель линейной комбинации
• Пример +slove Radicals и Roots
• математический тест по алгебраическим выражениям гр.

  No related posts.