Радианная мера угла – методическая разработка для учителей, Әнапияев Нұрбол Раманқұлұлы
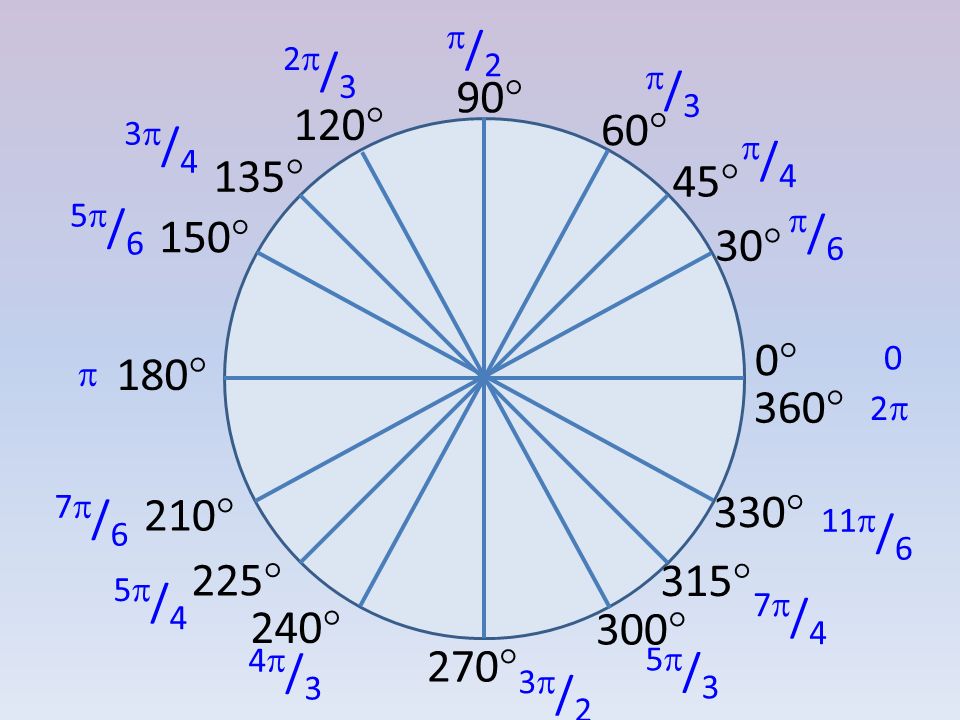
Цели обучения: | 9.1.1.2 — знать понятие радианной меры угла и уметь переводить градусы в радианы и обратно; 9.1.1.3 — отмечать на единичной окружности точки, соответствующие углам, заданным в радианной или градусной мере. |
Цели урока: | Учащиеся будут:
|
Критерии оценивания: | — знают понятие радианной меры угла; — умеют переводить градусы в радианы и обратно;  |
Языковые цели: | Лексика и терминология, специфичная для предмета:
Полезные выражения для диалогов и письма:
|
Навыки использования ИКТ: | Использование на уроке казахстанского образовательного сайта bilimland.kz, а также использование интерактивной доски. |
Предварительные знания: | Знание понятий «функция», «аргумент». Знание графика функции и его свойств. Знание определения тригонометрических функций острого угла из курса геометрии. |
Ход урока
Этапы урока | Деятельность учителя Деятельность ученика | Ресурсы |
Начало 1 урок 2 минуты
3 минуты
15 минут
20 минут
2 урок 5 минут
10 минут
5 минут
17 минут | 1.
2. Подготовка к восприятию новых знаний.
3.Сообщить учащимся тему и цель сегодняшнего урока.
Провести устный опрос: — что такое угол? — какие единицы измерения углов вы знаете?
Новая тема – Радианная мера угла. Ученики берут по одному ноутбуку из тележки. Включают ноутбуки и переходят на сайт
Если у учащихся возникают вопросы, я им объясняю. С помощью презентации на интерактивной доске показываю формулу длина дуги в a радиан.
Устная работа по ссылке https://bilimland.kz/ru/courses/math-ru/algebra/trigonometriya/lesson/gradusnye-i-radiannye-mery-ugla С помощью презентаций показываю формулы: и обратно: Самостоятельная работа на ноутбуках: https://bilimland. Когда ученики заполняют таблицу, я веду проверку. Учащиеся в курсе того, что если они введут неправильный ответ, то звук им укажет на это.
Парная работа. Заполните таблицу.
Интеграция с физикой. Видео урок по ссылке https://bilimland.kz/ru/courses/math-ru/algebra/trigonometriya/lesson/gradusnye-i-radiannye-mery-ugla
Формативное оценивание. Колесо автомобиля с радиусом 0,5 м вращается с постоянной скоростью \({80 \over 3} рад/с\). 1) Какое расстояние проедет автомобиль за 1 минуту? 2) За какое время автомобиль проедет путь, равный 12 км?
Дифференцированные задания |
Интерактивная доска Казахстанский образовательный сайт Bilimland. Презентация
Казахстанский образовательный сайт Bilimland.kz
Ю.
Казахстанский образовательный сайт Bilimland.kz
Ю.Н. Макарычев и др. Алгебра. Учебник для 9 класса. М.: 2000г. -272 с.
Ю.Н. Макарычев и др. Алгебра. Учебник для 9 класса. М.: 2000г. -272 с.
|
Конец 3 минуты | Рефлексия Я узнал……………… Я хочу научиться………….. Я запомнил……… Домашнее задание
3. Радиус окружности равен 1,5 см. Найти: 1) градусную и радианную меры угла, стягиваемого дугой окружности длиной 4; 2) длину дуг окружности, стягивающих углы величиной . Которое не должно превышать 15 минут. | Стикеры
Ю.Н. Макарычев и др. Алгебра. Учебник для 9 класса. М.: 2000г. -272 с.
|
Дифференциация – каким образом вы планируете оказать больше поддержки? Какие задачи вы планируете поставить перед более способными учащимися? | Оценивание – как вы планируете проверить уровень усвоения материала учащимися? | Здоровье и соблюдение техники безопасности |
Ученики делятся на группы по самостоятельности. Учитель занимается с отстающей группой. | В ходе урока учитель проверяет записи учащихся, ведет наблюдение за учениками. С помощью «Светофора» учащиеся оценивают свое усвоение материала. | Проветривание кабинета |
Рефлексия по уроку Были ли цели урока/цели обучения реалистичными? Все ли учащиеся достигли ЦО? Если нет, то почему? Правильно ли проведена дифференциация на уроке? Какие отступления были от плана урока и почему? | Используйте данный раздел для размышлений об уроке. Ответьте на самые важные вопросы о вашем уроке из левой колонки. | |
| ||
Общая оценка
Какие два аспекта урока прошли хорошо (подумайте как о преподавании, так и об обучении)? 1:
2:
Что могло бы способствовать улучшению урока (подумайте как о преподавании, так и об обучении)? 1:
2:
Что я выявил(а) за время урока о классе или достижениях/трудностях отдельных учеников, на что необходимо обратить внимание на последующих уроках?
| ||
Колесо автомобиля с радиусом 0,5 м вращается с постоянной скоростью \({80 \over 3} рад/с\).
1) Какое расстояние проедет автомобиль за 1 минуту?
2) За какое время автомобиль проедет путь, равный 12 км?
Домашнее задание
- Переведите в радианную меру градусы:
- Переведите в градусы радианы:
3. Радиус окружности равен 1,5 см. Найти: 1) градусную и радианную меры угла, стягиваемого дугой окружности длиной 4;
2) длину дуг окружности, стягивающих углы величиной .
Которое не должно превышать 15 минут.
Градусная и радианная мера угла
Похожие презентации:
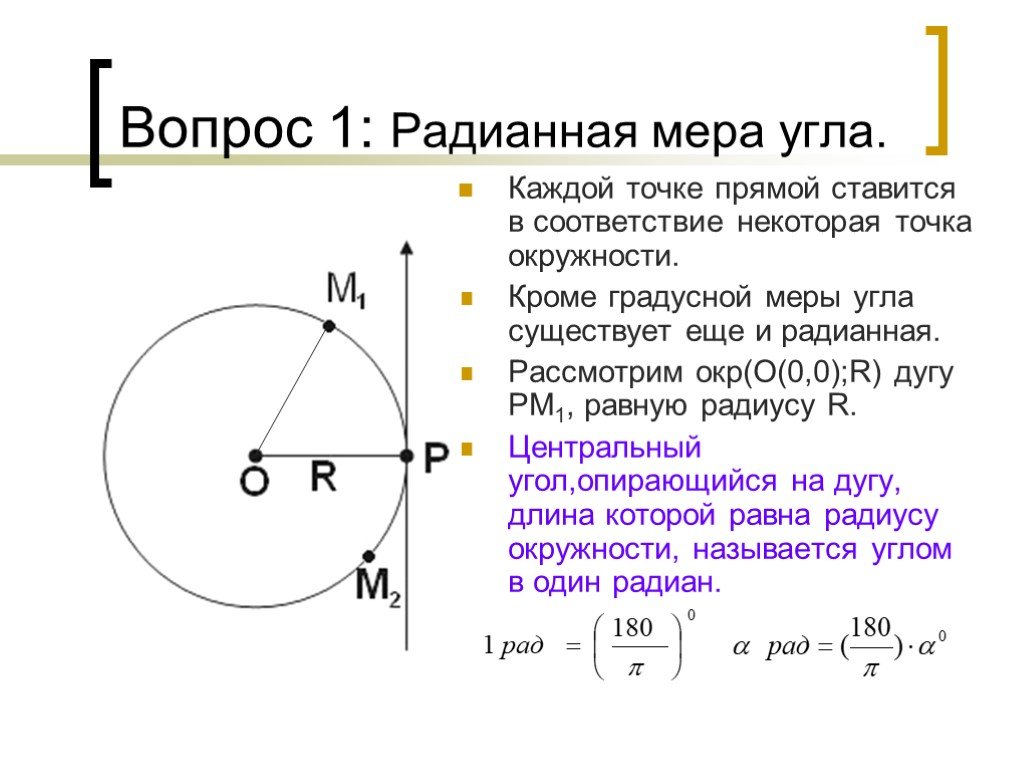
Радианная мера угла
Радианная мера угла
Тригонометрия. Радианная мера угла
Угол поворота. Радианная мера угла
Радианная мера угла. Угол поворота
Радианная мера угла
Угол поворота. Радианная мера угла
Угол поворота. Радианная мера угла
Градусная и радианная меры угла. Вращательное движение. Синус, косинус, тангенс и котангенс
Радианная мера угла
Градусная
и радианная
мера угла
Цели занятия:
1. Изучить способы измерения углов в градусах и
Изучить способы измерения углов в градусах и
радианах;
2. Сформировать умение пользоваться измерением
углов при решении практических задач.
Компетенции по ФГОС:
• применять математические методы для решения
профессиональных и прикладных задач;
• использовать приемы и методы математического
анализа в различных профессиональных ситуациях;
• анализировать результаты измерения величин с
допустимой погрешностью, представлять их графически.
Тригонометрия в искусстве
Тригонометрия
в пожарной службе
α
Тригонометрия в авиации
6. Тригонометрия в биологии
Тригонометрия(«три» — три, «гониа» — угол,
«метриа» — измеряю)
раздел математики,
изучающий
соотношение сторон и
углов в треугольнике
Чему равен угол квадрата?
0
90
На какой угол поворачивается
солдат по команде «кругом»?
0
180
Чему равен угол между минутной и
часовой стрелками на часах,
когда они показывают 2 часа?
0
60
Единицы
измерения углов
Градусы
Радианы
Градусная мера угла
=1
1 – цена одного деления
окружности, разделенной на
360 частей
14.
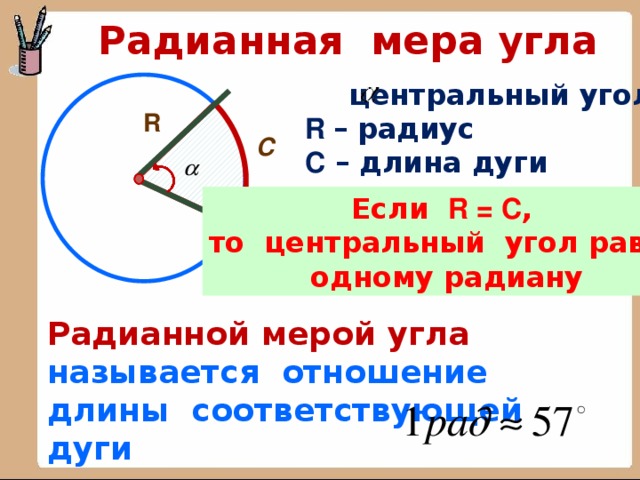
 Радианная мера углау
Радианная мера углау1 радиан это центральный
угол, длина дуги которого
равна радиусу окружности
90°
Р
1 радиан 57 °
180°
О
0°
360°
270°
х
Единицы измерения
углов
Радианы
Градусы
радиан=180
Перевод из градусной
меры в радианную:
радиан=180
рад
Пример:
1.
2.
Перевод из радианной
меры в градусную:
радиан=180
Примеры:
1.
2.
Таблица перехода из
градусной
в радианную меру угла
Градусы 0 30
45
60
6
4
3
Радианы
0
900
120 135 150 180 270
2
2 3
3 5
4 6
3
2
3600
2
Точка осмотра 3D рисунков
для зрителей
25. Практическая работа
Первый шаг. Нам понадобится жесткая бумага. Сгибаем листровно по середине. Рисуем в обе стороны прямые линии
под одинаковым углом. Линии должны зеркально отражать
друг друга. Примерно 35-40 градусов.
Второй шаг. Рисуем ступеньки лестницы с двух
сторон, параллельно сгибу листа.

Третий шаг. Берем линейку и соединяем прямой линией
вершины лестницы. Это будет тень. Берем мягкий
карандаш и делаем тень. Давить на карандаш не стоит,
тень не должна быть слишком темной.
Последний шаг. Поднимаем одну часть бумаги вверх и
разворачиваем бумагу под углом к зрителю. Важно
подобрать такой угол, чтобы лестница казалась прямой.
Из-за тени будет казаться, что это объемный рисунок:
http://wikibit.me/v/
30. Вывод:
Мы узнали, что тригонометрияприменяется не только в алгебре и
началах анализа, но и в строительстве,
пожарной службе, биологии и т.д.
Тригонометрия является основой для
создания многих шедевров архитектуры;
Научились использовать тригонометрию
в задачах с практическим содержанием.
English Русский Правила
Радиан Измерение угла
по
Измерение углов в радианах и градусах и преобразование одного в другой
Измерение угла разрешается от начальной стороны числом оборотов к конечной сторона.
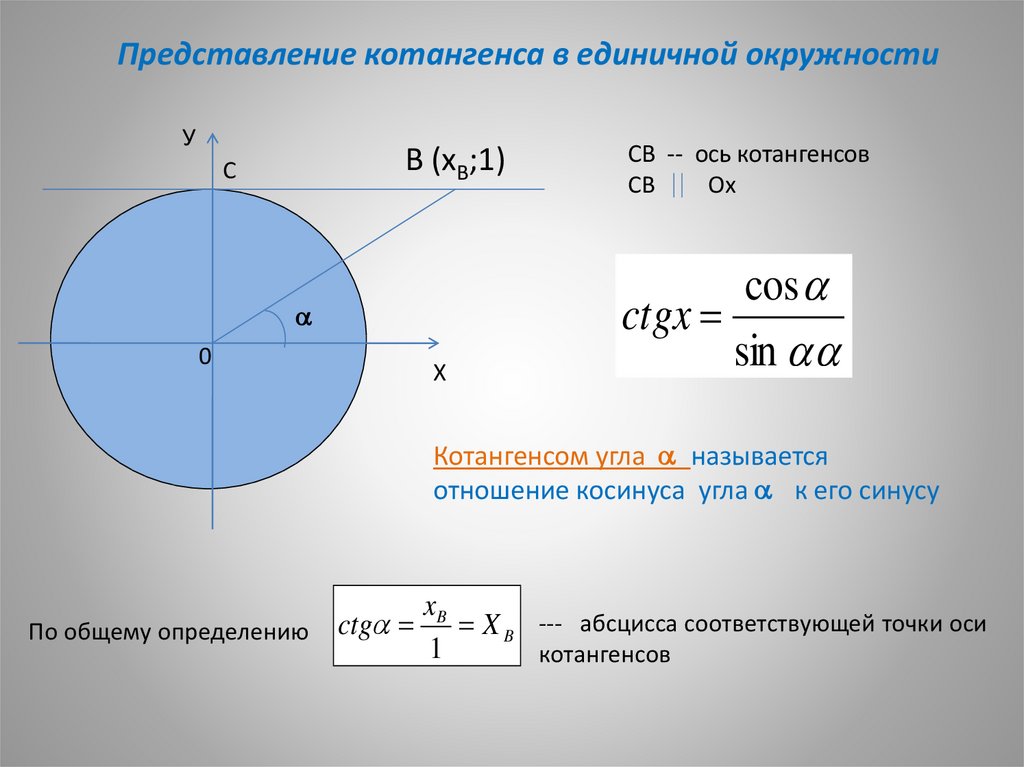
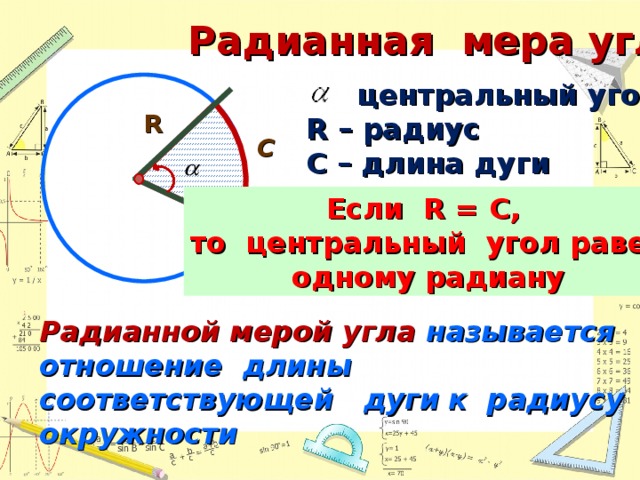
Один из методов измерения углов — в радианах. Чтобы определить, что такое радиан, используйте центральный угол окружности (угол, вершина или вершина которого является центром окружности).
Радиан — это мера центрального угла, который пересекает дугу, обозначенную буквой «s» на рисунке ниже и равную длине радиуса «r» окружности.
Принимая во внимание длину окружности, которая составляет 2πr, один оборот вокруг окружности радиуса r соотносится с углом 2π радиан как с / r = 2πr / r = 2π радиан.
Измерение углов в градусной форме.
В одном полном обороте 360 градусов, и под одним полным оборотом мы подразумеваем один полный круг.
The Degree Symbol: °
For instance – 90° = 90 degrees
Measuring Degrees
Oftentimes we do measure degrees with the help of a protractor:
Радиан известен как угол дуги в окружности, который образован радиусом окружности, окружающей ее окружность.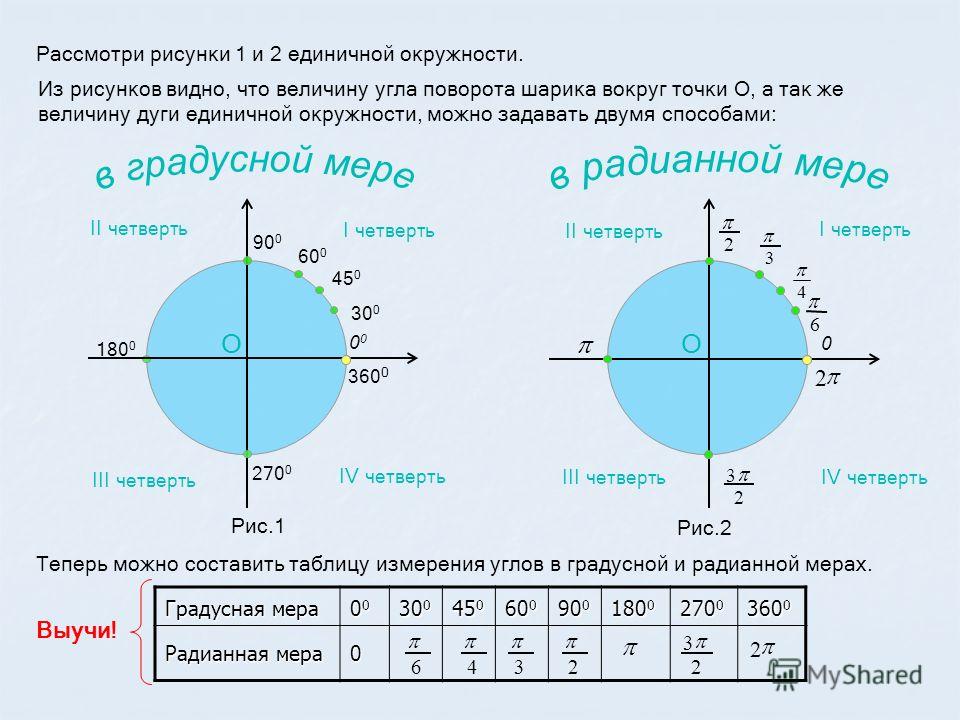 Представление угла находится между двумя линиями через градусы и радианы.
Представление угла находится между двумя линиями через градусы и радианы.
Общий угол окружности равен 360 градусам или может быть понят как 2 радиана. Преимущество преобразования радианов в градусы позволяет преобразовать углы, которые описаны в форме радианов, в форму градусов.
Радианы в градусы Формула задается как
Градусы = радианы × 180 / π
Решаемые примеры
Вопрос: Преобразовать 2,56
9 °?
Ответ:
Ниже приведена формула для преобразования радианов в градусы: стандартная единица измерения. Измерение угла в радианах, которое математически равно длине соответствующей дуги единичного круга.
Связь или соотношение между радиусом и длиной дуги окружности иллюстрирует радианы окружности.
Формула радиан и градус используются для преобразования радианов в градусы или градусов в радианы.
Radian in Deground Formula
Radian = Длина дуги / Длина радиуса
Radian = степень * π / 180
Итак, здесь несколько углов и их относительные радиан. / 60
/ 60
Please Share
Radian Angle System
Radian Angle System
- Применение
- Определение
- Измерение углов
- Триггерные функции
- Радиан против Градусов
- Ссылки
- Ссылки
Радианы измеряют углы как отношение длины дуги угла к радиусу окружности, используемой для рисования дуги. Полный оборот в радианах равен (тау) радианам.
Примечание: Этот веб-сайт использует константу (тау) вместо (пи) в качестве постоянной окружности по умолчанию. Подстановку можно использовать для перевода между двумя константами.
Подстановку можно использовать для перевода между двумя константами.
Применение
Радианная система используется для измерения углов и в качестве предпочтительной единицы для тригонометрических функций. В то время как система углов в градусах часто используется для введения понятий, радианная система со временем становится предпочтительной единицей измерения углов в математике [1] .
Определение
радиана — это единица измерения угла как отношение длины дуги угла к радиусу окружности. (Эквивалентный) символ используется для представления свойства инвариантности к радиусу определения [2] . Полный оборот равен (тау) радианам, где естественная постоянная окружности определяется делением длины окружности на ее радиус.
Измерение углов
Углы, измеренные в радианах, обычно выражаются с помощью постоянной окружности (тау). Ниже показаны некоторые примеры углов, измеренных в радианах.

 Организационный момент.
Организационный момент.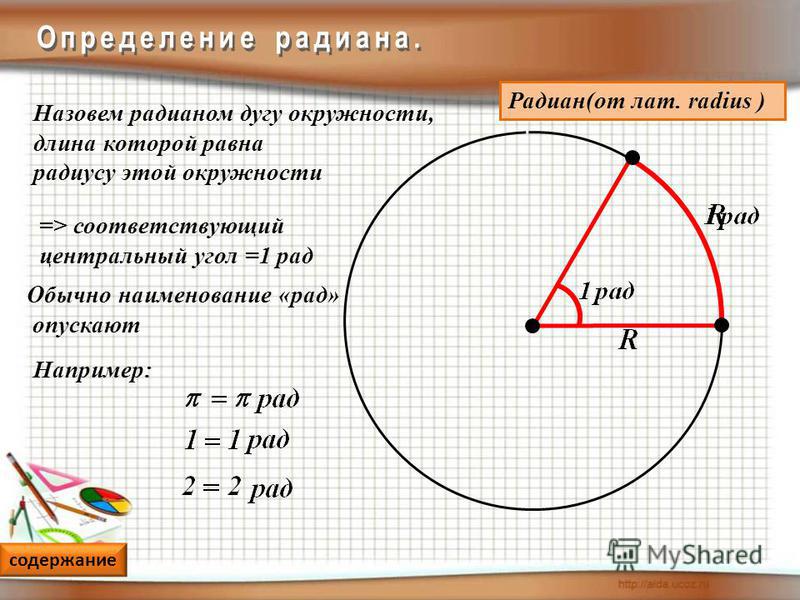 kz/ru/courses/math-ru/algebra/trigonometriya/lesson/gradusnye-i-radiannye-mery-ugla
kz/ru/courses/math-ru/algebra/trigonometriya/lesson/gradusnye-i-radiannye-mery-ugla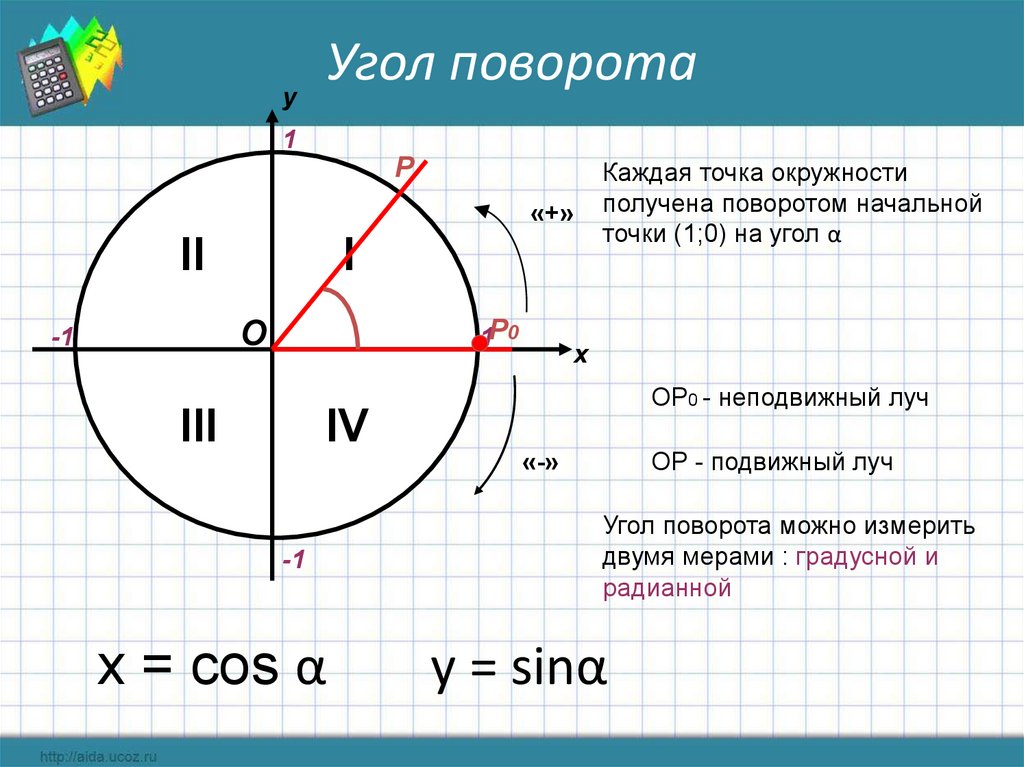
 Н. Макарычев и др. Алгебра. Учебник для 9 класса. М.: 2000г. -272 с.
Н. Макарычев и др. Алгебра. Учебник для 9 класса. М.: 2000г. -272 с.