Четверть числовой окружности
Если посмотреть на числовую окружность, то можно заметить, что оси абсцисс и ординат разбивают ее на четыре части. Эти части называют четвертями и нумеруют в том порядке как их проходят, двигаясь в положительном направлении (против часовой стрелки).
|
\((\)\(\frac{π}{2}\)\(;π)\)- вторая четверть |
\((0;\)\(\frac{π}{2}\)\()\) — первая четверть |
|
|
|
|
|
|
\((π;\)\(\frac{3π}{2}\)\()\) — третья четверть |
\((\)\(\frac{3π}{2}\)\(;2π)\) — четвертая четверть |
Почему так важно определять какой четверти принадлежит угол?
Дело в том, что каждая четверть уникальна в плане знаков тригонометрических функций.
Например, для любого угла из второй четверти — синус положителен, а косинус, тангенс и котангенс отрицательны. А для любого угла из первой четверти — все четыре функции будут положительны.
Теперь давайте рассмотрим пример задачи, которую не решить без использования знаний про четверти.
Пример (ЕГЭ):
|
Найдите \(\sina\), если \(\cosa=-0,6\) и \(π<a<\)\(\frac{3π}{2}\) |
Нам известен косинус, а найти нужно синус того же угла. Какая тригонометрическая формула связывает синус и косинус того же угла? |
|||
|
\(\sin^2a+\cos^2a=1\) |
Подставим известное, и проведем вычисления. |
|||
|
\(\sina=0,8\) или \(\sina=-0,8\) |
У нас два ответа, и оба нам подходят. Но у угла не может быть два синуса! Один лишний! А какой? |
Ответ: \(\sina=-0,8\).
Про непостоянство четвертей:
Важно понимать, что, например, первой четверти принадлежат не только углы от \(0\) до \(\frac{π}{2}\), но и углы от \(2π\) до \(\frac{5π}{2}\), и от \(4π\) до \(\frac{9π}{2}\), и от \(6π\) до \(\frac{13π}{2}\) и так далее. Ведь как только мы заканчиваем полный оборот – кончается четвертая четверть и опять начинается первая.
Ведь как только мы заканчиваем полный оборот – кончается четвертая четверть и опять начинается первая.
Кроме того, нужно помнить, что углы могут откладываться в отрицательную сторону (по часовой стрелке), и тогда мы попадем в первую четверть только в конце круга. Ведь сначала мы пройдем четвертую четверть, потом в третью и т.д.
|
\((-π;-\)\(\frac{3π}{2}\)\()\)- вторая четверть |
\((-\)\(\frac{3π}{2}\)\(;-2π)\) — первая четверть |
|
|
|
|
|
|
\((-\)\(\frac{π}{2}\)\(;-π)\) — третья четверть |
\((0;-\)\(\frac{π}{2}\)\()\) — четвертая четверть |
Ну и, конечно, мы можем в отрицательную сторону делать обороты, так же как и в положительную.
Смотрите также:
Числовая окружность (шпаргалка)
Тригонометрическая таблица с кругом
Как обозначать точки на числовой окружности
Отсчёт углов на тригонометрическом круге. Положительные и отрицательные углы. Распределение углов по четвертям
В прошлом уроке мы с вами успешно освоили (или повторили — кому как) ключевые понятия всей тригонометрии. Это тригонометрический круг, угол на круге, синус и косинус этого угла, а также освоили знаки тригонометрических функций по четвертям. Освоили подробно. На пальцах, можно сказать.
Но этого пока мало. Для успешного практического применения всех этих простых понятий нам необходим ещё один полезный навык. А именно — правильная работа с углами в тригонометрии. Без этого умения в тригонометрии — никак. Даже в самых примитивных примерах.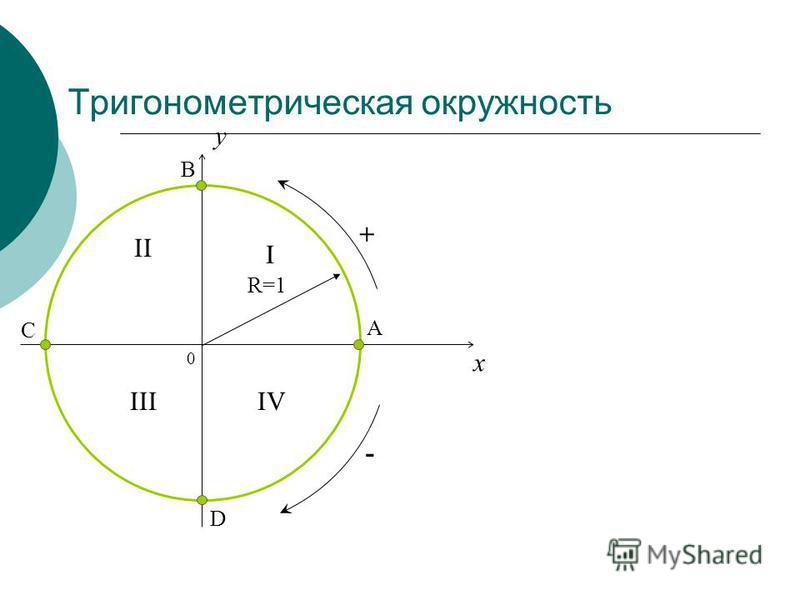 Почему? Да потому, что угол — ключевая действующая фигура во всей тригонометрии! Нет, не тригонометрические функции, не синус с косинусом, не тангенс с котангенсом а именно сам угол. Нет угла — нету и тригонометрических функций, да…
Почему? Да потому, что угол — ключевая действующая фигура во всей тригонометрии! Нет, не тригонометрические функции, не синус с косинусом, не тангенс с котангенсом а именно сам угол. Нет угла — нету и тригонометрических функций, да…
Как правильно работать с углами на круге? Для этого нам надо железно усвоить два пункта.
1) Как отсчитываются углы на круге?
2) В чём они считаются (измеряются)?
Ответ на первый вопрос — и есть тема сегодняшнего урока. С первым вопросом мы детально разберёмся прямо здесь и сейчас. Ответ на второй вопрос здесь не дам. Ибо достаточно развёрнутый он. Как и сам второй вопрос очень скользкий, да.) Вдаваться в подробности пока не буду. Это — тема следующего отдельного урока.
Приступим?
Как отсчитываются углы на круге? Положительные и отрицательные углы.
У прочитавших название параграфа, возможно, уже волосы встали дыбом.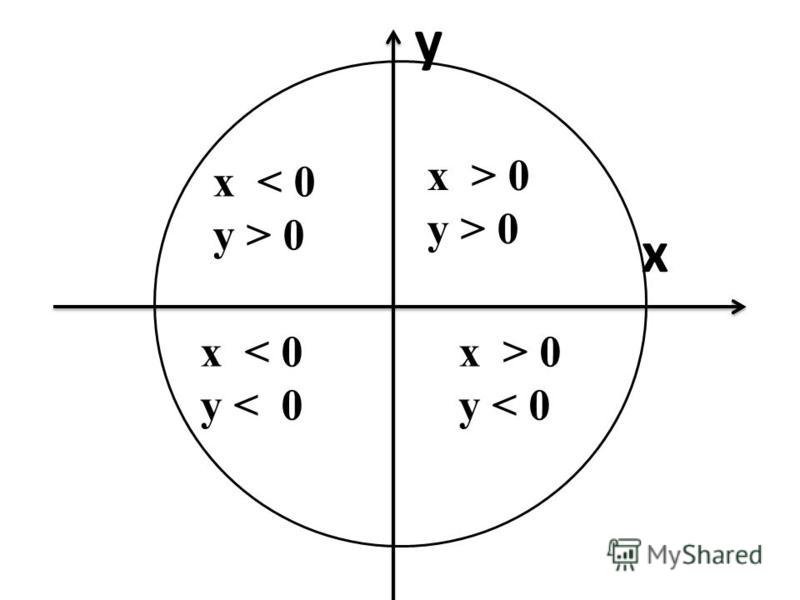 Как так?! Отрицательные углы? Разве такое вообще возможно?
Как так?! Отрицательные углы? Разве такое вообще возможно?
К отрицательным числам мы с вами уже попривыкли. На числовой оси их изображать умеем: справа от нуля положительные, слева от нуля отрицательные. Да и на градусник за окном поглядываем периодически. Особенно зимой, в мороз.) И денежки на телефоне в «минус» (т.е. долг) иногда уходят. Это всё знакомо.
А что же с углами? Оказывается, отрицательные углы в математике тоже бывают! Всё зависит от того, как отсчитывать этот самый угол… нет, не на числовой прямой, а на числовой окружности! То бишь, на круге. Круг — вот он, аналог числовой прямой в тригонометрии!
Итак, как же отсчитываются углы на круге? Ничего не поделать, придётся нам для начала этот самый круг нарисовать.
Я нарисую вот такую красивую картинку:
Она очень похожа на картинки из прошлого урока. Есть оси, есть окружность, есть угол. Но есть и новая информация.
Во-первых, я добавил номера четвертей (или квадрантов). Напоминаю, что четверти всегда нумеруются против часовой стрелки.
Напоминаю, что четверти всегда нумеруются против часовой стрелки.
Также я добавил циферки 0°, 90°, 180°, 270° и 360° на осях. Вот это уже поинтереснее.) Что это за циферки? Правильно! Это значения углов, отсчитанные от нашей неподвижной стороны, которые попадают на координатные оси. Вспоминаем, что неподвижная сторона угла у нас всегда крепко-накрепко привязана к положительной полуоси ОХ. И любой угол в тригонометрии отсчитывается именно от этой полуоси. Это базовое начало отсчёта углов надо держать в голове железно. А оси — они же под прямым углом пересекаются, верно? Вот и прибавляем по 90° в каждой четверти.
И ещё добавлена красная стрелочка. С плюсом. Красная — это специально, чтобы в глаза бросалась. И в память хорошенько врезалась. Ибо это надо запомнить надёжно.) Что же означает эта стрелочка?
Так вот оказывается, если наш угол мы будем крутить по стрелочке с плюсом (против часовой стрелки, по ходу нумерации четвертей), то угол будет считаться положительным! В качестве примера на рисунке показан угол +45°. Кстати, обратите внимание, что осевые углы 0°, 90°, 180°, 270° и 360° также отмотаны именно в плюс! По красной стрелочке.
Кстати, обратите внимание, что осевые углы 0°, 90°, 180°, 270° и 360° также отмотаны именно в плюс! По красной стрелочке.
А теперь посмотрим на другую картинку:
Здесь почти всё то же самое. Только углы на осях пронумерованы в обратную сторону. По часовой стрелке. И имеют знак «минус».) Ещё нарисована синяя стрелочка. Также с минусом. Эта стрелочка — направление отрицательного отсчёта углов на круге. Она нам показывает, что, если мы будем откладывать наш угол по ходу часовой стрелки, то угол будет считаться отрицательным. Для примера я показал угол -45°.
Кстати, прошу заметить, что нумерация четвертей никогда не меняется! Неважно, в плюс или в минус мы мотаем углы. Всегда строго против часовой стрелки.)
Запоминаем:
1. Начало отсчёта углов — от положительной полуоси ОХ. По часам — «минус», против часов — «плюс».
2. Нумерация четвертей всегда против часовой стрелки вне зависимости от направления исчисления углов.
Нумерация четвертей всегда против часовой стрелки вне зависимости от направления исчисления углов.
Кстати говоря, подписывать углы на осях 0°, 90°, 180°, 270°, 360°, каждый раз рисуя круг — вовсе не обязаловка. Это чисто для понимания сути сделано. Но эти циферки обязательно должны присутствовать в вашей голове при решении любой задачи по тригонометрии. Почему? Да потому, что эти элементарные знания дают ответы на очень многие другие вопросы во всей тригонометрии! Самый главный вопрос — в какую четверть попадает интересующий нас угол? Хотите верьте, хотите нет, но правильный ответ на этот вопрос решает львиную долю всех остальных проблем с тригонометрией. Этим важным занятием (распределением углов по четвертям) мы займёмся в этом же уроке, но чуть позже.
Величины углов, лежащих на осях координат (0°, 90°, 180°, 270° и 360°), надо запомнить! Запомнить накрепко, до автоматизма. Причём как в плюс, так и в минус.
А вот с этого момента начинаются первые сюрпризы. И вместе с ними и каверзные вопросы в мой адрес, да…) А что будет, если отрицательный угол на круге совпадёт с положительным? Выходит, что одну и ту же точку на круге можно обозначить как положительным углом, так и отрицательным???
Совершенно верно! Так и есть.) Например, положительный угол +270° занимает на круге то же самое положение, что и отрицательный угол -90°. Или, например, положительный угол +45° на круге займёт то же самое положение, что и отрицательный угол -315°.
Смотрим на очередной рисунок и всё видим:
Точно так же положительный угол +150° попадёт туда же, куда и отрицательный угол -210°, положительный угол +230° — туда же, куда и отрицательный угол -130°. И так далее…
И что теперь делать? Как именно считать углы, если можно и так и сяк? Как правильно?
Ответ: по-всякому правильно! Ни одно из двух направлений отсчёта углов математика не запрещает. А выбор конкретного направления зависит исключительно от задания. Если в задании ничего не сказано прямым текстом про знак угла (типа «определите наибольший отрицательный угол» и т.п.), то работаем с наиболее удобными нам углами.
А выбор конкретного направления зависит исключительно от задания. Если в задании ничего не сказано прямым текстом про знак угла (типа «определите наибольший отрицательный угол» и т.п.), то работаем с наиболее удобными нам углами.
Конечно, например, в таких крутых темах, как тригонометрические уравнения и неравенства направление исчисления углов может колоссально влиять на ответ. И в соответствующих темах мы эти подводные камни рассмотрим.
Запоминаем:
Любую точку на круге можно обозначить как положительным, так и отрицательным углом. Любым! Каким хотим.
А теперь призадумаемся вот над чем. Мы выяснили, что угол 45° в точности совпадает с углом -315°? Как же я узнал про эти самые 315°? Не догадываетесь? Да! Через полный оборот.) В 360°. У нас есть угол 45°. Сколько не хватает до полного оборота? Отнимаем 45° от 360° — вот и получаем 315°. Мотаем в отрицательную сторону — и получаем угол -315°.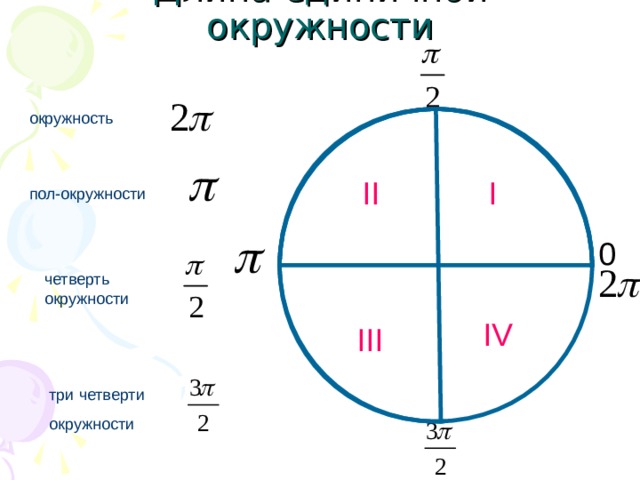 Всё равно непонятно? Тогда смотрим на картинку выше ещё раз.
Всё равно непонятно? Тогда смотрим на картинку выше ещё раз.
И так надо поступать всегда при переводе положительных углов в отрицательные (и наоборот) — рисуем круг, отмечаем примерно заданный угол, считаем, сколько градусов не хватает до полного оборота, и мотаем получившуюся разность в противоположную сторону. И всё.)
Чем ещё интересны углы, занимающие на круге одно и то же положение, как вы думаете? А тем, что у таких углов совершенно одинаковые синус, косинус, тангенс и котангенс! Всегда!
Например:
sin45° = sin(-315°)
cos120° = cos(-240°)
tg249° = tg(-111°)
ctg333° = ctg(-27°)
И так далее и тому подобное. В общем, вы поняли… Кстати, прошу заметить, что углы в этих парочках различны. Зато тригонометрические функции у них — одинаковы! Идея ясна?
А вот это уже крайне важно! Зачем? Да всё за тем же!) Для упрощения выражений. Ибо упрощение выражений — ключевая процедура успешного решения любых заданий по математике. И по тригонометрии в том числе.
Ибо упрощение выражений — ключевая процедура успешного решения любых заданий по математике. И по тригонометрии в том числе.
Итак, с общим правилом отсчёта углов на круге разобрались. Ну а коли мы тут заикнулись про полные обороты, про четверти, то пора бы уже покрутить и порисовать эти самые углы. Порисуем?)
Начнём пока с положительных углов. Они попроще в рисовании будут.
Рисуем углы в пределах одного оборота (между 0° и 360°).
Нарисуем, например, угол 60°. Тут всё просто, никаких заморочек. Рисуем координатные оси, круг. Можно прямо от руки, безо всякого циркуля и линейки. Рисуем схематично: у нас не черчение с вами. Никаких ГОСТов соблюдать не надо, не накажут.)
Можно (для себя) отметить значения углов на осях и указать стрелочку в направлении против часов. Ведь мы же в плюс откладывать собираемся?) Можно этого и не делать, но в голове держать всяко надо.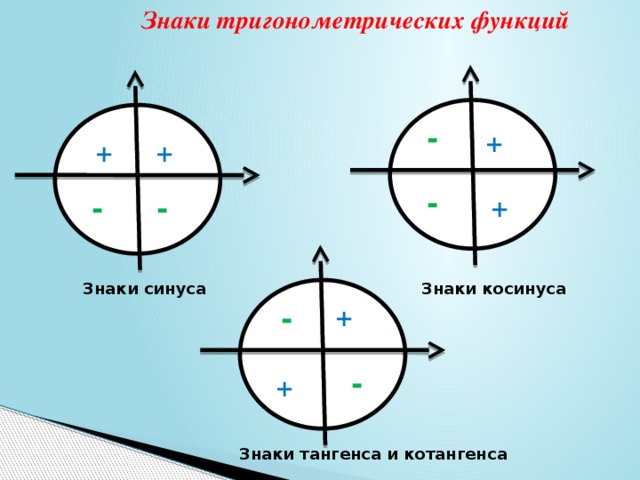
И теперь проводим вторую (подвижную) сторону угла. В какой четверти? В первой, разумеется! Ибо 60 градусов — это строго между 0° и 90°. Вот и рисуем в первой четверти. Под углом примерно 60 градусов к неподвижной стороне. Как отсчитать примерно 60 градусов без транспортира? Легко! 60° — это две трети от прямого угла! Делим мысленно первую чертвертинку круга на три части, забираем себе две трети. И рисуем… Сколько у нас там по факту получится (если приложить транспортир и померить) — 55 градусов или же 64 — неважно! Важно, что всё равно где-то около 60°.
Получаем картинку:
Вот и всё. И инструментов не понадобилось. Развиваем глазомер! В задачах по геометрии пригодится.) Этот неказистый рисунок бывает незаменим, когда надо нацарапать круг и угол на скорую руку, не особо задумываясь о красоте. Но при этом нацарапать правильно, без ошибок, со всей необходимой информацией. Например, как вспомогательное средство при решении тригонометрических уравнений и неравенств.
Например, как вспомогательное средство при решении тригонометрических уравнений и неравенств.
Нарисуем теперь угол, например, 265°. Прикидываем, где он может располагаться? Ну, ясное дело, что не в первой четверти и даже не во второй: они на 90 и на 180 градусов оканчиваются. Можно сообразить, что 265° — это 180° плюс ещё 85°. То есть, к отрицательной полуоси ОХ (там, где 180°) надо добавить примерно 85°. Или, что ещё проще, догадаться, что 265° не дотягивает до отрицательной полуоси OY (там, где 270°) каких-то несчастных 5°. Одним словом, в третьей четверти будет этот угол. Очень близко к отрицательной полуоси OY, к 270 градусам, но всё-таки в третьей!
Рисуем:
Повторюсь, абсолютная точность здесь не требуется. Пускай в реальности этот угол получился, скажем 263 градуса. Но на самый главный вопрос (какая четверть?) мы ответили безошибочно. Почему этот вопрос самый главный? Да потому, что любая работа с углом в тригонометрии (неважно, будем мы рисовать этот угол или не будем) начинается с ответа именно на этот вопрос! Всегда. Если этот вопрос проигнорировать или пробовать на него ответить мысленно, то ошибки почти неизбежны, да… Оно вам надо?
Если этот вопрос проигнорировать или пробовать на него ответить мысленно, то ошибки почти неизбежны, да… Оно вам надо?
Запоминаем:
Любая работа с углом (в том числе и рисование этого самого угла на круге) всегда начинается с определения четверти, в которую попадает этот угол.
Теперь, я надеюсь, вы уже безошибочно изобразите углы, например, 182°, 88°, 280°. В правильных четвертях. В третьей, первой и четвёртой, если что…)
Четвёртая четверть заканчивается углом 360°. Это один полный оборот. Ясен перец, что этот угол занимает на круге то же самое положение, что и 0° (т.е. начало отсчёта). Но углы на этом не заканчиваются, да…
Что делать с углами, большими 360°?
«А такие разве бывают?» — спросите вы. Бывают, ещё как! Бывает, например, угол 444°. А бывает, скажем, угол 1000°. Всякие углы бывают.) Просто визуально такие экзотические углы воспринимаются чуть сложнее, чем привычные нам углы в пределах одного оборота.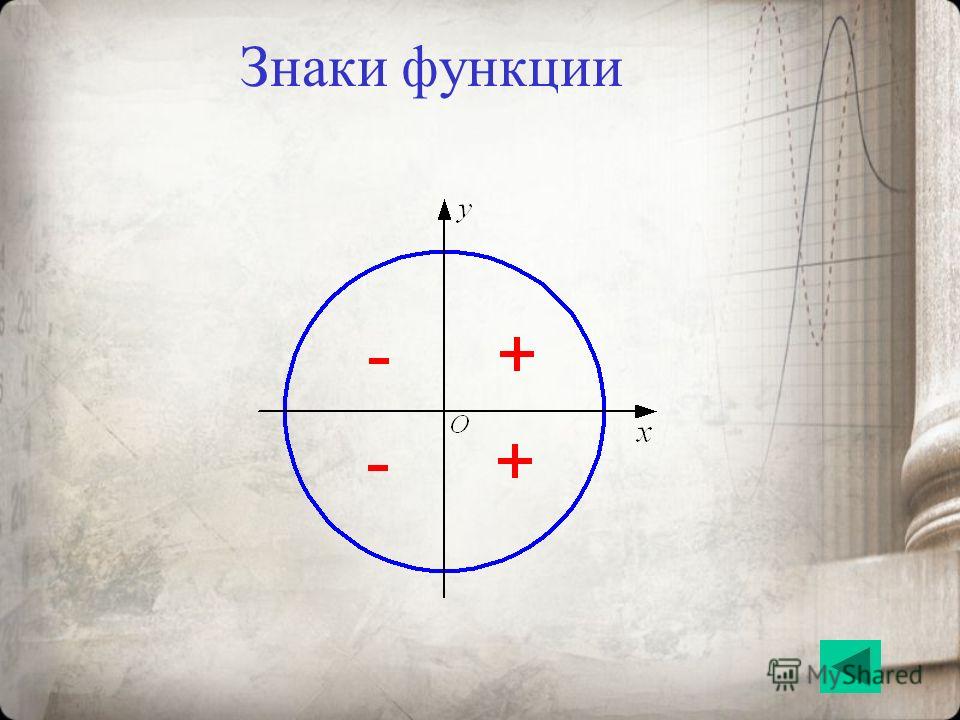 Но рисовать и просчитывать такие углы тоже надо уметь, да.
Но рисовать и просчитывать такие углы тоже надо уметь, да.
Для правильного рисования таких углов на круге необходимо всё то же самое — выяснить, в какую четверть попадает интересующий нас угол. Здесь умение безошибочно определять четверть куда более важно, чем для углов от 0° до 360°! Сама процедура определения четверти усложняется всего одним шагом. Каким, скоро увидите.
Итак, например, нам надо выяснить, в какую четверть попадает угол 444°. Начинаем крутить. Куда? В плюс, разумеется! Угол-то нам дали положительный! +444°. Крутим, крутим… Крутанули на один оборот — дошли до 360°.
Ну и крутим себе дальше!
Сколько там осталось до 444°? Считаем оставшийся хвостик:
444°-360° = 84°.
Итак, 444° — это один полный оборот (360°) плюс ещё 84°. Очевидно, это первая четверть. Итак, угол 444° попадает в первую четверть. Полдела сделано.
Осталось теперь изобразить этот угол. Как? Очень просто! Делаем один полный оборот по красной (плюсовой) стрелке и добавляем ещё 84°.
Как? Очень просто! Делаем один полный оборот по красной (плюсовой) стрелке и добавляем ещё 84°.
Вот так:
Здесь я уж не стал загромождать рисунок — подписывать четверти, рисовать углы на осях. Это всё добро уже давно в голове быть должно.)
Зато я «улиткой» или спиралькой показал, как именно складывается угол 444° из углов 360° и 84°. Пунктирная красная линия — это один полный оборот. К которому дополнительно прикручиваются 84° (сплошная линия). Кстати, обратите внимание, что, если этот самый полный оборот отбросить, то это никак не повлияет на положение нашего угла!
А вот это важно! Положение угла 444° полностью совпадает с положением угла 84°. Никаких чудес нет, так уж получается.)
А можно ли отбросить не один полный оборот, а два или больше?
А почему — нет? Если угол здоровенный, то не просто можно, а даже нужно! Угол-то не изменится! Точнее, сам-то угол по величине, конечно же, изменится. А вот его положение на круге — никак нет!) На то они и полные обороты, что сколько экземпляров ни добавляй, сколько ни убавляй, всё равно будешь в одну и ту же точку попадать. Приятно, правда?
А вот его положение на круге — никак нет!) На то они и полные обороты, что сколько экземпляров ни добавляй, сколько ни убавляй, всё равно будешь в одну и ту же точку попадать. Приятно, правда?
Запоминаем:
Если к углу прибавить (отнять) любое целое число полных оборотов, положение исходного угла на круге НЕ изменится!
Например:
В какую четверть попадает угол 1000°?
Никаких проблем! Считаем, сколько полных оборотов сидит в тысяче градусов. Один оборот — это 360°, ещё один — уже 720°, третий — 1080°… Стоп! Перебор! Значит, в угле 1000° сидит два полных оборота. Выбрасываем их из 1000° и считаем остаток:
1000° — 2·360° = 280°
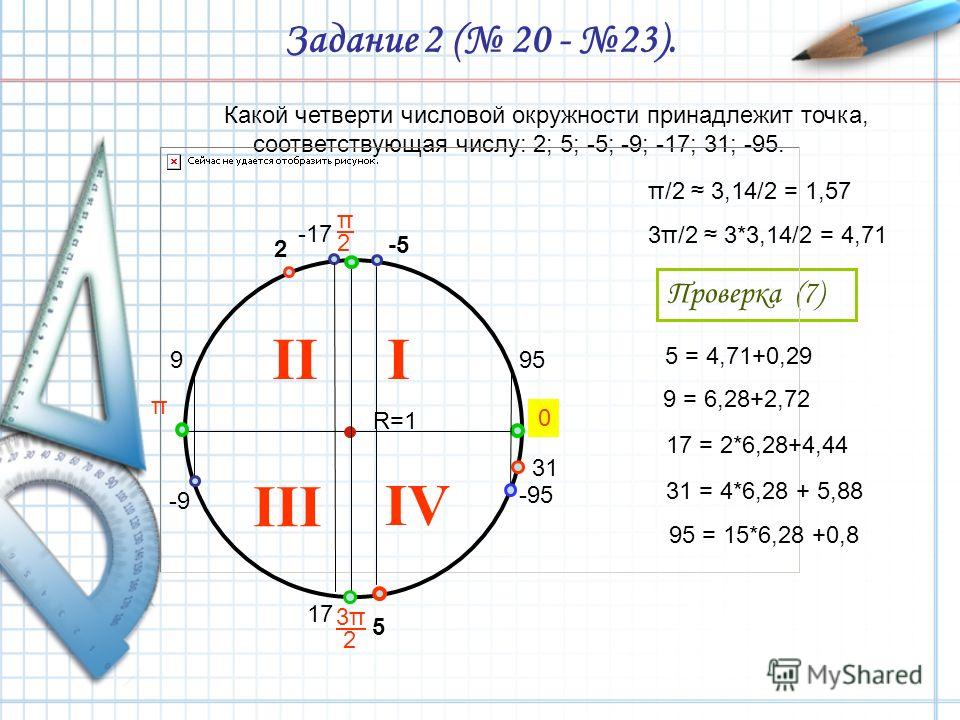
Значит, положение угла 1000° на круге то же самое, что и у угла 280°. С которым работать уже гораздо приятнее.) И куда же попадает этот угол? В четвёртую четверть он попадает: 270° (отрицательная полуось OY) плюс ещё десяточка.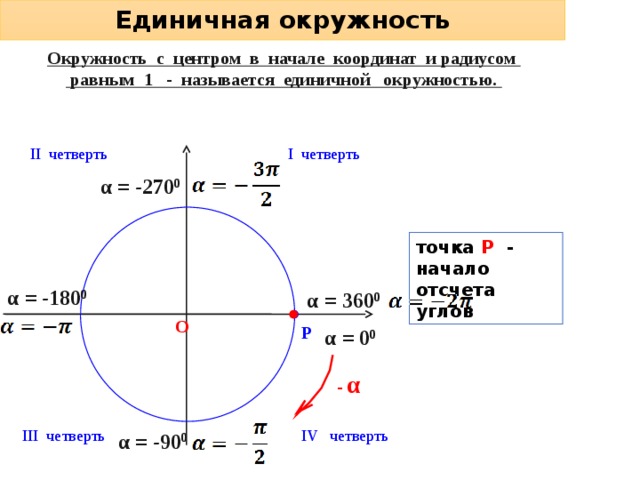
Рисуем:
Здесь я уже не рисовал пунктирной спиралькой два полных оборота: уж больно длинная она получается. Просто нарисовал оставшийся хвостик от нуля, отбросив все лишние обороты. Как будто бы их и не было вовсе.)
И ещё раз. По-хорошему, углы 444° и 84°, а также 1000° и 280° — разные. Но для синуса, косинуса, тангенса и котангенса эти углы — одинаковые!
Как вы видите, для того чтобы работать с углами, большими 360°, надо определить, сколько полных оборотов сидит в заданном большом угле. Это и есть тот самый дополнительный шаг, который обязательно надо предварительно проделывать при работе с такими углами. Ничего сложного, правда?
Отбрасывание полных оборотов, конечно, занятие приятное.) Но на практике при работе с совсем уж кошмарными углами случаются и затруднения.
Например:
В какую четверть попадает угол 31240° ?
И что же, будем много-много раз прибавлять по 360 градусов? Можно, если не горит особо. Но мы же не только складывать можем.) Ещё и делить умеем!
Но мы же не только складывать можем.) Ещё и делить умеем!
Вот и поделим наш большущий угол на 360 градусов!
Этим действием мы как раз и узнаем, сколько полных оборотов запрятано в наших 31240 градусах. Можно уголком поделить, можно (шепну на ушко :)) на калькуляторе.)
Получим 31240:360 = 86,777777….
То, что число получилось дробным — не страшно. Нас же только целые обороты интересуют! Стало быть, до конца делить и не надо.)
Итак, в нашем лохматом угле сидит аж 86 полных оборотов. Ужас…
В градусах это будет 86·360° = 30960°
Вот так. Именно столько градусов можно безболезненно выкинуть из заданного угла 31240°. Останется:
31240° — 30960° = 280°
Всё! Положение угла 31240° полностью идентифицировано! Там же, где и 280°. Т.е. четвёртая четверть.) Кажется, мы уже изображали этот угол ранее? Когда угол 1000° рисовали?) Там мы тоже на 280 градусов вышли. Совпадение.)
Совпадение.)
Итак, мораль сей басни такова:
Если нам задан страшный здоровенный угол, то:
1. Определяем, сколько полных оборотов сидит в этом угле. Для этого делим исходный угол на 360 и отбрасываем дробную часть.
2. Считаем, сколько градусов в полученном количестве оборотов. Для этого умножаем число оборотов на 360.
3. Отнимаем эти обороты от исходного угла и работаем с привычным углом в пределах от 0° до 360°.
Как работать с отрицательными углами?
Не вопрос! Точно так же, как и с положительными, только с одним единственным отличием. Каким? Да! Крутить углы надо в обратную сторону, в минус! По ходу часовой стрелки.)
Нарисуем, например, угол -200°. Сначала всё как обычно для положительных углов — оси, круг. Ещё синюю стрелочку с минусом изобразим да углы на осях по-другому подпишем.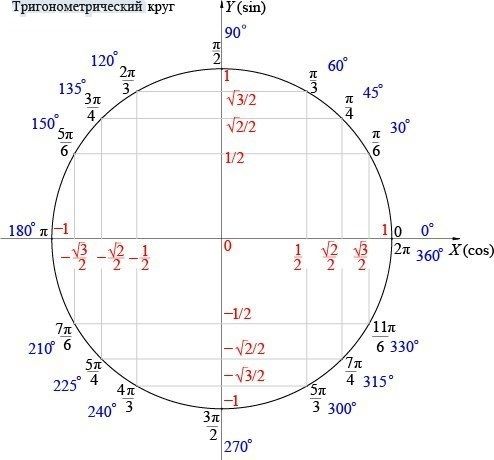 Их, естественно, также придётся отсчитывать в отрицательном направлении. Это будут всё те же самые углы, шагающие через 90°, но отсчитанные в обратную сторону, в минус: 0°, -90°, -180°, -270°, -360°.
Их, естественно, также придётся отсчитывать в отрицательном направлении. Это будут всё те же самые углы, шагающие через 90°, но отсчитанные в обратную сторону, в минус: 0°, -90°, -180°, -270°, -360°.
Картинка станет вот такой:
При работе с отрицательными углами часто возникает чувство лёгкого недоумения. Как так?! Получается, что одна и та же ось — это одновременно, скажем, и +90° и -270°? Неее, что-то тут нечисто…
Да всё чисто и прозрачно! Мы ведь же уже в курсе, что любую точку на круге можно обозвать как положительным углом, так и отрицательным! Совершенно любую. В том числе и на какой-то из координатных осей. В нашем случае нам нужно отрицательное исчисление углов. Вот и отщёлкиваем в минус все углы.)
Теперь нарисовать правильно угол -200° никакого труда не составляет. Это -180° и минус ещё 20°. Начинаем мотать от нуля в минус: четвёртую четверть пролетаем, третью тоже мимо, доходим до -180°. Куда мотать оставшуюся двадцатку? Да всё туда же! По часам.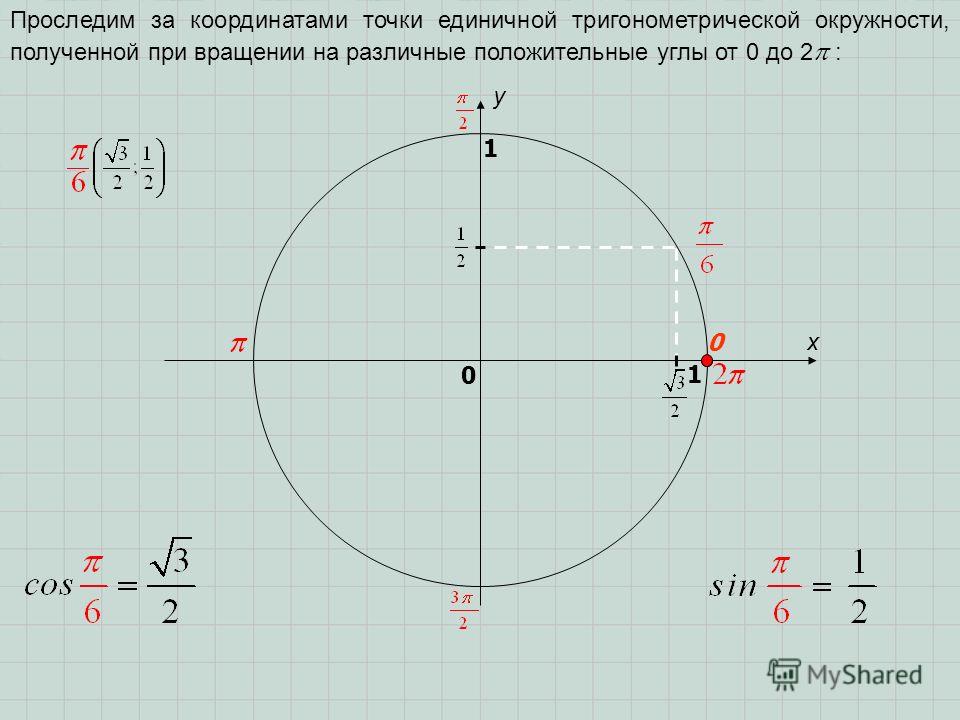 ) Итого угол -200° попадает во вторую четверть.
) Итого угол -200° попадает во вторую четверть.
Теперь вы понимаете, насколько важно железно помнить углы на осях координат?
Углы на осях координат (0°, 90°, 180°, 270°, 360°) надо помнить именно для того, чтобы безошибочно определять четверть, куда попадает угол!
А если угол большой, с несколькими полными оборотами? Ничего страшного! Какая разница, куда эти самые полные обороты крутить — в плюс или в минус? Точка-то на круге не изменит своего положения!
Например:
В какую четверть попадает угол -2000°?
Всё то же самое! Для начала считаем, сколько полных оборотов сидит в этом злом угле. Чтобы не косячить в знаках, оставим минус пока в покое и просто поделим 2000 на 360. Получим 5 с хвостиком. Хвостик нас пока не волнует, его чуть позже сосчитаем, когда рисовать угол будем. Считаем пять полных оборотов в градусах:
5·360° = 1800°
Воот. Именно столько лишних градусов можно смело выкинуть из нашего угла без ущерба для здоровья.
Именно столько лишних градусов можно смело выкинуть из нашего угла без ущерба для здоровья.
Считаем оставшийся хвостик:
2000° — 1800° = 200°
А вот теперь можно и про минус вспомнить.) Куда будем мотать хвостик 200°? В минус, конечно же! Нам же отрицательный угол задан.)
-2000° = -1800° — 200°
Вот и рисуем угол -200°, только уже без лишних оборотов. Только что его рисовали, но, так уж и быть, накалякаю ещё разок. От руки.
Ясен перец, что и заданный угол -2000°, так же как и -200°, попадает во вторую четверть.
Итак, мотаем себе на кру… пардон… на ус:
Если задан очень большой отрицательный угол, то первая часть работы с ним (поиск числа полных оборотов и их отбрасывание) та же самая, что и при работе с положительным углом. Знак «минус» на данном этапе решения не играет никакой роли. Учитывается знак лишь в самом конце, при работе с углом, оставшимся после удаления полных оборотов.
Как видите, рисовать отрицательные углы на круге ничуть не сложнее, чем положительные.
Всё то же самое, только в другую сторону! По часам!
А вот теперь — самое интересное! Мы рассмотрели положительные углы, отрицательные углы, большие углы, маленькие — полный ассортимент. Также мы выяснили, что любую точку на круге можно обозвать положительным и отрицательным углом, отбрасывали полные обороты… Нету никаких мыслей? Должно отложиться…
Да! Какую точку на круге ни возьми, ей будет соответствовать бесконечное множество углов! Больших и не очень, положительных и отрицательных — всяких! И разница между этими углами будет составлять целое число полных оборотов. Всегда! Так уж тригонометрический круг устроен, да…) Именно поэтому обратная задача — найти угол по известным синусу/косинусу/тангенсу/котангенсу — решается неоднозначно. И куда сложнее. В отличие от прямой задачи — по заданному углу найти весь набор его тригонометрических функций. И в более серьёзных темах тригонометрии (арки, тригонометрические уравнения и неравенства) мы с этой фишкой будем сталкиваться постоянно. Привыкаем.)
И куда сложнее. В отличие от прямой задачи — по заданному углу найти весь набор его тригонометрических функций. И в более серьёзных темах тригонометрии (арки, тригонометрические уравнения и неравенства) мы с этой фишкой будем сталкиваться постоянно. Привыкаем.)
Итак, будем считать, что самые-самые азы работы с углами на круге мы с вами освоили. Можно и на вопросы поотвечать. Самостоятельно.)
1. В какую четверть попадает угол -345°?
2. В какую четверть попадает угол 666°?
3. В какую четверть попадает угол 5555°?
4. В какую четверть попадает угол -3700°?
Всё хорошо? Поехали дальше.
5. Какой знак имеет cos999°?
6. Какой знак имеет ctg999°?
И это получилось? Прекрасно! Есть проблемы? Тогда вам сюда.
Ответы:
1. 1
2. 4
4
3. 2
4. 3
5. «+»
6. «-«
В этот раз ответы выданы по порядку в нарушение традиций. Ибо четвертей всего четыре, а знаков так и вовсе два. Особо не разбежишься…)
В следующем уроке мы с вами поговорим про радианы, про загадочное число «пи», научимся легко и просто переводить радианы в градусы и обратно. И с удивлением обнаружим, что даже этих простых знаний и навыков нам будет уже вполне достаточно для успешного решения многих нетривиальных задачек по тригонометрии!
| Табличка на двери |
| Синусоида | Косинусоида |
|---|---|
| y = sin x | y = cos x |
| ОДЗ [-1; 1] | ОДЗ [-1; 1] |
| sin x = 0, при x = πk, где k ϵ Z | cos x = 0, при x = π/2 + πk, где k ϵ Z |
| sin x = 1, при x = π/2 + 2πk, где k ϵ Z | cos x = 1, при x = 2πk, где k ϵ Z |
| sin x = — 1, при x = 3π/2 + 2πk, где k ϵ Z | cos x = — 1, при x = π + 2πk, где k ϵ Z |
| sin (-x) = — sin x, т. е. функция нечетная | cos (-x) = cos x, т. е. функция четная |
| функция периодическая, наименьший период — 2π | |
| sin x › 0, при x принадлежащем I и II четвертям или от 0° до 180° (2πk, π + 2πk) | cos x › 0, при x принадлежащем I и IV четвертям или от 270° до 90° (- π/2 + 2πk, π/2 + 2πk) |
| sin x ‹ 0, при x принадлежащем III и IV четвертям или от 180° до 360° (π + 2πk, 2π + 2πk) | cos x ‹ 0, при x принадлежащем II и III четвертям или от 90° до 270° (π/2 + 2πk, 3π/2 + 2πk) |
| возрастает на промежутке [- π/2 + 2πk, π/2 + 2πk] | возрастает на промежутке [-π + 2πk, 2πk] |
| убывает на промежутках [ π/2 + 2πk, 3π/2 + 2πk] | убывает на промежутках |
| производная (sin x)’ = cos x | производная (cos x)’ = — sin x |
Определить является ли функция четной или нет очень просто. Достаточно представить тригонометрический круг со знаками тригонометрических величин и мысленно «сложить» график относительно оси OX. Если знаки совпадают, функция четная, в противном случае — нечетная.
Достаточно представить тригонометрический круг со знаками тригонометрических величин и мысленно «сложить» график относительно оси OX. Если знаки совпадают, функция четная, в противном случае — нечетная.
Введение радиан и перечисление основных свойств синусоиды и косинусоиды позволяют привести следующую закономерность:
Убедиться в верности формулы очень просто. Например, для x = π/2 синус равен 1, как и косинус x = 0. Проверку можно осуществить обративших к таблицам или проследив кривые функций для заданных значений.
Свойства тангенсоиды и котангенсоиды
Графики функций тангенса и котангенса значительно отличаются от синусоиды и косинусоиды. Величины tg и ctg являются обратными друг другу.
- Y = tg x.
- Тангенсоида стремится к значениям y при x = π/2 + πk, но никогда не достигает их.
- Наименьший положительный период тангенсоиды равен π.
- Tg (- x) = — tg x, т. е. функция нечетная.
- Tg x = 0, при x = πk.

- Функция является возрастающей.
- Tg x › 0, при x ϵ (πk, π/2 + πk).
- Tg x ‹ 0, при x ϵ (— π/2 + πk, πk).
- Производная (tg x)’ = 1/cos 2 x .
Рассмотрим графическое изображение котангенсоиды ниже по тексту.
Основные свойства котангенсоиды:
- Y = ctg x.
- В отличие от функций синуса и косинуса, в тангенсоиде Y может принимать значения множества всех действительных чисел.
- Котангенсоида стремится к значениям y при x = πk, но никогда не достигает их.
- Наименьший положительный период котангенсоиды равен π.
- Ctg (- x) = — ctg x, т. е. функция нечетная.
- Ctg x = 0, при x = π/2 + πk.
- Функция является убывающей.
- Ctg x › 0, при x ϵ (πk, π/2 + πk).
- Ctg x ‹ 0, при x ϵ (π/2 + πk, πk).
- Производная (ctg x)’ = — 1/sin 2 x Исправить
Если вы уже знакомы с тригонометрическим кругом , и хотите лишь освежить в памяти отдельные элементы, или вы совсем нетерпеливы, – то вот он, :
Мы же здесь будем все подробно разбирать шаг за шагом.
Тригонометрический круг – не роскошь, а необходимость
Тригонометрия у многих ассоциируется с непроходимой чащей. Вдруг наваливается столько значений тригонометрических функций, столько формул… А оно ведь, как, – незаладилось вначале, и… пошло-поехало… сплошное непонимание…
Очень важно не махать рукой на значения тригонометрических функций , – мол, всегда можно посмотреть в шпору с таблицей значений.
Если вы постоянно смотрите в таблицу со значениями тригонометрических формул, давайте избавляться от этой привычки!
Нас выручит ! Вы несколько раз поработаете с ним, и далее он у вас сам будет всплывать в голове. Чем он лучше таблицы? Да в таблице-то вы найдете ограниченное число значений, а на круге – ВСЕ!
К примеру, скажите, глядя в стандартную таблицу значений тригонометрических формул , чему равен синус, скажем, 300 градусов, или -45.
Никак?.. можно, конечно, подключить формулы приведения … А глядя на тригонометрический круг, легко можно ответить на такие вопросы. И вы скоро будете знать как!
И вы скоро будете знать как!
А при решении тригонометрических уравнений и неравенств без тригонометрического круга – вообще никуда.
Знакомство с тригонометрическим кругом
Давайте по порядку.
Сначала выпишем вот такой ряд чисел:
А теперь такой:
И, наконец, такой:
Конечно, понятно, что, на самом-то деле, на первом месте стоит , на втором месте стоит , а на последнем – . То есть нас будет больше интересовать цепочка .
Но как красиво она получилась! В случае чего – восстановим эту «лесенку-чудесенку».
И зачем оно нам?
Эта цепочка – и есть основные значения синуса и косинуса в первой четверти.
Начертим в прямоугольной системе координат круг единичного радиуса (то есть радиус-то по длине берем любой, а его длину объявляем единичной).
От луча «0-Старт» откладываем в направлении стрелки (см. рис.) углы .
Получаем соответствующие точки на круге. Так вот если спроецировать точки на каждую из осей, то мы выйдем как раз на значения из указанной выше цепочки.
Это почему же, спросите вы?
Не будем разбирать все. Рассмотрим принцип , который позволит справиться и с другими, аналогичными ситуациями.
Треугольник АОВ – прямоугольный, в нем . А мы знаем, что против угла в лежит катет вдвое меньший гипотенузы (гипотенуза у нас = радиусу круга, то есть 1).
Значит, АВ= (а следовательно, и ОМ=). А по теореме Пифагора
Надеюсь, уже что-то становится понятно?
Так вот точка В и будет соответствовать значению , а точка М – значению
Аналогично с остальными значениями первой четверти.
Как вы понимаете, привычная нам ось (ox) будет осью косинусов , а ось (oy) – осью синусов . позже.
Слева от нуля по оси косинусов (ниже нуля по оси синусов) будут, конечно, отрицательные значения.
Итак, вот он, ВСЕМОГУЩИЙ , без которого никуда в тригонометрии.
А вот как пользоваться тригонометрическим кругом, мы поговорим в .
Назад
Вперёд
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации.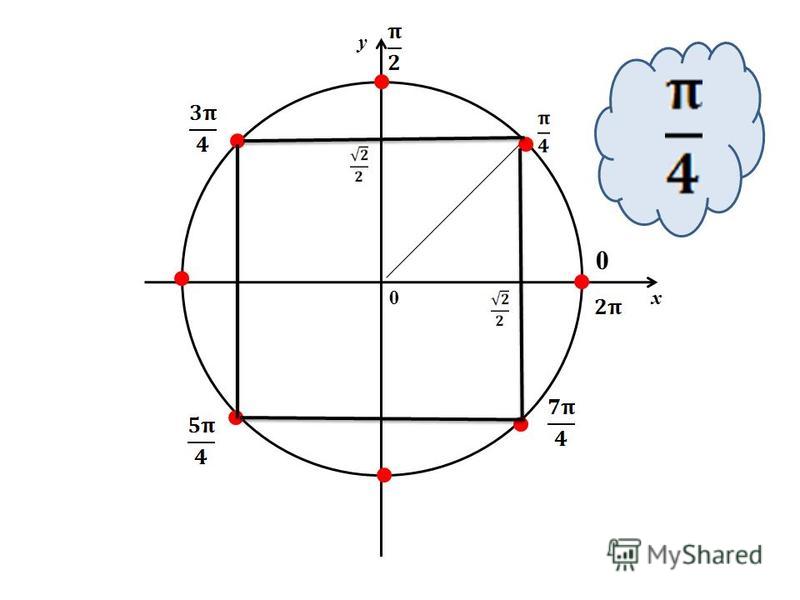 Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Цель: научить использовать единичную окружность при решении различных тригонометрических заданий.
В школьном курсе математики возможны различные варианты введения тригонометрических функций. Наиболее удобной и часто используемой является «числовая единичная окружность». Её применение в теме «Тригонометрия» весьма обширно.
Единичная окружность используется для:
– определения синуса, косинуса, тангенса и котангенса угла;
– нахождения значений тригонометрических функций для некоторых значений числового и углового аргумента;
– выведение основных формул тригонометрии;
– выведения формул приведения;
– нахождения области определения и области значений тригонометрических функций;
– определения периодичности тригонометрических функций;
– определения четности и нечетности тригонометрических функций;
– определения промежутков возрастания и убывания тригонометрических функций;
– определения промежутков знакопостоянства тригонометрических функций;
– радианного измерения углов;
– нахождения значений обратных тригонометрических функций;
– решение простейших тригонометрических уравнений;
– решение простейших неравенств и др.
Таким образом, активное осознанное владение учащимися данным видом наглядности дает неоспоримые преимущества для овладения разделом математики «Тригонометрия».
Использование ИКТ на уроках преподавания математики позволяет облегчить овладение числовой единичной окружностью. Конечно, интерактивная доска имеет широчайший диапазон применения, однако не во всех классах она есть. Если же говорить о применении презентаций, то на просторах Интернета и их выбор велик, и каждый педагог может найти наиболее приемлемый вариант для своих уроков.
В чем особенность представляемой мною презентации?
Данная презентация предполагает различные варианты использования и не является наглядностью к конкретному уроку в теме «Тригонометрия». Каждый слайд данной презентации можно использовать обособлено, как на этапе объяснения материала, формирования навыков, так и для рефлексии. При создании данной презентации особое внимание уделялось «читаемости» её с дальнего расстояния, поскольку количество учеников со сниженным зрением постоянно растет. Продумано цветовое решение, логически связанные объекты объединены единым цветом. Презентация анимирована таким образом, чтобы учитель имел возможность комментировать фрагмент слайда, а ученик задать вопрос. Таким образом, данная презентация – это своего рода «подвижные» таблицы. Последние слайды не анимированы и используются для проверки усвоения материала, в ходе решения тригонометрических заданий. Окружность на слайдах максимально упрощена внешне и максимально приближена к изображаемой на тетрадном листе учениками. Это условие я считаю принципиальным. У учащихся важно сформировать мнение о единичной окружности, как о доступном и мобильном (хотя и не единственном) виде наглядности при решении тригонометрических заданий.
Продумано цветовое решение, логически связанные объекты объединены единым цветом. Презентация анимирована таким образом, чтобы учитель имел возможность комментировать фрагмент слайда, а ученик задать вопрос. Таким образом, данная презентация – это своего рода «подвижные» таблицы. Последние слайды не анимированы и используются для проверки усвоения материала, в ходе решения тригонометрических заданий. Окружность на слайдах максимально упрощена внешне и максимально приближена к изображаемой на тетрадном листе учениками. Это условие я считаю принципиальным. У учащихся важно сформировать мнение о единичной окружности, как о доступном и мобильном (хотя и не единственном) виде наглядности при решении тригонометрических заданий.
Данная презентация поможет педагогам познакомить учеников с единичной окружностью в 9 классе на уроках геометрии при изучении темы «Соотношения между сторонами и углами треугольника». И, конечно, она поможет расширить и углубить навык работы с единичной окружностью при решении тригонометрических заданий у учащихся старшего звена обучения на уроках алгебры.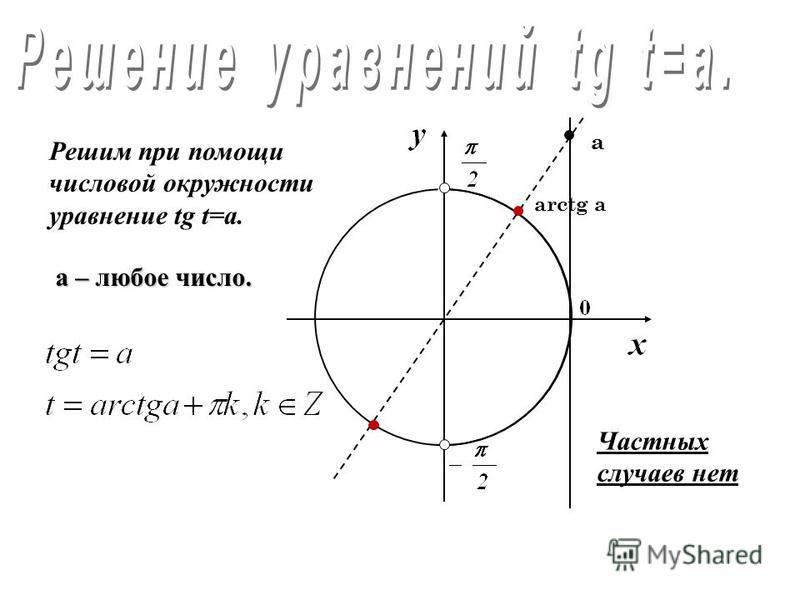
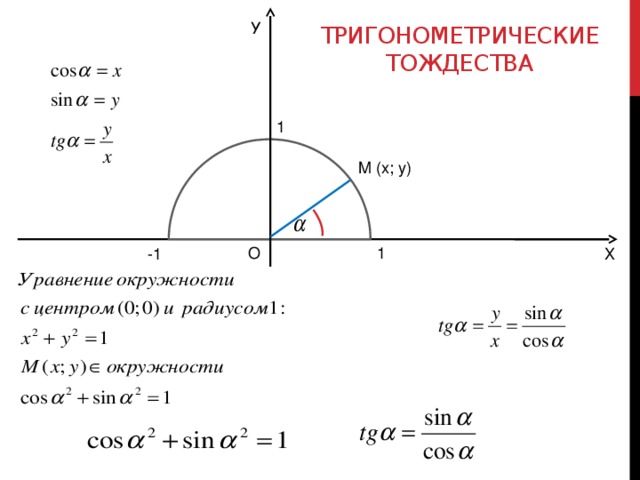
Слайды 3, 4 поясняют построение единичной окружности; принцип определения местоположения точки на единичной окружности в I и II координатных четвертях; переход от геометрических определений функций синус и косинус (в прямоугольном треугольнике) к алгебраическим на единичной окружности.
Слайды 5-8 поясняют, как найти значения тригонометрических функций для основных углов I координатной четверти.
Слайды 9-11 поясняет знаки функций в координатных четвертях; определение промежутков знакопостоянства тригонометрических функций.
Слайд 12 используется для формирования представлений о положительных и отрицательных значениях углов; знакомством с понятием периодичности тригонометрических функций.
Слайды 13, 14 используются при переходе на радианную меру угла.
Слайды 15-18 не анимированы и используются при решении различных тригонометрических заданий, закрепления и проверки результатов усвоения материала.
- Титульный лист.

- Целеполагание.
- Построение единичной окружности. Основные значения углов в градусной мере.
- Определение синуса и косинуса угла на единичной окружности.
- Табличные значения для синуса в порядке возрастания.
- Табличные значения для косинуса в порядке возрастания.
- Табличные значения для тангенса в порядке возрастания.
- Табличные значения для котангенса в порядке возрастания.
- Знаки функции sin α.
- Знаки функции cos α.
- Знаки функций tg α и ctg α.
- Положительные и отрицательные значения углов на единичной окружности.
- Радианная мера угла.
- Положительные и отрицательные значения углов в радианах на единичной окружности.
- Различные варианты единичной окружности для закрепления и проверки результатов усвоения материала.
Числовая окружность тригонометрия. Тригонометрический круг
Тригонометрический круг. Единичная окружность.
 Числовая окружность. Что это такое?
Числовая окружность. Что это такое?Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)
Очень часто термины тригонометрический круг, единичная окружность, числовая окружность плохо понимаются учащимся народом. И совершенно зря. Эти понятия – мощный и универсальный помощник во всех разделах тригонометрии. Фактически, это легальная шпаргалка! Нарисовал тригонометрический круг – и сразу увидел ответы! Заманчиво? Так давайте освоим, грех такой вещью не воспользоваться. Тем более, это совсем несложно.
Для успешной работы с тригонометрическим кругом нужно знать всего три вещи.
Если Вам нравится этот сайт…Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.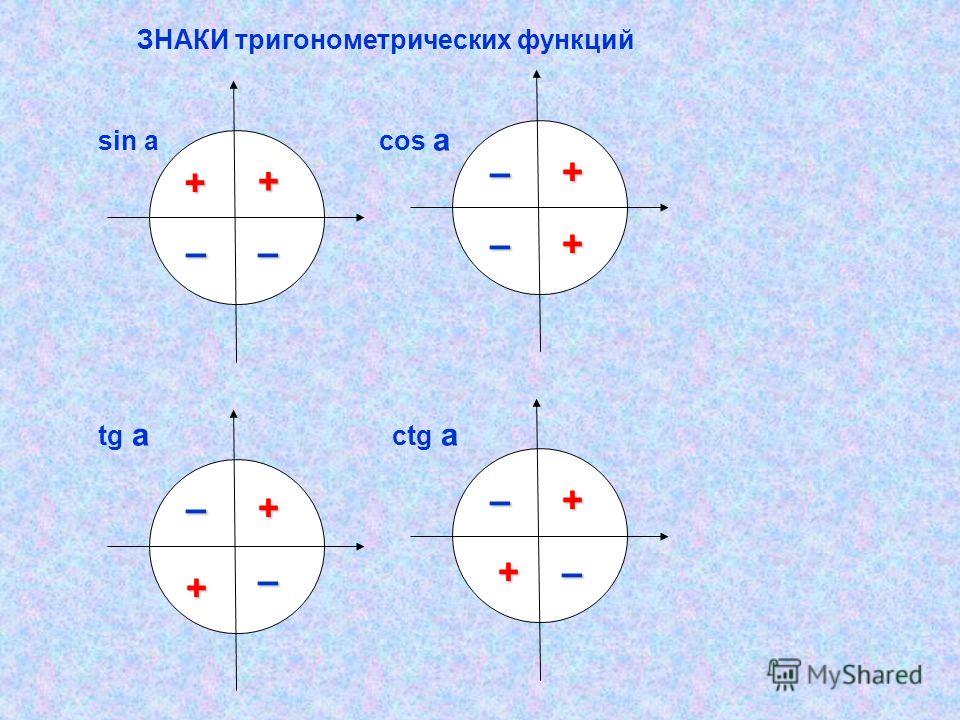
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.

- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.

- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Тригонометрия, как наука, зародилась на Древнем Востоке. Первые тригонометрические соотношения были выведены астрономами для создания точного календаря и ориентированию по звездам. Данные вычисления относились к сферической тригонометрии, в то время как в школьном курсе изучают соотношения сторон и угла плоского треугольника.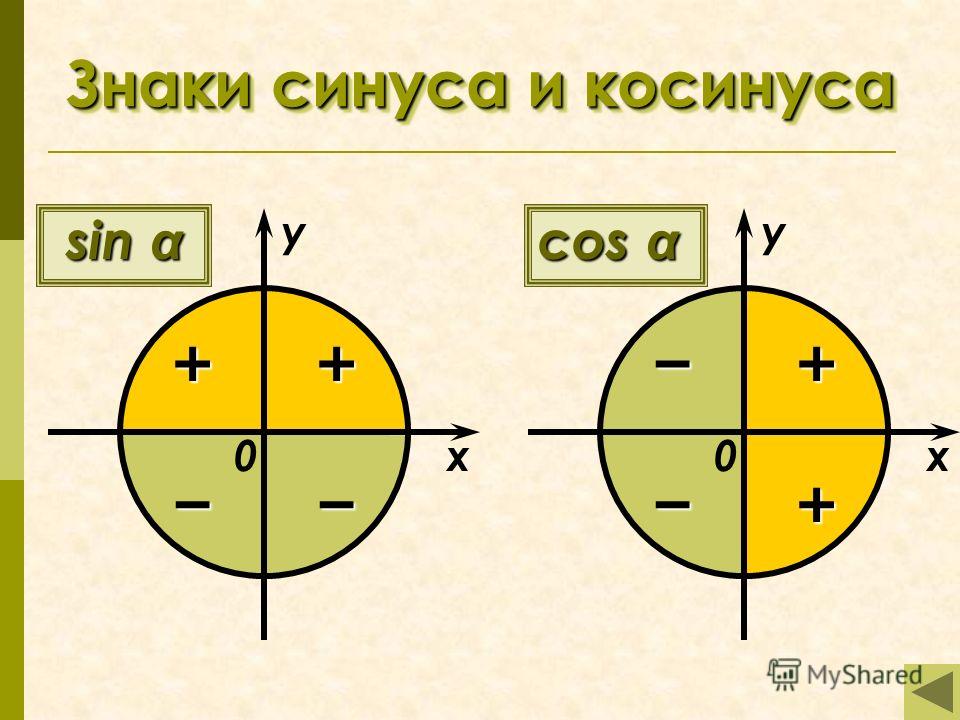
Тригонометрия – это раздел математики, занимающийся свойствами тригонометрических функций и зависимостью между сторонами и углами треугольников.
В период расцвета культуры и науки I тысячелетия нашей эры знания распространились с Древнего Востока в Грецию. Но основные открытия тригонометрии – это заслуга мужей арабского халифата. В частности, туркменский ученый аль-Маразви ввел такие функции, как тангенс и котангенс, составил первые таблицы значений для синусов, тангенсов и котангенсов. Понятие синуса и косинуса введены индийскими учеными. Тригонометрии посвящено немало внимания в трудах таких великих деятелей древности, как Евклида, Архимеда и Эратосфена.
Основные величины тригонометрии
Основные тригонометрические функции числового аргумента – это синус, косинус, тангенс и котангенс. Каждая из них имеет свой график: синусоида, косинусоида, тангенсоида и котангенсоида.
В основе формул для расчета значений указанных величин лежит теорема Пифагора. Школьникам она больше известна в формулировке: «Пифагоровы штаны, во все стороны равны», так как доказательство приводится на примере равнобедренного прямоугольного треугольника.
Школьникам она больше известна в формулировке: «Пифагоровы штаны, во все стороны равны», так как доказательство приводится на примере равнобедренного прямоугольного треугольника.
Синус, косинус и другие зависимости устанавливают связь между острыми углами и сторонами любого прямоугольного треугольника. Приведем формулы для расчета этих величин для угла A и проследим взаимосвязи тригонометрических функций:
Как видно, tg и ctg являются обратными функциями. Если представить катет a как произведение sin A и гипотенузы с, а катет b в виде cos A * c, то получим следующие формулы для тангенса и котангенса:
Тригонометрический круг
Графически соотношение упомянутых величин можно представить следующим образом:
Окружность, в данном случае, представляет собой все возможные значения угла α — от 0° до 360°. Как видно из рисунка, каждая функция принимает отрицательное или положительное значение в зависимости от величины угла. Например, sin α будет со знаком «+», если α принадлежит I и II четверти окружности, то есть, находится в промежутке от 0° до 180°.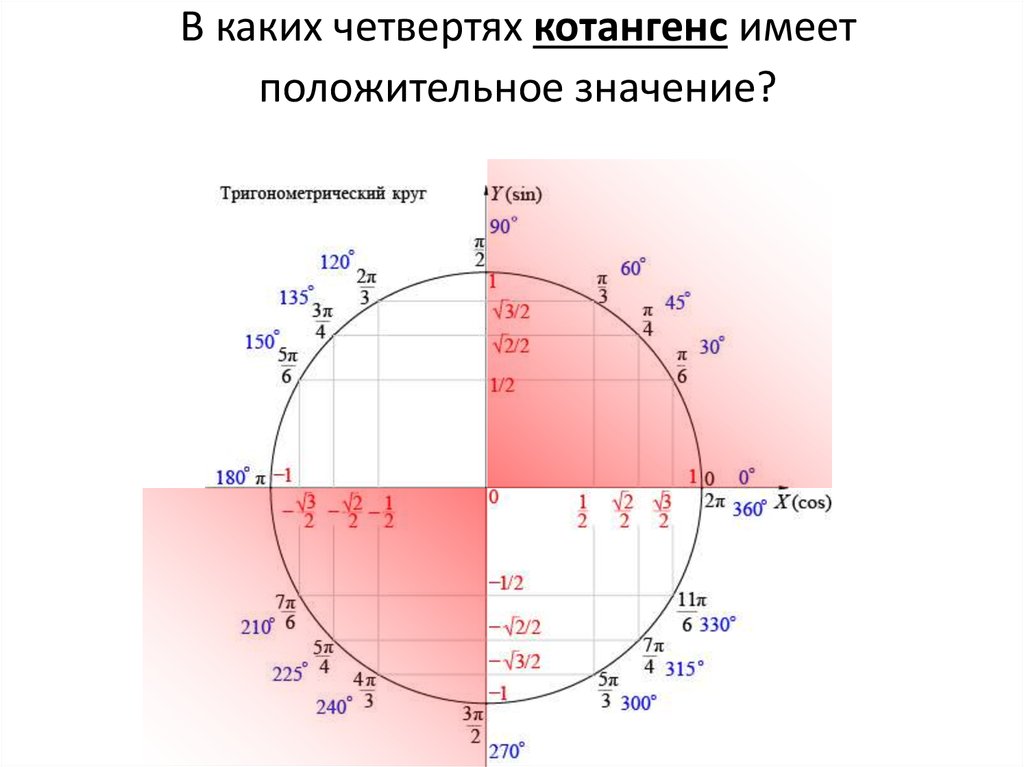 При α от 180° до 360° (III и IV четверти) sin α может быть только отрицательным значением.
При α от 180° до 360° (III и IV четверти) sin α может быть только отрицательным значением.
Попробуем построить тригонометрические таблицы для конкретных углов и узнать значение величин.
Значения α равные 30°, 45°, 60°, 90°, 180° и так далее – называют частными случаями. Значения тригонометрических функций для них просчитаны и представлены в виде специальных таблиц.
Данные углы выбраны отнюдь не случайно. Обозначение π в таблицах стоит для радиан. Рад — это угол, при котором длина дуги окружности соответствует ее радиусу. Данная величина была введена для того, чтобы установить универсальную зависимость, при расчетах в радианах не имеет значение действительная длина радиуса в см.
Углы в таблицах для тригонометрических функций соответствуют значениям радиан:
Итак, не трудно догадаться, что 2π – это полная окружность или 360°.
Свойства тригонометрических функций: синус и косинус
Для того, чтобы рассмотреть и сравнить основные свойства синуса и косинуса, тангенса и котангенса, необходимо начертить их функции.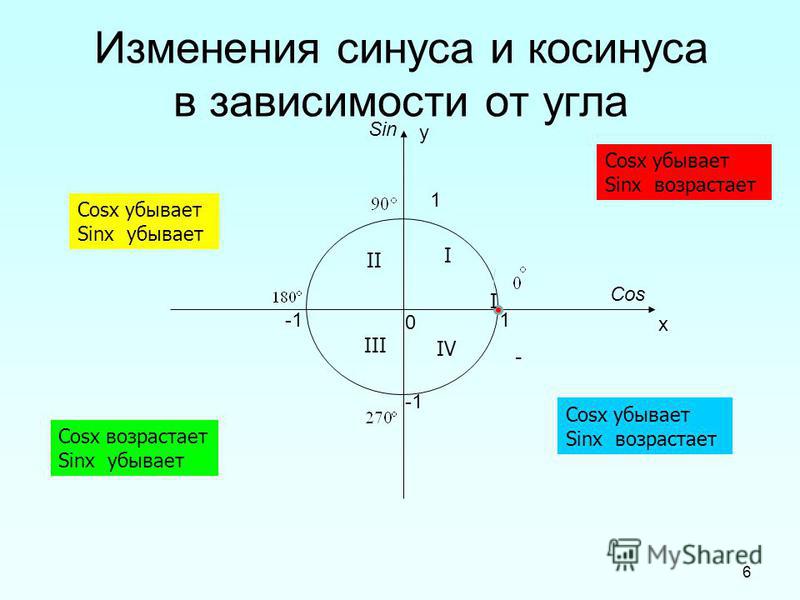 Сделать это можно в виде кривой, расположенной в двумерной системе координат.
Сделать это можно в виде кривой, расположенной в двумерной системе координат.
Рассмотри сравнительную таблицу свойств для синусоиды и косинусоиды:
| Синусоида | Косинусоида |
|---|---|
| y = sin x | y = cos x |
| ОДЗ [-1; 1] | ОДЗ [-1; 1] |
| sin x = 0, при x = πk, где k ϵ Z | cos x = 0, при x = π/2 + πk, где k ϵ Z |
| sin x = 1, при x = π/2 + 2πk, где k ϵ Z | cos x = 1, при x = 2πk, где k ϵ Z |
| sin x = — 1, при x = 3π/2 + 2πk, где k ϵ Z | cos x = — 1, при x = π + 2πk, где k ϵ Z |
| sin (-x) = — sin x, т. е. функция нечетная | cos (-x) = cos x, т. е. функция четная |
| функция периодическая, наименьший период — 2π | |
| sin x › 0, при x принадлежащем I и II четвертям или от 0° до 180° (2πk, π + 2πk) | cos x › 0, при x принадлежащем I и IV четвертям или от 270° до 90° (- π/2 + 2πk, π/2 + 2πk) |
| sin x ‹ 0, при x принадлежащем III и IV четвертям или от 180° до 360° (π + 2πk, 2π + 2πk) | cos x ‹ 0, при x принадлежащем II и III четвертям или от 90° до 270° (π/2 + 2πk, 3π/2 + 2πk) |
| возрастает на промежутке [- π/2 + 2πk, π/2 + 2πk] | возрастает на промежутке [-π + 2πk, 2πk] |
| убывает на промежутках [ π/2 + 2πk, 3π/2 + 2πk] | убывает на промежутках |
| производная (sin x)’ = cos x | производная (cos x)’ = — sin x |
Определить является ли функция четной или нет очень просто. Достаточно представить тригонометрический круг со знаками тригонометрических величин и мысленно «сложить» график относительно оси OX. Если знаки совпадают, функция четная, в противном случае — нечетная.
Достаточно представить тригонометрический круг со знаками тригонометрических величин и мысленно «сложить» график относительно оси OX. Если знаки совпадают, функция четная, в противном случае — нечетная.
Введение радиан и перечисление основных свойств синусоиды и косинусоиды позволяют привести следующую закономерность:
Убедиться в верности формулы очень просто. Например, для x = π/2 синус равен 1, как и косинус x = 0. Проверку можно осуществить обративших к таблицам или проследив кривые функций для заданных значений.
Свойства тангенсоиды и котангенсоиды
Графики функций тангенса и котангенса значительно отличаются от синусоиды и косинусоиды. Величины tg и ctg являются обратными друг другу.
- Y = tg x.
- Тангенсоида стремится к значениям y при x = π/2 + πk, но никогда не достигает их.
- Наименьший положительный период тангенсоиды равен π.
- Tg (- x) = — tg x, т. е. функция нечетная.
- Tg x = 0, при x = πk.

- Функция является возрастающей.
- Tg x › 0, при x ϵ (πk, π/2 + πk).
- Tg x ‹ 0, при x ϵ (— π/2 + πk, πk).
- Производная (tg x)’ = 1/cos 2 x .
Рассмотрим графическое изображение котангенсоиды ниже по тексту.
Основные свойства котангенсоиды:
- Y = ctg x.
- В отличие от функций синуса и косинуса, в тангенсоиде Y может принимать значения множества всех действительных чисел.
- Котангенсоида стремится к значениям y при x = πk, но никогда не достигает их.
- Наименьший положительный период котангенсоиды равен π.
- Ctg (- x) = — ctg x, т. е. функция нечетная.
- Ctg x = 0, при x = π/2 + πk.
- Функция является убывающей.
- Ctg x › 0, при x ϵ (πk, π/2 + πk).
- Ctg x ‹ 0, при x ϵ (π/2 + πk, πk).
- Производная (ctg x)’ = — 1/sin 2 x Исправить
Назад
Вперёд
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Цель: научить использовать единичную окружность при решении различных тригонометрических заданий.
В школьном курсе математики возможны различные варианты введения тригонометрических функций. Наиболее удобной и часто используемой является «числовая единичная окружность». Её применение в теме «Тригонометрия» весьма обширно.
Единичная окружность используется для:
– определения синуса, косинуса, тангенса и котангенса угла;
– нахождения значений тригонометрических функций для некоторых значений числового и углового аргумента;
– выведение основных формул тригонометрии;
– выведения формул приведения;
– нахождения области определения и области значений тригонометрических функций;
– определения периодичности тригонометрических функций;
– определения четности и нечетности тригонометрических функций;
– определения промежутков возрастания и убывания тригонометрических функций;
– определения промежутков знакопостоянства тригонометрических функций;
– радианного измерения углов;
– нахождения значений обратных тригонометрических функций;
– решение простейших тригонометрических уравнений;
– решение простейших неравенств и др.
Таким образом, активное осознанное владение учащимися данным видом наглядности дает неоспоримые преимущества для овладения разделом математики «Тригонометрия».
Использование ИКТ на уроках преподавания математики позволяет облегчить овладение числовой единичной окружностью. Конечно, интерактивная доска имеет широчайший диапазон применения, однако не во всех классах она есть. Если же говорить о применении презентаций, то на просторах Интернета и их выбор велик, и каждый педагог может найти наиболее приемлемый вариант для своих уроков.
В чем особенность представляемой мною презентации?
Данная презентация предполагает различные варианты использования и не является наглядностью к конкретному уроку в теме «Тригонометрия». Каждый слайд данной презентации можно использовать обособлено, как на этапе объяснения материала, формирования навыков, так и для рефлексии. При создании данной презентации особое внимание уделялось «читаемости» её с дальнего расстояния, поскольку количество учеников со сниженным зрением постоянно растет. Продумано цветовое решение, логически связанные объекты объединены единым цветом. Презентация анимирована таким образом, чтобы учитель имел возможность комментировать фрагмент слайда, а ученик задать вопрос. Таким образом, данная презентация – это своего рода «подвижные» таблицы. Последние слайды не анимированы и используются для проверки усвоения материала, в ходе решения тригонометрических заданий. Окружность на слайдах максимально упрощена внешне и максимально приближена к изображаемой на тетрадном листе учениками. Это условие я считаю принципиальным. У учащихся важно сформировать мнение о единичной окружности, как о доступном и мобильном (хотя и не единственном) виде наглядности при решении тригонометрических заданий.
Продумано цветовое решение, логически связанные объекты объединены единым цветом. Презентация анимирована таким образом, чтобы учитель имел возможность комментировать фрагмент слайда, а ученик задать вопрос. Таким образом, данная презентация – это своего рода «подвижные» таблицы. Последние слайды не анимированы и используются для проверки усвоения материала, в ходе решения тригонометрических заданий. Окружность на слайдах максимально упрощена внешне и максимально приближена к изображаемой на тетрадном листе учениками. Это условие я считаю принципиальным. У учащихся важно сформировать мнение о единичной окружности, как о доступном и мобильном (хотя и не единственном) виде наглядности при решении тригонометрических заданий.
Данная презентация поможет педагогам познакомить учеников с единичной окружностью в 9 классе на уроках геометрии при изучении темы «Соотношения между сторонами и углами треугольника». И, конечно, она поможет расширить и углубить навык работы с единичной окружностью при решении тригонометрических заданий у учащихся старшего звена обучения на уроках алгебры.
Слайды 3, 4 поясняют построение единичной окружности; принцип определения местоположения точки на единичной окружности в I и II координатных четвертях; переход от геометрических определений функций синус и косинус (в прямоугольном треугольнике) к алгебраическим на единичной окружности.
Слайды 5-8 поясняют, как найти значения тригонометрических функций для основных углов I координатной четверти.
Слайды 9-11 поясняет знаки функций в координатных четвертях; определение промежутков знакопостоянства тригонометрических функций.
Слайд 12 используется для формирования представлений о положительных и отрицательных значениях углов; знакомством с понятием периодичности тригонометрических функций.
Слайды 13, 14 используются при переходе на радианную меру угла.
Слайды 15-18 не анимированы и используются при решении различных тригонометрических заданий, закрепления и проверки результатов усвоения материала.
- Титульный лист.

- Целеполагание.
- Построение единичной окружности. Основные значения углов в градусной мере.
- Определение синуса и косинуса угла на единичной окружности.
- Табличные значения для синуса в порядке возрастания.
- Табличные значения для косинуса в порядке возрастания.
- Табличные значения для тангенса в порядке возрастания.
- Табличные значения для котангенса в порядке возрастания.
- Знаки функции sin α.
- Знаки функции cos α.
- Знаки функций tg α и ctg α.
- Положительные и отрицательные значения углов на единичной окружности.
- Радианная мера угла.
- Положительные и отрицательные значения углов в радианах на единичной окружности.
- Различные варианты единичной окружности для закрепления и проверки результатов усвоения материала.
Если вы уже знакомы с тригонометрическим кругом , и хотите лишь освежить в памяти отдельные элементы, или вы совсем нетерпеливы, – то вот он, :
Мы же здесь будем все подробно разбирать шаг за шагом.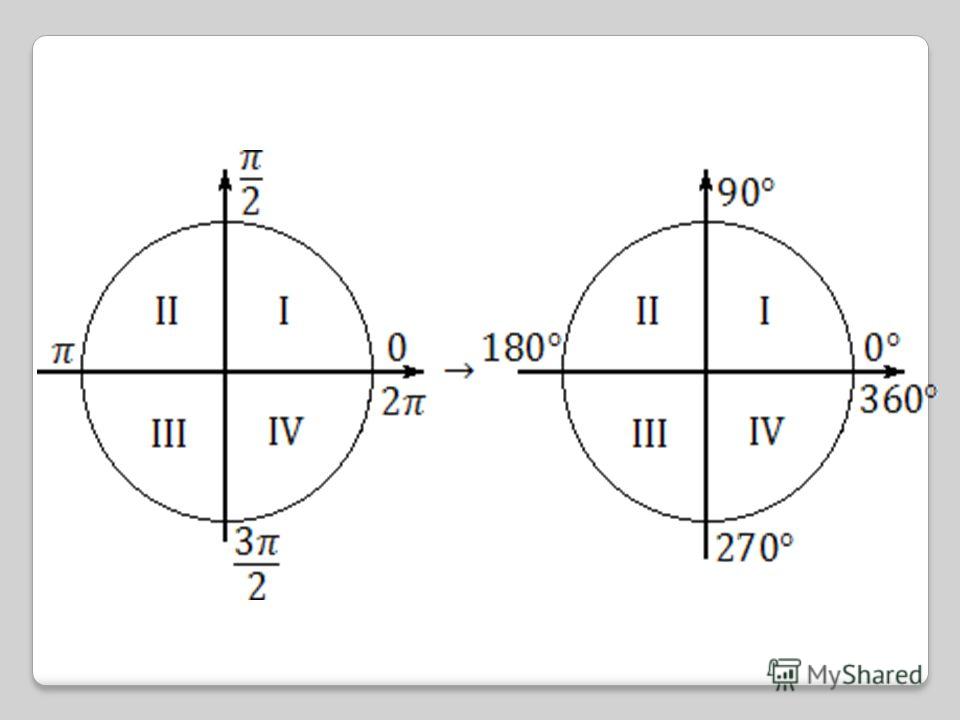
Тригонометрический круг – не роскошь, а необходимость
Тригонометрия у многих ассоциируется с непроходимой чащей. Вдруг наваливается столько значений тригонометрических функций, столько формул… А оно ведь, как, – незаладилось вначале, и… пошло-поехало… сплошное непонимание…
Очень важно не махать рукой на значения тригонометрических функций , – мол, всегда можно посмотреть в шпору с таблицей значений.
Если вы постоянно смотрите в таблицу со значениями тригонометрических формул, давайте избавляться от этой привычки!
Нас выручит ! Вы несколько раз поработаете с ним, и далее он у вас сам будет всплывать в голове. Чем он лучше таблицы? Да в таблице-то вы найдете ограниченное число значений, а на круге – ВСЕ!
К примеру, скажите, глядя в стандартную таблицу значений тригонометрических формул , чему равен синус, скажем, 300 градусов, или -45.
Никак?.. можно, конечно, подключить формулы приведения … А глядя на тригонометрический круг, легко можно ответить на такие вопросы.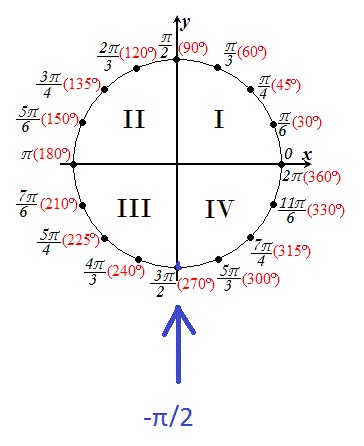 И вы скоро будете знать как!
И вы скоро будете знать как!
А при решении тригонометрических уравнений и неравенств без тригонометрического круга – вообще никуда.
Знакомство с тригонометрическим кругом
Давайте по порядку.
Сначала выпишем вот такой ряд чисел:
А теперь такой:
И, наконец, такой:
Конечно, понятно, что, на самом-то деле, на первом месте стоит , на втором месте стоит , а на последнем – . То есть нас будет больше интересовать цепочка .
Но как красиво она получилась! В случае чего – восстановим эту «лесенку-чудесенку».
И зачем оно нам?
Эта цепочка – и есть основные значения синуса и косинуса в первой четверти.
Начертим в прямоугольной системе координат круг единичного радиуса (то есть радиус-то по длине берем любой, а его длину объявляем единичной).
От луча «0-Старт» откладываем в направлении стрелки (см. рис.) углы .
Получаем соответствующие точки на круге. Так вот если спроецировать точки на каждую из осей, то мы выйдем как раз на значения из указанной выше цепочки.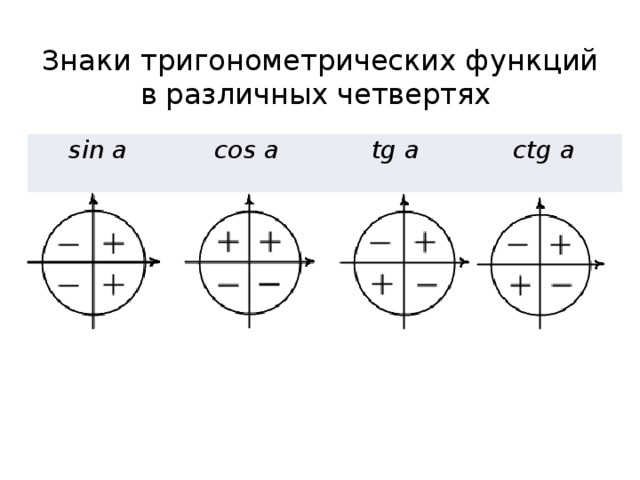
Это почему же, спросите вы?
Не будем разбирать все. Рассмотрим принцип , который позволит справиться и с другими, аналогичными ситуациями.
Треугольник АОВ – прямоугольный, в нем . А мы знаем, что против угла в лежит катет вдвое меньший гипотенузы (гипотенуза у нас = радиусу круга, то есть 1).
Значит, АВ= (а следовательно, и ОМ=). А по теореме Пифагора
Надеюсь, уже что-то становится понятно?
Так вот точка В и будет соответствовать значению , а точка М – значению
Аналогично с остальными значениями первой четверти.
Как вы понимаете, привычная нам ось (ox) будет осью косинусов , а ось (oy) – осью синусов . позже.
Слева от нуля по оси косинусов (ниже нуля по оси синусов) будут, конечно, отрицательные значения.
Итак, вот он, ВСЕМОГУЩИЙ , без которого никуда в тригонометрии.
А вот как пользоваться тригонометрическим кругом, мы поговорим в .
Тригонометрические функции произвольного угла с примерами решения
Содержание:
Угол поворотаДо недавнего времени говоря об угле мы имели в виду угол, полученный между двумя неподвижными сторонами. Угол также можно рассматривать как измерение поворота. Например, радиус колеса, расположенного по горизонтали при вращении вокруг неподвижной оси, через определённое время относительно начального положения образует некоторый угол. К тому же значение угла зависит от направления поворота. Любой угол можно рассматривать как фигуру, полученную вращением луча вокруг начальной точки.
Угол также можно рассматривать как измерение поворота. Например, радиус колеса, расположенного по горизонтали при вращении вокруг неподвижной оси, через определённое время относительно начального положения образует некоторый угол. К тому же значение угла зависит от направления поворота. Любой угол можно рассматривать как фигуру, полученную вращением луча вокруг начальной точки.
Начальное положение луча соответствует одной стороне угла, конечное положение — другой стороне. При вращении луча на координатной плоскости относительно начала координат в направлении по часовой стрелке или против часовой стрелки, можно получить различные углы.
Начальная сторона угла поворота совпадает с положительным направлением оси абсцисс. Сторону, полученную при вращении относительно начала координат (вершины угла), назовём конечной стороной. Принято считать, что если поворот происходит в направлении против часовой стрелки, то угол имеет положительное значение, при повороте в направлении по часовой стрелке, угол имеет отрицательное значение,
положительный угол отрицательный угол
Координатные оси разбивают координатную плоскость на 4 четверти.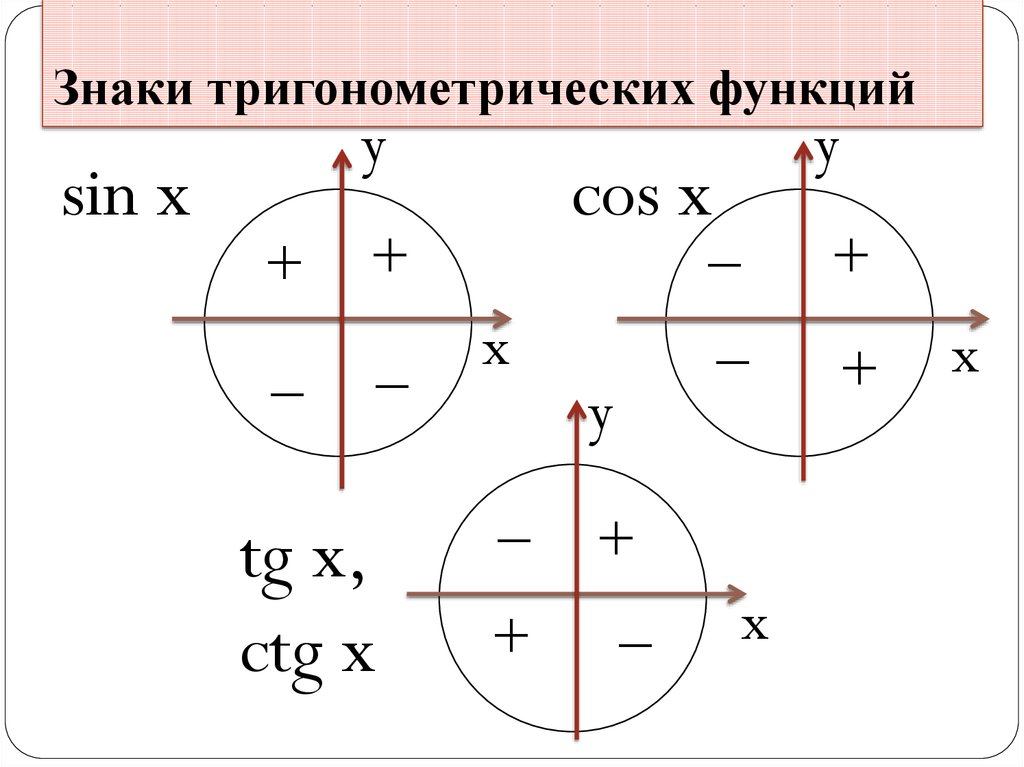 Значение угла, в зависимости от того, в какой четверти расположена его конечная сторона, меняется в определенном интервале.
Значение угла, в зависимости от того, в какой четверти расположена его конечная сторона, меняется в определенном интервале.
Конечная сторона угла может совершить один или несколько оборотов относительно начала координат. Один полный оборот соответствует углу 360°. Существует бесконечное число углов поворота, у которых начальная и конечная стороны совпадают. Например, конечные стороны углов 30°и 390° совпадают. В общем, для углов поворота и (здесь произвольное целое число) конечные стороны совпадают.
Радианная и градусная мера углаПример 1. Нарисуйте угол заданной величины. Определите какой четверти принадлежит конечная сторона угла.
Пример 2. На координатной плоскости покажите и запишите градусные меры двух положительных и одного отрицательного угла поворота, конечные стороны которых совпадают с конечной стороной угла 60°.
Радианное измерение угловУгол в один радиан-это центральный угол, у которого длина дуги равна радиусу.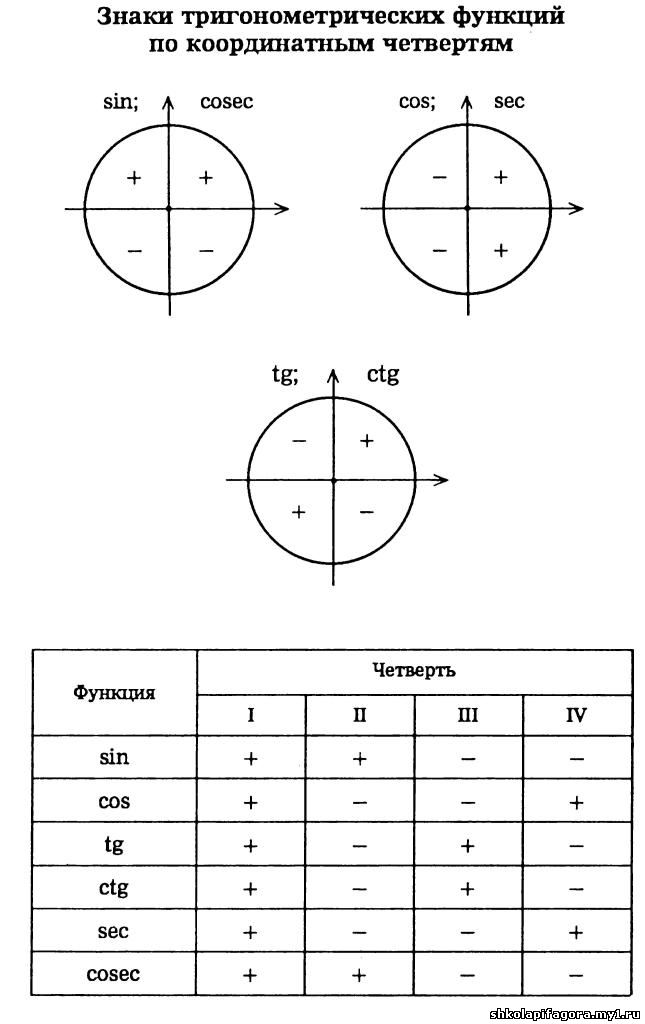 Радианная мера угла есть отношение длины соответствующей дуги к радиусу окружности: . Величина угла, выраженная в радианах не зависит от длины радиуса (объясните, воспользуясь подобием фигур на рисунке).
Радианная мера угла есть отношение длины соответствующей дуги к радиусу окружности: . Величина угла, выраженная в радианах не зависит от длины радиуса (объясните, воспользуясь подобием фигур на рисунке).
Пример 1. Сколько радиан составляет центральный угол, длина дуги которого равна 12 см, если радиус окружности равен 4 см?
Решение: 1 радиан соответствует длине дуги 4 см. Дуге длиной 12 см будет соответствовать угол 12 : 4 = 3 радиан. Длина окружности . Если центральный угол, соответствующий дуге окружности радиуса равен 1 радиану, то дуге, равной; соответствует центральный угол . Ниже показаны радианные меры углов поворота.
Радианная мера одного целого оборота равна , градусная мера 360°. То есть, радиан = 360°. Отсюда можно установить следующую связь между радианной и градусной мерой. Преобразование радиан в градусы:
Преобразование градусов в радианы:
Таким образом, рад = 180°. Обозначение «рад’ часто опускают. Вместо рад = 180° обычно пишут = 180°. Отсюда получаем, что
Вместо рад = 180° обычно пишут = 180°. Отсюда получаем, что
Используя соответствующие радианные и градусные меры углов, расположенных в первой четверти, можно найти увеличенные в разы значения других углов. Например, если 30° = , тогда 150° =
Пример 2. Выразите углы, заданные в градусах радианами, а углы, заданные радианами в градусах, а) 60° ; б)
Решение.
а)60° = радиан — радиан 1,047 радиан
б) радиан
Пример 3. Выразите углы, конечная сторона которых совпадает с углом 45°, в градусах и радианах.
Решение: Конечная сторона угла 45°совпадает с углами 405° и 315°, а также существует бесконечно много углов, конечные стороны которых совпадают с конечной стороной угла 45°: ;
,
или,
.
В радианах это можно записать как
и т.д. Все углы, конечные стороны которых совпадают с углом в общем виде записываются так:
Пример, а)
Все углы поворота, конечные стороны которых совпадают с углом
можно найти но формуле .
Как видно, в заданном интервале, расположен всего один угол 425°. Пример. д) Все углы поворота, конечные стороны которых, совпадают с этим углом можно найти по формуле .
Интервалу принадлежат углы
Длина дугиЗапишем формулу нахождения длины дуги, соответствующей центральному углу окружности радиуса . Используя радианную меру длину окружности можно найти ещё проще. По определению радиана, если , тогда длина дуги равна произведению радиуса и радианной меры угла: Длина дуги окружности находится с радиусом в прямо пропорциональной зависимости.
Площадь сектораЦентральному углу соответствует сектор площадь которого равна . Учитывая что радиальная мера центрального угла равна и обозначив её через , запишем формулу нахождения площади сектора . Пример 1. Длина секундной стрелки часов равна 12 см. Определите длину дуги, которую описывает конец секундной стрелки за 15 секунд.
Решение. Секундная стрелка за 60 минут совершают один полный оборот. Это соответствует радианам. 15 секунд соответствуют части полного оборота: радиан. То есть, минутная стрелка за 15 секунд чертит дугу, соответствующую центральному углу . Длина этой дуги:
Пример 2. Найдите площадь и периметр закрашенного сектора на рисунке, если радиус круга равен 8 см. Закрашенной части круга соответствует центральный угол:
Площадь сектора равна:
(см2).
Периметр сектора равен сумме длин двух радиусов и длины дуги: (см)
Линейная скорость и угловая скоростьСкорость при движении по окружности, например, скорость движения произвольной точки Р колеса, которое вращается вокруг точки О, может быть вычислена двумя способами.
В первом случае, её можно найти используя расстояние и время. Эта скорость называется линейной скоростью. Во втором случае — используя угол поворота (центральный угол).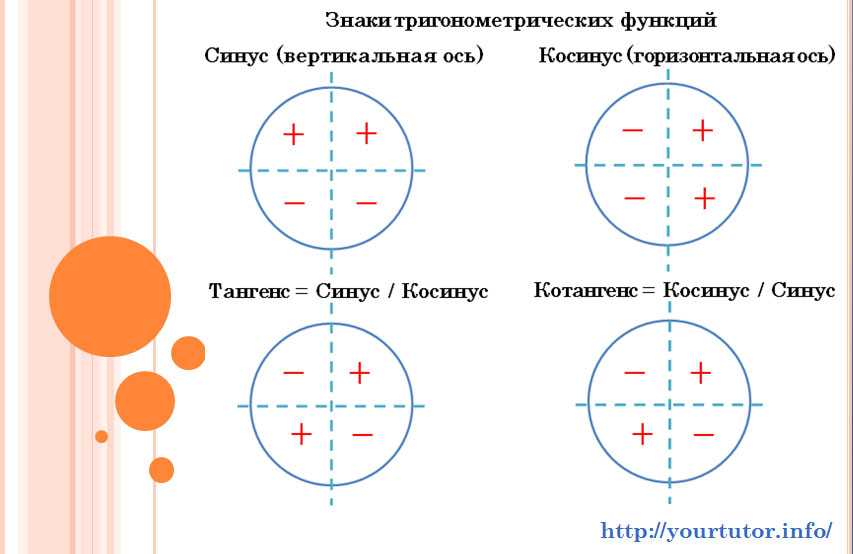 Эта скорость называется угловой скоростью.
Эта скорость называется угловой скоростью.
Если тело движется но окружности, то линейная скорость равна отношению пройденного пути (длины дуги окружности) к промежутку времени.
Если тело движется по окружности, то угловая скорость равна отношению угла поворота к промежутку времени.
Здесь (в радианах) — угол вращения за промежуток времени . Между линейной и угловой скоростью существует следующая связь:
линейная скорость = угловая скорость
Пример 3. Карусель совершает за минуту 8 полных оборотов.
а)Чему равна угловая скорость карусели за минуту(в радианах)?
б)На сколько метров за минуту передвигается лошадь, которая находится на расстоянии 3 м от центра окружности?
в)На сколько метров за минуту передвигается лошадь, которая находится на расстоянии 2 м от центра окружности?
Решение:
а) Один целый оборот при вращении соответствует центральному углу . За 8 оборотов этот угол равен .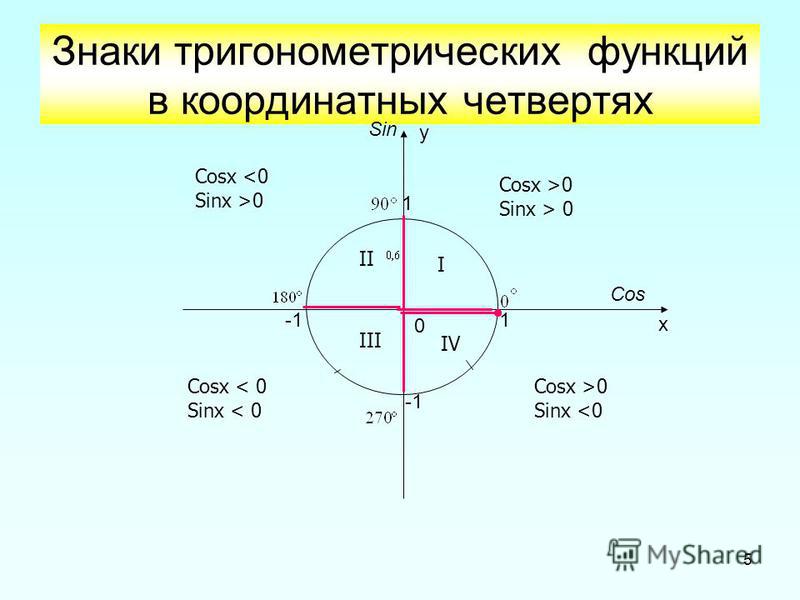 Угловая скорость за минуту равна радиан/мин.
Угловая скорость за минуту равна радиан/мин.
б)Если лошадь находится на расстоянии 3 м от центра, то она движется по окружности радиуса 3 м.
Линейная скорость:м/мин
в)Если лошадь находится на расстоянии 2 м от центра, то она движется по окружности радиуса 2 м.
Линейная скорость:м/мин
Тригонометрические функцииТригонометрические отношении для угла зависят только от значения угла.
Пусть конечная сторона угла а при повороте пересекается с окружностью радиусом г, центр которой находится в начале координат, в точке Р(х; у).
Отношение ординаты точки Р к длине радиуса называется синусом угла :
Отношение абсциссы точки Р к длине радиуса называется косинусом угла :
Отношение ординаты точки Р к абсциссе называется тангенсом угла :
(здесь , то есть точка Р не расположена на оси ординат)
Отношение абсциссы точки Р к ординате называется котангенсом угла : (здесь , то есть точка Р не расположена на оси абсцисс)
Косинусом угла называется обратное значение для синуса:
(здесь )
Секансом угла называется обратное значение для косинуса:
(здесь )
Пример 1.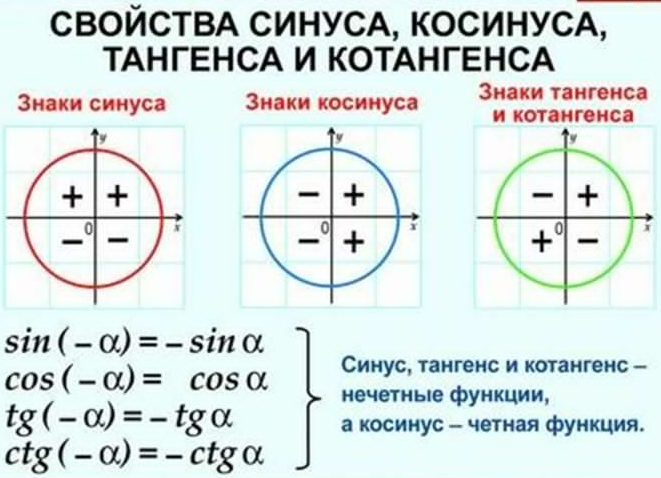 Точка А (- 3; 4) расположена на конечной стороне угла поворота .
Точка А (- 3; 4) расположена на конечной стороне угла поворота .
а) Изобразите решение примера.
б) Определите значения тригонометрических отношений для угла поворота .
Решение:
а)
б)
Координаты точки на окружности
Если заданная точка Р окружности находится на конечной стороне угла поворота , то она имеет координаты .
Пример 2. По данным рисунка найдите координаты точки Р.
Точка Р находится во II четверти и косинус отрицательный.
Для некоторых углов, конечная сторона расположена на одной из координатной оси. В этом случае, градусная мера угла поворота равна: или радиан, или радиан, или радиан, или радиан.
В этом случае координаты х или у равны или нулю, или абсолютному значению длины радиуса.
Пример 3. Найдём значения тригонометрических отношений для:
а) а = 90° ; б) а = 180°; в) а = 270° .
При всех допустимых значениях, каждому значению , соответствует единственное значение . Поэтому тригонометрические отношения являются функциями угла и называются тригонометрическими функциями.
Так как , то знак косинуса совпадает со знаком х.
Так как , то знак синуса совпадает со знаком у.
Тригонометрические функции произвольного угла. Нахождение значений тригонометрических функций произвольного угла при помощи острого углаЧтобы вычислить тригонометрические отношения для углов больше 90°, удобно использовать тригонометрические отношения острого угла.
Для любого угла поворота существует образованный конечной стороной и прямой, содержащий ось абсцисс.
Используя соответствующие острые углы можно определить тригонометрические отношения для любого произвольного угла. Эти значения можно вычислить точно для углов 30°, 45°, 60°, а для остальных острых углов — при помощи калькулятора.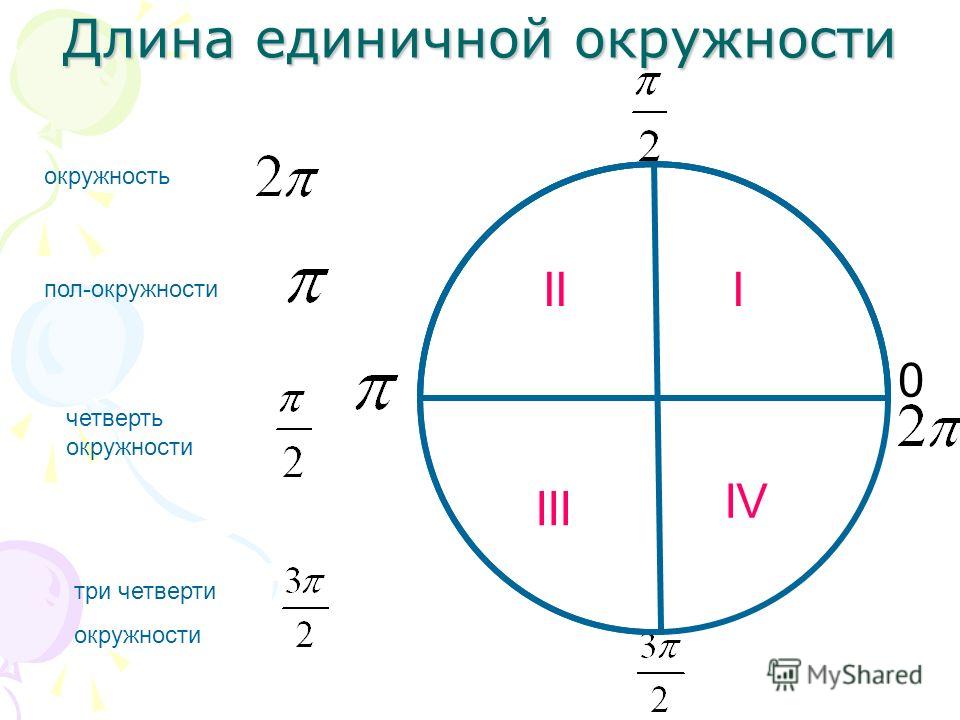
Пример 1. Для следующих углов, определите острые углы:
а) б)
Решение:
а) конечная сторона угла 300° расположена в IV четверти. Соответствующий острый угол равен: 360°- 300° = 60°
б) конечная сторона угла расположена в III четверти. Соответствующий
острый угол равен:
Пример 2. Найдём значение основных тригонометрических функций для угла . Шаги решения:
1.Найдём наименьший положительный угол, конечная сторона которого совпадает с заданным углом и дополняет его до 360°: -135° + 360° = 225°
2.Для угла 225° найдём соответствующий острый угол 225° — 180° = 45°.
3.Определим какой четверти принадлежит угол -135° — угол III четверти.
4.Найдём значение тригонометрических функций для угла 45° и учтём знак этих функций в III четверти. Получим:
Тригонометрические функции для произвольного угла можно определить следующим образом:
•определяем соответствующий острый угол;
•находим значение тригонометрических функций для этого угла;
•определяем знак значения тригонометрических функций в зависимости от четверти.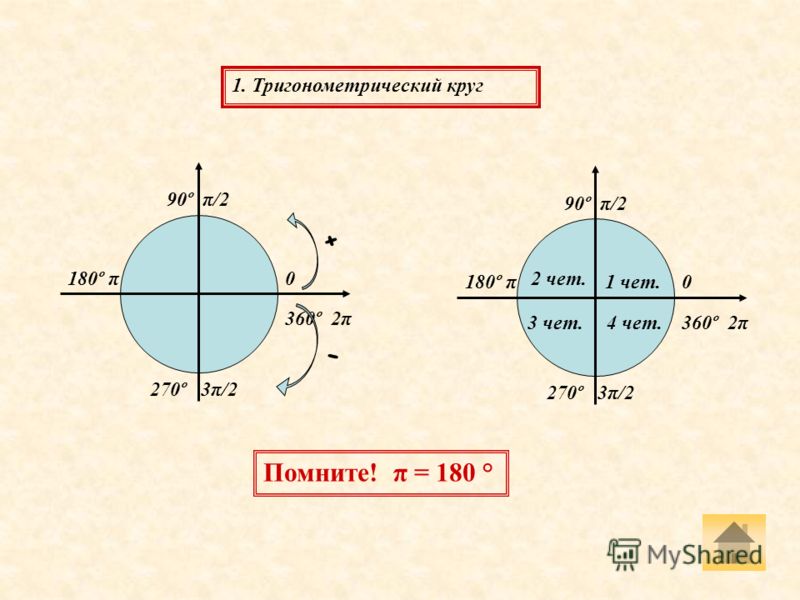
Так как конечные стороны углов и совпадают, то значения тригонометрических функций этих углов одинаковы. Если угол изменяется на целое число оборотов, то значение тригонометрических функций не меняется.
Заметим, что если угол меняется на пол оборота, то значения тангенса и котангенса не изменяются.
На самом деле, если углу поворота соответствует точка , а углу поворота (или ) соответствует точка , то :
В общем случае выполняются равенство:
Пример 3. Найдём допустимые значения , если . Так как в I и во II четвертях синус положителен.
, значит если , то
Абсцисса этой точки
Тогда или
Единичная окружность и тригонометрические функцииЗначения тригонометрических функций зависят только от значения угла и не зависят от радиуса окружности. Поэтому, не нарушая общности, можно принять . Окружность, центр которой находится в начале координат, с радиусом равным единице, называется единичной окружностью. Координаты точки, принадлежащей окружности удовлетворяют уравнению .
Координаты точки, принадлежащей окружности удовлетворяют уравнению .
Если точка является точкой пересечения единичной окружности и конечной стороны угла поворота , то между ней и тригонометрическими функциями существует следующая связь: Таким образом, координаты точки принадлежащей единичной окружности, можно записать как: .
Также по заданным координатам можно найти следующие тригонометрические функции: . Зная, что при определённом повороте на единичной окружности, можно найти соответствующие координаты точки.
Для этого надо выполнить следующие шаги:
1) На единичной окружности отметим точки, соотвегствующие углу поворота , найдём координаты этих точек по формуле: .
2)Для некоторой точки, принадлежащей единичной окружности, например ,определите координаты симметричной точки. Как видно но рисунку, существует 3 точки, симметричные точке А, которые расположены во II, III и IV четвертях.
Точка В симметрична точке А относительно оси у, точка С — относительно начала координат, а точка D — относительно оси х.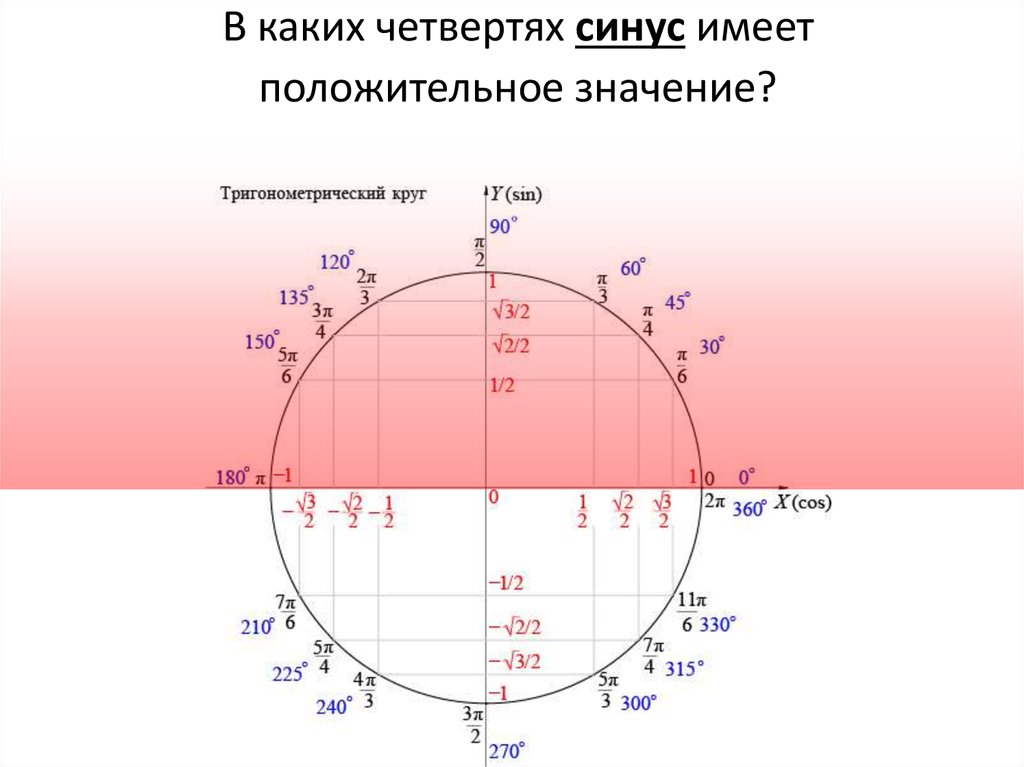 Абсолютные значения координат этих точек равны и отличаются только знаком.
Абсолютные значения координат этих точек равны и отличаются только знаком.
3)Таким образом, можно определить координаты новых точек, зная координаты точки, принадлежащей I четверти. Т.е. получаем единичную окружность, на которой отмечены углы поворота и координаты точек.
- Заказать решение задач по высшей математике
Так как координаты точек на единичной окружности удовлетворяют условиям , то Наибольшее значение и равно 1, а наименьшее значение равно -1.
Пример 1. Для угла поворота вычислите значения основных тригонометрических функций.
Решение: Конечная сторона угла поворота расположена в III четверти. Этому углу соответствует острый угол . Точка пересечения конечной стороны угла с единичной окружностью симметрична точке относительно начала координат и соответствует точке .
Тогда ,
Пример 2. Точка А, с абсциссой расположена в III четверти и пересекается с единичной окружностью на стороне угла .
Точка А, с абсциссой расположена в III четверти и пересекается с единичной окружностью на стороне угла .
а)Найдём ординату точки А.
б)Изобразим рисунок, соответствующий условию и для угла найдём значения шести тригонометрических функций.
Решение:
а), . Так как точка расположена в III четверти .
б),,,,
,.
Пример 3. Найдём наибольшее и наименьшее значение выражения .
Решение:
Таким образом, для выражения a НМЗ равно 1, а НБЗ равно 5.
Формулы приведенияЕсли объект находится в I четверти, то симметричный ему относительно оси у объект находится во II четверти. Симметричный последнему относительно оси х, объект находится в III четверти, и он совпадает с объектом, симметричным начальному объекту из I относительно начала координат. Обратите внимание, что отображение относительно оси у и отображение, относительно оси х, совпадают с поворотом на 180°.
При отображении относительно оси х, точка расположенная на конечной стороне угла изменяет координаты, как показано на рисунке.
То есть, при этом знак меняет только координата у. Таким образом, так как косинус зависит от х он не меняется, зато меняется знак синуса. Отсюда, для углов можно записать следующие зависимости между тригонометрическими функциями.
То есть, синус, тангенс и котангенс нечётные функции, косинус-чётная.
Пример 1:
Конечные стороны углов поворота и 360° — симметричны относительно оси х. То есть .
Отсюда получаем:
Запишем для углов и 90° — прямоугольного треугольника с острым углом тригонометрические отношения:
При попарном сравнении равенств можно увидеть следующую связь-между значениями тригонометрических функций углов и 90° — .
Повернём конечную сторону угла поворота ещё на 90°. При этом точка Р(х; у), расположенная на стороне преобразуется в точку . По определению тригонометрических функций:
При этом точка Р(х; у), расположенная на стороне преобразуется в точку . По определению тригонометрических функций:
Запишем эти формулы в следующем виде:
Как видно но рисунку отображения относительно оси у и оси х эквивалентны повороту на 180°. Изменение координат, можно записать следующим образом:
Как видно по рисунку, при повороте угла а на 180° конечная сторона расположена в противоположных четвертях, но на одной прямой.
Пример 2.
Для получения аналогичных формул тригонометрических функций угла поворота достаточно записать и применить последовательность соответствующих формул.
Например:
Теперь запишем соответствующие формулы для угла поворота . Например:
При помощи полученных формул можно найти значения тригонометрических функций произвольного угла, зная значения для соответствующего острого угла. Эти формулы называются формулами приведения. Для формул приведений можно легко увидеть следующую закономерность
1)Если аргумент имеет вид или , то функция преобразуется в «сопряжённую» функцию (то есть синус в косинус или наоборот, а тангенс в котангенс или наоборот) угла .
2)Если аргумент имеет вид 180° ± или 360° ± , то функция преобразуется в одноимённую функцию угла .
В каждом из обоих случаев, знак полученной в результате преобразования функции имеет одинаковое значение со знаком острого угла в соответствующей четверти.
Тригонометрические тождестваДля острого угла прямоугольного треугольника покажите, что , выполнив следующие шаги:
1)Запишите теорему Пифагора:
2)Каждую из сторон равенства разделите на с2:
3)Примените свойство степени:
4) Примите во внимание, что:
Связь между тригонометрическими функциями одного и того же углаТождество можно доказать и при помощи координат точки, принадлежащей единичной окружности.
По координатам точки на единичной окружности и по определениям тригонометрических функций имеем:
Для всех значений , при которых
Для всех значений , при которых
Из данных равенств имеем,что если для угла одновременно выполняются условия и , то справедливо тождество
Разделив обе чаете равенства поочередно на и на будем иметь:
Полученные выше равенства являются тождествами. Их называют основными тригонометрическими тождествами. На основании основных тригонометрических можно написать:
Их называют основными тригонометрическими тождествами. На основании основных тригонометрических можно написать:
При помощи основных тригонометрических тождеств можно упрощать тригонометрические выражения и вычислять модуль значения всех остальных функций, зная значение одной из них.
Пример 1. Используя основные тригонометрические тождества, докажите,что:
Доказательство:
Пример 2. Зная, что и угол принадлежит III четверти, найдите
остальные тригонометрические функции.
Из формул получаем:
Так как угол принадлежит III четверти, то
Тогда:
Формулы сложенияПрактическая работа .
1)Покажем по шагам, равенство выражения
a)Для значений и, вычислим значения выражения в левой части.
б)Для значений и, вычислим значения выражения в правой части.
2)Как можно вычислить значение тригонометрических функций для угла 15°, используя разность значений углов 45° и 30°(15° = 45° — 30°)?
Тригонометрические функции суммы и разности двух углов. Сначала докажем тождество
Сначала докажем тождество
На рисунке
а)для угла координаты точки Р1, взятой на единичной окружности равны , а для угла координаты точки Р2 равны . Разместим углы — , как показано на рисунке б).
Тогда, для угла координаты точки Рз будут . Из того, что (по признаку СУС ) следует, что .
Доказательство тождества
учитывая, что
справедливость тождества доказана.
Доказательство тождества
no формулам приведения группируя
no формуле косинуса разности с учётом формул приведения.
Доказательство тождества :
Пример 1. Найдём значение выражения если
Решение.
Пример 2.
Найдём значение выражения если
.
Решение.
Известно что . Если углу соответствует острый угол , то . Так как противолежащий катет равен 3, а гипотенуза 5, тогда прилежащий катет равен и учитывая, что угол III четверти, получим:.
Аналогично, если зная, что , получаем,
что .
Можно записать формулы сложения для тангенса и котангенса:
no определению no формулам сложения
Аналогичным образом можно показать, что :
Следствия из формул сложенияПрактическая работа.
Преобразуйте сумму в произведение, выполнив следующие шаги:
1)
решив систему уравнений найдите такие углы, чтобы их сумма была равна 70°, а разность
2)Запишите следующее 70° = 40° + 30°, 10° = 40° — 30° и упростите
Преобразование суммы(разности) в произведениеФормулы преобразования произведенияСправедливость данных тождеств можно показать при помощи формул сложения:
почленно складываем почленно складываем
Следующее тождество можно доказать аналогичным образом.
Тригонометрические функции двойного аргументаФормулы сложения позволяют выразить через тригонометрические функции угла .
Таким образом, получаем тождества, которые называются формулами двойного аргумента:
Формулы половинного аргументаИмеем, что
Отсюда: Заменяем в данной формуле на получаем:
Для половинных аргументов справедливы тождества. Знак в правой части в данном равенстве зависит от того, в какой четверги находится угол .
Пример 1. Упростим выражение .
Решение.
Пример 2. He используя калькулятор, вычислим значения и , зная, что угол принадлежит IV четверти и
Решение.
Пример 3. Найдём значений .
Решение:
Используем формулу половинного аргумента
угол I четверти и в этой четверти косинус положителен.
Упрощение тригонометрических выраженийПример 1. Раскроем скобки и упростим выражение.
Пример 2. Разложим на множители и упростим выражение.
Разложим на множители и упростим выражение.
Пример 3. Упростим рациональное выражение, содержащее тригонометрические функции.
Пример 4. Освободим знаменатель от радикала
Здесь .
Тригонометрический круг со всеми значениями, круг синусов и косинусов, линия, ось тангенса на окружности, как пользоваться и находить точки
В каждой профессии существуют свои инструменты, обеспечивающие решение и качественное выполнение определенных задач. Математики применяют тригонометрический круг, позволяющий легко и быстро вычислить значение какой-либо функции. Однако не все могут им правильно пользоваться, поскольку не понимают основных понятий.
Общие сведения
Для правильного решения тригонометрических задач следует изучить основные понятия, формулы, а также методы нахождения основных величин. Раздел математики, изучающий функции косинуса, синуса, тангенса, котангенса, арксинуса, арккосинуса, арктангенса и арккотангенса, называется тригонометрией. Окружность, которая используется для решения геометрических задач на плоскости, имеет единичный радиус.
Окружность, которая используется для решения геометрических задач на плоскости, имеет единичный радиус.
Значения функций, которые можно по ней находить, называются тригонометрическими. Однако существует множество способов нахождения их значений, но в некоторых ситуациях при использовании формул приведения решение затянется на продолжительное время, а вычисления будут громоздкими. Чтобы этого избежать, нужно использовать тригонометрический круг со всеми значениями. С его помощью также можно определить, является ли функция четной или нечетной.
Углы и их классификация
Перед тем как понять основное назначение тригонометрических функций, следует обратить внимание на классификацию углов. Она является важной для вычисления тригонометрических выражений. Углы в математических дисциплинах делятся на следующие типы:
- Острые.
- Прямые.

- Тупые.
- Развернутые.
- Выпуклые.
- Полные.
К первому типу относятся углы любой размерности градусной единицы измерения, которая не превышает 90 (а<90). Если значение соответствует 90, то он является прямым (а=90). Угол считается тупым, при выполнении следующего условия: 90<a<180. Если градусная размерность угла соответствует 180, то он является развернутым (а = 180). Выпуклым считается угол, когда выполняется такое условие: 180 < a < 360. Следует отметить, что он является смежным с острым углом. В случае, когда значение градусной размерности соответствует 360 градусам, то он является полным (а=360).
Однако углы измеряются не только в градусах, но и в радианах. Для решения тригонометрических задач оптимальным выбором градусной меры является радиан. Для соотношения между двумя единицами измерения применяется простая формула: 180 (град) = ПИ (рад). Из соотношения можно вывести формулу для перевода градусов в радианы: Pрад = (а * ПИ) / 180. Переменная «а» — значение величины градусной меры заданного угла. Обратное соотношение принимает следующий вид: а = (Ррад * 180) / ПИ.
Переменная «а» — значение величины градусной меры заданного угла. Обратное соотношение принимает следующий вид: а = (Ррад * 180) / ПИ.
Для быстрого перевода единиц измерения применяют такие инструменты: радианная табличка, программное обеспечение и тригонометрическая окружность. Однако для начала следует обратить внимание на тригонометрические функции, которые присутствуют в задачах физико-математического уклона.
Информация о функциях
Тригонометрических функций всего четыре вида: синус (sin), косинус (cos), тангенс (tg) и котангенс (ctg). Существует столько же типов обратных функций: арксинус (arcsin), арккосинус (arccos), арктангенс (arctg) и арккотангенс (arcctg). Они получили широкое применение не только в математических задачах, но также используются в физике, электронике, электротехнике и других дисциплинах. Основной их особенностью считается возможность представления какого-либо закона.
Например, зависимость амплитуды напряжения переменного тока от времени описывается следующим законом: u = Um * cos (w*t) (графиком является косинусоида). Гармонические звуковые колебания также подчиняются определенному закону, в котором присутствует тригонометрическая функция. Кроме того, можно находить значения корня тригонометрического уравнения.
Синусом угла называется величина, равная отношению противолежащего катета прямоугольного треугольника к его гипотенузе. Следовательно, косинус — отношение прилежащего катета к гипотенузе. Тангенс — отношение величины противолежащего катета к прилежащему. Котангенс является обратной функцией тангенсу, т. е. отношение прилежащего к противолежащему.
youtube.com/embed/2x0sdaNBZD8″/>Функции arcsin, arccos, arctg, arcctg применяются в том случае, когда нужно найти значение угла в градусах или радианах. Вычисления выполняются по специальным таблицам Брадиса или с помощью программ. Также можно использовать тригонометрическую окружность.
Тригонометрический круг
Чтобы воспользоваться тригонометрической окружностью для решения задач, нужны такие базовые знания: понятие о синусе, косинусе, тангенсе, котангенсе, системе координат и теореме Пифагора. Для построения единичной окружности используется декартовая система координат с двумя осями. Точка «О» — центр пересечения координатных осей, ОХ — ось абсцисс, ОУ — ординат.
Для решения задач различного типа применяется и теорема Пифагора. Она справедлива только для прямоугольного треугольника (один из углов — прямой). Ее формулировка следующая: квадрат гипотенузы в произвольном прямоугольном треугольнике равен сумме квадратов катетов. Следует также знать основные соотношения между функциями острых углов в заданном прямоугольном треугольнике:
- a + b = 180.
- cos(a) = sin(b).
- cos(b) = sin(a).
- tg(a) = ctg(b).
- tg(b) = ctg(a).
- tg(a) = 1 / ctg(a).

- tg(b) = 1 / ctg(b).
Существуют и другие тригонометрические тождества, но для работы с кругом этого перечня будет достаточно.
Построение «инструмента»
Построить окружность, которая ускорит процесс решения задач, довольно просто. Для этого потребуются бумага, карандаш, резинка и циркуль. Далее необходимо нарисовать любую немаленькую окружность. После этого отметить ее центр карандашом, поставив точку. Пусть она будет называться «О». Через эту точку следует провести две перпендикулярные прямые (угол пересечения равен 90 градусам). Обозначить их следующим образом: «х» (горизонтальная) и «у» (вертикальная).
Окружность является единичной, но не стоит рисовать ее такой, поскольку работать будет неудобно. Этот прием называется масштабированием. Он широко применяется практически во всех сферах человеческой деятельности. Например, инженеры не чертят двигатель космического корабля в натуральную величину, поскольку с таким «рисунком» будет неудобно и невозможно работать. Они используют его макет.
Они используют его макет.
Окружность пересекается с осями декартовой системы координат в 4 точках со следующими координатами: (1;0), (0;1), (-1;0) и (0;-1). Области, которые делят декартовую систему координат на 4 части, называются четвертями. Их четыре:
- Первая состоит из положительных координат по х и у.
- Вторая имеет по х отрицательные и положительные по у.
- Третья — только отрицательные значения.
- Четвертая — положительные значения по х и отрицательные по у.
Исходя из этих особенностей, определяется числовой знак функции, позволяющий определить ее четность и нечетность. Кроме того, на ней следует отметить углы следующим образом: 0 и 2ПИ соответствует точке с координатами (1;0), ПИ/2 — (0;1), ПИ — (-1;0) и 3ПИ/2 — (0;-1).
Готовый макет
Для решения задач специалисты рекомендуют иметь рабочий и готовый макеты тригонометрических окружностей. Первый применяется для нахождения значений нестандартных углов (например, синуса 185 градусов). Тригонометрическим кругом (рис. 1) удобно пользоваться в том случае, когда значение угла является стандартным (90, 60 и т. д.).
Первый применяется для нахождения значений нестандартных углов (например, синуса 185 градусов). Тригонометрическим кругом (рис. 1) удобно пользоваться в том случае, когда значение угла является стандартным (90, 60 и т. д.).
Рисунок 1. Готовый макет тригонометрического круга синусов и косинусов.
Для нахождения необходимых значений объединяют две фигуры — единичную окружность и прямоугольный треугольник. Гипотенуза последнего равна 1 и соответствует радиусу окружности. Ось ОХ — косинусы, ОУ — синусы. С помощью этого «инструмента» определение синусов и косинусов становится намного проще. Для нахождения значения sin(30) необходимо воспользоваться следующим алгоритмом:
- Отметить угол на окружности и достроить его до прямоугольного треугольника.
- Если катет лежит напротив угла в 30 градусов, то он равен 0,5 от длины гипотенузы.
- sin(30) = 1 * 0,5 = 0,5.
Для нахождения косинуса необходимо использовать основное тригонометрическое тождество, которое связывает sin и cos: (sin(a))^2 + (cos(a))^2 = 1. 2] = sqrt(3) / 2.
2] = sqrt(3) / 2.
Однако после всех вычислений следует выбрать знак функции. В данном случае угол находится в первой четверти. Следовательно, функция имеет положительный знак. Для нахождения тангенса и котангенса можно воспользоваться следующими формулами: tg(a) = sin(a) / cos(a) и ctg(a) = cos(a) / sin(a). Подставив значения синуса и косинуса, можно определить значение tg: tg(30) = 0,5 / (sqrt(3) / 2) = 1 / sqrt(3) = sqrt(3) / 3. Тогда котангенс можно найти двумя способами:
- Через известный тангенс: ctg(30) = 1 / (1 / sqrt(3)) = sqrt(3).
- Использовать основное отношение: ctg(30) = (sqrt(3) / 2) / (1/2) = sqrt(3).
Вычислить значения синуса и косинуса для угла 60 градусов очень просто. Для этого нужно воспользоваться основными тождествами: sin(60) = сos(30) = sqrt(3) / 2, cos(60) = sin(30) = 1/2, tg(30) = ctg(60) = sqrt(3) / 3, tg(60) = ctg(30) = sqrt(3). Значения для 45 градусов определяются следующим образом:
- Прямоугольный треугольник с углом 45 градусов является равносторонним (катеты равны).
 2 = 1.
2 = 1. - sin(45) + cos(45) = sqrt(2) / 2.
Тангенс и котангенс равен 1. Если угол равен 90, то необходимо внимательно посмотреть на рисунок 1. Следовательно, sin(90) = 1, cos(90) = 0, tg(90) = 1 и ctg(90) не существует. Линия тангенса на окружности не отображается. В этом случае нужно пользоваться основными тригонометрическими тождествами.
Правила использования
Инструмент позволяет легко и быстро находить значения тригонометрических функций любых углов. Если при решении задачи требуется найти sin(270), то нужно выполнить простые действия:
- Пройти против часовой стрелки (положительное направление) 180 градусов, а затем еще 90.
- На оси синусов значение составляет -1 (точка лежит на оси).
Существуют задачи, в которых угол представлен отрицательным значением. Например, нужно определить синус, косинус, тангенс и котангенс угла (-7ПИ/6). В некоторых случаях заданное значение следует перевести в градусы: -7ПИ/6 = -210 (градусам). Если в условии отрицательный угол, то движение следует осуществлять по часовой стрелке от нулевого значения (пройти полкруга, а затем еще 30). Можно сделать вывод о том, что значение -210 соответствует 30. Следовательно, синус вычисляется следующим образом: sin(-210) = -(sin(ПИ + 30)) = — 1/2, cos(-210) = sqrt(3)/2, tg(-210) = sqrt(3)/3 и ctg(-210) = sqrt(3).
В некоторых случаях заданное значение следует перевести в градусы: -7ПИ/6 = -210 (градусам). Если в условии отрицательный угол, то движение следует осуществлять по часовой стрелке от нулевого значения (пройти полкруга, а затем еще 30). Можно сделать вывод о том, что значение -210 соответствует 30. Следовательно, синус вычисляется следующим образом: sin(-210) = -(sin(ПИ + 30)) = — 1/2, cos(-210) = sqrt(3)/2, tg(-210) = sqrt(3)/3 и ctg(-210) = sqrt(3).
Пример случая, когда нет необходимости переводить радианы в градусы, является следующим: нужно вычислить значения тригонометрических функций угла 5ПИ/4. Необходимо расписать значение угла таким образом: 5ПИ/4 = ПИ + ПИ/4. Против часовой стрелки следует пройти половину круга (ПИ), а затем его четвертую часть (ПИ/4). Далее нужно спроецировать координаты точки на ось синусов и косинусов. Это соответствует значению sqrt(2)/2. Тангенс и котангенс заданного угла будут равны 1.
Встречаются задачи, в которых значение угла превышает 360 градусов. Например, требуется найти значения тригонометрических функций угла (-25ПИ/6). Для решения необходимо разложить угол следующим образом: (-25ПИ/6) = — (4ПИ + ПИ/6). Можно не делать обороты, поскольку 4ПИ соответствует двойному обороту и возврату в точку (-ПИ/6). Это объясняется периодом функций синуса и косинуса, который равен 2ПИ. Значения функций sin, сos, tg и ctg равны следующим значениям: — 1/2, sqrt(3)/2, sqrt(3)/3 и sqrt(3) соответственно.
Например, требуется найти значения тригонометрических функций угла (-25ПИ/6). Для решения необходимо разложить угол следующим образом: (-25ПИ/6) = — (4ПИ + ПИ/6). Можно не делать обороты, поскольку 4ПИ соответствует двойному обороту и возврату в точку (-ПИ/6). Это объясняется периодом функций синуса и косинуса, который равен 2ПИ. Значения функций sin, сos, tg и ctg равны следующим значениям: — 1/2, sqrt(3)/2, sqrt(3)/3 и sqrt(3) соответственно.
Таким образом, тригонометрический круг позволяет оптимизировать вычисления в дисциплинах с физико-математическим уклоном, в которых используются тригонометрические функции. Не имеет смысла устанавливать дополнительное программное обеспечение, пользоваться таблицами, поскольку это занимает некоторое время. При помощи этого «универсального инструмента» можно найти значение любого угла.
Площадь четверти круга — Формула, Примеры, Определение
Прежде чем узнать, что такое площадь четверти круга , вспомним, что такое круг и четверть круга . Окружность — это геометрическое место (набор) точек, находящихся на фиксированном расстоянии от фиксированной точки. Эта фиксированная точка и фиксированное расстояние называются «центром» и «радиусом» соответственно. Четверть круга составляет одну четвертую часть круга. Таким образом, площадь четверти круга составляет ровно одну четвертую площади полного круга.
Окружность — это геометрическое место (набор) точек, находящихся на фиксированном расстоянии от фиксированной точки. Эта фиксированная точка и фиксированное расстояние называются «центром» и «радиусом» соответственно. Четверть круга составляет одну четвертую часть круга. Таким образом, площадь четверти круга составляет ровно одну четвертую площади полного круга.
Давайте выучим формулу площади круга вместе с ее доказательством, несколькими решенными примерами и практическими вопросами.
| 1. | Что такое четверть круга (квадрант)? |
| 2. | Формулы площади четверти круга |
| 3. | Как найти площадь четверти круга? |
| 4. | Часто задаваемые вопросы о площади четверти круга |
Что такое четверть круга (квадрант)?
Площадь (или) часть, образованная двумя радиусами, перпендикулярными друг другу и одной четвертой части окружности круга, называется четвертью окружности. Это также известно как квадрант круга. т. е. если мы разделим круг на 4 равные части, каждая часть будет четвертью круга (или) квадрантом.
Это также известно как квадрант круга. т. е. если мы разделим круг на 4 равные части, каждая часть будет четвертью круга (или) квадрантом.
Формулы площади четверти круга
Рассмотрим круг радиуса ‘r’ и диаметра ‘d’. Мы знаем, что d = 2r. Выведем формулы площади четверти круга через радиус и диаметр.
Площадь четверти круга с использованием радиуса
Мы знаем, что площадь круга равна πr 2 . Как мы уже узнали в предыдущем разделе, четверть круга составляет одну четвертую часть полного круга, и, следовательно, его площадь составляет одну четвертую площади круга.
Таким образом , площадь четверти круга в терминах радиуса = πr 2 / 4
Площадь четверти круга с использованием диаметра
Так как d = 2r, мы имеем r = d/2. Подставив это в приведенную выше формулу, мы можем получить площадь четверти круга через диаметр.
Площадь четверти круга = π(d/2) 2 / 4 = πd 2 / 16
Таким образом, площадь четверти круга по диаметру = πd 2 / 16
Примечание: Здесь π — математическая константа, значение которой считается равным 22/7 (или) 3,14159. 2…
2…
Как найти площадь четверти круга?
Рассмотрим круг радиуса ‘r’. Вот шаги, чтобы найти площадь четверти круга.
- Если радиус (r) дан, то сразу подставьте его в формулу πr 2 / 4.
- Если диаметр (d) дан, то либо решить d = 2r относительно ‘r’ и использовать формулу πr 2 / 4 (или) сразу подставить значение d в формулу πd 2 / 16.
- Если длина окружности (C) дана, то решите C = 2πr для ‘r’ и подставьте его в формулу πr 2 / 4.
- Если площадь (A) дана, то либо решите A = πr 2 для ‘r’ и подставьте его в формулу πr 2 / 4 (или) просто найдите A / 4.
Теперь, когда мы поняли формулу и метод нахождения площади четверти круга, давайте взглянем на несколько решенных примеров для лучшего понимания.
Примеры площади четверти круга
Пример 1: Радиус круглого парка составляет 40 ярдов.
 Четверть круга этой части отведена под игровое оборудование. Найдите площадь участка, отведенного под игровое оборудование. Используйте π = 3,142.
Четверть круга этой части отведена под игровое оборудование. Найдите площадь участка, отведенного под игровое оборудование. Используйте π = 3,142.Решение:
Радиус круглого парка, r = 40 ярдов.
Площадь участка, отведенного под игровое оборудование, можно найти по формуле площади четверти круга.
Часть парка, отведенная под игровое оборудование = πr 2 / 4 = (3,142)(40) 2 / 4 = 1256,8 квадратных ярдов.
Ответ: Требуемая площадь игрового оборудования = 1256,8 кв.
Пример 2: Джеймс заказал пиццу для себя и 3 своих друзей. Они хотят разделить его поровну. Пицца имеет круглую форму и ее диаметр составляет 16 дюймов. Используя формулу площади четверти круга, найдите количество пиццы, которое получил каждый из них. Используйте π = 3,14.
Решение:
Диаметр данной пиццы d = 16 дюймов.
Поскольку пицца разделена на 4 равные части, каждая часть представляет собой четверть круга, поэтому ее площадь можно найти по формуле площади четверти круга.

Метод 1
Радиус пиццы r = d/2 = 16/2 = 8 дюймов.
Площадь каждой части = πr 2 / 4 = (3,14)(8) 2 / 4 = 50,24 квадратных дюйма.
Метод 2
Площадь каждой части = πd 2 / 16 = (3,14)(16) 2 / 16 = 50,24 квадратных дюйма.
Ответ: Площадь каждой порции пиццы = 50,24 квадратных дюйма.
перейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Забронировать бесплатный пробный урок
Практические вопросы по площади четверти круга
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о площади четверти круга
Как называется четверть круга?
Когда круг делится на 4 равные части, образуются 4 четверти, и каждая из этих четвертей известна как «квадрант».
Какова площадь четверти круга?
Площадь четверти круга составляет одну четвертую площади полного круга радиуса ‘r’. т. е. площадь четверти круга = πr 2 / 4.
Как вычислить площадь четверти круга?
Если r, d, C и A являются радиусом, диаметром, длиной окружности и площадью круга, одной из этих частей информации достаточно, чтобы найти площадь четверти круга, как описано ниже.
- Если дано r, используйте формулу πr 2 / 4.
- Если дано d, используйте формулу πd 2 / 16.
- Если C задано, то решите C = 2πr для ‘r’ и используйте формулу πr 2 / 4.
- Если дано А, то найти А/4.
Какова площадь четверти круга по радиусу?
Рассмотрим круг радиуса ‘r’. Тогда площадь четверти круга по r равна πr 2 / 4.
Как найти площадь четверти круга, используя диаметр?
Если r и d — радиус и диаметр окружности, то мы знаем, что d = 2r. Если задано значение «d», то мы можем найти площадь четверти круга одним из следующих способов:
Если задано значение «d», то мы можем найти площадь четверти круга одним из следующих способов:
- Найдите ‘r’, используя r = d/2, а затем используйте формулу πr 2 / 4 (или)
- Сразу подставьте значение d в формулу πd 2 / 16.
Какова площадь квадранта круга?
Площадь квадранта круга есть не что иное, как площадь четверти круга, и, следовательно, она составляет одну четвертую площади полного круга. т. е. если «r» — радиус полного круга, то площадь квадранта круга = πr 2 / 4.
Какова формула периметра четверти круга?
Четверть окружности состоит из двух радиусов и одной четвертой части окружности. Таким образом, периметр четверти круга радиуса «r» равен r + r + (2πr)/4 = 2r + πr/2.
Скачать БЕСПЛАТНЫЕ учебные материалы
Рабочий лист площади
Четверть круга
- Часть внутренней части круга, имеющая две границы радиуса под углом 90° и дугу.
- Центр круга, в котором все точки на линии окружности находятся на равном расстоянии от центральной точки.

- Четверть круга — это структурная форма, используемая в строительстве.
Ссылки на статьи
- Геометрические свойства структурных форм
дуга Формула длины четверти круга
| \(\large{ L = \frac {2 \; \pi \; r} {4} }\) |
Где:
| Единицы | Английский | Метрическая система |
| \(\large{L}\) = длина дуги | \(\большой{в}\) | \(\большой{мм}\) |
| \(\большой{\пи}\) = Пи | \(\большой{3.141 592 653 …}\) | |
| \(\большой{r}\) = радиус | \(\большой{в}\) | \(\большой{мм}\) |
площадь четверти круга формула 92 }\)
 141 592 653 …}\)
141 592 653 …}\)
Расстояние от центроида четверти круга формулы
| \(\large{ C_x = \frac {4 \; r} {3 \; \pi} }\) | |
| \(\large{ C_y = \frac {4 \; r} {3 \; \pi} }\) |
Где:
| Единицы | Английский | Метрическая система |
| \(\large{C_x, C_y}\) = расстояние от центра тяжести | \(\большой{в}\) | \(\большой{мм}\) |
| \(\большой{\пи}\) = Пи | \(\большой{3.141 592 653 …}\) | |
| \(\large{r}\) = радиус | \(\большой{в}\) | \(\большой{мм}\) |
Модуль упругого сечения четверти круга формула
| \(\large{ S = \frac { I_x } { C_y } }\) |
Где:
| Единицы | Английский | Метрическая система |
| \(\large{S}\) = модуль упругого сечения 94 }\) |
Формулы периметра четверти круга
| \(\large{ P = \frac {2 \; \pi \; r} {4} + 2 \; r }\) | |
| \(\large{ P = L + 2 \; r }\) |
Где:
| Единицы | Английский | Метрическая система |
| \(\large{P}\) = периметр | \(\большой{в}\) | \(\большой{мм}\) |
| \(\large{L}\) = длина дуги | \(\большой{в}\) | \(\большой{мм}\) |
| \(\большой{\пи}\) = Пи | \(\большой{3. 141 592 653 …}\) 141 592 653 …}\) | |
| \(\большой{r}\) = радиус | \(\большой{в}\) | \(\большой{мм}\) |
| \(\большой{\пи}\) = Пи | \(\большой{3.141 592 653 …}\) | |
| \(\большой{r}\) = радиус | \(\большой{в}\) | \(\большой{мм}\) |
Формула радиуса четверти круга
Где:
| \(\large{ k_{x1} = \frac { r } { 2 } }\) | |
| \(\large{ k_{y1} = \frac { r } { 2 } }\) | |
| \(\large{ k_{z1} = \frac { \sqrt {2} } { 2 } \; r }\) |
Где:
| Единицы | Английский | Метрическая система |
| \(\large{k}\) = радиус вращения | \(\большой{в}\) | \(\большой{мм}\) |
| \(\большой{\пи}\) = Пи | \(\большой{3. 141 592 653 …}\) 141 592 653 …}\) | |
| \(\большой{r}\) = радиус | \(\большой{в}\) | \(\большой{мм}\) |
Второй момент площади полукруга формулы 94 }\)
Четверть круга в квадрате – какова площадь? – Следите за своими решениями
Если вы покупаете по ссылке в этом посте, я могу заработать комиссию. Это не влияет на цену, которую вы платите. Как партнер Amazon я зарабатываю на соответствующих покупках. Узнать больше.
Опубликовано 14 ноября 2019 г. Прешем Талвалкаром. Прочитайте обо мне или напишите мне .
В квадрате со стороной 20 между углами квадрата начерчены четверти окружности. Найдите площадь синей, зеленой и оранжево-желтой фигур.
Задача состоит в том, чтобы использовать только геометрию, а не тригонометрию или исчисление.
Посмотрите видео, чтобы найти решение.
Какова площадь? СЛОЖНАЯ геометрическая задача
Я благодарю многих людей во всем мире, которые предложили мне эту задачу, в том числе:
Доктор Перкинс из Австралии
Матье из Канады
Цезар Тан из Малайзии
Акаруид из Индии
Наим из Турции
Или продолжайте читать.
.
.
«Все будет хорошо, если вы будете использовать свой разум для принятия решений и думать только о своих решениях.» С 2007 года я посвятил свою жизнь разделению радости теории игр и математики. MindYourDecisions теперь содержит более 1000 бесплатных статей без рекламы благодаря поддержке сообщества! Помогите и получите ранний доступ к публикациям с залогом на Patreon.
.
.
.
.
.
.
М
И
Н
Д
.
Y
O
U
R
.
D
E
C
I
S
I
O
N
S
.
P
U
Z
Z
L
E
.
.
.
.
Ответ на четверть круга в квадрате — что такое площадь
(Практически все сообщения быстро расшифровываются после того, как я делаю для них видео — пожалуйста, дайте мне знать, если есть какие-либо опечатки / ошибки, и я их исправлю, Благодарность).
Доктор Перкинс прислал мне следующее доказательство, и я отдаю ему должное.
Решим задачу в общем случае для квадрата, длина стороны которого r . Обозначьте площади трех областей внутри квадрата как a , b и c , как показано на диаграмме.
Площадь квадрата можно выразить как в виде суммы площадей отдельных областей, так и в виде квадрата длины его стороны. Отсюда имеем:
4 a + 4 b + c = r 2
Теперь рассмотрим площадь одной четверти круга.
Его площадь можно выразить как сумму площадей отдельных областей, так и 1/4 площади круга. Отсюда имеем:
2 a + 3 b + c = π r 2 /4
Наконец, найдем площадь следующей формы:
27 0 9
Его площадь равна a + 2 b + c .
Мы также посчитаем его площадь геометрически. Для этого мы нарисуем радиусы двух пересекающихся четвертей круга, как показано на рисунке. Поскольку каждая четверть окружности имеет радиус, равный стороне квадрата, два радиуса и сторона квадрата образуют равносторонний треугольник.
Нужную форму можно найти как сумму круглого сектора с центральным углом 60 градусов (1/6 окружности) плюс площадь круглого сегмента (найденная как площадь сектора минус равносторонний треугольник.)
Площадь, Таким образом,:
π R 2 /6 + (π R 2 /6 — R 2 √3 /4)
= π9950 2 √3 /4)
= π949950509950995099509999999999999999999999999999999999999999999999999999999999999999999999999999999999тельно 2 √3 /4). 2 /3 — R 2 √3 /4
2 /3 — R 2 √3 /4
Вспоменный эта область была A + 2 B + C , мы получаем уравнение:
A + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 . c = π r 2 /3 – r 2 √3/4
Таким образом, мы имеем серию из 3 уравнений:
4 A + 4 B + C = R 2
2 A + 3 B + 9 C. . . C. C C. r 2 /4
a + 2 b + c = π r 2 /3 – r 2 √3/4
It is routine to solve for each переменная (сделано в видео около 3:06). Получаем решение:
а = r 2 (1 – π/6 – √3/4)
b = r 2 (π/12 – 1 + √3/2) r 2 (1 + π/3 – √3)
Если r = 20, то:
a &приблизительно; 17,36
б &прибл. 51.13
51.13
c &прибл. 126.06
Дополнительные баллы: решение синей фигуры с помощью тригонометрии
Я подумал, что было бы интересно показать быстрое решение тригонометрии для закругленного квадрата в центре рисунка.
Сначала нарисуйте равносторонний треугольник, чтобы мы могли сделать вывод, что угол между радиусом и стороной квадрата равен 30 градусам.
Теперь нарисуйте еще один радиус, и по симметрии мы можем сделать вывод, что все три угла равны 30 градусам.
Теперь сосредоточимся на следующем сегменте треугольника и круга. Угол 30 градусов выражается как π/6 радиан.
Площадь кругового сектора вычисляем по формуле:
круговой сектор = (1/2) r 2 (π/6 – sin(π/6))
круговой сектор = (1/2) r 2 (π/6 – 1/2)
Тогда используем Аль-Каши Закон косинусов решить для значения x 2 .
x 2 = r 2 + r 2 – 2 r r cos (π/6)
x 2 = r 2 (2 – 2 cos (π/6))
x 2 = r 2 (2 – √3)
Площадь закругленного квадрата равна площади 4 круглых сегментов плюс квадрат между ними (это квадрат, так как все хорды имеют одинаковую длину, а хорды перпендикулярны друг другу. )
)
4(круговой сектор) + (квадрат)
= 4((1/2) r 2 (π/6 – 1/2)) + r 2 (2 – √3)
= r 2 (1 + π/3 – √3)
Я видел подобные задачи во многих классах по всему миру, поэтому надеюсь, что этот пост и видео поможет многим студентам по всему миру!
Источники
Есть много других способов решить эту проблему. Вот веб-сайт с еще несколькими способами:
https://www.mathalino.com/reviewer/plane-geometry/02-area-common-arcs-quarter-circles
Я благодарю многих людей во всем мире, которые предложили эту задачу. мне, в том числе:
Доктор Перкинс из Австралии
Матье из Канады
Цезар Тан из Малайзии
Акаруиде из Индии
Наим из Турции
МОИ КНИГИ
Если вы совершаете покупку по этим ссылкам, я могу получить компенсацию за покупки, сделанные на Amazon . Как партнер Amazon я зарабатываю на соответствующих покупках. Это не влияет на цену, которую вы платите.
Рейтинги книг по состоянию на январь 2022 г. 1) Радость теории игр: введение в стратегическое мышление
(2) 40 парадоксов логики, теории вероятностей и теории игр
(3) Иллюзия иррациональности: как принимать разумные решения и преодолевать предубеждения
(4) Лучший менталитет Математические трюки
(5) Умножение чисел путем рисования линий
Радость теории игр показывает, как вы можете использовать математику, чтобы перехитрить своих конкурентов. (оценка 4,2/5 звезд в 224 обзорах)
40 парадоксов в логике, теории вероятностей и теории игр содержит наводящие на размышления и противоречивые результаты. (рейтинг 4,1/5 звезд в 38 обзорах)
Иллюзия иррациональности: как принимать разумные решения и преодолевать предубеждения — это руководство, в котором объясняется множество причин, по которым мы предвзято относимся к принятию решений, и предлагаются методы принятия разумных решений. (рейтинг 4/5 звезд по 24 отзывам)
Лучшие приемы ментальной математики учит, как можно выглядеть математическим гением, решая задачи в уме (оценка 4,2/5 звезд в 76 обзорах)
Умножение чисел путем рисования линий Эта книга является справочником руководство для моего видео, которое имеет более 1 миллиона просмотров о геометрическом методе умножения чисел. (оценка 4,3/5 звезд в 30 обзорах)
(оценка 4,3/5 звезд в 30 обзорах)
Загадывайте свои головоломки представляет собой сборник из трех книг «Математические головоломки», тома 1, 2 и 3. Темы головоломок включают математические предметы, включая геометрию, вероятность, логика и теория игр.
Math Puzzles Volume 1 содержит классические головоломки и загадки с полными решениями задач по счету, геометрии, вероятности и теории игр. Том 1 получил оценку 4,4/5 звезд по 87 отзывам.
Математические головоломки, том 2 — это продолжение книги с большим количеством больших задач. (оценка 4,1/5 звезд по 24 отзывам)
Math Puzzles Volume 3 — третья книга в серии. (рейтинг 4,2/5 звезд по 22 отзывам)
KINDLE UNLIMITED
Преподаватели и студенты со всего мира часто пишут мне о книгах. Поскольку образование может иметь такое огромное влияние, я стараюсь сделать электронные книги доступными как можно большему числу людей по минимально возможной цене.
В настоящее время вы можете читать большинство моих электронных книг через программу Amazon Kindle Unlimited. Включенный в подписку, вы получите доступ к миллионам электронных книг. Вам не нужно устройство Kindle: вы можете установить приложение Kindle на любой смартфон/планшет/компьютер и т. д. Ниже я собрал ссылки на программы в некоторых странах. Пожалуйста, проверьте доступность и условия программы на местном веб-сайте Amazon.
Включенный в подписку, вы получите доступ к миллионам электронных книг. Вам не нужно устройство Kindle: вы можете установить приложение Kindle на любой смартфон/планшет/компьютер и т. д. Ниже я собрал ссылки на программы в некоторых странах. Пожалуйста, проверьте доступность и условия программы на местном веб-сайте Amazon.
США, список моих книг (США)
Великобритания, список моих книг (Великобритания)
Канада, список моих книг (CA)
Германия, список моих книг (Германия)
Франция, список моих книг (Франция)
Индия, список моих книг (IN)
Австралия, список моих книг (AU)
Италия, список моих книг (IT)
Испания, список моих книг (ES)
Япония, список моих книг (JP)
Бразилия, результаты книги (BR)
Мексика, результаты книги (MX)
ТОВАРЫ
Возьмите кружку, футболку и многое другое на официальном сайте товаров: Обдумывайте свои решения в Teespring .
Квадрат в четверть круга — обдумывайте свои решения
Если вы покупаете по ссылке в этом посте, я могу заработать комиссию. Это не влияет на цену, которую вы платите. Как партнер Amazon я зарабатываю на соответствующих покупках. Узнать больше.
Это не влияет на цену, которую вы платите. Как партнер Amazon я зарабатываю на соответствующих покупках. Узнать больше.
Опубликовано 7 декабря 2021 г. Прешем Талвалкаром. Прочитайте обо мне или напишите мне .
Спасибо Джону Х. за предложение!
Площадь ABCD вписано в четверть окружности O так, что B и C лежат на дуге четверти окружности. Если четверть круга имеет радиус, равный 1, какова площадь квадрата?
Мне сказали, что это было дано ученикам 7-го класса (возраст 12-13 лет), и я думаю, что это очень сложная задача для этой возрастной группы. На самом деле я думаю, что это хорошая задача для любого изучающего геометрию.
Как обычно, посмотрите видео для решения.
Сложная задача для 12-летних – квадрат в квадранте
Или продолжайте читать.
.
.
«Все будет хорошо, если вы будете использовать свой разум для принятия решений и думать только о своих решениях. » С 2007 года я посвятил свою жизнь разделению радости теории игр и математики. MindYourDecisions теперь содержит более 1000 бесплатных статей без рекламы благодаря поддержке сообщества! Помогите и получите ранний доступ к публикациям с залогом на Patreon.
» С 2007 года я посвятил свою жизнь разделению радости теории игр и математики. MindYourDecisions теперь содержит более 1000 бесплатных статей без рекламы благодаря поддержке сообщества! Помогите и получите ранний доступ к публикациям с залогом на Patreon.
.
.
.
.
.
.
М
И
Н
Д
.
Y
O
U
R
.
D
E
C
I
S
I
O
N
S
.
P
U
Z
Z
L
E
.
.
.
.
Ответить на квадрат в четверть круга
(Практически все сообщения быстро расшифровываются после того, как я делаю для них видео — пожалуйста, дайте мне знать, если есть какие-либо опечатки / ошибки, и я их исправлю, спасибо).
Сторона BC хорда окружности O . Постройте биссектрису г. до н.э. г. . Он пройдет через центр O (поскольку O равноудалено от B и C ) и пометит его пересечение с BC как E , а его пересечение с AD F . Поскольку ABCD — квадрат, серединный перпендикуляр к BC также является серединным перпендикуляром к 9.0949 г. н.э. г. .
Поскольку ABCD — квадрат, серединный перпендикуляр к BC также является серединным перпендикуляром к 9.0949 г. н.э. г. .
Треугольники AFO и DFO находятся в конгруэнтах по боковой стороне с AF = FD , углы AFO и DFO . Таким образом, AOF = DOF , а поскольку AOD = 90°, мы имеем AOF = DOF = 45°. Таким образом, OFD является равнобедренным прямоугольным треугольником, где OF = FD .
Конструкция Radius OB , которая имеет длину 1. Предположим, что половина стороны квадратного = CD = 2 х . Тогда OEB представляет собой прямоугольный треугольник с катетами х , х + 2 х = 3 х и гипотенузой, равной 1. Таким образом, мы имеем:
х
254 + (3
x ) 2 = 1 2
10 x 2 = 1
x 2 = 1/10
. x ) 2
x ) 2
= 4 x 2
= 4 (1/10)
= 4/10
= 0,4
Специальная благодарность в этом месяце:
Robert Zarker
5
Robert Zarnke
5.
Майкл Анвари
Дэниел Льюис
Спасибо всем подписчикам на Patreon!
Ссылки
Я благодарю этих людей, которые помогли мне подтвердить первый шаг в Твиттере:
@ahmed_elashraf
https://twitter.com/ahmed_elashraf/status/1450213493798494211
- 71 @Stwitter com/ScottRollison/status/1450251161798430728
@OkanAtalay1970
https://twitter.com/OkanAtalay1970/status/1450305206378434562
МОИ КНИГИ
Вы можете получить компенсацию за эти ссылки на Amazon. Как партнер Amazon я зарабатываю на соответствующих покупках. Это не влияет на цену, которую вы платите.
Рейтинги книг по состоянию на январь 2022 г. 1) Радость теории игр: введение в стратегическое мышление
(2) 40 парадоксов логики, теории вероятностей и теории игр
(3) Иллюзия иррациональности: как принимать разумные решения и преодолевать предубеждения
(4) Лучший менталитет Математические трюки
(5) Умножение чисел путем рисования линий
Радость теории игр показывает, как вы можете использовать математику, чтобы перехитрить своих конкурентов. (оценка 4,2/5 звезд в 224 обзорах)
(оценка 4,2/5 звезд в 224 обзорах)
40 парадоксов в логике, теории вероятностей и теории игр содержит наводящие на размышления и противоречивые результаты. (рейтинг 4,1/5 звезд в 38 обзорах)
Иллюзия иррациональности: как принимать разумные решения и преодолевать предубеждения — это руководство, в котором объясняется множество причин, по которым мы предвзято относимся к принятию решений, и предлагаются методы принятия разумных решений. (рейтинг 4/5 звезд по 24 отзывам)
Лучшие приемы ментальной математики учит, как можно выглядеть математическим гением, решая задачи в уме (оценка 4,2/5 звезд в 76 обзорах)
Умножение чисел путем рисования линий Эта книга является справочником руководство для моего видео, которое имеет более 1 миллиона просмотров о геометрическом методе умножения чисел. (оценка 4,3/5 звезд в 30 обзорах)
Загадывайте свои головоломки представляет собой сборник из трех книг «Математические головоломки», тома 1, 2 и 3. Темы головоломок включают математические предметы, включая геометрию, вероятность, логика и теория игр.
Темы головоломок включают математические предметы, включая геометрию, вероятность, логика и теория игр.
Math Puzzles Volume 1 содержит классические головоломки и загадки с полными решениями задач по счету, геометрии, вероятности и теории игр. Том 1 получил оценку 4,4/5 звезд по 87 отзывам.
Математические головоломки, том 2 — это продолжение книги с большим количеством больших задач. (оценка 4,1/5 звезд по 24 отзывам)
Math Puzzles Volume 3 — третья книга в серии. (рейтинг 4,2/5 звезд по 22 отзывам)
KINDLE UNLIMITED
Преподаватели и студенты со всего мира часто пишут мне о книгах. Поскольку образование может иметь такое огромное влияние, я стараюсь сделать электронные книги доступными как можно большему числу людей по минимально возможной цене.
В настоящее время вы можете читать большинство моих электронных книг через программу Amazon Kindle Unlimited. Включенный в подписку, вы получите доступ к миллионам электронных книг. Вам не нужно устройство Kindle: вы можете установить приложение Kindle на любой смартфон/планшет/компьютер и т. д. Ниже я собрал ссылки на программы в некоторых странах. Пожалуйста, проверьте доступность и условия программы на местном веб-сайте Amazon.
Вам не нужно устройство Kindle: вы можете установить приложение Kindle на любой смартфон/планшет/компьютер и т. д. Ниже я собрал ссылки на программы в некоторых странах. Пожалуйста, проверьте доступность и условия программы на местном веб-сайте Amazon.
США, список моих книг (США)
Великобритания, список моих книг (Великобритания)
Канада, список моих книг (CA)
Германия, список моих книг (Германия)
Франция, список моих книг (Франция)
Индия, список моих книг (IN)
Австралия, список моих книг (AU)
Италия, список моих книг (IT)
Испания, список моих книг (ES)
Япония, список моих книг (JP)
Бразилия, результаты книги (BR)
Мексика, результаты книги (MX)
ТОВАРЫ
Возьмите кружку, футболку и многое другое на официальном сайте товаров: Обдумывайте свои решения в Teespring .
Использование тригонометрических функций для вычисления площади треугольника
Все ресурсы для предварительного исчисления
12 диагностических тестов 380 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 3 Следующая →
Precalculus Help » Тригонометрические приложения » Площадь треугольника » Используйте тригонометрические функции для вычисления площади треугольника
У вас есть треугольное пространство на заднем дворе, которое вы хотите покрыть мульчей, и его стороны имеют длину 5, 6 и 8 метров. Если мешок мульчи покрывает 2 квадратных метра земли и стоит 10 долларов, сколько денег вам потребуется, чтобы выполнить эту работу? Предположим, что стороны треугольника обозначены как a, b и c в порядке, указанном выше.
Если мешок мульчи покрывает 2 квадратных метра земли и стоит 10 долларов, сколько денег вам потребуется, чтобы выполнить эту работу? Предположим, что стороны треугольника обозначены как a, b и c в порядке, указанном выше.
Возможные ответы:
Правильный ответ:
Пояснение:
Используйте формулу Герона для вычисления площади косоугольного треугольника.
где .
Поскольку мешки с мульчей покрывают 2 квадратных метра, для работы потребуется 7,5 мешков. Однако в магазине не продаются половинчатые пакеты, поэтому требуется 8 штук и нужно потратить 80 долларов.
Сообщить об ошибке
Найдите площадь треугольника со сторонами 25 м, 42 м и 23 м.
Возможные ответы:
Ничего из перечисленного.
Правильный ответ:
Пояснение:
Мы используем формулу Герона для нахождения площади косоугольного треугольника или треугольника без прямого угла.
Формула Герона:
.
Находим s по
Находим s.
Ввод в формулу Герона:
Сообщить об ошибке
На декартовой плоскости начертите окружность с центром в начале радиуса . Теперь нарисуйте отрезок от до . Заштрихуйте область между сегментом и границей круга над сегментом.
Какова площадь заштрихованной области?
Возможные ответы:
Правильный ответ:
Пояснение:
Заштрихованная площадь равна одной четверти площади круга за вычетом площади равнобедренного прямоугольного треугольника с катетами по радиусу.
Круг имеет радиус , поэтому площадь круга равна
.
Часть круга в первом квадранте равна
Если мы вычтем площадь под соединяющей линией, мы получим правильный ответ.
Чтобы найти эту область, распознайте геометрию как треугольник. Две точки дают вам основание и высоту, поэтому ее площадь равна
.
Следовательно, площадь интересующей области составляет .
Сообщить об ошибке
Найти площадь заштрихованного сегмента данного круга радиусом 8 см:
Возможные ответы:
Правильный ответ:
Пояснение:
Площадь сегмента можно рассчитать по следующей формуле:
Площадь сектора вычисляется следующим образом:
Чтобы найти площадь треугольника, 120-градусный равнобедренный треугольник можно разделить на два треугольника 30 60 90:
Площадь треугольника можно рассчитать следующим образом:
Возвращаясь к исходной формуле для площади сегмента:
Сообщить об ошибке
Найти площадь заштрихованного сегмента: 9037
Возможные ответы:
Правильный ответ:
Объяснение:
Площадь сегмента можно рассчитать по следующей формуле:
Площадь сектора можно найти следующим образом:
Площадь треугольника можно легко определить, потому что это прямоугольный треугольник под углом 90 градусов:
Теперь, когда нам нужны обе переменные по формуле можно определить площадь отрезка:
Сообщить об ошибке
Найти площадь заштрихованного отрезка ВС:
Возможные ответы:
Правильный ответ:
Объяснение:
Площадь сегмента можно вычислить следующим образом:
Мы можем найти площадь сектора как такового:
Чтобы найти площадь треугольника, мы должны разделить равнобедренный треугольник на две равные части. треугольники с биссектрисой:
треугольники с биссектрисой:
Для определения основания вычисляем:
Для определения высоты вычисляем:
Теперь, когда у нас есть все необходимые значения, мы можем вычислить площадь треугольника:
Теперь можно рассчитать общую площадь сегмента BC:
Сообщить об ошибке
Найти
7 площадь отрезка ВС:
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти площадь сегмента, мы должны сначала найти площадь сектора и треугольника, чтобы выполнить данную формулу:
Чтобы найти площадь сектора:
Чтобы найти площадь треугольника, мы сначала должны разделить его на два прямоугольных треугольника:
Мы можем найти высоту треугольника как таковую:
Мы можем найти базу с использованием аналогичного метода:
Площадь треугольника может быть рассчитана как таковая:
, чтобы найти область сегмента. , теперь мы можем вычесть площадь треугольника из площади сектора:
, теперь мы можем вычесть площадь треугольника из площади сектора:
Сообщить об ошибке
Найдите площадь четверти круга радиусом 9см.
Возможные ответы:
Правильный ответ:
Пояснение:
Чтобы найти площадь четверти круга, сначала вспомните, что такое площадь круга. Формула такова. Поскольку нас интересует только четверть круга, воспользуемся формулой. Затем подставьте радиус так, чтобы ваш ответ был: .
Сообщить об ошибке
← Предыдущая 1 2 3 Следующая →
Уведомление об авторских правах
Все ресурсы Precalculus
12 Диагностические тесты 380 практических тестов Вопрос дня Карточки Learn by Concept
Видео-урок: Площади и окружности окружностей
Стенограмма видео
В этом видео мы научимся
найти площадь и длину окружности по радиусу или диаметру и как
соотносить как площадь, так и окружность для решения различных задач.
Давайте начнем с повторения некоторых ключевой язык, связанный с кругами. Окружность – это множество точек, которые имеют постоянное расстояние от точки в центре, здесь обозначается буквой 𝑀. Радиусом окружности является любая линия отрезок, соединяющий центр круга с его краем, здесь обозначен с помощью буква 𝑟. Диаметр круга это линия отрезок, оба конца которого лежат на краю окружности и который проходит через центр. Обозначим диаметр с помощью букву 𝑑 и обратите внимание, что она всегда в два раза длиннее радиуса той же круг.
Длина окружности равна
расстояние по всему периметру. И обозначим это буквой
𝐶. Круги — очень особенные формы
потому что их свойства связаны математической константой, которую мы называем 𝜋
и обозначать с помощью греческой буквы. 𝜋 примерно равно 3,142
до трех знаков после запятой. Но на самом деле 𝜋 — это то, что известно как
иррациональное число, что означает, что оно имеет бесконечно длинную строку цифр после
десятичная точка без повторяющегося шаблона. Если бы мы попытались написать все эти
цифры вниз, мы будем пытаться вечно.
𝜋 примерно равно 3,142
до трех знаков после запятой. Но на самом деле 𝜋 — это то, что известно как
иррациональное число, что означает, что оно имеет бесконечно длинную строку цифр после
десятичная точка без повторяющегося шаблона. Если бы мы попытались написать все эти
цифры вниз, мы будем пытаться вечно.
Первая ключевая формула, относящаяся к круги, которые нам нужно знать, это. Окружность круга равно 𝜋, умноженному на диаметр. 𝐶 равно 𝜋𝑑. Поскольку диаметр в два раза больше радиуса, это также можно записать как 𝐶 равно двум 𝜋𝑟.
Начнем с рассмотрения Пример, в котором мы вычисляем длину окружности, зная длину ее диаметр.
Расчет окружности обведите кружком, давая ответ с точностью до двух знаков после запятой.
Прежде всего напомним, что
Окружность круга — это расстояние вокруг его края. Формула расчета
длина окружности 𝐶 равна 𝜋𝑑, где 𝐶 представляет длину окружности
а 𝑑 представляет диаметр круга. Глядя на диаграмму, мы были
Учитывая, мы можем видеть, что этот отрезок является диаметром круга, потому что его два
конечные точки лежат на краю круга, и он проходит через центр
круг. Длина этой линии равна шести, поэтому
значение 𝑑 равно шести. Окружность круга
поэтому 𝜋 умножается на шесть, что мы можем записать как шесть 𝜋.
Формула расчета
длина окружности 𝐶 равна 𝜋𝑑, где 𝐶 представляет длину окружности
а 𝑑 представляет диаметр круга. Глядя на диаграмму, мы были
Учитывая, мы можем видеть, что этот отрезок является диаметром круга, потому что его два
конечные точки лежат на краю круга, и он проходит через центр
круг. Длина этой линии равна шести, поэтому
значение 𝑑 равно шести. Окружность круга
поэтому 𝜋 умножается на шесть, что мы можем записать как шесть 𝜋.
Теперь, если нам нужно дать точное
ответ или, если у нас не было доступа к калькулятору, мы могли оставить наш ответ в
эта форма. Но нас просят дать ответ
с точностью до двух знаков после запятой. Поэтому нам нужно оценить это. Поскольку 𝜋 — иррациональное число,
мы получаем ответ, который также иррационален, 18,84955, продолжающийся. Округление до двух знаков после запятой
дает 18,85.
Нам не дали единиц для диаметр в вопросе, поэтому у нас нет единиц измерения длины окружности. Но так как окружность мера длины, единицы измерения будут общими единицами длины. Мы обнаружили, что окружность окружность до двух знаков после запятой равна 18,85.
Итак, мы узнали, как рассчитать длину окружности по этой формуле. Мы также можем применить эти формулы к найти периметр других фигур, связанных с кругами. Например, предположим, что у нас есть полукруг. Периметр этой фигуры равен состоит из двух частей: прямой ребра, которая является длиной круга диаметр, и эта изогнутая часть, которую мы называем дугой.
Поскольку это полукруг, длина
этой дуги будет половина окружности полного круга. Итак, используя формулу, которую мы уже
записано, будет 𝜋𝑑 больше двух. Если мы найдем общее
периметр этого полукруга, а не просто изогнутая длина, мы должны помнить
чтобы добавить на прямой край. Итак, мы имеем, что периметр a
полукруг, представленный 𝑃, равен 𝑑 плюс 𝜋𝑑 больше двух.
Итак, мы имеем, что периметр a
полукруг, представленный 𝑃, равен 𝑑 плюс 𝜋𝑑 больше двух.
Мы можем применить те же рассуждения к Найдите формулу периметра четверти окружности. На этот раз у нас есть два подряд ребра, каждое из которых является радиусом исходной окружности. Тогда у нас есть изогнутый край, который четверть полной окружности круга, поэтому его длина будет 𝜋𝑑 больше четыре. Периметр четверти круга поэтому равно двум 𝑟 плюс 𝜋𝑑 больше четырех. А так как два 𝑟 равно 𝑑, мы также можно написать как 𝑑 плюс 𝜋𝑑 больше четырех.
Мы также можем выразить каждое из этих
формулы через 𝐶, длину окружности исходного круга. Для полукруга периметр
равно 𝑑 плюс 𝐶 больше двух. А для четверти круга
периметр равен 𝑑 плюс 𝐶 больше четырех. Давайте теперь рассмотрим пример
с участием частей кругов.
Используя 3.14 для аппроксимации 𝜋 и тот факт, что 𝐴𝐵𝐶𝐷 является квадратом, вычислить периметр заштрихованной части.
Сначала может показаться, что периметр этой заштрихованной области будет сложно определить, так как это необычный форма. Но если мы посмотрим внимательно, то увидим что каждая из этих незаштрихованных частей представляет собой четверть круга. Заштрихованная область окружена изогнутые части этих четырех четвертей кругов. Каждая из этих длин дуг четверть окружности круга, а так как их четыре, вместе они образуют полную окружность круга.
Мы знаем, что формула для вычисление длины окружности 𝐶 равно 𝜋𝑑, где 𝑑 представляет диаметр окружности. Итак, вопрос в том, что такое диаметр этого круга?
Учитывая четверть круга в
в левом нижнем углу рисунка мы видим, что радиус этой окружности будет
половина длины стороны квадрата. Это 68 больше двух. Значит радиус 34
сантиметры. Диаметр круга в два раза больше
радиус, значит, диаметр в два раза больше 34; это 68 сантиметров. На самом деле, мы могли бы вывести это
от цифры без деления пополам и повторного удвоения. Два радиуса четверти
окружности лежат вдоль стороны квадрата, поэтому удвоенный радиус равен 68
сантиметры. А так как диаметр в два раза больше
радиуса, снова находим, что диаметр равен 68 сантиметрам. Мы уже говорили, что
периметр заштрихованной области равен длине полной окружности, сделанной
из этих четырех четвертей кругов.
Это 68 больше двух. Значит радиус 34
сантиметры. Диаметр круга в два раза больше
радиус, значит, диаметр в два раза больше 34; это 68 сантиметров. На самом деле, мы могли бы вывести это
от цифры без деления пополам и повторного удвоения. Два радиуса четверти
окружности лежат вдоль стороны квадрата, поэтому удвоенный радиус равен 68
сантиметры. А так как диаметр в два раза больше
радиуса, снова находим, что диаметр равен 68 сантиметрам. Мы уже говорили, что
периметр заштрихованной области равен длине полной окружности, сделанной
из этих четырех четвертей кругов.
Таким образом, использование формулы 𝐶 равно
𝜋𝑑, мы находим, что периметр заштрихованной области равен 𝜋, умноженному на 68. В вопросе сказано использовать
3.14 в качестве приближения для 𝜋. Таким образом, умножение дает 213,52. Единицы для этого периметра
такие же, как единицы длины, используемые в вопросе. Итак, мы находим, что периметр
заштрихованная часть с использованием 3,14 в качестве приближения для 𝜋 составляет 213,52 сантиметра.
Итак, мы находим, что периметр
заштрихованная часть с использованием 3,14 в качестве приближения для 𝜋 составляет 213,52 сантиметра.
Теперь рассмотрим площадь круги. Район также имеет отношение к размеры окружности константой 𝜋. В этом случае отношения что площадь равна 𝜋, умноженной на квадрат радиуса. Площадь равна 𝜋𝑟 в квадрате. Так как радиус равен половине диаметра, мы могли бы эквивалентно записать это как 𝜋, умноженное на 𝑑 на два в квадрате, или 𝜋𝑑 в квадрате над четырьмя, но это встречается гораздо реже. Обычно, если нам дают диаметр круга, мы просто разделим это значение на два, чтобы вычислить радиус круга, а затем используйте первую версию формулы. Теперь рассмотрим пример в что мы применяем эту формулу, чтобы найти площадь круга.
Использование 3.14 в качестве приближения для
𝜋, найдите площадь круга.
Начнем с того, что вспомним, что формула для нахождения площади круга 𝜋𝑟 в квадрате, где 𝑟 представляет собой радиус окружности. Из рисунка мы определяем, что радиус этого круга равен 12 сантиметрам, потому что нам дана длина отрезок, соединяющий центр окружности с точкой на окружности длина окружности.
Таким образом, подставив 12 вместо 𝑟, мы получим что площадь этого круга равна 𝜋, умноженному на 12 в квадрате. Мы должны помнить, что это просто 12 мы возводим в квадрат. Мы тоже не в квадрат 𝜋. Таким образом, это равно 𝜋, умноженному на 144. Нам говорят, что мы должны использовать 3,14 как приближение для 𝜋. Таким образом, оценивая 3,14, умноженное на 144 дает 452,16. Единицы площади квадратные единицы.
Итак, мы обнаружили, что площадь этого
круг, который имеет радиус длины 12 сантиметров, составляет приблизительно 452,16
сантиметр в квадрате.
Так же, как мы считали периметров полу- и четверти кругов, мы также можем найти формулы для площадей эти формы. А по факту чуть больше на этот раз просто, потому что нам просто нужно разделить площадь полного круга на два для полукруга или на четыре для четверти круга. Итак, мы имеем, что площадь полукруг равен 𝜋𝑟 в квадрате над двумя, а площадь четверти круга равна 𝜋𝑟 в квадрате более четырех. Теперь рассмотрим пример в которым мы связываем площадь и периметр полукруга.
Площадь данного полукруга равна 51,04 сантиметра в квадрате. Найдите периметр полуокружность с точностью до сантиметра.
Напомним, что формула для
найти площадь полукруга 𝜋𝑟 в квадрате над двумя, где 𝑟 — радиус
круг. 𝜋𝑟 в квадрате дает площадь
полный круг, а затем мы делим его на два. Периметр полукруга равен
состоит из прямого края, который является диаметром круга, и изогнутой части,
что составляет половину окружности круга. Значит периметр полукруга
равно 𝑑 плюс 𝐶 больше двух. И формула нахождения
длина окружности равна 𝜋𝑑, 𝜋 раз больше диаметра. Периметр полукруга может
быть записано как 𝑑 плюс 𝜋𝑑 над двумя.
Значит периметр полукруга
равно 𝑑 плюс 𝐶 больше двух. И формула нахождения
длина окружности равна 𝜋𝑑, 𝜋 раз больше диаметра. Периметр полукруга может
быть записано как 𝑑 плюс 𝜋𝑑 над двумя.
Для определения периметра этого полукруга, то нам сначала нужно вычислить его диаметр. Используя заданную площадь полуокружности и формулы для вычисления площади полукруга, мы можем составить уравнение: 𝜋𝑟 в квадрате над двумя равно 51,04. Если мы сможем решить это уравнение, чтобы определить значение 𝑟, мы можем затем вычислить диаметр круга по напомнив, что диаметр в два раза больше радиуса. Начнем с умножения обеих сторон уравнения на два, чтобы получить 𝜋𝑟 в квадрате равно 102,08.
Далее разделяем обе стороны
уравнение на 𝜋, дающее 𝑟 в квадрате равно 102,08 по 𝜋, а затем возьмите квадрат
корень каждой части уравнения. Оценка дает 𝑟 равно 5,7002
продолжение. Итак, мы нашли радиус
круг, и мы можем удвоить его, чтобы найти диаметр, который дает 11,4005
продолжение.
Оценка дает 𝑟 равно 5,7002
продолжение. Итак, мы нашли радиус
круг, и мы можем удвоить его, чтобы найти диаметр, который дает 11,4005
продолжение.
Теперь мы можем заменить это значение 𝑑 в нашу формулу для периметра полукруга. И нам нужно убедиться, что мы держим это значение как можно точнее. Вы можете сохранить это значение в память вашего калькулятора, чтобы вы могли затем вызвать его непосредственно, когда оценка периметра. Подставляя это точное значение 𝑑 а затем оценка дает 29.3084. Нас просят указать периметр ближайший сантиметр, поэтому округляем до 29. Вспоминая формулы для вычислив площадь и периметр полукруга, мы нашли, что периметр этого полукруга с точностью до сантиметра равен 29 сантиметрам.
Теперь рассмотрим один последний
пример, в котором мы применим наши знания о кругах к реальной задаче.
Козел привязан на 10 метров длинная веревка к углу сарая. Какую площадь поля может козел достигать?
Во-первых, нам нужно мыслить практически о том, как коза может передвигаться по этому полю. Если бы козу просто привязали где-нибудь в середине поля, тогда это было бы гораздо проще проблема. Коза могла бродить где угодно в пределах круга радиусом 10 метров. Но поскольку вместо этого коза привязанный к углу сарая, в какой-то момент амбар попадет в путь.
Предположим сначала, что коза ходит
насколько они могут вдоль верхней стены амбара. Поскольку веревка имеет длину 10 метров, но
эта стена 12 метров в длину, козел не сможет пройти весь путь до
конец. Так они дойдут до точки 10 метров
подальше от другого угла, прежде чем у них кончится веревка. Если веревка остается полностью натянутой,
затем коза может начать ходить по кругу с центром в углу сарая с
радиус 10 метров.
На самом деле мы можем отследить три четверти круга, пока коза не достигнет вот этой точки. Но давайте подумаем, что происходит следующий. В этот момент веревка собирается застрять в правом нижнем углу амбара, и козе придется повернуться вокруг этой точки. Пять метров веревки будет израсходован, потому что теперь он будет лежать вдоль восточного края амбара. И это длина этого край. Значит, у козла всего пять метров веревка, оставленная для поворота. Таким образом, коза может ходить в меньший круг радиусом пять метров, пока они не достигнут южного края сарай. Конечно, все это происходит если коза остается прямо на конце веревки, значит, это трассировка по периметру области, которую может покрыть коза.
Коза тоже может ходить везде
внутри этой области, если не используется вся длина веревки. Итак, что мы обнаружили тогда, так это то, что
общая площадь, которую может покрыть коза, составляет три четверти круга радиусом 10 метров.
и четверть круга радиусом пять метров.
Итак, что мы обнаружили тогда, так это то, что
общая площадь, которую может покрыть коза, составляет три четверти круга радиусом 10 метров.
и четверть круга радиусом пять метров.
Напомним, что формула для вычисление площади круга 𝜋 умножается на его радиус в квадрате. Итак, для круга в три четверти площадь равна 𝜋, умноженному на 10 в квадрате, умноженному на три четверти. А для четверти круга площадь равна 𝜋, умноженному на пять в квадрате, умноженному на одну четверть. Оценка дает 300 за четыре 𝜋 и 25 больше четырех 𝜋. Общая площадь поля, которое коза может достичь, то это сумма этих двух значений, которая равна 325 по четырем 𝜋 квадратные метры.
Давайте теперь суммируем ключевые моменты
из этого видео. Окружность круга
равно 𝜋, умноженному на диаметр, или двум 𝜋, умноженным на радиус. Площадь круга 𝜋𝑟
в квадрате.

 2a=0,64\)
2a=0,64\)
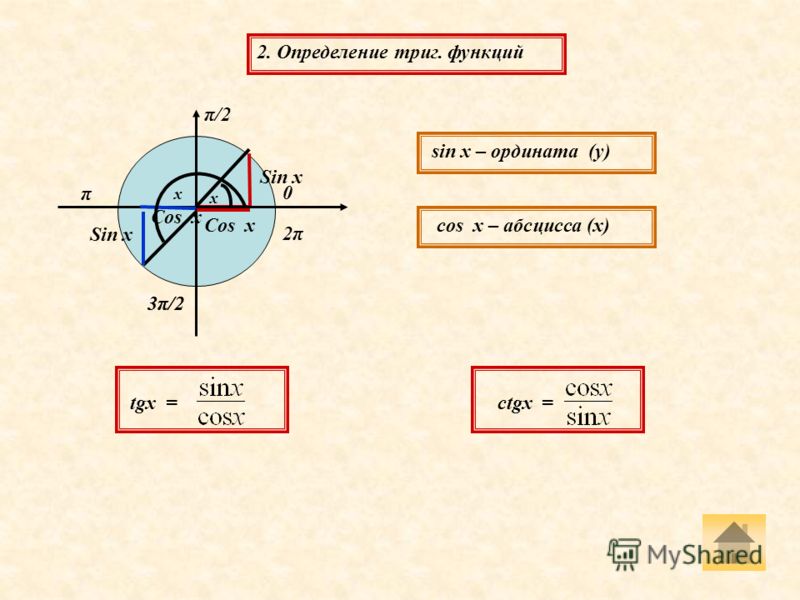 Когда Ахиллес пробежит сто шагов, черепаха проползёт ещё десять шагов, и так далее. Процесс будет продолжаться до бесконечности, Ахиллес так никогда и не догонит черепаху.
Когда Ахиллес пробежит сто шагов, черепаха проползёт ещё десять шагов, и так далее. Процесс будет продолжаться до бесконечности, Ахиллес так никогда и не догонит черепаху.  Применение же нашей обычной логики приводит нас в ловушку. Мы, по инерции мышления, применяем постоянные единицы измерения времени к обратной величине. С физической точки зрения это выглядит, как замедление времени до его полной остановки в момент, когда Ахиллес поравняется с черепахой. Если время останавливается, Ахиллес уже не может перегнать черепаху.
Применение же нашей обычной логики приводит нас в ловушку. Мы, по инерции мышления, применяем постоянные единицы измерения времени к обратной величине. С физической точки зрения это выглядит, как замедление времени до его полной остановки в момент, когда Ахиллес поравняется с черепахой. Если время останавливается, Ахиллес уже не может перегнать черепаху.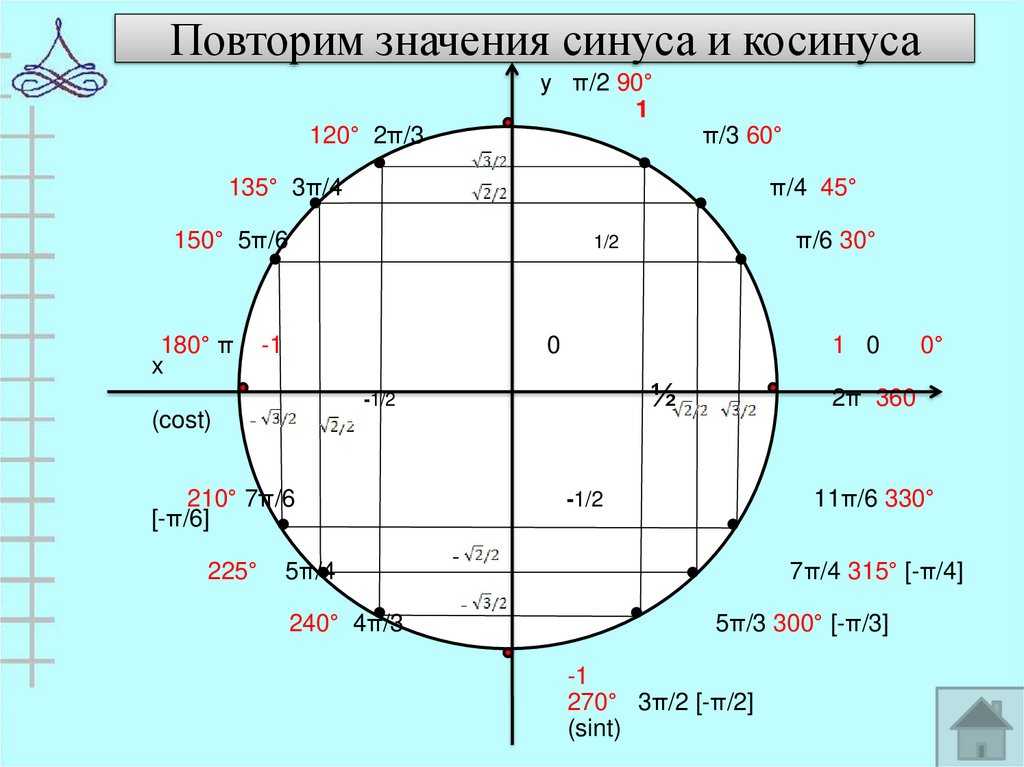 За следующий интервал времени, равный первому, Ахиллес пробежит ещё тысячу шагов, а черепаха проползет сто шагов. Теперь Ахиллес на восемьсот шагов опережает черепаху.
За следующий интервал времени, равный первому, Ахиллес пробежит ещё тысячу шагов, а черепаха проползет сто шагов. Теперь Ахиллес на восемьсот шагов опережает черепаху. 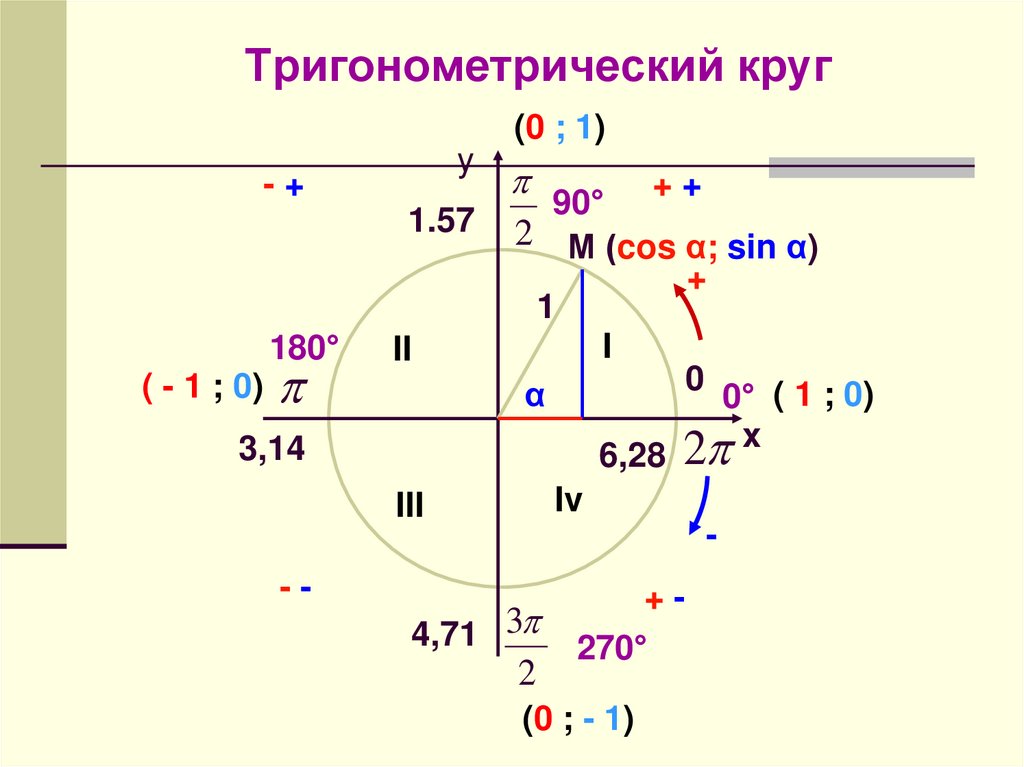
 Подобную логику абсурда разумным существам не понять никогда. Это уровень говорящих попугаев и дрессированных обезьян, у которых разум отсутствует от слова «совсем». Математики выступают в роли обычных дрессировщиков, проповедуя нам свои абсурдные идеи.
Подобную логику абсурда разумным существам не понять никогда. Это уровень говорящих попугаев и дрессированных обезьян, у которых разум отсутствует от слова «совсем». Математики выступают в роли обычных дрессировщиков, проповедуя нам свои абсурдные идеи. Затем берем с каждой стопки по одной купюре и вручаем математику его «математическое множество зарплаты». Поясняем математику, что остальные купюры он получит только тогда, когда докажет, что множество без одинаковых элементов не равно множеству с одинаковыми элементами. Вот здесь начнется самое интересное.
Затем берем с каждой стопки по одной купюре и вручаем математику его «математическое множество зарплаты». Поясняем математику, что остальные купюры он получит только тогда, когда докажет, что множество без одинаковых элементов не равно множеству с одинаковыми элементами. Вот здесь начнется самое интересное.

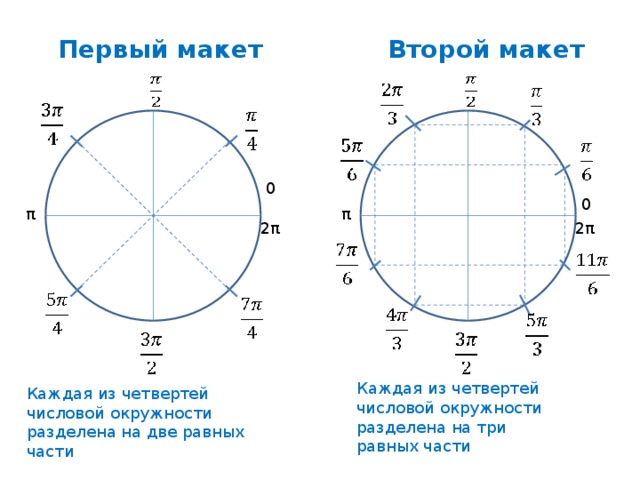 Это не математическое действие.
Это не математическое действие.
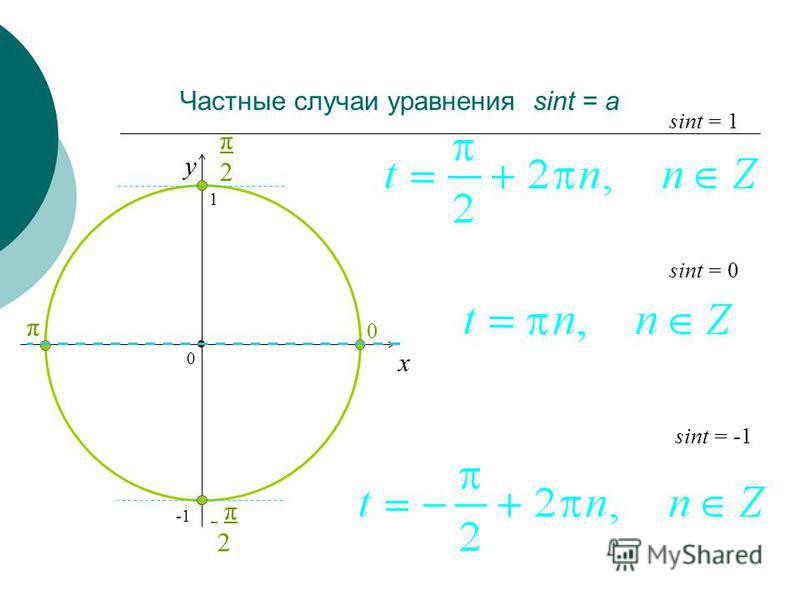 Какой еще туалет?
Какой еще туалет?
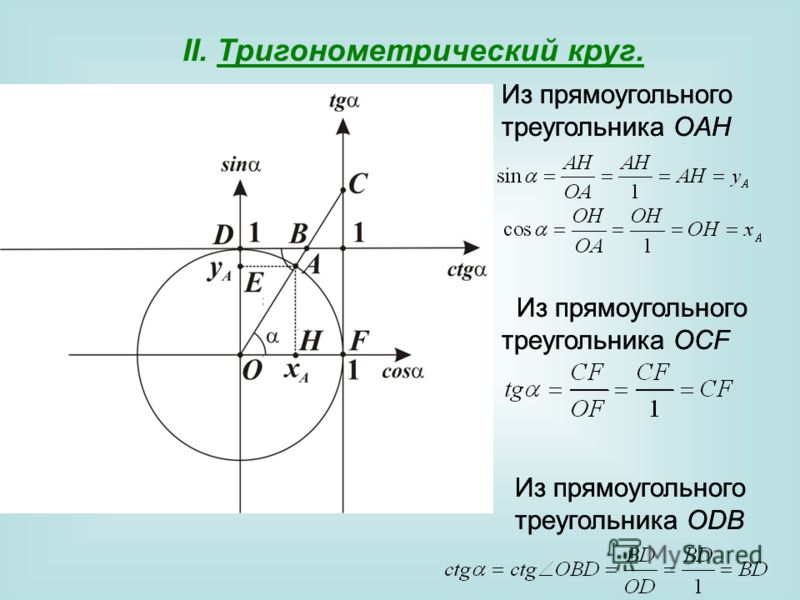 Данные вычисления относились к сферической тригонометрии, в то время как в школьном курсе изучают соотношения сторон и угла плоского треугольника.
Данные вычисления относились к сферической тригонометрии, в то время как в школьном курсе изучают соотношения сторон и угла плоского треугольника.
 Например, sin α будет со знаком «+», если α принадлежит I и II четверти окружности, то есть, находится в промежутке от 0° до 180°. При α от 180° до 360° (III и IV четверти) sin α может быть только отрицательным значением.
Например, sin α будет со знаком «+», если α принадлежит I и II четверти окружности, то есть, находится в промежутке от 0° до 180°. При α от 180° до 360° (III и IV четверти) sin α может быть только отрицательным значением.