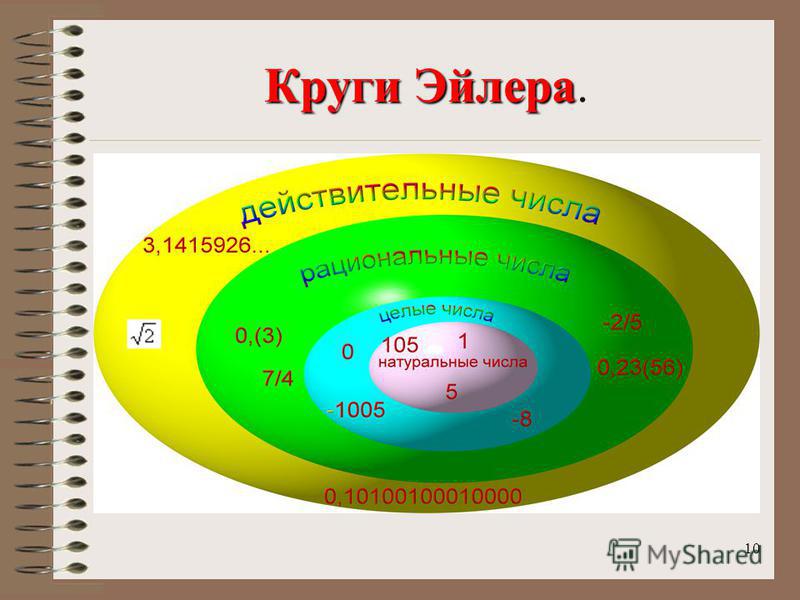
| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | cos(pi/4) | ||
| 9 | Найти точное значение | sin(45 град. ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) | |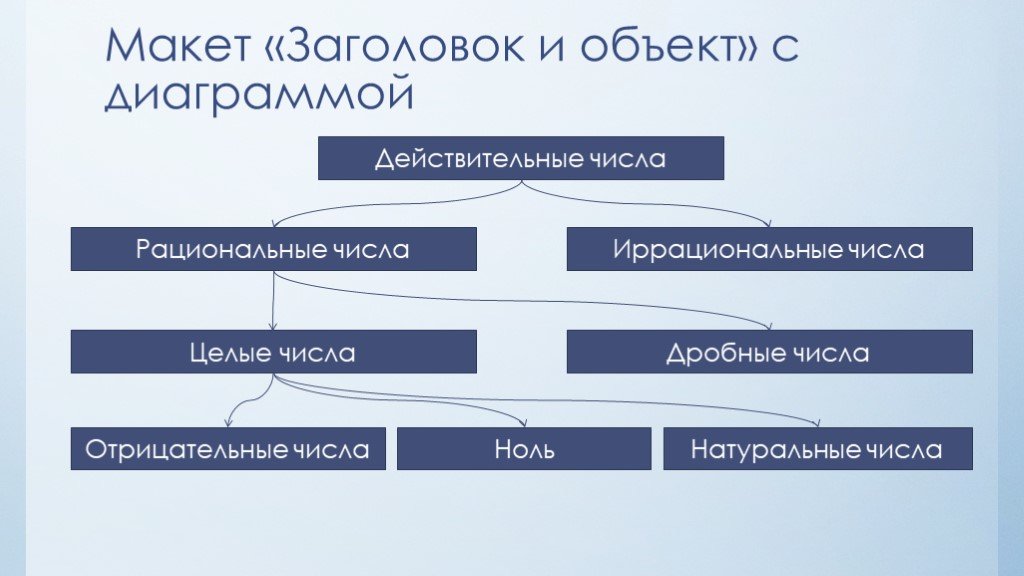
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | tan(45) | ||
| 69 | Вычислить | sin(30 град. ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град. ) | |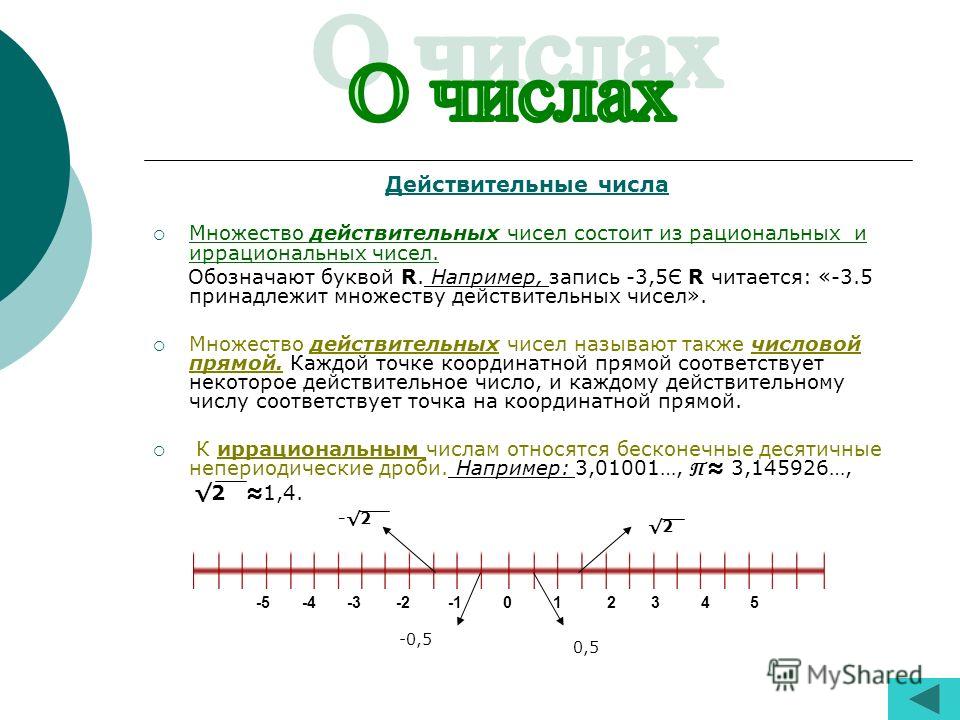
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
Основные виды чисел и формирование понятия об арифметических действиях
Оглавление
Введение
1. Основные виды чисел и формирования понятия об арифметических действиях над натуральными и рациональными числами
1.
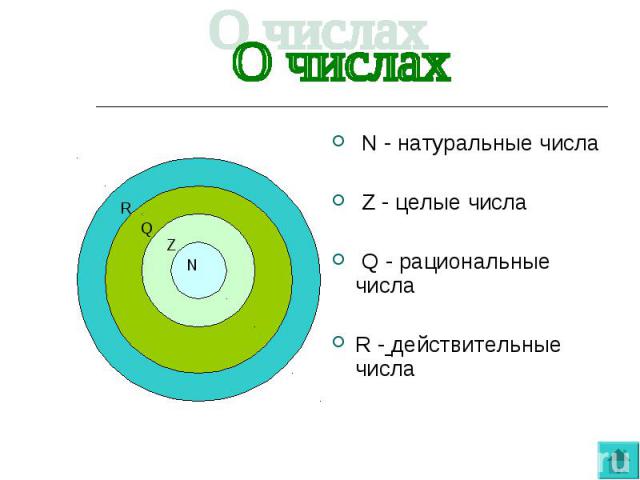1. Историческая справка
1.2. Основные виды чисел
1.3. Натуральные числа
1.4. Арифметические действия над натуральными числами
1.5. Рациональные числа
1.6. Арифметические действия над натуральными числами
2. Практические задачи по теме «Основные виды чисел и формирования понятия об арифметических действиях над натуральными и рациональными числами»
2.1. Натуральные числа
2.2. Рациональные числа
2.3. Задачи для самостоятельного решения
Заключение
Список использованной литературы:
Приложение
Введение
Число — абстракция, используемая для количественной характеристики объектов. Числа возникли еще в первобытном обществе в связи с потребностью людей считать предметы. С течением времени по мере развития науки число превратилось в важнейшее математическое понятие.
Актуальность темы обусловлена тем, что для решения задач и доказательства различных теорем необходимо понимать, какие бывают виды чисел.
Цель данной работы – проанализировать основные виды чисел и сформировать понятия об арифметических действиях над натуральными и рациональными числами.
Для достижения поставленной цели необходимо решить ряд задач:
— рассмотреть основные виды чисел, а именно: натуральные, целые, рациональные, вещественные, комплексные;
— раскрыть свойства натуральных и рациональных чисел, их множество, запись и аксиомы;
— подробно разобрать арифметические действия над натуральными и рациональными числами, такие как сложение, умножение, вычитание, деление и натуральная степень числа;
— рассмотреть примеры с подробными решениями;
— подобрать задачи для самостоятельного решения.
Для решения поставленных задач и проверки гипотезы в курсовой работе использовались следующие методы исследования:
— теоретический анализ математической, историко-математической литературы и научных изданий;
— анализ и обобщение знаний, полученных многими учеными в процессе развития науки математика;
— подробное рассмотрение формул, аксиом и законов, на которых строится научный материал по заданной теме;
— подробный разбор примеров заданий с решениями.
Структура и содержание данной работы состоят в следующем: курсовая работа состоит из введения; двух глав, первая из которых содержит теоретический анализ материала, вторая – практическое решение задач и заданий для самостоятельного решения; заключения, приложения и библиографического списка.
1. Основные виды чисел и формирования понятия об арифметических действиях над натуральными и рациональными числами
1.1. Историческая справка
Основной объект арифметики – число. Натуральные числа, то есть 1, 2, 3, 4, … и так далее, возникли еще в доисторические времена из потребности счета конкретных предметов.
Важная задача арифметики – научиться преодолевать конкретный смысл названий считаемых предметов, отвлекаться от их формы, размера, цвета и тому подобное. Эта задача в процессе развития человеческого общества была постепенно достигнута параллельно с развитием письменности: понятие натурального числа принимает все более отвлеченную форму, все более закрепляется отвлеченное от всякой конкретности понятие числа, воспроизводимого в форме слов в устной речи и в форме обозначения специальными знаками в письменной.
Важным шагом в развитии понятия натурального числа является осознание бесконечности натурального ряда чисел, т.е. потенциальной возможности его безграничного продолжения. Отчетливое представление о бесконечности натурального ряда отражено в знаменитых памятниках античной математики (3 век до н.э.), в трудах Евклида и Архимеда
Появление дробных (положительных рациональных) чисел был связано с необходимостью производить измерения, т.е. процедуру, в которой какая-либо величина сравнивается с другой величиной того же рода, выбираемой в качестве эталона (единицы измерения). Но так как единица измерения не всегда укладывалась в целое число раз в измеряемой величине, и пренебречь этим обстоятельством в ряде случаев было нельзя, то возникла практическая потребность ввести более «мелкие» числа, нежели натуральные. Это и было источником возникновения наиболее «простых» дробей, таких как половина, треть, четверть и т. д. Дальнейшее развитие понятия числа было обусловлено уже не только непосредственной практической деятельностью человека, но и следствием развития математики.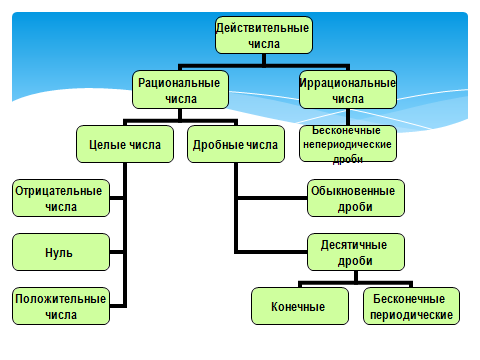
Число – это важнейшее математическое понятие. Возникновение понятия натурального числа относится к первобытному обществу, и было обусловлено необходимостью счета в практической деятельности человека. Первоначально понятие отвлеченного числа отсутствовало – число было «привязано» к тем предметам, которые пересчитывали, и в языке первобытных народов существовали различные словесные обороты для обозначения числа разных предметов. Отвлеченное понятие натурального числа (т.е. числа, не связанного с пересчетом конкретных предметов) появляется и закрепляется вместе с развитием письменности и введением для обозначения чисел определенных символов.
Введение отрицательных чисел было вызвано развитием алгебры как науки, дающей общие способы решения арифметических задач, независимо от их конкретного содержания и исходных числовых данных. Отрицательные числа систематически употреблялись индийскими математиками еще в VI – XI веках. В европейской науке отрицательные числа окончательно вошли в употребление лишь после работ Р.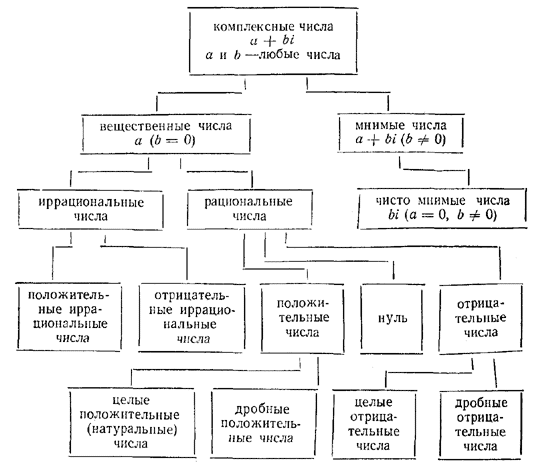
Декарта в XVII веке, давшего их геометрическое истолкование.
Множество рациональных чисел оказывается достаточным для удовлетворения большинства практических потребностей – с помощью рациональных чисел измерения можно выполнять с любой степенью точности.
Дальнейшее расширение понятия числа произошло в XVII веке в период зарождения современной математики, когда возникла необходимость ввести четкое определение понятия числа. Такое определение было дано одним из основоположников математического анализа И.Ньютоном во «Всеобщей арифметике»: «Под числом мы понимаем не столько множество единиц, сколько отвлеченное отношение какой-нибудь величины к другой величине того же рода, принятой нами за единицу». Эта формулировка дает единое определение действительного числа, как рационального, так и иррационального. (О существовании несоизмеримых отрезков, отношение которых есть число иррациональное, было известно еще ученым Древней Греции.) В дальнейшем, в 70-х годах XIX века строгая теория действительного числа была развита в работах Р.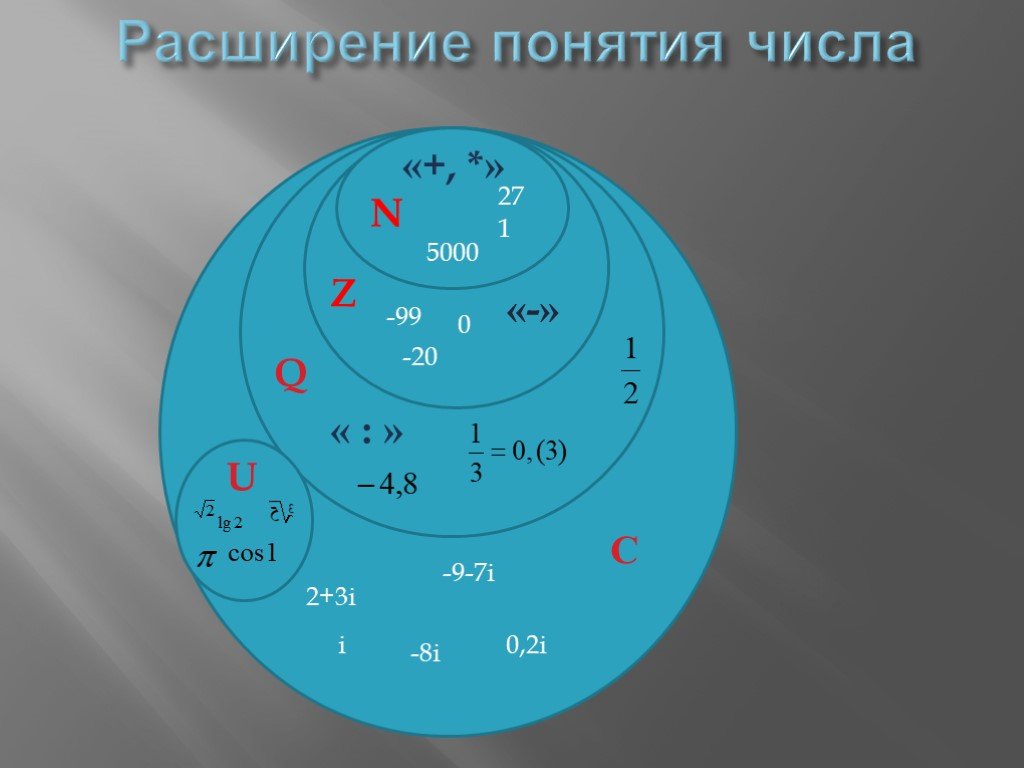
Дедекинда, Г.Кантора и К.Вейерштрасса.
Основными математическими объектами с незапамятных времен являются числа, множества и элементы множества, их свойства. Число́ — абстракция, используемая для количественной характеристики объектов. Возникнув ещё в первобытном обществе из потребностей счёта, понятие числа изменялось и обогащалось и превратилось в важнейшее математическое понятие. Письменными знаками (символами) для записи чисел служат цифры. Современная математика оперирует несколько другими математическими понятиями. Если внимательно проанализировать их суть, то они в общем–то являются эквивалентными или изоморфными понятиям «число», «множество», «отображение», «свойство».
В теоретико–множественном смысле числа являются классом множеств с определенными свойствами. Эти свойства выражаются через тип упорядоченности, размерность, топологические и метрические свойства основанных на них множеств. Основное свойство чисел – это их мощность, которая может быть конечной, счетной или континуальной.
Соответственно, числа могут быть представителями любого класса множеств с подходящей мощностью. Даже множества с мощностью больше континуума можно представить как множество всех функций, определенных на числовом множестве. В этом проявляется универсальность понятия «число».
Другое важное свойство чисел – это их размерность. Есть несколько классов чисел с различающимися свойствами. Есть линейные (одномерные) числа – это натуральные N, положительные N+, целые Z, рациональные R и вещественные Q числа. Есть составные многомерные или гиперкомплексные числа – это комплексные числа C, кватернионы H, бикватернионы B, невырожденные квадратные матрицы M, числа Клиффорда K и другие.
Выводы:
В параграфе 1.1. были рассмотрены следующие вопросы:
— история появления и развития определения числа;
— задачи арифметики;
— расширение понятия числа;
— основные математические объекты – числа;
— размерность чисел.
1.2. Основные виды чисел
Самыми простыми числами являются целые, рациональные, вещественные и комплексные числа.
Они коммутативны, ассоциативны и дистрибутивны.
Основными видами чисел, обладающими похожими свойствами, являются четыре вида чисел. Это действительные числа, комплексные, кватернионы и октавы. Коммутативность умножения для последних двух видов чисел не выполняется. Но они все обладают алгебрами без делителей нуля.
Дальнейшие расширения чисел могут не иметь и свойство ассоциативности. Дистрибутивность соблюдается.
Натуральные числа, получаемые при естественном счёте; множество натуральных чисел обозначается N. Таким образом, (иногда к множеству натуральных чисел также относят ноль, то есть N = {0, 1, 2, 3, …}). Натуральные числа замкнуты относительно сложения и умножения (но не вычитания или деления). Натуральные числа коммутативны и ассоциативны относительно сложения и умножения, а умножение натуральных чисел дистрибутивно относительно сложения.
Целые числа, получаемые объединением натуральных чисел с множеством отрицательных чисел и нулём, обозначаются Z = {–2, –1, 0, 1, 2, …}.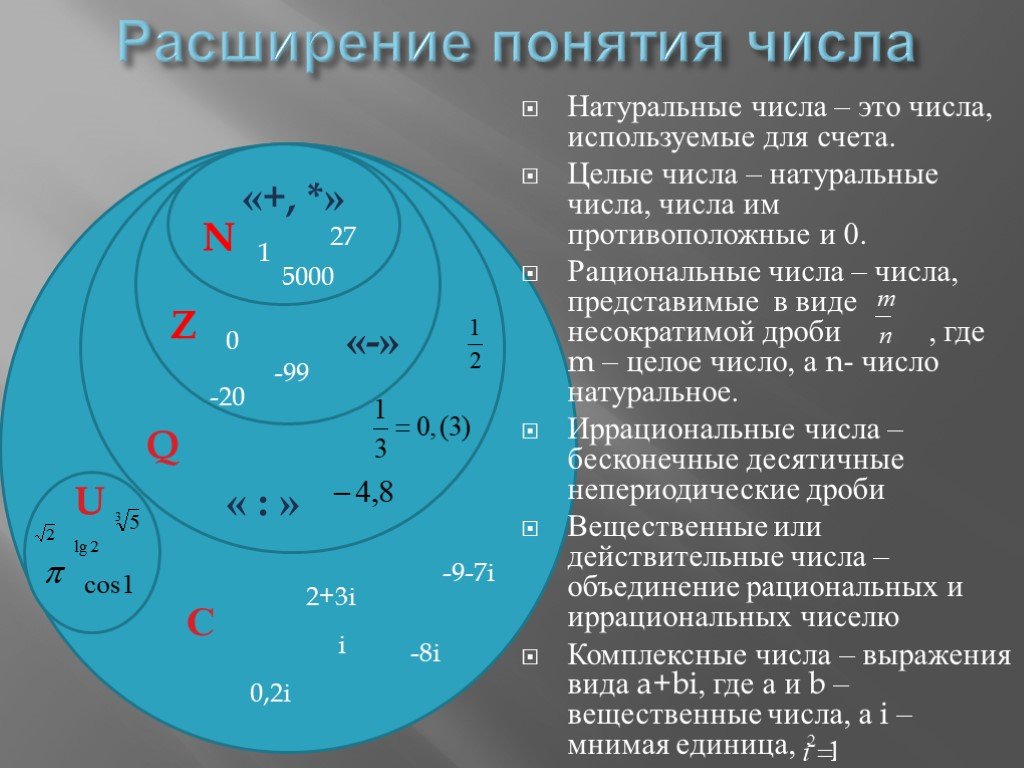
Целые числа замкнуты относительно сложения, вычитания и умножения (но не деления).
Рациональные числа — числа, представленные в виде дроби (n ≠ 0), где m — целое число, а n — натуральное число. Для рациональных чисел определены все четыре «классические» арифметические действия: сложение, вычитание, умножение и деление (кроме деления на ноль). Для обозначения рациональных чисел используется знак Q.
Действительные (вещественные) числа представляют собой расширение множества рациональных чисел, замкнутое относительно некоторых (важных для математического анализа) операций предельного перехода. Множество вещественных чисел обозначается R. Его можно рассматривать как пополнение поля рациональных чисел Q при помощи нормы, являющейся обычной абсолютной величиной. Кроме рациональных чисел, R включает множество иррациональных чисел, не представимых в виде отношения целых. Кроме подразделения на рациональные и иррациональные, действительные числа также подразделяются на алгебраические и трансцендентные.
При этом каждое трансцендентное число является иррациональным, каждое рациональное число — алгебраическим.
Комплексные числа C, являющиеся расширением множества действительных чисел. Они могут быть записаны в виде z = x + iy, где i — так называемая мнимая единица, для которой выполняется равенство i2 = − 1. Комплексные числа используются при решении задач квантовой механики, гидродинамики, теории упругости и пр.
Для перечисленных множеств чисел справедливо следующее выражение: N Z Q R C.
Гипердействительные числа – это числа вида
1) a + e, где a – обычное число, a — бесконечно малое число;
2) ∞ = 1/e – бесконечно большое число.
Гипердействительные числа не являются числами в обычном понимании. Они применяются во многих разделах математики, особенно в дифференциальном и интегральном исчислениях, а также везде, где используются предельные числовые последовательности, даже при определении вещественных чисел.
Выводы:
В параграфе 1.
2. были рассмотрены:
— общие сведения об основных видах чисел;
— натуральные, целые, рациональные, действительные и комплексные числа, их представление, обозначение и особенности;
— гипердействительные числа.
1.3. Натуральные числа
Понятия «число» и «элемент множества» появилось у человечества в связи с необходимостью счета и различения различных предметов. Множество чисел, необходимых для этого, объединяются понятием «натуральные числа» – N+. Обычно под натуральными числами понимаются числа от единицы до бесконечности. Иногда к ним присоединяется и число «ноль». Число «ноль» означает отсутствие чего–бы то ни было в счете.
Важным шагом в развитии понятия натурального числа является осознание бесконечности натурального ряда чисел, т.е. потенциальной возможности его безграничного продолжения.
Считается, что термин «натуральное число» впервые применил римский государственный деятель, философ, автор трудов по математике и теории музыки Боэций (480 — 524 гг.
), но еще греческий математик Никомах из Геразы говорил о натуральном, то есть природном ряде чисел.
Натуральные числа имеют две основные функции: характеристика количества предметов и характеристика порядка предметов, размещенных в ряд. В соответствии с этими функциями возникли понятия порядкового числа (первый, второй и т.д.) и количественного числа (один, два и т.д.).
Четыре аксиомы натуральных чисел:
1) существует минимальное натуральное число «единица» = 1, но иногда это число «ноль» = 0. Они отличаются своими свойствами.
2) для каждого числа существует единственное следующее число: a → a’. Отношение «следующее число» является отношением частичного порядка.
Классификация действительных чисел | Математика для гуманитарных наук Базовый курс
Результаты обучения
- Классифицировать действительные числа как счетные, целые, рациональные, иррациональные или целые числа
Мы видели, что все счетные числа являются целыми числами, все целые числа являются целыми числами и все целые числа являются рациональными числами.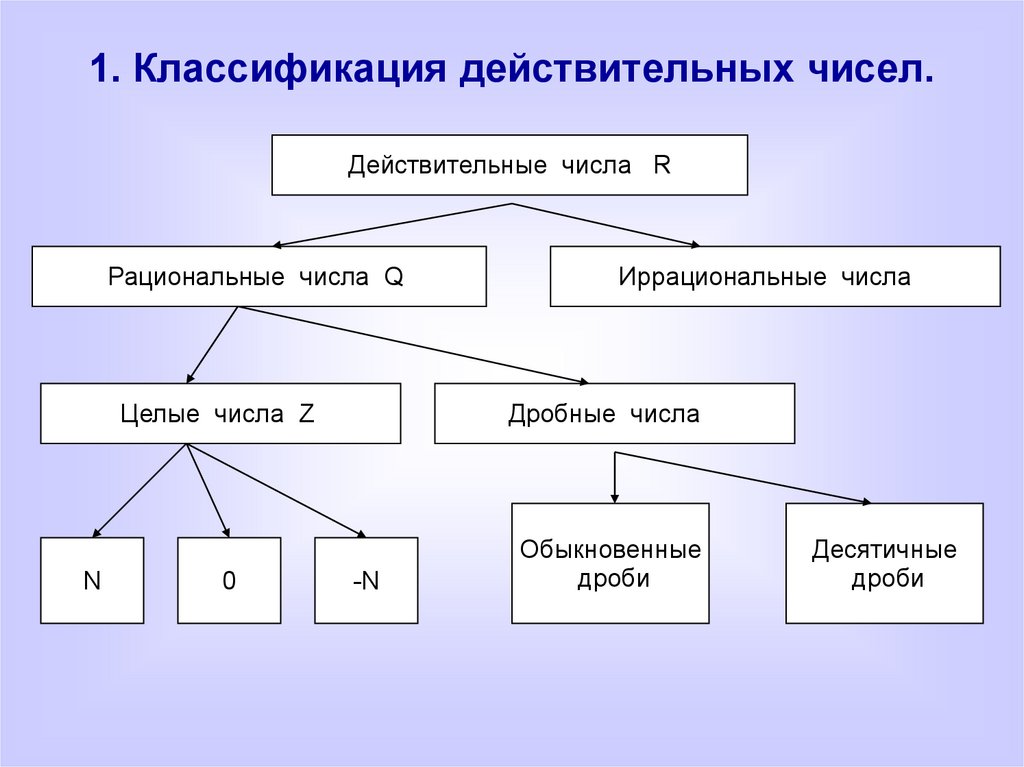
Иррациональные числа представляют собой отдельную категорию. Когда мы складываем рациональные числа и иррациональные числа, мы получаем множество действительных чисел.
На этой диаграмме показаны отношения между различными типами действительных чисел.
Вещественные числа
Вещественные числа — это числа, которые являются либо рациональными, либо иррациональными.
Термин «действительные числа» кажется вам странным? Существуют ли числа, которые не являются «настоящими», и если да, то какими они могут быть? На протяжении веков единственными числами, о которых люди знали, были те, которые мы сейчас называем реальными числами. Затем математики открыли множество мнимые числа. В этом курсе вы не столкнетесь с мнимыми числами, но вы столкнетесь с ними позже, изучая алгебру.
пример
Определите, является ли каждое из чисел в следующем списке 1. целым числом, 2. целым числом, 3. рациональным числом, 4. иррациональным числом и 5.
действительным числом.
[латекс]-7,\Large\frac{14}{5}\normalsize ,8,\sqrt{5},5.9,-\sqrt{64}[/latex]
Решение:
1. Целое числа [латекс]0,1,2,3\точки[/латекс] Число [латекс]8[/латекс] — единственное заданное целое число.
2. Целые числа — это целые числа, их противоположности и [латекс]0[/латекс]. Из заданных чисел [латекс]-7[/латекс] и [латекс]8[/латекс] являются целыми числами. Также обратите внимание, что [латекс]64[/латекс] является квадратом [латекса]8[/латекса], поэтому [латекс]-\sqrt{64}=-8[/латекс]. Итак, целые числа равны [латекс]-7,8,-\sqrt{64}[/латекс].
3. Поскольку все целые числа рациональны, числа [латекс]-7,8,\текст{и}-\sqrt{64}[/латекс] также рациональны. Рациональные числа также включают дроби и десятичные дроби, которые заканчиваются или повторяются, поэтому [latex]\Large\frac{14}{5}\normalsize\text{and}5.9[/latex] рациональны.
4. Число [латекс]5[/латекс] не является полным квадратом, поэтому [латекс]\sqrt{5}[/латекс] иррационально.
5. Все указанные номера действительны.
Сведем результаты в таблицу.
| Номер | Целиком | Целое число | Рационал | Иррациональный | Реальный |
|---|---|---|---|---|---|
| [латекс]-7[/латекс] | [латекс]\quad\галочка [/латекс] | [латекс]\quad\галочка [/латекс] | [латекс]\quad\галочка [/латекс] | ||
| [латекс]\большой\фрак{14}{5}[/латекс] | [латекс]\quad\галочка [/латекс] | [латекс]\quad\галочка [/латекс] | |||
| [латекс]8[/латекс] | [латекс]\quad\галочка [/латекс] | [латекс]\quad\галочка [/латекс] | [латекс]\quad\галочка [/латекс] | [латекс]\quad\галочка [/латекс] | |
| [латекс]\sqrt{5}[/латекс] | [латекс]\quad\галочка [/латекс] | [латекс]\quad\галочка [/латекс] | |||
[латекс]5. 9[/латекс] | [латекс]\quad\галочка [/латекс] | [латекс]\quad\галочка [/латекс] | |||
| [латекс]-\sqrt{64}[/латекс] | [латекс]\quad\галочка [/латекс] | [латекс]\quad\галочка [/латекс] | [латекс]\quad\галочка [/латекс] |
попробуйте
В следующем мини-уроке приведены дополнительные примеры классификации действительных чисел.
Классификация вещественных чисел — ChiliMath
Представленная ниже диаграмма «стека воронок» поможет нам легко классифицировать любые вещественные числа. Но сначала нам нужно описать, какие элементы входят в каждую группу чисел. Воронка представляет каждую группу или набор чисел.
Натуральные числа (также известные как счетные числа) — это числа, которые мы используем для счета.
Начинается с 1, затем 2, 3 и так далее.
Целые числа — это небольшое «обновление» натуральных чисел, потому что мы просто добавляем элемент ноль к текущему набору натуральных чисел. Думайте о целых числах как о натуральных числах вместе с нулем.
Целые числа включают все целые числа вместе с «отрицательными» или противоположными натуральными числами.
Рациональные числа — это числа, которые могут быть выражены как отношение целых чисел. Это означает, можем ли мы записать данное число в виде дроби, где числитель и знаменатель являются целыми числами; тогда это рациональное число.
Символически мы можем записать рациональное число как:
Внимание! Знаменатель не может быть равен нулю.
Рациональные числа также могут встречаться в десятичной форме . Если десятичное число либо оканчивается, либо повторяется, то его можно записать в виде дроби с целыми числителем и знаменателем.
Значит, это еще и рационально.
Иррациональные числа — это все числа, которые при записи в десятичной форме не повторяются и не заканчиваются. Другими словами, это продолжается бесконечно бесконечно, не имея определенного шаблона.
Действительные числа включают как рациональные, так и иррациональные числа. Помните, что под множеством рациональных чисел у нас есть подкатегории или подмножества целых чисел, целых чисел и натуральных чисел.
Классификация действительных чисел Примеры
Пример 1 : Натуральное число также является целым числом. ( Правда или Ложь )
Набор целых чисел включает ноль и все натуральные числа. Это истинное утверждение .
Пример 2 : Целое число всегда является целым числом. ( Правда или Ложь )
Набор целых чисел состоит из нуля, натуральных чисел и «отрицательных» натуральных чисел.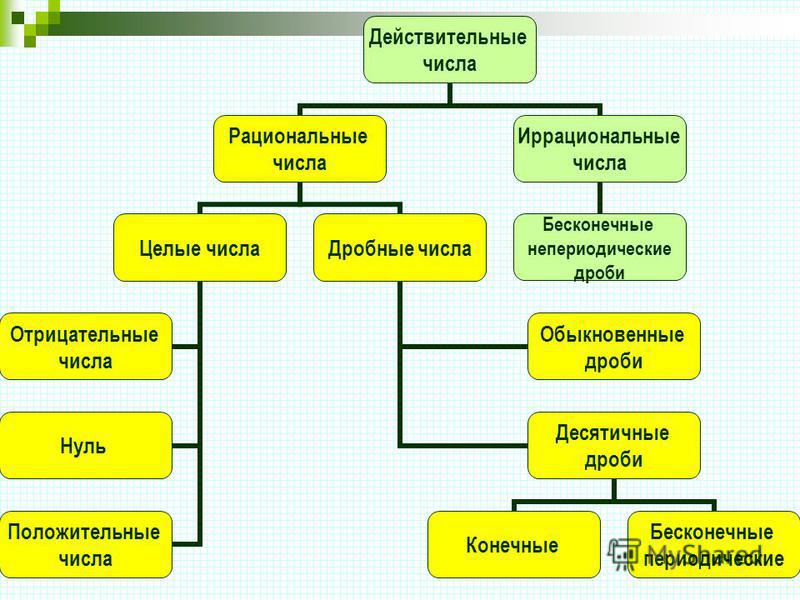
Это означает, что некоторые целые числа являются целыми числами, но не все.
Например, — 2 является целым, но не целым числом. Это утверждение ложно .
Пример 3 : Каждое рациональное число также является целым числом. ( Правда или Ложь )
Слово «каждый» означает «все». Можете ли вы придумать рациональное число, не являющееся целым? Вам нужен только один контрпример, чтобы показать, что это утверждение ложно.
Дробь \Large{1 \over 2} является примером рационального числа, которое НЕ является целым числом. Таким образом, это утверждение ложь .
Пример 4 : каждое целое число является рациональным числом. ( True or False )
Это верно , потому что каждое целое число можно представить в виде дроби со знаменателем 1.
количество. ( Правда или Ложь )
Если рассматривать вышеприведенные описания, то можно заметить, что натуральные числа находятся в наборах целых чисел, целых чисел и рациональных чисел.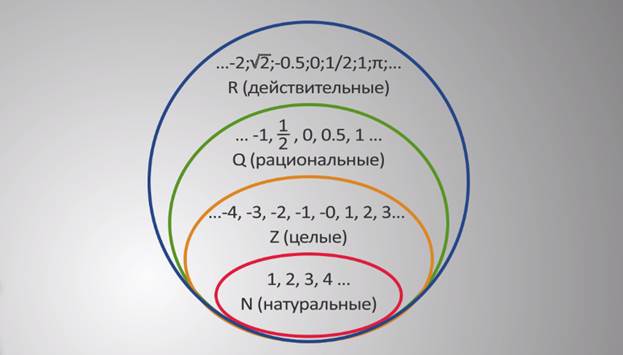
Это делает его истинное утверждение .
Мы также можем использовать диаграмму воронок выше, чтобы помочь нам ответить на этот вопрос. Если мы нальем воду в «воронку натуральных чисел», вода также должна пройти через все воронки, расположенные ниже нее. Таким образом, проходя через воронки целых чисел, целых чисел и рациональных чисел.
Пример 6 : Каждое целое число является натуральным, целым и рациональным числом. ( Правда или Ложь )
Используя ту же аналогию с «воронкой»; если мы нальем немного жидкости в воронку целых чисел, она должна пройти через воронки целых и рациональных чисел, спускаясь вниз. Поскольку воронка натуральных чисел находится над набором целых чисел, с которого мы начали, мы не может включить эту воронку в группу.
Это ложное утверждение, поскольку целые числа принадлежат множествам целых и рациональных чисел, но не множеству натуральных чисел.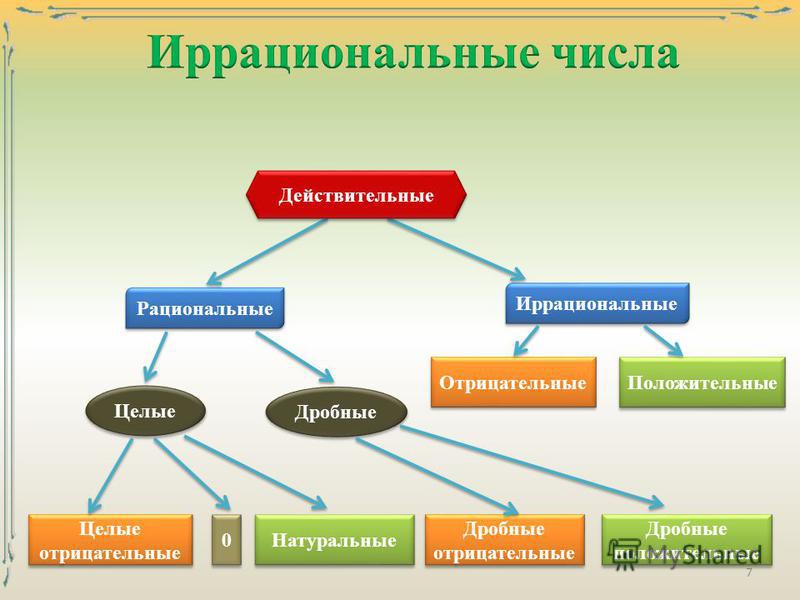
Проще говоря, число ноль (0) является контрпримером, поскольку это целое число, а не натуральное число. Так что действительно, это ложное утверждение.
Пример 7 : классифицируйте число ноль, 0.
Определенно не натуральное число, но это целое, целое, рациональное и действительное число. Может быть неочевидно, что ноль также является рациональным числом. Однако запись его в виде дроби с ненулевым знаменателем ясно показывает, что это действительно рациональное число.
Пример 8 : классифицируйте число 5.
Это натуральное или счетное число, целое число и целое число. Поскольку мы можем записать его в виде дроби со знаменателем 1, то есть \Large{5 \over 1}, это также рациональное число. И, конечно же, это реальная цифра.
Пример 9 : классифицируйте число 0,25.
Данное десятичное число заканчивается, поэтому мы можем записать его в виде дроби, что является характеристикой рационального числа.
Это число также является действительным числом.
\Large{0,25 = {{25} \более {100}} = {1 \более 4}}
Пример 10 : классифицируйте число {\rm{2}}{1 \более 5}.
Мы можем переписать эту смешанную дробь как неправильную дробь, чтобы было ясно, что у нас есть отношение двух целых чисел.
\Large{{\rm{2}}{1 \более 5} = {{11} \более 5}}
Это число является рациональным и действительным числом.
Пример 11 : классифицируйте число {\rm{5,241879132…}}.
Десятичное число не заканчивается и не повторяется, что означает, что это иррациональное число. Конечно, любое иррациональное число также является действительным числом.
Пример 12 : классифицируйте число 1,7777…
Поскольку десятичная дробь повторяется, это рациональное число. Любое рациональное число также должно быть действительным числом.
Пример 13 : классифицируйте число \sqrt 2 .