Какая классификация настоящих чисел? | Ресурсы самопомощи
вещественные числа является набор рациональных и иррациональных чисел чем существующие, из которых также можно найти различные типы. Они возникли в связи с необходимостью, обнаруженной между XV и XVII веками, когда расчет невозможно было описать логически и точно, поскольку часто использовались ненадежные термины или выражения, такие как «малый» или «предел».
Хотя египтяне уже использовали дроби, это было до тех пор, пока математика греков не изучала «число» более философски, когда последователи Пифагора пришли к выводу, что все вокруг них является числами; и поэтому они применялись в различных областях.
Индекс
- 1 Классификация действительных чисел по их типу
- 1.1 1. Рациональные числа
- 1.1.1 а) Целые числа
- 1.1.2 б) Дробное
- 1.2 2. Иррациональные числа
- 1.1 1. Рациональные числа
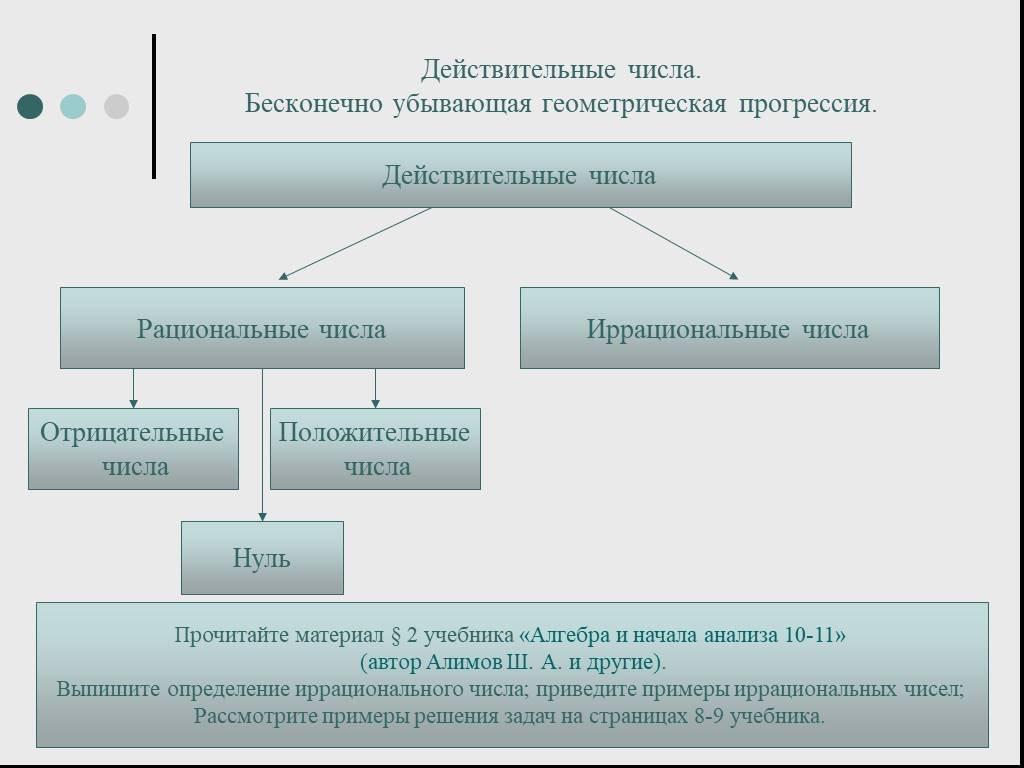
Эти числа можно разделить на два типа, о которых мы упоминали ранее, то есть рациональные числа (положительные, отрицательные и нулевые) и иррациональные (алгебраические и трансцендентные).
Это имя, данное числам, которые могут быть представлены как деление целых чисел или, что то же самое, обыкновенная и текущая дробь, в которой числитель и знаменатель не равны нулю и не меньше его.
Они, в свою очередь, также делятся на несколько типов: целые (натуральные, нулевые и отрицательные целые числа) и дробные (правильные и неправильные дроби).
а) Целые числаЦелые числа представляют собой набор натуральных чисел, отрицательных целых чисел и нуля, которые обозначаются буквой «Z». Целые числа также обычно представлены в числовой строке, где положительные или натуральные числа находятся справа, ноль — в середине, а отрицательные — слева.
- Считается «натуральные числа”Для тех, кто привык считать предметы или выполнять некоторые из наиболее распространенных и простых расчетных операций.
- El Cero Это нулевое значение, то есть в нем отсутствует значащая цифра, когда оно не сопровождается.
 Однако его положение в числе может полностью изменить значение, поскольку, когда оно находится справа от него, значение умножается на десять; а с другой стороны модификации нет.
Однако его положение в числе может полностью изменить значение, поскольку, когда оно находится справа от него, значение умножается на десять; а с другой стороны модификации нет. - отрицательные целые числа они используются противоположно положительным или естественным, то есть вместо того, чтобы считать, их использование состоит в том, чтобы вычитать, иметь, тратить или быть ниже. Чтобы их упомянуть, необходимо перед числом указать термин «минус», например «минус четыре».
Также среди вещественных чисел можно найти этот тип в рациональных числах, которые возникли с целью решать задачи относительно деления натуральных чисел.
Дроби характеризуются числителем и знаменателем, которые отделены друг от друга диагональной или горизонтальной чертой. Однако, несмотря на то, что в целых числах мы также можем найти «простую дробь», в этом разделе типы дробей, которые мы находим, правильные и неправильные.
- Правильные состоят из тех, у которых числитель меньше знаменателя.
- Неподходящие будут наоборот, то есть знаменатель больше знаменателя.
Иррациональные числа — это числа, которые нельзя записать в виде дроби, поскольку их десятичные дроби продолжают повторяться бесконечно. Например, невозможно записать дробь, включающую число Пи, е, соотношение золота и корней квадратные, кубические и другие.
Иррациональные числа возникли благодаря потребности ученика Пифагора записать корень в виде дроби; понимая, что это невозможно и что сегодня мы знаем это число под термином «иррациональное». Однако Пифагор не согласился с его открытием, хотя оно приписывается ему не меньше, чем его школе.
Кроме того, их можно разделить на два типа: алгебраические и трансцендентные.
- алгебраический те, которые позволяют решить алгебраическое уравнение.
- трансцендентный Это те, которые не могут быть представлены конечным числом корней (в отличие от алгебраических) и которые не следуют шаблону в своих десятичных дробях.
 Среди них находим число Пи.
Среди них находим число Пи.
Пока что мы подошли к классификации действительных чисел, которую, как мы надеемся, было легко читать и понимать; поскольку многие люди не любят математику, и мы сделали все возможное, чтобы дать подробное и простое объяснение.
Рациональные и иррациональные числа — презентация онлайн
Похожие презентации:
Деятельность пришкольного лагеря с дневным пребыванием детей «Дружба» МОУ школа № 71
Моя будущая профессия: юрист
Развитие интеллектуальной одаренности детей Новосибирской области с использованием дистанционных образовательных технологий
Элементы комбинаторики ( 9-11 классы)
Творческий проект «Планирование кухни-столовой»
Моя будущая профессия — военный
Кейсы (ситуации взаимодействия ребёнка и взрослого)
Творческий проект «мой профессиональный выбор»
Развитие связной речи у дошкольников
Технология В.А. Илюхиной «Письмо с открытыми правилами» для учащихся начальных классов
1.
 «Рациональные и иррациональные числа»Тема урока:
«Рациональные и иррациональные числа»Тема урока:«Рациональные и
иррациональные числа»
Потапенко И.В.
МБОУ СОШ №6
г.Владикавказ
Необходимость вести счёт – вот что
заставило людей ввести понятие –
натуральные числа
Характеристика порядка предметов,
расположенных в ряд – еще одна функция,
которые выполняют натуральные числа
Натуральные числа
Сумма и произведение натуральных
чисел есть число натуральное.
1, 2, 3, 4, 5, 6…
n — натуральное
n∈ N
Дроби появились при исчислении
времени.
Дробные числа
23
;
67
5
;
1
21
;
5
1
;
8
3
;
16
1
;
3600
34
;
1
1
;
123
1
;
16
1
.
2
1
;
4
1
;
100
При решении
алгебраических
уравнений возникло
понятие
отрицательные
числа
Отрицательные числа
трактовались
так же как долг при финансовых и
бартерных расчетах.
Числа,
им противоположные
-6
-5
-4
-3
-2
-1
Натуральные числа
1 2 3 4 5 6
Z
Целые
Целые числа
Сумма, произведение и разность
целых чисел есть число целое.
m
— целое
m Z
…-3;-2;-1;0,1, 2, 3,…
Целые числа
Дробные числа
2/7
2
5
7,1
3,2
0,(2)
0,1
1
0
-4
9
58
10
Q
Рациональные
Рациональные числа
r — рациональное
r Q
Сумма, произведение, разность и
частное рациональных чисел есть
число рациональное.
Отношения между множествами
натуральных,
целых и рациональных чисел наглядно
демонстрирует
геометрическая иллюстрация –
круги Эйлера.
N
Z
Q
Задание:
Найдите значения числовых выражений и изобразите
их на диаграмме Эйлера.
Вместо недостающего числа впишите букву к.
а 1 : 5 0,8
2
в 0,6 : 0,2 2
с 17 : 3 5
3
2
d ( 1) ( 1)
m 13 : 2 0,5
N
Z
Q
k
Задание.
 Выясните, какие из высказываний
Выясните, какие из высказыванийистинные:
1 )k ошибся
N
и
л
2 )k ошибся
Z
и
л
3 )k
Q
молодец
и
4 )а ∈молодец
N
молодец
л
и
л
5 )а ∈молодец
Z
молодец
и
и
6 )а ∈
Q
молодец
л
молодец
л
8 )d молодец
Z
ошибся
и
л
ошибся
и
7 )d
N
ошибся
ошибся
л
9 )d молодец
Q
ошибся
и
ошибся
л
ошибс
Задание. Замените данные рациональные числа
десятичными дробями.
1
2
0,5
1
0,2
5
1
1
0,125
0 ,333…
8
3
1
0,25
4
2
0,4
5
3
0,375
8
2
0 ,666…
3
3
0,75
4
3
0,6
5
5
0,625
8
1
0 ,1666..
6
15. Сравните числа:
3,00491,011
-67
11,333…
-12,9
0,007
1,2424
<
>
<
>
>
>
<
3,10004
1,008
0,002
11,333
-12,93
74
1,(24)
16.
 Иррациональные числа – это бесконечные десятичные непериодические дроби.2,121121112…
Иррациональные числа – это бесконечные десятичные непериодические дроби.2,121121112…7, 02002…
-1,1010010110…
Действительные
числа R
Рациональные
числа
Иррациональные
числа
R
Q
Z
N
19. Укажите, рациональное или иррациональное это число?
432-3,2
0,1010010001…
5,13113111…
1,2333…
-2,121121112…
-10,353535…
Рациональные
Иррациональные
-3,2 ; 1,2333… ; 432 ;
5,13113111…
-10,353535…
0,1010010001…
-2,121121112…
20. ТЕСТ: +согласен, -несогласен
1.2.
3.
4.
5.
6.
7.
Всякое целое число является натуральным
Всякое натуральное число является рациональным
Число -7 является рациональным
Сумма двух натуральных чисел всегда есть число
натуральное
Разность двух натуральных чисел есть число
натуральное
Действительное число не может быть
натуральным
Всякое иррациональное число является
действительным
21.
 Проверим:1
Проверим:12
3
4
5
6
7
___
+
+
+
__
___
+
22. Спасибо за внимание!
English Русский Правила
2. Квадратные и n-е корни натуральных чисел: рациональные или иррациональные?
Теперь мы рассмотрим некоторые свойства квадратных корней натуральных чисел, начиная с одного из самых известных примеров, √2. Вот удивительно простое доказательство иррациональности, которое мы позже обобщим на другие случаи. b — целые числа, а b — ненулевое значение. Это означает, что: a/b = √2 A 2 /B 2 = 2 A 2 = 2B 2 СМОТ из 2 в а. 2 будет иметь в 2 раза больше множителей, чем 2 в a, поэтому следует, что 2 имеет четное количество таких множителей (которое все еще может быть равно нулю). Интересно отметить, что это доказательство может
быть адаптирована и к другим простым числам с небольшими изменениями аргумента.
Во всех случаях приходим к противоречию о количестве некоторых
факторы в результате. Кроме того, доказательство можно использовать и для
составные числа путем разложения их на произведение простых множителей
а затем учет числа каждого из этих факторов.
Например, извлекая квадратный корень из 6, мы видим, что a 2 = 2 * 3 * b 2 и
одно и то же число имеет как нечетное, так и четное количество делителей 2 и 3. Это разумно полагать, что мы можем использовать описанный выше метод, чтобы показать, что за исключением идеальных квадратов, квадратный корень из целого числа равен иррациональный. Однако я также создал общее доказательство, которое охватывает все эти случаи вместе. Это работает от противного. Мы будем временно предположим, что для некоторого несовершенного квадратного целого числа c рациональное число a/b в простейшей форме, где a и b не имеют общих множители, отличные от 1, является его квадратным корнем. Это означает, что: (a/b) 2 = c a 2 /b 2 = c Мы думаем, что эта дробь каким-то образом должна быть сведена к целому числу. *Это не единственное возможное доказательство этого факта; другие методы существуют. Мы можем, например, использовать многочлен x 2 — 2 и теорему о рациональном корне (см. «Рациональность или иррациональность корней многочленов»), чтобы продемонстрировать
иррациональность. |

 Однако его положение в числе может полностью изменить значение, поскольку, когда оно находится справа от него, значение умножается на десять; а с другой стороны модификации нет.
Однако его положение в числе может полностью изменить значение, поскольку, когда оно находится справа от него, значение умножается на десять; а с другой стороны модификации нет. Среди них находим число Пи.
Среди них находим число Пи. Применяя те же рассуждения, мы видим, что b 2 также имеет четное число множителей, равных 2. Итак, с левой стороны,
у нас есть четное число множителей 2, и справа у нас есть
четное число множителей 2 плюс один лишний от коэффициента, поэтому
правая часть имеет нечетное количество множителей, равных 2. Это означает, что
одно и то же число имеет как четное, так и нечетное число делителей 2, что
просто невозможно. Поэтому, наоборот, квадратный корень из
2 иррационально.
Применяя те же рассуждения, мы видим, что b 2 также имеет четное число множителей, равных 2. Итак, с левой стороны,
у нас есть четное число множителей 2, и справа у нас есть
четное число множителей 2 плюс один лишний от коэффициента, поэтому
правая часть имеет нечетное количество множителей, равных 2. Это означает, что
одно и то же число имеет как четное, так и нечетное число делителей 2, что
просто невозможно. Поэтому, наоборот, квадратный корень из
2 иррационально.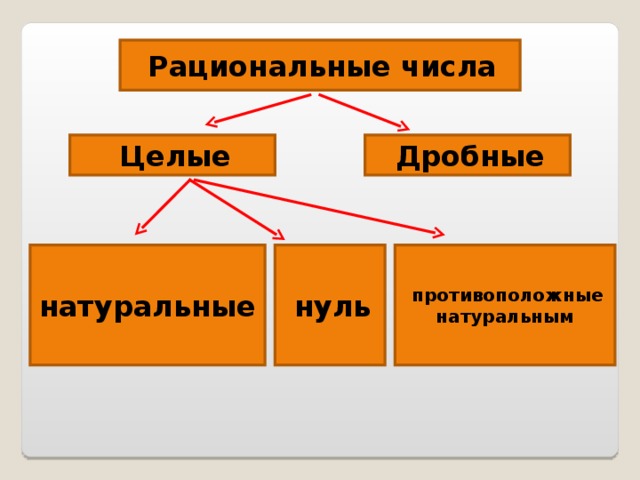 (Случаи идеального квадрата, такие как квадратный корень из 4, терпят неудачу, когда мы не можем
пришли к противоречию о количестве некоторых простых множителей. В этом
частный случай, у нас есть 2 = 4b 2 , что дает четное число множителей по 2 с каждой стороны; следовательно, такого противоречия нет.)
(Случаи идеального квадрата, такие как квадратный корень из 4, терпят неудачу, когда мы не можем
пришли к противоречию о количестве некоторых простых множителей. В этом
частный случай, у нас есть 2 = 4b 2 , что дает четное число множителей по 2 с каждой стороны; следовательно, такого противоречия нет.) Однако, поскольку a и b взаимно просты, a 2 и b 2 также относительно просты (квадрат числа не вводит никаких новых
множители) и единственный общий множитель числителя и знаменателя
1. Из этого следует, что единственный способ для этой дроби быть
integer означает, что b равно 1, что также делает a/b целым числом и
противоречит нашему предположению, что c не является полным квадратом. Поэтому,
если целое число не является полным квадратом, его квадратный корень иррационален.
С помощью обобщения это доказательство также можно распространить на любое n
Однако, поскольку a и b взаимно просты, a 2 и b 2 также относительно просты (квадрат числа не вводит никаких новых
множители) и единственный общий множитель числителя и знаменателя
1. Из этого следует, что единственный способ для этой дроби быть
integer означает, что b равно 1, что также делает a/b целым числом и
противоречит нашему предположению, что c не является полным квадратом. Поэтому,
если целое число не является полным квадратом, его квадратный корень иррационален.
С помощью обобщения это доказательство также можно распространить на любое n 