2 корня из 10 как посчитать. Формулы корней. Свойства корней. Как умножать корни? Примеры
2 корня из 10 как посчитать. Формулы корней. Свойства корней. Как умножать корни? Примеры
Формулы корней. Свойства квадратных корней.
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)
В предыдущем уроке мы разобрались, что такое квадратный корень . Пришла пора разобраться, какие существуют формулы для корней , каковы свойства корней , и что со всем этим можно делать.
Формулы корней, свойства корней и правила действий с корнями — это, по сути, одно и то же. Формул для квадратных корней на удивление немного. Что, безусловно, радует! Вернее, понаписать всяких формул можно много, но для практической и уверенной работы с корнями достаточно всего трёх. Все остальное из этих трёх проистекает. Хотя и в трех формулах корней многие плутают, да.
..
Начнём с самой простой. Вот она:
Если Вам нравится этот сайт…Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Желательно инженерный – такой, в котором имеется кнопочка со знаком корня: «√». Обычно для извлечения корня достаточно набрать само число, а потом нажать на кнопку: «√».
В большинстве современных мобильных телефонов имеется приложение «калькулятор» с функцией извлечения корня. Порядок нахождения корня числа с помощью телефонного калькулятора аналогичен вышеизложенному.
Пример.
Найти из 2.
Включаем калькулятор (если он выключен) и последовательно нажимаем кнопки с изображением двойки и корня («2» «√»). Нажимать на клавишу «=», как правило, не нужно. В результате получаем число типа 1,4142 (количество знаков и «округленность» зависит от разрядности и настроек калькулятора).
Примечание: при попытке найти корень калькулятор обычно выдает об ошибке.
Если есть доступ к компьютеру, то найти корень числа очень просто.
1. Можно воспользоваться приложением «Калькулятор», имеющемся практически на любом компьютере. Для Windows ХР эту программу можно запустить следующим образом:
«Пуск» — «Все программы» — «Стандартные» — «Калькулятор».
Вид лучше установить «обычный». Кстати, в отличие от реального калькулятора кнопка для извлечения корня помечена как «sqrt», а не «√».
Если добраться до калькулятора указанным способом не , то можно запустить стандартный калькулятор «вручную»:
«Пуск» — «Выполнить» — «calc».
2. Для нахождения корня числа можно также воспользоваться некоторыми программами, установленными на компьютере. Кроме того, программы собственный встроенный калькулятор.
Например, для приложения MS Excel можно проделать следующую последовательность действий:
Запускаем MS Excel.
Записываем в любую клетку число, из которого нужно извлечь корень.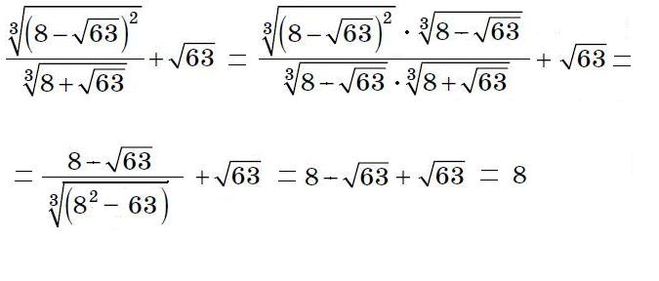
Помещаем указатель клетки на другое место
Нажимаем кнопочку выбора функции (fx)
Выбираем функцию «КОРЕНЬ»
В качестве аргумента функции указываем клетку с числом
Нажимаем «ОК» или «Еnter»
Преимуществом данного способа является то, что теперь достаточно ввести в клетку с числом любое значение, как в с функцией тут же появляется .
Примечание.
Имеется несколько других, более экзотических способа найти корень числа. Например, «уголком», с помощью логарифмической линейки или таблиц Брадиса. Однако, в этой статье эти методы не рассматриваются ввиду их сложности и практической бесполезности.
Видео по теме
Источники:
- как находить корень числа
Иногда возникают ситуации, когда приходится выполнять какие-либо математические вычисления, в том числе извлекать корни квадратные и корни большей степени из числа. Корень степени «n» из числа «a» представляет собой число, n-я степень которого и есть число «a».
Инструкция
Чтобы найти корень «n» из , сделайте следующее.
Нажмите на своем компьютере «Пуск» — «Все программы» — «Стандартные». Затем войдите в подраздел «Служебные» и выберите «Калькулятор». Можете сделать это вручную: нажмите «Пуск», введите «calk» в строку «выполнить» и нажмите «Enter». Откроется . Для извлечения корня квадратного из какого-либо числа, введите это в строку калькулятора и нажмите кнопку с надписью «sqrt». Калькулятор произведет извлечение из введенного числа корня второй степени, называемого квадратным.
Для того чтобы извлечь корень, степень которого выше второй, нужно воспользоваться другим видом калькулятора. Для этого в интерфейсе калькулятора нажмите кнопку «Вид» и в меню выберите строку «Инженерный» или «Научный». Этот вид калькулятора имеет необходимую для вычисления корня n-й степени функцию.
Для извлечения корня третьей степени (), на «инженерном» калькуляторе наберите нужное число и нажмите кнопку «3√». Для получения корня, степень которого выше 3-й, наберите нужное число, нажмите кнопку со значком «y√x» и затем введите число – показатель степени.
После этого нажмите знак равенства (кнопка «=») и вы получите искомый корень.
Если на вашем калькуляторе отсутствует функция «y√x», следующее.
Для извлечения кубического корня введите подкоренное выражение, потом поставьте в чек боксе, который расположен рядом с надписью «Inv», отметку. Этим действием вы переведете функции кнопок калькулятора на обратные, т.е., щелкнув по кнопке для возведения в куб, вы произведете извлечение корня кубического. На кнопке, которая вам
Библиографическое описание: Прямостанов С. М., Лысогорова Л. В. Методы извлечения квадратного корня // Юный ученый. 2017. №2.2. С. 76-77..02.2019).
Ключевые слова : квадратный корень, извлечение квадратного корня.
На уроках математики я познакомился с понятием квадратного корня, и операцией извлечения квадратного корн. Мне стало интересно извлечение квадратного корня возможно только по таблице квадратов, с помощью калькулятора или есть способ извлечения вручную.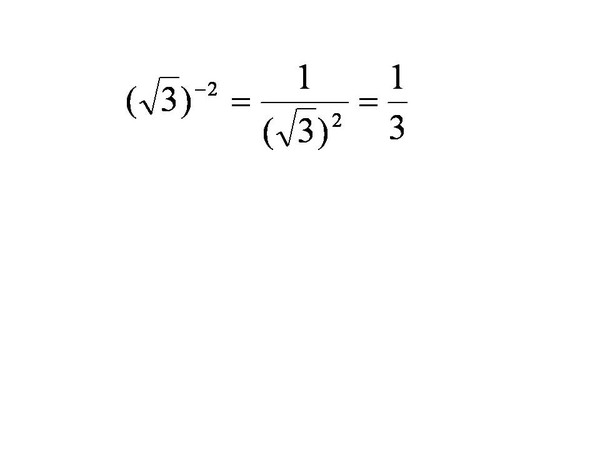
Я нашел несколько способов: формула Древнего Вавилона, через решение уравнений, способ отбрасывания полного квадрата, метод Ньютона, геометрический метод, графический метод (, ), метод подбора угадыванием, метод вычетов нечётного числа.
Рассмотрим следующие способы:
Разложим на простые множители, используя признаки делимости 27225=5*5*3*3*11*11. Таким образом
- Канадский метод. Этот быстрый метод был открыт молодыми учёными одного из ведущих университетов Канады в 20 веке. Его точность — не более двух — трёх знаков после запятой.
где х-число, из которого надо извлечь корень, с-число ближайшего квадрата), например:
=5,92
- Столбиком. Этот способ позволяет найти приближённое значение корня из любого действительного числа с любой наперёд заданной точностью. К недостаткам способа можно отнести увеличивающуюся сложность вычисления с увеличением количества найденных цифр. Для ручного извлечения корня применяется запись, похожая на деление столбиком
Алгоритм извлечения квадратного корня
1.
От запятой отдельно дробную и отдельно целую части делим на грани по две цифры в каждой грани (целую часть — справа налево; дробную — слева направо). Возможно, что в целой части может оказаться одна цифра, а в дробной — нули.
2.Извлечение начинается слева направо, и подбираем число, квадрат которого не превосходит числа, стоящего в первой грани. Это число возводим в квадрат и записывает под числом, стоящим в первой грани.
3.Находим разность между числом, стоящим в первой грани, и квадратом подобранного первого числа.
4.К получившейся разности сносим следующую грань, полученное число будет делимым . Образовываем делитель . Первую подобранную цифру ответа удваиваем (умножаем на 2), получаем число десятков делителя, а число единиц должно быть таким, чтобы его произведение на весь делитель не превосходило делимого. Подобранную цифру записываем в ответ.
5.К получившейся разности сносим следующую грань и выполняем действия по алгоритму.
Если данная грань окажется гранью дробной части, то в ответе ставим запятую. (Рис. 1.)
Данным способом можно извлекать числа с разной точностью, например с точностью до тысячных. (Рис.2)
Рассматривая различные способы извлечения квадратного корня, можно сделать вывод: в каждом конкретном случае нужно определиться с выбором наиболее эффективного для того, чтобы меньше затратить времени для решения
Литература:
- Киселев А. Элементы алгебры и анализа. Часть первая.-М.-1928 г
Ключевые слова: квадратный корень, извлечение квадратного корня .
Аннотация: В статье описываются способы извлечения квадратного корня, и приведены примеры извлечения корней.
Как извлечь корень из числа. В этой статье мы будем учиться извлекать квадратный корень из четырехзначных и пятизначных чисел.
Давайте, для примера, извлечем квадратный корень из числа 1936.
Следовательно, .
Последняя цифра в числе 1936 — цифра 6. На 6 заканчивается квадрат числа 4 и числа 6. Следовательно, 1936 может быть квадратом числа 44 или числа 46. Осталось проверить с помощью умножения.
Значит,
Извлечем квадратный корень из числа 15129.
Следовательно, .
Последняя цифра в числе 15129 — цифра 9. На 9 заканчивается квадрат числа 3 и числа 7. Следовательно, 15129 может быть квадратом числа 123 или числа 127. Проверим с помощью умножения.
Значит,
Как извлечь корень — видеоА теперь предлагаю вам посмотреть видео Анны Денисовой — «Как извлечь корень «, автора сайта » Простая физика «, в котором она рассказывает, как извлекать квадратные и кубические корни без калькулятора.
В видео рассматривается несколько способов извлечения корней:
1. Самый простой способ извлечения квадратного корня.
2. Подбором, используя квадрат суммы.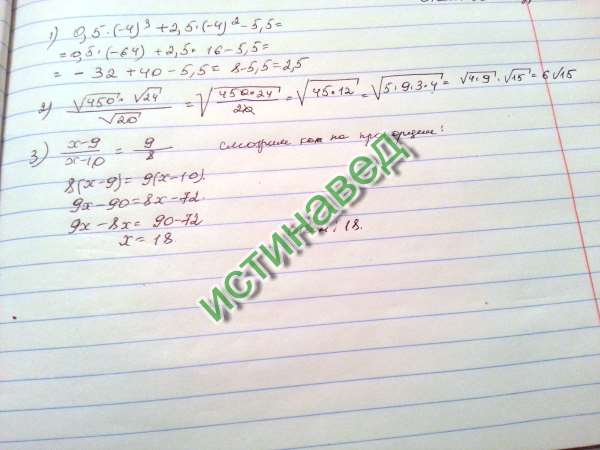
3. Вавилонский способ.
4. Способ извлечения квадратного корня в столбик.
5. Быстрый способ извлечения кубического корня.
6. Способ извлечения кубического корня в столбик.
Пожалуйста помогите!!!! Сколько будет 2 корень из 21 умно… -reshimne.ru
Новые вопросы
Ответы
2√3•√7•6•√7•√5:7√60=
2√15•42:7√60=
12√5:√60=
12√3•√5:√12•√5=
12√3:√4•√3=
12:2=6
Ответ 6
Похожие вопросы
Помогите пожалуйста Составьте числовое выражение и найдите его знаение: Частное разности чисел 11 и 5,8 и числа -1,3…
Сумма цифр двузначного числа равна 9. Если это число разделить на разность его цифр, то получится 12. Найдите это число.
Объясните подробно…
2*4^x — 3*10^x — 5*25^x = 0.
..
Люди помагите решить если что то не правильно исправте и в конце 2 примера помагите не могу решить…
Пожалуйста помогите!!!! Сколько будет 2 корень из 21 умножить на 6 корень из 35 делить на 7 корень из 60. Дам макс. баллов, кто поможет И ЖЕЛАТЕЛЬНО СКАЖИТЕ КАК ВЫ СДЕЛАЛИ А ТО Я НЕ ПОНИМАЮ…
Помогите решить уравнение:)…
Математика
Литература
Алгебра
Русский язык
Геометрия
Английский язык
Химия
Физика
Биология
Другие предметы
История
Обществознание
Окружающий мир
География
Українська мова
Українська література
Қазақ тiлi
Беларуская мова
Информатика
Экономика
Музыка
Право
Французский язык
Немецкий язык
МХК
ОБЖ
Психология
Квадратный корень из 2
Древнегреческие философы-пифагорейцы глубоко почитали числа.
Арифметика и геометрия охранялись как форма тайного знания, доступная только избранным.
Они считали, что сама Вселенная является проявлением чисел и геометрии, поэтому, исследуя математику, они проникали в более глубокие слои космической реальности. Поэтому пифагорейцы были потрясены, когда обнаружили, что некоторые числа лежат за пределами их аккуратной интеллектуальной схемы.
В детстве мы сначала учимся считать целые числа 1, 2, 3… которые математики называют «натуральными» числами. Затем нас учат дробям, которые выражаются как отношение натуральных чисел, например 2/5 или 1/3. После этого идут десятичные дроби.
Каждая дробь, как мы узнали, может быть представлена в виде десятичной дроби — например, 2/5 = 0,4 и 1/3 = 0,33333… (где «…» означает, что последовательность троек продолжается вечно). Но верно ли обратное? Можно ли представить каждую десятичную дробь в виде дроби?
Разумеется, десятичные числа конечной длины всегда можно выразить в виде дробей, например, 0,43857 = 43857/100000.
А как насчет десятичных дробей бесконечной длины? Ну, повторяющиеся десятичные расширения могут быть выражены в виде дробей, например. 0,33333… = 1/3 и 0,285714285714285714… = 2/7. Но предположим, что десятичное расширение не повторяется? Ведь таких чисел бесконечность!
Ранние пифагорейцы были убеждены, что любое мыслимое число в принципе можно записать в виде дроби, как отношение двух натуральных чисел. Поскольку существует бесконечное количество натуральных чисел, думали они, их должно быть достаточно, чтобы выполнить эту работу. Открытие того, что это ошибочное мнение, возможно, сделанное геометром Гиппасом в V веке до н. э., стало шокирующей новостью. Согласно легенде, Гиппас был сброшен с лодки и утонул, чтобы истина не стала широко известной, такова была ее угроза пифагорейской концепции порядка во Вселенной.
Даже сегодня числа, которые не могут быть выражены в виде отношения натуральных чисел, называются иррациональными числами, несмотря на то, что они имеют смысл для современных математиков.
На самом деле легко понять, почему некоторые числа иррациональны. Известным примером является квадратный корень из 2, который примерно равен 1,4142 и обозначается √2.
Если бы √2 было рациональным, оно должно быть выражено в форме a/b, где a и b — натуральные числа (то есть целые числа). Мы можем записать это в виде уравнения, √2 = a/b, а затем придать ему быстрый математический удар по шинам.
Для начала мы знаем, что по крайней мере одно из двух неизвестных чисел, a и b, должно быть нечетным. Если бы оба были четными, мы могли бы разделить верх и низ на 2 и сократить дробь до соотношения меньших чисел (например, 2/8, которое сводится к 1/4).
Теперь давайте посмотрим на уравнение с нескольких разных точек зрения. Если возвести в квадрат обе части уравнения √2 = a/b, мы получим
2 = a 2 /b 2 (1)
, что можно записать как
a 2 = 2b 2 . (2)
Мы можем сразу заключить, что 2 — четное число.
Почему? Потому что это дважды b 2 . Умножьте любое натуральное число на два (а мы знаем, что b — натуральное число), и ответ будет четным. Таким образом, 2 должны быть четными.
Теперь, если 2 четно, то и а (квадрат нечетного числа всегда нечетен). Поскольку мы уже указали, что a и b не могут быть одновременно четными, мы можем сделать вывод, что b должно быть нечетным. Все идет нормально. Однако тревожные звоночки начинают звенеть, когда мы замечаем, что если а четно, то его всегда можно выразить как 2с, где с — другое натуральное число. Подставляя это в уравнение (1), получаем
2 = 4c 2 /b 2
или, переставляя уравнение и деля на 2,
b 2 = 2c 2 .
Рассуждая так же, как и уравнение (2), мы заключаем, что b должно быть четным числом. Но мы уже определили, что b нечетно, поэтому приходим к абсурдному выводу, что b и четно, и нечетно — заведомо невозможно. Ошибочное рассуждение проистекает из исходного предположения, что √2 можно выразить как отношение целых чисел.
Оно не может; это «иррационально».
Оказывается, почти все числа иррациональны, в том числе такие известные, как π и φ, золотое сечение ( Космос 65, стр. 120).
Существует безграничное количество как рациональных, так и иррациональных чисел, но каким-то образом иррациональных чисел на больше, чем рациональных — они образуют больший класс бесконечности.
Непонимание этого факта часто вводило древних греков в заблуждение и приводило ко всевозможным парадоксам, пока вопрос о бесконечности не был окончательно решен в 19 веке.век.
Сегодня мы видим, что иррациональные числа — это не катастрофа, а просто расширение системы счисления, точно так же, как дроби были введены как расширение натуральных чисел. В более поздние века система счисления была расширена и другими способами, но это тема для следующей статьи.
Читать по теме:
Получайте свежие научные новости прямо на свой почтовый ящик.
- Одни бесконечности больше других
- Как решить магический квадрат
Пол Дэвис
Пол Дэвис — профессор Риджентс и директор Центра фундаментальных концепций науки Университета штата Аризона.
Он также является плодовитым автором и обозревателем Cosmos.
Читайте научные факты, а не художественную литературу…
Никогда не было более важного времени, чтобы объяснять факты, ценить научно обоснованные знания и демонстрировать последние научные, технологические и инженерные достижения. Cosmos издается Королевским институтом Австралии, благотворительной организацией, призванной связывать людей с миром науки. Финансовые взносы, большие или малые, помогают нам предоставлять доступ к достоверной научной информации в то время, когда мир больше всего в ней нуждается. Пожалуйста, поддержите нас, сделав пожертвование или купив подписку сегодня.
Доказательство того, что квадратный корень из 2 является действительным числом
Доказательство того, что квадратный корень из 2 является действительным числом — MathonlineДоказательство того, что квадратный корень из 2 является действительным числом
Сложите Содержание Доказательство того, что квадратный корень из 2 является действительным числом |
Напомним, что ранее мы доказали на Доказательстве того, что квадратный корень из 2 является иррациональной страницей, что $\sqrt{2} \not \in \mathbb{Q}$.