Числа рациональные целые: Целые и рациональные числа — урок. Математика, 6 класс.

Противоположные числа. Целые числа. Рациональные числа – онлайн-тренажер для подготовки к ЕНТ, итоговой аттестации и ВОУД

Запомнить

Восстановить пароль

Регистрация

Конспект

Числа, которые отличаются друг от друга только знаком, называются противоположными.

Например: числа 2 и –2; 6 и –6; –10 и 10. Противоположные числа расположены на числовой оси в противоположных направлениях от точки О, но на одинаковом расстоянии от нее.

Натуральные числа, а также все числа, противоположные им по знаку, и число ноль называют целыми числами. Все целые числа образуют множество целых чисел. Множество целых чисел бесконечно. Множество целых чисел обозначают буквой:

\(Z= \{…,-n,…,-2, -1, 0, 1, 2,…,n,…\}\).

Положительные числа (целые и дробные), отрицательные числа (целые и дробные) и число 0 составляют группу рациональных чисел.

Рациональные числа – это числа, которые могут быть представлены в виде \(\frac{m}{n}\). Обозначение:

\(Q=\{\frac{m}{n}, \ m\in Z, \ n\in N\}\).

Например: \(-4\frac13; -2,6;\ 1;\ 3\frac12;\ 14\).

Вопросы

1. Найдите наибольшее целое решение неравенства.

   \(x\le-6\)

Сообщить об ошибке

Обязательные

Математическая грамотность

Грамотность чтения

История Казахстана

Предметы по профилю

Биология

Химия

Английский язык

Французский язык

География

Немецкий язык

Информатика

Основы права

Русская литература

Математика

Физика

Русский язык

Всемирная история

Укажите предмет *

Скопируйте и вставьте вопрос задания *

Опишите подробнее найденную ошибку в задании *

Прикрепите скриншот

Объем файла не должен превышать 1МБ

Казахский

Русский

Обратите внимание! По выбранным Вами предметам ГРАНТЫ не предоставлены. В AlmaU, Университете Нархоз и Каспийском Университете представлены специальности, где профильными предметами являются математика, физика, география, иностранный язык, Человек. Общество. Право, всемирная история, биология, химия и творческий экзамен.

1. Скачайте приложение iTest, используя QR-код или строку поиска в AppStore или Play Market

2. Авторизуйтесь в приложении и готовьтесь к экзаменам вместе с нами

Целые и рациональные числа

Вы уже знаете, что числа, которые мы используем в счёте, называют натуральными. Кстати, натуральные числа – это один из первых математических объектов, который стал изучать человек, так как повседневная жизнь требовала использования натуральных чисел на практике, и в частности, в счёте.

Поэтому и изучение математики в школе мы начинали именно со знакомства с натуральными числами.

Итак, давайте перечислим натуральные числа: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 и так далее. Все натуральные числа образуют множество натуральных чисел, которое обозначают заглавной латинской буквой .

С понятием натуральных чисел мы с вами разобрались, а теперь давайте перейдём к действиям с ними. И ответим на вопрос: какие числа получают при сложении и умножении натуральных чисел?

Конечно же, вам не составит труда ответить на этот вопрос. И вы сразу скажете, что при сложении натуральных чисел всегда получают натуральные числа.

И при умножении натуральных чисел тоже всегда получают натуральные числа.

Тогда возникает новый вопрос: а какие числа мы получим при вычитании и делении натуральных чисел?

Так вот, при нахождении разности и частного натуральных чисел не всегда получаются натуральные числа.

В связи с этим математикам пришлось расширять знания, связанные с числами.

Если мы добавим к натуральным числам нуль и отрицательные числа (то есть числа, которые противоположны натуральным), то множество натуральных чисел расширится до множества

целых чисел.

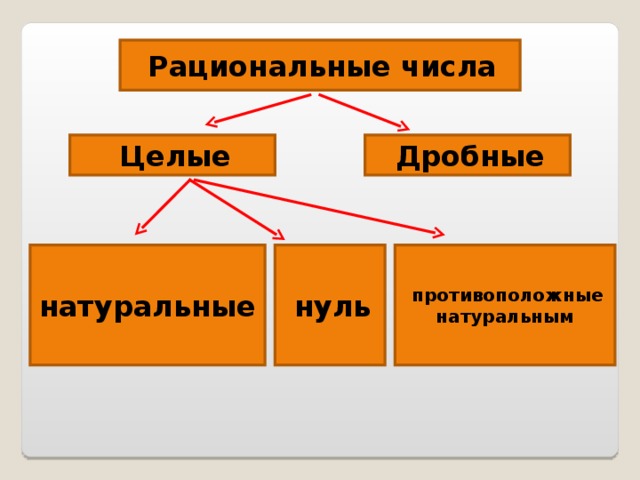
Множество целых чисел принято обозначать заглавной латинской буквой . Оно состоит из следующих элементов: .

Мы с вами разобрались с понятием целых чисел, а теперь давайте перейдём к действиям с ними. Понятно, что при сложении, вычитании и умножении целых чисел всегда получают целые числа.

Чего нельзя сказать о делении целых чисел. При нахождении частного двух целых чисел в результате не всегда получают целые числа.

(

Следовательно, понятия, связанные с числами, пришлось расширять дальше. Так, множество целых чисел расширили, введя множество рациональных чисел.

Итак, числа вида , где m – целое число, n – натуральное число, составляют

множество рациональных чисел. Это множество принято обозначать заглавной латинской буквой . Кстати, любое целое число можно представить в виде рационального, например, число m можно представить в виде .

Множество рациональных чисел позволило находить частное любых двух целых чисел при условии, что делитель не равен нулю.

Кроме того, при выполнении всех четырёх арифметических действий (кроме деления на нуль) над рациональными числами всегда получают рациональные числа.

Рациональное число можно представить в виде дроби , где m – целое число, k – натуральное число. Если рациональное число можно представить в виде дроби , где m – целое число, k – натуральное число, то его можно записать в виде конечной десятичной дроби.

 

Заметим, что одно и то же рациональное число можно представить различными дробями, которые получаются из несократимой дроби умножением её числителя и знаменателя на одно и то же целое число, отличное от нуля.

Существуют и рациональные числа, которые нельзя записать в виде конечной десятичной дроби.

 

Если, например, мы попытаемся записать число  в виде десятичной дроби, используя алгоритм деления уголком, то получим бесконечную десятичную дробь ….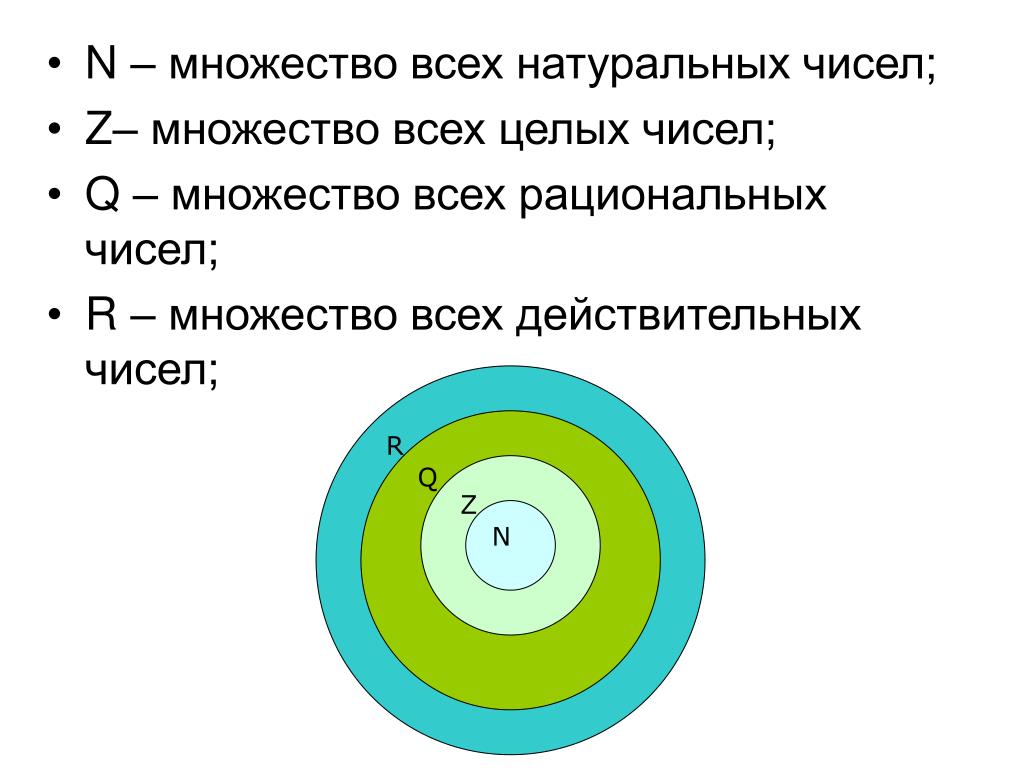

Напомним, что такую бесконечную десятичную дробь называют периодической, а повторяющуюся цифру 3 – её периодом. Нашу периодическую дробь … коротко записывают так: . А читают нашу периодическую дробь так: «нуль целых и три в периоде».

Тогда можем сделать такой вывод: любая

периодическая дробь – это бесконечная десятичная дробь, у которой, начиная с некоторого десятичного знака, повторяется одна и та же цифра или группа цифр – период дроби.

Например, десятичная дробь …. Она равна . Это периодическая дробь с периодом 23. Читают эту дробь так: «пятнадцать целых семнадцать сотых и двадцать три в периоде».

Заметим, что каждое целое число или конечную десятичную дробь можно считать и бесконечной десятичной периодической дробью с периодом, равным нулю.

Вообще, любую конечную десятичную дробь можно записать в виде бесконечной дроби двумя способами: с периодом 0 и с периодом 9.

Давайте договоримся в дальнейшем не использовать бесконечные десятичные дроби с периодом 9. Вместо таких дробей будем записывать конечные десятичные дроби или бесконечные десятичные дроби с периодом 0.

Таким образом, можем сделать следующий вывод: каждое рациональное число можно представить в виде бесконечной периодической десятичной дроби. Справедливо и обратное утверждение: каждая бесконечная периодическая десятичная дробь является рациональным числом, так как может быть представлена в виде дроби , где m – целое число, n – натуральное число.

Вообще, при делении целого числа m на натуральное число n на некотором шаге остаток может стать равным нулю, тогда в результате деления получается целое число или конечная десятичная дробь. Либо же при делении целого числа m на натуральное число n на некотором шаге остатки начинают повторяться, так как каждый из остатков меньше n, тогда в результате деления получается бесконечная десятичная периодическая дробь.

А теперь давайте приступим к практической части нашего урока.

Итак, задание первое. Запишите в виде бесконечной десятичной дроби: а) ;     б) .

Решение.

Задание второе. Запишите в виде обыкновенной дроби: а) ;     б) .

Решение.

И последнее задание. Покажите, что … .

Решение.

определение рационального+целого по The Free Dictionary

Рациональное+целое — определение рационального+целого по The Free Dictionary

Рациональное+целое — определение рационального+целого в The Free Dictionary

---

Слово, не найденное в Словаре и Энциклопедии.

Возможно, Вы имели в виду:

Пожалуйста, попробуйте слова по отдельности:

рациональный целое число

Некоторые статьи, соответствующие вашему запросу:

Не можете найти то, что ищете? Попробуйте выполнить поиск по сайту Google или помогите нам улучшить его, отправив свое определение.

Полный браузер ?

• ▲
• Rational Test Lab Manager
• Рациональный тест в реальном времени
• Рациональное богословие
• Рациональное богословие
• рациональная терапия
• Рациональная мысль
• Рациональная мысль
• Рациональная мысль
• Рациональное пороговое значение
• Рабочий стол Rational Transformation
• рациональное лечение
• рациональное лечение
• рациональное лечение
• рациональное лечение
• рациональное лечение
• Рациональная тригонометрия
• Партнерская программа Rational Unified
• Рациональный унифицированный процесс
• Рациональный унифицированный процесс
• Продукт Rational Unified Process

• Рациональное использование лекарств
• Рациональное использование энергии
• Рациональное использование лекарственных средств
• Группа пользователей Rational
• Формула рациональной оценки
• Рациональный сорт
• Рациональная молодежь
• Рациональная молодежь (EP)
• Проверка рациональных нулей
• Серия Rational zeta
• рациональное+целое число
• Рациональное, надежное и безопасное согласование в многоагентных системах
• гипотеза рациональных ожиданий
• блокировка рациональных гармоник
• Рационально-правовая власть
• Рационально-правовая власть
• обоснование
• обоснование
• обоснование
• обоснование
• Обоснование (облачение)

• Обоснование (облачение)
• Обоснование подхода к разработке лекарств
• Обоснование программ для одаренных
• Обоснование войны в Ираке
• Обоснование грязной шутки
• Обоснование, Цели, Оценка, Мониторинг, Оценка
• Обоснование, цели, оценка, мониторинг, оценка и обратная связь
• обоснования
• обоснования
• обоснования
• Рационалибус Дивисис
• Рационалис
• рационализируется
• рационализация
• рационализация
• рационализация
• рационализация
• рационализация
• рационализации
• рационализации
• ▼

Сайт: Следовать:

Делиться:

Открыть / Закрыть

 

Классификация рациональных чисел — УРОКИ КЕЙТ ПО МАТЕМАТИКЕ

Готовы узнать о целых числах, целых числах и рациональных числах? Прокрутите вниз до первого зеленого заголовка. Если вы также хотите узнать о натуральных числах, иррациональных числах и действительных числах, вам лучше перейти к моему уроку «Классификация действительных чисел».

Сопроводительный ресурс: ​ Карточки Boom Classification Rational Numbers

Типы номеров

Знаете ли вы, что цифры существуют не вечно? Давным-давно у людей не было слов или символов для таких простых чисел, как 1, 2, 3. . . До того, как были изобретены числа и их символы, люди использовали палки и делали отметки на камнях, чтобы следить за вещами. К счастью, со временем система счисления развилась, поэтому нам больше не нужно использовать палочки или поднимать пальцы, чтобы считать! Теперь у нас есть имена и символы, которые мы используем для представления чисел. (Хотите увидеть некоторые из более ранних символов, которые использовались? Прочтите эту статью об истории системы счисления. )

Система счисления, которую мы используем сегодня, имеет различные типы чисел. В этом уроке мы рассмотрим 3 типа: целые числа, целые числа и рациональные числа.​

Целые числа

 0, 1, 2, 3 . . .
Целые числа начинаются с нуля и идут вверх. Я думаю об этом как о числах, которые вы изучаете, когда молоды. Они не включают отрицательные числа, дроби или десятичные дроби.

Примеры целых чисел:
5
23
167
14

Не целые числа:
8,9
-2
3/5

Бонус Примечание: 0 как число? Раньше они думали, что это безумие, когда число обозначает «ничего». Я надеюсь, вы рады, что он был изобретен, потому что у нас не было бы компьютеров без числа 0! Ознакомьтесь с этой историей числа ноль, чтобы узнать больше интересных фактов о нуле (знали ли вы, что кто-то думал, что это зло?).

Целые числа

. . . -3, -2, -1, 0, 1, 2, 3. . .
Этот набор чисел похож на целые числа, но включает и отрицательные числа. Целые числа не включают дроби или десятичные дроби. Все целые числа также являются целыми числами.

Примеры целых чисел:
8
-34
721
-5

Не целых чисел:
6.2
-7/8

Rational Числа

, которые могут быть написаны как номера.

Любое число, которое можно представить в виде дроби, считается рациональным числом. Я бы перечислил их для вас, но это невозможно, потому что их так много! Все целые числа также являются рациональными числами, потому что вы можете переписать любое из них в виде дроби, используя 1 в знаменателе (например, 5 можно переписать как дробь 5/1). К рациональным числам также относятся конечные десятичные дроби (десятичные дроби, которые останавливаются в какой-то точке), повторяющиеся десятичные дроби (например, . 2323…) и числа, которые уже записаны в виде дробей.
​
Примеры рациональных чисел:
13,25
-7 (это можно записать в виде дроби -7/1)
2/5
.4444 . . . . (Это можно записать в виде дроби 4/9)

НЕ рациональные числа:
Десятичная дробь, которая идет бесконечно без конца или повторения, не является рациональной. Вот два примера:

Использование графических организаторов для классификации рациональных чисел

Вот графический органайзер, который поможет вам понять, как эти три типа чисел связаны друг с другом. Целые числа находятся внутри целых чисел на диаграмме, потому что все целые числа также являются целыми числами. Целые числа находятся внутри рациональных чисел на диаграмме, потому что все целые числа также являются рациональными числами.

Допустим, вам нужно классифицировать следующие числа:
-10
8,2
23

выход из положения. Начнем с -10. -10 — это целое число? Нет. Целые числа начинаются с 0 и не включают отрицательные числа, поэтому это не целое число. Является ли -10 целым числом? Да. Целые числа включают -1, -2, -3, -4 и т. д., поэтому -10 является целым числом .

Обратите внимание, что -10 также является рациональным числом, поскольку его можно записать в виде дроби (-10/1). Это похоже на то, как квадрат также является прямоугольником, но термин «квадрат» является более конкретным. Термин целое число более конкретен, чем рациональное число.

Как насчет 8.2? Это целое число? Нет, целые числа не включают десятичные. Это целое число? Нет, целые числа также не включают десятичные дроби. Является ли это рациональным числом (может ли оно быть записано в виде дроби)? Да, это завершающее десятичное число (десятичное число, которое останавливается), поэтому его можно записать в виде дроби. 8.2 можно записать в виде дроби 82/10. Это означает 8.2 — рациональное число .