1.3.7 Расстояние от точки до прямой
Для вычисления расстояния D от точки М(X0, Y0) до прямой Ах + Ву + С = 0 используется Формула
. (1.20)
Приведем пример ее применения.
Пример 1.16. Найти расстояние между прямыми (L1) 2Х + 3У – 1 = 0 и(L2) 4Х + 6У + 5 = 0.
Решение. Векторы нормали данных прямых и коллинеарны , т. е. прямые параллельны. Выберем на прямой L1 фиксированную точку М(–1, 1), координаты которой удовлетворяют уравнению прямой (рисунок 1.10).
Воспользуемся теперь формулой (1.20) и вычислим расстояние от точки М1 до прямой L2:
Найденное расстояние является расстоянием между параллельными прямыми L1 и L2.
Рисунок 1.10
Рисунок 1.11
Задачу вычисления расстояния от данной точки до данной прямой Можно решить и другим способом, используя уже полученные знания.
Пусть дана точка М(–1, 1) и прямая 3Х – 4У + 12 = 0. Необходимо найти расстояние от этой точки до прямой ЕF. Расстояние D от точки М до прямой EF равно длине перпендикуляра MN, опущенного из М на ЕF (рисунок 1.11).
Запишем алгоритм решения этой задачи.
1. Найдем угловой коэффициент К1 прямой EF, для этого разрешим уравнение прямой ЕF относительно У:
(1.21)
.
2. Используя условие перпендикулярности двух прямых, найдем угловой коэффициент K2 перпендикуляра MN:
Или , отсюда .
3. Теперь напишем уравнение прямой MN, проходящей через точку М(–1, 1) с угловым коэффициентом .
Или
(1.22)
4. Вычислим координаты точки N – точки пересечения прямой ЕF с перпендикуляром MN. Координаты этой точки удовлетворяют уравнениям (1.21) и (1.22), мы их получим, решив совместно эти уравнения.
И вычислим отсюда абсциссу Х Точки N
или , откуда .
Подставив найденное значение, например, в уравнение (1.21), вычислим ординату точки N:
или , откуда .
Итак, точка N имеет координаты .
5. Найдем теперь расстояние между точками М и N:
.
Конечно, использованный выше алгоритм является достаточно громоздким. Он был приведен для того и продемонстрирован для того, чтобы показать различные способы решения задач такого типа.
Эту задачу можно легко решить, используя общую формулу вычисления расстояния D от точки М(Х0, У0) до прямой Ax + By + C = 0, которая была рассмотрена выше и имеет вид
(1.23)
Для нашей задачи мы получим
.
Разумеется, результаты, полученные различными способами, совпадают.
| < Предыдущая | Следующая > |
|---|
21.
 Расстояние от точки до прямой на плоскости (вывод).
Расстояние от точки до прямой на плоскости (вывод).Вывод формулы расстояния от точки до прямой
Вариант 1
Пусть на плоскости дана прямая l : ax + by + c = 0 и точка M1(x1;y1), не принадлежащая этой прямой. Найдем расстояние от точки до прямой. Под расстоянием ρ от точки M1 до прямой l понимают длину отрезка M0 M1⏊l.
Для определения расстояния удобно использовать единичный вектор, коллинеарный нормальному вектору прямой.
Пояснение: поскольку точка M0 лежит в на прямой l, то ее координаты должны удовлетворять уравнению данной прямой, т.е. ax0 + by0 + c = 0Вариант 2
Если
задана точка М(х0,
у0),
то расстояние до прямой Ах + Ву + С =0
определяется как .
Доказательство. Пусть точка М1(х1, у1) – основание перпендикуляра, опущенного из точки М на заданную прямую. Тогда расстояние между точками М и М1: (1) Координаты x1 и у1 могут быть найдены как решение системы уравнений: Второе уравнение системы – это уравнение прямой, проходящей через заданную точку М0 перпендикулярно заданной прямой. Если преобразовать первое уравнение системы к виду: A(x – x0) + B(y – y0
22. Условия параллельности и перпендикулярности прямых на плоскости (вывод).
1)
Если прямые R1 и R2 параллельны,
то φ = 0. Тогда tg φ = 0 и из формулы (7) имеем
k2 — k1 =
0 или k2 = k1.
Таким образом, условием параллельности
двух прямых на плоскости является
равенство их угловых коэффициентов.
2) Если прямые R1 и R2 перпендикулярны, то φ = . Так как φ = φ2 – φ1 , то
φ2 = + φ1 и tg φ2 = tg(+ φ1) = ctg φ1 = — , т.е.
k2 = — . (8)
Таким образом, условие перпендикулярности двух прямых состоит в том, что их угловые коэффициенты обратны по величине и противоположны по знаку.
23. Уравнение плоскости. Нормальное уравнение плоскости (вывод). Геометрический смысл коэффициентов.
Получение уравнения плоскости в нормальном виде представляет интерес даже с формальной точки зрения: как развитие аналитических моделей геометрических фигур при переходе от двумерного пространства к 3-мерному. С другой стороны, от нормального уравнения плоскости мы ожидаем расширения наших возможностей при решении более сложных геометрических задач. Пусть точкаи. Пусть единичный векторсовпадает по направлению с вектором. Известно, что любой вектор можно представить как:, где– направляющие косинусы вектора.
Учитывая: =1, представим векторв виде:. Отметим на плоскостипроизвольную точку:==.
Используя заданные условия и принятые обозначения, запишем (используя скалярное произведение векторов и формулу для вычисления проекции вектора на направление):====×=,
откуда получаем: . (1)
Уравнение
(1) называют нормальным
уравнением
Отнесёмся к выражению: формально. Учитывая способ получения нормального уравнения (1), нетрудно догадаться, что для всех точек пространства, принадлежащих плоскостивеличина=0. А что будет происходить с величиной, если выбирать произвольные точки пространства?
Пусть – произвольная точка пространства и– некоторая плоскость пространства. Пусть точка, причём. Пусть единичный векторсовпадает по направлению с вектороми представлен в виде:.
Найдём
проекцию точки
на
направление:
обозначим
проекцию как точку. В
таком случае длина отрезкаравна
расстоянию точкиот
начала координат.
Вычислим=+.
При
получении нормального уравнения
плоскости было показано, что=.
Тогда:=,
В
таком случае длина отрезкаравна
расстоянию точкиот
начала координат.
Вычислим=+.
При
получении нормального уравнения
плоскости было показано, что=.
Тогда:=,
после чего можем записать: =–==[вспомним обозначение]=.
Итак, геометрический смысл величины –отклонение произвольной точки пространства от плоскости, причём=–расстояние этой точки до этой плоскости.
Возникает вопрос: почему для нахождения расстояния потребовался модуль? Ответ легко видеть из рисунка:
а) если точки ирасполагаются по разные стороны от плоскости, то>0;
б) если точки ирасполагаются по одну сторону от плоскости, то<0.
Ещё раз отметим, что величина – это расстояние произвольной точки пространства до заданной плоскости, причёмсо знаком! Знак отражает процесс проектирования вектора на направление вектора, а именно:=. Так как векторединичный, то получаем длину отрезка:==, измеренную при помощи единичного вектора.
Если
уравнение плоскости задано в общем
виде:
,
то
его можнонормировать,
то есть привести к записи (1).
1). Умножим общее уравнение плоскости на число :. (2)
2). Пусть получили тождество: . Тогда необходимо:→;→(3)Замечания: 1). В результате нормализации вектор нормали плоскости преобразован в единичный вектор: =→=, причем=1.
2). Смысл правил выбора знака величины t в преобразованиях (3), будет установлен при рассмотрении задачи вычисления отклонения произвольной точки от заданной плоскости.Замечание: При решении задачи «Пересекает ли отрезок плоскость» достаточно подставить координаты этих точек в заданное уравнение плоскости (не обязательно нормированное!), чтобы установить:пересекает плоскость, если вычисленные значения правой части уравнения плоскости имеют разные знаки;не пересекает плоскость, если знаки совпадают.
1. Рассмотрим вектор с проекциями на координатные оси, соответственно равнымиA, B и C, т. е. .
2.
Возьмем на плоскости Ax + By + Cz + D = 0 две произвольные точки M(x1, y1, z1)
и N(x2, y2, z2)
и рассмотрим вектор
. Этот вектор лежит в плоскостиAx + By + Cz + D = 0. Его проекции на координатные оси
соответственно равны x2 — x1, y2 — y1, z2 — z1 и
.
Этот вектор лежит в плоскостиAx + By + Cz + D = 0. Его проекции на координатные оси
соответственно равны x2 — x1, y2 — y1, z2 — z1 и
.
3. Так как точки M и N лежат в плоскости Ax + By + Cz + D = 0, то имеют место равенства
Ax1 + By1 + Cz1 + D = 0
и
Ax2 + By2 + Cz2 + D
Вычитая первое уравнение из второго, получим
A(x2 — x1) + B(y2 — y1) + C(z2 — z1) = 0. (1)
Скалярное произведение вектора на векторравно
A(x2 — x1)
+ B(y2 — y1)
+ C(z2 — z1).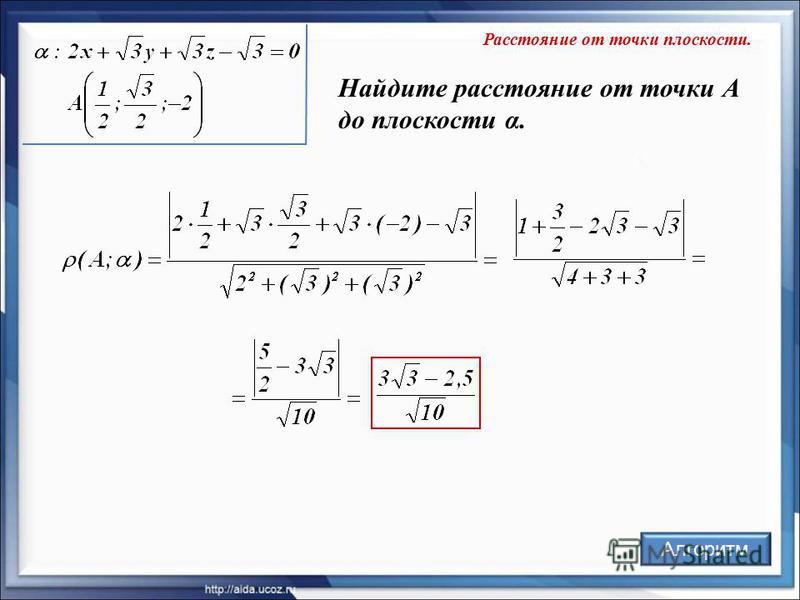
Так как на основании (1) это скалярное произведение равно нулю, то вектор перпендикулярен вектору, а тем самым и той плоскости, в которой лежит этот вектор, т. е. векторперпендикулярен плоскостиAx + By + Cz + D = 0.
Геометрическое значение коэффициентов A, B и C в общем уравнении плоскости Ax + By + Cz + D = 0 состоит в том, что они являются проекциями на координатные оси Ox, Oy, Oz вектора, перпендикулярного этой плоскости.
Перпендикулярное расстояние от точки до линии
Далее на этой странице…
Пример использования формулы перпендикулярного расстояния
(Кстати, нам не нужно говорить «перпендикулярно», потому что расстояние от точки до линии всегда означает кратчайшее расстояние.)
Это большая проблема, потому что она использует все эти вещи, которые мы узнали до сих пор:
- формула расстояния
- наклон параллельных и перпендикулярных линий
- прямоугольные координаты 92`
После доказательства есть несколько примеров использования этой формулы.

Начнем со строки Ax + By + C = 0 и назовем ее DE. Он имеет уклон `-A/B`.
xyAx + By + C = 0DEОткрыть изображение на новой страницеЛиния DE с наклоном −A/B.
У нас есть точка P с координатами ( m , n ). Мы хотим найти расстояние по перпендикуляру от точки P до линии DE (то есть расстояние `PQ`).
xyP (m, n)QDEОткрыть изображение на новой страницеПерпендикулярно прямой линии.
Теперь мы проделаем трюк, чтобы облегчить себе задачу (иначе алгебра действительно ужасна). Проведем прямую, параллельную DE через ( м , n ). Эта линия также будет иметь наклон «-A/B», так как она параллельна DE. Мы назовем эту линию FG.
xyP (m, n)QDEFGОткрыть изображение на новой страницеПерпендикулярные и параллельные построения.
Теперь построим еще одну прямую, параллельную PQ, проходящую через начало координат.
Эта линия будет иметь наклон `B/A`, поскольку она перпендикулярна DE.

Назовем это линией RS. Мы расширяем его до начала координат `(0, 0)`.
Мы найдем расстояние RS, которое, надеюсь, вы согласны с тем, что оно равно расстоянию PQ, которое мы хотели в начале.
xyP (m, n)QDEFGRS(0, 0)Открыть изображение на новой страницеПерпендикулярно через начало координат.
Так как FG проходит через ( м , n ) и имеет наклон `-A/B`, его уравнение `y-n=-A/B(x-m)` или 92))`
Пользователи телефонов
ПРИМЕЧАНИЕ: Если вы пользуетесь телефоном, вы можете прокручивать любые широких уравнений на этой странице вправо или влево, чтобы увидеть выражение целиком.
Точка S является пересечением линий `y=B/Ax` и Ax + By + C = 0, что можно записать как `y=-(Ax+C)/B`.
Это происходит, когда (то есть мы решаем их одновременно)
92``-(Ах+С)/В=В/Ах`
`=(|(-2)(5)+(3)(6)+4|)/(sqrt(4+9)`
`=3.
 328`
328`Вот график ситуации Мы видим, что наш ответ чуть более 3 единиц является разумным
246-22468-2xy(5, 6)Открыть изображение на новой страницеПерпендикулярно через (5, 6) к линии −2 x + 3 y + 4 = 0.
Таким образом, требуемое расстояние составляет «3,3» единицы, с точностью до 1 знака после запятой
Пример 2
Найти расстояние от точки `(-3, 7)` до линии 92`
`=(|(6)(-3)+(-5)(7)+10|)/кв.кв.(36+25)`
`=|-5.506|`
`=5,506`
Таким образом, требуемое расстояние составляет «5,506» единиц, с точностью до 3 знаков после запятой.
Нужна помощь в решении другой графической задачи? Попробуйте решение проблем.
Отказ от ответственности: IntMath.com не гарантирует точность результатов. Решатель задач предоставлен Mathway.
Что такое формула расстояния в геометрии?
Формула геометрического расстояния используется для определения расстояния между двумя точками на плоскости.
 Это важная идея для студентов, изучающих геометрию, и людей, работающих в таких областях, как инженерия и физика. В этой статье рассматриваются основы формул расстояния, включая то, что они собой представляют, почему они полезны и как их использовать.
Это важная идея для студентов, изучающих геометрию, и людей, работающих в таких областях, как инженерия и физика. В этой статье рассматриваются основы формул расстояния, включая то, что они собой представляют, почему они полезны и как их использовать.Как формула расстояния используется в геометрии?
Чтобы использовать формулы расстояний в вашей геометрии, выполните следующие действия:
1. Определите координаты двух точек.
- Эти точки могут быть представлены в системе координат, например в декартовой системе координат с осями x и y.
- Координаты точки записываются как (x, y), где координата x представляет положение точки по оси x, а координата y представляет ее положение по оси y.
2. Подставить координаты точки в формулу расстояния. Формула d = √((x2 – x1)2 + (y2 – y1)2) , где:
- d – расстояние между двумя точками и
- (x1, y1) и (x2, y2 ) — координаты
3.
 Вычислить расстояние между точками. Подставьте координаты точек в уравнение и найдите d. Пожалуйста, используйте правильные единицы измерения для координат и окончательного ответа.
Вычислить расстояние между точками. Подставьте координаты точек в уравнение и найдите d. Пожалуйста, используйте правильные единицы измерения для координат и окончательного ответа.Формулы расстояний имеют множество применений в геометрии, например, для определения расстояния между точками на графике, вычисления длины сегмента линии и определения расстояния между двумя линиями. Его можно использовать для многих целей, например, для поиска кратчайшего пути между двумя точками или для определения скорости движения объекта по прямой. Мы используем формулу расстояния, чтобы определить расстояние между двумя точками на единичной окружности. Если вы понимаете и знаете, как использовать формулы расстояний, вы можете использовать их для решения любой задачи геометрии.
Какая формула для вычисления расстояния в геометрии?
Следующая формула вычисляет расстояние в геометрии:
d = √((x2 – x1)2 + (y2 – y1)2)
Формула использует теорему Пифагора, которая утверждает, что квадрат гипотенуза треугольника (противоположная сторона прямого угла) равна сумме двух других его квадратов.
 В этом случае гипотенуза — это расстояние между двумя точками, а две другие стороны — это разница между координатами x и y соответственно.
В этом случае гипотенуза — это расстояние между двумя точками, а две другие стороны — это разница между координатами x и y соответственно.Подставьте координаты двух точек в формулу расстояния и найдите d. Например, если две точки имеют координаты (3, 4) и (6, 8), расстояние между ними равно (3, 4).
Это эквивалентно
√((6 — 3)2 + (8 — 4)2
= √((3)2 + (4)2)
= √(9 + 16)
= √25
= 5
Другими словами, расстояние между двумя точками равно пяти единицам
В декартовой системе координат формула расстояния применяется только к точкам на двумерной плоскости Другая формула для точек в Используется трехмерное пространство, известное как формула трехмерного расстояния.0005
Почему важна формула расстояния?
Формула расстояния является важным математическим инструментом по многим причинам.
- Вы можете рассчитать точное расстояние между двумя точками на плоскости или в пространстве. Это полезно в технике, физике, навигации и других областях, где важно измерение расстояния.

- Использование Для расчета кратчайшего пути между двумя точками, расчета скорости объекта и расчета расстояния, пройденного объектом.
- Крайне важно понимать и работать с геометрией. Формула расстояния является фундаментальным понятием в геометрии, и ее базовое понимание необходимо для решения более сложных задач о расстояниях на плоскости и в пространстве. Имеет практическое применение в повседневной жизни.
- Формула расстояния используется в повседневных приложениях, таких как навигация по карте, строительство и спорт, что делает ее ценным инструментом для решения реальных задач.
Применение формулы расстояния в реальных ситуациях
Формулы расстояний можно использовать по-разному в реальном мире, особенно в технике и физике. Вот пример использования формулы расстояния:
Навигация: Формулы расчета расстояния можно использовать для определения расстояния между двумя местами или точками на заданном маршруте или для определения того, до какого места потребуется меньше всего времени, чтобы добраться до него.
 . Это особенно полезно при путешествии по воздуху или по морю, когда важны расстояние и расход топлива.
. Это особенно полезно при путешествии по воздуху или по морю, когда важны расстояние и расход топлива.Архитектура и строительство: Для определения размеров зданий и других сооружений и организации размещения фундаментных опор и других элементов конструкций используются формулы расстояний.
Физика: Формулы расстояния используются для расчета расстояния, которое объект проходит по прямой линии, и скорости этого объекта. Он также вычисляет расстояние между двумя ее объектами в космосе, такими как планеты и спутники.
Спорт: Формулы расстояния могут измерять расстояние, пройденное спортсменом, или расстояние между игроками на спортивной площадке.
Географические информационные системы (ГИС) : Формулы расстояний используются в программном обеспечении ГИС для измерения расстояния между двумя точками на карте или для нахождения кратчайшего пути между двумя точками.
Хотите начать применять математику в своей карьере? Найди пару с репетиторами по математике для взрослых!
Советы по решению задач с формулой расстояния в геометрии
Вот несколько советов по решению задач с формулой расстояния в геометрии.

- Убедитесь, что вы понимаете суть проблемы и то, что от вас ожидается. Имея две точки и единицу измерения, определите, хотите ли вы расстояние между точками или длину отрезка, который их соединяет.
- Определите координаты двух точек. Эти точки могут быть представлены в системе координат, такой как декартова система координат с осями x и y. Точка описывается двумя числами, где первое число x представляет расстояние от нее по оси x, а второе число y представляет расстояние по оси y.
- Подставить координаты точки в формулу расстояния. Формулы состоят из d = √((x2 – x1)2 + (y2 – y1)2) , где d – расстояние
- Рассчитать расстояние между точками. Подставьте координаты точек в уравнение и найдите d. Пожалуйста, используйте правильные единицы измерения для координат и окончательного ответа.
- Проверьте свою работу. Убедитесь, что ваш окончательный ответ дан в правильных единицах и что ваше решение разумно, учитывая контекст проблемы.

Распространенные ошибки, которых следует избегать при использовании формулы расстояния в геометрии
Таким образом, при решении формул, связанных с расстоянием, люди совершают следующие распространенные ошибки:
Путаница между формулами расстояния и средней точки: формулы расстояния определяют расстояние между две точки, в то время как формулы средней точки находят координаты точки на полпути вдоль сегмента. Убедитесь, что вы используете правильную формулу для решения проблемы.
Забыли возвести в квадрат разницу между координатами x и y. Формула расстояния требует возведения в квадрат разницы между координатами x и y перед их сложением. Игнорирование этого приведет к неправильному ответу.
Забыв про квадратный корень: Формула расстояния требует нахождения квадратного корня из суммы квадратов разностей между координатами x и y. Если вы забудете и об этом, это будет неправильно.
Использование неправильных единиц измерения: Убедитесь, что вы используете правильные координаты и окончательный ответ.
 Если единицы измерения не указаны, обязательно укажите единицы, которые вы используете.
Если единицы измерения не указаны, обязательно укажите единицы, которые вы используете.Перепутаны координаты двух точек: Убедитесь, что вы используете правильные координаты для двух точек. Если вы перепутаете координаты, вы получите неправильный ответ.
Заинтересованы в изучении тригонометрии? Прочтите это
Общие заблуждения относительно формулы расстояния
Некоторые распространенные заблуждения относительно формулы расстояния могут привести к ошибкам при использовании. Вот некоторые заблуждения и пояснения к ним:
- Формула расстояния может использоваться только для определения расстояния между двумя точками на плоскости. Он обычно используется для нахождения расстояний между двумя точками на координатной плоскости, но его также можно использовать для нахождения расстояний между любыми двумя точками, независимо от того, перекрываются ли они.
- Формула расстояния и формула средней точки одинаковы. Формула расстояния вычисляет расстояние между двумя точками, а формула средней точки вычисляет координаты средней точки отрезка, соединяющего две точки.
 Хотя обе формулы не эквивалентны, их не следует путать.
Хотя обе формулы не эквивалентны, их не следует путать. - Формулы расстояний в основном используются для нахождения расстояний между точками на плоскости. Однако их можно применять и к трехмерным пространствам. С помощью x1, y1, z1 и x2, y2, z2 идентифицируются две трехмерные точки. Последнее число представляет собой длину стороны коробки, где одно измерение пространства представляет собой бесконечную прямую линию.
- Формула расстояния используется только в геометрии. Хотя формула расстояния обычно используется в геометрии, она также находит применение в других областях, таких как физика и инженерия.
Поняв эти распространенные заблуждения и прояснив их, вы сможете адекватно пользоваться формулой расстояния и точно рассчитывать расстояние между точками на плоскости или в пространстве.
Заинтересованы ли вы в изучении основ геометрии или вам нужен репетитор по математике
В Learner мы предлагаем лучших онлайн-репетиторов для каждого учащегося, подобранных по индивидуальному заказу с помощью нашего собственного процесса отбора и проверки.
 Наши преподаватели должны знать больше, чем просто предмет, который они преподают. Они также должны обладать правильными техническими и человеческими навыками, чтобы вдохновлять и мотивировать сегодняшних студентов.
Наши преподаватели должны знать больше, чем просто предмет, который они преподают. Они также должны обладать правильными техническими и человеческими навыками, чтобы вдохновлять и мотивировать сегодняшних студентов.Вот что мы предлагаем:
- Специально подобранный математический эксперт для решения любых задач.
- Преподаватели мирового класса, являющиеся экспертами в области педагогики, разрабатывают планы уроков в вашем собственном темпе и доводят их до вашего стиля обучения.
- Наставники учащихся выходят за рамки предмета, помогая определить траектории после проходного балла. Нажмите здесь, чтобы прочитать отзывы наших счастливых клиентов.
Заключение
В заключение отметим, что формула расстояния эффективно определяет расстояние между двумя точками на плоскости или в пространстве. Это применимо независимо от того, расположены ли точки в одной или разных плоскостях. Это важная часть изучения геометрии или работы с ней, поскольку она используется в инженерии, физике и навигации, а также в других областях.




 328`
328` Это важная идея для студентов, изучающих геометрию, и людей, работающих в таких областях, как инженерия и физика. В этой статье рассматриваются основы формул расстояния, включая то, что они собой представляют, почему они полезны и как их использовать.
Это важная идея для студентов, изучающих геометрию, и людей, работающих в таких областях, как инженерия и физика. В этой статье рассматриваются основы формул расстояния, включая то, что они собой представляют, почему они полезны и как их использовать. Вычислить расстояние между точками. Подставьте координаты точек в уравнение и найдите d. Пожалуйста, используйте правильные единицы измерения для координат и окончательного ответа.
Вычислить расстояние между точками. Подставьте координаты точек в уравнение и найдите d. Пожалуйста, используйте правильные единицы измерения для координат и окончательного ответа.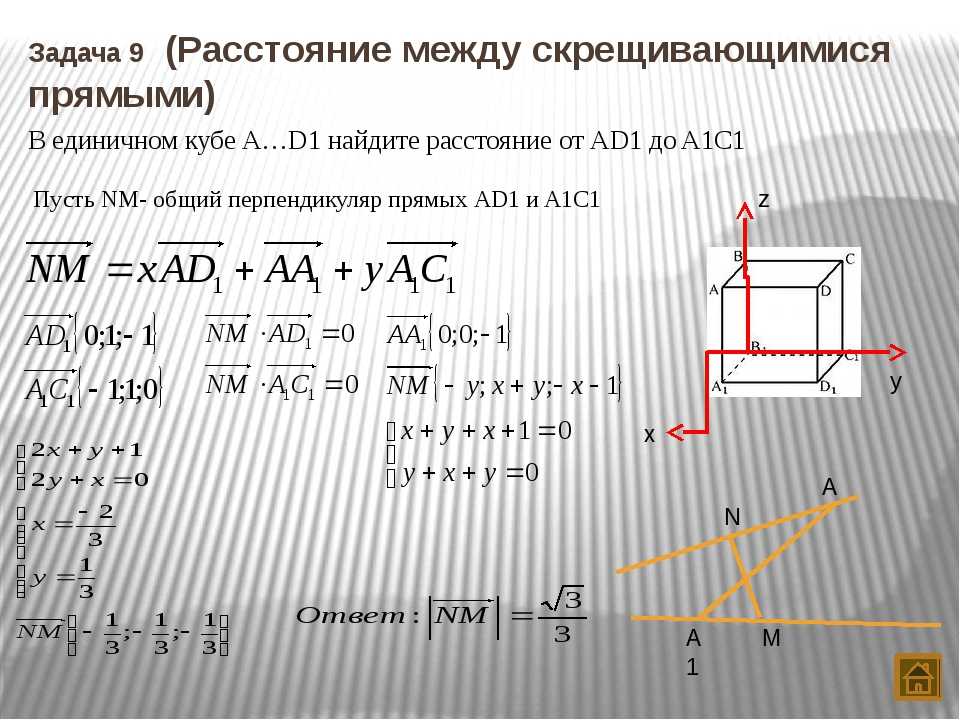 В этом случае гипотенуза — это расстояние между двумя точками, а две другие стороны — это разница между координатами x и y соответственно.
В этом случае гипотенуза — это расстояние между двумя точками, а две другие стороны — это разница между координатами x и y соответственно.
 . Это особенно полезно при путешествии по воздуху или по морю, когда важны расстояние и расход топлива.
. Это особенно полезно при путешествии по воздуху или по морю, когда важны расстояние и расход топлива.

 Если единицы измерения не указаны, обязательно укажите единицы, которые вы используете.
Если единицы измерения не указаны, обязательно укажите единицы, которые вы используете. Хотя обе формулы не эквивалентны, их не следует путать.
Хотя обе формулы не эквивалентны, их не следует путать. Наши преподаватели должны знать больше, чем просто предмет, который они преподают. Они также должны обладать правильными техническими и человеческими навыками, чтобы вдохновлять и мотивировать сегодняшних студентов.
Наши преподаватели должны знать больше, чем просто предмет, который они преподают. Они также должны обладать правильными техническими и человеческими навыками, чтобы вдохновлять и мотивировать сегодняшних студентов.