Запись an означает что число a должно быть умножено n раз: |
Пример 1. 53=5*5*5=125
Деление это обратная операция умножению. Отрицательная степень означает сколько раз нужно разделить число.
Число в отрицательной степени a-n может быть записано в виде: |
Пример 2. 5-3=1÷5÷5÷5=0,008
| Пример 2 может быть записан в виде. |
| Определение. Если a≠0 и n — целое отрицательное число, то |
Для вычисления числа a-n в отрицательной степени нужно:
1.Вычислить an
2.Затем разделить 1 на полученный результат, т.е. |
правила возведения числа и наглядные примеры
В одной из предыдущих статей мы уже упоминали о степени числа. Сегодня мы постараемся сориентироваться в процессе нахождения ее значения. Научно говоря, мы будем выяснять, как правильно возводить в степень. Мы разберемся, как производится этот процесс, одновременно затронем все вероятные показатели степени: натуральный, иррациональный, рациональный, целый.Итак, давайте подробно рассмотрим решения примеров и выясним, что значит:
- Определение понятия.
- Возведение в отрицательную ст.
- Целый показатель.
- Возведение числа в иррациональную степень.
Определение понятия
Вот точно отражающее смысл определение: «Возведением в степень называют определение значения степени числа».
Соответственно, возведение числа a в ст. r и процесс нахождения значения степени a с показателем r — это идентичные понятия. К примеру, если стоит задача вычислить значение степени (0,6)6″, то ее можно упростить до выражения «Возвести число 0,6 в степень 6».
После этого можно приступать напрямую к правилам возведения.

Возведение в отрицательную степень
Минусовая степень обозначает, что число множат на него самого такое количество раз, какое значится в ст., а после этого единицу делят на вычисленный результат.
Для наглядности следует обратить внимание на такую цепочку выражений:
110=0,1=1* 10 в минус 1 ст.,
1100=0,01=1*10 в минус 2 степ.,
11000=0,0001=1*10 в минус 3 ст.,
110000=0,00001=1*10 в минус 4 степeни.
Благодаря данным примерам можно четко просмотреть возможность моментально вычислить 10 в любой минусовой степени. Для этой цели достаточно банально сдвигать десятичную составляющую:
- 10 в -1 степeни — перед единицей 1 ноль;
- в -3 — три нуля перед единицей;
- в -9 — это 9 нулей и проч.
Так же легко понять по данной схеме, сколько будет составлять 10 в минус 5 ст. —
1100000=0,000001=(1*10)-5.

Как возвести число в натуральную степeнь
Вспоминая определение, учитываем, что натуральное число a в ст. n равняется произведению из n множителей, при этом каждый из них равняется a. Проиллюстрируем: (а*а*…а)n, где n — это количество чисел, которые умножаются. Соответственно, чтобы a возвести в n, необходимо рассчитать произведение следующего вида: а*а*…а разделить на n раз.
Отсюда становится очевидно, что возведение в натуральную ст. опирается на умение осуществлять умножение
Возведите -2 в 4-ю ст.
Решение:
Мы имеем дело с натуральным показателем. Соответственно, ход решения будет следующим: (-2) в cт. 4 = (-2)*(-2)*(-2)*(-2). Теперь осталось только осуществить умножение целых численностей:(-2)*(-2)*(-2)*(-2). Получаем 16.
Ответ на задачу:
(-2) в ст. 4=16.
Пример:
Вычислите значение: три целых две седьмых в квадрате.
Решение:
Данный пример равняется следующему произведению: три целых две седьмых умножить на три целых две седьмых. Припомнив, как осуществляется умножение смешанных чисел, завершаем возведение:
- 3 целых 2 седьмых умножить на самих себя;
- равно 23 седьмых умножить на 23 седьмых;
- равно 529 сорок девятых;
- сокращаем и получаем 10 тридцать девять сорок девятых.
Ответ: 10 39/49
Возведение в иррациональную стeпeнь
Касаемо вопроса возведения в иррациональный показатель, следует отметить что расчеты начинают проводить после завершения предварительного округления основы степени до какого-либо разряда, который позволил бы получить величину с заданной точностью. К примеру, нам необходимо возвести число П (пи) в квадрат.
Начинаем с того, что округляем П до сотых и получаем:
П в квадрате = (3,14)2=9,8596. Однако если сократить П до десятитысячных, получим П=3,14159. Тогда возведение в квадрат получает совсем другое чиcло: 9,8695877281.
Здесь следует отметить, что во многих задачах нет надобности возводить иррациональные числа в cтeпeнь. Как правило, ответ вписывается или в виде, собственно, степени, к примеру, корень из 6 в степени 3, либо, если позволит выражение, проводится его преобразование: корень из 5 в 7 cтепeни = 125 корень из 5.
Как возвести чиcло в целую степень
Эту алгебраическую манипуляцию уместно принимать во внимание для следующих случаев:
- для целых чисел;
- для нулевого показателя;
- для целого положительного показателя.
Поскольку практически все целые положительные числа совпадают с массой чисел натуральных, то постановка в положительную целую степень — это тот же процесс, что и постановка в ст. натуральную. Данный процесс мы описали в предшествующем пункте.
Теперь поговорим о вычислении ст. нулевой. Мы уже выяснили выше, что нулевую степень числа a можно определить для любого отличного от нуля a (действительного), при этом a в ст. 0 будет равно 1.
Соответственно, возведение какого угодно действительного числа в нулевую ст. будет давать единицу.
К примеру, 10 в ст.0=1, (-3,65)0=1, а 0 в ст. 0 нельзя определить.
Для того чтобы завершить возведение в целую степень, остается определиться с вариантами целых отрицательных значений. Мы помним, что ст. от a с целым показателем -z будет определяться как дробь. В знаменателе дроби располагается ст. с целым положительным значением, значение которой мы уже научились находить. Теперь остается лишь рассмотреть пример возведения.
Пример:
Вычислить значение числа 2 в кубе с целым отрицательным показателем.
Процесс решения:
Согласно определению стeпeни с отрицательным показателем обозначаем: два в минус 3 ст. равняется один к двум в третьей cтепeни.
Знаменатель рассчитывается просто: два в кубе;
3 = 2*2*2=8.
Ответ: два в минус 3-й ст. = одна восьмая.
Видео
Из этого видео вы узнаете, что делать, если степень с отрицательным показателем.
Отрицательная степень числа | Алгебра
Степень с отрицательным показателем
Число с отрицательным показателем степени равно дроби, числителем которой является единица, а знаменателем данное число с положительным показателем.
| d -c = | 1 | ; 7 -5 = | 1 | ; a -5 = | 1 | . |
| d c | 7 5 | a 5 |
Чтобы разобраться, почему число в отрицательной степени равно дроби, надо вспомнить правило деления степеней с одинаковыми основаниями:
При делении степеней с одинаковыми основаниями из показателя степени делимого вычитают показатель степени делителя.
Следовательно, если степень делимого будет меньше степени делителя, то в результате получится число с отрицательной степенью:
a 5 : a 8 = a5 — 8 = a -3.
Если записать деление в виде дроби, то при сокращении в числителе останется 1, а в знаменателе число будет иметь положительную степень:
Значит:
Пример 1. Замените дробь степенью с отрицательным показателем:
Решение:
Пример 2. Представьте в виде степени с отрицательным показателем:
Решение:
| 1 | = (m + n) -2. |
| (m + n) 2 |
Действия над степенями с отрицательными показателями
При умножении отрицательных степеней с одинаковыми основаниями показатели степеней складываются:
Чтобы возвести произведение в отрицательную степень, надо возвести в эту степень каждый сомножитель отдельно:
Чтобы возвести дробь в отрицательную степень, надо возвести в эту степень отдельно числитель и знаменатель:
При возведении одной степени (положительной или отрицательной) в степень (положительную или отрицательную) показатели степеней перемножаются:
Отрицательная степень | Алгебра
Что такое степень с отрицательным показателем (отрицательная степень)? Как выполнить возведение числа в отрицательную степень? Как возвести в отрицательную степень дробь?
Определение.
В частности, число в степени минус один — это число, обратное данному:
Если n — целое число, то речь идет о степени с целым отрицательным показателем и равенство верно для любого a, отличного от нуля (т.е. при a≠0).
Если n — дробное число, то речь идет о степени с рациональным показателем:
(m — целое число, n — натуральное число). Степень с дробным показателем определена только для положительных a (a>0).
В частности,
Дробь в степени с отрицательным показателем равна обратному этой дроби числу в степени с показателем, противоположным данному:
Другими словами, чтобы возвести дробь в отрицательную степень, надо эту дробь «перевернуть»(числитель и знаменатель поменять местами) и изменить знак в показателе степени.
Дробь в минус первой степени — это «перевернутая» дробь.
В частности,
Рассмотрим примеры возведения чисел в степень с отрицательным показателем.
Для ускорения вычислений используем таблицу степеней.
Примеры.
Чтобы возвести в отрицательную степень смешанное число, надо сначала перевести его в неправильную дробь:
Возведем числа в степень с дробным отрицательным показателем:
При возведении в отрицательную степень десятичной дроби можно сначала перевести ее в обыкновенную и, если возможно, сократить:
Если в показателе степени стоит десятичная дробь, нужно перевести ее в обыкновенную:
Возведение в степень с отрицательным показателем в алгебре встречается достаточно часто, поэтому важно вовремя усвоить эту тему.
Одной из главных характеристик в алгебре, да и во всей математике является степень. Конечно, в 21 веке все расчеты можно проводить на онлайн-калькуляторе, но лучше для развития мозгов научиться делать это самому.
В данной статье рассмотрим самые важные вопросы, касающиеся этого определения. А именно, поймем что это вообще такое и каковы основные его функции, какие имеются свойства в математике.
Степень, свойства и действия со степенями, сложение, умножение, деление отрицательных степеней, степень с натуральным показателем, правила и формулы

Рассмотрим на примерах то, как выглядит расчет, каковы основные формулы. Разберем основные виды величины и то, чем они отличаются от других функций.
Поймем, как решать с помощью этой величины различные задачи. Покажем на примерах, как возводить в нулевую степень, иррациональную, отрицательную и др.
Что такое степень числа
Что же подразумевают под выражением «возвести число в степень»?
Степенью n числа а является произведение множителей величиной а n-раз подряд.

Математически это выглядит следующим образом: an = a * a * a * …an.
Причем, левая часть уравнения будет читаться, как a в степ. n.
Например:
- 23 = 2 в третьей степ. = 2 * 2 * 2 = 8,
- 42 = 4 в степ. два = 4 * 4 = 16,
- 54 = 5 в степ. четыре = 5 * 5 * 5 * 5 = 625,
- 105 = 10 в 5 степ. = 10 * 10 * 10 * 10 * 10 = 100000,
- 104 = 10 в 4 степ. = 10 * 10 * 10 * 10 = 10000.
Ниже будет представлена таблица квадратов и кубов от 1 до 10.
Таблица степеней от 1 до 10
Ниже будут приведены результаты возведения натуральных чисел в положительные степени – «от 1 до 100».
| Ч-ло | 2-ая ст-нь | 3-я ст-нь |
| 1 | 1 | 1 |
| 2 | 4 | 8 |
| 3 | 9 | 27 |
| 4 | 16 | 64 |
| 5 | 25 | 125 |
| 6 | 36 | 216 |
| 7 | 49 | 343 |
| 8 | 64 | 512 |
| 9 | 81 | 279 |
| 10 | 100 | 1000 |
Свойства степеней
Что же характерно для такой математической функции? Рассмотрим базовые свойства.
Учеными установлено следующие признаки, характерные для всех степеней:
- an * am = (a)(n+m),
- an : am = (a)(n-m),
- (ab ) m=(a)(b*m).
Проверим на примерах:
- 23 * 22 = 8 * 4 = 32. С другой стороны 25 = 2 * 2 * 2 * 2 * 2 =32.
Аналогично:
- 23 : 22 = 8 / 4 =2. Иначе 23-2 = 21 =2.
- (23)2 = 82 = 64. А если по-другому? 26 = 2 * 2 * 2 * 2 * 2 * 2 = 32 * 2 = 64.
Как видим, правила работают.

А как же быть со сложением и вычитанием? Всё просто. Выполняется сначала возведение в степень, а уж потом сложение и вычитание.
Посмотрим на примерах:
- 33 + 24 = 27 + 16 = 43,
- 52 – 32 = 25 – 9 = 16. Обратите внимание: правило не будет выполняться, если сначала произвести вычитание: (5 3)2 = 22 = 4.
- А вот в этом случае надо вычислять сначала сложение, поскольку присутствуют действия в скобках: (5 + 3)3 = 83 = 512.
Как производить вычисления в более сложных случаях? Порядок тот же:
- при наличии скобок – начинать нужно с них,
- затем возведение в степень,
- потом выполнять действия умножения, деления,
- после сложение, вычитание.
Есть специфические свойства, характерные не для всех степеней:
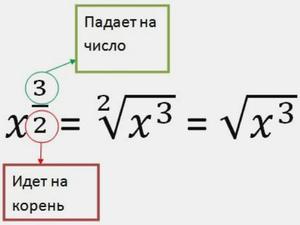
- Корень n-ой степени из числа a в степени m запишется в виде: am/n.
- При возведении дроби в степень: этой процедуре подвержены как числитель, так и ее знаменатель.
- При возведении произведения разных чисел в степень, выражение будет соответствовать произведению этих чисел в заданной степени. То есть: (a * b)n = an * bn.
- При возведении числа в отрицательную степ., нужно разделить 1 на число в той же ст-ни, но со знаком «+».
- Если знаменатель дроби находится в отрицательной степени, то это выражение будет равно произведению числителя на знаменатель в положительной степени.
- Любое число в степени 0 = 1, а в степ. 1 = самому себе.
Степень с отрицательным показателем
Что делать при минусовой степени, т. е. когда показатель отрицательный?

Исходя из свойств 4 и 5 (смотри пункт выше), получается:
- A(-n) = 1 / An, 5(-2) = 1 / 52 = 1 / 25.
И наоборот:
- 1 / A(-n) = An, 1 / 2(-3) = 23 = 8.
А если дробь?
- (A / B)(-n) = (B / A)n, (3 / 5)(-2) = (5 / 3)2 = 25 / 9.
Степень с натуральным показателем
Под ней понимают степень с показателями, равными целым числам.
Что нужно запомнить:
- A0 = 1, 10 = 1, 20 = 1, 3.150 = 1, (-4)0 = 1… и т. д.
- A1 = A, 11 = 1, 21 = 2, 31 = 3 … и т. д.
Кроме того, если (-a)2n+2, n=0, 1, 2…то результат будет со знаком «+». Если отрицательное число возводится в нечетную степень, то наоборот. Общие свойства, да и все специфические признаки, описанные выше, также характерны для них.
Дробная степень
Этот вид можно записать схемой: Am/n. Читается как: корень n-ой степени из числа A в степени m.

С дробным показателем можно делать, что угодно: сокращать, раскладывать на части, возводить в другую степень и т. д.
Степень с иррациональным показателем
Пусть α – иррациональное число, а А ˃ 0.
Чтобы понять суть степени с таким показателем, рассмотрим разные возможные случаи:
- А = 1. Результат будет равен 1. Поскольку существует аксиома – 1 во всех степенях равна единице,
- А˃1.
- Аr1 ˂ Аα ˂ Аr2, r1 ˂ r2 – рациональные числа.
В этом случае наоборот: Аr2 ˂ Аα ˂ Аr1 при тех же условиях, что и во втором пункте.
Например, показатель степени число π. Оно рациональное.
- r1 – в этом случае равно 3,
- r2 – будет равно 4.
- Тогда, при А = 1, 1π = 1.
- А = 2, то 23 ˂ 2π ˂ 24, 8 ˂ 2π ˂ 16.
- А = 1/2, то (½)4 ˂ (½)π ˂ (½)3, 1/16 ˂ (½)π ˂ 1/8.
Для таких степеней характерны все математические операции и специфические свойства, описанные выше.
Заключение
Подведём итоги для чего же нужны эти величины, в чем преимущество таких функций? Конечно, в первую очередь они упрощают жизнь математиков и программистов при решении примеров, поскольку позволяют минимизировать расчеты, сократить алгоритмы, систематизировать данные и многое другое.
Где еще могут пригодиться эти знания? В любой рабочей специальности: медицине, фармакологии, стоматологии, строительстве, технике, инженерии, конструировании и т. д.
Источник: https://tvercult.ru/nauka/stepen-svoystva-pravila-deystviya-i-formulyi
Степенные выражения (выражения со степенями) и их преобразование
Рассмотрим тему преобразования выражений со степенями, но прежде остановимся на ряде преобразований, которые можно проводить с любыми выражениями, в том числе со степенными. Мы научимся раскрывать скобки, приводить подобные слагаемые, работать с основанием и показателем степени, использовать свойства степеней.
Что представляют собой степенные выражения?
В школьном курсе мало кто использует словосочетание «степенные выражения», зато этот термин постоянно встречается в сборниках для подготовки к ЕГЭ. В большинства случаев словосочетанием обозначаются выражения, которые содержат в своих записях степени. Это мы и отразим в нашем определении.
Степенное выражение – это выражение, которое содержит степени.
Приведем несколько примеров степенных выражений, начиная со степени с натуральным показателем и заканчивая степенью с действительным показателем.
- Самыми простыми степенными выражениями можно считать степени числа с натуральным показателем: 32, 75+1, (2+1)5, (−0,1)4, 2233, 3·a2−a+a2, x3−1, (a2)3.
- А также степени с нулевым показателем: 50, (a+1)0, 3+52−3,20. И степени с целыми отрицательными степенями: (0,5)2+(0,5)-22.
- Чуть сложнее работать со степенью, имеющей рациональный и иррациональный показатели: 26414-3·3·312, 23,5·2-22-1,5, 1a14·a12-2·a-16·b12, xπ·x1-π, 233+5.
- В качестве показателя может выступать переменная 3x-54-7·3x-58 или логарифм x2·lgx−5·xlgx.
С вопросом о том, что такое степенные выражения, мы разобрались. Теперь займемся их преобразованием.
Основные виды преобразований степенных выражений
В первую очередь мы рассмотрим основные тождественные преобразования выражений, которые можно выполнять со степенными выражениями.
Вычислите значение степенного выражения 23·(42−12).
Решение
Все преобразования мы будем проводить с соблюдением порядка выполнения действий. В данном случае начнем мы с выполнения действий в скобках: заменим степень на цифровое значение и вычислим разность двух чисел. Имеем 23·(42−12)=23·(16−12)=23·4.
Нам остается заменить степень 23 ее значением 8 и вычислить произведение 8·4=32. Вот наш ответ.
Ответ: 23·(42−12)=32.
Упростите выражение со степенями 3·a4·b−7−1+2·a4·b−7.
Решение
Данное нам в условии задачи выражение содержит подобные слагаемые, которые мы можем привести: 3·a4·b−7−1+2·a4·b−7=5·a4·b−7−1.
Ответ: 3·a4·b−7−1+2·a4·b−7=5·a4·b−7−1.
Источник: https://Zaochnik.com/spravochnik/matematika/vyrazhenija/stepennye-vyrazhenija/
Возведение в степень
Возведение в степень — это арифметическая операция повторяющегося умножения. Если требуется перемножить число n-ное количество раз, то достаточно возвести его в n-ную степень.
Основные действия со степенями
В первую очередь степень — это повторяющееся умножение. Число 134 — это 13 × 13 × 13 × 13, где перемножаются четыре одинаковых сомножителя. Если умножить 134 на 132, то мы получим (13 × 13 × 13 × 13) × (13 × 13), что логично превращается в 136.
Это и есть первое правило возведения в степень, которое гласит: при умножении чисел, возведенных в степень, их показатели суммируются. Математически это записывается как:
Если разделить 134 на 132, то нам потребуется вычислить дробь вида:
- (13 × 13 × 13 × 13) / (13 × 13).
Мы можем просто сократить числа в числителе и знаменателе, и в результате останется 13 × 13 = 132. Очевидно, деление чисел, возведенных в степень, соответствует вычитанию их показателей. Второе правило действий со степенями математически выглядит так: am / an = a(m – n).
Теперь давайте возведем 114 в куб, то есть в третью степень. Для этого нам потребуется вычислить выражение (11 × 11 × 11 × 11) × (11 × 11 × 11 × 11) × (11 × 11 × 11 × 11). Получилось 12 сомножителей, следовательно, при возведении в n-ную степень числа в степени m, показатели перемножаются. Третье правило записывается так: (am)n = a(m × n).
Это основные правила работы со степенными выражениями. Однако число можно возвести в отрицательную степень, дробную и нулевую. Какой результат даст выражение 150? Давайте воспользуемся вторым правилом действий степенями и попробуем разделить 154 на 154, что запишется как дробь: 154 / 154.
Очевидно, что в числителе и знаменателе стоят одни и те же числа, а когда число делится само на себя, оно превращается в единицу. Но согласно правилу действий со степенными числами это будет эквивалентно 150.
Следовательно: 154 / 154 = 150 = 1.
Таким образом, четвертое правило гласит, что любое положительное число в нулевой степени равняется единице. Выглядит это правило так: a0 = 1.
При помощи второго правила легко объяснить и работу с отрицательными степенями. К примеру, давайте разделим 82 на 84 и запишем выражение в виде дроби.
(8 × 8) / (8 × 8 × 8 × 8).
Мы можем сократить две восьмерки в числителе и знаменателе и преобразовать дробь в 1 / (8 × 8). Но согласно правилу в ответе мы должны получить 8-2. В знаменателе у нас как раз стоит восьмерка в квадрате. Таким образом:
При этом для значения -1 правило трансформируется в элегантную формулу:
И последнее правило, которое пригодится вам при работе со степенными функциями, гласит о дробных степенях. Что мы можем сделать с выражением 7(1/2). Очевидно, что возвести его в квадрат, и тогда по третьему правилу в результате у нас останется только семерка.
Степень 1/2 — это извлечение квадратного корня, так как при возведении его в квадрат мы получаем целое число. Степень 1/3 соответствует извлечению кубического корня, но как быть с показателем 2/3? Логично, что это кубический корень из числа, возведенного в квадрат.
Последнее правило гласит, что знаменатель дробного показателя означает извлечение корня, а числитель — возведение в степень. Математически это выглядит как: a(m/n) есть корень n-ной степени из am. Теперь вы знаете, как проводить любые арифметические операции со степенными выражениями.
Вы можете использовать наш калькулятор для вычисления степенных функций. Программа позволяет определить основание, показатель и результат операции. Кроме того, калькулятор сопровождается иллюстрацией графика функций: параболы, кубической параболы и параболы в n-ной степени. Рассмотрим пару примеров.
Примеры из реальной жизни
Депозит в банке
Если мы положим на банковский депозит $1 000 под годовую ставку в размере 9% годовых, то сколько денег на счету будет через 20 лет? Рост с течением времени рассчитываются по экспоненциальной формуле вида:
Рост = a × e(kt),
- где a – начальное значение,
- e – константа, равная 2,718;
- k – коэффициент роста;
- t – время.
Для решения банковской задачи нам потребуется возвести 2,718 в степень, равную 20 × 0,09 = 1,8. Воспользуемся нашим калькулятором и введем в ячейку «Число, x =» значение 2,718, а в ячейку «Степень, n =» значение 1,8. Мы получим ответ, равный 6,049. Теперь, для подсчета суммы на банковском счету нам необходимо умножить начальное значение $1 000 на прирост в размере 6,049. В итоге, через 20 лет на депозите будет $6 049.
Школьная задача
Пусть в школьной задаче требуется построить график функции y = x2,5. Это алгебраическая задача, для решения которой требуется задаться тремя значениями «x» и вычислить соответствующие ему значения «y». После чего по найденным точкам построить график функции.
Введите в ячейку «Степень, n =» значение 2,5. После этого последовательно рассчитайте значения «y», вводя в «Число, x =» аргументы 1, 2, 3. Вы получите соответствующие значения функции 1; 5,657; 15,588. Вам останется только нарисовать кривую по найденным точкам.
Источник: https://BBF.ru/calculators/73/
Степень с отрицательным показателем определение
Пусть число a есть любое действительное число, отличное от нуля. Число m – отрицательное целое число.
Степень с отрицательным показателем определение:
Действительное, отличное от нуля число a, возведенное в отрицательную целую степень -m, равно дроби, в числителе которой 1 и в знаменателе a, возведенное в положительную целую степень m.
Отрицательная степень формула
Для вычислений отрицательных степеней используем формулу:
a-m = 1/am
Эта формула применяется, если имеется отрицательное значение степени.
Положительная и отрицательная степень
Чтоб лучше понять сравним положительные и отрицательные степени.
Пусть число a есть любое действительное число, отличное от нуля. Число m – любое целое число.
Тогда a в положительной степени m равно:
am = a * a * a * … (m раз)
Теперь a в отрицательной степени -m:
a-m = 1/am
Степень с целым отрицательным показателем
Обратите внимание, что в этой статье речь идет именно о целом отрицательном показателе. Здесь существенным является то, что показатель целый.
Пример степени с целым отрицательным показателем:
12-3 = 1/123
Отрицательное основание степени
Отрицательная степень числа и отрицательное основание степени – это разные вещи.
Отрицательное основание степени рассмотрим на примере.
Пример отрицательного основания степени:
(-2)3 = -2 * (-2) * (-2) = -8
А теперь пример отрицательной степени числа.
Пример (отрицательная степень числа):
2-3 = 1/23 = 1/8
90000 Negative Exponents | Purplemath 90001 90002 Purplemath 90003 90004 Once you’ve learned about negative numbers, you can also learn about negative powers. A negative exponent just means that the base is on the wrong side of the fraction line, so you need to flip the base to the other side. For instance, «90005 x 90006 90007 -2 90008» (pronounced as «ecks to the minus two») just means «90005 x 90006 90007 2 90008, but underneath, as in 1 / (90005 x 90006 90007 2 90008)».90017 90018 90019 90020 90021 Write 90005 x 90006 90007 -4 90008 using only positive exponents. 90026 90027 90028 90004 I know that the negative exponent means that the base, the 90005 x 90006, belongs on the other side of the fraction line. But there is not a fraction line! 90017 90002 MathHelp.com 90003 90035 90004 To fix this, I’ll first convert the expression into a fraction in the way that 90005 any 90006 expression can be converted into a fraction: by putting it over «1». Of course, once I move the base to the other side of the fraction line, there will be nothing left on top.But since anything can also be regarded as being multiplied by 1, I’ll leave a 1 on top. 90017 90004 Here’s what it looks like: 90017 90004 90017 90004 Once I no longer needed the «1» underneath (to create the fraction), I omitted it, because I had the variable expression underneath, and the «times one» does not change anything. 90017 90018 90019 90020 90021 Write 90005 x 90006 90007 2 90008/90005 x 90006 90007 -3 90008 using only positive exponents.90026 90027 90028 90004 Only one of the terms has a negative exponent. This means that I’ll only be moving one of these terms. The term with the negative power is underneath; this means that I’ll be moving it up top, to the other side of the fraction line. There already is a term on top; I’ll be using exponent rules to combine these two terms. 90017 90004 Once I move that denominator up top, I will not having anything left underneath (other than the «understood» 1), so I’ll drop the denominator.90017 90004 90017 90018 90019 90020 90021 Write 2 90005 x 90006 90007 -1 90008 using only positive exponents. 90026 90027 90028 90004 The negative power will become just «1» once I move the base to the other side of the fraction line.Anything to the power 1 is just itself, so I’ll be able to drop this power once I’ve moved the base. 90017 90004 90081 90017 90004 Make sure you understand why the «2» above does not move with the variable: the negative exponent is only on the «90005 x 90006», so only the 90005 x 90006 moves .. 90017 90018 90019 90020 90021 Write (3 90005 x 90006) 90007 -2 90008 using only positive exponents.90026 90027 90028 90004 I’ve got a number inside the power this time, as well as a variable, so I’ll need to remember to simplify the numerical squaring. 90017 90004 Unlike the previous exercise, the parentheses meant that the negative power did indeed apply to the three as well as the variable. 90017 90018 90019 90020 90021 Write (-5 90005 x 90006 90007 -1 90008) / (90005 y 90006 90007 3 90008) using only positive powers.90026 90027 90028 90004 The «minus one» power on the 90005 x 90006 means that I’ll need to move that 90005 x 90006 to the other side of the fraction line. But the «minus» on the 5 means only that the 5 is negative. This «minus» is 90005 not 90006 a power, so it does not say 90005 anything 90006 about moving the 5 90005 anywhere! 90006 90017 90004 Moving only the one bit that actually needs to be moved, I get: 90017 90004 (-5 90005 x 90006 90007 -1 90008) / (90005 y 90006 90007 3 90008) = -5 / (90005 x 90006 90007 1 90008 90005 y 90006 90007 3 90008) = -5 / (90005 x 90006 90005 y 90006 90007 3 90008) 90017 90018 90019 90020 90021 Write (90005 x 90006 90007 -2 90008/90005 y 90006 90007 -3 90008) 90007 -2 90008 using only positive exponents.90026 90027 90028 90004 There is more than one way to do the steps for this simplification. I’ll start by noting that the negative exponent on the outside of the parentheses means that the numerator should be moved underneath and the denominator should be moved on top. In other words, the fraction inside the parentheses should be flipped. 90017 90004 Once I’ve flipped the fraction and converted the negative outer power to a positive, I’ll move this power inside the parentheses, using the power-on-a-power rule; namely, I’ll multiply.In this case, this will result in negative powers on each of the numerator and the denominator, so I’ll flip again. (Yes, I’m kind of taking the long way ’round.) 90017 90004 The above simplification can also be done as: 90017 90004 90017 90004 Instead of flipping twice, I noted that all the powers were negative, and moved the outer power onto the inner ones; since «minus times minus is plus», I ended up with all positive powers.90017 90004 Note: While this second solution would be a faster way of getting the exercise done, «faster» does not mean «more right». Either way is fine. 90017 90004 Since exponents indicate multiplication, and since order does not matter in multiplication, there will often be more than one sequence of steps that will lead to a valid simplification of a given exercise of this type. Do not worry if the steps in your homework look quite different from the steps in a classmate’s homework.As long as your steps were correct, you should both end up with the same answer in the end. 90017 90018 90004 You can use the Mathway widget below to practice simplifying expressions with negative exponents. Try the entered exercise, or type in your own exercise. Then click the button to compare your answer to Mathway’s. (Or skip the widget and continue with the lesson.) 90017 90004 90005 (Click here to be taken directly to the Mathway site, if you’d like to check out their software or get further info.) 90006 90017 90018 90004 By the way, now that you know about negative exponents, you can understand the logic behind the «anything to the power zero» rule: 90017 90004 Anything to the power zero is just «1». 90017 90004 Why is this so? There are various explanations. One might be stated as «because that’s how the rules work out.» Another would be to trace through a progression like the following: 90017 90004 3 90007 5 90008 = 3 90007 6 90008 ÷ 3 = 3 90007 6 90008 ÷ 3 90007 1 90008 = 3 90007 6-1 90008 = 3 90007 5 90008 = 243 90017 90004 3 90007 4 90008 = 3 90007 5 90008 ÷ 3 = 3 90007 5 90008 ÷ 3 90007 1 90008 = 3 90007 5-1 90008 = 3 90007 4 90008 = 81 90017 90004 3 90007 3 90008 = 3 90007 4 90008 ÷ 3 = 3 90007 4 90008 ÷ 3 90007 1 90008 = 3 90007 4-1 90008 = 3 90007 3 90008 = 27 90017 90004 3 90007 2 90008 = 3 90007 3 90008 ÷ 3 = 3 90007 3 90008 ÷ 3 90007 1 90008 = 3 90007 3-1 90008 = 3 90007 2 90008 = 9 90017 90004 3 90007 1 90008 = 3 90007 2 90008 ÷ 3 = 3 90007 2 90008 ÷ 3 90007 1 90008 = 3 90007 2-1 90008 = 3 90007 1 90008 = 3 90017 90004 At each stage, with each stage having a power than was one less than what came before, the simplified value was equal to the previous value, divided by 3.Then logically, since 3 ÷ 3 = 1, we must then have: 90017 90004 3 90007 0 90008 = 3 90007 1 90008 ÷ 3 = 3 90007 1 90008 ÷ 3 90007 1 90008 = 3 90007 1-1 90008 = 3 90007 0 90008 = 1 90017 90004 A negative-exponents explanation of the «anything to the zero power is just 1» might be as follows: 90017 90004 90005 m 90006 90007 0 90008 = 90005 m 90006 90007 (90005 n — n 90006) 90008 = 90005 m 90006 90007 90005 n 90006 90008 × 90005 m 90006 90007 — 90005 n 90006 90008 = 90005 m 90006 90007 90005 n 90006 90008 ÷ 90005 m 90006 90007 90005 n 90006 90008 = 1 90017 90004…since anything divided by itself is just «1». 90017 90018 90004 Comment: Please do not ask me to «define» 0 90007 0 90008. There are at least two ways of looking at this quantity: 90017 90004 Anything to the zero power is «1», so 0 90007 0 90008 = 1. 90017 90004 Zero to any power is zero, so 0 90007 0 90008 = 0. 90017 90004 As far as I know, the «math gods» have not yet settled on a firm «definition» of 0 90007 0 90008 — though, to be fair, an informal consensus seems to be building that the value «should» be 1, and just about any programming language will spit out the value 1.90017 90004 In calculus, «0 90007 0 90008» will be called an «indeterminate form», meaning that, mathematically, it makes no sense and tells you nothing useful. If this quantity comes up in your class, do not assume: ask your instructor what you should do with it. 90017 90018 90004 For loads more worked examples, try here. Or continue with this lesson; scientific notation comes next. 90017 90018 90004 URL: https: // www.purplemath.com/modules/exponent2.htm 90017 .90000 Negative exponents — how to solve 90001 90002 How to calculate negative exponents. 90003 90004 Negative exponents rule 90005 90002 The base b raised to the power of minus n is equal to 1 divided by the base b raised to the power of n: 90003 90002 90009 b 90010 -n 90011 90012 = 1/90009 b 90010 n 90011 90012 90003 90018 Negative exponent example 90019 90002 The base 2 raised to the power of minus 3 is equal to 1 divided by the base 2 raised to the power of 3: 90003 90002 2 90010 -3 90011 = 1/2 90010 3 90011 = 1 / (2⋅2⋅2) = 1/8 = 0.125 90003 90018 Negative fractional exponents 90019 90002 The base b raised to the power of minus n / m is equal to 1 divided by the base b raised to the power of n / m: 90003 90002 90033 b 90034 90010 -n / m 90011 = 1/90033 b 90034 90010 n / m 90011 = 1/90009 90012 (90009 90010 m 90011 √ 90012 90033 b 90034) 90010 90033 n 90034 90011 90003 90002 The base 2 raised to the power of minus 1/2 is equal to 1 divided by the base 2 raised to the power of 1/2: 90003 90002 2 90010 -1/2 90011 = 1/2 90010 1/2 90011 = 1/90009 √ 90012 2 = 0.7071 90003 90018 Fractions with negative exponents 90019 90002 The base a / b raised to the power of minus n is equal to 1 divided by the base a / b raised to the power of n: 90003 90002 (90033 a 90034/90033 b 90034) 90010 — 90033 n 90034 90011 = 1 / (90033 a 90034/90033 b 90034) 90010 90033 n 90034 90011 = 1 / (90033 a 90034 90010 n 90011/90033 b 90034 90010 n 90011) = 90033 b 90034 90010 n 90011/90033 a 90034 90010 n 90011 90003 90002 The base 2 raised to the power of minus 3 is equal to 1 divided by the base 2 raised to the power of 3: 90003 90002 (2/3) 90010 -2 90011 = 1 / (2/3) 90010 2 90011 = 1 / (2 90010 2 90011/3 90010 2 90011) = 3 90010 2 90011/2 90010 2 90011 = 9/4 = 2.25 90003 90018 Multiplying negative exponents 90019 90002 For exponents with the same base, we can add the exponents: 90003 90002 90009 a 90010 -n 90011 90012 ⋅ 90009 a 90010 -m 90011 90012 = 90009 a 90010 — (n + m 90011 90012 90010) 90011 = 1 / 90009 a 90010 n + m 90011 90012 90003 90002 Example: 90003 90002 2 90010 -3 90011 ⋅ 2 90010 -4 90011 = 2 90010 — (3 + 4) 90011 = 2 90010 -7 90011 = 1/2 90010 7 90011 = 1 / (2⋅2⋅2⋅2⋅2⋅2⋅2) = 1/128 = 0.0078125 90003 90002 90003 90002 When the bases are diffenrent and the exponents of a and b are the same, we can multiply a and b first: 90003 90002 90009 a 90010 -n 90011 90012 ⋅ 90009 b 90010 -n 90011 90012 = (90009 a 90012 ⋅ 90009 b 90012) 90009 90010 -n 90011 90012 90003 90002 Example: 90003 90002 3 90010 -2 90011 ⋅ 4 90010 -2 90011 = (3⋅4) 90010 -2 90011 = 12 90010 -2 90011 = 1/12 90010 2 90011 = 1 / (12⋅12) = 1/144 = 0.0069444 90003 90002 90003 90002 When the bases and the exponents are different we have to calculate each exponent and then multiply: 90003 90002 90009 a 90010 -n 90011 90012 ⋅ 90009 b 90010 -m 90011 90012 90003 90002 Example: 90003 90002 3 90010 -2 90011 ⋅ 4 90010 -3 90011 = (1/9) ⋅ (1/64) = 1 / 576 = 0.0017361 90003 90002 90003 90018 Dividing negative exponents 90019 90002 For exponents with the same base, we should subtract the exponents: 90003 90002 90009 a 90010 n 90011 90012/90009 a 90010 m 90011 90012 = 90009 a 90010 n-m 90011 90012 90003 90002 Example: 90003 90002 2 90010 6 90011/2 90010 3 90011 = 2 90010 6-3 90011 = 2 90010 3 90011 = 2⋅2⋅2 = 8 90003 90002 90003 90002 When the bases are diffenrent and the exponents of a and b are the same, we can divide a and b first: 90003 90002 90009 a 90010 n 90011 90012/90009 b 90010 n 90011 90012 = (90009 a / B 90012) 90009 90010 n 90011 90012 90003 90002 Example: 90003 90002 6 90010 3 90011/2 90010 3 90011 = (6/2) 90010 3 90011 = 3 90010 3 90011 = 3⋅3⋅3 = 27 90003 90002 90003 90002 When the bases and the exponents are different we have to calculate each exponent and then divide: 90003 90002 90009 a 90010 n 90011 90012/90009 b 90010 m 90011 90012 90003 90002 Example: 90003 90002 6 90010 2 90011/3 90010 3 90011 = 36/27 = 1.333 90003 90002 90003 90302 90018 See also 90019 .90000 Algebra Topics: Negative Numbers 90001 90002 Lesson 3: Negative Numbers 90003 90004 / en / algebra-topics / exponents / content / 90005 90006 What are negative numbers? 90007 90004 A 90009 negative number 90010 is any number that is less than zero. For instance, -7 is a number that is 90009 seven less 90010 than 0. 90005 90004 -7 90005 90004 It might seem a little odd to say that a number is 90009 less 90010 90009 than 90010 0. After all, we often think of zero as meaning 90009 nothing 90010.For instance, if you have 0 pieces of chocolate left in your candy bowl, you have 90009 no 90010 candy. There’s 90009 nothing 90010 left. It’s difficult to imagine having less than nothing in this case. 90005 90004 However, there are instances in real life where you use numbers that are less than zero. For example, have you ever been outside on a really cold winter day when the temperature was below zero? Any temperature below zero is a negative number. For instance, the temperature on this thermometer is 90009 -20 90010, or twenty degrees 90009 below 90010 zero.90005 90034 90005 90004 You can also use negative numbers for more abstract ideas. For instance, in finances negative numbers can be used to show 90009 debt 90010. If I overdraw my account (take out more money than I actually have), my new bank balance will be a 90009 negative number 90010. Not only will I have no money in the bank-I’ll actually have 90009 less 90010 than none because I owe the bank money 90009. 90010 90005 90004 Watch the video below to learn more about negative numbers.90005 90004 90049 90050 90005 90004 Any number without a minus sign in front of it is considered to be a 90009 positive 90010 number, meaning a number that’s 90009 greater than 90010 zero. So while -7 is 90009 negative seven 90010, 7 is 90009 positive seven 90010, or simply 90009 seven 90010. 90005 90002 Understanding negative numbers 90003 90004 As you might have noticed, you write negative numbers with the same symbol you use in subtraction: the minus sign (-). The minus sign does not mean you should think of a number like -4 as 90009 subtract four 90010.After all, how would you subtract this? 90005 90004 -4 90005 90004 You couldn’t-because there’s nothing to subtract it from. We can write -4 on its own precisely because it 90009 does not 90010 mean 90009 subtract 90010 90009 4 90010. It means the 90009 opposite 90010 of four. 90005 90004 Take a look at 4 and -4 on the number line: 90005 90034 90005 90004 You can think of a number line as having three parts: a 90009 positive 90010 direction, a 90009 negative 90010 direction, and 90009 zero 90010.Everything to the right of zero is 90009 positive 90010 and everything to the left of zero is 90009 negative 90010. We think of positive and negative numbers as being 90009 opposites 90010 because they are on 90009 opposite 90010 sides of the number line. 90005 90004 Another important thing to know about negative numbers is that they get 90009 smaller 90010 the farther they get from 0. On this number line, the farther 90009 left 90010 a number is, the smaller it is. So 90009 1 90010 is smaller than 90009 3 90010.90009 -2 90010 is smaller than 90009 1 90010, and 90009 -7 90010 is smaller than 90009 -2 90010. 90005 90034 90005 90002 Understanding absolute value 90003 90004 When we talk about the 90009 absolute value 90010 of a number, we are talking about that number’s distance from 0 on the number line. Remember how we said 4 and -4 were the same distance from 0? That means 4 and -4 have the same absolute value. We represent taking the absolute value of a number with two straight vertical lines 90009 | | 90010.For example, | -3 | = 3. This is read «the absolute value of negative three is three.» 90005 90034 90005 90004 Something important to remember: even though negative numbers get 90009 smaller 90010 as they get further from 0, their absolute value gets 90009 bigger 90010. For example, -10 is smaller than -6. However, | -10 | is bigger than | -6 | because -10 has a greater distance from 0 than -6. 90005 90006 Calculating with negative numbers 90007 90004 Using negative numbers in arithmetic is fairly simple.There are just a few special rules to keep in mind. 90005 90006 Adding and subtracting negative numbers 90007 90004 When you’re adding and subtracting negative numbers, it helps to think about a number line, at least at first. Let’s take a look at this problem: 90009 6 — 7 90010. Even though 7 is larger than 6, you can subtract it in the exact same way as any other number, as long as you understand there are numbers 90009 smaller 90010 than 0. 90005 90034 90005 90004 6 — 7 = -1 90005 90004 While the number line makes it easy to picture this problem, there’s also a trick you could have used to solve it.90005 90004 First, ignore the negative signs for a moment. Just find the 90009 difference 90010 between the two numbers. In this case, it means solving for 90009 7 — 6 90010, which is 1. Next, look at your original problem. Which number has the 90009 highest absolute value 90010? In this case, it’s -7. Because -7 is a negative number, our answer will be one too: -1. Because the absolute value of 90009 -7 90010 is greater than the distance between 90009 6 90010 and 90009 0 90010, our answer ends up being 90009 less than 0 90010.90005 90002 Adding negative numbers 90003 90004 How would you solve this problem? 90005 90004 6 + -7 90005 90004 Believe it or not, this is the exact same problem we just solved! 90005 .90000 c # — Calculate power of a negative number 90001 Stack Overflow 90002 90003 Products 90004 90003 Customers 90004 90003 Use cases 90004 90009 90010 90003 Stack Overflow Public questions and answers 90004 90003 Teams Private questions and answers for your team 90004 90003 Enterprise Private self-hosted questions and answers for your enterprise 90004 90003 Jobs Programming and related technical career opportunities 90004 90003 Talent Hire technical talent 90004 90003 Advertising Reach developers worldwide 90004 90009 .