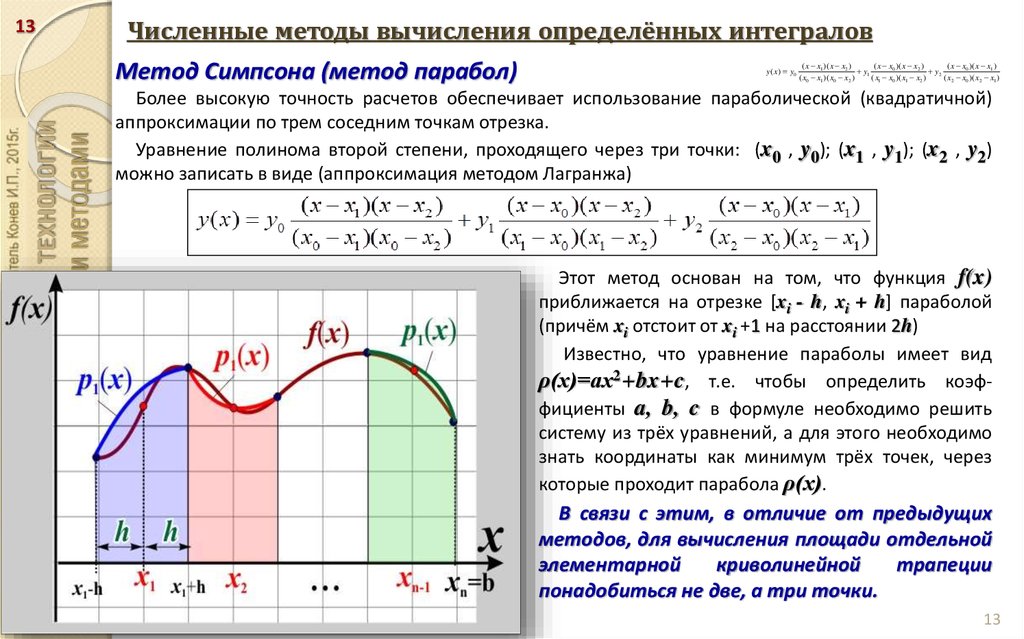
Метод трапеций
Сегодня мы познакомимся с еще одним методом численного интегрирования, методом трапеций. С его помощью мы будем вычислять определенные интегралы с заданной степенью точности. В статье мы опишем суть метода трапеций, разберем, как выводится формула, сравним метод трапеции с методом прямоугольника, запишем оценку абсолютной погрешности метода. Каждый из разделов мы проиллюстрируем примерами для более глубокого понимания материала.
Метод трапеций
Предположим, что нам нужно приближенно вычислить определенный интеграл ∫abf(x)dx, подынтегральная функция которого y=f(x) непрерывна на отрезке [a;b]. Для этого разделим отрезок [a;b] на несколько равных интервалов длины h точками a=x0<x1<x2<…<xn-1<xn=b. Обозначим количество полученных интервалов как n.
Найдем шаг разбиения: h=b-an. Определим узлы из равенства xi=a+i·h, i=0, 1,…, n.
На элементарных отрезках рассмотрим подынтегральную функцию xi-1; xi, i=1, 2,.., n.
При бесконечном увеличении n сведем все случаи к четырем простейшим вариантам:
Выделим отрезки xi-1; xi, i=1, 2,. .., n. Заменим на каждом из графиков функцию y=f(x) отрезком прямой, который проходит через точки с координатами xi-1; fxi-1 и xi; fxi. Отметим их на рисунках синим цветом.
.., n. Заменим на каждом из графиков функцию y=f(x) отрезком прямой, который проходит через точки с координатами xi-1; fxi-1 и xi; fxi. Отметим их на рисунках синим цветом.
Возьмем выражение f(xi-1)+f(xi)2·h в качестве приближенного значения интеграла ∫xi-1xif(x)dx. Т.е. примем ∫xi-1xif(x)dx≈f(xi-1)+f(xi)2·h.
Давайте посмотрим, почему метод численного интегрирования, который мы изучаем, носит название метода трапеций. Для этого нам нужно выяснить, что с точки зрения геометрии означает записанное приближенное равенство.
Для того, чтобы вычислить площадь трапеции, необходимо умножить полусуммы ее оснований на высоту. В первом случае площадь криволинейной трапеции примерно равна трапеции с основаниями f(xi-1), f(xi) высотой h. В четвертом из рассматриваемых нами случаев заданный интеграл ∫xi-1xf(x)dx приближенно равен площади трапеции с основаниями -f(xi-1), -f(xi) и высотой h, которую необходимо взять со знаком «-». Для того, чтобы вычислить приближенное значение определенного интеграла ∫xi-1xif(x)dx во втором и третьем из рассмотренных случаев, нам необходимо найти разность площадей красной и синей областей, которые мы отметили штриховкой на расположенном ниже рисунке.
Подведем итоги. Суть метода трапеций заключается в следующем: мы можем представить определенный интеграл ∫abf(x)dx в виде суммы интегралов вида ∫xi-1xif(x)dx на каждом элементарном отрезке и в последующей приближенной замене ∫xi-1xif(x)dx≈f(xi-1)+f(xi)2·h.
Формула метода трапеций
Вспомним пятое свойство определенного интеграла: ∫abf(x)dx=∑i=1n∫xi-1xif(x)dx. Для того, чтобы получить формулу метода трапеций, необходимо вместо интегралов ∫xi-1xif(x)dx подставить их приближенные значения: ∫xi-1xif(x)dx=∑i=1n∫xi-1xif(x)dx≈∑i=1nf(xi-1)+f(xi)2·h==h3·(f(x0)+f(x1)+f(x1)+f(x2)+f(x2)+f(x3)+…+f(xn))==h3·f(x0)+2∑i=1n-1f(xi)+f(xn)⇒∫xi-1xif(x)dx≈h3·f(x0)+2∑i=1n-1f(xi)+f(xn)
Определение 1Формула метода трапеций: ∫xi-1xif(x)dx≈h3·f(x0)+2∑i=1n-1f(xi)+f(xn)
Оценка абсолютной погрешности метода трапеций
Оценим абсолютную погрешность метода трапеций следующим образом:
Определение 2δn≤maxx∈[a;b]f»(x)·n·h412=maxx∈[a;b]f»(x)·b-a312n2
Графическая иллюстрация метода трапеций
Графическая иллюстрация метода трапеций приведена на рисунке:
Примеры вычислений
Разберем примеры использования метода трапеций для приближенного вычисления определенных интегралов.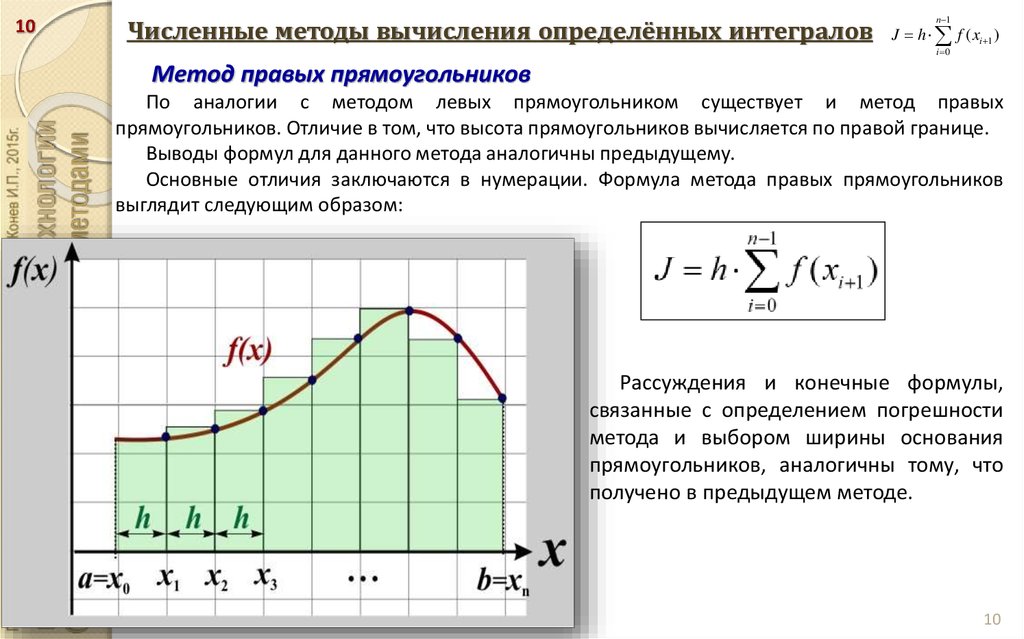 Особое внимание уделим двум разновидностям заданий:
Особое внимание уделим двум разновидностям заданий:
- вычисление определенного интеграла методом трапеций для данного числа разбиения отрезка n;
- нахождение приближенного значения определенного интеграла с оговоренной точностью.
При заданном n все промежуточные вычисления необходимо проводить с достаточно высокой степенью точности. Точность вычислений должна быть те выше, чем больше n.
Если мы имеем заданную точность вычисления определенного интеграла, то все промежуточные вычисления необходимо проводить на два и более порядков точнее. Например, если задана точность до 0,01, то промежуточные вычисления мы проводим с точностью до 0,0001 или 0,00001. При больших n промежуточные вычисления необходимо проводить с еще более высокой точностью.
Рассмотрим приведенное выше правило на примере. Для этого сравним значения определенного интеграла, вычисленного по формуле Ньютона-Лейбница и полученного по методу трапеций.
Итак, ∫057dxx2+1=7arctg(x)05=7arctg 5≈9,613805.
Вычислим по методу трапеций определенный интеграл ∫057×2+1dx для n равным 10.
Решение
Формула метода трапеций имеет вид ∫xi-1xif(x)dx≈h3·f(x0)+2∑i=1n-1f(xi)+f(xn)
Для того, чтобы применить формулу, нам необходимо вычислить шаг h по формуле h=b-an , определить узлы xi=a+i·h, i=0, 1,…, n, вычислить значения подынтегральной функции f(x)=7×2+1.
Шаг разбиения вычисляется следующим образом: h=b-an=5-010=0.5. Для вычисления подынтегральной функции в узлах xi=a+i·h, i=0, 1,…, n будем брать четыре знака после запятой:
i=0: x0=0+0·0.5=0⇒f(x0)=f(0)=702+1=7i=1: x1=0+1·0.5=0.5⇒f(x1)=f(0.5)=70,52+1=5,6…i=10: x10=0+10·0.5=5⇒f(x10)=f(5)=752+1≈0,2692
Внесем результаты вычислений в таблицу:
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| xi | 0 | 0.5 | 1 | 2 | 2,5 | 3 | 3,5 | 4 | 4,5 | 5 | |
| f(xi) | 7 | 5,6 | 3,5 | 2,1538 | 1,4 | 0,9655 | 0,7 | 0,5283 | 0,4117 | 0,3294 | 0,2692 |
Подставим полученные значения в формулу метода трапеций: ∫057dxx2+1≈h3·f(x0)+2∑i=1n-1f(xi)+f(xn)==0,52·7+2·5,6+3,5+2,1538+1,4+0,9655+0,7+0,5283+0,4117+0,3294+0,2692=9,6117
Сравним наши результаты с результатами, вычисленными по формуле Ньютона-Лейбница. Полученные значения совпадают до сотых.
Полученные значения совпадают до сотых.
Ответ: ∫057dxx2+1=9,6117
Пример 2Вычислим по методу трапеций значение определенного интеграла ∫12112×4+13x-160dx с точностью до 0,01.
Решение
Согласно условию задачи a = 1; b = 2, f(x)=112×4+13x-160; δn≤0,01.
Найдем n, которое равно количеству точек разбиения отрезка интегрирования, с помощью неравенства для оценки абсолютной погрешности δn≤maxx∈[a;b]f»(x)·(b-a)312n2. Сделаем мы это следующим образом: мы найдем значения n, для которых будет выполняться неравенство maxx∈[a;b]f»(x)·(b-a)312n2≤0,01. При данных n формула трапеций даст нам приближенное значение определенного интеграла с заданной точностью.
Для начала найдем наибольшее значение модуля второй производной функции на отрезке [1; 2].
f'(x)=112×4+13x-160’=13×3+13⇒f»(x)=13×3+13’=x2
Вторая производная функция является квадратичной параболой f»(x)=x2. Из ее свойств мы знаем, что она положительная и возрастает на отрезке [1; 2]. В связи с этим maxx∈[a;b]f»(x)=f»(2)=22=4.
В связи с этим maxx∈[a;b]f»(x)=f»(2)=22=4.
В приведенном примере процесс нахождения maxx∈[a;b]f»(x) оказался достаточно простым. В сложных случаях для проведения вычислений можно обратиться к наибольшим и наименьшим значениям функции. После рассмотрения данного примера мы приведем альтернативный метод нахождения maxx∈[a;b]f»(x).
Подставим полученное значение в неравенство maxx∈[a;b]f»(x)·(b-a)312n2≤0,01
4·(2-1)312n2≤0,01⇒n2≥1003⇒n≥5,7735
Количество элементарных интервалов, на которые разбивается отрезок интегрирования n является натуральным числом. Для поведения вычислений возьмем n равное шести. Такое значение n позволит нам достичь заданной точности метода трапеций при минимуме расчетов.
Вычислим шаг: h=b-an=2-16=16.
Найдем узлы xi=a+i·h, i=1, 0,…, n, определим значения подынтегральной функции в этих узлах:
i=0: x0=1+0·16=1⇒f(x0)=f(1)=112·14+13·1-160=0,4i=1: x1=1+1·16=76⇒f(x1)=f76=112·764+13·76-160≈0,5266…i=6: x10=1+6·16=2⇒f(x6)=f(2)=112·24+13·2-160≈1,9833
Результаты вычислений запишем в виде таблицы:
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| xi | 1 | 76 | 43 | 32 | 53 | 116 | 2 |
| fxi | 0,4 | 0,5266 | 0,6911 | 0,9052 | 1,1819 | 1,5359 | 1,9833 |
Подставим полученные результаты в формулу трапеций:
∫12112×4+13x-160dx≈h3·f(x0)+2∑i=1n-1f(xi)+f(xn)==112·0,4+2·0,5266+0,6911+0,9052+1,1819+1,5359+1,9833≈1,0054
Для проведения сравнения вычислим исходный интеграл по формуле Ньютона-Лейбница:
∫12112×4+13x-160dx=x560+x26-x6012=1
Как видим, полученной точности вычислений мы достигли.
Ответ: ∫12112×4+13x-160dx≈1,0054
Для подынтегральных функций сложного вида нахождение числа n из неравенства для оценки абсолютной погрешности не всегда просто. В этом случае будет уместен следующий метод.
Обозначим приближенное значение определенного интеграла, которое было получено по методу трапеций для n узлов, как In. Выберем произвольное число n. По формуле метода трапеций вычислим исходный интеграл при одинарном (n=10) и удвоенном (n=20) числе узлов и найдем абсолютную величину разности двух полученных приближенных значений I20-I10.
Если абсолютная величина разности двух полученных приближенных значений меньше требуемой точности I20-I10<δn, то мы прекращаем вычисления и выбираем значение I20 , которое можно округлить до требуемого порядка точности.
Если абсолютная величина разности двух полученных приближенных значений больше требуемой точности, то необходимо повторить действия с удвоенным количеством узлов (n=40).
Такой метод требует проведения большого объема вычислений, поэтому разумно использовать вычислительную технику для экономии времени.
Решим с помощью приведенного выше алгоритма задачу. С целью экономии времени опустим промежуточные вычисления по методу трапеций.
Пример 3Необходимо вычислить определенный интеграл ∫02xexdx по методу трапеций с точностью до 0,001.
Решение
Возьмем n равное 10 и 20. По формуле трапеций получим I10=8,4595380, I20=8,4066906.
I20-I10=8,4066906-8,4595380=0,0528474>0,001, что требует продолжения вычислений.
Возьмем n равное 40: I40=8,3934656.
I40-I20=8,3934656-8,4066906=0,013225>0,001, что также требует продолжения вычислений.
Возьмем n равное 80: I80=8,3901585.
I80-I40=8,3901585-8,3934656=0,0033071>0,001, что требует проведения еще одного удвоения числа узлов.
Возьмем n равное 160: I160=8,3893317.
I160-I80=8,3893317-8,3901585=0,0008268<0,001
Получить приближенное значение исходного интеграла можно округлив I160=8,3893317 до тысячных: ∫02xexdx≈8,389.
Для сравнения вычислим исходный определенный интеграл по формуле Ньютона-Лейбница: ∫02xexdx=ex·(x-1)02=e2+1≈8,3890561.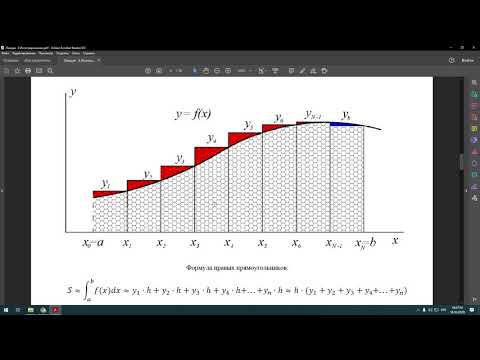
Ответ: ∫02xexdx≈8,389
Погрешности
Промежуточные вычисления для определения значения определенного интеграла проводят в большинстве своем приближенно. Это значит, что при увеличении n начинает накапливаться вычислительная погрешность.
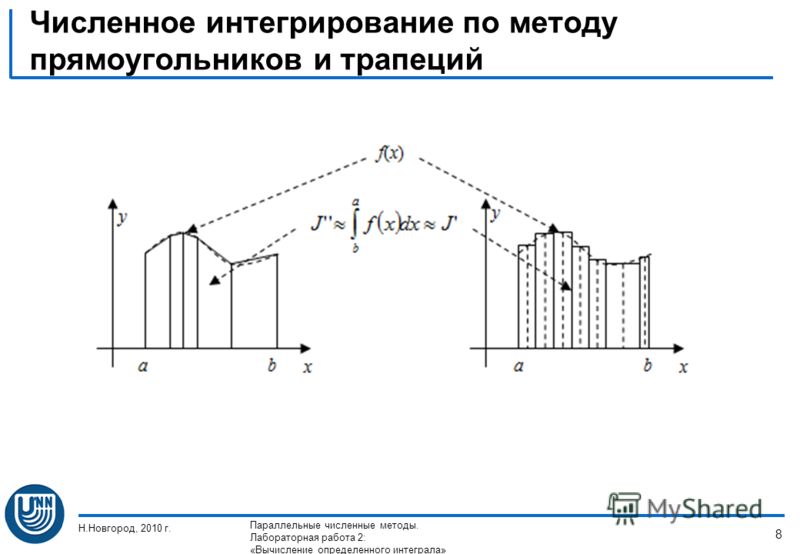
Сравним оценки абсолютных погрешностей метода трапеций и метода средних прямоугольников:
δn≤maxx∈[a;b]f»(x)n·h412=maxx∈[a;b]f»(x)·b-a312n2δn≤maxx∈[a;b]f»(x)n·h424=maxx∈[a;b]f»(x)·b-a324n2.
Метод прямоугольников для заданного n при одинаковом объеме вычислительной работы дает вдвое меньшую погрешность. Это делает метод более предпочтительным в тех случаях, когда известны значения функции в средних отрезках элементарных отрезков.
В тех случаях, когда интегрируемые функции задаются не аналитически, а в виде множества значений в узлах, мы можем использовать метод трапеций.
Если сравнивать точность метода трапеций и метода правых и левых прямоугольников, то первый метод превосходит второй в точности результата.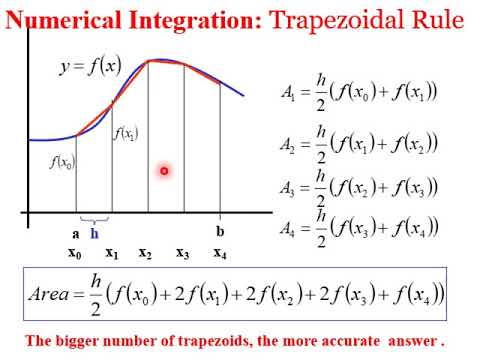
Метод трапеций
Сегодня мы познакомимся с еще одним методом численного интегрирования, методом трапеций. С его помощью мы будем вычислять определенные интегралы с заданной степенью точности. В статье мы опишем суть метода трапеций, разберем, как выводится формула, сравним метод трапеции с методом прямоугольника, запишем оценку абсолютной погрешности метода. Каждый из разделов мы проиллюстрируем примерами для более глубокого понимания материала.
Метод трапеций
Предположим, что нам нужно приближенно вычислить определенный интеграл ∫abf(x)dx, подынтегральная функция которого y=f(x) непрерывна на отрезке [a;b]. Для этого разделим отрезок [a;b] на несколько равных интервалов длины h точками a=x0<x1<x2<…<xn-1<xn=b. Обозначим количество полученных интервалов как n.
Найдем шаг разбиения: h=b-an. Определим узлы из равенства xi=a+i·h, i=0, 1,…, n.
На элементарных отрезках рассмотрим подынтегральную функцию xi-1; xi, i=1, 2,.., n.
При бесконечном увеличении n сведем все случаи к четырем простейшим вариантам:
Выделим отрезки xi-1; xi, i=1, 2,. .., n. Заменим на каждом из графиков функцию y=f(x) отрезком прямой, который проходит через точки с координатами xi-1; fxi-1 и xi; fxi. Отметим их на рисунках синим цветом.
.., n. Заменим на каждом из графиков функцию y=f(x) отрезком прямой, который проходит через точки с координатами xi-1; fxi-1 и xi; fxi. Отметим их на рисунках синим цветом.
Возьмем выражение f(xi-1)+f(xi)2·h в качестве приближенного значения интеграла ∫xi-1xif(x)dx. Т.е. примем ∫xi-1xif(x)dx≈f(xi-1)+f(xi)2·h.
Давайте посмотрим, почему метод численного интегрирования, который мы изучаем, носит название метода трапеций. Для этого нам нужно выяснить, что с точки зрения геометрии означает записанное приближенное равенство.
Для того, чтобы вычислить площадь трапеции, необходимо умножить полусуммы ее оснований на высоту. В первом случае площадь криволинейной трапеции примерно равна трапеции с основаниями f(xi-1), f(xi) высотой h. В четвертом из рассматриваемых нами случаев заданный интеграл ∫xi-1xf(x)dx приближенно равен площади трапеции с основаниями -f(xi-1), -f(xi) и высотой h, которую необходимо взять со знаком «-». Для того, чтобы вычислить приближенное значение определенного интеграла ∫xi-1xif(x)dx во втором и третьем из рассмотренных случаев, нам необходимо найти разность площадей красной и синей областей, которые мы отметили штриховкой на расположенном ниже рисунке.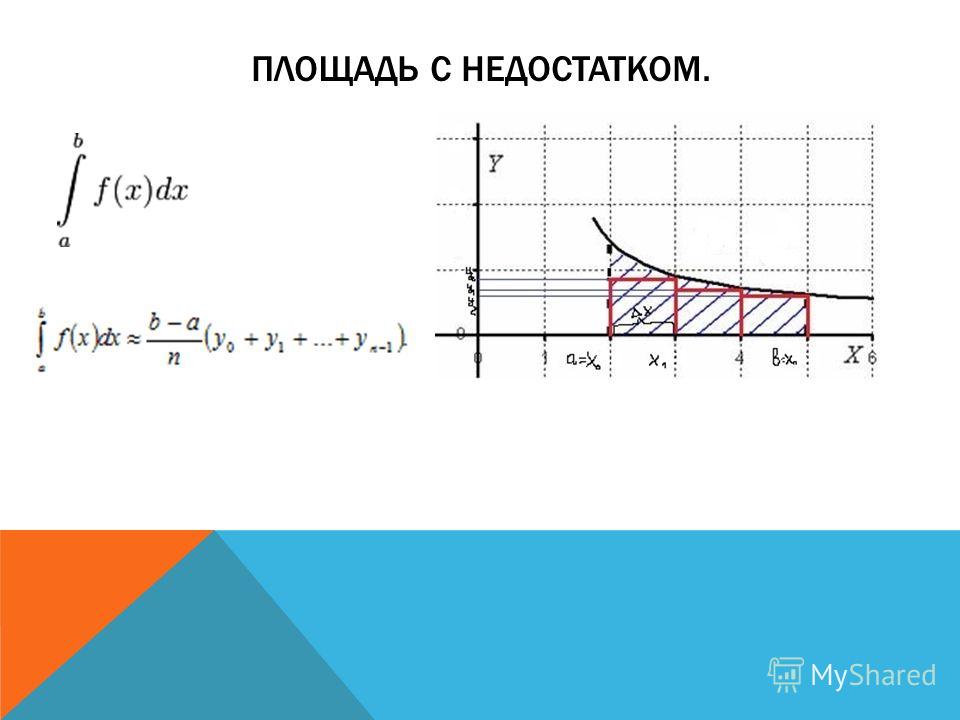
Подведем итоги. Суть метода трапеций заключается в следующем: мы можем представить определенный интеграл ∫abf(x)dx в виде суммы интегралов вида ∫xi-1xif(x)dx на каждом элементарном отрезке и в последующей приближенной замене ∫xi-1xif(x)dx≈f(xi-1)+f(xi)2·h.
Формула метода трапеций
Вспомним пятое свойство определенного интеграла: ∫abf(x)dx=∑i=1n∫xi-1xif(x)dx. Для того, чтобы получить формулу метода трапеций, необходимо вместо интегралов ∫xi-1xif(x)dx подставить их приближенные значения: ∫xi-1xif(x)dx=∑i=1n∫xi-1xif(x)dx≈∑i=1nf(xi-1)+f(xi)2·h==h3·(f(x0)+f(x1)+f(x1)+f(x2)+f(x2)+f(x3)+…+f(xn))==h3·f(x0)+2∑i=1n-1f(xi)+f(xn)⇒∫xi-1xif(x)dx≈h3·f(x0)+2∑i=1n-1f(xi)+f(xn)
Определение 1Формула метода трапеций: ∫xi-1xif(x)dx≈h3·f(x0)+2∑i=1n-1f(xi)+f(xn)
Оценка абсолютной погрешности метода трапеций
Оценим абсолютную погрешность метода трапеций следующим образом:
Определение 2δn≤maxx∈[a;b]f»(x)·n·h412=maxx∈[a;b]f»(x)·b-a312n2
Графическая иллюстрация метода трапеций
Графическая иллюстрация метода трапеций приведена на рисунке:
Примеры вычислений
Разберем примеры использования метода трапеций для приближенного вычисления определенных интегралов.
- вычисление определенного интеграла методом трапеций для данного числа разбиения отрезка n;
- нахождение приближенного значения определенного интеграла с оговоренной точностью.
При заданном n все промежуточные вычисления необходимо проводить с достаточно высокой степенью точности. Точность вычислений должна быть те выше, чем больше n.
Если мы имеем заданную точность вычисления определенного интеграла, то все промежуточные вычисления необходимо проводить на два и более порядков точнее. Например, если задана точность до 0,01, то промежуточные вычисления мы проводим с точностью до 0,0001 или 0,00001. При больших n промежуточные вычисления необходимо проводить с еще более высокой точностью.
Рассмотрим приведенное выше правило на примере. Для этого сравним значения определенного интеграла, вычисленного по формуле Ньютона-Лейбница и полученного по методу трапеций.
Итак, ∫057dxx2+1=7arctg(x)05=7arctg 5≈9,613805.
Вычислим по методу трапеций определенный интеграл ∫057×2+1dx для n равным 10.
Решение
Формула метода трапеций имеет вид ∫xi-1xif(x)dx≈h3·f(x0)+2∑i=1n-1f(xi)+f(xn)
Для того, чтобы применить формулу, нам необходимо вычислить шаг h по формуле h=b-an , определить узлы xi=a+i·h, i=0, 1,…, n, вычислить значения подынтегральной функции f(x)=7×2+1.
Шаг разбиения вычисляется следующим образом: h=b-an=5-010=0.5. Для вычисления подынтегральной функции в узлах xi=a+i·h, i=0, 1,…, n будем брать четыре знака после запятой:
i=0: x0=0+0·0.5=0⇒f(x0)=f(0)=702+1=7i=1: x1=0+1·0.5=0.5⇒f(x1)=f(0.5)=70,52+1=5,6…i=10: x10=0+10·0.5=5⇒f(x10)=f(5)=752+1≈0,2692
Внесем результаты вычислений в таблицу:
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| xi | 0 | 0.5 | 1 | 1,5 | 2 | 2,5 | 3 | 3,5 | 4 | 4,5 | 5 |
| f(xi) | 7 | 5,6 | 3,5 | 2,1538 | 1,4 | 0,9655 | 0,7 | 0,5283 | 0,4117 | 0,3294 | 0,2692 |
Подставим полученные значения в формулу метода трапеций: ∫057dxx2+1≈h3·f(x0)+2∑i=1n-1f(xi)+f(xn)==0,52·7+2·5,6+3,5+2,1538+1,4+0,9655+0,7+0,5283+0,4117+0,3294+0,2692=9,6117
Сравним наши результаты с результатами, вычисленными по формуле Ньютона-Лейбница.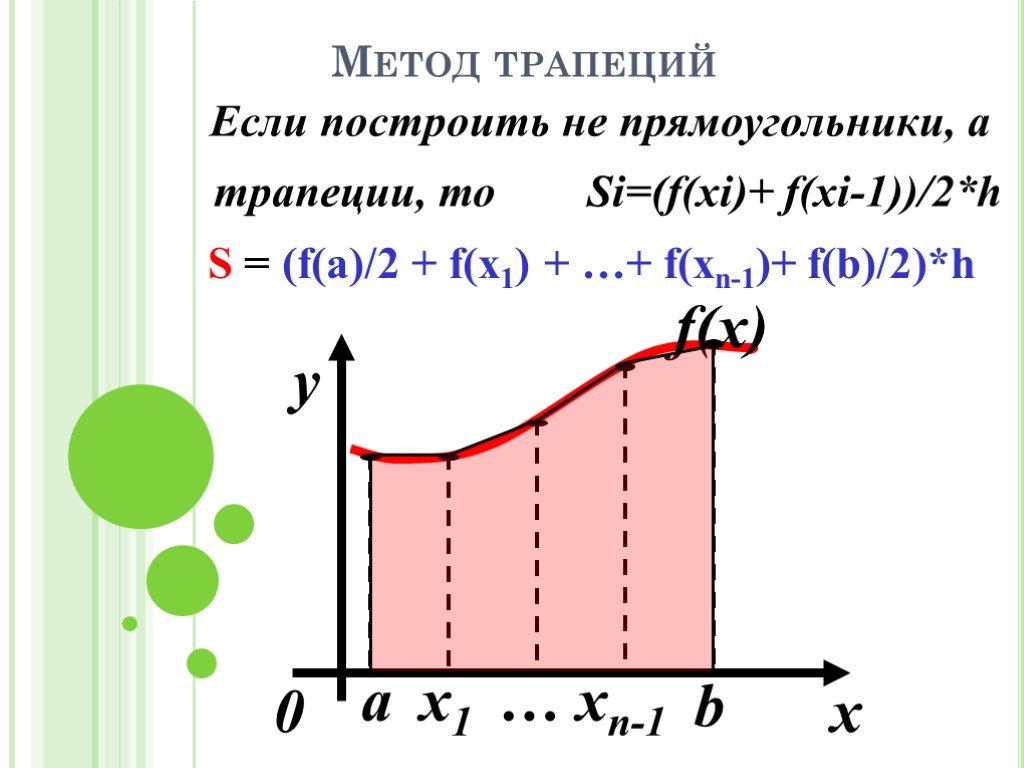 Полученные значения совпадают до сотых.
Полученные значения совпадают до сотых.
Ответ: ∫057dxx2+1=9,6117
Пример 2Вычислим по методу трапеций значение определенного интеграла ∫12112×4+13x-160dx с точностью до 0,01.
Решение
Согласно условию задачи a = 1; b = 2, f(x)=112×4+13x-160; δn≤0,01.
Найдем n, которое равно количеству точек разбиения отрезка интегрирования, с помощью неравенства для оценки абсолютной погрешности δn≤maxx∈[a;b]f»(x)·(b-a)312n2. Сделаем мы это следующим образом: мы найдем значения n, для которых будет выполняться неравенство maxx∈[a;b]f»(x)·(b-a)312n2≤0,01. При данных n формула трапеций даст нам приближенное значение определенного интеграла с заданной точностью.
Для начала найдем наибольшее значение модуля второй производной функции на отрезке [1; 2].
f'(x)=112×4+13x-160’=13×3+13⇒f»(x)=13×3+13’=x2
Вторая производная функция является квадратичной параболой f»(x)=x2. Из ее свойств мы знаем, что она положительная и возрастает на отрезке [1; 2].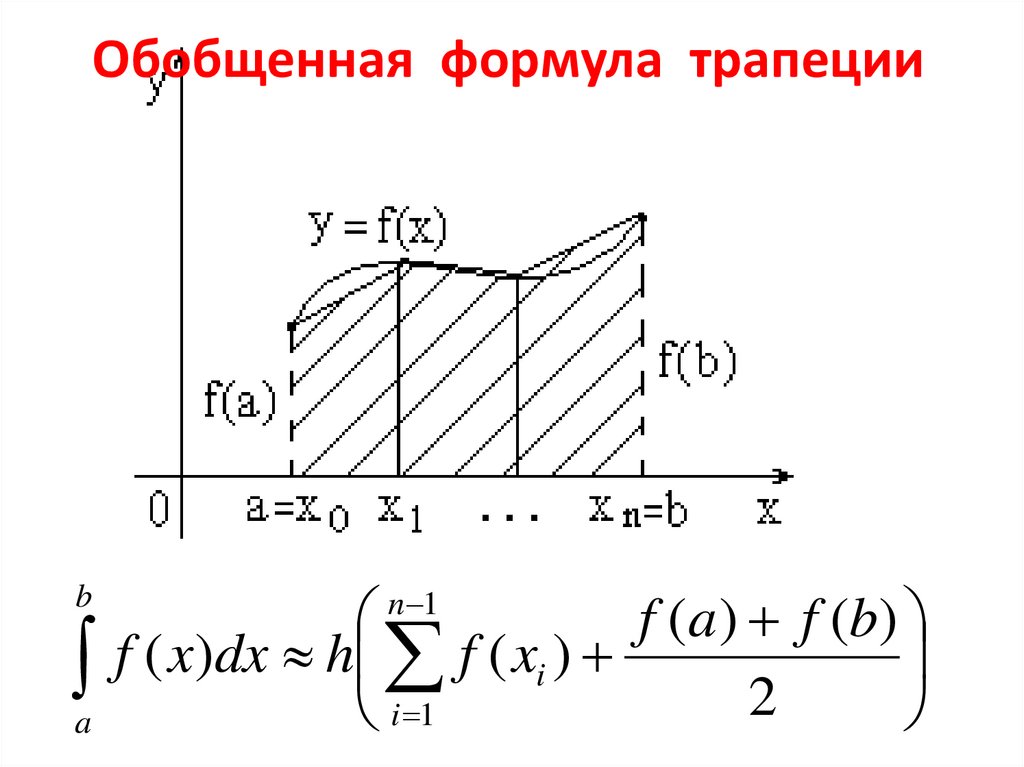 В связи с этим maxx∈[a;b]f»(x)=f»(2)=22=4.
В связи с этим maxx∈[a;b]f»(x)=f»(2)=22=4.
В приведенном примере процесс нахождения maxx∈[a;b]f»(x) оказался достаточно простым. В сложных случаях для проведения вычислений можно обратиться к наибольшим и наименьшим значениям функции. После рассмотрения данного примера мы приведем альтернативный метод нахождения maxx∈[a;b]f»(x).
Подставим полученное значение в неравенство maxx∈[a;b]f»(x)·(b-a)312n2≤0,01
4·(2-1)312n2≤0,01⇒n2≥1003⇒n≥5,7735
Количество элементарных интервалов, на которые разбивается отрезок интегрирования n является натуральным числом. Для поведения вычислений возьмем n равное шести. Такое значение n позволит нам достичь заданной точности метода трапеций при минимуме расчетов.
Вычислим шаг: h=b-an=2-16=16.
Найдем узлы xi=a+i·h, i=1, 0,…, n, определим значения подынтегральной функции в этих узлах:
i=0: x0=1+0·16=1⇒f(x0)=f(1)=112·14+13·1-160=0,4i=1: x1=1+1·16=76⇒f(x1)=f76=112·764+13·76-160≈0,5266…i=6: x10=1+6·16=2⇒f(x6)=f(2)=112·24+13·2-160≈1,9833
Результаты вычислений запишем в виде таблицы:
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| xi | 1 | 76 | 43 | 32 | 53 | 116 | 2 |
| fxi | 0,4 | 0,5266 | 0,6911 | 0,9052 | 1,1819 | 1,5359 | 1,9833 |
Подставим полученные результаты в формулу трапеций:
∫12112×4+13x-160dx≈h3·f(x0)+2∑i=1n-1f(xi)+f(xn)==112·0,4+2·0,5266+0,6911+0,9052+1,1819+1,5359+1,9833≈1,0054
Для проведения сравнения вычислим исходный интеграл по формуле Ньютона-Лейбница:
∫12112×4+13x-160dx=x560+x26-x6012=1
Как видим, полученной точности вычислений мы достигли.
Ответ: ∫12112×4+13x-160dx≈1,0054
Для подынтегральных функций сложного вида нахождение числа n из неравенства для оценки абсолютной погрешности не всегда просто. В этом случае будет уместен следующий метод.
Обозначим приближенное значение определенного интеграла, которое было получено по методу трапеций для n узлов, как In. Выберем произвольное число n. По формуле метода трапеций вычислим исходный интеграл при одинарном (n=10) и удвоенном (n=20) числе узлов и найдем абсолютную величину разности двух полученных приближенных значений I20-I10.
Если абсолютная величина разности двух полученных приближенных значений меньше требуемой точности I20-I10<δn, то мы прекращаем вычисления и выбираем значение I20 , которое можно округлить до требуемого порядка точности.
Если абсолютная величина разности двух полученных приближенных значений больше требуемой точности, то необходимо повторить действия с удвоенным количеством узлов (n=40).
Такой метод требует проведения большого объема вычислений, поэтому разумно использовать вычислительную технику для экономии времени.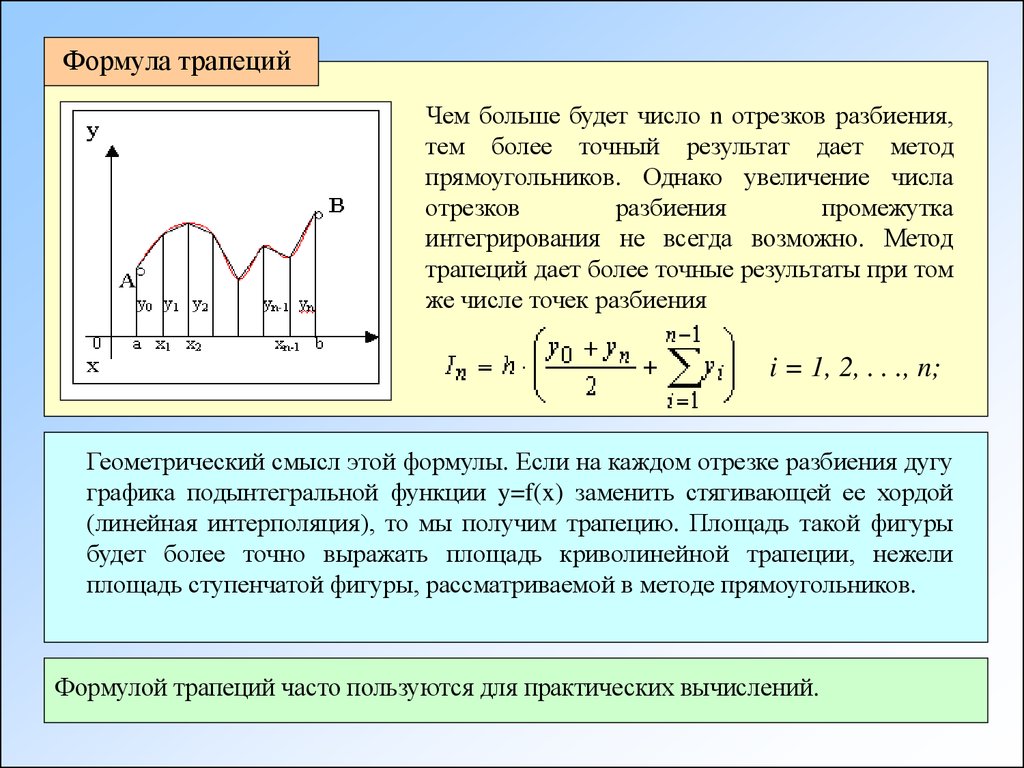
Решим с помощью приведенного выше алгоритма задачу. С целью экономии времени опустим промежуточные вычисления по методу трапеций.
Пример 3Необходимо вычислить определенный интеграл ∫02xexdx по методу трапеций с точностью до 0,001.
Решение
Возьмем n равное 10 и 20. По формуле трапеций получим I10=8,4595380, I20=8,4066906.
I20-I10=8,4066906-8,4595380=0,0528474>0,001, что требует продолжения вычислений.
Возьмем n равное 40: I40=8,3934656.
I40-I20=8,3934656-8,4066906=0,013225>0,001, что также требует продолжения вычислений.
Возьмем n равное 80: I80=8,3901585.
I80-I40=8,3901585-8,3934656=0,0033071>0,001, что требует проведения еще одного удвоения числа узлов.
Возьмем n равное 160: I160=8,3893317.
I160-I80=8,3893317-8,3901585=0,0008268<0,001
Получить приближенное значение исходного интеграла можно округлив I160=8,3893317 до тысячных: ∫02xexdx≈8,389.
Для сравнения вычислим исходный определенный интеграл по формуле Ньютона-Лейбница: ∫02xexdx=ex·(x-1)02=e2+1≈8,3890561. Требуемая точность достигнута.
Требуемая точность достигнута.
Ответ: ∫02xexdx≈8,389
Погрешности
Промежуточные вычисления для определения значения определенного интеграла проводят в большинстве своем приближенно. Это значит, что при увеличении n начинает накапливаться вычислительная погрешность.
Сравним оценки абсолютных погрешностей метода трапеций и метода средних прямоугольников:
δn≤maxx∈[a;b]f»(x)n·h412=maxx∈[a;b]f»(x)·b-a312n2δn≤maxx∈[a;b]f»(x)n·h424=maxx∈[a;b]f»(x)·b-a324n2.
Метод прямоугольников для заданного n при одинаковом объеме вычислительной работы дает вдвое меньшую погрешность. Это делает метод более предпочтительным в тех случаях, когда известны значения функции в средних отрезках элементарных отрезков.
В тех случаях, когда интегрируемые функции задаются не аналитически, а в виде множества значений в узлах, мы можем использовать метод трапеций.
Если сравнивать точность метода трапеций и метода правых и левых прямоугольников, то первый метод превосходит второй в точности результата.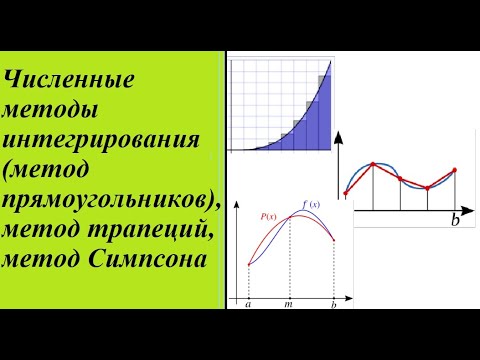
Правило трапеций: метод численного интегрирования | Кази Абу Русан
Познание, к которому стремится геометрия, есть познание вечного. — Платон
В физике большую часть времени нам приходится применять интегрирование . Но есть некоторые интеграции, которые не могут быть решены обычными методами. Для них у нас есть специальные приемы, такие как интегральный прием Фейнмана, преобразование Фурье, преобразование Лапласа, теорема об остатках и так далее.
Но бывают случаи, когда даже они не могут помочь . Даже если мы оставим эти интеграции, в современном мире, когда мы занимаемся интеграциями с помощью наших компьютеров, мы видим, что машины не могут решать интеграции аналитически. Чтобы преодолеть обе эти проблемы, мы используем некоторые методы, называемые числовым интегрированием. Сердцем этого метода является наша геометрия . Как гласили такие легенды, как Платон , Архимед , Гаусс и другие, Вселенная разговаривает с нами на языке геометрии, в данном случае не исключение.
Используя простую трапецию , мы можем решать интегрирования (лучше всего то, что мы даже можем позволить компьютерам использовать этот метод, и с некоторыми ограничениями, мы также можем некоторые из обычно нерешаемых интегрирований) численно с желаемым уровнем точность.
Мы знаем, что если построить заданную функцию , то ее интегрирование будет равно площади, замкнутой кривой функции с осью независимой переменной.
Рис. 1. Наша функция f(x), построенная в координатной плоскости с горизонтальной осью по оси xПредположим, у нас есть функция f(x) и x — независимая переменная . Давайте построим нашу функцию. После построения f(x) и x, если мы возьмем две точки, такие как x = a и x = b . Тогда каково значение интегрирования между в пределе a и b ?
Рис.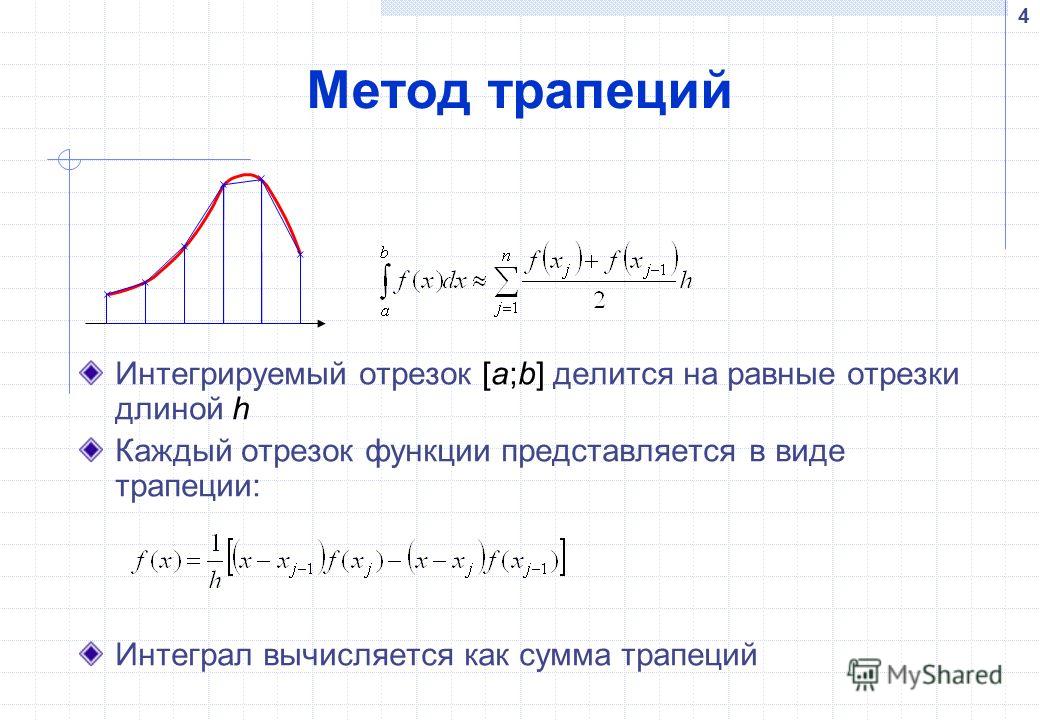 2: Первый указатель находится в точке x= a, а второй — в точке x=b. Указатель принимает все значения x по мере продвижения.
2: Первый указатель находится в точке x= a, а второй — в точке x=b. Указатель принимает все значения x по мере продвижения.Как видите, я взял две случайные точки на оси x (x = a и x = b), соответствующие этим значениям x, мы получим два значения y, которые равны y = f(a) и y = f(b) . Мы получим значения y для всех значений x между линейной областью. Теперь мы можем нарисовать прямоугольников , используя последовательных точек по оси x и точек на графике (как мы делаем для , определяем сами интеграции ).
Обычно мы используем прямоугольных блоков для аппроксимации площади под кривой (сделав ширину каждого прямоугольника = dx как можно меньше, чтобы получить максимально точный результат), что работает нормально. Но в этом случае мы должны использовать много термов (прямоугольников), что не так эффективно.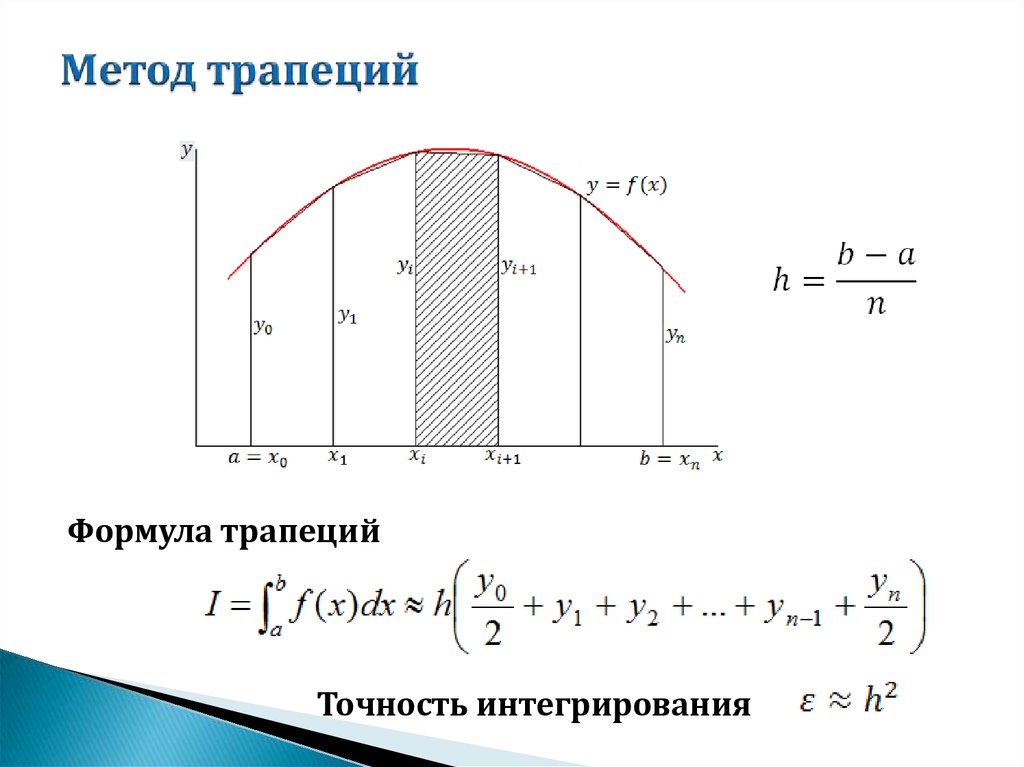 .
.
Как видите, я использовал одинаковое количество прямоугольников и трапеций в обоих случаях с одинаковой шириной. Теперь ясно, что трапеции аппроксимируют площадь лучше, чем прямоугольники, что является основной идеей использования Трапеции вместо Прямоугольников.
Предположим, у нас есть функция f(x) , и нас интересует интегрирование в линейном диапазоне x = a и x = b. Тогда значение интегрирования равно:
См. рис. 2Мы разделили ось x равномерно на малые длины, каждая из которых имеет ширину h = (b-a)/n . Здесь n (номер трапеции) — это огромное число. большее n даст нам лучший результат .
Поскольку длина делится поровну на n равных частей, следовательно, мы можем записать любую точку на оси x как
Помните, что мы создали n равных отрезков, что означает, что у нас есть n + 1 точка.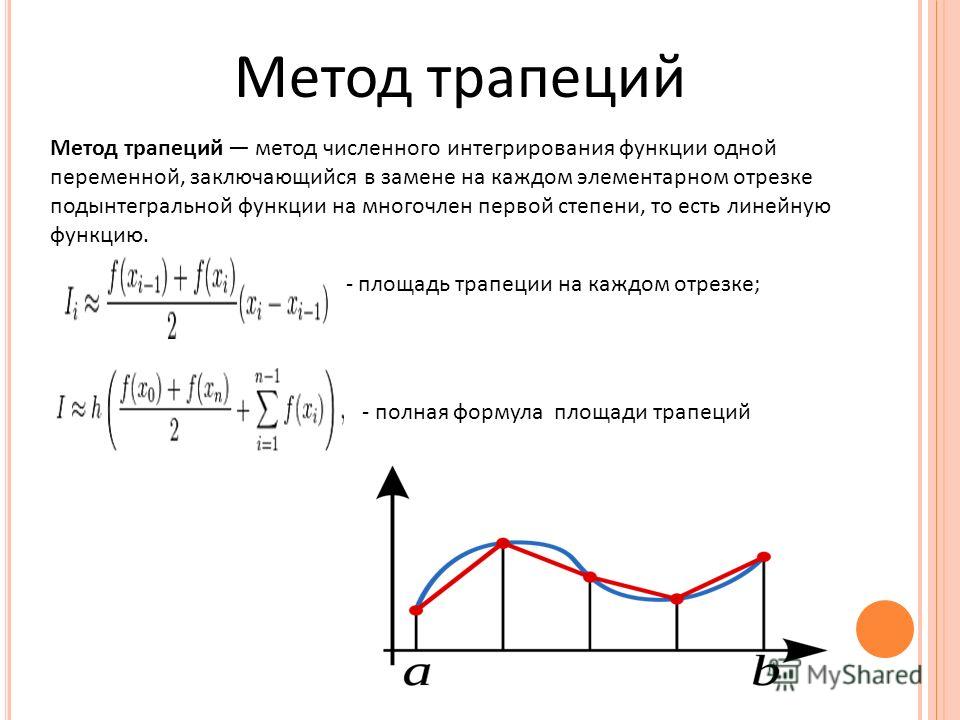 В качестве примера посмотрите на свои руки. У вас 5 пальцев(Если 6 то ошибка🤣), но пробелов всего 4.
В качестве примера посмотрите на свои руки. У вас 5 пальцев(Если 6 то ошибка🤣), но пробелов всего 4.В соответствии с каждым из этих значений x. Если мы нарисуем линий, параллельных оси y , то точек, в которых они пересекают кривую, являются соответствующими значениями функции и, следовательно, длина каждой пунктирной линии .
Следовательно, каждая фиолетовая точка на красном графике представляет (x_r,f(x_r)) , и здесь используется x_0 = a . Рис. 4: Здесь h = 2 единицы. Как видите, когда мы двигаемся по стрелкам от 1-го x ко 2-му x, мы добавляем букву h. Вы можете спросить, почему x_r имеет такое значение? Вы можете видеть на рисунке-4, как мы движемся от x_0=a к конец из первая трапеция , мы добавляем ее ширину к нашему x значение .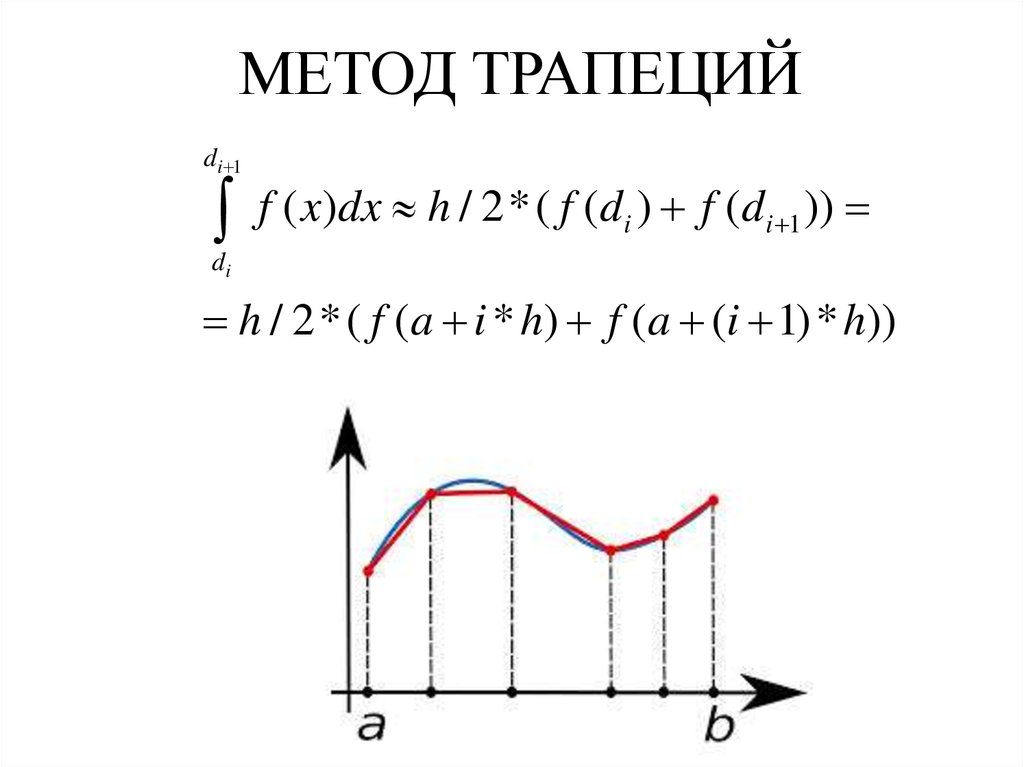 Следовательно, каждый раз, когда мы пересекаем трапецию, мы должны добавить h к
Следовательно, каждый раз, когда мы пересекаем трапецию, мы должны добавить h к 8 9. Таким образом, чтобы достичь точки
r-th на оси x ( r-th x value ), мы должны добавить h , r-times к нашему x_0 .
Как видите, каждая фигура представляет собой трапецию. Следовательно, нам просто нужно найти площадь каждой трапеции и , сложив их, мы получим общую площадь под кривой .
Рис-5: r-ая трапеция аппроксимации площади, параллельные стороны длины f(x_r) и f(x_(r+1)) Теперь вы видите, что мы берем две точки x_r и х_(г+1) . Для этих двух точек у нас есть две линии, параллельные двум осям y, длины которых равны f(x_r) и f(x_(r+1)) .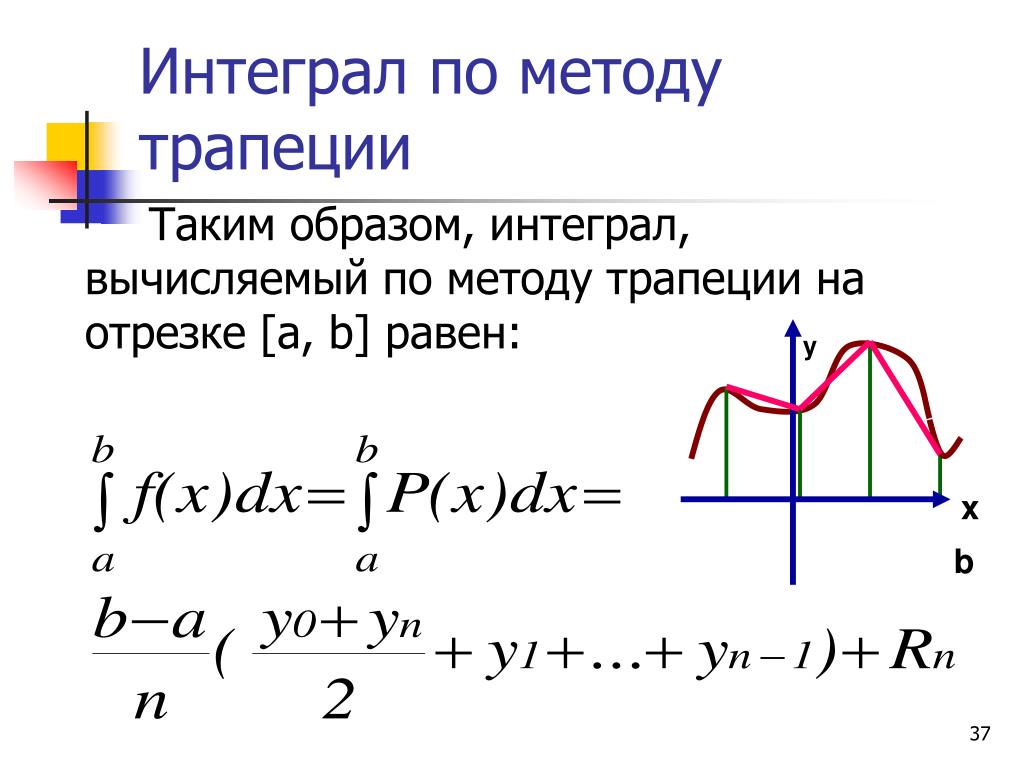 Вы можете ясно видеть, что это действительно трапеция с высотой h(x_(r+1)-x_r) и длина двух параллельных сторон равна длине линий, которые параллельны оси y . Используя обычную геометрическую формулу площади трапеции, мы получаем,
Вы можете ясно видеть, что это действительно трапеция с высотой h(x_(r+1)-x_r) и длина двух параллельных сторон равна длине линий, которые параллельны оси y . Используя обычную геометрическую формулу площади трапеции, мы получаем,
Итак, для одиночной трапеции площадь такая, как показано на рисунке. Теперь для 9Всего 0007 равно , а мы просто суммируем все. Индекс (r) будет варьироваться от r = 0 до r = (n-1) , где n — номер 9. трапеции или №. деления между x= a и x = b . Отсюда общая площадь региона или значение интегрирования равно (с небольшой погрешностью):
Используя обозначение суммирования, получаем:
В 1-й строке мы суммировали до n-1 , так как при r = n-1 f(a+(r+1)h)=f(b), что и должно быть.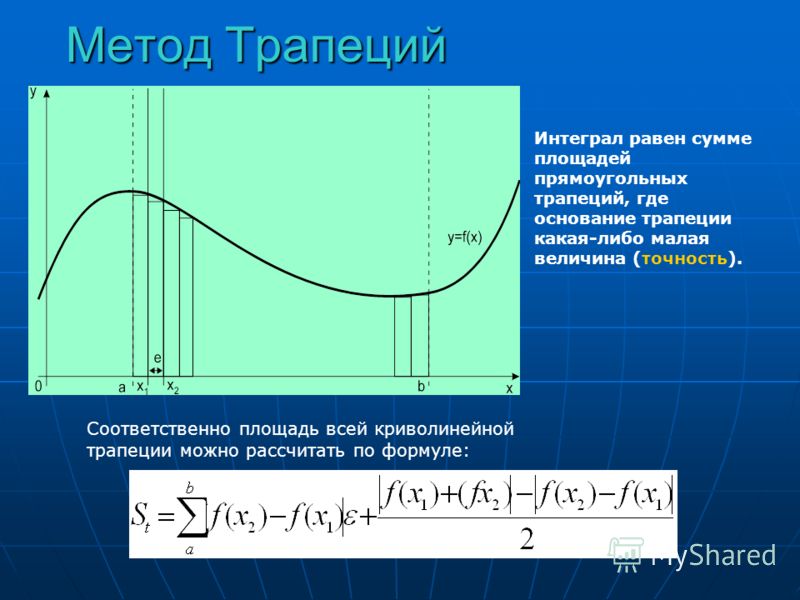 Для 2-й строки, поскольку средние члены (f(a+h),f(a+2h) и т. д. существуют в двух последовательных трапециях) встречаются дважды, мы умножаем их на 2 и добавляем каждый член один раз.
Для 2-й строки, поскольку средние члены (f(a+h),f(a+2h) и т. д. существуют в двух последовательных трапециях) встречаются дважды, мы умножаем их на 2 и добавляем каждый член один раз.Верхняя формула работает нормально, но для лучшего приближения мы должны сделать n больше, что делает h намного меньше, давая нам результат, настолько совершенный, насколько мы желаем .
Рис. 6: Уменьшение значения h и соответствующие ему трапецииКак видно на видео выше, по мере того как мы уменьшаем значение h , т. е. увеличиваем значение n , аппроксимация площади ( значение интегрирования) 9000 идет к этому истинное значение (т.е. уменьшает значение ошибка ). Теперь давайте посмотрим, как можно использовать компьютер для численного решения любого интегрирования (мы будем использовать Python):
Алгоритм
- Определите f(x) функцию, которую мы хотим интегрировать.

- Получить значения a , b , допуск (значение ошибки, т.е. |действительное значение — вычисленное значение|).
- Присвоить значения fa = f(a), fb = f(b), n .
- Используйте цикл для суммирования.
- Вернуть или распечатать значение.
Я написал это как функцию, чтобы мы могли использовать ее в любое время (она просто использует numpy , хотя программа будет работать и без него, просто уберите значение pi во 2-й строке с его истинным значением):
Это простая программа. Вы можете сделать его немного более удобным для пользователя, указав значение n при вызове функции.
Вот еще один (он просто использует numpy и matplotlib ):
График с использованием Matplotlib, чтобы показать, как введение большего количества трапеций помогает в лучшем приближении. Этот код не только дает вам свободу задавать любое значение n, но также показывает, как трапеции покрывают площадь под кривой. Но, как вы можете видеть, я удалил допуск, поскольку он не имеет смысла, когда вы пытаетесь узнать, как он сходится. Хотя вы можете добавить его самостоятельно, как это сделал я в предыдущем.
Но, как вы можете видеть, я удалил допуск, поскольку он не имеет смысла, когда вы пытаетесь узнать, как он сходится. Хотя вы можете добавить его самостоятельно, как это сделал я в предыдущем.
Вы видите, что в обоих случаях есть ошибка (я включил ошибку в вывод). Величина ошибки в этом методе пропорциональна произведению производной второго порядка нашей функции f(x) и h² .
Если мы включим член ошибки, то окончательное выражение будет
Это можно доказать с помощью теоремы о промежуточных значенияхИз приведенного выше выражения ясно видно, что при уменьшении h (т. срок уменьшается.
Как видите, как прекрасно мы можем использовать простую элементарную геометрию трапеций для аппроксимации и вычислять интегрирования численно. Это действительно мощно и намного лучше, чем классической прямоугольной аппроксимации площади . Попробуйте сами, решите некоторую интеграцию, используя это правило трапеций.
Надеюсь, вам понравилось узнавать что-то новое.
Все используемые здесь программы, изображения и гифки созданы мной с использованием разных 9Библиотека Python 0007 и все уравнения написаны с использованием Tex. Связанный PDF-файл взят из книги « Что такое математика? » от Ричарда Куранта и Герберта Роббинса .
Engineering at Alberta Courses » Трапециевидное правило
Трапециевидная линейка
Пусть . Разделив интервал на множество подинтервалов, правило трапеций аппроксимирует площадь под кривой путем линейной интерполяции между значениями функции на стыках подинтервалов, и, таким образом, на каждом подинтервале вычисляемая площадь имеет форму трапеция. Для простоты ширина трапеций выбрана постоянной. Позвольте быть количество интервалов с и постоянный интервал . Метод трапеций может быть реализован следующим образом:
Следующий инструмент иллюстрирует реализацию правила трапеций для интегрирования функции, определенной как:
Используйте ползунок, чтобы увидеть влияние увеличения количества интервалов на аппроксимацию.
 2 + Sin[2 Pi*x] + Cos[2 Pi*x/0,5];
ИТ[f, 0, 1,5, 1,0]
IT[f, 0, 1,5, 18,0] Посмотреть код Python
2 + Sin[2 Pi*x] + Cos[2 Pi*x/0,5];
ИТ[f, 0, 1,5, 1,0]
IT[f, 0, 1,5, 18,0] Посмотреть код Pythonимпортировать numpy как np def IT(f, a, b, n): h = (б - а)/n возвращаемая сумма([(f(a + i*h) + f(a + (i + 1)*h))*h/2 для i в диапазоне (int(n))]) def f(x): вернуть 2 + 2*x + x**2 + np.sin(2*np.pi*x) + np.cos(2*np.pi*x/0,5) напечатать (IT (f, 0, 1,5, 1,0)) напечатать (IT (f, 0, 1,5, 18,0))
По следующей ссылке представлены коды MATLAB для реализации правила трапеций.
Файлы MATLAB: Файл 1 (trap.m)
Анализ ошибок
Расширение теоремы Тейлора можно использовать для определения того, как изменяется ошибка при уменьшении размера шага. Для данной функции и ее интерполяционного полинома степени () погрешность между интерполяционным полиномом и функцией определяется выражением (доказательство см. в разделе «Математические основы»):
Где находится в области определения функции и зависит от точки . Погрешность вычисления трапециевидного числа между точками и будет оцениваться по приведенной выше формуле в предположении линейной интерполяции между точками и .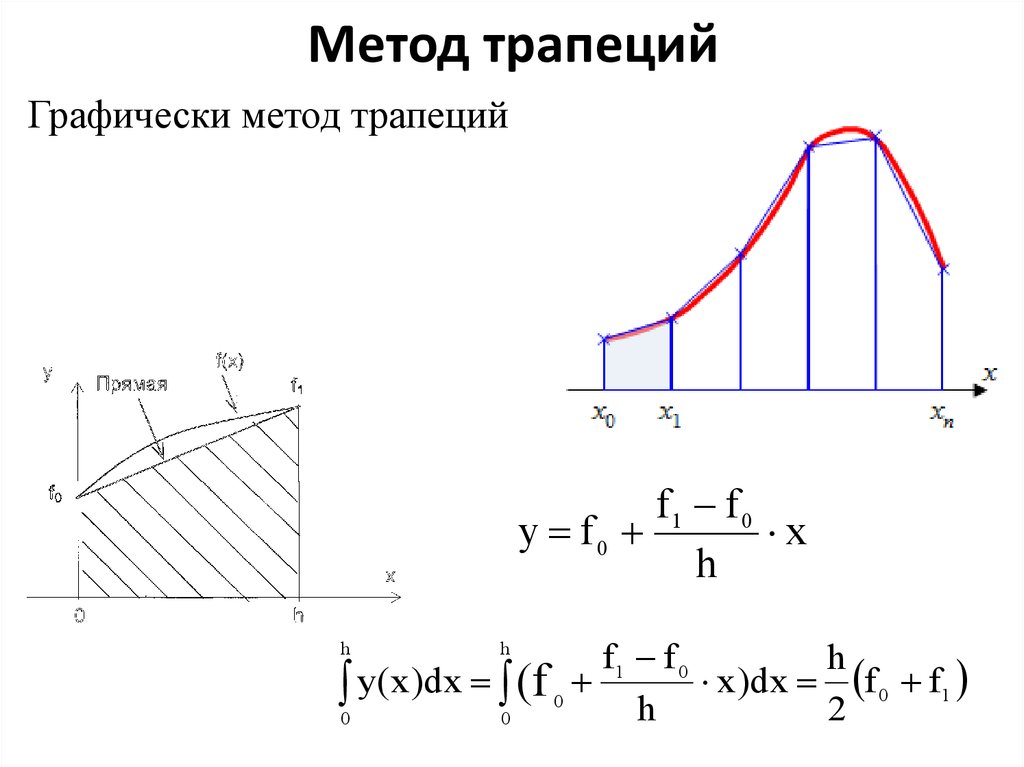 Следовательно:
Следовательно:
Если – количество подразделений (количество трапеций), т. е. , то:
В приведенном выше анализе ошибок мы не учитывали члены более высокого порядка, чем . Хотя это упростило вычисления и удовлетворило наши цели, здесь мы демонстрируем общий анализ ошибок, содержащий члены более высокого порядка. Позже мы воспользуемся результатами для объяснения метода Ромберга.
Рассмотрим непрерывную функцию, заданную на интервале . Если интервал дискретизирован на подинтервалы таким образом, что правило трапеций оценивает интегрирование по подинтервалу как:
где
Чтобы найти порядок ошибки приведенной выше оценки, мы должны найти члены, представленные в:
(Я)
где в порядке точности (подлежит уточнению).
С этой целью мы сначала рассмотрим запись для его разложения в ряд Тейлора о том, что это середина интервала . Таким образом, подстановка разложения в ряд Тейлора приводит к
, который в конечном итоге оценивается как
.
(II)
Оставив пока этот результат и вернувшись к правилу трапеций, мы можем написать, используя его разложение в ряд Тейлора, следующим образом.
Если расширения ряда Тейлора для и записываются как,
поэтому
Обратите внимание, что производные нечетного порядка, т.е. обращаются в нуль.
Решая приведенное выше уравнение и подставляя полученное выражение в правую часть уравнения. II, ведет к,
Сравнивая этот результат с уравнением. I, мы можем сказать, что правило трапеций имеет точность третьего порядка на подынтервале, другими словами,
(Я)
Теперь мы должны перейти к анализу погрешности правила трапеций на всем интервале. Если мы рассмотрим аналогичную длину, для каждого подинтервала дискретизированного как , мы можем написать,
Сумма членов производных может быть заменена их значениями, определенными с помощью теоремы о промежуточном значении.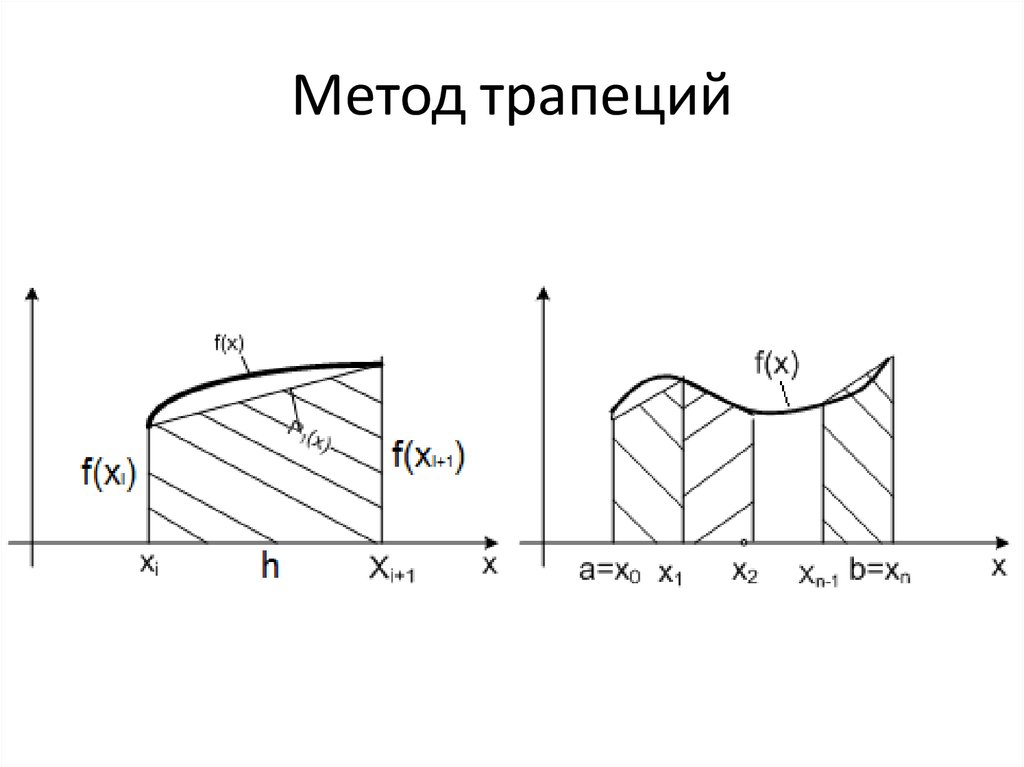 Теорема о промежуточном значении утверждает, что если функция непрерывна на интервале , то существует такое, что для любого попадания в значения и .
Теорема о промежуточном значении утверждает, что если функция непрерывна на интервале , то существует такое, что для любого попадания в значения и .
Следовательно, для непрерывной функции над , если мы установим и в пределах таких, что и , мы можем написать,
означает, что существует такое число, что . Следовательно,
Таким же образом мы можем записать как
для .
Используя приведенные выше значения суммирования, мы получаем,
Так как , мы можем заключить, что
Указывает, что правило трапеций для интегрирования по любому интервалу имеет второй порядок точности.
Пример
Используя правило трапеций с , вычислите и сравните с точным интегралом функции на интервале . Найдите такое значение, чтобы ошибка была меньше 0,001.
Решение
Поскольку расстояние можно рассчитать как:
Следовательно, , , , , и .