|
Введение Задачи по алгебре. Выпуск 1. Задачи по алгебре. Выпуск 2. Задачи по теории алгоритмов. Выпуск 1. Задачи по алгебре. Выпуск 1.
1. Вычислить определитель . Согласно определению определителя 2-го порядка .
2. Пользуясь определениями, решить систему уравнение: . Найдем определитель из коэффициентов системы: . Определитель отличен от нуля, поэтому к системе применимо правило Крамера согласно которому значение неизвестных определяется по формулам: , , где определитель получается из определителя заменой первого столбца столбцом свободных членов системы: , а определитель . Таким образом, , .
3. Вычислить определитель 3-го порядка: . Согласно определению определителя 3-го порядка: .
4. Пользуясь определителями, решить систему уравнений: Найдем определитель из коэффициентов системы: . Определитель отличен от нуля, поэтому к системе применимо правило Крамера согласно которому значение неизвестных определяется по формулам: , , , где определитель получается из определителя заменой первого столбца столбцом свободных членов системы: , определитель получается из определителя заменой второго столбца столбцом свободных членов системы: , определитель получается из определителя заменой третьего столбца столбцом свободных членов системы: . Таким образом, , , .
5. Определить число инверсий в перестановке 2, 3, 5, 4, 1. Инверсии образуют следующие пары чисел (2,1), (3,1), (5,1), (5,4), (4,1). Таким образом, число инверсий в данной перестановке равно 5.
6. Определить число инверсий в перестановке 1, 3, 5, 7,…,2n-1, 2, 4, 6, 8,…, 2n. Число 1 не образует инверсий. Число 3 образует 1 инверсию с 2. Число 5 образует 2 инверсию с 2 и 4. Число7 образует 3 инверсию с 2, 4 и 6. Число 2n-1 образует n-1 инверсию с 2, 4, 6, … , 2n-2. Таким образом, число всех инверсий в данной перестановки равно .
7. Вычислить определитель . Выполним сначала следующие преобразования:
Получим . Разложим этот определитель по третьему столбцу, содержащий лишь один не равный нулю элемент, расположенный на пересечении 1-ой строки и 3-го столбца, получим . Согласно определению определителя 3-го порядка получим: .
8. Пользуясь теоремой Лапласа вычислить определитель: . Разложим его по 2-ой и 4-ой строкам, содержащим лишь один не равный нулю минор , элементы которого стоят на пересечении 2-ой, 4-ой строк и 1-го, 4-го столбцов, получим: 9. Пользуясь теоремой Лапласа вычислить определитель: . Разложим определитель по 3-му и 5-му столбцу, содержащих три не равных минора: минор , элементы которого стоят на пересечении 3-го, 5-го столбцов и 1-ой, 3-ей строк; минор , элементы которого стоят на пересечении 3-го, 5-го столбцов и 1-ой, 4-ой строк; минор , элементы которого стоят на пересечении 3-го,
5-го столбцов и 3-ей, 4-ой строк. Получим: .
10.Решить систему методом исключения неизвестных: . Рассмотрим расширенную матрицу системы: . Поменяем местами 1-ую и 3-юю строки, получим: . Прибавим ко 2-ой строке 1-ую, умноженную на (-2), прибавим к 3-ей строке 1-ую, умноженную на (-3), прибавим к 4-ой строке 1-ую, умноженную на (-1), получим: . Прибавим ко 2-ой строке 3-ю строку, умноженную на (-1) получим: . Прибавим к 3-ей строке 2-ю строку, умноженную на 8, прибавим к 4-ой строке 2-ю, умноженную на 3, получим . Прибавим к 3-ей строке 4-ю строку, умноженную на (-3) получим: . Прибавим к 4-ой строке 3-ю строку, умноженную на (-14) получим . Умножим 4-ю строку на , получим: .  Прибавим к 3-ей строке 4-ю строку, умноженную на 26, прибавим к 1-ой 4-ую, умноженную на 4, получим: ~~.
11. Найдем ранг матрицы методом окаймления минора: . Минор, второго порядка, стоящем в левом верхнем углу данной матрицы равен нулю: . Однако в матрице содержится и отличный от нуля минор второго порядка, например . Все миноры третьего порядка, окаймляющие минор d, равны 0: , , . Таким образом, ранг матрицы равен 2.
12. Выяснить, является ли следующая система векторов линейно зависимой или линейно независимой: , , , . Составим матрицу, для которой данные вектора служат столбцами (строками) и вычислим ранг этой матрицы: . Таким образом, ранг равен 4 Следовательно, все 4 вектора данной системы линейно независимы.
|
НОУ ИНТУИТ | Лекция | Подстановки, перестановки
< Лекция 10 || Лекция 10: 1234
Аннотация: В данной лекции рассматриваются подстановки и перестановки. Приведены основные определения, рассмотрена транспозиция, разложение подстановок в произведение циклов с непересекающимися орбитами. Рассмотрен ряд характерных задач, доказаны основные теоремы, а также приведены задачи для самостоятельного рассмотрения
Ключевые слова: группа, операции, подгруппа, моноид, доказательство, подстановка, множества, перестановка, орбита цикла, разбиение на классы сопряженных элементов, инверсия, гомоморфизм групп
Подстановки, перестановки
Теорема 5.0.4. Множество S(U) всех биекций
с операцией произведения (композиции) отображений gf для , , обладает следующими свойствами:
- intuit.ru/2010/edi»>операция произведения ассоциативна ( h(gf)=(hg)f для всех ),
- нейтральным элементом для этой операции является тождественное отображение 1 U ( 1Uf=f=f1U для всех ),
- для всякой биекции существует обратный элемент — биекция g=f-1 ( fg=1U=gf ).
(Другими словами, S(U) — группа относительно операции произведения отображений; S(U) — подгруппа моноида T(U): .)
Доказательство. следует из теоремы 1.6.4 и леммы 1.8.4.
Биекции множества U часто называются подстановками . Наиболее важный для нас случай U={1,2,…,n}, в этом случае группу Sn = S({1,2,…,n}) называют группой подстановок множества {1,2,…,n} из n элементов (иногда называемой симметрической группой).
Запись подстановок. Перестановки
Если — подстановка, то рассмотрим ее каноническую запись
В нижней строчке (f(1), f(2),…, f(n)), поскольку f — биекция, встречаются все элементы i, , при этом только по одному разу. Такие строчки элементов (i1,…,in), , где каждый элемент i_j, , встречается один и только один раз, называются перестановками элементов 1,2,…,n .
Лемма 5.1.1. Число всех перестановок (i1,…,in) из n элементов равно .
Доказательство. Для i1 имеем n возможностей. При выбранном i1 для i2 имеем (n-1) возможность. Таким образом, число различных перестановок равно !.
Лемма 5.1.2. Число различных подстановок множества {1,2,…,n} равно n! (т. е. | S_n|=n!).
е. | S_n|=n!).
Доказательство. Для рассмотрим каноническую запись
Таким образом, различных подстановок столько же, сколько различных перестановок n элементов, т. е. n!.
Во многих случаях удобно рассматривать записи подстановки , располагая в верхней строчке произвольную перестановку (i1,i2,…,in):
Каждый столбец этой таблицы имеет вид
Пример 5.1.3
- Для тождественной подстановки в S2 имеем Для биекции , f(1)=2, f(2)=1, имеем
- Если то
- Так как , то В частности,
- Обозначим через (i1 i2… ir) цикл длины r в группе подстановок S
 ..,n}, отличные от i1,…,ir, на месте. Тогда в S3 имеем шесть подстановок:
При этом в Sn для имеем
следовательно, группа S3 и любая группа Sn при некоммутативны. Так как S1={e} и S2={e, (1 2)} — коммутативные группы, то получаем, что группа Sn коммутативна тогда и только тогда, когда n=1 или n=2.
..,n}, отличные от i1,…,ir, на месте. Тогда в S3 имеем шесть подстановок:
При этом в Sn для имеем
следовательно, группа S3 и любая группа Sn при некоммутативны. Так как S1={e} и S2={e, (1 2)} — коммутативные группы, то получаем, что группа Sn коммутативна тогда и только тогда, когда n=1 или n=2.
Дальше >>
< Лекция 10 || Лекция 10: 1234
Алгоритм— подсчет инверсий в массиве
Этот ответ содержит результаты тестов timeit , созданных кодом в моем основном ответе. Пожалуйста, смотрите этот ответ для деталей!
count_inversions результаты теста скорости Размер = 5, прим = 2, 4096 петель ltree_count_PM2R : 0,04871, 0,04872, 0,04876 bruteforce_loops_PM2R : 0,05696, 0,05700, 0,05776 решение_TimBabych: 0,05760, 0,05822, 0,05943 решениеE_TimBabych: 0,06642, 0,06704, 0,06760 брутфорс_сумма_PM2R : 0,07523, 0,07545, 0,07563 перм_сумма_PM2R : 0,09873, 0,09875, 0,09935 rank_sum_PM2R : 0,10449, 0,10463, 0,10468 решение_python: 0,13034, 0,13061, 0,13221 fenwick_inline_PM2R : 0,14323, 0,14610, 0,18802 perm_radixR_PM2R : 0,15146, 0,15203, 0,15235 merge_count_BM : 0,16179, 0,16267, 0,16467 perm_radixI_PM2R : 0,16200, 0,16202, 0,16768 perm_fenwick_PM2R : 0,16887, 0,16920, 0,17075 слияние_PM2R: 0,18262, 0,18271, 0,18418 count_inversions_NiklasB : 0,19183, 0,19279, 0,20388 count_inversion_mkso : 0,20060, 0,20141, 0,20398 inv_cnt_ZheHu: 0,20815, 0,20841, 0,20906 Фенвик_PM2R : 0,22109, 0,22137, 0,22379 reversePairs_nomanpouigt: 0,29620, 0,29689, 0,30293 Значение: 5 Размер = 10, прибавка = 5, 2048 петель решение_TimBabych: 0,05954, 0,05989, 0,05991 решениеE_TimBabych: 0,05970, 0,05972, 0,05998 perm_sum_PM2R : 0,07517, 0,07519, 0,07520 ltree_count_PM2R : 0,07672, 0,07677, 0,07684 bruteforce_loops_PM2R : 0,07719, 0,07724, 0,07817 rank_sum_PM2R : 0,08587, 0,08823, 0,08864 брутфорс_сумма_PM2R : 0,09470, 0,09472, 0,09484 решение_python: 0,13126, 0,13154, 0,13185 perm_radixR_PM2R : 0,14239, 0,14320, 0,14474 perm_radixI_PM2R : 0,14632, 0,14669, 0,14679 fenwick_inline_PM2R : 0,16796, 0,16831, 0,17030 perm_fenwick_PM2R : 0,18189, 0,18212, 0,18638 merge_count_BM : 0,19816, 0,19870, 0,19948 count_inversions_NiklasB : 0,21807, 0,22031, 0,22215 слияние_PM2R: 0,22037, 0,22048, 0,26106 Фенвик_PM2R : 0,24290, 0,24314, 0,24744 count_inversion_mkso : 0,24895, 0,24899, 0,25205 inv_cnt_ZheHu: 0,26253, 0,26259, 0,26590 reversePairs_nomanpouigt: 0,35711, 0,35762, 0,35973 Стоимость: 20 Размер = 20, прибавка = 10, 1024 петли решениеE_TimBabych: 0,05687, 0,05696, 0,05720 решение_TimBabych: 0,06126, 0,06151, 0,06168 perm_sum_PM2R : 0,06875, 0,06906, 0,07054 rank_sum_PM2R : 0,07988, 0,07995, 0,08002 ltree_count_PM2R : 0,11232, 0,11239, 0,11257 брутфорс_лупс_PM2R : 0,12553, 0,12584, 0,12592 решение_python: 0,13472, 0,13540, 0,13694 брутфорс_сумма_PM2R : 0,15820, 0,15849, 0,16021 perm_radixI_PM2R : 0,17101, 0,17148, 0,17229 perm_radixR_PM2R : 0,17891, 0,18087, 0,18366 perm_fenwick_PM2R : 0,20554, 0,20708, 0,21412 fenwick_inline_PM2R : 0,21161, 0,21163, 0,22047 merge_count_BM : 0,24125, 0,24261, 0,24565 count_inversions_NiklasB : 0,25712, 0,25754, 0,25778 слияние_PM2R: 0,26477, 0,26566, 0,31297 Фенвик_PM2R : 0,28178, 0,28216, 0,29069 count_inversion_mkso : 0,30286, 0,30290, 0,30652 inv_cnt_ZheHu: 0,32024, 0,32041, 0,32447 reversePairs_nomanpouigt: 0,45812, 0,45822, 0,46172 Значение: 98 Размер = 40, прибавка = 20, 512 петель решениеE_TimBabych: 0,05784, 0,05787, 0,05958 решение_TimBabych: 0,06452, 0,06475, 0,06479 perm_sum_PM2R : 0,07254, 0,07261, 0,07263 rank_sum_PM2R : 0,08537, 0,08540, 0,08572 ltree_count_PM2R : 0,11744, 0,11749, 0,11792 решение_python: 0,14262, 0,14285, 0,14465 perm_radixI_PM2R : 0,18774, 0,18776, 0,18922 perm_radixR_PM2R : 0,19425, 0,19435, 0,19609 bruteforce_loops_PM2R : 0,21500, 0,21511, 0,21686 perm_fenwick_PM2R : 0,23338, 0,23375, 0,23674 fenwick_inline_PM2R : 0,24947, 0,24958, 0,25189 брутфорс_сумма_PM2R : 0,27627, 0,27646, 0,28041 merge_count_BM : 0,28059, 0,28128, 0,28294 count_inversions_NiklasB : 0,28557, 0,28759, 0,29022 слияние_PM2R: 0,29886, 0,29928, 0,30317 Фенвик_PM2R : 0,30241, 0,30259, 0,35237 count_inversion_mkso : 0,34252, 0,34356, 0,34441 inv_cnt_ZheHu: 0,37468, 0,37569, 0,37847 reversePairs_nomanpouigt: 0,50725, 0,50770, 0,50943 Стоимость: 369 Размер = 80, прибавка = 40, 256 петель решениеE_TimBabych: 0,06339, 0,06373, 0,06513 решение_TimBabych : 0,06984, 0,06994, 0,07009 perm_sum_PM2R : 0,09171, 0,09172, 0,09186 rank_sum_PM2R : 0,10468, 0,10474, 0,10500 ltree_count_PM2R : 0,14416, 0,15187, 0,18541 решение_python: 0,17415, 0,17423, 0,17451 perm_radixI_PM2R : 0,20676, 0,20681, 0,20936 perm_radixR_PM2R : 0,21671, 0,21695, 0,21736 perm_fenwick_PM2R : 0,26197, 0,26252, 0,26264 fenwick_inline_PM2R : 0,28111, 0,28249, 0,28382 count_inversions_NiklasB : 0,31746, 0,32448, 0,32451 merge_count_BM : 0,31964, 0,33842, 0,35276 слияние_PM2R: 0,32890, 0,32941, 0,33322 Фенвик_PM2R : 0,34355, 0,34377, 0,34873 count_inversion_mkso : 0,37689, 0,37698, 0,38079 inv_cnt_ZheHu: 0,42923, 0,42941, 0,43249 bruteforce_loops_PM2R : 0,43544, 0,43601, 0,43902 брутфорс_сумма_PM2R : 0,52106, 0,52160, 0,52531 reversePairs_nomanpouigt: 0,57805, 0,58156, 0,58252 Стоимость: 1467 Размер = 160, прибавка = 80, 128 петель решениеE_TimBabych: 0,06766, 0,06784, 0,06963 решение_TimBabych: 0,07433, 0,07489, 0,07516 perm_sum_PM2R : 0,13143, 0,13175, 0,13179 rank_sum_PM2R : 0,14428, 0,14440, 0,14922 решение_python: 0.20072, 0.20076, 0.20084 ltree_count_PM2R : 0,20314, 0,20583, 0,24776 perm_radixI_PM2R : 0,23061, 0,23078, 0,23525 perm_radixR_PM2R : 0,23894, 0,23915, 0,24234 perm_fenwick_PM2R : 0,30984, 0,31181, 0,31503 fenwick_inline_PM2R : 0,31933, 0,32680, 0,32722 merge_count_BM : 0,36003, 0,36387, 0,36409count_inversions_NiklasB : 0,36796, 0,36814, 0,37106 слияние_PM2R: 0,36847, 0,36848, 0,37127 Фенвик_PM2R : 0,37833, 0,37847, 0,38095 count_inversion_mkso : 0,42746, 0,42747, 0,43184 inv_cnt_ZheHu: 0,48969, 0,48974, 0,49293 reversePairs_nomanpouigt: 0,67791, 0,68157, 0,72420 bruteforce_loops_PM2R : 0,82816, 0,83175, 0,83282 брутфорс_сумма_PM2R : 1.03322, 1.03378, 1.03562 Стоимость: 6194 Размер = 320, прибавка = 160, 64 петли решениеE_TimBabych: 0,07467, 0,07470, 0,07483 решение_TimBabych : 0,08036, 0,08066, 0,08077 perm_sum_PM2R : 0,21142, 0,21201, 0,25766 решение_python: 0,22410, 0,22644, 0,22897 rank_sum_PM2R : 0,22820, 0,22851, 0,22877 ltree_count_PM2R : 0,24424, 0,24595, 0,24645 perm_radixI_PM2R : 0,25690, 0,25710, 0,26191 perm_radixR_PM2R : 0,26501, 0,26504, 0,26729 perm_fenwick_PM2R : 0,33483, 0,33507, 0,33845 fenwick_inline_PM2R : 0,34413, 0,34484, 0,35153 merge_count_BM : 0,39875, 0,39919, 0,40302 Фенвик_PM2R : 0,40434, 0,40439, 0,40845 слияние_PM2R: 0,40814, 0,41531, 0,51417 count_inversions_NiklasB : 0,41681, 0,42009, 0,42128 count_inversion_mkso : 0,47132, 0,47192, 0,47385 inv_cnt_ZheHu: 0,54468, 0,54750, 0,54893 reversePairs_nomanpouigt: 0,76164, 0,76389, 0,80357 брутфорс_лупс_PM2R : 1,59125, 1,60430, 1,64131 bruteforce_sum_PM2R : 2.
03734, 2.03834, 2.03975 Стоимость: 24959 Запуск 2 Размер = 640, прибавка = 320, 8 петель решениеE_TimBabych: 0,04135, 0,04374, 0,04575 ltree_count_PM2R : 0,06738, 0,06758, 0,06874 perm_radixI_PM2R : 0,06928, 0,06943, 0,07019 fenwick_inline_PM2R : 0,07850, 0,07856, 0,08059perm_fenwick_PM2R : 0,08151, 0,08162, 0,08170 perm_sum_PM2R : 0,09122, 0,09133, 0,09221 rank_sum_PM2R : 0,09549, 0,09603, 0,11270 merge_count_BM : 0,10733, 0,10807, 0,11032 count_inversions_NiklasB : 0,12460, 0,19865, 0,20205 решение_python: 0,13514, 0,13585, 0,13814 Размер = 1280, прибавка = 640, 8 петель решениеE_TimBabych: 0,04714, 0,04742, 0,04752 perm_radixI_PM2R : 0,15325, 0,15388, 0,15525 решение_python: 0,15709, 0,15715, 0,16076 fenwick_inline_PM2R : 0,16048, 0,16160, 0,16403 ltree_count_PM2R : 0,16213, 0,16238, 0,16428 perm_fenwick_PM2R : 0,16408, 0,16416, 0,16449count_inversions_NiklasB : 0,19755, 0,19833, 0,19897 merge_count_BM : 0,23736, 0,23793, 0,23912 perm_sum_PM2R : 0,32946, 0,32969, 0,33277 rank_sum_PM2R : 0,34637, 0,34756, 0,34858 Размер = 2560, прибавка = 1280, 8 петель решениеE_TimBabych: 0,10898, 0,11005, 0,11025 perm_radixI_PM2R : 0,33345, 0,33352, 0,37656 ltree_count_PM2R : 0,34670, 0,34786, 0,34833 perm_fenwick_PM2R : 0,34816, 0,34879, 0,35214 fenwick_inline_PM2R : 0,36196, 0,36455, 0,36741 решение_python: 0,36498, 0,36637, 0,40887 count_inversions_NiklasB : 0,42274, 0,42745, 0,42995 merge_count_BM : 0,50799, 0,50898, 0,50917 perm_sum_PM2R : 1,27773, 1,27897, 1,27951 rank_sum_PM2R : 1.
29728, 1.30389, 1.30448 Размер = 5120, прибавка = 2560, 8 петель решениеE_TimBabych: 0,26914, 0,26993, 0,27253 perm_radixI_PM2R : 0,71416, 0,71634, 0,71753 perm_fenwick_PM2R : 0,71976, 0,72078, 0,72078 fenwick_inline_PM2R : 0,72776, 0,72804, 0,73143 ltree_count_PM2R : 0,81972, 0,82043, 0,82290 решение_python: 0,83714, 0,83756, 0,83962 count_inversions_NiklasB : 0,87282, 0,87395, 0,92087 merge_count_BM: 1.09496, 1.09584, 1.10207 rank_sum_PM2R : 5.02564, 5.06277, 5.06666 perm_sum_PM2R : 5.09088, 5.12999, 5.13512 Размер = 10240, прибавка = 5120, 8 петель решениеE_TimBabych: 0,71556, 0,71718, 0,72201 perm_radixI_PM2R : 1,54785, 1,55096, 1,55515 perm_fenwick_PM2R : 1.55103, 1.55353, 1.59298 fenwick_inline_PM2R : 1,57118, 1,57240, 1,57271 ltree_count_PM2R : 1,76240, 1,76247, 1,80944 count_inversions_NiklasB : 1,86543, 1,86851, 1,87208 решение_python: 2.01490, 2.01519, 2.06423 merge_count_BM: 2.35215, 2.35301, 2.40023 rank_sum_PM2R : 20.07048, 20.08399, 20.13200 perm_sum_PM2R : 20.10187, 20.12551, 20.
12683 Запуск 3 Размер = 20480, прим = 10240, 4 петли решениеE_TimBabych: 1.07636, 1.08243, 1.09569 perm_radixI_PM2R : 1,59579, 1,60519, 1,61785 perm_fenwick_PM2R : 1.66885, 1.68549, 1.71109 fenwick_inline_PM2R : 1.72073, 1.72752, 1.77217 ltree_count_PM2R : 1,96900, 1,97820, 2,02578 count_inversions_NiklasB : 2.03257, 2.05005, 2.18548 merge_count_BM : 2,46768, 2,47377, 2,52133 решение_python: 2.49833, 2.50179, 3.79819 Размер = 40960, прим = 20480, 4 петли решениеE_TimBabych: 3.51733, 3.52008, 3.56996 perm_radixI_PM2R : 3,51736, 3,52365, 3,56459 perm_fenwick_PM2R : 3.76097, 3.80900, 3.87974 fenwick_inline_PM2R : 3,95099, 3,96300, 3,99748 ltree_count_PM2R : 4,49866, 4,54652, 5,39716 count_inversions_NiklasB : 4.61851, 4.64303, 4.73026 merge_count_BM : 5,31945, 5.35378, 5.35951 решение_python: 6.78756, 6.82911, 6.98217 Размер = 81920, прим = 40960, 4 петли perm_radixI_PM2R : 7,68723, 7,71986, 7,72135 perm_fenwick_PM2R : 8.52404, 8.53349, 8.53710 fenwick_inline_PM2R : 8.97082, 8.97561, 8.98347 ltree_count_PM2R : 10.
01142, 10.01426, 10.03216 count_inversions_NiklasB : 10.60807, 10.62424, 10.70425 merge_count_BM: 11.42149, 11.42342, 11.47003 решениеE_TimBabych: 12.83390, 12.83485, 12.89747 решение_python : 19.66092, 19.67067, 20.72204 Размер = 163840, прим = 81920, 4 петли perm_radixI_PM2R : 17.14153, 17.16885, 17.22240 perm_fenwick_PM2R : 19.25944, 19.27844, 20.27568 fenwick_inline_PM2R : 19.78221, 19.80219, 19.80766 ltree_count_PM2R : 22.42240, 22.43259, 22.48837 count_inversions_NiklasB : 22.97341, 23.01516, 23.98052 merge_count_BM: 24.42683, 24.48559, 24.51488 решениеE_TimBabych: 60.96006, 61.20145, 63.71835 решение_python: 73.75132, 73.79854, 73.95874 Размер = 327680, прибавка = 163840, 4 петли perm_radixI_PM2R : 36.56715, 36.60221, 37.05071 perm_fenwick_PM2R : 42.21616, 42.21838, 42.26053 fenwick_inline_PM2R : 43.04987, 43.09075, 43.13287 ltree_count_PM2R : 49.87400, 50.08509, 50.69292 count_inversions_NiklasB : 50.74591, 50.75012, 50.75551 merge_count_BM: 52.37284, 52.51491, 53.43003 решениеE_TimBabych: 373.
67198, 377.03341, 377.42360 решение_python: 411.69178, 411.92691, 412.83856 Размер = 655360, прибавка = 327680, 4 петли perm_radixI_PM2R : 78,51927, 78.66327, 79.46325 perm_fenwick_PM2R : 90.64711, 90.80328, 91.76126 fenwick_inline_PM2R : 93.32482, 93.39086, 94.28880 count_inversions_NiklasB : 107.74393, 107.80036, 108.71443 ltree_count_PM2R : 109.11328, 109.23592, 110.18247 merge_count_BM: 111.05633, 111.07840, 112.05861 решениеE_TimBabych: 1830.46443, 1836.39960, 1849.53918 решение_python: 1911.03692, 1912.04484, 1914.69786
алгоритм — Подсчет инверсий в диапазонах
Я участвовал в соревновании по программированию, в котором не смог решить задачу, проблема была:
Учитывая массив A из n целых чисел, мне нужно подсчитать количество инверсий в заданных диапазонах. Вводится целое число m, указывающее количество диапазонов, затем следуют m строк, в каждой строке заданы два целых числа li и ri.
Мы должны считать инверсии только в указанном диапазоне, т.е. от li до ri включительно (индексация на основе 0).
от li до ri включительно (индексация на основе 0).
Два элемента A[i] и A[j] складываются в инверсию, если A[i]>A[j] и i
например: Я знаю методы для вычисления числа инверсий в O(nlogn) (например, BIT или сортировка слиянием) для всего массива, и если я применю то же самое здесь ко всем диапазонам, сложность будет O(mnlogn), что, безусловно, неприемлемо в качестве ограничения по времени составляет 1 секунду. 1 Вот алгоритм времени O((n + m) sqrt n log n). Вероятно, этого недостаточно, чтобы пройти, но что-то здесь кажется не совсем правильным — обычные трюки на соревнованиях по программированию не работают. (O((n + m) sqrt n) может быть достигнуто с большей осторожностью.) Разделить входной массив на sqrt n подмассивов длины sqrt n, называемых блоками . Для каждого входного диапазона разложить его на объединение нескольких блоков (заблокированных элементов) и менее 2 sqrt n элементов (незаблокированных элементов). Используя предварительно вычисленные результаты и включение-исключение, найдите количество инверсий в диапазоне, где хотя бы один элемент заблокирован. (O(sqrt n)) Вычислите и добавьте к этой величине количество инверсий в диапазоне, включающем два незаблокированных элемента. (O(кв. n log n)) 1 O((n + m) * sqrt(n) * log(n)) время, O(n + m) пространственный алгоритм с автономными запросами (все диапазоны запросов должны быть известны заранее): Дерево BIT/Fenwick может быть использовано здесь как эффективная реализация дерева статистики заказов. В этом случае необходима некоторая предварительная обработка: подстановка значений массива их индексами в отсортированную копию массива для сжатия диапазона значений. O((n + m) * sqrt(n)) временной, O(n * sqrt(n)) пространственный алгоритм с оперативными запросами. Как намекнул Дэвид Эйзенштат. Предварительная обработка: После предварительной обработки у нас есть несколько LUT, содержащих количество инверсий в префиксах/суффиксах блоков ( Запрос: 1 Вот разработка предыдущего ответа, также с заполнением потенциального пробела. Сначала вы вычисляете и сохраняете количество инверсий для всех префиксов вашего массива за время O (n log n), добавляя по одному элементу за раз справа налево и выполняя поиск по двоичному дереву поиска, чтобы найти элемент в дереве все предыдущие элементы, чтобы определить дополнительное количество добавленных инверсий, а затем вставить элемент в двоичное дерево (и поддерживать дерево как самобалансирующееся двоичное дерево поиска). Затем для данного диапазона вы берете префикс и суффикс и округляете суффикс до ближайшего кратного sqrt(n) большего числа, и ищете количество инверсий за время O(1). Затем вы берете оставшиеся элементы в суффиксе и ищете количество инверсий в префиксе, который заканчивается ближайшим кратным sqrt (n) ниже, за время O (sqrt (n)). Затем вы берете оставшиеся элементы в суффиксе и оставшиеся элементы в префиксе (не включенные в конечные точки sqrt (n)), и грубой силой вычисляете количество инверсий между ними за время O (sqrt (n) log n) . Общее время вычислений составляет O(sqrt(n) log n) на диапазон, что дает общее время выполнения O((m + n) sqrt(n) log n) времени, что должно удовлетворять ограничению времени в 1 секунду. 3-й диапазон: индексы 0–3 содержат 1-й и 2-й диапазоны. Если вы знаете, сколько инверсий содержалось в предыдущих диапазонах, вы их пропускаете. Таким образом, в третьем диапазоне вы можете пропустить сравнение 1 с 2 и пропустить сравнение 2 с 3. A=[3 2 1 4] 99  Используя инкрементный алгоритм подсчета инверсий, для каждой пары, состоящей из блока и префикса массива, вычислить количество инверсий, где первый элемент происходит от первого, а второй элемент происходит от второго. (O(n sqrt n log n)) Сделайте то же самое для пар префикс-блок.
Используя инкрементный алгоритм подсчета инверсий, для каждой пары, состоящей из блока и префикса массива, вычислить количество инверсий, где первый элемент происходит от первого, а второй элемент происходит от второго. (O(n sqrt n log n)) Сделайте то же самое для пар префикс-блок.
Pbegin , Pmid , Pend ) так, чтобы все они указывали на конец текущей части массива (а еще лучше на самое правое начало диапазона, принадлежащего этой части). Ожидающий ; обновить дерево статистики заказов, которое определяет количество инверсий между Pmid и Pend ; когда Pend совпадает с концом некоторого диапазона, имеющего начало в текущей части массива, выполнить шаги 5...7. Pbegin назад, пока он не совпадет с началом диапазона, найденного на шаге 4. Накопить количество элементов в дереве порядковой статистики меньше значений, указанных Pbegin (но не обновлять дерево). Pbegin и Pmid (используя либо сортировку слиянием, либо отдельное дерево статистики порядка).
B массива выполнить шаги 4...8. P и массив сумм суффиксов S .
C предыдущей детали B выполните шаг 6. v части C и двигаясь назад, сложите все значения P[v] и запишите результаты sqrt(n) в справочную таблицу E . Сложность этого шага O(n * sqrt(n)). D следующей детали B выполнить шаг 8. v части D и далее, сложите все значения S[v] и запишите результаты sqrt(n) в справочную таблицу F . Сложность этого шага O(n * sqrt(n)). sqrt(n) ). Запишите результаты в интерполяционную таблицу G . Сложность этого шага составляет O(n * log n).
H . Сложность этого шага составляет O(n * log n). E или F и любой из G или H для вычисления числа инверсий в последовательных блоках (с любой парой блоков для начальной и конечной позиции). Запишите результаты в интерполяционную таблицу R . Сложность этого шага O(n). G , H , O(n) пробел), количество инверсий между полными блоками и префиксами/суффиксами блоков ( E , F , O(n * sqrt(n)) пробел), и количество инверсий в последовательных блоках ( R , O(n) пробел). (При желании мы можем объединить E и F с R , что увеличивает время предварительной обработки, но дает время O(1) для первого шага запроса).
R , чтобы получить количество инверсий в последовательных полных блоках, используйте E и F , чтобы добавить количество инверсий между префиксом/суффиксом и каждым из этих полных блоков, используйте G и H , чтобы добавить количество инверсий в префиксе и в суффиксе. sqrt(n) счетчиков, 2 прохода подсчета и 2 прохода для распределения значений) и объедините их. (3/2) log n).
(3/2) log n).






 ..,n}, отличные от i1,…,ir, на месте. Тогда в S3 имеем шесть подстановок:
При этом в Sn для имеем
следовательно, группа S3 и любая группа Sn при некоммутативны. Так как S1={e} и S2={e, (1 2)} — коммутативные группы, то получаем, что группа Sn коммутативна тогда и только тогда, когда n=1 или n=2.
..,n}, отличные от i1,…,ir, на месте. Тогда в S3 имеем шесть подстановок:
При этом в Sn для имеем
следовательно, группа S3 и любая группа Sn при некоммутативны. Так как S1={e} и S2={e, (1 2)} — коммутативные группы, то получаем, что группа Sn коммутативна тогда и только тогда, когда n=1 или n=2.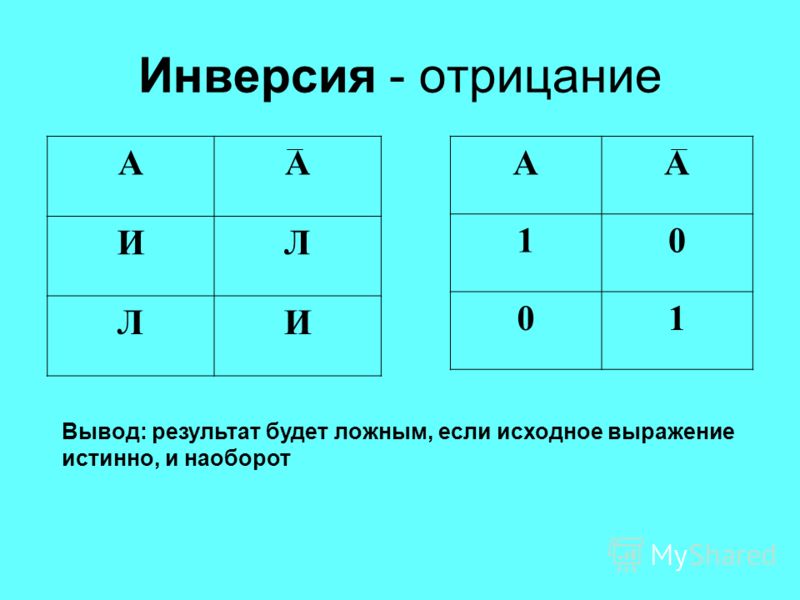 20072, 0.20076, 0.20084
ltree_count_PM2R : 0,20314, 0,20583, 0,24776
perm_radixI_PM2R : 0,23061, 0,23078, 0,23525
perm_radixR_PM2R : 0,23894, 0,23915, 0,24234
perm_fenwick_PM2R : 0,30984, 0,31181, 0,31503
fenwick_inline_PM2R : 0,31933, 0,32680, 0,32722
merge_count_BM : 0,36003, 0,36387, 0,36409count_inversions_NiklasB : 0,36796, 0,36814, 0,37106
слияние_PM2R: 0,36847, 0,36848, 0,37127
Фенвик_PM2R : 0,37833, 0,37847, 0,38095
count_inversion_mkso : 0,42746, 0,42747, 0,43184
inv_cnt_ZheHu: 0,48969, 0,48974, 0,49293
reversePairs_nomanpouigt: 0,67791, 0,68157, 0,72420
bruteforce_loops_PM2R : 0,82816, 0,83175, 0,83282
брутфорс_сумма_PM2R : 1.03322, 1.03378, 1.03562
Стоимость: 6194
Размер = 320, прибавка = 160, 64 петли
решениеE_TimBabych: 0,07467, 0,07470, 0,07483
решение_TimBabych : 0,08036, 0,08066, 0,08077
perm_sum_PM2R : 0,21142, 0,21201, 0,25766
решение_python: 0,22410, 0,22644, 0,22897
rank_sum_PM2R : 0,22820, 0,22851, 0,22877
ltree_count_PM2R : 0,24424, 0,24595, 0,24645
perm_radixI_PM2R : 0,25690, 0,25710, 0,26191
perm_radixR_PM2R : 0,26501, 0,26504, 0,26729
perm_fenwick_PM2R : 0,33483, 0,33507, 0,33845
fenwick_inline_PM2R : 0,34413, 0,34484, 0,35153
merge_count_BM : 0,39875, 0,39919, 0,40302
Фенвик_PM2R : 0,40434, 0,40439, 0,40845
слияние_PM2R: 0,40814, 0,41531, 0,51417
count_inversions_NiklasB : 0,41681, 0,42009, 0,42128
count_inversion_mkso : 0,47132, 0,47192, 0,47385
inv_cnt_ZheHu: 0,54468, 0,54750, 0,54893
reversePairs_nomanpouigt: 0,76164, 0,76389, 0,80357
брутфорс_лупс_PM2R : 1,59125, 1,60430, 1,64131
bruteforce_sum_PM2R : 2.
20072, 0.20076, 0.20084
ltree_count_PM2R : 0,20314, 0,20583, 0,24776
perm_radixI_PM2R : 0,23061, 0,23078, 0,23525
perm_radixR_PM2R : 0,23894, 0,23915, 0,24234
perm_fenwick_PM2R : 0,30984, 0,31181, 0,31503
fenwick_inline_PM2R : 0,31933, 0,32680, 0,32722
merge_count_BM : 0,36003, 0,36387, 0,36409count_inversions_NiklasB : 0,36796, 0,36814, 0,37106
слияние_PM2R: 0,36847, 0,36848, 0,37127
Фенвик_PM2R : 0,37833, 0,37847, 0,38095
count_inversion_mkso : 0,42746, 0,42747, 0,43184
inv_cnt_ZheHu: 0,48969, 0,48974, 0,49293
reversePairs_nomanpouigt: 0,67791, 0,68157, 0,72420
bruteforce_loops_PM2R : 0,82816, 0,83175, 0,83282
брутфорс_сумма_PM2R : 1.03322, 1.03378, 1.03562
Стоимость: 6194
Размер = 320, прибавка = 160, 64 петли
решениеE_TimBabych: 0,07467, 0,07470, 0,07483
решение_TimBabych : 0,08036, 0,08066, 0,08077
perm_sum_PM2R : 0,21142, 0,21201, 0,25766
решение_python: 0,22410, 0,22644, 0,22897
rank_sum_PM2R : 0,22820, 0,22851, 0,22877
ltree_count_PM2R : 0,24424, 0,24595, 0,24645
perm_radixI_PM2R : 0,25690, 0,25710, 0,26191
perm_radixR_PM2R : 0,26501, 0,26504, 0,26729
perm_fenwick_PM2R : 0,33483, 0,33507, 0,33845
fenwick_inline_PM2R : 0,34413, 0,34484, 0,35153
merge_count_BM : 0,39875, 0,39919, 0,40302
Фенвик_PM2R : 0,40434, 0,40439, 0,40845
слияние_PM2R: 0,40814, 0,41531, 0,51417
count_inversions_NiklasB : 0,41681, 0,42009, 0,42128
count_inversion_mkso : 0,47132, 0,47192, 0,47385
inv_cnt_ZheHu: 0,54468, 0,54750, 0,54893
reversePairs_nomanpouigt: 0,76164, 0,76389, 0,80357
брутфорс_лупс_PM2R : 1,59125, 1,60430, 1,64131
bruteforce_sum_PM2R : 2. 03734, 2.03834, 2.03975
Стоимость: 24959
Запуск 2
Размер = 640, прибавка = 320, 8 петель
решениеE_TimBabych: 0,04135, 0,04374, 0,04575
ltree_count_PM2R : 0,06738, 0,06758, 0,06874
perm_radixI_PM2R : 0,06928, 0,06943, 0,07019
fenwick_inline_PM2R : 0,07850, 0,07856, 0,08059perm_fenwick_PM2R : 0,08151, 0,08162, 0,08170
perm_sum_PM2R : 0,09122, 0,09133, 0,09221
rank_sum_PM2R : 0,09549, 0,09603, 0,11270
merge_count_BM : 0,10733, 0,10807, 0,11032
count_inversions_NiklasB : 0,12460, 0,19865, 0,20205
решение_python: 0,13514, 0,13585, 0,13814
Размер = 1280, прибавка = 640, 8 петель
решениеE_TimBabych: 0,04714, 0,04742, 0,04752
perm_radixI_PM2R : 0,15325, 0,15388, 0,15525
решение_python: 0,15709, 0,15715, 0,16076
fenwick_inline_PM2R : 0,16048, 0,16160, 0,16403
ltree_count_PM2R : 0,16213, 0,16238, 0,16428
perm_fenwick_PM2R : 0,16408, 0,16416, 0,16449count_inversions_NiklasB : 0,19755, 0,19833, 0,19897
merge_count_BM : 0,23736, 0,23793, 0,23912
perm_sum_PM2R : 0,32946, 0,32969, 0,33277
rank_sum_PM2R : 0,34637, 0,34756, 0,34858
Размер = 2560, прибавка = 1280, 8 петель
решениеE_TimBabych: 0,10898, 0,11005, 0,11025
perm_radixI_PM2R : 0,33345, 0,33352, 0,37656
ltree_count_PM2R : 0,34670, 0,34786, 0,34833
perm_fenwick_PM2R : 0,34816, 0,34879, 0,35214
fenwick_inline_PM2R : 0,36196, 0,36455, 0,36741
решение_python: 0,36498, 0,36637, 0,40887
count_inversions_NiklasB : 0,42274, 0,42745, 0,42995
merge_count_BM : 0,50799, 0,50898, 0,50917
perm_sum_PM2R : 1,27773, 1,27897, 1,27951
rank_sum_PM2R : 1.
03734, 2.03834, 2.03975
Стоимость: 24959
Запуск 2
Размер = 640, прибавка = 320, 8 петель
решениеE_TimBabych: 0,04135, 0,04374, 0,04575
ltree_count_PM2R : 0,06738, 0,06758, 0,06874
perm_radixI_PM2R : 0,06928, 0,06943, 0,07019
fenwick_inline_PM2R : 0,07850, 0,07856, 0,08059perm_fenwick_PM2R : 0,08151, 0,08162, 0,08170
perm_sum_PM2R : 0,09122, 0,09133, 0,09221
rank_sum_PM2R : 0,09549, 0,09603, 0,11270
merge_count_BM : 0,10733, 0,10807, 0,11032
count_inversions_NiklasB : 0,12460, 0,19865, 0,20205
решение_python: 0,13514, 0,13585, 0,13814
Размер = 1280, прибавка = 640, 8 петель
решениеE_TimBabych: 0,04714, 0,04742, 0,04752
perm_radixI_PM2R : 0,15325, 0,15388, 0,15525
решение_python: 0,15709, 0,15715, 0,16076
fenwick_inline_PM2R : 0,16048, 0,16160, 0,16403
ltree_count_PM2R : 0,16213, 0,16238, 0,16428
perm_fenwick_PM2R : 0,16408, 0,16416, 0,16449count_inversions_NiklasB : 0,19755, 0,19833, 0,19897
merge_count_BM : 0,23736, 0,23793, 0,23912
perm_sum_PM2R : 0,32946, 0,32969, 0,33277
rank_sum_PM2R : 0,34637, 0,34756, 0,34858
Размер = 2560, прибавка = 1280, 8 петель
решениеE_TimBabych: 0,10898, 0,11005, 0,11025
perm_radixI_PM2R : 0,33345, 0,33352, 0,37656
ltree_count_PM2R : 0,34670, 0,34786, 0,34833
perm_fenwick_PM2R : 0,34816, 0,34879, 0,35214
fenwick_inline_PM2R : 0,36196, 0,36455, 0,36741
решение_python: 0,36498, 0,36637, 0,40887
count_inversions_NiklasB : 0,42274, 0,42745, 0,42995
merge_count_BM : 0,50799, 0,50898, 0,50917
perm_sum_PM2R : 1,27773, 1,27897, 1,27951
rank_sum_PM2R : 1. 29728, 1.30389, 1.30448
Размер = 5120, прибавка = 2560, 8 петель
решениеE_TimBabych: 0,26914, 0,26993, 0,27253
perm_radixI_PM2R : 0,71416, 0,71634, 0,71753
perm_fenwick_PM2R : 0,71976, 0,72078, 0,72078
fenwick_inline_PM2R : 0,72776, 0,72804, 0,73143
ltree_count_PM2R : 0,81972, 0,82043, 0,82290
решение_python: 0,83714, 0,83756, 0,83962
count_inversions_NiklasB : 0,87282, 0,87395, 0,92087
merge_count_BM: 1.09496, 1.09584, 1.10207
rank_sum_PM2R : 5.02564, 5.06277, 5.06666
perm_sum_PM2R : 5.09088, 5.12999, 5.13512
Размер = 10240, прибавка = 5120, 8 петель
решениеE_TimBabych: 0,71556, 0,71718, 0,72201
perm_radixI_PM2R : 1,54785, 1,55096, 1,55515
perm_fenwick_PM2R : 1.55103, 1.55353, 1.59298
fenwick_inline_PM2R : 1,57118, 1,57240, 1,57271
ltree_count_PM2R : 1,76240, 1,76247, 1,80944
count_inversions_NiklasB : 1,86543, 1,86851, 1,87208
решение_python: 2.01490, 2.01519, 2.06423
merge_count_BM: 2.35215, 2.35301, 2.40023
rank_sum_PM2R : 20.07048, 20.08399, 20.13200
perm_sum_PM2R : 20.10187, 20.12551, 20.
29728, 1.30389, 1.30448
Размер = 5120, прибавка = 2560, 8 петель
решениеE_TimBabych: 0,26914, 0,26993, 0,27253
perm_radixI_PM2R : 0,71416, 0,71634, 0,71753
perm_fenwick_PM2R : 0,71976, 0,72078, 0,72078
fenwick_inline_PM2R : 0,72776, 0,72804, 0,73143
ltree_count_PM2R : 0,81972, 0,82043, 0,82290
решение_python: 0,83714, 0,83756, 0,83962
count_inversions_NiklasB : 0,87282, 0,87395, 0,92087
merge_count_BM: 1.09496, 1.09584, 1.10207
rank_sum_PM2R : 5.02564, 5.06277, 5.06666
perm_sum_PM2R : 5.09088, 5.12999, 5.13512
Размер = 10240, прибавка = 5120, 8 петель
решениеE_TimBabych: 0,71556, 0,71718, 0,72201
perm_radixI_PM2R : 1,54785, 1,55096, 1,55515
perm_fenwick_PM2R : 1.55103, 1.55353, 1.59298
fenwick_inline_PM2R : 1,57118, 1,57240, 1,57271
ltree_count_PM2R : 1,76240, 1,76247, 1,80944
count_inversions_NiklasB : 1,86543, 1,86851, 1,87208
решение_python: 2.01490, 2.01519, 2.06423
merge_count_BM: 2.35215, 2.35301, 2.40023
rank_sum_PM2R : 20.07048, 20.08399, 20.13200
perm_sum_PM2R : 20.10187, 20.12551, 20. 12683
Запуск 3
Размер = 20480, прим = 10240, 4 петли
решениеE_TimBabych: 1.07636, 1.08243, 1.09569
perm_radixI_PM2R : 1,59579, 1,60519, 1,61785
perm_fenwick_PM2R : 1.66885, 1.68549, 1.71109
fenwick_inline_PM2R : 1.72073, 1.72752, 1.77217
ltree_count_PM2R : 1,96900, 1,97820, 2,02578
count_inversions_NiklasB : 2.03257, 2.05005, 2.18548
merge_count_BM : 2,46768, 2,47377, 2,52133
решение_python: 2.49833, 2.50179, 3.79819
Размер = 40960, прим = 20480, 4 петли
решениеE_TimBabych: 3.51733, 3.52008, 3.56996
perm_radixI_PM2R : 3,51736, 3,52365, 3,56459
perm_fenwick_PM2R : 3.76097, 3.80900, 3.87974
fenwick_inline_PM2R : 3,95099, 3,96300, 3,99748
ltree_count_PM2R : 4,49866, 4,54652, 5,39716
count_inversions_NiklasB : 4.61851, 4.64303, 4.73026
merge_count_BM : 5,31945, 5.35378, 5.35951
решение_python: 6.78756, 6.82911, 6.98217
Размер = 81920, прим = 40960, 4 петли
perm_radixI_PM2R : 7,68723, 7,71986, 7,72135
perm_fenwick_PM2R : 8.52404, 8.53349, 8.53710
fenwick_inline_PM2R : 8.97082, 8.97561, 8.98347
ltree_count_PM2R : 10.
12683
Запуск 3
Размер = 20480, прим = 10240, 4 петли
решениеE_TimBabych: 1.07636, 1.08243, 1.09569
perm_radixI_PM2R : 1,59579, 1,60519, 1,61785
perm_fenwick_PM2R : 1.66885, 1.68549, 1.71109
fenwick_inline_PM2R : 1.72073, 1.72752, 1.77217
ltree_count_PM2R : 1,96900, 1,97820, 2,02578
count_inversions_NiklasB : 2.03257, 2.05005, 2.18548
merge_count_BM : 2,46768, 2,47377, 2,52133
решение_python: 2.49833, 2.50179, 3.79819
Размер = 40960, прим = 20480, 4 петли
решениеE_TimBabych: 3.51733, 3.52008, 3.56996
perm_radixI_PM2R : 3,51736, 3,52365, 3,56459
perm_fenwick_PM2R : 3.76097, 3.80900, 3.87974
fenwick_inline_PM2R : 3,95099, 3,96300, 3,99748
ltree_count_PM2R : 4,49866, 4,54652, 5,39716
count_inversions_NiklasB : 4.61851, 4.64303, 4.73026
merge_count_BM : 5,31945, 5.35378, 5.35951
решение_python: 6.78756, 6.82911, 6.98217
Размер = 81920, прим = 40960, 4 петли
perm_radixI_PM2R : 7,68723, 7,71986, 7,72135
perm_fenwick_PM2R : 8.52404, 8.53349, 8.53710
fenwick_inline_PM2R : 8.97082, 8.97561, 8.98347
ltree_count_PM2R : 10. 01142, 10.01426, 10.03216
count_inversions_NiklasB : 10.60807, 10.62424, 10.70425
merge_count_BM: 11.42149, 11.42342, 11.47003
решениеE_TimBabych: 12.83390, 12.83485, 12.89747
решение_python : 19.66092, 19.67067, 20.72204
Размер = 163840, прим = 81920, 4 петли
perm_radixI_PM2R : 17.14153, 17.16885, 17.22240
perm_fenwick_PM2R : 19.25944, 19.27844, 20.27568
fenwick_inline_PM2R : 19.78221, 19.80219, 19.80766
ltree_count_PM2R : 22.42240, 22.43259, 22.48837
count_inversions_NiklasB : 22.97341, 23.01516, 23.98052
merge_count_BM: 24.42683, 24.48559, 24.51488
решениеE_TimBabych: 60.96006, 61.20145, 63.71835
решение_python: 73.75132, 73.79854, 73.95874
Размер = 327680, прибавка = 163840, 4 петли
perm_radixI_PM2R : 36.56715, 36.60221, 37.05071
perm_fenwick_PM2R : 42.21616, 42.21838, 42.26053
fenwick_inline_PM2R : 43.04987, 43.09075, 43.13287
ltree_count_PM2R : 49.87400, 50.08509, 50.69292
count_inversions_NiklasB : 50.74591, 50.75012, 50.75551
merge_count_BM: 52.37284, 52.51491, 53.43003
решениеE_TimBabych: 373.
01142, 10.01426, 10.03216
count_inversions_NiklasB : 10.60807, 10.62424, 10.70425
merge_count_BM: 11.42149, 11.42342, 11.47003
решениеE_TimBabych: 12.83390, 12.83485, 12.89747
решение_python : 19.66092, 19.67067, 20.72204
Размер = 163840, прим = 81920, 4 петли
perm_radixI_PM2R : 17.14153, 17.16885, 17.22240
perm_fenwick_PM2R : 19.25944, 19.27844, 20.27568
fenwick_inline_PM2R : 19.78221, 19.80219, 19.80766
ltree_count_PM2R : 22.42240, 22.43259, 22.48837
count_inversions_NiklasB : 22.97341, 23.01516, 23.98052
merge_count_BM: 24.42683, 24.48559, 24.51488
решениеE_TimBabych: 60.96006, 61.20145, 63.71835
решение_python: 73.75132, 73.79854, 73.95874
Размер = 327680, прибавка = 163840, 4 петли
perm_radixI_PM2R : 36.56715, 36.60221, 37.05071
perm_fenwick_PM2R : 42.21616, 42.21838, 42.26053
fenwick_inline_PM2R : 43.04987, 43.09075, 43.13287
ltree_count_PM2R : 49.87400, 50.08509, 50.69292
count_inversions_NiklasB : 50.74591, 50.75012, 50.75551
merge_count_BM: 52.37284, 52.51491, 53.43003
решениеE_TimBabych: 373. 67198, 377.03341, 377.42360
решение_python: 411.69178, 411.92691, 412.83856
Размер = 655360, прибавка = 327680, 4 петли
perm_radixI_PM2R : 78,51927, 78.66327, 79.46325
perm_fenwick_PM2R : 90.64711, 90.80328, 91.76126
fenwick_inline_PM2R : 93.32482, 93.39086, 94.28880
count_inversions_NiklasB : 107.74393, 107.80036, 108.71443
ltree_count_PM2R : 109.11328, 109.23592, 110.18247
merge_count_BM: 111.05633, 111.07840, 112.05861
решениеE_TimBabych: 1830.46443, 1836.39960, 1849.53918
решение_python: 1911.03692, 1912.04484, 1914.69786
67198, 377.03341, 377.42360
решение_python: 411.69178, 411.92691, 412.83856
Размер = 655360, прибавка = 327680, 4 петли
perm_radixI_PM2R : 78,51927, 78.66327, 79.46325
perm_fenwick_PM2R : 90.64711, 90.80328, 91.76126
fenwick_inline_PM2R : 93.32482, 93.39086, 94.28880
count_inversions_NiklasB : 107.74393, 107.80036, 108.71443
ltree_count_PM2R : 109.11328, 109.23592, 110.18247
merge_count_BM: 111.05633, 111.07840, 112.05861
решениеE_TimBabych: 1830.46443, 1836.39960, 1849.53918
решение_python: 1911.03692, 1912.04484, 1914.69786