Компоненты вектора: Что такое компоненты вектора? Это не базис случайно? — Спрашивалка

Координаты и компоненты вектора

По этой ссылке вы найдёте полный курс лекций по математике:

Решение задач по математике

Выберем в пространстве прямоугольную декартову систему координат. Обозначим через i, j, к единичные векторы (орты) положительных направлений осей Ох. Оу, Oz (рис. 19). Рассмотрим произвольный вектор а, начало которого лежит в начале координат О, а коней — в точке А. Проведем через точку А плоскости, перпендикулярные .осям Ох, Оу и Oz. Эти плоскости пересекут координатные оси в точках Ру Q и R соответственно.

Из рис. 20 видно, что Векторы OP, OQ и OR коллинеарны соответственно единичным векторам i, j, k. поэтому найдутся числа х, у, 2 такие, что и, следовательно, Координаты и компоненты вектора Формула (2) называется разложением вектора и по век/порам i, j, к. Указанным способом всякий вектор может быть разложен по векторам i, j, k.

Векторы i, j, k попарно ортогональны, и их длины равны единице. Тройку i, j, k называют ортонормированным (координатным) базисом (ортобазисом).

Можно показать, что для каждого вектора а разложение (2) по базису i, j, к единственно, т. с. коэффициенты!, у, z в разложении вектора а по векторам i, j, к определены однозначно.

Эти коэффициенты называются координатами вектора а. Они совпадают с координатами х, у, z точки Л — конца вектора а. Мы пишем в этом случае Эта запись означает, что свободный вектор а однозначно задастся упорядоченной тройкой своих координат. Векторы х\, t/j, zk, сумма которых равна вектору а, называются компонентами вектора а.

Возможно вам будут полезны данные страницы:

Схема построения графика функции

Оптимальность по Парето. Множество. Метод идеальной точки

Сечение цилиндра плоскостью

Деформационные швы (разделяющий здание на отдельные отсеки)

Из вышеизложенного следует, что два вектора а = {x\,y\,z\} и Ь = {х2,у2,22} равны тогда и только тогда, когда соответственно равны их координаты, т. и начальной М\ точек этого вектора.

Компоненты вектора — Энциклопедия по экономике

Состояние окружающей среды характеризовалось пятью безразмерными показателями, компонентами вектора V, три из которых описывают сте-  [c.38]
Различные производственные способы могут отличаться как объемами выпуска и затрат при единичной интенсивности, так и номенклатурой продукции и ресурсов. Поэтому в математических моделях, в которых присутствует несколько производственных способов, в описание отдельных способов вводят продукты и ресурсы, не используемые и не производящиеся в них. Для этих ресурсов и продуктов соответствующие компоненты векторов х и г/° полагают равными нулю.  [c.100]

В соотношении (4.16) нет деления на ресурсы и продукцию. Роль каждого вида материальных благ определяется знаком соответствующей компоненты вектора v° при v° > 0. это выпуска-  [c.100]

В дальнейшем ту часть модели месторождения, которая формирует компоненты вектора (127), используемые при построении Qt и Qt, будем называть имитационным блоком модели месторождения.  [c.217]

Г есть дисперсии компонент векторов оценок Ьц и bh то дис-  [c.95]

Из рисунка видно, что ряд вариантов векторов оценок (1, 2 3, 4) порождает одинаковую динамику з /Л, что можно объяснить некоторой инерционностью модели, т. е.. реакция на уровень различия и , равный единице, отсутствует. Вместе с тем заметна и некоторая направленность изменения (жу ). состоящая в смещении вниз при больших значениях компоненты вектора w (6, 7 8, 9).  [c.124]

Отличительной особенностью моделей с переменными параметрами является то, что в этих моделях коэффициенты матрицы условий 11й/у11 могут целенаправленно варьироваться в непрерывном спектре технологических способов производства. В некоторых случаях может осуществляться и варьирование в непрерывной области компонентов вектора ограничений 6г- .  [c.26]

III. Известна часть базисного или оптимального решения задачи (2.28) или (2.34), известны номера или численные значения части компонентов вектора  [c.35]

Формируется смешанное» базисное решение, включающее известные компоненты вектора X, искусственные и дополнительные переменные.  [c.35]

Здесь х и j. «— компоненты вектора V», являющиеся, соответственно, входными и выходными потоками подсистемы v s — q-Я качественный показатель /-го потока и» (/-=Г, Л ) — r-е управляющее воздействие (2.41) — условие материального баланса (2.42) — (2.44) — позиционные ограничения, налагаемые на входные потоки, качественные показатели и управления (2.45) — целевая функция.  [c.39]

В зависимости от условий функционирования производственного комплекса в задаче (3.10) — (3.12) случайными параметрами могут быть элементы матрицы условий Нд -Н, компоненты вектора ограничений b,- , коэффициенты целевой функции сД. Построчные вероятностные ограничения позволяют отразить в данной постановке различную значимость для целевого функционала невязок, возникающих в отдельных ограничениях.  [c.57]

Здесь а ,..-(и ) и a(/(ui) — предельные случайные границы изменения технологического коэффициента a(-.(tj) (3.27) — функциональные ограничения, налагаемые на компоненты вектора R а ц и /3 (oj) — величины, учитывающие особенности реализации технологических процессов НПП /у — номер функционального ограничения, налагаемого нау -й способ производства.

 [c.61]

В постановке (3.74)-(3.79) искомыми (оптимизируемыми) величинами в подзадачах (3.75) — (3.79) являются компоненты векторов -/Г,, и К — случайные величины a iv и . При формировании подзадач эти величины в ограничениях вида (3.77), (3.78) оказываются только в правой части, что обеспечивает линейный вид их детерминированных аналогов. При линейном виде функции H(aiv), описывающей параметрические связи, в соответствии с рассмотренными в [47] случаями детерминированный аналог задачи (3.74) —(3.79), в отличие от (3.73), после соответствующих преобразований может быть представлен в виде задачи обобщенного линейного программирования, решение которого осуществляется на базе известного алгоритма [16].  [c.72]

Здесь Ош — дисперсия компонентов вектора ресурсов xf — параметр, зависящий от заданного уровня риска.  [c.95]

Искомые значения v и компонентов вектора (, д) определятся из следующей системы уравнений  [c.129]

Интересно, что компоненты вектора д,- на выбор замыкания / не оказывают влияния определяющим фактором здесь является  [c.

142]

Задаваемые построчные вероятности (уровни надежности) для каждого вида сырьевого ресурса и продукта определяются дифференциально, на основе экспертных оценок, или в зависимости от дисперсии рассматриваемых случайных величин. При этом в соответствии с [43] по тем продуктам, для которых невыполнение вероятностного ограничения вызывает большие потери или дополнительные расходы, уровень надежности задан большим. Как показали проведенные исследования, в соответствии с практическими требованиями оказывается целесообразным уровень надежности для случайных технологических коэффициентов выбирать в зависимости от дисперсии, а для случайных компонентов вектора ограничений — в ряде случаев на базе рекомендаций экспертов-технологов, работников планового отдела предприятия (так как ограничения на объемы переработки сырья, полу продуктов и вы пуск товарных продуктов определяются также вышестоящими органами и подвергаются неоднократным изменениям на этапе составления и реализации плана). При практических расчетах задаваемые вероятности изменяются от 0,75 до 0,96.

 [c.173]

Решается задача при произвольно выбранном векторе Ъ . В случае допустимого решения, для тех компонентов вектора, для которых соот-  [c.206]

Элементами множества Б являются возможные значения компонентов вектора ограничений.  [c.209]

В комментариях к блок-схеме приняты следующие обозначения Р -область допустимых значений bi и > . — верхняя и нижняя границы варьирования компонент вектора признаков.  [c.210]

Компоненты вектора есть элементы множеств Gqk вида  [c.210]

Обе из приведенных выше моделей (как (4.1.1), так и (4.1.4)) дают представление о положении изучаемого объекта (банка) для каждого момента времени t в отдельности. Однако можно привести немало примеров того, когда возникает необходимость в переходе от такого точечного представления к интегральному описанию поведения/-й характеристики на некотором заданном промежутке (среднего значения характеристики (/-и компоненты вектора состояния) на интервале ,.  [c.148]

Если произвести те же преобразования, что и выше, то система в матричной форме примет вид, аналогичный (11. 3.4), но вектор свободных членов будет иметь только один ненулевой элемент Я. Это первая компонента вектора свободных членов. Решая систему относительно q /x. по правилу Крамера, получим простой результат  [c.230]

Компоненты вектора ограничений At — максимально возможный объем поставок всех видов нефтепродуктов I -M поставщиком Лф — фиктивный потребитель Qp, S k — максимально возможные годовые пропускные способности соответственно р-й нефтебазы и -го филиала В]г —величина спроса /-го потребителя в г-м виде нефтепродукта в период t.  [c.120]

Компоненты вектора ограничений Qpi, 8ы — пропускные способности соответственно рг-й нефтебазы и fer-го филиала на начало планового периода AQp/.ASw —приросты пропускной способности соответственно pt -и нефтебазы и kt -го филиала в году t В / Гв—потребность /г-го потребителя в га -м нефтепродукте в году t.  [c.152]

Блок 14—формирует компоненты вектора ограничений по ресурсам, пропускным способностям объектов нефтебазового хозяйства и по потребностям агрегированных потребителей [1, 4].  [c.84]

Блок 9— формирование компонентов вектора ограничений по потребностям агрегированных потребителей в автобензине и дизельном топливе на первый контрольный год планового периода и  [c.106]

Блок 10— формирование компонентов вектора ограничений по пропускным способностям. Последняя принимается максимальной и учитывает результаты решения задачи текущего планирования нефтеснабжения региона и приростов пропускной способности по контрольным годам планового периода, полученных из данных проектных организаций [1, 2].  [c.107]

Блок 14 — получение оптимальных вариантов прогнозных транспортно-экономических связей по массовым светлым нефтепродуктам при изменении компонентов вектора ограничений по потребностям агрегированных потребителей.  [c.107]

Будем говорить, что первое состояние предпочтительнее второго, если последняя отличная от нуля компонента вектора сравнения меньше нуля. Если последняя отличная от нуля компонента вектора сравнения больше нуля, предпочтительнее второе состояние. Если вектор состояния есть нуль-вектор, сравниваемые состояния эквивалентны.  [c.85]

Введем, как и в однопродуктовой задаче, вектор сравнения двух состояний, полученный как разность соответствующих компонент векторов состояний. И аналогично однопродуктовому случаю будем говорить, что первое состояние предпочтительнее второго, если последняя отличная от нуля компонента вектора  [c.85]

Для устранения мультиколлинеарности может быть использован переход от исходных объясняющих переменных Х, А ,…, Х , связанных между собой достаточно тесной корреляционной зависимостью, к новым переменным, представляющим линейные комбинации исходных. При этом новые переменные должны быть слабокоррелированными либо вообще некоррелированными. В качестве таких переменных берут, например, так называемые главные компоненты вектора исходных объясняющих переменных, изучаемые в компонентном анализе, и рассматривают регрессию на главных компонентах,. в которой последние выступают в качестве обобщенных объясняющих переменных, подлежащих в дальнейшем содержательной (экономической) интерпретации.  [c.111]

Здесь ац и я,у (о>) — соответственно, детерминированный и случайный коэффициенты матрицы условий bjubi(u>) -детерминированная испуганная компоненты вектора ограничений шел — случайный параметр 5″,- и в»,у — математическое ожидание случайных величин и,- (и>) и а,у (о>) у/ — вероятность выполнения г -го условия Ф»1 (7г-) — обратная функция нормального распределения о — — дисперсия случайной величины в,у (и ) f — дисперсия случайной величины 1ц (ш) лу — интенсивность /-го способа производства.  [c.18]

Для оценки компонент вектора признаков были определены следующие термы допустимо», недопустимо», на грани», почти допустимо», почти недопустимо». Причем при ответе на вопрос о реализуемости производственной ситуации были использованы первые три терма. Функция допустимо» была определена через х-функцию  [c.213]

Компоненты вектора — формула, приложения, примеры

Компоненты вектора помогают разделить данный вектор на части по разным направлениям. Иногда возникает необходимость разбить вектор на его компоненты, чтобы облегчить выполнение многочисленных арифметических операций с векторами. Компоненты вектора представляют часть вектора относительно каждой из осей системы координат. Компоненты вектора также могут быть вычислены для вектора в трехмерной геометрической плоскости.

Давайте узнаем больше о компонентах вектора, о том, как найти компоненты вектора и о различных арифметических операциях с компонентами вектора.

1.	Каковы компоненты вектора?
2.	Как найти компоненты вектора?
3.	Алгебраические операции с использованием компонентов вектора
4.	Примеры компонентов вектора
5.	Практические вопросы
6.	Часто задаваемые вопросы о компонентах вектора

Что такое компоненты вектора?

Компоненты вектора дают разбиение вектора. Вектор разбивается относительно каждой из осей, и мы можем вычислить компоненты вектора. Отдельные компоненты вектора можно позже объединить, чтобы получить представление всего вектора. Векторы обычно представлены в двумерной координатной плоскости с осью x, осью y или трехмерным пространством, содержащим ось x, ось y, ось z соответственно. Векторы — это общие математические представления с направлением и величиной. 92}\)

Кроме того, векторы также представлены в виде \(\overrightarrow A = a\hat i + b \hat j + c \hat k\) в трехмерном пространстве. Здесь \(\hat i\), \(\hat j\), \(\hat k\) — единичные векторы вдоль оси x, оси y и оси z соответственно. Эти единичные векторы помогают идентифицировать компоненты векторов относительно каждой из осей. Компоненты вектора A относительно оси x, оси y, оси z равны a, b, c соответственно.

Как найти компоненты вектора? 92}\)

Алгебраические операции с использованием компонентов вектора

Различные алгебраические операции над векторами можно легко выполнять, используя различные компоненты вектора. Рассмотрим два вектора \(\overrightarrow A = a_1\hat i + b_1 \hat j + c_1 \hat k\) и \(\overrightarrow B = a_2\hat i + b_2 \hat j + c_2 \hat k\ ).

• Для сложения двух векторов \(\overrightarrow A\) и \(\overrightarrow B\) имеем: \(\overrightarrow A + \overrightarrow B = (a_1 + a_2)\hat i + (b_1 + b_2 )\шляпа j + (c_1 + c_2)\шляпа k\).
• Для вычитания двух векторов \(\overrightarrow A\) и \(\overrightarrow B\) имеем: \(\overrightarrow A — \overrightarrow B = (a_1 — a_2)\hat i + (b_1 — b_2)\ шляпа j + (c_1 — c_2)\шапка k\).
• Два вектора \(\overrightarrow A\) и \(\overrightarrow B\) равны, если: \(a_1 = a_2\), \(b_1 = b_2\), \(c_1 = c_2\).
• Умножение вектора на скаляр λ дает: \(λ\overrightarrow A = λa_1\hat i + λb_1 \hat j + λc_1 \hat k\).

Связанные темы

Следующие темы полезны для лучшего понимания компонентов вектора.

• Векторы
• Единичный вектор
• Векторные формулы
• Векторные количества
• Типы векторов
• Перекрестное произведение двух векторов

 

Примеры компонентов вектора

1. Пример 1: Найдите компоненты x и y вектора, имеющего модуль 12 и образующего угол 45 градусов с положительной осью x.

   Решение:

   Дан вектор V= 12, образующий угол θ = 45º.

   Компонент x вектора = \(V_x\) = VCosθ = 12.Cos45º = 12.(1/√2) = 6√2.

   Y-компонента вектора = \(V_y\) = VSinθ = 12.Sin45º = 12.(1/√2) = 6√2.

   Следовательно, компоненты x и компоненты y вектора равны 6√2.​​​​​​​

2. Пример 2: Найдите вектор из компонентов вектора, имеющего x-компоненту из 5 единиц, y-компоненту из 12 единиц и z-компоненту из 4 единиц соответственно.

   Решение:

   Компонента X вектора = a = 5

   Компонента Y вектора = b = 12

   Компонента Z вектора = c = 4

   Искомый вектор равен \(\overrightarrow V = a\hat i + b \hat j + c \hat k\)

   Отсюда \(\overrightarrow V = 5\hat i + 12 \hat j + 4 \hat k\).

   Следовательно, искомый вектор равен \(\overrightarrow V = 5\hat i + 12 \hat j + 4 \hat k\).

перейти к слайдуперейти к слайду

Разбивайте сложные концепции с помощью простых визуальных средств.

Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.

Забронировать бесплатный пробный урок

Практические вопросы по компонентам вектора

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы о компонентах вектора

Каковы три компонента вектора?

Тремя компонентами вектора являются компоненты вдоль оси x, оси y и оси z соответственно. Для вектора \(\overrightarrow A = a\hat i + b \hat j + c \hat k\) a, b, c называются скалярными компонентами вектора A, а a\(\hat i\), b\(\hat j\), c\(\hat k\) называются компонентами вектора.

Являются ли компоненты вектора тоже вектором?

Компоненты вектора также являются векторами. Вектор \(\overrightarrow A = a\hat i + b \hat j + c \hat k\) имеет компоненты a, b, c вдоль осей x, y и z соответственно. Поскольку компоненты вектора имеют величину и аргумент, направленные вдоль соответствующих осей, эти компоненты также являются векторами.

Являются ли компоненты векторов скалярными?

Компоненты вектора не являются скалярами. Компоненты вектора также являются векторами и имеют величину и направление. Компоненты вектора также определяются относительно одной из осей в координатной плоскости или в трехмерном пространстве. 9{-1}\frac{V_y}{V_x}\).

Как определить коллинеарность векторов на основе компонентов вектора?

Коллинеарность двух векторов можно доказать, если один вектор получается умножением другого вектора с постоянным значением. Также для двух коллинеарных векторов соответствующие компоненты двух векторов пропорциональны. Два вектора \(\overrightarrow A = a_1\hat i + b_1 \hat j + c_1 \hat k\) и \(\overrightarrow B = a_2\hat i + b_2 \hat j + c_2 \hat k\) называются быть коллинеарным, если \(\overrightarrow A\) = λ\(\overrightarrow B\), а также \(\frac{a_1}{a_2} = \frac{b_1}{b_2} = \frac{c_1}{c_2 }\) = λ.

Компоненты вектора

Можно считать, что любой вектор, направленный в двух измерениях, оказывает влияние в двух разных направлениях. Это означает, что можно считать, что он состоит из двух разных частей. Каждая часть двумерного вектора называется компонентой. Компоненты вектора помогают изобразить влияние этого вектора в определенном направлении. Суммарное влияние обоих этих компонентов равно влиянию двухмерных одиночных векторов. Один двумерный вектор можно заменить двумя компонентами вектора.

Компонентами вектора в двумерной системе координат обычно считаются x-компонента и y-компонента. Вы можете представить это как

V = \[(v_{x}, v_{y})\]

, где V называется вектором.

Это части векторов, которые генерируются вдоль осей системы координат. В этой статье вы будете находить компоненты заданного вектора, используя формулы как для двумерной, так и для трехмерной системы координат.

Вектор и его компоненты — краткий обзор

• Вектор имеет два компонента, на которые он может быть разбит, то есть на величину и направление.

• Используя метод гипотенузы, мы можем вычислить горизонтальную составляющую и вертикальную составляющую вектора, используя угол, который вектор образует с двумя составляющими.

• Скалярные величины (например, масса, высота, объем и площадь) — это физические величины, представленные одним числом, тогда как векторные величины (например, скорость, смещение и ускорение) — это величины, представленные в виде два компонента, то есть направление и величина.

• Векторные величины можно разбить на компоненты горизонтальной и вертикальной осей.

• Вектор, величина которого равна 1, называется единичным вектором.

• Векторы в основном представляют собой стрелки с величиной и направлением, поэтому, если вектор представляет какую-либо величину, то эта величина имеет и величину, и направление.

• Наиболее распространенными физическими величинами, которые представляются в виде векторов, являются перемещение, ускорение и скорость.

• Поскольку ускорение представляет скорость изменения скорости по отношению ко времени, требуется направление и величина.

• Перемещение, скорость и ускорение связаны друг с другом, поскольку для вычисления одного требуется значение другого, из-за чего все три являются векторными величинами.

 

Компоненты вектора Определение

В двумерной системе координат вы можете разбить любой вектор на его x-компоненту и y-компоненту. Обозначается как:

\[\overrightarrow{v}\] = \[(v_{x}, v_{y})\]

Рассмотрим следующий пример:

На диаграмме, показанной ниже, вектор v разделен на два его компоненты, которые являются \[v_{x}\] и . \[v_{y}\].

Считайте, что угол между вектором и его x-компонентой равен θ.

(Изображение будет загружено в ближайшее время)

Вектор и компоненты вектора здесь образуют прямоугольный треугольник, как показано ниже:

(Изображение будет загружено в ближайшее время)

Тригонометрические отношения дадут вам отношение между величиной вектора и компонентами вектора.

• \[cos\theta = \frac{\text{прилежащая сторона}}{\text{гипотенуза}} = \frac{v_{x}}{v}\]

• \[sin\theta = \frac{\text{противоположная сторона}}{\text{гипотенуза}} = \frac{v_{y}}{v}\]

• \[v_{x} = vcos\theta\]

• \[v_{y} = vsin\theta\]

Когда вы используете теорему Пифагора в прямоугольном треугольнике с длинами \[v_{x}\] и \[v_{y}\], ты понял, 9{2}}\]

1.

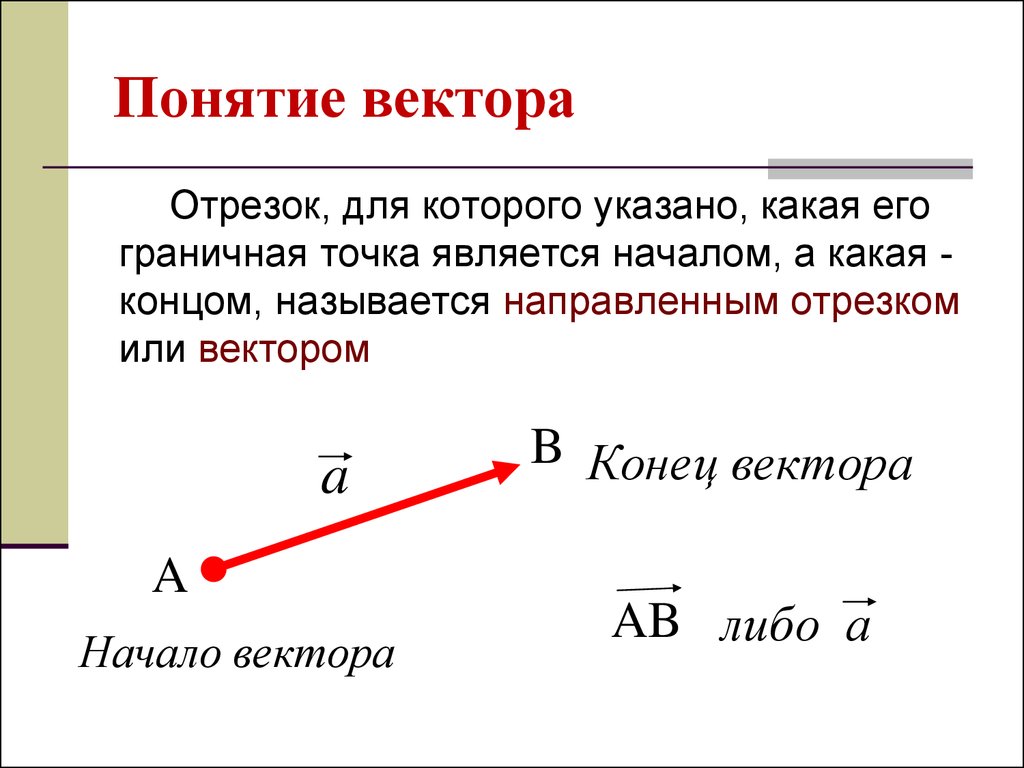Компоненты двумерного вектора

Рассмотрим, например, двумерный вектор \[\overrightarrow{a}\], который имеет начальную точку O в системе координат и имеет конечную также точка А.

Теперь, если вы проведете линии из точек O и A так, чтобы они пересекались в точке C и образовывали угол 90 друг с другом, вы получили бы два вновь сформированных вектора \[\overrightarrow{a_{x}}\] и \[\overrightarrow{a_{y}}\].

Говорят, что это компоненты вектора \[\overrightarrow{a}\].

(Изображение будет загружено в ближайшее время)

2. Компоненты трехмерного вектора

Точно так же, как двухмерные компоненты вектора, если вы разложите заданный вектор \[\overrightarrow{a}\]на его компоненты в трехмерной системе с осями x, y, z вы получите

\[\overrightarrow{a_{x}}\], \[\overrightarrow{a_{y}}\] и \[\overrightarrow {a_{z}}\]

Три вновь сформированных вектора известны как компоненты x, y, z вектора в 3D соответственно вектора \[\overrightarrow{a}\].

(Изображение будет загружено в ближайшее время)

Компоненты вектора Пример

Величина заданного вектора F и направление его вектора равны 60 по горизонтали. Найдите компоненты его вектора.

(Изображение будет загружено в ближайшее время)

Решение

\[F_{x} = F cos60\]

Решив это, вы получите \[10\times \frac{1}{2} = 5\].

\[F_{y} = F sin60\]

Решив это, вы получите \[10\times \frac{\sqrt{3}}{2} = 5\sqrt{3}\]

Следовательно, вектор F равен 5, \[5\sqrt{3}\].

Задача о компонентах вектора

Сила 20 Н образует с осью x угол 30 градусов. Найдите компоненты x и y данной силы.

Решение

Первый шаг — нарисовать схему. Ваша диаграмма будет выглядеть так:

(Изображение будет загружено в ближайшее время)

Затем найдите компоненты вектора заданной силы 20 Н.

Для этого найдите F _x = F cos 30 и F _y = F sin 30. 

Решив их, вы получите 3})\]

Следовательно, ваш ответ: \[10\sqrt{3}\] Ньютон.

F _y = F sin 30 = 20 x sin 30

= 20 x 0,5

Следовательно, ваш ответ 10 ньютонов.

Каковы будут результаты изучения векторов и их компонентов?

Векторы и их компоненты являются очень важной главой, которую преподают учащимся, и из этой главы задают много вопросов как на школьных, так и на конкурсных экзаменах. Расширенная версия векторов также включена в будущие главы. Основным результатом изучения векторов и их компонентов будет то, что учащиеся смогут различать, во-первых, двухмерные и трехмерные векторы и, во-вторых, скалярные величины и векторные величины. Учащиеся смогут разработать графическую модель для вычислений, таких как сложение и вычитание векторов, а также смогут обобщить взаимосвязь между скалярными величинами и векторными величинами.