Чему равен периметр: Периметр — урок. Математика, 2 класс.

Содержание

Чему равен периметр и площадь треугольника. Как найти площадь и периметр треугольника? Периметр и площадь треугольника

Любого треугольника равен сумме длин трёх его сторон. Общая формула для нахождения периметра треугольников:

P = a + b + c

где P — это периметр треугольника, a , b и c — его стороны.

Можно найти сложив последовательно длины его сторон или умножив длину боковой стороны на 2 и прибавив к произведению длину основания. Общая формула для нахождения периметра равнобедренных треугольников будет выглядеть так:

P = 2a + b

где P — это периметр равнобедренного треугольника, a — любая из боковых сторон, b — основание.

Можно найти сложив последовательно длины его сторон или умножив длину любой его стороны на 3. Общая формула для нахождения периметра равносторонних треугольников будет выглядеть так:

P = 3a

где P — это периметр равностороннего треугольника, a — любая из его сторон.

Площадь

Для измерения площади треугольника можно сравнить его с параллелограммом . Рассмотрим треугольник ABC :

Если взять равный ему треугольник и приставить его так, чтобы получился параллелограмм, то получится параллелограмм с той же высотой и основанием, что и у данного треугольника:

В данном случае общая сторона сложенных вместе треугольников является диагональю образованного параллелограмма. Из свойства параллелограммов известно, что диагональ всегда делит параллелограмм на два равных треугольника, значит площадь каждого треугольника равна половине площади параллелограмма.

Так как площадь параллелограмма равна произведению его основания на высоту, то площадь треугольника будет равна половине этого произведения. Значит для ΔABC площадь будет равна

Теперь рассмотрим прямоугольный треугольник:

Два равных прямоугольных треугольника можно сложить в прямоугольник, если прислонить их друг к другу гипотенузой.

Так как площадь прямоугольника равна произведению его смежных сторон, то площадь данного треугольника равна:

Из это можно сделать вывод, что площадь любого прямоугольного треугольника равна произведению катетов, разделённому на 2.

Из данных примеров можно сделать вывод, что площадь любого треугольника равна произведению длин основания и высоты, опущенной на основание, разделённому на 2 . Общая формула для нахождения площади треугольников будет выглядеть так:

S =	ah a
	2

где S — это площадь треугольника, a — его основание, h a — высота, опущенная на основание a .

В предложенном задании нас просят рассказать, как найти периметр и площадь треугольника. Для этого необходимо иметь представление, что собой представляет геометрическая фигура треугольник.

Треугольник

В математике треугольником называют геометрическую фигуру, которая образована тремя отрезками, которые соединяют между собой три точки, не лежащие на одной прямой.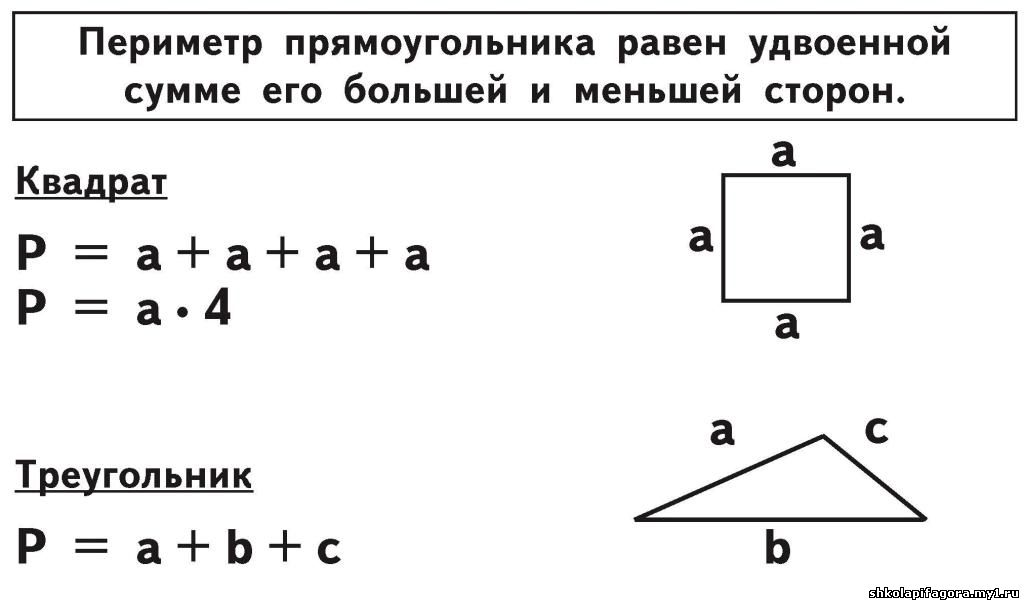 При этом эти точки называют вершинами треугольника, а отрезки их соединяющие сторонами треугольника.

Периметр и площадь треугольника

Нахождение периметра треугольника. Чтобы найти периметр треугольника необходимо знать длину всех его сторон. Тогда периметр находится путём их сложения.
Нахождение площади треугольника через основание и высоту. Зная основание и высоту треугольника мы можем найти его площадь по формуле:

S = 1/2 * a * h, где a — основание, а h — высота.

Нахождение площади треугольника через две стороны и угол между ними. Если нам известны две стороны треугольника и угол между ними, то мы можем найти его площадь по следующей формуле:

S = 1/ 2 * a * b * sin a (угла между сторонами).

Нахождение площади треугольника через три его стороны. Если нам известны три стороны треугольника, то мы можем найти его площадь, для чего сначала находим периметр, а затем решаем по формуле:

S = √(p·(p-a)·(p-b)·(p-c)).

Таким образом, мы рассмотрели геометрическую фигуру треугольник, формулу для нахождения его периметра и все возможные формулы для нахождения его площади.

Треугольник — это одна из базовых фигур, образованная тремя пресекающимися отрезками прямых. Точки пересечения называются вершинами, а сами отрезки сторонами треугольника. Периметр треугольника — это сумма длин его сторон. Находить площадь треугольника учат еще в школе и впоследствии эти знания используются многими людьми включая студентов, математиков и инженеров. В зависимости от исходный данных площадь треугольника может быть надена различными способами. Рассмотрим их все по порядку.

1 способ Если известны длины всех сторон треугольника a, b и с, то в данном случае периметр определяется как сумма длин всех сторон:

P = a + b + c

где P — периметр треугольника;
a, b, c — длины сторон треугольника.

В частном случае для равнобедренного треугольника данная формула примет следующий вид:

P = 3a

то есть длина стороны, умноженная на три.
Если треугольник будет равнобедренный, то формула может быть записана в виде:

P = 2a + c

где a — боковая сторона, c — основание.

2 способ

Но длины всех сторон могут быть заданы не всегда. Если известны только две стороны и величина угла между ними, то периметр треугольника может быть определен через нахождение третьей стороны, лежащей напротив угла β. Эта сторона (назовем ее с) будет равна квадратному корню из выражения

a2+b2-2∙a∙b∙cosβ

В этом случае периметр треугольника может быть найден по формуле:

P = a+b+√(a2+b2-2∙a∙b∙cosα)

где a, b — длины сторон;
α — величина угла между сторонами a и b.

3 способ
Если известна сторона и два прилегающих к ней угла, то периметр треугольника определяется по теореме синусов по формуле:

P = а+sinα∙а/(sin(180°-α-β)) + sinβ∙а/(sin(180°-α-β))

где — a — длина стороны треугольника;
α, β — величина прилегающих к стороне a углов.

4 способ
Если задача предполагает нахождение периметра треугольника по радиусу вписанной в него окружности и площади треугольника, то в данном случае периметр может быть определен по формуле.

В геометрии, а также в реальной жизни, каждый человек хотя бы несколько раз сталкивается с такой геометрической фигурой как треугольник. Это фигура с тремя углами, тремя противолежащими сторонами, которая является простейшим многоугольником. При желании можно распределить любой многоугольник на треугольники. Таким образом, при необходимости вычитать периметр или площадь многоугольника можно применить формулы расчета треугольника.

Основные характеристики треугольника это: периметр треугольника и площадь треугольника . Дополнительные характеристики это радиус вписанной и радиус описанной окружности. При расчете периметра и площади надо помнить, что расчет делается в зависимости от вида треугольников: остроугольники, тупо угольники, прямоугольники, равнобедренные, равносторонние .

Расчет периметра треугольника определяется достаточно просто с помощью простой формулы, которая суммирует размеры всех сторон. Таким образом, если обозначить стороны треугольника буквами а, b, c, в то время когда периметр треугольника обозначен буквой p, то соответственно формуле расчета периметра получаем:

p= a+ b+ c .

В случае расчета площади треугольника все намного сложнее. Таким образом, если вы не уверены в своих силах, то вы можете использовать специальную программу, которая позволит рассчитать треугольник (http://2mb.ru/matematika/kalkulyatory/on-line-raschet-treugolnika/) за считанные секунды. Но, а если все, же вам интересно, откуда взялся этот результат, то стоит углубляться в деталях.

Расчет площади треугольника делается в зависимости от того, какие данные о треугольнике известны, и в зависимости от типа треугольник. Существует множество формул, которые позволяют сделать расчет. Одна из формул позволяет сделать расчет площади тогда, когда известен периметр треугольника, и она носит название – формула Герона.

Формула Герона заключается в использовании значения полу периметра для расчета площади треугольника. Полу периметр это? часть периметра. Формула Герона: S=?p(p-a)(p-b)(p-c) , где буквой S обозначена площадь.

Расчет площади треугольника, когда известна одна сторона (а) и высота треугольника (h ), опущенная на эту сторону: S=(a*h)/2.

Расчет площади равностороннего треугольника : длину надо возвести на вторую степень, умножить на корень квадратный из трех и разделить на 4.

Расчет площади прямоугольного треугольника : длина катетов умножается между собой и разделяется на 2. Катеты это те стороны треугольника, которые образуют прямой угол.

Если материал был полезен, вы можете или поделиться данным материалом в социальных сетях:

Треугольник — двумерная фигура с тремя ребрами и таким же количеством вершин. Это одна из основных форм в геометрии. Объект имеет три угла, их суммарная градусная мера всегда равна 180°. Вершины принято обозначать латинскими буквами, например, ABC.

Теория

Треугольники можно классифицировать по разным признакам.

Если градусная мера всех его углов меньше 90 градусов, то его называют остроугольным, если один из них равен этому значению — прямоугольным, ну и в иных случаях — тупоугольным.

Когда треугольник имеет все стороны одинаковой величины, то именуют его равносторонним. На рисунке это отмечают перпендикулярной отрезку меткой. Углы в в таком случае всегда равны 60°.

Если же только две стороны треугольника равны, то его называют равнобедренным. В таком случае углы, находящиеся у основания, равны.

Треугольник, не подходящий под два предыдущих варианта, называют разносторонним.

Когда говорят, что два треугольника равны, это означает, что они имеют одинаковые размер и форму. Также они имеют одинаковые углы.

Если же совпадают исключительно градусные меры, то фигуры называют подобными. Тогда соотношение соответствующих сторон можно выразить определенным числом, которое называется коэффициентом пропорциональности.

Периметр треугольника через площадь или стороны

Как и в любом многоугольнике, периметр — это сумма длин всех сторон.

Для треугольника формула выглядит так: P = а + b + c, где a, b и c — длины сторон.

Существует еще один способ решения данной задачи. Он заключается в том, чтобы найти периметр треугольника через площадь.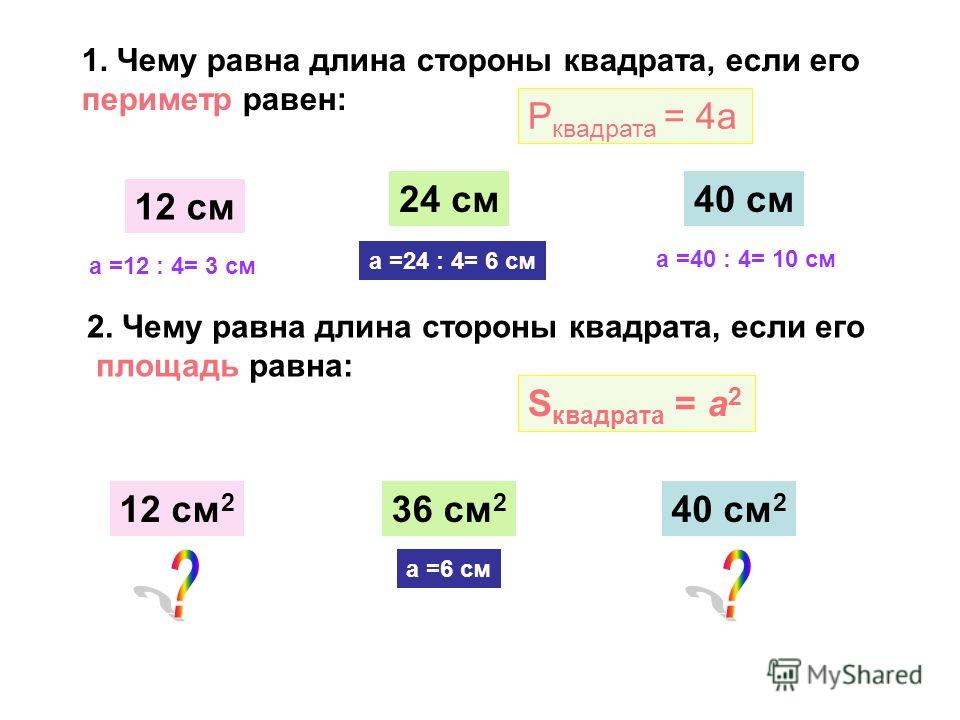 Для начала нужно знать уравнение, связывающее эти две величины.

S = p × r, где p — полупериметр, а r — радиус вписанной в объект окружности.

Весьма просто можно преобразовать уравнение в необходимый для нас вид. Получим:

Не забываем, что настощий периметр будет в 2 раз больше полученного.

Вот так просто решаются подобные примеры.

Чему равен периметр 8 см? – Обзоры Вики

Периметр — это расстояние вокруг прямоугольника. У прямоугольника 4 стороны: 2 из них будут длиной (8 см) и 2 из них шириной (3 см). Чтобы получить периметр, нужно сложить 2 длины и 2 ширины: 2 х 8 + 2 х 3. Следовательно, ответ таков: 22cm (не забудьте единицы измерения!)

Чему равен периметр квадрата со стороной 8 см? Следовательно, периметр и площадь квадрата равны 32 см и 64 см, а расстояние, пройденное мальчиком, равно 2 км.

Дополнительно Каков периметр 3 и 8? Периметр это сумма сторон. а если каждая сторона 38 см. тогда периметр равен 38+38+38 или 3×38=98 см.

Чему равна площадь 7см? Площадь квадрата равна A = s², где s — длина одной из 4 равных сторон квадрата. А = 49 см² это площадь квадрата со стороной 7см.

Как найти периметр восьмиугольника из площади?

Если длины всех сторон и измерения всех углов равны, восьмиугольник называется правильным восьмиугольником.
…
Формулы восьмиугольника.

Формулы для восьмиугольника
Площадь восьмиугольника	2a ² (1+√2)
Периметр восьмиугольника	8a

Как найти периметр равностороннего восьмиугольника? 1 Ответ

Для равностороннего треугольника: P=3×сторона=3s.
Для квадрата: P=4×сторона=4s. У правильного восьмиугольника 8 равных сторон, т.
Р=8×сторона=8с. Общая формула для периметра правильной фигуры будет выглядеть так:
P=n×сторона=n×s. n = количество сторон. и s = длина каждой стороны. В таком случае.

Каков диаметр восьмиугольника? Я предполагаю, что вы имеете в виду правильный восьмиугольник, в котором все стороны имеют одинаковую длину и все углы имеют одинаковую меру. д = (1 + √2) × 60 = 144.85 ноги.

Как мы находим периметр квадрата?

Периметр квадрата — это общая длина всех сторон квадрата. Следовательно, мы можем найти периметр квадрата с помощью складывая все четыре стороны. Периметр данного квадрата равен a + a + a + a. Поскольку все стороны квадрата равны, нам нужна только одна сторона, чтобы найти его периметр.

Также Как найти периметр квадрата? Формула периметра квадрата:

= Сторона+Сторона+Сторона+Сторона. Теперь, как мы знаем, длины всех четырех сторон квадрата равны, поэтому периметр в четыре раза больше длины любой стороны квадрата. Периметр квадрата = 4 х стороны.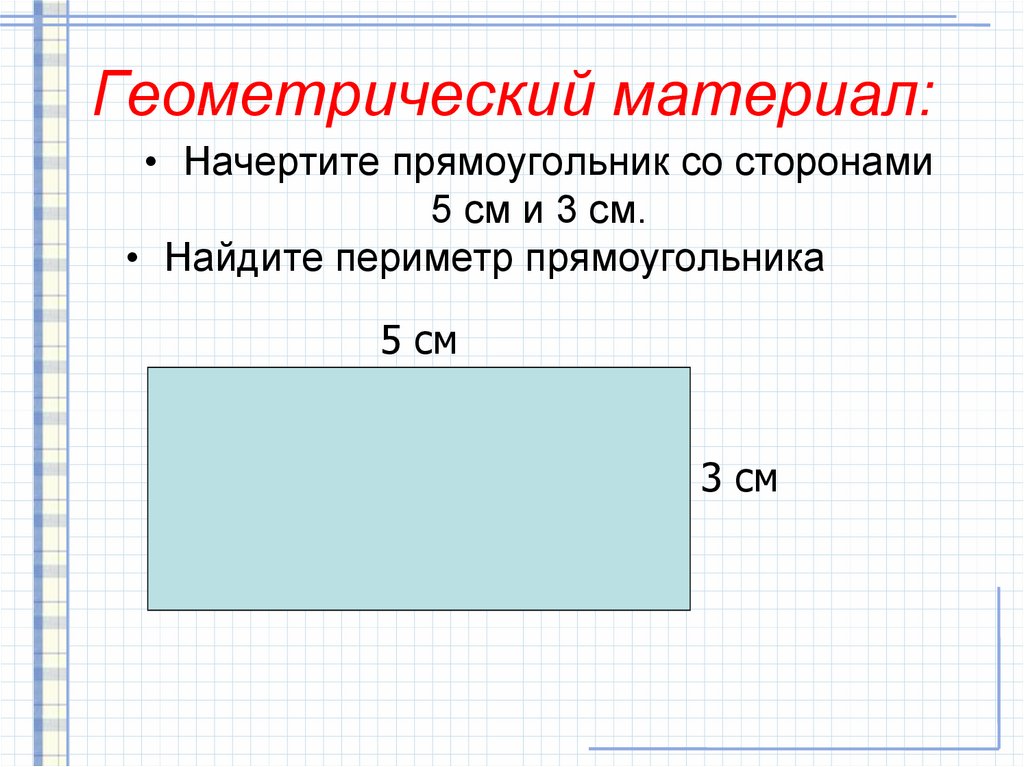 Возьмем в качестве примера квадрат со стороной «а».

Какова площадь и периметр квадрата?

Ответ: площадь квадрата равна квадрату длины его стороны, а периметр квадрата в 4 раза больше длины его стороны. Пусть длина стороны квадрата равна единицам «а».

Как найти периметр фигур? Чтобы найти периметр фигуры, вы складываете длину всех его ребер. Детям можно дать периметр фигуры и попросить вычислить длину немаркированных ребер.

Как найти периметр разных форм?

Как преобразовать площадь в периметр?

Разделите периметр на 4: это дает вам длину одной стороны. Затем возведите эту длину в квадрат: это даст вам площадь. В этом примере 14 ÷ 4 = 3.5. (3.5) ² = 12.25 квадратных футов.

Чему равен периметр 7 см? Теперь мы знаем, что периметр = сумма всех сторон. Следовательно, периметр квадрата со стороной 7 см равен 28cm.

Можем ли мы нарисовать квадрат со стороной 7 см да или нет? Можем ли мы нарисовать квадрат со стороной, равной 7 см? Объяснение: У квадрата все стороны равны по длине, а все углы равны 90 градусов. Следовательно, мы можем взять любые пять измерений, чтобы построить квадрат.

Как найти площадь круга диаметром 8 см?

Примеры предалгебры

Площадь круга равна Pi π умножить на радиус r в квадрате. Подставьте значение радиуса r = 8 в формулу площади круга. Pi π примерно равно 3.14. Возведи 8 в степень 2.

Сколько сторон в восьмиугольнике?

В геометрии восьмиугольник (от греческого ὀκτάγωνον oktágōnon, «восемь углов») — это 8 -сторонний многоугольник или 8-угольник.
…
Октагон.

Правильный восьмиугольник
Ребра и вершины	8
Символ Шляфли	{8}, т {4}
Диаграммы Кокстера – Дынкина
Группа симметрии	Двугранный (D ₈ ), заказ 2 × 8

Все ли стороны восьмиугольника равны? В правильном восьмиугольнике все стороны равны по длине, и все углы равны.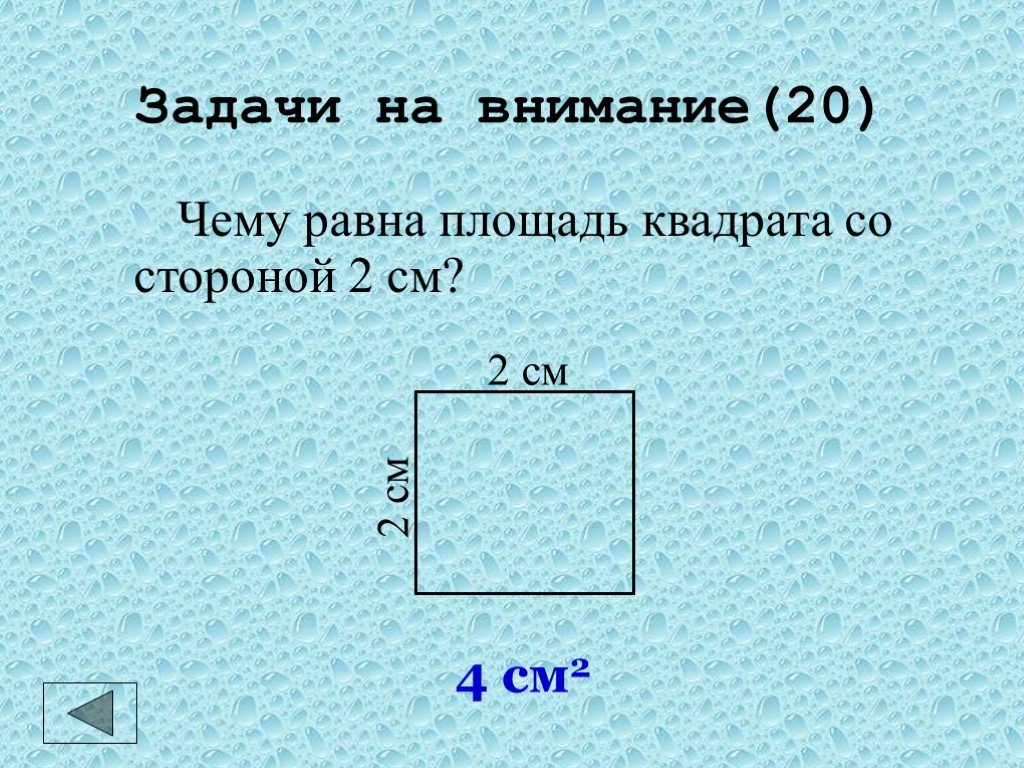 Внутренние углы в сумме составляют 1080°, а внешние углы в сумме составляют 360°. Внутренний угол при каждой вершине правильного восьмиугольника равен 135°.

Как найти периметр восьмиугольника по апофеме?

Re: Апофема

После того, как площадь найдена, используйте формулу P = 2 ⋅ площадь стиль отображения P=frac{2cdottext{область}}{a} P=a2⋅площадь найти периметр. a=длина апофемы и n=количество сторон.

Как найти размеры восьмиугольника?

Умножьте длину диаметра на расстояние от вершины до противоположной вершины., на 0.383, чтобы вычислить длину стороны. Например, диаметр составляет 10 дюймов — 10 дюймов, умноженных на 0.383, дают 3.83 дюйма.

Периметр – определение, значение и синонимы

ПЕРЕЙТИ К СОДЕРЖАНИЮ

периметры

Существительное периметр относится к границе замкнутого пространства. периметр дома — это линия его собственности. Для страны это будут границы этой страны.

От латинского слова, означающего «вокруг» ( per ) и «мера» ( metron ), периметр в основном представляет собой границу любого вида, измеряемую вокруг формы. По математике периметр относится к длине этой границы. На уроке геометрии вас могут попросить вычислить периметра многоугольника, который представляет собой сумму длин каждой стороны. Вы также можете услышать это слово, используемое военнослужащими или полицией, например, «защитить периметр » или «периметр был нарушен». Говорят, что баскетболист, который любит бросать с трехочковой линии, «действует на периметре ».

Определения периметра

существительное
линия, ограничивающая плоскую площадь
существительное
линия границы или область непосредственно внутри границы
синонимы: граница, край
существительное
размер чего-либо, определяемый расстоянием вокруг него
синонимы: длина окружности

ОТКАЗ ОТ ОТВЕТСТВЕННОСТИ: Эти примеры предложений появляются в различных источниках новостей и книгах, чтобы отразить использование слова «периметр» . Мнения, выраженные в примерах, не отражают мнение Vocabulary.com или его редакции. Отправьте нам отзыв

Слова, которые часто путают

параметр / периметр

Параметр — это ограничение, которое влияет на то, как что-то может быть сделано, а периметр — это контур физической области. Оба слова имеют особое значение в математике, но они снимают свои карманные протекторы и смягчают свои определения, когда присоединяются к остальным из нас.

Продолжить чтение…

ВЫБОР РЕДАКТОРА

Посмотреть

периметр в последний раз

Закройте пробелы в словарном запасе с помощью персонализированного обучения, которое фокусируется на обучении слова, которые нужно знать.

Начните изучение словарного запаса

Независимо от того, являетесь ли вы учителем или учеником, Vocabulary.com может направить вас или ваш класс на путь систематического улучшения словарного запаса.

Начать

Что такое периметр? — Измерение фигур в KS2 Maths

«Что такое периметр?» – Хорошо бы понять определение математических понятий начальной школы, прежде чем пытаться объяснить на примере. Периметр фигуры — это сумма длины внешнего края фигуры. Его можно найти, сложив длины всех отдельных ребер.

Содержание страницы

Что такое периметр?

На уровне математики в начальной школе KS2 мы можем думать о периметре как о пути. Если бы вы обошли фигуру, полностью следуя каждому краю и производя измерения на ходу, сумма этих измерений составила бы периметр.

Давайте подумаем о нескольких примерах, которые помогут вам и вашим детям найти периметр. Это поможет сделать его более понятным! В конце этого блога вы также можете найти несколько вопросов о периметре KS2 SAT. Они будут посвящены темам «5-й класс находит периметр» и «6-й класс находит периметр».

Итак, теперь, когда вы знаете, что такое периметр, давайте визуализируем его:

Полезным способом представления периметра и других понятий в математике KS2 является реальный пример, который часто помогает как учителям, так и учащимся визуализировать понятие. Давайте представим пример парка с одним входом и одним выходом. В этом парке есть дорожка, которая охватывает всю территорию парка и проходит по внешнему краю.

Измерение периметра в этом случае скажет нам длину этого пути. Теперь, когда мы знаем, как думать о периметре в некоторых примерах из реальной жизни, мы можем перейти к некоторым математическим примерам. Использование визуальных стимулов и графики является ключевым преимуществом математики в начальной школе онлайн.

Как вы учите детей периметру?

Обучение детей периметру может сбивать с толку, а также методы визуализации и сравнения с реальной жизнью, описанные выше, вы можете использовать распространенные примеры форм. Вопросы могут включать как простые, так и сложные формы. Хороший метод состоит в том, чтобы понять периметры простых фигур, чтобы затем использовать это для разбивки и решения более сложных вопросов. Также может быть полезно рисовать фигуры и использовать измерительные инструменты и канцелярские принадлежности, чтобы помочь учащимся найти периметр. Достаньте линейки всех форм и размеров и попросите детей начать самостоятельно измерять стороны фигур и складывать единицы измерения на линейке!

Как найти периметр треугольника:

Мы знаем, что треугольник является трехсторонней фигурой, поэтому периметр можно найти, просто сложив длины этих трех сторон. Давайте рассмотрим треугольник на изображении ниже;

Мы можем ясно видеть три стороны этой фигуры и их размеры. Чтобы найти периметр, все, что нам нужно сделать, это сложить эти длины. Итак, в этом случае периметр этой фигуры будет:

Периметр = 3 см + 5 см + 5 см = 13 см

Онлайн-уроки математики, которые повысят успеваемость вашего ребенка в школе!

В рамках нашей миссии по поддержке родителей в течение 2020 года Think Academy UK приглашала сотни британских учащихся начальной школы на наши успешные онлайн-курсы по математике.

Мы начинаем набор учеников начальной школы KS1 и KS2 на наш Весенний курс, который начнется в январе 2021 года! Родители используют наших онлайн-репетиторов по математике в качестве дополнения к обучению, которое происходит в школе. Все наши онлайн-курсы по математике с несколькими уровнями сложности используют современную платформу онлайн-обучения, являющуюся новаторской в Великобритании системой с двумя преподавателями. Это создает комплексный опыт обучения с руководством, подходящий для каждого ребенка, позволяя им наверстать упущенное и добиться прогресса в математике.

Как найти периметр квадрата:

Мы снова видим четыре стороны, каждая из которых имеет длину ребра. Как мы уже говорили, это квадрат, поэтому все стороны имеют одинаковую длину.
Теперь давайте подумаем о том, как найти периметр квадрата. Хотя у квадрата на одну сторону больше, чем у треугольника, найти периметр на самом деле может быть проще. Это потому, что мы знаем, что в квадрате все стороны имеют одинаковую длину. Итак, давайте подумаем о квадрате, изображенном ниже;

Периметр = 6 см + 6 см + 6 см + 6 см = 4×6 см = 24 см

Из этого следует, что для вычисления периметра квадрата нужно просто знать длину одной стороны, затем умножить ее на 4 , и вы отработали периметр! Это будет частый вопрос в начальной школе по математике KS2, но для 5-го и 6-го классов начальной школы он обычно будет немного сложнее. Тем не менее всегда важно знать эти формулы, поскольку они могут быть частью более сложного вопроса о периметре KS2 SAT.

Как найти периметр прямоугольника?

Вот еще один пример математических вопросов KS2, содержащий больше примеров из реальной жизни. Вы часто обнаружите, что вопросы относятся к реальному сценарию или объекту, часто это может быть что-то вроде спортивной площадки или бассейна, и в этих двух конкретных примерах вы часто найдете прямоугольники, назовем эти подходы (а) и (б). Иногда эти вопросы будут представлены ниже; в стиле (а)

В этом примере (а), как и в случае с квадратом и треугольником, вам даны длины всех четырех сторон, и вам просто нужно сложить это, то есть периметр на фото прямоугольный бассейн;

Периметр = 10 м + 10 м + 6 м + 6 м = 32 м

Однако есть и другой способ найти этот вопрос, таким образом (б) вам будут даны только две стороны. Как этот пример;

Ответ на этот вопрос зависит от понимания фигур учащимся начальной школы, поэтому он должен заметить, что это прямоугольник и, следовательно, можно найти две неуказанные стороны.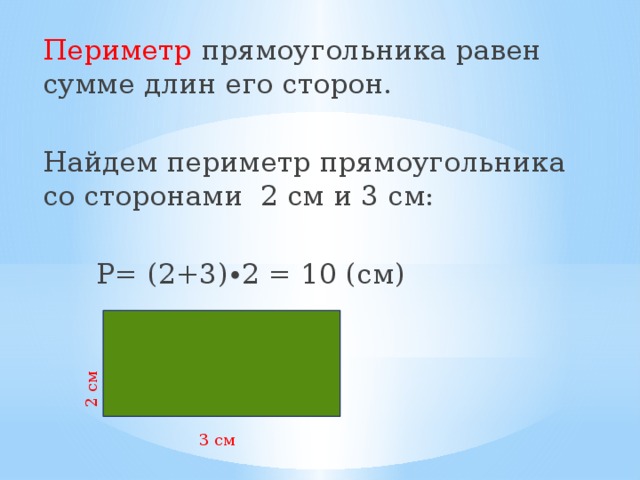 т.е. в прямоугольнике две параллельные стороны всегда имеют одинаковую длину. Следовательно, из такого примера; более длинная сторона, которая не указана, также будет равна 12 м, а более короткая — 5 м.

Следовательно, периметр этого прямоугольника можно вычислить как;

Периметр = 12 м + 5 м + 12 м + 5 м = 34 м

Как найти периметр круга поэтому мы должны использовать другой метод. Для математического уровня KS2 мы делаем это с помощью простой формулы, которую мы должны запомнить. Периметр круга = 2 x π

x r = 2πr, где π — математическая константа числа пи, а r — радиус окружности.

Давайте посмотрим на пример;

Как мы видим из вопроса, мы должны знать радиус круга, чтобы узнать периметр. Радиус просто половина диаметра.

Итак, в этом примере мы видим, что радиус окружности равен 3, теперь мы можем просто использовать формулу 2πr со значением r равным 3.

Периметр = 2 x π х 3 = 6π или 18,84956….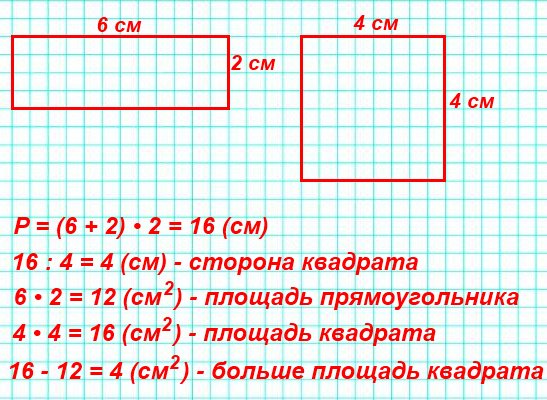

Какова длина окружности?

Теперь вы можете увидеть слово окружность круга, встречающееся в вопросах KS2 по математике для начальной школы. Окружность круга — это периметр, просто как! Они означают одно и то же. Таким образом, для вычисления длины окружности используется тот же метод, что и выше. Легкий!

Периметр круга = длина окружности

Как найти периметр многоугольника?

Запоминание общей формулы, которая поможет ученику 5 или 6 класса найти периметр многоугольника, поможет вам всегда быть в курсе дел. Во-первых, напоминание — многоугольник — это любая фигура с более чем тремя сторонами и прямыми ребрами, т. е. та, которую можно нарисовать на плоской поверхности.

Для правильного многоугольника , т. е. все стороны имеют одинаковую длину, периметр определяется как;

Периметр = длина одной стороны x количество сторон

Для неправильного многоугольника , , т. е. стороны равны , а не , все они одинаковой длины, периметр определяется как;

Периметр = сумма всех длин сторон

Площадь и периметр одинаковы?

Нет! Важно помнить о разнице между площадью и периметром, так как они часто используются вместе в вопросах. Хороший способ подумать о разнице между этими двумя понятиями — это внутреннее и внешнее. Периметр формы — это измерение вне ее, как мы видели, траектории вокруг формы. Принимая во внимание, что площадь формы — это измерение всего, что находится внутри формы. Еще одним ключевым отличием является единица измерения: площадь будет измеряться в «единицах в квадрате», тогда как периметр будет измеряться только в единицах. т.е. Вы можете обнаружить, что площадь фигуры равна 3 метрам в квадрате, но периметр фигуры равен 3 метрам. Визуально картинка ниже помогает нам понять это.

Площадь этих двух фигур находится путем подсчета квадратов внутри фигур, то есть части, выделенной красным цветом. Периметр этих фигур задается черной линией, окружающей край формы.

Вопрос-головоломка

Здесь нам дан прямоугольный кусок дерева. ПЕРИМЕТР этого куска дерева равен 14 м, и нам известно, что самая длинная сторона равна 5 м. Можно узнать длины других сторон?

Комбинирование фигур

Многие вопросы по математике в начальной школе KS2 будут включать комбинированные фигуры, иногда давая вам только одну или две длины, поэтому вы должны 1) выяснить, каковы длины других сторон, и 2) работать каков общий периметр. Вот пример.

В этом вопросе у нас есть 6 равносторонних треугольников двух разных размеров. Они окрашены по-разному, поэтому мы можем сказать, но может быть так, что они не разделены так явно.

Нам только говорят, что длина стороны меньшего равностороннего треугольника равна 2 см (помните, что равносторонний означает, что все стороны имеют одинаковую длину). Итак, давайте посмотрим, что мы замечаем на картинке;

Сторона большего треугольника = 3 сторонам меньшего треугольника. т.е. Следовательно, сторона большего треугольника равна 6 см.
Низ фигуры состоит из 2 сторон меньшего треугольника, т.е. = 4см.
Есть 2 зеленые стороны = 2 х 2см.
Снаружи также есть 2 стороны синего треугольника. т.е. 6см х 2.
Итак, теперь мы хотим сложить все эти стороны вместе:

Периметр = 6 см + 6 см + 2 см + 2 см + 4 см

КС2 Рабочие листы по периметру и практику

1 балл за правильный расчет; (13 + (12-5)) x 4.

Онлайн-обучение математике для учащихся начальной школы с 1 по 6 классы.

В ответ на большое количество запросов от родителей мы открыли регистрацию на наш весенний курс, который начнется в январе 2021 года. Для родителей, решивших записать своего ребенка сегодня, мы предлагаем ограниченную по времени скидку для раннего бронирования. Узнайте больше здесь.

Родители используют наших онлайн-репетиторов по математике в качестве дополнения к школьному обучению.