Иррациональное число » задачи — страница 3
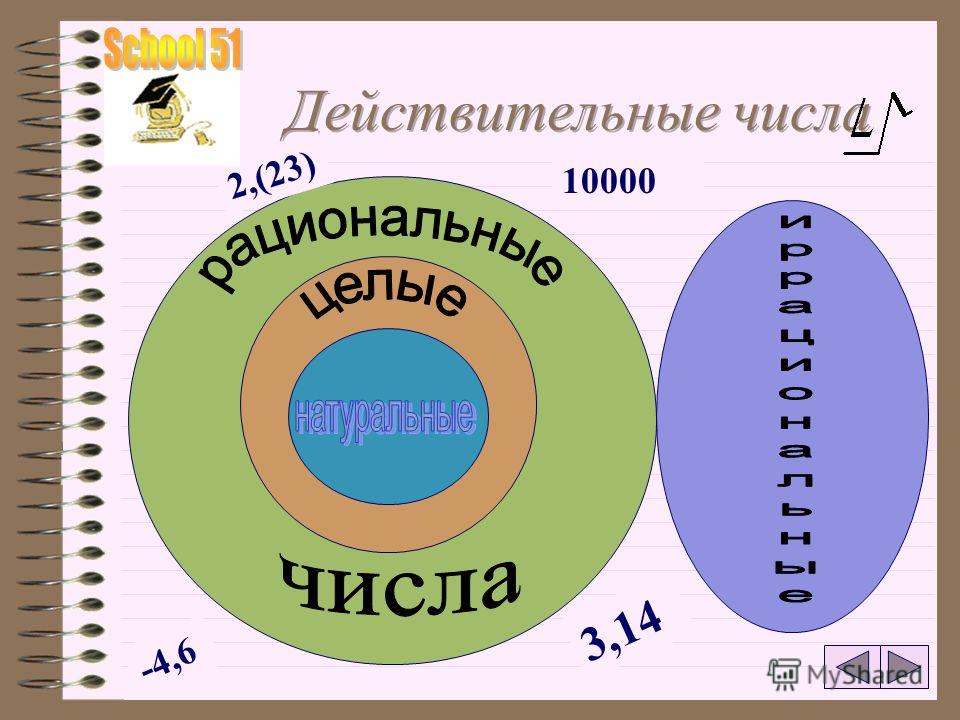
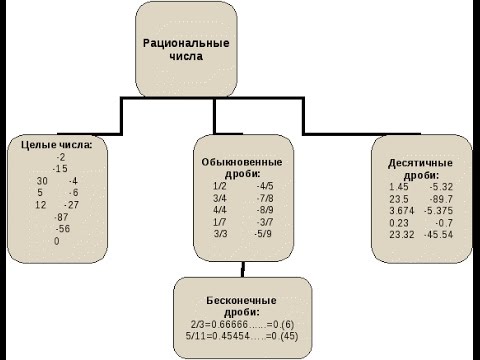
числа »
Приведите пример числа которое:
а) является рациональным, но не является целым
б) является целым, но не является натуральным
в) является действительным, но не является рациональным
г) является действительным, но не является иррациональным
Решение: А) Рациональное число — такое, которое можно выразить отношением двух целых чисел. Например, дробь 1/2 — рациональное, но не целое число.
б) К целым числам, помимо натуральных, относятся им противоположные и нуль. Например, число -5 будет целым и не натуральным.
в) Не является рациональным — не выразимо в виде отношения целых чисел. Например, корень из 2 — действительное иррациональное.
г) А например число 0,(3), оно же 1/3, является действительным рациональнымОтветьте на вопросы:
1) Может ли сумма двух действительных чисел быть
рациональным числом, а разность – иррациональным? Обоснуйте свой ответ. {\frac{1}{3}} = \frac{2}{3} $$
{\frac{1}{3}} = \frac{2}{3} $$
Подставляем в исходное выражение
$$ 3*3* \frac{2}{3}- \frac{2}{3} = \frac{16}{3}=5 \frac{1}{3} $$Верно ли утверждение, что квадратный корень из рационального числа есть иррациональное число ?
Решение: Иррациональное число — это число, не являющееся рациональным, то есть такое, которое нельзя представить в виде отношения двух целых чисел.
Если Вы помните, рациональные числа были введены потому, что во множестве целых чисел не всегда можно выполнить деление. Например, существует целое число, которое является результатом деления 8 на 2, но не существует целого числа, которое является результатом деления 8 на 3. Поэтому были введены рациональные числа, то есть дроби вида p/q. Целые числа стали их подмножеством, когда q=1.
Для выполнимости деления рациональных чисел достаточно, но вот для извлечения корней — нет. Например, не существует рационального числа, которое было бы результатом извлечения квадратного корня из двух. Поэтому производят дальнейшее расширение системы чисел. К рациональным числам добавляют ещё и иррациональные, и все они вместе образуют множество действительных чисел.
Поэтому производят дальнейшее расширение системы чисел. К рациональным числам добавляют ещё и иррациональные, и все они вместе образуют множество действительных чисел.
Если не вдаваться в подробности, то рациональные числа можно отличить от иррациональных следующим образом. Рациональные числа, если их записать десятичной дробью, обязательно дадут конечную или бесконечную периодическую дробь. Это тоже легко доказать. Иррациональные же числа, записанные в виде десятичной дроби, оказываются представленными бесконечной НЕпериодической дробью.
Типичным примером иррационального числа является корень квадратный из двух. Пи — тоже иррациональное число, причем в определенном смысле более сложное, чем корень из двух, потому что Пи нельзя представить в виде корня из рационального числа. Но это уже немножко высший пилотаж.
Есть вопросы — пишите в комментарий.Рациональное число это число m/n m целое число n натуральное число к примеру 1/10
ираациональное которое не может быть преставлено как m/n m целоеt n натуральное
к примеру корень (2/3) иррациональное число
но корень (1/4)=1/1 или корень (1/25) = 1/5
поэтому утверждение неверноПочему при сложении иррационального и рационального чисел, всегда в ответе получается иррациональное число?
Решение: Потому что иррациональное число это бесконечная непериодическая дробь. Оно при сложении с рациональным никак не может дать рациональный ответ
Оно при сложении с рациональным никак не может дать рациональный ответИррациональное число- число, которое не может быть представлено в виде дроби, эти числа содержат период и писать их можно до бесконечность( к примеру 2,(34)), а рациональные числа можно представить в виде дроби.
А теперь попробуйте сложить 1,7676767676.+2,3, у вас всё равно получится число, которое представить в виде дроби не возможно, а это значит, что оно является иррациональным.
123
Иррациональное число
Иррациональное число — это вещественное число, которое не является рациональным, то есть не может быть представлено в виде обыкновенной дроби m n {displaystyle {frac {m}{n}}} , где m , n {displaystyle m,n} — целые числа, n ≠ 0 {displaystyle n
eq 0} .
Другими словами, множество иррациональных чисел есть разность I = R ∖ Q {displaystyle mathbb {I} =mathbb {R} ackslash mathbb {Q} } множеств вещественных и рациональных чисел.
О существовании иррациональных чисел (точнее отрезков, несоизмеримых с отрезком единичной длины), знали уже древние математики: им была известна, например, несоизмеримость диагонали и стороны квадрата, что равносильно иррациональности числа 2 {displaystyle {sqrt {2}}} .
Иррациональными являются, среди прочих, отношение длины окружности к диаметру круга (число π), число Эйлера e, золотое сечение φ, квадратный корень из двух. Все квадратные корни натуральных чисел, кроме полных квадратов, иррациональны.
Иррациональные числа также могут рассматриваться через бесконечные непрерывные дроби. Следствием доказательства Кантора является то, что действительные числа не счётны, а рациональные — счётны, отсюда следует, что почти все действительные числа иррациональны.
Свойства
- Сумма двух положительных иррациональных чисел может быть рациональным числом.
- Иррациональные числа определяют дедекиндовы сечения во множестве рациональных чисел, у которых в нижнем классе нет наибольшего, а в верхнем нет наименьшего числа.
- Множество иррациональных чисел всюду плотно на числовой прямой: между любыми двумя различными числами имеется иррациональное число.
Алгебраические и трансцендентные числа
Каждое иррациональное число является либо алгебраическим, либо трансцендентным. Множество алгебраических чисел является счётным множеством. Так как множество вещественных чисел несчётно, то множество иррациональных чисел также несчётно.
Каждое вещественное трансцендентное число является иррациональным; алгебраическое число может быть как рациональным, так и иррациональным. .
.
Множество иррациональных чисел является множеством второй категории.
Иррациональные числа и непрерывные дроби
Иррациональное число представляются бесконечной непрерывной дробью. Пример, число e:
e = [ 2 ; 1 , 2 , 1 , 1 , 4 , 1 , 1 , 6 , 1 , … , 1 , 2 n , 1 , … ] . {displaystyle e=[2;1,2,1,1,4,1,1,6,1,ldots ,1,2n,1,ldots ].}
Квадратичным иррациональностям соответствуют периодические непрерывные дроби.
ϕ = 1 + 5 2 = [ 1 ; 1 , 1 , 1 , 1 , … ] . {x}} для любого рационального x ≠ 0 {displaystyle x
eq 0}
{x}} для любого рационального x ≠ 0 {displaystyle x
eq 0}
Примеры доказательства иррациональности
Корень из 2
Допустим противное: 2 {displaystyle {sqrt {2}}} рационален, то есть представляется в виде дроби m n {displaystyle {frac {m}{n}}} , где m {displaystyle m} — целое число, а n {displaystyle n} — натуральное число.
Возведём предполагаемое равенство в квадрат:
2 = m n ⇒ 2 = m 2 n 2 ⇒ m 2 = 2 n 2 {displaystyle {sqrt {2}}={frac {m}{n}}Rightarrow 2={frac {m^{2}}{n^{2}}}Rightarrow m^{2}=2n^{2}} . {2}} невозможно. Значит, исходное предположение было неверным, и 2 {displaystyle {sqrt {2}}} — иррациональное число.
{2}} невозможно. Значит, исходное предположение было неверным, и 2 {displaystyle {sqrt {2}}} — иррациональное число.
Двоичный логарифм числа 3
Допустим противное: log 2 3 {displaystyle log _{2}3} рационален, то есть представляется в виде дроби m n {displaystyle {frac {m}{n}}} , где m {displaystyle m} и n {displaystyle n} — целые числа. Поскольку log 2 3 > 0 {displaystyle log _{2}3>0} , m {displaystyle m} и n {displaystyle n} могут быть выбраны положительными. {m}} чётно, а правая часть получившегося равенства нечётна. Получаем противоречие.
{m}} чётно, а правая часть получившегося равенства нечётна. Получаем противоречие.
См. раздел «Доказательство иррациональности» в статье «e».
История
Античность
Концепция иррациональных чисел была неявным образом воспринята индийскими математиками в VII веке до нашей эры, когда Манава (приблизительно 750—690 года до нашей эры) выяснил, что квадратные корни некоторых натуральных чисел, таких как 2 и 61, не могут быть явно выражены.
Первое доказательство существования иррациональных чисел, а точнее существование несоизмеримых отрезков, обычно приписывается пифагорейцу Гиппасу из Метапонта (приблизительно 470 год до нашей эры). Нет точных данных о том, иррациональность какого числа была доказана Гиппасом. Согласно легенде он нашёл его, изучая длины сторон пентаграммы. Поэтому разумно предположить, что это было золотое сечение, так как это и есть отношение диагонали к стороне в правильном пятиугольнике.
Греческие математики назвали это отношение несоизмеримых величин алогос (невыразимым), однако согласно легендам не воздали Гиппасу должного уважения. Существует легенда, что Гиппас совершил открытие, находясь в морском походе, и был выброшен за борт другими пифагорейцами «за создание элемента вселенной, который отрицает доктрину, что все сущности во вселенной могут быть сведены к целым числам и их отношениям». Открытие Гиппаса поставило перед пифагорейской математикой серьёзную проблему, разрушив лежавшее в основе всей теории предположение, что числа и геометрические объекты едины и неразделимы.
Существует легенда, что Гиппас совершил открытие, находясь в морском походе, и был выброшен за борт другими пифагорейцами «за создание элемента вселенной, который отрицает доктрину, что все сущности во вселенной могут быть сведены к целым числам и их отношениям». Открытие Гиппаса поставило перед пифагорейской математикой серьёзную проблему, разрушив лежавшее в основе всей теории предположение, что числа и геометрические объекты едины и неразделимы.
Феодор Киренский доказал иррациональность корней натуральных чисел до 17 (исключая, естественно, точные квадраты — 1, 4, 9 и 16), но остановился на этом, так как имевшаяся в его инструментарии алгебра не позволяла доказать иррациональность квадратного корня из 17. По поводу того, каким могло быть это доказательство, историками математики было высказано несколько различных предположений. Согласно наиболее правдоподобному предположению Жана Итара, оно было основано на теореме о том, что нечётное квадратное число делится на восемь с остатком один.
Позже Евдокс Книдский (410 или 408 г. до н. э. — 355 или 347 г. до н. э.) развил теорию пропорций, которая принимала во внимание как рациональные, так и иррациональные отношения. Это послужило основанием для понимания фундаментальной сути иррациональных чисел. Величина стала считаться не числом, но обозначением сущностей, таких как отрезки прямых, углы, площади, объёмы, промежутки времени — сущностей, которые могут меняться непрерывно (в современном понимании этого слова). Величины были противопоставлены числам, которые могут меняться лишь «прыжками» от одного числа к соседнему, например, с 4 на 5. Числа составляются из наименьшей неделимой величины, в то время как величины можно уменьшать бесконечно.
Поскольку никакое количественное значение не сопоставлялось величине, Евдокс смог охватить и соизмеримые, и несоизмеримые величины при определении дроби как отношения двух величин, и пропорции как равенства двух дробей. Убрав из уравнений количественные значения (числа), он избежал ловушки, состоящей в необходимости назвать иррациональную величину числом. Теория Евдокса позволила греческим математикам совершить невероятный прогресс в геометрии, предоставив им необходимое логическое обоснование для работы с несоизмеримыми величинами. Десятая книга «Начал» Евклида посвящена классификации иррациональных величин.
Теория Евдокса позволила греческим математикам совершить невероятный прогресс в геометрии, предоставив им необходимое логическое обоснование для работы с несоизмеримыми величинами. Десятая книга «Начал» Евклида посвящена классификации иррациональных величин.
Средние века
Средние века ознаменовались принятием таких понятий как ноль, отрицательные числа, целые и дробные числа, сперва индийскими, затем китайскими математиками. Позже присоединились арабские математики, которые первыми стали считать отрицательные числа алгебраическими объектами (наряду и на равных правах с положительными числами), что позволило развить дисциплину, ныне называемую алгеброй.
Арабские математики соединили древнегреческие понятия «числа» и «величины» в единую, более общую идею вещественных чисел. Они критически относились к представлениям Евклида об отношениях, в противовес ей они развили теорию отношений произвольных величин и расширили понятие числа до отношений непрерывных величин. В своих комментариях на Книгу 10 «Начал» Евклида, персидский математик аль-Махани (ок. 800 года н. э.) исследовал и классифицировал квадратичные иррациональные числа и более общие кубические иррациональные числа. Он дал определение рациональным и иррациональным величинам, которые он и называл иррациональными числами. Он легко оперировал этими объектами, но рассуждал как об обособленных объектах, например:
800 года н. э.) исследовал и классифицировал квадратичные иррациональные числа и более общие кубические иррациональные числа. Он дал определение рациональным и иррациональным величинам, которые он и называл иррациональными числами. Он легко оперировал этими объектами, но рассуждал как об обособленных объектах, например:
В противовес концепции Евклида, что величины суть в первую очередь отрезки прямых, Аль Махани считал целые числа и дроби рациональными величинами, а квадратные и кубические корни — иррациональными. Он также ввел арифметический подход к множеству иррациональных чисел, поскольку именно он показал иррациональность следующих величин:
Египетский математик Абу Камил (ок. 850 г. н. э. — ок. 930 г. н. э.) был первым, кто счел приемлемым признать иррациональные числа решением квадратных уравнений или коэффициентами в уравнениях — в основном, в виде квадратных или кубических корней, а также корней четвёртой степени. В X веке иракский математик Аль-Хашими вывел общие доказательства (а не наглядные геометрические демонстрации) иррациональности произведения, частного и результатов иных математических преобразований над иррациональными и рациональными числами. Аль-Хазин (900 г. н. э. — 971 г. н. э.) приводит следующее определение рациональной и иррациональной величины:
Аль-Хазин (900 г. н. э. — 971 г. н. э.) приводит следующее определение рациональной и иррациональной величины:
Многие из этих идей были позже переняты европейскими математиками после перевода на латынь арабских текстов в XII веке. Аль Хассар, арабский математик из Магриба, специализировавшийся на исламских законах о наследстве, в XII веке ввел современную символьную математическую нотацию для дробей, разделив числитель и знаменатель горизонтальной чертой. Та же нотация появилась затем в работах Фибоначчи в XIII веке. В течение XIV—XVI вв. Мадхава из Сангамаграмы и представители Керальской школы астрономии и математики исследовали бесконечные ряды, сходящиеся к некоторым иррациональным числам, например, к π {displaystyle pi } , а также показали иррациональность некоторых значений тригонометрических функций. Джестадева привёл эти результаты в книге «Йуктибхаза».
Новое время
В XVII—XVIII веке в математике прочно укрепились комплексные числа, вклад в изучение которых внесли Абрахам де Муавр (1667—1754) и Леонард Эйлер (1707—1783). Когда теория комплексных чисел в XIX веке стала замкнутой и чёткой, стало возможным классифицировать иррациональные числа на алгебраические и трансцендентные (доказав при этом существование трансцендентных чисел), тем самым переосмыслив работы Евклида по классификации иррациональных чисел. По этой теме в 1872 году были опубликованы работы Вейерштрасса, Гейне, Кантора и Дедекинда. Хотя ещё в 1869 году Мерэ начал рассмотрения, схожие с работами Гейне, именно 1872 год принято считать годом рождения теории. Метод Вейерштрасса был полностью изложен Сальваторе Пинкерле в 1880 году, а Дедекинд получил дополнительную известность благодаря более поздней работе автора (1888) и одобрению Поля Таннери (1894). Вейерштрасс, Кантор и Гейне обосновывали свои теории при помощи бесконечных рядов, в то время как Дедекинд работал с (ныне так называемыми) дедекиндовыми сечениями множества вещественных чисел, разделяя все рациональные числа на два множества с определёнными характеристическими свойствами.
Когда теория комплексных чисел в XIX веке стала замкнутой и чёткой, стало возможным классифицировать иррациональные числа на алгебраические и трансцендентные (доказав при этом существование трансцендентных чисел), тем самым переосмыслив работы Евклида по классификации иррациональных чисел. По этой теме в 1872 году были опубликованы работы Вейерштрасса, Гейне, Кантора и Дедекинда. Хотя ещё в 1869 году Мерэ начал рассмотрения, схожие с работами Гейне, именно 1872 год принято считать годом рождения теории. Метод Вейерштрасса был полностью изложен Сальваторе Пинкерле в 1880 году, а Дедекинд получил дополнительную известность благодаря более поздней работе автора (1888) и одобрению Поля Таннери (1894). Вейерштрасс, Кантор и Гейне обосновывали свои теории при помощи бесконечных рядов, в то время как Дедекинд работал с (ныне так называемыми) дедекиндовыми сечениями множества вещественных чисел, разделяя все рациональные числа на два множества с определёнными характеристическими свойствами.
Цепные дроби, тесно связанные с иррациональными числами (цепная дробь, представляющая данное число, бесконечна тогда и только тогда, когда число является иррациональным), были впервые исследованы Катальди в 1613 году, затем снова привлекли к себе внимание в работах Эйлера, а в начале XIX века — в работах Лагранжа. {2}} иррационально, откуда иррациональность π {displaystyle pi } следует тривиально (рациональное число в квадрате дало бы рациональное).
{2}} иррационально, откуда иррациональность π {displaystyle pi } следует тривиально (рациональное число в квадрате дало бы рациональное).
Существование трансцендентных чисел было доказано Лиувиллем в 1844—1851 годах. Позже Георг Кантор (1873) показал их существование, используя другой метод, и обосновал, что любой интервал вещественного ряда содержит бесконечно много трансцендентных чисел. Шарль Эрмит доказал в 1873 году, что e трансцендентно, а Фердинанд Линдеман в 1882 году, основываясь на этом результате, показал трансцендентность π {displaystyle pi } . Доказательство Линдеманна было затем упрощено Вейерштрассом в 1885 году, ещё более упрощено Давидом Гильбертом в 1893 году и, наконец, доведено до почти элементарного Адольфом Гурвицем и Паулем Горданом.
7.1 Рациональные и иррациональные числа. Предварительная алгебра 2e
Цели обучения
К концу этого раздела вы сможете:
- Определение рациональных и иррациональных чисел
- Классифицировать различные типы действительных чисел
Будь готов 7.
 1
1Прежде чем начать, пройдите этот тест на готовность.
Запишите 3.193.19 в виде неправильной дроби.
Если вы пропустили эту проблему, просмотрите пример 5.4.
Будь готов 7.2
Запишите 511511 в виде десятичного числа.
Если вы пропустили эту проблему, просмотрите пример 5.30.
Будь готов 7.3
Упрощение: 144.144.
Если вы пропустили эту проблему, просмотрите пример 5.69.
Определение рациональных и иррациональных чисел
Поздравляем! Вы завершили первые шесть глав этой книги! Пришло время подвести итоги того, что вы уже сделали в этом курсе, и подумать о том, что впереди. Вы научились складывать, вычитать, умножать и делить целые числа, дроби, целые числа и десятичные дроби. Вы познакомились с языком и символами алгебры, упростили и оценили алгебраические выражения. Вы решили множество различных типов приложений. Вы заложили хорошую прочную основу, необходимую для достижения успеха в алгебре.
В этой главе мы проверим ваши навыки. Мы еще раз взглянем на типы чисел, с которыми мы работали во всех предыдущих главах. Мы будем работать со свойствами чисел, которые помогут вам улучшить ваше чувство числа. И мы попрактикуемся в их использовании так, как будем использовать при решении уравнений и других алгебраических процедурах.
Мы уже описали числа как счетные числа, целые числа и целые числа. Вы помните, в чем разница между этими типами чисел?
| счет чисел | 1,2,3,4…1,2,3,4… |
| целые числа | 0,1,2,3,4…0,1,2,3,4… |
| целых | …−3,−2,−1,0,1,2,3,4……−3,−2,−1,0,1,2,3,4… |
Рациональные числа
Какие числа вы бы получили, если бы начали со всех целых чисел, а затем включили все дроби? Числа, которые вы получили бы, образуют множество рациональных чисел. Рациональное число — это число, которое можно записать как отношение двух целых чисел.
Рациональное число — это число, которое можно записать как отношение двух целых чисел.
Рациональное число
Рациональное число — это число, которое можно записать в виде pq,pq, где pp и qq — целые числа, а q≠o.q≠o.
Все дроби, как положительные, так и отрицательные, являются рациональными числами. Несколько примеров
45,-78,134 и-20345,-78,134 и-203
Каждый числитель и каждый знаменатель являются целыми числами.
Нам нужно просмотреть все числа, которые мы использовали до сих пор, и убедиться, что они рациональны. Определение рациональных чисел говорит нам, что все дроби рациональны. Теперь мы рассмотрим счетные числа, целые числа, целые числа и десятичные дроби, чтобы убедиться, что они рациональны.
Являются ли целые числа рациональными числами? Чтобы решить, является ли целое число рациональным, мы пытаемся записать его как отношение двух целых чисел. Самый простой способ сделать это — записать дробь со знаменателем один.
3=31−8=−810=013=31−8=−810=01
Поскольку любое целое число можно представить как отношение двух целых чисел, все целые числа являются рациональными числами. Помните, что все счетные числа и все целые числа тоже целые, а значит, они тоже рациональны.
Что насчет десятичных знаков? Являются ли они рациональными? Давайте рассмотрим несколько, чтобы увидеть, можем ли мы записать каждое из них как отношение двух целых чисел. Мы уже видели, что целые числа являются рациональными числами. Целое число -8-8 может быть записано как десятичное число -8.0.-8.0. Итак, ясно, что некоторые десятичные дроби рациональны.
Подумайте о десятичной дроби 7.3.7.3. Можем ли мы записать это как отношение двух целых чисел? Поскольку 7.37.3 означает 7310,7310, мы можем записать это как неправильную дробь, 7310,7310. Итак, 7,37,3 — это отношение целых чисел 7373 и 10,10. Это рациональное число.
В общем случае любое десятичное число, которое заканчивается после ряда цифр (например, 7,37,3 или -1,2684)-1,2684), является рациональным числом.
Пример 7.1
Запишите каждое как отношение двух целых чисел: ⓐ−15−15ⓑ6,816,81ⓒ−367,−367.
Решение
| ⓐ | |
| −15−15 | |
| Запишите целое число в виде дроби со знаменателем 1. | −151−151 |
| ⓑ | |
| 6.816.81 | |
| Запишите десятичную дробь как смешанное число. | 681100681100 |
| Затем преобразуйте его в неправильную дробь. | 681100681100 |
| ⓒ | |
| −367−367 | |
Преобразуйте смешанное число в неправильную дробь. | −277−277 |
Попробуй 7.1
Запишите каждое как отношение двух целых чисел: ⓐ−24−24ⓑ3,57,3,57.
Попробуй 7.2
Запишите каждое как отношение двух целых чисел: ⓐ−19−19 ⓑ8,41,8,41.
Давайте посмотрим на десятичную форму чисел, которые, как мы знаем, являются рациональными. Мы видели, что каждое целое число является рациональным числом, поскольку a=a1a=a1 для любого целого числа, п.в. Мы также можем преобразовать любое целое число в десятичное, добавив десятичную точку и ноль.
Целое-2,-1,0,1,2,3Десятичное-2.0,-1.0,0.0,1.0,2.0,3.0Эти десятичные числа останавливаются. Целое-2,-1,0,1,2,3Десятичное-2.0, −1.0,0.0,1.0,2.0,3.0Эти десятичные числа останавливаются.
Мы также видели, что каждая дробь является рациональным числом. Посмотрите на десятичную форму дробей, которые мы только что рассмотрели.
Соотношение целых чисел45,-78,134,-203 Десятичные формы 0,8,-0,875,3,25,-6,666… Эти десятичные дроби либо останавливаются, либо повторяются. −6,666… Эти десятичные дроби либо останавливаются, либо повторяются. −6,66—
−6,666… Эти десятичные дроби либо останавливаются, либо повторяются. −6,66—
О чем говорят вам эти примеры? Каждое рациональное число можно записать как в виде отношения целых чисел, так и в виде десятичной дроби, которая либо останавливается, либо повторяется. В таблице ниже показаны числа, которые мы рассмотрели, выраженные в виде отношения целых чисел и десятичных дробей.
| Рациональные числа | ||
|---|---|---|
| Дроби | Целые числа | |
| Номер | 45,-78,134,-20345,-78,134,-203 | -2,-1,0,1,2,3-2,-1,0,1,2,3 |
| Отношение целого числа | 45,-78,134,-20345,-78,134,-203 | −21,−11,01,11,21,31−21,−11,01,11,21,31 |
| Десятичное число | 0,8,-0,875,3,25,-6,6-,0,8,-0,875,3,25,-6,6-, | −2,0,−1,0,0,0,1,0,2,0,3,0−2,0,−1,0,0,0,1,0,2,0,3,0 |
Иррациональные числа
Существуют ли какие-либо десятичные дроби, которые не останавливаются и не повторяются? Да. Число ππ (греческая буква пи, произносится как «пирог»), которое очень важно для описания кругов, имеет десятичную форму, которая не заканчивается и не повторяется.
Число ππ (греческая буква пи, произносится как «пирог»), которое очень важно для описания кругов, имеет десятичную форму, которая не заканчивается и не повторяется.
π=3,141592654…….π=3,141592654…….
Точно так же десятичные представления квадратных корней целых чисел, которые не являются полными квадратами, никогда не останавливаются и никогда не повторяются. Например,
5=2,236067978…..5=2,236067978…..
Десятичное число, которое не заканчивается и не повторяется, не может быть записано как отношение целых чисел. Мы называем такие числа иррациональными числами.
Иррациональное число
Иррациональное число — это число, которое нельзя записать как отношение двух целых чисел. Его десятичная форма не прерывается и не повторяется.
Давайте обобщим метод, который мы можем использовать, чтобы определить, является ли число рациональным или иррациональным.
Если десятичная форма числа
- останавливается или повторяется, число рациональное.

- не останавливается и не повторяется, число иррациональное.
Пример 7.2
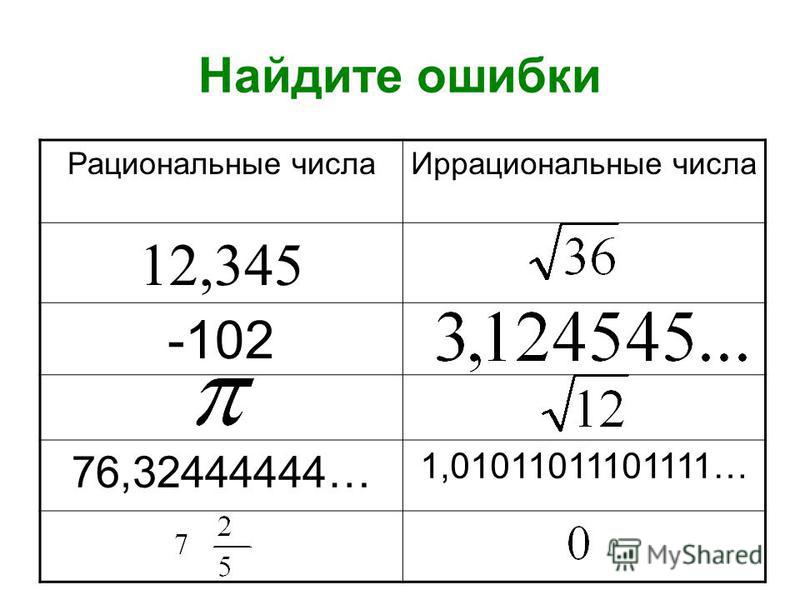
Определите каждое из следующего как рациональное или иррациональное:
- ⓐ0,583–0,583–
- ⓑ0.4750.475
- ⓒ3,605551275…3,605551275…
Решение
ⓐ 0,583–0,583–
Полоска над числом 33 указывает на то, что оно повторяется. Следовательно, 0,583–0,583– — это повторяющаяся десятичная дробь и, следовательно, рациональное число.
ⓑ 0,4750,475
Это десятичное число заканчивается после 55, поэтому это рациональное число.
ⓒ 3,605551275…3,605551275…
Многоточие (…)(…) означает, что это число не заканчивается. Нет повторяющегося набора цифр. Поскольку число не останавливается и не повторяется, оно иррационально.
Попробуй 7.3
Определите каждое из следующего как рациональное или иррациональное:
ⓐ0,290,29ⓑ0,816–0,816–ⓒ2,515115111…2,515115111…
Попробуй 7.
 4
4Определите каждое из следующего как рациональное или иррациональное:
ⓐ0,23–0,23–ⓑ0,1250,125ⓒ0,418302…0,418302…
Давайте теперь подумаем о квадратных корнях. Квадратные корни из полных квадратов всегда являются целыми числами, поэтому они рациональны. Но десятичные формы квадратных корней чисел, которые не являются идеальными квадратами, никогда не останавливаются и никогда не повторяются, поэтому эти квадратные корни иррациональны.
Пример 7.3
Определите каждое из следующего как рациональное или иррациональное:
- ⓐ3636
ⓑ4444
Решение
ⓐ Число 3636 является полным квадратом, так как 62=36,62=36. Итак, 36=6,36=6. Поэтому 3636 рационально.
ⓑ Помните, что 62=3662=36 и 72=49,72=49, поэтому 4444 не является полным квадратом.
Это означает, что число 4444 иррационально.
Попробуй 7,5
Определите каждое из следующего как рациональное или иррациональное:
- ⓐ8181
- ⓑ1717
Попробуй 7.
 6
6Определите каждое из следующего как рациональное или иррациональное:
ⓐ116116
ⓑ121121
Классификация действительных чисел
Мы видели, что все счетные числа являются целыми числами, все целые числа являются целыми числами и все целые числа являются рациональными числами. Иррациональные числа представляют собой отдельную категорию. Когда мы складываем рациональные числа и иррациональные числа, мы получаем множество действительных чисел.
На рис. 7.2 показано, как связаны наборы чисел.
Рисунок 7.2 Эта диаграмма иллюстрирует отношения между различными типами действительных чисел.
Вещественные числа
Действительные числа — это числа, которые могут быть рациональными или иррациональными.
Вам не кажется странным термин «действительные числа»? Существуют ли числа, которые не являются «настоящими», и если да, то какими они могут быть? На протяжении веков единственными числами, о которых люди знали, были те, которые мы сейчас называем реальными числами. Затем математики открыли множество мнимых чисел. В этом курсе вы не столкнетесь с мнимыми числами, но вы столкнетесь с ними позже, изучая алгебру.
Затем математики открыли множество мнимых чисел. В этом курсе вы не столкнетесь с мнимыми числами, но вы столкнетесь с ними позже, изучая алгебру.
Пример 7.4
Определите, является ли каждое из чисел в следующем списке ⓐ целым числом, ⓑ целым числом, ⓒ рациональным числом, ⓓ иррациональным числом и ⓔ действительным числом.
−7 145,8,5,5,9,−64−7 145,8,5,5,9,−64
Решение
ⓐ Целые числа 0,1,2,3,… 0,1,2,3,… Число 88 — единственное заданное целое число.
ⓑ Целые числа — это целые числа, их противоположности и 0,0. Из заданных чисел −7−7 и 88 — целые числа. Также обратите внимание, что 6464 — это квадрат 88, поэтому −64=−8,−64=−8. Таким образом, целые числа равны −7,8,−64,−7,8,−64.
ⓒ Поскольку все целые числа рациональны, числа −7,8 и −64−7,8 и −64 также рациональны. Рациональные числа также включают дроби и десятичные дроби, которые заканчиваются или повторяются, поэтому 145 и 5,9145 и 5,9 являются рациональными.
ⓓ Число 55 не является полным квадратом, поэтому 55 иррационально.
ⓔ Все указанные номера действительны.
Сведем результаты в таблицу.
| Номер | Целиком | Целое число | Рационал | Иррациональный | Реальный |
|---|---|---|---|---|---|
| −7−7 | ✓✓ | ✓✓ | ✓✓ | ||
| 145145 | ✓✓ | ✓✓ | |||
| 88 | ✓✓ | ✓✓ | ✓✓ | ✓✓ | |
| 55 | ✓✓ | ✓✓ | |||
5. 95.9 95.9 | ✓✓ | ✓✓ | |||
| −64−64 | ✓✓ | ✓✓ | ✓✓ |
Попробуй 7.7
Определите, является ли каждое число ⓐ целым числом, ⓑ целым числом, ⓒ рациональным числом, ⓓ иррациональным числом и ⓔ действительным числом: −3,−2,0,3–,95,4,49,−3,−2,0,3 –,95,4,49.
Попробуй 7,8
Определите, является ли каждое число ⓐ целым числом, ⓑ целым числом, ⓒ рациональным числом, ⓓ иррациональным числом и ⓔ действительным числом: −25,−38,−1,6,121,2,041975…−25,−38,−1, 6,121,2.041975…
Раздел 7.1 Упражнения
Практика ведет к совершенству
Рациональные числа
В следующих упражнениях запишите как отношение двух целых чисел.
1.
- ⓐ 55
- ⓑ 3.193.19
2.
- ⓐ 88
- ⓑ −1,61−1,61
3.
- ⓐ −12−12
- ⓑ 9.2799.279
4.
- ⓐ−16−16
- ⓑ4.3994.399
В следующих упражнениях определите, какие из данных чисел рациональны, а какие иррациональны.
5.
0,750,75, 0,223–0,223–, 1,39174…1,39174…
6.
0,360,36, 0,94729…0,94729…, 2,528–2,528–
7.
0,45—0,45—, 1,919293…1,919293…, 3,593,59
8.
0,13–,0,42982…0,13–,0,42982…, 1,8751,875
В следующих упражнениях определите, является ли каждое число рациональным или иррациональным.
9.
- ⓐ 2525
- ⓑ 3030
10.
- ⓐ4444
- ⓑ4949
11.
- ⓐ 164164
- ⓑ 169169
12.
- ⓐ 225225
- ⓑ 216216
Классификация действительных чисел
В следующих упражнениях определите, является ли каждое число целым, целым, рациональным, иррациональным и действительным.
13.
−8−8, 0,1,95286….0,1,95286…., 125125, 3636, 99
14.
−9−9, −349−349, −9−9, 0,409—0,409—, 116116, 77
15.
−100−100, −7−7, −83−83, −1−1, 0,770,77, 314314
Математика на каждый день
16.
Экскурсия Все пятиклассники начальной школы Линкольна отправятся на экскурсию в музей науки. С учетом всех детей, учителей и сопровождающих будет 147147 человек. Каждый автобус вмещает 4444 человека.
ⓐ Сколько потребуется автобусов?
ⓑ Почему ответ должен быть целым числом?
ⓒ Почему нельзя округлить ответ обычным способом?
17.
Уход за детьми Серена хочет открыть лицензированный детский сад. Ее штат требует, чтобы на каждого учителя приходилось не более 1212 детей. Она хотела бы, чтобы ее детский сад обслуживал 4040 детей.
ⓐ Сколько потребуется учителей?
ⓑ Почему ответ должен быть целым числом?
ⓒ Почему нельзя округлить ответ обычным способом?
Письменные упражнения
18.
Своими словами объясните разницу между рациональным числом и иррациональным числом.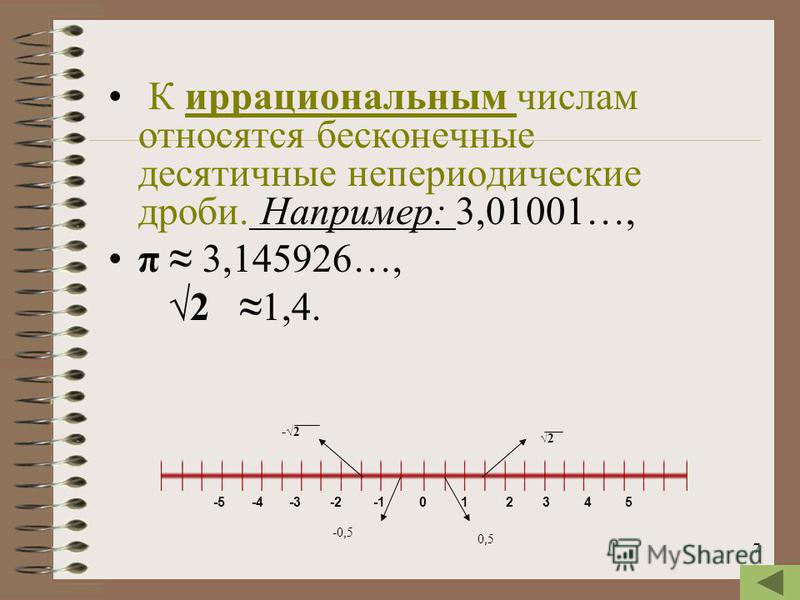
19.
Объясните, как наборы чисел (счетные, целые, целые, рациональные, иррациональные, действительные) связаны друг с другом.
Самопроверка
ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство в выполнении целей этого раздела.
ⓑ Если большинство ваших чеков:
…уверенно. Поздравляем! Вы достигли целей в этом разделе. Подумайте об учебных навыках, которые вы использовали, чтобы вы могли продолжать их использовать. Что вы сделали, чтобы обрести уверенность в своих способностях делать эти вещи? Быть конкретной.
…с некоторой помощью. Это нужно решать быстро, потому что темы, которые вы не осваиваете, становятся выбоинами на вашем пути к успеху. В математике каждая тема основывается на предыдущей работе. Прежде чем двигаться дальше, важно убедиться, что у вас есть прочная основа. Кого вы можете попросить о помощи? Ваши одноклассники и преподаватель являются хорошими ресурсами. Есть ли в кампусе место, где есть репетиторы по математике? Можно ли улучшить свои учебные навыки?
Есть ли в кампусе место, где есть репетиторы по математике? Можно ли улучшить свои учебные навыки?
… нет, я не понимаю! Это предупреждающий знак, и вы не должны его игнорировать. Вы должны немедленно обратиться за помощью, иначе вы быстро будете поражены. Как можно скорее обратитесь к инструктору, чтобы обсудить вашу ситуацию. Вместе вы можете придумать план, как получить необходимую вам помощь.
4 примера рациональных чисел
В контексте математики рациональное число — это число, которое может быть выражено как отношение двух целых чисел. Рациональное число — это число, равное частному двух целых чисел стр. и кв. Другими словами, рациональное число можно представить в виде некоторой дроби, в которой числитель и знаменатель являются целыми числами. Вот некоторые примеры рациональных чисел:
- Число 8 является рациональным, потому что его можно выразить как дробь 8/1 (или дробь 16/2)
- дробь 5/7 является рациональным числом, потому что это частное из двух целых чисел 5 и 7
- десятичное число 1,5 является рациональным, поскольку его можно представить в виде дроби 3/2
- повторяющееся десятичное число 0,333… эквивалентно рациональному числу 1/3
Традиционно множество всех рациональных чисел обозначается жирным шрифтом Q . Рациональные числа отличаются от натуральных, целых и действительных чисел тем, что являются надмножеством первых 2 и подмножеством последних. Также существует иррациональных чисел ; числа, которые не могут быть выражены как отношение двух целых чисел. Примером иррационального числа является √2. √2 нельзя записать как частное двух целых чисел.
Рациональные числа отличаются от натуральных, целых и действительных чисел тем, что являются надмножеством первых 2 и подмножеством последних. Также существует иррациональных чисел ; числа, которые не могут быть выражены как отношение двух целых чисел. Примером иррационального числа является √2. √2 нельзя записать как частное двух целых чисел.
Давайте сделаем шаг назад и поговорим о различных видах чисел.
Виды чисел
Некоторых может удивить, что существуют разные классы чисел. В конце концов, число есть число, так как же некоторые числа могут фундаментально отличаться от других чисел? Короче говоря, числа можно различать по тому, как они ведут себя при сложении, вычитании, умножении или делении.
Натуральные числа
Авторы и права: Good Free Photos CC0 1.0
Начнем с самой основной группы чисел, натуральных чисел . Набор натуральных чисел (обозначается N ) состоит из набора всех обычных целых чисел {1, 2, 3, 4,…} Натуральные числа также иногда называют счетными числами , потому что числа, которые мы используем для подсчета дискретных количеств вещей. Ключевой особенностью натуральных чисел является то, что они могут быть представлены без какой-либо дробной или десятичной части . Существует бесконечное количество натуральных чисел от 1 до бесконечности.
Ключевой особенностью натуральных чисел является то, что они могут быть представлены без какой-либо дробной или десятичной части . Существует бесконечное количество натуральных чисел от 1 до бесконечности.
Натуральные числа считаются самым основным типом чисел, потому что все другие виды чисел могут быть определены как расширения натуральных чисел. Традиционно натуральные числа не содержат числа ноль (0), хотя некоторые математики считают 0 натуральным числом.
Натуральные числа закрыты при сложении и умножении. Это означает, что если вы сложите или умножите любые два натуральных числа, вашим ответом будет еще одно натуральное число. Сложение 4 и 4 дает натуральное число 8, а умножение 5 на 1 000 000 дает натуральное число 5 000 000. Сложение или умножение двух натуральных чисел всегда дает другое натуральное число, без исключений.
А как насчет вычитания? Натуральные числа — это , а не , замкнутые при вычитании. Это означает, что если вы вычтете два натуральных числа, ваш ответ не всегда может быть натуральным числом, что приводит нас к…
Целые числа
Далее следуют целые числа. Целые числа (обозначаемые Z ) состоят из всех натуральных чисел и всех отрицательных целых чисел (…-4, -3, -2, -1). Множество целых чисел строится путем добавления аддитивной инверсии каждого натурального числа, поэтому он содержит все положительные и отрицательные целые числа {…-4, -3, -2, -1, 0, 1, 2, 3, 4,…}. Как следствие, все натуральные числа также являются целыми. Как и в случае с натуральными числами, существует бесконечное количество целых чисел, простирающихся от отрицательной бесконечности до положительной бесконечности.
Целые числа (обозначаемые Z ) состоят из всех натуральных чисел и всех отрицательных целых чисел (…-4, -3, -2, -1). Множество целых чисел строится путем добавления аддитивной инверсии каждого натурального числа, поэтому он содержит все положительные и отрицательные целые числа {…-4, -3, -2, -1, 0, 1, 2, 3, 4,…}. Как следствие, все натуральные числа также являются целыми. Как и в случае с натуральными числами, существует бесконечное количество целых чисел, простирающихся от отрицательной бесконечности до положительной бесконечности.
Предоставлено: WikiCommons CC0 1.0
Как и натуральные числа, целые числа замкнуты при сложении и вычитании. Сложение или умножение любых двух целых чисел всегда дает другое целое число. Введение отрицаний в наши системы счисления приводит к тому, что целые числа также замыкаются при вычитании. Вычитание любых двух целых чисел всегда даст вам другое целое число. 6−3 = -3 и 12−40 = -28.
Теперь у нас есть набор чисел, закрытый при сложении, умножении и вычитании. А как же деление? Недолгое размышление должно сказать вам, что нет, целые числа равны 9.0669, а не закрыто под подразделением. Деление двух целых чисел не всегда может привести к другому целому числу. Это понимание приводит нас к следующему набору чисел…
А как же деление? Недолгое размышление должно сказать вам, что нет, целые числа равны 9.0669, а не закрыто под подразделением. Деление двух целых чисел не всегда может привести к другому целому числу. Это понимание приводит нас к следующему набору чисел…
Рациональные числа
Авторы и права: Pixabay CC0 1.0
Введите рациональные числа. Сложение рациональных чисел (обозначаемое как Q ) позволяет нам выражать числа как частное двух целых чисел. Каждое рациональное число может быть однозначно представлено некоторой неприводимой дробью. Число 3/2 является рациональным числом, потому что оно выражается в виде дроби в простейшей форме. Следовательно, рациональное число 6/4 также равно 3/2, потому что 6/4 можно упростить до 3/2. Все целые числа (и, следовательно, все натуральные числа) можно представить в виде неприводимой дроби (8 = 8/1 и -5 = -5/1), поэтому все целые и натуральные числа также являются рациональными числами.
Рациональные числа добавляются в систему счисления, чтобы можно было закрыть числа при делении (за единственным исключением деления на 0).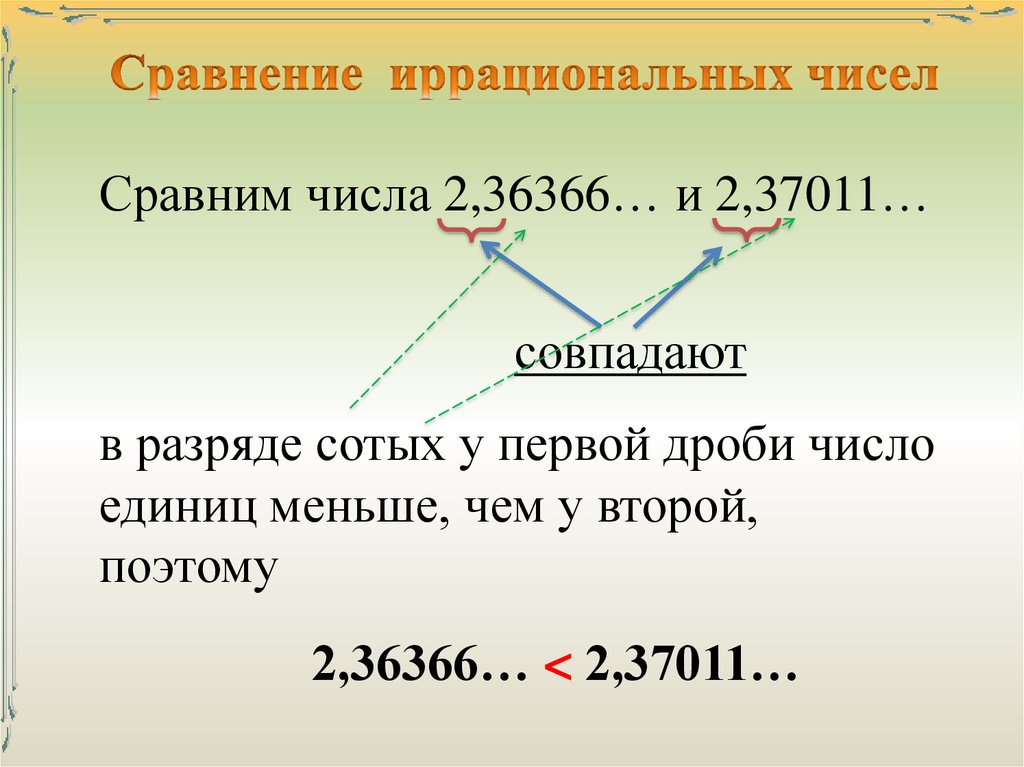 Частное любых двух рациональных чисел всегда может быть выражено как другое рациональное число. Это понимание можно увидеть в общем правиле деления дробей (то есть рациональных чисел).
Частное любых двух рациональных чисел всегда может быть выражено как другое рациональное число. Это понимание можно увидеть в общем правиле деления дробей (то есть рациональных чисел).
a/b ÷ c/d = ad/bc, когда d и b ≠ 0
a/b и c/d — рациональные числа, означающие, что по определению a, b, c и d — целые числа. Поскольку целые числа замкнуты относительно умножения, ad и bc также являются целыми числами. ad/bc представлен как отношение двух целых чисел, что является точным определением рационального числа. Следовательно, рациональные числа замкнуты относительно деления.
Рациональные числа также могут быть представлены в виде десятичных дробей. Преобразовать дробь в десятичную запись очень просто: все, что вам нужно сделать, это решить задачу деления в длинную и разделить числитель на знаменатель. Деление неприводимой дроби даст вам один из двух результатов: либо (i) длинное деление закончится некоторой конечной десятичной последовательностью, либо (ii) длинное деление даст бесконечно повторяющуюся последовательность десятичных знаков (например, 1/3 = 0,333… и 6). /11 = 0,5454…).
/11 = 0,5454…).
Преобразование десятичной дроби в дробь также просто. Все, что вам нужно сделать, это умножить десятичную дробь на некоторую степень 10, чтобы избавиться от десятичной точки и упростить полученную дробь.
например) 0,25 × 100/100 = 25/100 = 1/4
Рациональные числа представляют собой простейший набор чисел, который замыкается под действием 4 основных арифметических операций: сложения, вычитания, умножения и деления. Это свойство делает их чрезвычайно полезными в повседневной жизни. Однако рациональные числа — это еще не конец истории, поскольку существует очень важный класс чисел, для которых 90 669 нельзя выразить 90 360 как отношение двух целых чисел.
Иррациональные числа
Кредит: Дминасян через WikiCommons CC BY-SA 4.0
Иррациональное число — это число, которое не может быть выражено как отношение двух целых чисел. Иррациональные числа не могут быть представлены дробью в низшей форме. Два набора рациональных и иррациональных чисел исключают друг друга; никакое рациональное число не является иррациональным, и никакое иррациональное число не является рациональным. Типичные примеры иррациональных чисел включают π, число Эйлера e и золотое сечение φ. Ни одно из этих трех чисел не может быть выражено как частное двух целых чисел.
Типичные примеры иррациональных чисел включают π, число Эйлера e и золотое сечение φ. Ни одно из этих трех чисел не может быть выражено как частное двух целых чисел.
Откуда мы вообще знаем, что иррациональное число существует? Вот простое доказательство от противного, которое показывает, что √2 — иррациональное число:
Предположим, что √2 — рациональное число. Если √2 — рациональное число, то это означает, что его можно представить в виде неприводимой дроби двух целых чисел. Назовем эти два целых числа p и q .
(1.) √2 = p/q
Поскольку p/q — неприводимая дробь (согласно определению рационального числа), у них нет общих делителей. Возведение обеих сторон в квадрат, чтобы избавиться от левого радикала, дает нам:
(2.) 2 = P 2 /Q 2
, который мы можем переставить в:
(3.) 2Q 2 = P 2
2 — четное число, потому что 2 — один из его множителей. Единственный способ, которым p 2 может быть четным, состоит в том, что p само по себе четно. Если p четно, то существует некоторое число k такое, что p = 2 k . Замена 2 K для P в уравнении (3.) Дает нам:
Единственный способ, которым p 2 может быть четным, состоит в том, что p само по себе четно. Если p четно, то существует некоторое число k такое, что p = 2 k . Замена 2 K для P в уравнении (3.) Дает нам:
(4.) 2Q 2 = (2K) 2
(5.) 2Q 2 = 4K 2
9 (5.) можно переписать как:
(6.) q 2 = 2k 2
По аналогичным рассуждениям q 2 и q должны быть четными. Следовательно, и p , и q являются четными числами. Однако это противоречит нашему требованию из (1.), что p и q не имеют общих факторов. Поскольку мы получили противоречие, наше исходное предположение (что √2 рационально) должно быть ложным. Следовательно, √2 — иррациональное число, и его нельзя выразить как частное двух целых чисел.
Иррациональные числа поднимают голову повсюду. Как оказалось, квадратные корни большинства натуральных чисел иррациональны. Многие часто встречающиеся числа в математике иррациональны. Например, число π, которое представляет собой отношение диаметра круга к его длине окружности, иррационально. Кроме того, число Эйлера e , уникальное число, натуральный логарифм которого равен 1, также является иррациональным.
Какое-то время считалось, что все числа рациональные. Озабоченность рациональными числами восходит к Древней Греции с учением пифагорейцев. Пифагорейцы были квазирелигиозной сектой, верившей, что числа являются основными составляющими Вселенной. Центральным элементом их убеждений была идея о том, что все количества можно выразить рациональными числами. Легенда гласит, что пифагорейец Гиппас впервые обнаружил существование иррациональных чисел, пытаясь найти гипотенузу прямоугольного треугольника со сторонами равной длины. Гиппас обнаружил, что длину гипотенузы нельзя понимать как пропорциональную длинам ее сторон, и при этом открыл иррациональные числа.

 {\frac{1}{3}} = \frac{2}{3} $$
{\frac{1}{3}} = \frac{2}{3} $$ Поэтому производят дальнейшее расширение системы чисел. К рациональным числам добавляют ещё и иррациональные, и все они вместе образуют множество действительных чисел.
Поэтому производят дальнейшее расширение системы чисел. К рациональным числам добавляют ещё и иррациональные, и все они вместе образуют множество действительных чисел. 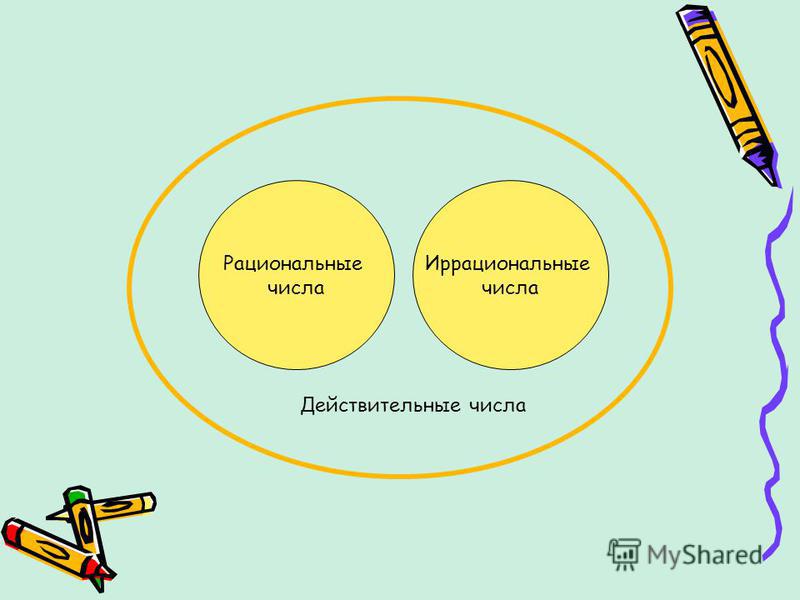 Оно при сложении с рациональным никак не может дать рациональный ответ
Оно при сложении с рациональным никак не может дать рациональный ответ