Площадь треугольника в заданиях ОГЭ
Площадь треугольника требуется уметь находить, чтобы успешно решить модуль “Геометрия” в ОГЭ. Умение находить площадь треугольника является одним из основополагающих умений в геометрии. Для того, чтобы находить площадь треугольника в заданиях ОГЭ – нужно иметь представления о том, по каким формулам вообще находится площадь треугольника. Ниже мы приводим их все, а также даем анализ того, как часто встретятся вам эти формулы при выполнении заданий по геометрии в ОГЭ.
Задачи самые разнообразные, как и треугольники, как и методы их решения. Однако, для того, чтобы решать такие задачи, нам понадобятся формулы и общие сведения.
Содержание
Площадь треугольника. Формулы. Задачи.
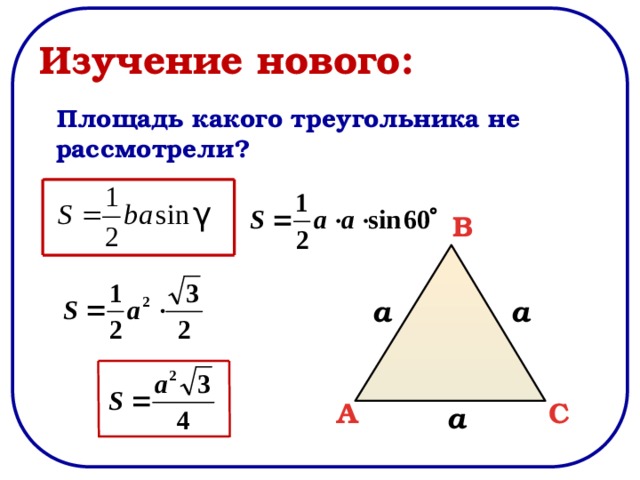
1. Формула нахождения площади треугольника по двум сторонам и углу между ними
Эта формула считается общей, ее очень часто используют, особенно если в треугольнике известен какой-либо угол. Ее кратко называют так “площадь треугольника через синус”. Итак, посмотрите на чертеж – нам дан треугольник ABC, известны две его стороны и угол между ними. Тогда площадь треугольника находится по формуле:
Итак, посмотрите на чертеж – нам дан треугольник ABC, известны две его стороны и угол между ними. Тогда площадь треугольника находится по формуле:
Задачи на определение площади треугольника при заданных сторонах треугольника и углу между ними.
Задача 1. Найдите площадь треугольника, две стороны которого равны 19 и 18, а угол между ними равен 300. Решение. Используем формулу площади треугольника через синус:
Ответ: 85,5 Задача 2. Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 150 0 . Боковая сторона треугольника равна 2. Найдите площадь этого треугольника. Решение. Нарисуем треугольник. Обозначим его вершины – A, B, C. Значит, нам дано: <ABC=1500. AB=BC=2. Тогда для того, чтобы найти площадь треугольника, воспользуемся формулой нахождения площади треугольника по двум сторонам и углу между ними:
В этой задаче мы применили метод приведения для тригонометрических функций.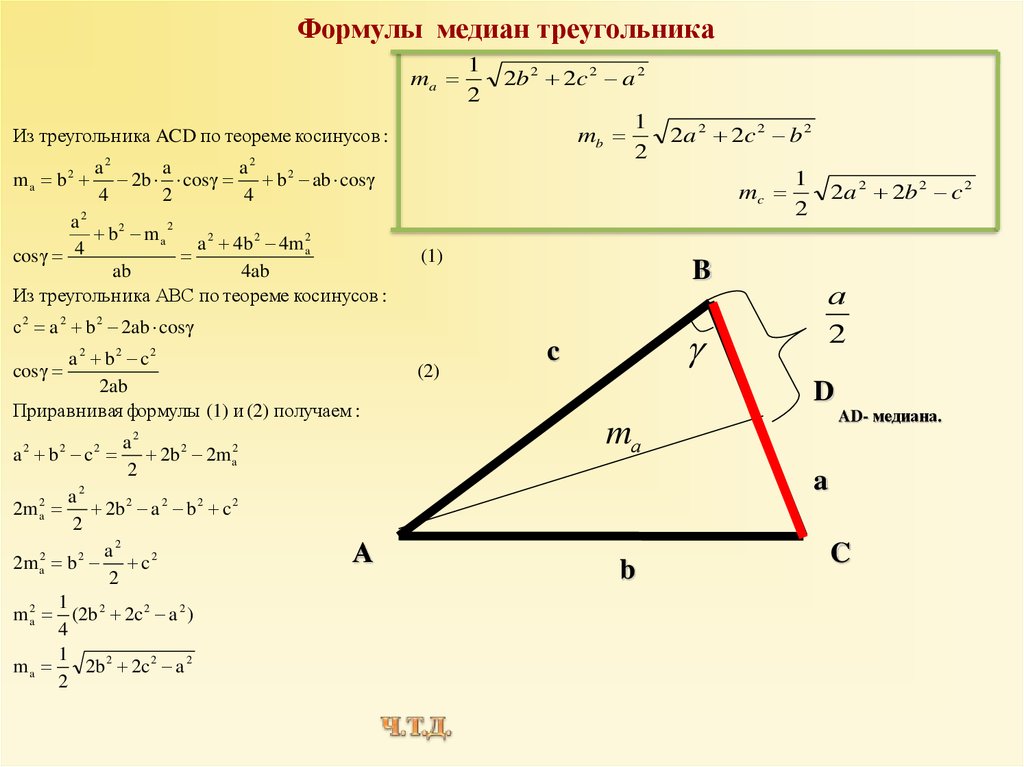
Ответ: 1.
2. Площадь треугольника через высоту.
Самая любимая школьниками формула определения площади треугольника – определение площади через высоту. В этой формуле всего нужно знать две величины – основание треугольника и высоту проведенную из вершины треугольника к этому основанию – смотрите рисунок.
Очень удобная формула для определения любого треугольника, если известны любые три его размера.
3. Площадь равнобедренного треугольника.
Равнобедренным называется треугольник, у которого две стороны равны. Нахождение площади равнобедренного треугольника ничем не отличается от нахождения площади обыкновенного треугольника, разве что формула площади равнобедренного треугольника несколько упрощается. Например, если дана боковая сторона треугольника и угол при вершине, то формула нахождения площади будет выглядеть так:
Вообще говоря, нет необходимости выводить и тем более запоминать некую мифическую формулу площади равнобедренного треугольника. Нужно просто помнить, что равнобедренный треугольник всего лишь частный случай общего, обыкновенного треугольника и все те формулы, которые применимы для нахождения площади треугольника, будут применимы и для равнобедренного треугольника.
Нужно просто помнить, что равнобедренный треугольник всего лишь частный случай общего, обыкновенного треугольника и все те формулы, которые применимы для нахождения площади треугольника, будут применимы и для равнобедренного треугольника.
Гораздо важнее не забыть свойства равнобедренного треугольника – высота (перпендикуляр), проведенная к основанию равнобедренного треугольника, есть медиана (делит основание пополам), биссектриса (делит угол напротив основания пополам). Углы при основании равнобедренного треугольника равны.
4. Площадь треугольника по координатам вершин
Никакой волшебной формулы тут нет – вы просто, используя координаты вершин, находите длины сторон треугольника, а затем подставляете их в формулу Герона.
5. Формула Герона для нахождения площади треугольника
,
где p – полупериметр треугольника, который находится по формуле:
а, b и c – стороны треугольника.
Таким образом, зная формулы, найти площадь треугольника не составит никакого труда.
Как находить площадь треугольника в заданиях ОГЭ.
В заданиях ОГЭ обычно площадь треугольника просят найти с помощью самой простой формулы – через основание и высоту.
Очень и очень редко встречается задача нахождения площади треугольника через две стороны и синус угла между ними, а уж формула Герона вообще не встречается, разве что вы можете ее использовать, если она вам очень нравится, да и то – в задачах второй части ОГЭ.
Найти площадь треугольника зная его стороны. Как найти площадь треугольника
Ниже приведены формулы нахождения площади произвольного треугольника которые подойдут для нахождения площади любого треугольника, независимо от его свойств, углов или размеров. Формулы представлены в виде картинки, здесь же приведены пояснения по применению или обоснованию их правильности. Также на отдельном рисунке указаны соответствия буквенных обозначений в формулах и графических обозначений на чертеже.
Примечание . Если же треугольник обладает особыми свойствами (равнобедренный, прямоугольный, равносторонний), можно использовать формулы, приведенные ниже, а также дополнительно специальные, верные только для треугольников с данными свойствами, формулы:
- «Формулы площади равностороннего треугольника»
Формулы площади треугольника
Пояснения к формулам :
a, b, c — длины сторон треугольника, площадь которого мы хотим найти
r — радиус вписанной в треугольник окружности
R — радиус описанной вокруг треугольника окружности
p — полупериметр треугольника, 1/2 суммы его сторон (периметра)
α — угол, противолежащий стороне a треугольника
β — угол, противолежащий стороне b треугольника
γ — угол, противолежащий стороне c треугольника
h a , h b , h c — высота треугольника, опущенная на сторону a , b , c
Обратите внимание, что приведенные обозначения соответствуют рисунку, который находится выше, чтобы при решении реальной задачи по геометрии Вам визуально было легче подставить в нужные места формулы правильные значения.
- Площадь треугольника равна половине произведения высоты треугольника на длину стороны на которую эта высота опущена (Формула 1). Правильность этой формулы можно понять логически. Высота, опущенная на основание, разобьет произвольный треугольник на два прямоугольных. Если достроить каждый из них до прямоугольника с размерами b и h, то, очевидно, площадь данных треугольников будет равна ровно половине площади прямоугольника (Sпр = bh)
- Площадь треугольника равна половине произведения двух его сторон на синус угла между ними (Формула 2) (см. пример решения задачи с использованием этой формулы ниже). Несмотря на то, что она кажется непохожей на предыдущую, она легко может быть в нее преобразована. Если из угла B опустить высоту на сторону b, окажется, что произведение стороны a на синус угла γ по свойствам синуса в прямоугольном треугольнике равно проведенной нами высоте треугольника, что и даст нам предыдущую формулу
- Площадь произвольного треугольника может быть найдена через произведение половины радиуса вписанной в него окружности на сумму длин всех его сторон (Формула 3), проще говоря, нужно полупериметр треугольника умножить на радиус вписанной окружности (так легче запомнить)
- Площадь произвольного треугольника можно найти, разделив произведение всех его сторон на 4 радиуса описанной вокруг него окружности (Формула 4)
- Формула 5 представляет собой нахождение площади треугольника через длины его сторон и его полупериметр (половину суммы всех его сторон)
- Формула Герона (6) — это представление той же самой формулы без использования понятия полупериметра, только через длины сторон
- Площадь произвольного треугольника равна произведению квадрата стороны треугольника на синусы прилежащих к этой стороне углов деленного на двойной синус противолежащего этой стороне угла (Формула 7)
- Площадь произвольного треугольника можно найти как произведение двух квадратов описанной вокруг него окружности на синусы каждого из его углов.
 (Формула 8)
(Формула 8) - Если известна длина одной стороны и величины двух прилежащих к ней углов, то площадь треугольника может быть найдена как квадрат этой стороны, деленный на двойную сумму котангенсов этих углов (Формула 9)
- Если известна только длина каждой из высот треугольника (Формула 10), то площадь такого треугольника обратно пропорциональна длинам этих высот, как по Формуле Герона
- Формула 11 позволяет вычислить площадь треугольника по координатам его вершин , которые заданы в виде значений (x;y) для каждой из вершин. Обратите внимание, что получившееся значение необходимо взять по модулю, так как координаты отдельных (или даже всех) вершин могут находиться в области отрицательных значений
Примечание . Далее приведены примеры решения задач по геометрии на нахождение площади треугольника. Если Вам необходимо решить задачу по геометрии, похожей на которую здесь нет — пишите об этом в форуме. В решениях вместо символа «квадратный корень» может применяться функция sqrt(), в которой sqrt — символ квадратного корня, а в скобках указано подкоренное выражение
 Иногда для простых подкоренных выражений может использоваться символ √ Задача. Найти площадь по двум сторонам и углу между ними
Иногда для простых подкоренных выражений может использоваться символ √ Задача. Найти площадь по двум сторонам и углу между ними Стороны треугольника равны 5 и 6 см. Угол между ними составляет 60 градусов. Найдите площадь треугольника .
Решение .
Для решения этой задачи используем формулу номер два из теоретической части урока.
Площадь треугольника может быть найдена через длины двух сторон и синус угла межу ними и будет равна
S=1/2 ab sin γ
Поскольку все необходимые данные для решения (согласно формуле) у нас имеются, нам остается только подставить значения из условия задачи в формулу:
S = 1/2 * 5 * 6 * sin 60
В таблице значений тригонометрических функций найдем и подставим в выражение значение синуса 60 градусов . Он будет равен корню из трех на два.
Ответ : 7,5 √3 (в зависимости от требований преподавателя, вероятно, можно оставить и 15 √3/2)
Задача. Найти площадь равностороннего треугольникаНайти площадь равностороннего треугольника со стороной 3см.
Решение .
Площадь треугольника можно найти по формуле Герона:
S = 1/4 sqrt((a + b + c)(b + c — a)(a + c — b)(a + b -c))
Поскольку a = b = c формула площади равностороннего треугольника примет вид:
S =
√3 / 4 * a 2
S =
√3 / 4 * 3 2
Ответ : 9 √3 / 4.
Задача. Изменение площади при изменении длины сторон
Во сколько раз увеличится площадь треугольника, если стороны увеличить в 4 раза?
Решение .
Поскольку размеры сторон треугольника нам неизвестны, то для решения задачи будем считать, что длины сторон соответственно равны произвольным числам a, b, c. Тогда для того, чтобы ответить на вопрос задачи, найдем площадь данного треугольника, а потом найдем площадь треугольника, стороны которого в четыре раза больше. Соотношение площадей этих треугольников и даст нам ответ на задачу.
Далее приведем текстовое пояснение решения задачи по шагам. Однако, в самом конце, это же самое решение приведено в более удобном для восприятия графическом виде. Желающие могут сразу опуститься вниз решения.
Желающие могут сразу опуститься вниз решения.
Для решения используем формулу Герона (см. выше в теоретической части урока). Выглядит она следующим образом:
S = 1/4 sqrt((a + b + c)(b + c — a)(a + c — b)(a + b -c))
(см. первую строку рисунка внизу)
Длины сторон произвольного треугольника заданы переменными a, b, c.
Если стороны увеличить в 4 раза, то площадь нового треугольника с составит:
S 2 = 1/4 sqrt((4a + 4b + 4c)(4b + 4c — 4a)(4a + 4c — 4b)(4a + 4b -4c))
Как видно, 4 — общий множитель, который можно вынести за скобки из всех четырех выражений по общим правилам математики.
Тогда
S 2 = 1/4 sqrt(4 * 4 * 4 * 4 (a + b + c)(b + c — a)(a + c — b)(a + b -c)) — на третьей строке рисунка
S 2 = 1/4 sqrt(256 (a + b + c)(b + c — a)(a + c — b)(a + b -c)) — четвертая строка
Из числа 256 прекрасно извлекается квадратный корень, поэтому вынесем его из-под корня
S 2 = 16 * 1/4 sqrt((a + b + c)(b + c — a)(a + c — b)(a + b -c))
S 2 = 4 sqrt((a + b + c)(b + c — a)(a + c — b)(a + b -c))
(см.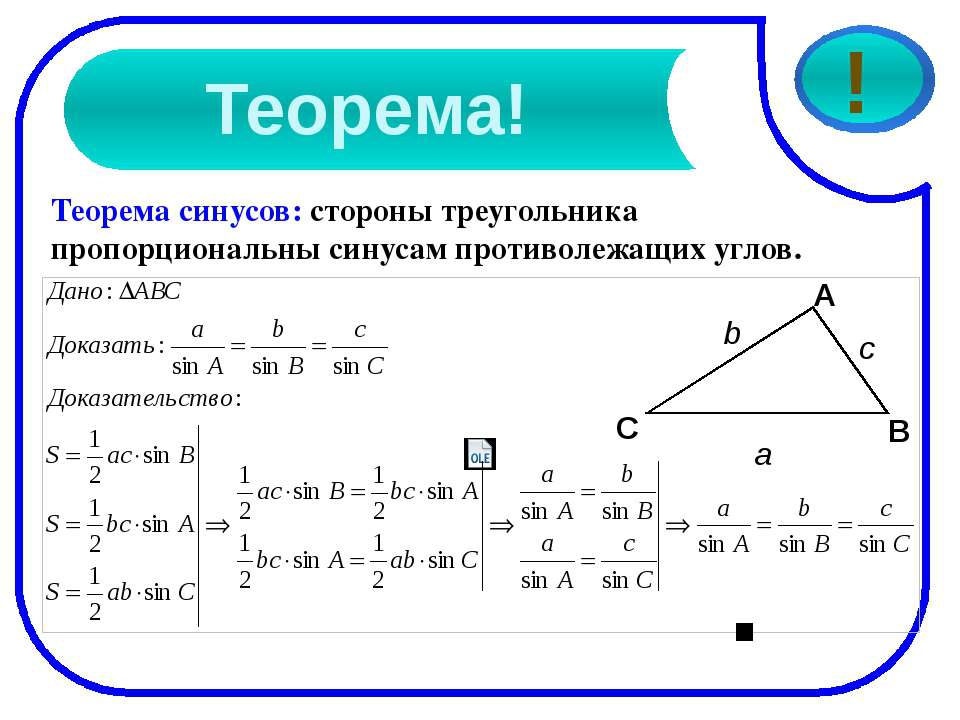 пятую строку рисунка внизу)
пятую строку рисунка внизу)
Чтобы ответить на вопрос, заданный в задаче, нам достаточно разделить площадь получившегося треугольника, на площадь первоначального.
Определим соотношения площадей, разделив выражения друг на друга и сократив получившуюся дробь.
Понятие площади
Понятие площади любой геометрической фигуры, в частности треугольника, будем связывать с такой фигурой, как квадрат. За единицу площади любой геометрической фигуры будем принимать площадь квадрата, сторона которого равняется единице. Для полноты, вспомним два основных свойства для понятия площадей геометрических фигур.
Свойство 1: Если геометрические фигуры равны, то значения их площадей также равны.
Свойство 2: Любая фигура может быть разбита на несколько фигур. Причем площадь первоначальной фигуры равняется сумме значений площадей всех составляющих её фигур.
Рассмотрим пример.
Пример 1
Очевидно, что одна из сторон треугольника является диагональю прямоугольника , у которого одна сторона имеет длину $5$ (так как $5$ клеток), а вторая $6$ (так как $6$ клеток).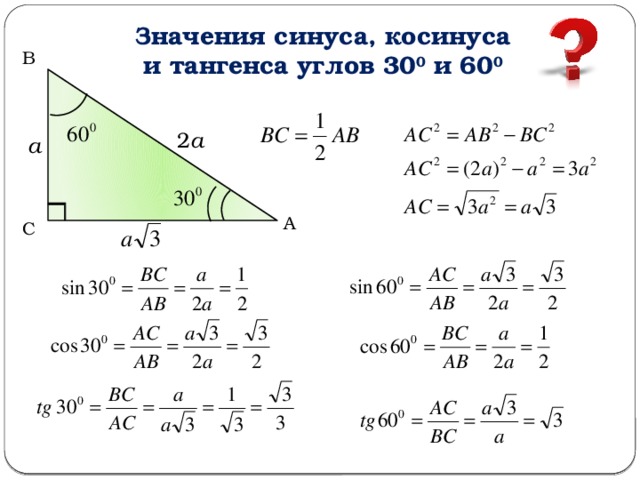
Тогда площадь треугольника равняется
Ответ: $15$.
Далее рассмотрим несколько методов для нахождения площадей треугольников, а именно с помощью высоты и основания, с помощью формулы Герона и площадь равностороннего треугольника.
Как найти площадь треугольника через высоту и основание
Теорема 1
Площадь треугольника можно найти как половину произведения длины стороны, на высоту, проведенную к этой стороне.
Математически это выглядит следующим образом
$S=\frac{1}{2}αh$
где $a$ — длина стороны, $h$ — высота, проведенная к ней.
Доказательство.
Рассмотрим треугольник $ABC$, в котором $AC=α$. К этой стороне проведена высота $BH$, которая равняется $h$. Достроим его до квадрата $AXYC$ как на рисунке 2.
Площадь прямоугольника $AXBH$ равняется $h\cdot AH$, а прямоугольника $HBYC$ равняется $h\cdot HC$.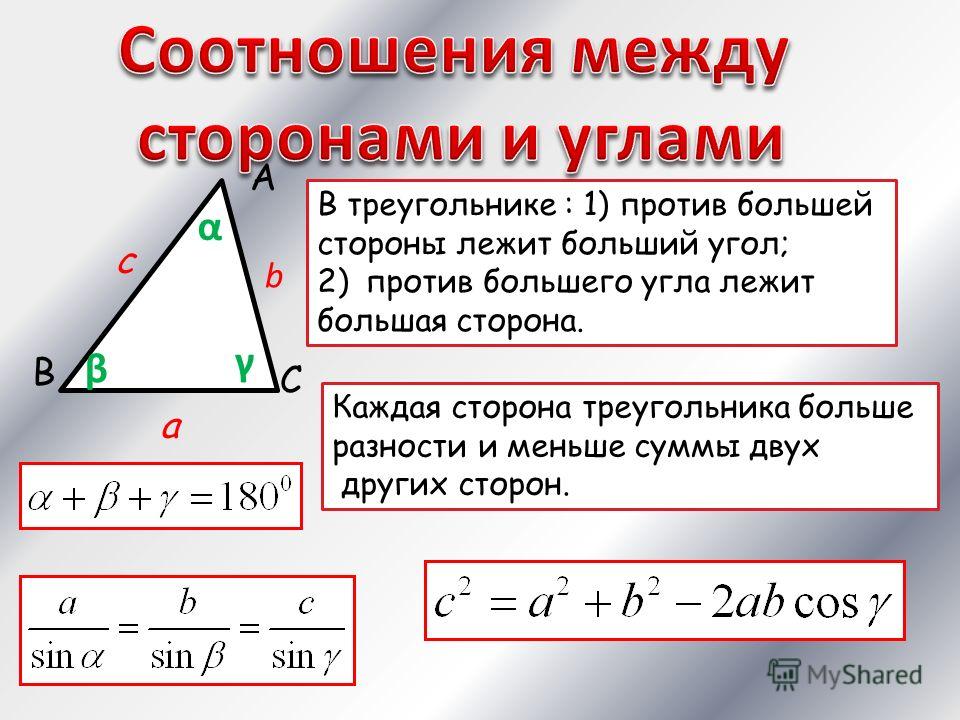
$S_ABH=\frac{1}{2}h\cdot AH$, $S_CBH=\frac{1}{2}h\cdot HC$
Следовательно, искомая площадь треугольника, по свойству 2, равняется
$S=S_ABH+S_CBH=\frac{1}{2}h\cdot AH+\frac{1}{2}h\cdot HC=\frac{1}{2}h\cdot (AH+HC)=\frac{1}{2}αh$
Теорема доказана.
Пример 2
Найти площадь треугольника на рисунке ниже, если клетка имеет площадь, равную единице
Основание этого треугольника равняется $9$ (так как $9$ составляет $9$ клеток). Высота также равняется $9$. Тогда, по теореме 1, получим
$S=\frac{1}{2}\cdot 9\cdot 9=40,5$
Ответ: $40,5$.
Формула Герона
Теорема 2
Если нам даны три стороны треугольника $α$, $β$ и $γ$, то его площадь можно найти следующим образом
$S=\sqrt{ρ(ρ-α)(ρ-β)(ρ-γ)}$
здесь $ρ$ означает полупериметр этого треугольника.
Доказательство.
Рассмотрим следующий рисунок:
По теореме Пифагора из треугольника $ABH$ получим
Из треугольника $CBH$, по теореме Пифагора, имеем
$h^2=α^2-(β-x)^2$
$h^2=α^2-β^2+2βx-x^2$
Из этих двух соотношений получаем равенство
$γ^2-x^2=α^2-β^2+2βx-x^2$
$x=\frac{γ^2-α^2+β^2}{2β}$
$h^2=γ^2-(\frac{γ^2-α^2+β^2}{2β})^2$
$h^2=\frac{(α^2-(γ-β)^2)((γ+β)^2-α^2)}{4β^2}$
$h^2=\frac{(α-γ+β)(α+γ-β)(γ+β-α)(γ+β+α)}{4β^2}$
Так как $ρ=\frac{α+β+γ}{2}$, то $α+β+γ=2ρ$, значит
$h^2=\frac{2ρ(2ρ-2γ)(2ρ-2β)(2ρ-2α)}{4β^2}$
$h^2=\frac{4ρ(ρ-α)(ρ-β)(ρ-γ)}{β^2 }$
$h=\sqrt{\frac{4ρ(ρ-α)(ρ-β)(ρ-γ)}{β^2}}$
$h=\frac{2}{β}\sqrt{ρ(ρ-α)(ρ-β)(ρ-γ)}$
По теореме 1, получим
$S=\frac{1}{2} βh=\frac{β}{2}\cdot \frac{2}{β} \sqrt{ρ(ρ-α)(ρ-β)(ρ-γ)}=\sqrt{ρ(ρ-α)(ρ-β)(ρ-γ)}$
Треугольник – это такая геометрическая фигура, которая состоит из трех прямых, соединяющихся в точках, не лежащих на одной прямой. Точки соединения прямых – это вершины треугольника, которые обозначаются латинскими буквами (например, A, B,C). Соединяющиеся прямые треугольника называются отрезками, которые также принято обозначать латинскими буквами. Различают следующие типы треугольников:
Точки соединения прямых – это вершины треугольника, которые обозначаются латинскими буквами (например, A, B,C). Соединяющиеся прямые треугольника называются отрезками, которые также принято обозначать латинскими буквами. Различают следующие типы треугольников:
- Прямоугольный.
- Тупоугольный.
- Остроугольный.
- Разносторонний.
- Равносторонний.
- Равнобедренный.
Общие формулы для вычисления площади треугольника
Формула площади треугольника по длине и высоте
S= a*h/2,
где а – это длина стороны треугольника, площадь которого нужно найти, h-длина проведенной к основанию высоты.
Формула Герона
S=√р*(р-а)*(р-b)*(p-c),
где √-это квадратный корень, p-полупериметр треугольника, a,b,c-это длина каждой стороны треугольника. Полупериметр треугольника можно вычислить по формуле p=(a+b+c)/2.
Формула площади треугольника по величине угла и длине отрезка
S = (a*b*sin(α))/2,
где b,c -это длина сторон треугольника, sin(α)- синус угла между двумя сторонами.
Формула площади треугольника по радиусу вписанной окружности и трем сторонам
S=p*r,
где p-это полупериметр треугольника, площадь которого нужно найти, r-радиус вписанной в этот треугольник окружности.
Формула площади треугольника по трем сторонам и радиусу описанной вокруг него окружности
S= (a*b*c)/4*R,
где a,b,c-это величина длины каждой стороны треугольника, R- радиус описанной вокруг треугольника окружности.
Формула площади треугольника по декартовым координатам точек
Декартовы координаты точек – это координаты в системе xOy, где x- это абсцисса, y- ордината. Декартовой системой координат xOy на плоскости называют взаимно перпендикулярные числовых оси Oх и Oy с общим началом отсчета в точке О. Если заданы координаты точек на этой плоскости в виде A(x1, y1), B(x2, y2) и C(x3, y3), то можно вычислить площадь треугольника по следующей формуле, которая получена из векторного произведения двух векторов.
S = |(x1 – x3) (y2 – y3) – (x2 – x3) (y1 – y3)|/2,
где || обозначает модуль.
Как найти площадь прямоугольного треугольника
Прямоугольный треугольник – это такой треугольник, у которого один угол составляет 90 градусов. Такой угол у треугольника может быть лишь один.
Формула площади прямоугольного треугольника по двум катетам
S= a*b/2,
где a,b – это длина катетов. Катетами называются стороны, прилежащие к прямому углу.
Формула площади прямоугольного треугольника по гипотенузе и острому углу
S = a*b*sin(α)/ 2,
где a, b – это катеты треугольника, а sin(α)- это синус угла, в котором пересекаются прямые a, b.
Формула площади прямоугольного треугольника по катету и противолежащему углу
S = a*b/2*tg(β),
где a, b – это катеты треугольника, tg(β) – это тангенс угла, в котором соединяются катеты a, b.
Как вычислить площадь равнобедренного треугольника
Равнобедренным называется такой треугольник, который имеет две равные стороны. Эти стороны называются боковыми, а другая сторона является основой. Для вычисления площади равнобедренного треугольника можно использовать одну из следующих формул.
Эти стороны называются боковыми, а другая сторона является основой. Для вычисления площади равнобедренного треугольника можно использовать одну из следующих формул.
Основная формула для вычисления площади равнобедренного треугольника
S=h*c/2,
где с – это основание треугольника, h-это высота треугольника, опущенного к основанию.
Формула равнобедренного треугольника по боковой стороне и основанию
S=(c/2)* √(a*a – c*c/4),
где с – основание треугольника, a- величина одной из боковых сторон равнобедренного треугольника.
Как найти площадь равностороннего треугольника
Равносторонний треугольник – это такой треугольник, у которого все стороны равны. Для вычисления площади равностороннего треугольника можно использовать следующую формулу:
S = (√3*a*a)/4,
где a-это длина стороны равностороннего треугольника.
Вышеприведенные формулы позволят вычислить искомую площадь треугольника. Важно помнить, что для вычисления пощади треугольников нужно учитывать тип треугольника и доступные данные, которые можно использовать для вычисления.
Понятие площади
Понятие площади любой геометрической фигуры, в частности треугольника, будем связывать с такой фигурой, как квадрат. За единицу площади любой геометрической фигуры будем принимать площадь квадрата, сторона которого равняется единице. Для полноты, вспомним два основных свойства для понятия площадей геометрических фигур.
Свойство 1: Если геометрические фигуры равны, то значения их площадей также равны.
Свойство 2: Любая фигура может быть разбита на несколько фигур. Причем площадь первоначальной фигуры равняется сумме значений площадей всех составляющих её фигур.
Рассмотрим пример.
Пример 1
Очевидно, что одна из сторон треугольника является диагональю прямоугольника , у которого одна сторона имеет длину $5$ (так как $5$ клеток), а вторая $6$ (так как $6$ клеток). Следовательно, площадь этого треугольника будет равняться половине такого прямоугольника. Площадь прямоугольника равняется
Тогда площадь треугольника равняется
Ответ: $15$.
Далее рассмотрим несколько методов для нахождения площадей треугольников, а именно с помощью высоты и основания, с помощью формулы Герона и площадь равностороннего треугольника.
Как найти площадь треугольника через высоту и основание
Теорема 1
Площадь треугольника можно найти как половину произведения длины стороны, на высоту, проведенную к этой стороне.
Математически это выглядит следующим образом
$S=\frac{1}{2}αh$
где $a$ — длина стороны, $h$ — высота, проведенная к ней.
Доказательство.
Рассмотрим треугольник $ABC$, в котором $AC=α$. К этой стороне проведена высота $BH$, которая равняется $h$. Достроим его до квадрата $AXYC$ как на рисунке 2.
Площадь прямоугольника $AXBH$ равняется $h\cdot AH$, а прямоугольника $HBYC$ равняется $h\cdot HC$. Тогда
$S_ABH=\frac{1}{2}h\cdot AH$, $S_CBH=\frac{1}{2}h\cdot HC$
Следовательно, искомая площадь треугольника, по свойству 2, равняется
$S=S_ABH+S_CBH=\frac{1}{2}h\cdot AH+\frac{1}{2}h\cdot HC=\frac{1}{2}h\cdot (AH+HC)=\frac{1}{2}αh$
Теорема доказана. 2}}$
2}}$
$h=\frac{2}{β}\sqrt{ρ(ρ-α)(ρ-β)(ρ-γ)}$
По теореме 1, получим
$S=\frac{1}{2} βh=\frac{β}{2}\cdot \frac{2}{β} \sqrt{ρ(ρ-α)(ρ-β)(ρ-γ)}=\sqrt{ρ(ρ-α)(ρ-β)(ρ-γ)}$
Формул для вычисления площади треугольника в интернете можно найти свыше 10. Немало из них применяется в задачах с известными сторонами и углами треугольника. Однако есть ряд сложных примеров где по условию задания известны только одна сторона и углы треугольника, или радиус описанной или вписанной окружности и еще одна характеристика. В таких случаях простую формулу применить не удастся.
Приведенные ниже формулы позволят решить 95 процентов задач в которых требуется найти площадь треугольника.
Перейдем к рассмотрению распространенных формул площади.
Рассмотрим треугольник изображен на рисунке ниже
На рисунке и далее в формулах введены классические обозначения всех его характеристик
a,b,c
– стороны треугольника,
R
– радиус описанной окружности,
r
– радиус вписанной окружности,
h[b],h[a],h[c]
– высоты, проведенные в соответствии со сторонами a,b,c.
alpha, beta,hamma –
углы возле вершин.
1. Площадь равна половине произведения стороны треугольника на высоту опущенной к этой стороне. На языке формул это определение можно записать так
Таким образом, если известна сторона и высота — то площадь найдет каждый школьник.
Кстати, из этой формулы можно вывести одну полезную зависимость между высотами
2. Если учесть, что высота треугольника через соседнюю сторону выражается зависимостью
То с первой формулы площади следуют однотипные вторые
Внимательно посмотрите на формулы — их легко запомнить, поскольку в произведении фигурирует две стороны и угол между ними. Если правильно обозначить стороны и углы треугольника (как на рисунке выше) то получим две стороны a,b и угол связан с третьей С (hamma).
3. Для углов треугольника справедливо соотношение
Зависимость позволяет применять в вычислениях следующие формулы площади треугольника
Примеры на эту зависимость встречаются крайне редко, но помнить что есть такая формула Вы должны.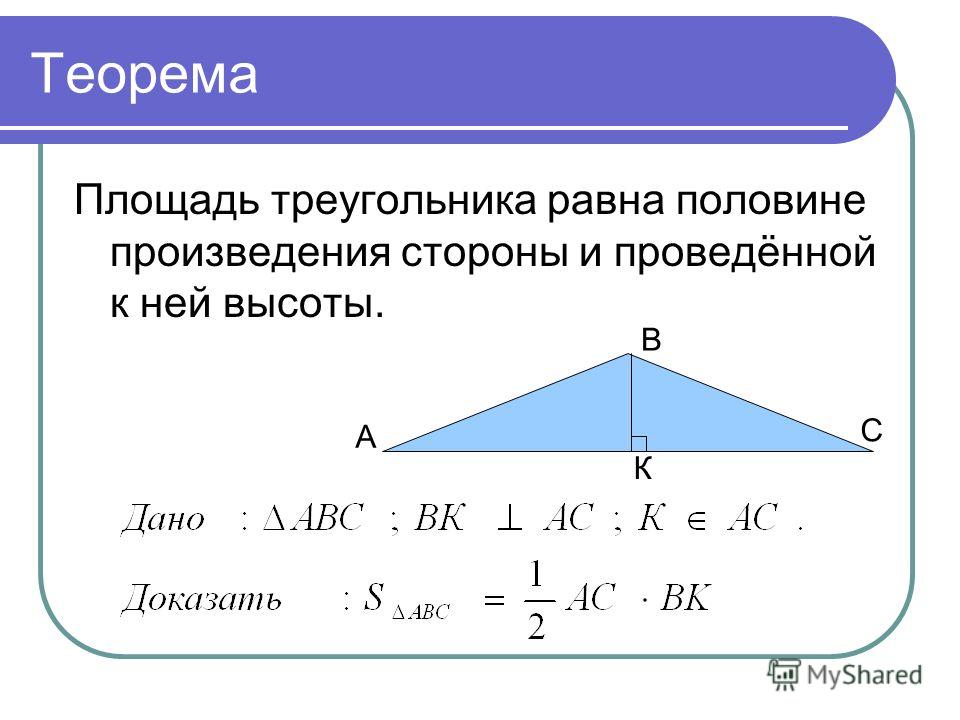
4. Если известна сторона и два прилегающих угла то площадь находится по формуле
5. Формула площади через сторону и котангенс прилегающих углов следующая
Перестановкой индексов можете получить зависимости для других сторон.
6. Приведенная ниже формула площади используется в задачах когда вершины треугольника заданы на плоскости координатами . В этом случае площадь равна половине определителя взятого по модулю.
7. Формула Герона
применяют в примерах с известными сторонами треугольника.
Сначала находят полупериметр треугольника
А затем определяют площадь по формуле
или
Ее довольно часто используют в коде программ калькуляторов.
8. Если известны все высоты треугольника то площадь определяют по формуле
Она сложна для вычисления на калькуляторе, однако в пакетах MathCad, Mathematica, Maple площадь находится на «раз два ».
9.
Следующие формулы используют известны радиусы вписанных и описанных окружностей.
В частности, если известно радиус и стороны треугольника, или его периметр то площадь вычисляется согласно формуле
10. В примерах где задано стороны и радиус или диаметр описанной окружности площадь находят по формуле
11. Следующая формула определяет площадь треугольника через сторону и углы треугольника.
Ну и напоследок — частные случаи:
Площадь прямоугольного треугольника
с катетами a
и b
равна половине их произведения
Формула площади равностороннего (правильного) треугольника
=
= одной четвертой произведения квадрату стороны на корень из тройки.
Площадь треугольника Trig — Математика GCSE
Введение
Чему равна площадь триггера треугольника?
Какую площадь формулы треугольника следует использовать?
Как найти площадь треугольника, используя Area = ½abSinC
Площадь рабочего листа триггера треугольника
Откуда взялась формула площадь = ½abSinC?
Распространенные заблуждения
Похожие уроки
Практическая область вопросов триггера треугольника
Площадь треугольника вопросы GCSE
Контрольный список обучения
Следующие уроки
Все еще застряли?
Индивидуальные занятия по математике, созданные для успеха KS4
Теперь доступны еженедельные онлайн-уроки повторения математики GCSE
Узнать больше
Введение
Чему равна площадь триггера треугольника?
Какую площадь формулы треугольника следует использовать?
Как найти площадь треугольника, используя Area = ½abSinC
Площадь рабочего листа триггера треугольника
Откуда взялась формула площадь = ½abSinC?
Распространенные заблуждения
Похожие уроки
Практическая область вопросов триггера треугольника
Площадь треугольника вопросы GCSE
Контрольный список обучения
Следующие уроки
Все еще застряли?
Вот все, что вам нужно знать о нахождении площади треугольника с помощью тригонометрии для выпускных экзаменов по математике (Edexcel, AQA и OCR). Вы узнаете, как сгенерировать формулу площади треугольника, использовать формулу для нахождения площади треугольника и применить эту формулу к другим многоугольникам.
Вы узнаете, как сгенерировать формулу площади треугольника, использовать формулу для нахождения площади треугольника и применить эту формулу к другим многоугольникам.
Ищите рабочие листы по площади треугольника и экзаменационные вопросы в конце.
Какова площадь треугольника ‘trig’ (½abSinC)
Площадь треугольника trig — это формула для вычисления площади любого треугольника:
\[\text{Площадь треугольника }=\frac{1} {2}ab\sin C \]
Ранее мы вычислили площадь треугольника по другой формуле:
\[\text{Площадь треугольника }=\frac{\text{основание} \times \text {height}}{2}\]
Чтобы использовать это, нам нужно знать вертикальную высоту (перпендикулярную высоту к основанию) треугольника и основания треугольника.
Мы можем адаптировать эту формулу, используя тригонометрическое отношение \sin(\theta)=\frac{O}{H}, чтобы вычислить площадь треугольника, когда мы не знаем его высоту по вертикали. Формула, которую мы получаем:
\[\text{Площадь треугольника }=\frac{1}{2}ab\sin C\]
Треугольник должен быть помечен следующим образом, со строчными буквами для каждой стороны напротив соответствующей заглавной буквы угла.
Нам нужно знать:
- Длина не менее 2-х сторон треугольника.
- Прилежащий угол между этими двумя сторонами.
Например, треугольник ABC был помечен, где C — угол между двумя сторонами треугольника a и b.
Какова площадь треугольника треугольника (½abSinC)?
Какую площадь треугольника следует использовать?
Если мы знаем или можем вычислить вертикальную высоту треугольника, может быть проще использовать следующую формулу:
\[\text{Площадь треугольника}=\frac{\text{основание} \times \ текст{высота}}{2}\]
Напр.
Однако, если высота по вертикали не указана и мы знаем две стороны и угол между ними, нам нужно будет использовать следующее:
\[\text{Площадь треугольника }=\frac{1}{2} ab\sin C\]
Как только мы узнаем, какую формулу использовать, нам нужно подставить в нее правильные значения, а затем решить уравнение для расчета площади. Площадь всегда записывается в квадратных единицах.
Помните : другие многоугольники можно разбить на треугольники, чтобы найти внутренние углы,
итак:
\[\text{Площадь треугольника }=\frac{1}{2}ab\sin C\]
можно применить для нахождения площади прямоугольника, площади равностороннего треугольника, площадь пятиугольника, площадь параллелограмма и т. д.
Пошаговая инструкция: Углы в многоугольниках.
Как найти площадь треугольника, используя Area = ½abSinC
Чтобы найти площадь треугольника, используя
\[\text{Площадь треугольника }=\frac{1}{2}ab\sin C \]
- Обозначьте угол, который мы собираемся использовать, угол C и его противоположную сторону c. Обозначьте два других угла B и A и соответствующие им стороны b и a.
- Подставьте данные значения в формулу \text{Площадь }=\frac{1}{2}absinC.
- Решите уравнение.
Как найти площадь треугольника, используя Area = ½abSinC.
Площадь треугольника триггера ½ листа abSinC
Получите бесплатную площадь треугольника треугольника ½ листа abSinC из 20+ вопросов и ответов. Включает рассуждения и прикладные вопросы.
Включает рассуждения и прикладные вопросы.
СКАЧАТЬ БЕСПЛАТНО
ИксПлощадь треугольника триггера ½ листа abSinC
Получите бесплатную площадь треугольника треугольника ½ листа abSinC из 20+ вопросов и ответов. Включает рассуждения и прикладные вопросы.
СКАЧАТЬ БЕСПЛАТНО
Площадь треугольника (½abSinC) примеры
Пример 1: с двумя сторонами и углом между ними
Вычислите площадь треугольника ABC. Запишите свой ответ с точностью до 2 знаков после запятой.
- 9{2}
\end{aligned}\]
Пример 2: с двумя сторонами и углом между ними
Вычислите площадь треугольника. Запишите свой ответ с точностью до 2 знаков после запятой.
Обозначьте угол, который мы собираемся использовать, угол C и его противоположную сторону c. Обозначьте два других угла A и B и соответствующие им стороны a и b.

Здесь мы обозначили каждую сторону a, b и c и каждую вершину A, B и C.
Подставляем данные значения в формулу 9{2} \end{aligned}\]
Пример 3: с тремя сторонами и одним углом
Вычислите площадь разностороннего треугольника PQR. Напишите свой ответ с тремя значащими цифрами.
Обозначьте угол, который мы собираемся использовать, угол C и его противоположную сторону c. Обозначьте два других угла A и B и соответствующие им стороны a и b.
Здесь мы помечаем каждую сторону и каждый угол.
Подставить данные значения в формулу 9{2} \end{aligned}\]
Пример 4: площадь равнобедренного треугольника с известным углом
Треугольник XYZ является равнобедренным. Найдите площадь треугольника с точностью до 2 знаков после запятой.
Обозначьте угол, который мы собираемся использовать, угол C и его противоположную сторону c.
 Обозначьте два других угла A и B и соответствующие им стороны a и b.
Обозначьте два других угла A и B и соответствующие им стороны a и b. Здесь мы помечаем каждую сторону и каждый угол.
Подставить данные значения в формулу 9{2} \end{aligned}\]
Пример 5: с двумя сторонами и двумя углами
Вычислите площадь треугольника ABC. Запишите свой ответ с точностью до 2 знаков после запятой.
Обозначьте угол, который мы собираемся использовать, угол C и его противоположную сторону c. Обозначьте два других угла А и В и соответствующие им стороны а и b.
Здесь мы обозначаем 22 o буквой C, так как этот угол лежит между двумя известными сторонами.
Подставить указанные значения в формулу . 9{2} \end{aligned}\]
Пример 6: с двумя сторонами и двумя углами
Вычислите площадь треугольника ABC. Запишите свой ответ до 4 значащих цифр.
Обозначьте каждый угол ( A , B , C ) и каждую сторону (a, b , c ) треугольника.

Здесь мы должны хорошо подумать, потому что a, b и C не соответствуют a, b и C в
\[A=\frac{1}{2}ab\sin(C)\]
Поскольку известные стороны b и c имеют внутренний угол в точке A со всеми тремя известными значениями, мы можем изменить правило синусов, чтобы получить 9{2} \end{aligned}\]
Пример 7: нахождение длины по площади
Площадь этого треугольника равна 30 см 2 . Найдите длину, обозначенную х.
Обозначьте каждый угол ( A , B , C ) и каждую сторону (a, b , c ) треугольника.
Подставьте данные значения в формулу .
\[A=\frac{1}{2}ab\sin(C)\]
На этот раз мы знаем площадь, одну сторону и угол.
Следовательно:
\[30=\frac{1}{2}\times x\times12\times\sin(38)\]
Решите уравнение.
\[\begin{выровнено} 30&=6 \х х \х 0,616\\ 30&=3,694x\\ 8.
 {\circ}
\конец{выровнено}\]
{\circ}
\конец{выровнено}\]Откуда взялась формула Площадь = ½abSinC?
Выведем формулу площади любого треугольника, взяв треугольник ABC с высотой по вертикали h:
Применив обычную формулу площади треугольника (\frac{\text{base}\times\text {height}}{2}) имеем A=\frac{1}{2}(a\times{h}).
Мы также можем утверждать, используя тригонометрию, что \sin(C)=\frac{h}{b}, которые мы можем переставить, чтобы сделать h предметом h=b\sin(C).
Подставляя h=b\sin(C) в A=\frac{1}{2}(a\times{h}), получаем: A=\frac{1}{2}ab\sin(C) .
Важно отметить, что C — это внутренний угол между сторонами a и b.
Распространенные заблуждения
- Неправильная маркировка треугольника, поэтому замена неверна
- Без использования внутреннего угла между a и b.
- Предполагается, что треугольник содержит прямой угол, поэтому площадь рассчитывается путем деления основания на высоту пополам.

- 9{2}=113,447
- Знать и применять \text{Area}=\frac{1}{2}ab\sin C для вычисления площади, сторон или углы любого треугольника
(1)
х=10,65 см
(1)
Учебный контрольный список
Теперь вы узнали, как:
Все еще застряли?
Подготовьте своих учеников KS4 к успешной сдаче выпускных экзаменов по математике с помощью программы Third Space Learning. Еженедельные онлайн-уроки повторения GCSE по математике, которые проводят опытные преподаватели математики.
Узнайте больше о нашей программе повторения GCSE по математике.
Мы используем необходимые и необязательные файлы cookie для улучшения работы нашего веб-сайта. Пожалуйста, ознакомьтесь с нашей Политикой использования файлов cookie для получения информации о том, как мы используем файлы cookie и как управлять вашими настройками файлов cookie или изменять их.
 Принять
ПринятьПлощадь треугольника с использованием формулы синуса
Площадь треугольника равна половине произведения двух сторон и угла, прилежащего к стороне. .
Рассмотрим приведенный ниже треугольник, в котором стороны, противоположные углам A, B и C, обозначены буквами a, b и c соответственно.
В приведенном выше треугольнике
AB = c (основание) и
CN = h(высота)
В треугольнике ANC,
sin A = Противоположная сторона/гипотенуза
sin A
3
sin A 9 = 0 003 h/03 h = b (sin A)
Итак, площадь треугольника ABC = (1/2) ⋅ основание ⋅ высота
= (1/2) ⋅ c ⋅ (b sin A)
Площадь треугольника = (1/ 2) ⋅ (bc sin A)
Найдите площадь приведенного ниже треугольника:
Пример 1:
Решение:
Площадь треугольника = (1/2) ⋅ (ac sin B)
= (1/2) ⋅ (13) ⋅ (12) sin 45
= (1/2) ⋅ (13) ⋅ (12 ) (0,707)
= 55,146 см 2
Пример 2:
Решение:
.
 2) ⋅ (ac sin C)
2) ⋅ (ac sin C)= (1/2) ⋅ (28) ⋅ (25) sin 82
= (1/2) ⋅ (28) ⋅ (25) (0,990)
= 346,5 км 2
Итак, площадь данного треугольника равна 347 км 2 .
Пример 3 :
Решение :
= (1/2) ⋅ (7,8) ⋅ (6,4) (0,927)
= 23,13 см 2
Итак, площадь данного треугольник 23,13 см 2 .
Пример 4 :
Решение :

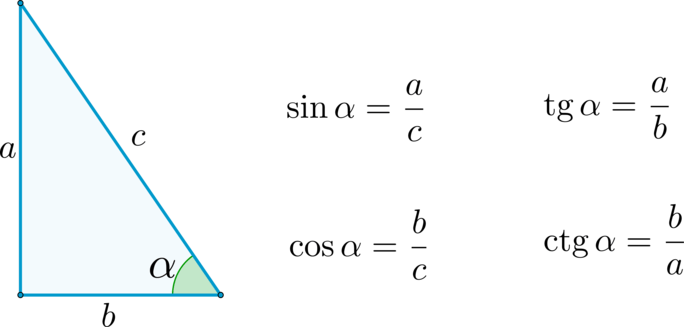 (Формула 8)
(Формула 8)
 Обозначьте два других угла A и B и соответствующие им стороны a и b.
Обозначьте два других угла A и B и соответствующие им стороны a и b. 
 {\circ}
\конец{выровнено}\]
{\circ}
\конец{выровнено}\]
 Принять
Принять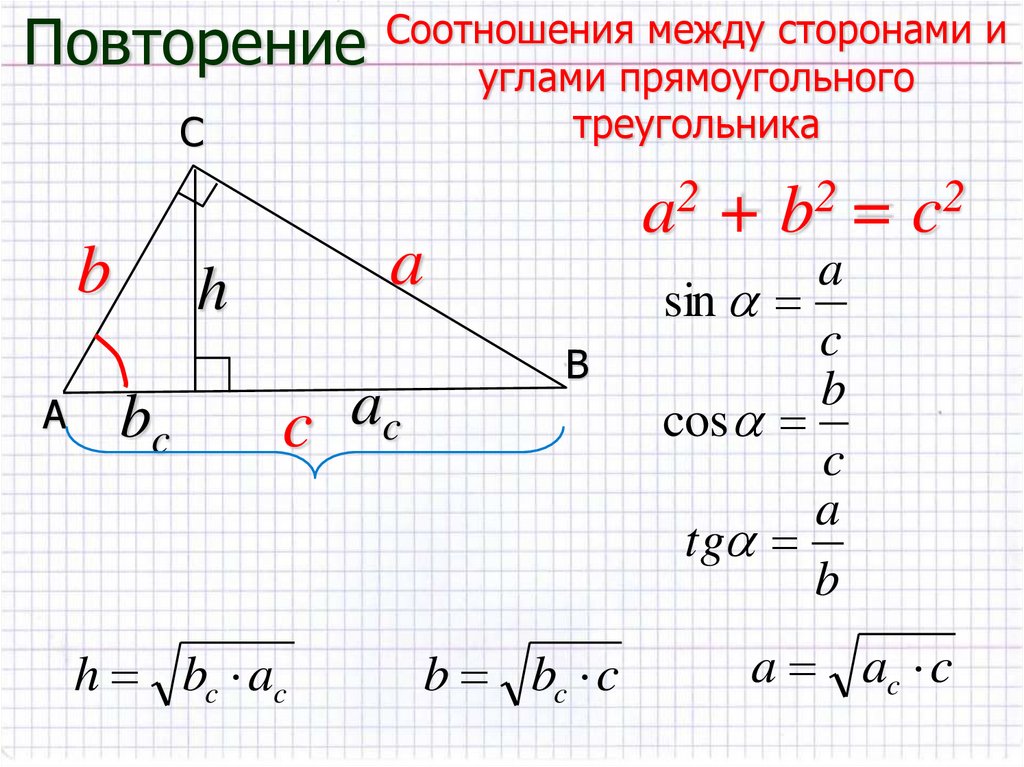 2) ⋅ (ac sin C)
2) ⋅ (ac sin C)
