Число пи круг: Окружность и круг. Число Пи. Длина окружности. Площадь круга. Математика, 6 класс: уроки, тесты, задания.

Содержание

чему равно, история самой популярной математической постоянной

Вообще π (пи) — это 16 буква греческого алфавита, которая используется для обозначения широко известной математической постоянной. Она равна отношению длины окружности к ее диаметру. Но как вообще вычислили число Пи?

Ирина Слепухина

Wikimedia Commons

Как мы уже отметили, по определению, π -это отношение длины окружности (C) к ее диаметру (d). Другими словами, π равно окружности, деленной на диаметр (π = c/d), и наоборот, окружность круга равна π, умноженному на диаметр (c = πd). Независимо от того, насколько велик или мал круг, π всегда будет одним и тем же числом — примерно 3,14.

Чему равно число Пи

Пи — это иррациональное число, то есть, его нельзя выразить простой дробью. Все дело в том, что число Пи, как его называют математики, является «бесконечной десятичной дробью», которое никогда не закончится.

В мире даже существует рекорд, зафиксированный в книге Гиннеса — 21 марта 2015 года индиец Раджвир Мине смог запомнить и воспроизвести 70 тысяч знаков числа Пи после запятой. Между тем, некоторые программисты высчитали значение числа Пи до более чем 22 триллионов цифр. О подобных достижениях часто заявляют в ежегодный праздник постоянной — День Пи, который отмечают каждый год 14 марта (3/14).

Но к счастью, в использовании всех цифр π нет необходимости — его сокращают до 3,14 или до 3,14159. Но если вам интересно, на сайте piday.org содержатся цифры числа Пи до первого миллиона.

Как вычислили значение Пи

Число Пи известно уже почти 4000 лет — впервые его стали использовать древние вавилоняне. До нас дошли древние таблички примерно 1900-1680-х годов до н.э., на которых написано, что Пи равно 3,125. Древние египтяне тоже делали подобные открытия, о чем свидетельствует папирус Ринда 1650 года до н.

э. В этом документе египтяне рассчитали площадь круга по формуле, которая также присваивает числу Пи приблизительное значение 3,1605.

Первое зафиксированное вычисление числа Пи было проведено Архимедом Сиракузским (287-212 гг. до н. э.) — это тот же ученый, который обещал сдвинуть Землю с места, если дать ему точку опоры. Он определил примерное значение числа Пи через теорему Пифагора — сначала с ее помощью он нашел площади двух многоугольников, а затем вычислил площадь окружности, основываясь на площади правильного многоугольника, вписанного в эту окружность, и площади правильного многоугольника, внутри которого была описана окружность. Так Архимед получил приблизительное значение числа Пи, которое находилось между 3,1428 и 3,1408.

А в 1706 году британский математик Уильям Джонс обозначил постоянную символом π и стал использовать значение 3,14159 для расчетов.

Любопытный факт о числе Пи

В честь числа Пи был даже создан свой язык — пилиш. Это диалект английского языка, суть которого заключается в том, чтобы составлять предложения таким образом, что количество букв в идущих по порядку словах будет соответствовать каждому последующему элементу постоянной. Сейчас приведем пример и станет понятнее.

Now I fall, a tired suburbian in liquid under the trees, Drifting alongside forests simmering red in the twilight over Europe

Это отрывок из книги Майка Кита «Not A Wake» — это первое произведение, полностью написанное на пилише.

Первым символом числа Пи является тройка, это значит, что и первое слово предложения должно состоять из трех букв — в приведенном предложении это слово now. Далее идет цифра 1, а затем 4 — соответственно, автор книги специально подбирает слова, подходящие по количеству знаков — однобуквенное местоимение I и четырехбуквенный глагол fall. Остальные слова подбираются по тому же принципу.

Где на практике применяется число Пи?

Число Пи активно используется в точных и прикладных науках. С его помощью можно найти периметр окружности, выполнить вычисления в статистике и квантовой механике. В астрономии число Пи применяют, когда необходимо рассчитать орбиту спутника.

Без числа Пи не было бы телефонов и радио — инженеры используют его для расчета и оптимизации звуковых волн.

Математическая константа нужна еще и для того, чтобы рассчитать время и расстояние полета на самолете, поскольку самолет движется по округлой дуге.

Число Пи внесло вклад, в том числе, и в спорт — благодаря нему мячи для тенниса, футбола и баскетбола идеально круглые.

Как набрать число Пи на клавиатуре

Если вы используете MAC, зажмите комбинацию клавиш option и P;
Если вы используется Windows, включите клавишу «Num Lock», затем зажмите «Alt» и комбинацию цифр 227 или 960 при помощи Number Pad, расположенного на клавиатуре справа;
Если вы хотите вставить π на телефоне, введите в поисковую строку пи и просто скопируйте знак, который выдаст сайт по запросу.

Как запомнить число Пи?

Чтобы сложная информация отложилась в памяти, рекомендуется использовать мнемотехники — методы запоминания, основанные на создании ассоциаций. Приводим несколько способов:

Создание рифмы

Можно попробовать запомнить число Пи с помощью стихотворения:

«Чтобы нам не ошибаться,

Надо правильно прочесть:

Три, четырнадцать, пятнадцать,

Девяносто два и шесть.

Ну и дальше надо знать,

Если мы вас спросим —

Это будет пять, три, пять,

Восемь, девять, восемь».

(С. Бобров «Волшебный двурог»)

Буквы в цифры

Суть следующего подхода в том, чтобы придумать фразы, где количество букв в слове будет совпадать с цифрой в числе Пи. Попробуйте способы, предложенные Перельманом:

Что я знаю о кругах? (3.1415)
Вот и знаю я число, именуемое Пи — Молодец! (3.1415926 — округленно)
Учи и знай в числе известном за цифрой цифру, как удачу примечать! (3.14159265359)

Структурирование данных

Разбейте цифры после запятой на пятерки или десятки по 4 цифры в каждой. Так вы последовательно запомните целых 20-40 знаков после запятой.

Как округлять число Пи?

Чтобы округлить число Пи, сначала нужно определить, до какого разряда необходимо провести округление. Далее отделить все цифры, стоящие справа от цифры округляемого разряда. Если после нее идет цифра, чье значение меньше пяти, то она остается без изменений, если больше или равно — увеличивается на один.

Значение числа Пи, округленного до тысячных, — 3,141;
До сотых — 3,14;
До десятых — 3,1;

До целого — 3.

От архимедова числа к числу π

Авторы
Руководители
Файлы работы
Наградные документы

Лукина К.К. 1

1Муниципальное автономное общеобразовательное учреждение «Средняя общеобразовательная школа №24

Паршева В.В. 1

1Муниципальное автономное общеобразовательное учреждение «Средняя общеобразовательная школа №24

Автор работы награжден дипломом победителя III степени

Диплом школьникаСвидетельство руководителя

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF

ВВЕДЕНИЕ

Уже много веков люди понимают важность и ценность для науки математической постоянной, равной отношению длины окружности к ее же диаметру. В учебнике мы сталкиваемся со следующим объяснением: «Длина окружности прямо пропорциональна длине её диаметра.

Это число обозначают греческой буквой π (читается «пи»),формула, выражающая длину окружности через её радиус C=2πR и площади круга S=πR²». Возникает много вопросов, связанных с числом Пи: когда возник интерес к этому загадочному числу, кто и когда впервые нашел значение отношения длины окружности к ее диаметру, какие математики внесли свой вклад в вычисление значения этого числа, какими способами находили значение числа Пи, как измерить диаметр окружности, как измерить длину окружности , когда было введено обозначение этого числа, сколько знаков после запятой у числа, как запомнить знаки числа. Школьные учебники такой информации для учеников не дают. Но такую информацию дают и энциклопедии по математике, и книги для внеклассного чтения, и интернет-ресурсы. «Вычисление точного значения π во все века неизменно оказывалось тем блуждающим огоньком, который увлек за собой сотни, если не тысячи, несчастных математиков, затративших бесценные годы в тщетной надежде решить задачу, не поддававшуюся усилиям предшественников, и тем самым снискать себе бессмертие.

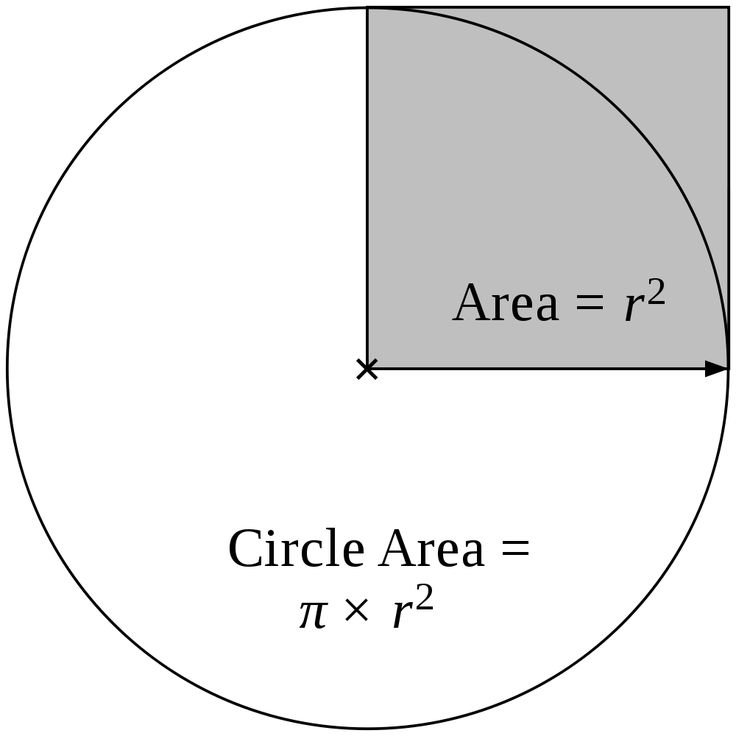» Л. Кэрролл (Чарльз Лютвидж До́джсон) .

Актуальность исследования заключается в том, что до сих пор так и неясно, кто открыл число Пи, кто впервые задумался над этой проблемой и произвел первые расчеты этого, по-настоящему мистического числа, несмотря на то, что к нему имели отношение самые лучшие математики на протяжении всей нашей истории. Кроме того актуальность выбранной темы в том, что многие технические специальности требуют прежде умения использовать формулы, таблицы, константы и т. д., но все они в том или ином виде содержат число Пи.

Объект исследования: число p (Пи).

Предмет исследования: Периоды в истории развития числа p (Пи) и вычисление значения ПИ экспериментальным путем.

Гипотеза: выполнив работу, мы установим историю числа p (Пи): что знали об этом числе в доисторические времена, в древние времена, вклад Архимеда в вычислении значения p, знания о числе число Пи в Средние века, кто ввел обозначение отношения длины окружности к диаметру буквой p, какие ученые занимались в ИГС GeoGebra, воссоздадим исторические способы вычисления значения вычислением Пи в более поздние времена. Выполнив эксперименты и моделирование Пи и установим некоторые интересные факты, связанные с числом ПИ.

Цель работы: установить историю вычисления числа Пи, провести эксперименты по нахождению значения ПИ, выполнив моделирование в ИГС GeoGebra? и найти значение ПИ методом Архимеда.

Задачи исследования:

1.Изучить информацию по теме в школьных учебниках, справочниках, Интернет – ресурсах.

2. Установить:

Истоки изучения вопроса об отношении длины окружности к ее диаметру

Значение работ Архимеда в поисках значения отношения длины окружности (L) к длине ее диаметр(d).

Выполнить компьютерное моделирование нахождения отношения L к d по способу Архимеда в ИГС GEOGEBRA.

Сравнить результаты и сделать вывод.

3. Установить историю дальнейшего изучения отношения L к d.

4. Способы запоминания этого волшебного числа.

5. Найти интересные факты, связанные с этим загадочным числом.

Методы исследования:

Анализ учебников, справочной математической литературы.

Построения с помощью циркуля и линейки.

Компьютерное моделирование математических объектов с помощью ИГС GeoGebra.

Анализ, сравнение, сопоставление и обобщение объектов, полученных в результате моделирования.

Обобщение найденных с помощью компьютерного моделирования закономерностей.

Проверка выдвинутых гипотез.

Аналитические рассуждения.

ОСНОВНАЯ ЧАСТЬ

От архимедова числа к числу π

1. Число Пи в доисторические времена

Число Пи обратило на себя внимание людей ещё в первобытном обществе, когда они не умели записывать ни своих знаний, ни своих переживаний, ни своих воспоминаний. Открывателями числа вполне можно считать людей доисторического времени, которые заметили, что при плетении корзин нужного диаметра необходимо брать прутья в 3 раза длиннее диаметра.Уже тогда люди заинтересовались соотношением длины окружности и её диаметра. Сначала по невежеству это отношение считали равным трём. Древнейшие известные попытки нахождения длины окружности и площади круга принадлежат Антифонту и Бризону (V в. до н. э.). Антифонт последовательно вписывал в круг правильные многоугольники, каждый раз удваивая количество сторон, и полагал, что в конце концов многоугольник совпадет с окружностью. Бризон строил два квадрата – вписанный в окружность и описанный вокруг нее – и считал, что площадь квадрата, лежащего между ними, равна площади круга. Письменная история числа начинается с египетского папируса, датируемого примерно 2000 годом до нашей эры, но оно было известно еще древним людям. Кто и когда впервые открыл число пи, до сих пор остается загадкой. Строители в Вавилоне уже пользовались им при проектировании различных сооружений. На клинописных табличках, которым тысячи лет, сохранились даже задачи, в решении которых использовали самую популярную ныне математическую константу. Правда, вавилоняне ее считали равной трем и одной восьмой. Античные математики не отличались такой точностью, как нынешние. В Древнем Египте пи было равно 3,16, в Древней Индии — 3,088, в Римской империи на рубеже двух эр — 3,125. Одним из первых заметил и вычислил интересную зависимость между длиной окружности и ее диаметром Архимед в III в. до н.э.. Одно из первых упоминаний о числе Пи можно встретить в текстах египетского писца Ахмес (около 1700-2000 г. до н. э), известный сейчас как папирус Ахмеса (Ринда) «Наставление к приобретению всех тайных вещей». Птолемей, использовав правильный 720-угольник, нашел, что отношение длины окружности к ее диаметру ≈ 377/120, что составляет приблизительно 3,14167 (ошибка меньше 0,003).Вавилонское царство возникло в начале II тысячелетия до н. э.. на территории современного Ирака. Вавилонские ученые изучали свойства окружности Учились измерять длину окружности. Они поступали так: чертили окружность и два квадрата: один т ак, чтобы его углы упирались в окружность изнутри, второй квадрат побольше рисовали так, чтобы окружность помещалась в нем.Потом измеряли стороны большого и меньшего квадратов (это легко сделать с помощью линейки).Получившиеся числа складывали и делили пополам, и это число считалось длиной окружности.

L =(P₁ + P₂)/2, L— длина окружности, Р₁ – периметр большого квадрата

Р₂ –периметр малого квадрата

2. Математический метод Архимеда

В III веке до н.э. египетский математик Архимед написал свою первую небольшую работу «Измерение круга»В ней он обосновал три положения:

Всякий круг равновелик прямоугольному треугольнику, катеты которого соответственно равны длине окружности и ее радиусу.

П лощади круга относятся к квадрату, построенному на диаметре, как 11 к 14.

Отношение длины любой окружности к ее диаметру.

Архимед из Сиракуз первым предложил использовать математический метод вычисления. Он построил вписанный и описанный вокруг окружности многоугольники по 96 сторон каждый, вычислил их периметры и справедливо отметил, что число пи «сидит где-то м ежду». По мнению древнегреческого ученого, достаточно было разделить 22 на 7.(22/7 -называется архимедовым числом) При вычислении такой дроби ошибка обнаруживается уже на третьем знаке после запятой (22:7 ≈3,1428571429, истинное 3,141).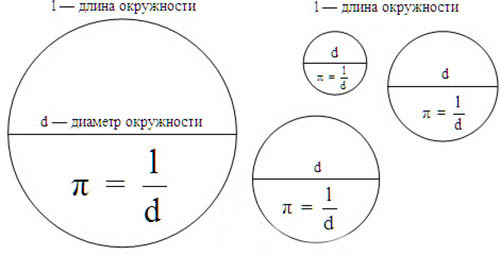 Примерно в 220 году до н.э. он вывел формулу площади круга путём приближения области окружности, основанной на области многоугольника, вписанного в окружность, и области многоугольника, вокруг которого была описана окружность. Архимед доказал, что площадь круга равна половине произведения длины окружности на ее радиус. Кроме того, с помощью вычисленных им периметров вписанных и описанных правильных многоугольников (от 6-угольника до 96-угольника) Архимед нашел в десятичных дробях, 3,1409… < π < 3,1428… (подлинное значение π = 3,14159…). Таким образом, он не только нашел приближенные значения π, но и оценил точность этих приближений. Уже найденная Архимедом верхняя оценка, равная 22/7, дает приближение π с точностью 0,04 %. Эту дробь часто называют «архимедовым числом». «Архимедово число»

В V веке до н. э. знаменитый астроном Цзу Чунчжи предложил простой способ вычисления. Надо было дважды написать нечетные числа 1, 3 и 5: 113355, а потом, разделив их пополам (113 и 355) , поместить первое в знаменатель дроби, а второе — в числитель: 355/113. Результат совпадает с современными вычислениями вплоть до седьмого знака. Найти точное число «пи» (отношение длины окружности к диаметру) является очень важной и очень трудной темой в математике. Многие древнекитайские математики прилагали усилия по вычислению числа «пи». В 5 веке до н.э. успехи китайского математика Цзу Чучжи, можно сказать, символизировали скачок в этом отношении. Чунчжи – великий математик и астроном. Когда Цзу Чунчжи было 35 лет, он начал заниматься вычислением числа «пи» вычислил значение числа пи с точностью до седьмого знака после запятой, им было найдено более точное значение этого числа: 377/120 ≈ 3,1415927.

Поиском значения отношения длины окружности к её диаметру занимались многие ученые — математики: индийский астроном и математик Ариабхаты , среднеазиатский учёный , математик, астроном, географ и историк аль Хорезми, в XIII в. вычислил 3 знака после запятой Леонардо Фибоначчи, в XIVв. – 9 знаков после запятой Франсуа Виет. К концу 1999 года количество верных знаков после запятой превысило 206 миллиардов.

3 .Собственные исследования по вычислению значения числа Пи

Для проведения собственных вычислений значения числа Пи мы применили ИГС GeoGebra. Использованы инструменты ИГС GeoGebra: Окружность по центру и точке, Расстояние или длина, Текст, Правильные многоугольники.

Эксперимент 1. Нахождение отношения периметра правильного многоугольника (a_n=2), вписанного в окружность к ее диаметру

n	P_n	d	P _n /d
3	6	2,31	2,597
4	8	2,83	2,829
5	10	3,4	2,940
6	12	4,0	3,0
7	14	4,38	3,196
12	24	7,73	3,105
20	40	12,78	3,129

При увеличении числа сторон правильных многоугольников, вписанных в окружность, число, выражающее отношение длины окружности к длине диаметра приближается к 3,14.

Эксперимент 2. Нахождение отношения периметров правильных многоугольников, описанных около окружности одного и того же диаметра (по идеи Архимеда)

О писываем около данной окружность правильные многоугольники при n=3, n=6, n=12. При увеличении числа сторон отношение периметра многоугольника к диаметру окружности увеличивается (5,18; 3,48; 3,20) и приближается к значению π=3,14.;

Эксперимент 3. По следам Архимеда(n=5)

О дин правильный пятиугольник вписывали в окружность, другой — описывали около этой окружности. В результате вычислений установили π ≈3 ,19.

У двоили число сторон многоугольников, выполнив вычисления получили π ≈ 3,17.
Удвоим еще раз число сторон многоугольника (n=40) и выполним вычисление числа ПИ: π ≈ 3,148.

Вывод. Повторив вычисление значения отношения длины периметра правильных вписанного и описанного многоугольников методом древних , убедились, что с увеличением числа сторон правильных многоугольников, значение ПИ приближается к классическому значению π ≈ 3,1415.

4.Интересные факты с числом ПИ.

Возникает вопрос: число π выражается бесконечной десятичной дробью. Как запомнить хотя бы несколько цифр после запятой. Оказалось, что есть фразы, с помощью которых можно запомнить до 10 знаков после запятой. Вот эти фразы:

— Что я знаю о круге (3,1415).

— Вот и Миши и Анюта прибежали, Пи узнать число они желали (3,1415926536)

-Учи и знай в числе известном за цифрой цифру как удачу примечать.

(3,14159265359).

В штате Юта (США) был принят закон с очень короткой формулировкой «Пи равно трем», а в штате Индиана властями было официально назначено, что Пи равно 4.

Сегодня проводятся мировые чемпионаты по запоминанию числа П и фиксируются мировые рекорды, последний принадлежит китайцу Лю Чао, за сутки с небольшим, назвал 67 890 знаков.

По данным на 2011 год уже установлено 10 триллионов цифр периода числа. В 2014 году компьютеры рассчитали 13,3 триллионов знаков после запятой.

Самое удивительное, что отмечается праздник числа Пи, который отмечается 14 марта — «День рождения числа Пи».

В США и в Англии установлены памятники числу π.

На Теле — шоу «Удивительные люди» проводились конкурсу по запоминанию десятичных знаков числа π.

ЗАКЛЮЧЕНИЕ

В результате исследования наша гипотеза подтвердилась и цель работы была достигнута.

Приобретен опыт работы с новой информацией.

В ходе выполнения работы мы ознакомились с историей и развитием одного из самых удивительных чисел. История числа π — это череда усилий величайших умов человечества по уточнению его знаков и поисков алгоритмов для их нахождения.

Значение числа π в современном мире представляет собой не только научную ценность, но и используется для точных вычислений.

С числом π связано много интересных фактов, поэтому оно вызывает интерес к изучению.

Совершенствовался опыт работы в ИГС GeoGebra.

Узнали, как запомнить несколько цифр после запятой в записи значения числа π.

Установили интересные факты, связанные с числом π.

ИСТОЧНИКИ ИНФОРМАЦИИ

Жуков А.В. Вездесущее число ПИ.- М.: Едиториал УРСС, 2004;

Жуков А.В. О числе ПИ. — М:МЦНМО, 2002;

Звонкин А. Что такое π / Квант,1978 №11;

Кыпман Ф. История числа π.- М.: Наука, Гл. ред. Физ-мат лит.,1971;

Мир математики: в 40т. Т7.Хоакин Наварро. Секреты числа π. Почему неразрешима задача о квадратуре круга.- М.:Де Агостини,2014

Перельман Я. И. Занимательная геометрия. Глава «Старое и новое о круге».- М.: Наука, Гл. ред. Физ-мат лит.,1955;

Райк Ф.Е. Очерки по истории математики в древности. -Саранск, 1987;

Сергей Бобров. Волшебный двурог. — М.: Детская литература,1967;

Сергей Бобров. Архимедово лето. — М.:Детгиз, 1962;

«Энциклопедическом словаре юного математика», сост. Савин А.П .// М., «Педагогика»,1989г.-352с.

ИНТЕРНЕТ-РЕСУРС. Как вычислить число ПИ. ru.wikinon.com (дата обращения: 12.01.22).

ИНТЕРНЕТ-РЕСУРС. Чему равно число ПИ? История, открытие, тайны, загадки.uchitelskaia.ru (дата обращения: 12.01.2022)

ИНТЕРНЕТ-РЕСУРС.Что такое число ПИ. Что значит число Пи… .kakprosto.ru (дата обращения: 12.01.2022)

ИНТЕРНЕТ-РЕСУРС.Кто открыл число ПИ? История вычислений. vseonauke.com (дата обращения 12.01.20122)

ИНТЕРНЕТ-РЕСУРС. Число ПИ. Интересное о математике. Siterid.ru (дата обращения12.01.2022)

ИНТЕРНЕТ-РЕСУРС.Число ПИ – значение, история, кто придумал.calcukator888.ru (дата обращения: 12.01.2022)

Интересные факты о числе ПИ. facty.by (дата обращения: 12.01.2022).

ПРИЛОЖЕНИЕ 1 Буклет «От архимедова числа к числу π»

Просмотров работы: 362

Можно ли вычислить число Пи, нарисовав круг?

Пи заставляет мир вращаться. Это сумасшедшее бесконечное число появляется практически везде, куда бы вы ни посмотрели. можете ли вы прибить с помощью этого метода?

Если подумать, число Пи действительно странное. Это иррациональное число появляется в самых безумных местах. Если вы раскачаете груз туда-сюда на веревке, там будет число Пи. Он появляется в принципе неопределенности Гейзенберга, общей теории относительности Эйнштейна и взаимодействии двух электрических зарядов.

Конечно, у большинства людей число пи ассоциируется с кругами. Это понятно, так как самое основное определение числа пи — это отношение длины окружности к диаметру круга:

Иллюстрация: Ретт Аллен

Теперь самое важное. Сегодня, как вы знаете, день Пи. Почему сегодня? Потому что сегодня 14 марта — да, 14 марта — и 3,14 — это число пи с точностью до двух знаков после запятой. Конечно, фактическое число продолжается до бесконечного числа знаков после запятой: 3,14159265359… и так далее до бесконечности. Вот почему это называется иррациональным.

Должен добавить, что США — почти единственное место, где используется формат даты со средним порядком байтов: месяц/день/год. Если вы придерживаетесь формата дня/месяца/года с прямым порядком байтов, то сегодня 14/3, что, очевидно, составляет , а не пи. (В таком случае я предлагаю 22 июля, так как дробь 7/22 является довольно приличным приближением для числа пи.)

В любом случае, мой традиционный способ празднования Дня числа числа числа числа числа числа числа числа числа числа числа числа числа числа числа числа числа числа числа и 2 000 000 000 000 000 000 000 000 000 000 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 . Это просто то, что я делаю. Я занимаюсь этим уже довольно давно, так что вот некоторые из моих любимых:

Finding pi using random numbers (and Python)
Determining the value of pi using a mass oscillating on a spring
Actually measuring the circumference and diameter of real circles

Самое важное число во Вселенной?

Эдвард Б. Бургер, доктор философии, Юго-Западный университет

Одним из самых важных чисел в нашей Вселенной является число Пи или π. Исследуйте одиссею человечества — попытки на протяжении веков, которые действительно выходят за рамки культур, — вычислить, приблизить и понять это загадочное число.

(Изображение: Константин Панкин/Shutterstock)

A Определение

Хотя происхождение π точно неизвестно, мы знаем, что вавилоняне приблизили π по основанию 60 около 1800 г. до н.э. Определение π сосредоточено вокруг кругов. Это отношение длины окружности к ее диаметру — число чуть больше трех.

Иоганн Ламберт, швейцарский математик, первым доказал, что число пи — иррациональное число. (Изображение: общественное достояние)

Константа π помогает нам лучше понять нашу вселенную. Определение π вдохновило на новое понятие измерения углов, новую единицу измерения. Эта важная угловая мера известна как «радианная мера» и привела к многим важным открытиям в нашем физическом мире. Что касается самого π, то Иоганн Ламберт в 1761 году показал, что π — иррациональное число, а позже, в 1882 году, Фердинанд фон Линдеманн доказал, что π не является решением ни одного полиномиального уравнения с целыми числами. Однако многие вопросы о π остаются без ответа.

Подробнее: Геометрия — многоугольники и окружности

Эксперименты с числом Пи

Длина окружности чуть более чем в три раза превышает ее диаметр. Точное соотношение называется π.
(Изображение: Kjoonlee/Public domain)

Любое обсуждение происхождения числа Пи должно начинаться с эксперимента с кругами, который мы все можем попробовать. Возьмите любой круг и возьмите длину окружности, то есть длину окружности, и измерьте ее через диаметр, то есть длину в поперечном направлении. В итоге вы получите три диаметра и чуть больше, и если вы внимательно посмотрите, это чуть больше, чем 1/10 пути. Этот эксперимент показывает нам, что это отношение окружности к диаметру будет числом около или немного больше, чем 3,1. Независимо от того, каков размер круга, длина окружности чуть больше, чем его диаметр в три раза.

Это расшифровка из серии видео От нуля до бесконечности . Смотрите прямо сейчас на The Great Courses.

Это фиксированное, постоянное значение получило имя, и мы называем его π. Как сказать точнее? Число π определяется как отношение длины окружности любого круга к его диаметру в поперечнике. Это соотношение постоянно. Независимо от того, с каким размером круга мы пытаемся это сделать, это число всегда будет одним и тем же. Это начинается 3.141592653589, и так продолжается.

Уильям Джонс, валлийский математик. (Изображение: Уильям Хогарт/общественное достояние)

Символ π происходит от греческой буквы π, потому что греческое слово «периферия» начинается с греческой буквы π. Периферия круга была предшественницей периметра круга, который сегодня мы называем окружностью. Символ π впервые появляется в тексте Уильяма Джонса 1709 года « Новое введение в математику », а позже этот символ стал популярен благодаря великому швейцарскому математику XVIII века Леонарду Эйлеру примерно в 1737 году9.0003

Узнайте больше: Теория чисел — простые числа и делители

От Вавилона к Библии

Переходя от названия к значению, существуют доказательства того, что вавилоняне приблизили число π по основанию 60 около 1800 г. до н. э. На самом деле они считали, что π = 25/8, или 3,125 — поразительное приближение для такого раннего периода человеческой истории. Древнеегипетский писец Ахмес, который связан со знаменитым папирусом Райнда, предложил приближение 256/81, которое составляет 3,16049. Опять же, мы видим впечатляющее приближение к этой константе. В Библии даже указано неявное значение π. В 3 Царств 7:23 сказано, что круглый бассейн имеет 30 локтей в окружности и 10 локтей в диаметре. Таким образом, в Библии неявно утверждается, что π равно 3 (30/10).

Индийский математик и астроном Арьябхата аппроксимировал π в ок. 500 г. н.э. с дробью 62 832/20 000, что равно 3,1416 — поистине удивительная оценка.

Неудивительно, что по мере того, как человечество развивалось в понимании чисел, росла и его способность лучше понимать и, таким образом, оценивать само число π. В 263 году китайский математик Лю Хуэй считал, что π = 3,141014.

Приблизительно 200 лет спустя индийский математик и астроном Арьябхата аппроксимировал число π дробью 62 832/20 000, что равно 3,1416 — поистине удивительная оценка. Около 1400 года персидский астроном Кашани правильно вычислил число π до 16 цифр.

Как измерять углы с помощью пи

Давайте отвлечемся от этой исторической охоты за цифрами числа π и рассмотрим π как важное число в нашей Вселенной. Учитывая связь π с измерением длины окружности, ученые были вдохновлены использовать его в качестве меры углового расстояния. Рассмотрим круг с радиусом 1. Радиус — это просто мера от центра в стороны. Это половина диаметра.

Традиционными единицами измерения углов, конечно же, являются градусы. С градусами один полный оборот вокруг окружности имеет меру 360 градусов, что примерно равно количеству дней в одном полном году и может объяснить, почему мы думаем об одном обороте как о 360.

Вместо произвольной меры 360, подразумевающей один оборот по кругу, давайте вычислим реальную длину путешествия по этому конкретному кругу, кругу радиуса 1, один раз. Какая у него длина и окружность? Если у нас есть радиус 1, то наш диаметр в два раза больше, чем 2, и поэтому мы знаем, что однократный оборот будет в 2 раза больше π, потому что длина окружности в π раз больше диаметра.

Когда-то вокруг будет 2π. Один полный оборот вокруг, который представляет собой угол в 360 градусов, будет выполнен с длиной окружности 2π в этом конкретном круге. На полпути будет 180 градусов, и мы выметем половину окружности, которая в данном случае будет равна π. Девяносто градусов охватывают четверть круга, и для этого конкретного круга длина этого круга будет равна π/2, или половине π.

Мы начинаем понимать, что каждый угол соответствует расстоянию, измеренному частично или полностью вокруг этой конкретной окружности радиуса 1. Другими словами, для любого угла мы можем измерить длину дуги этой окружности, охваченной под этим углом.

Эта длина дуги обеспечивает новый способ представления меры угла, и мы называем эту меру углов «радианной мерой». Например, 360 градусов = 2π радиан, это единицы; 180 градусов равны π радианам, а 90 градусов равны π/2 радианам. Помните, что все эти меры всегда основаны на специальной окружности с радиусом 1.

Узнайте больше о геометрии и тактике преобразования

Радианные измерения и сила числа Пи

Оказывается, что радианные измерения гораздо полезнее для измерения углов в математике и физике, чем более привычные градусные измерения. Этот факт неудивителен. Радианная мера естественным образом связана через длину окружности с углом, а не более произвольная градусная мера, не имеющая математической основы. Он представляет собой приближение через полный год.

Термин «радиан» впервые появился в печати в 1870-х годах, но к тому времени великие математики, в том числе великий математик Леонард Эйлер, использовали углы, измеряемые в радианах, уже более ста лет.

Число π появляется в бесчисленных важных формулах и теориях, включая принцип неопределенности Гейзенберга и уравнение поля Эйнштейна из общей теории относительности. Это важная формула и число во всем мире.

Общие вопросы о числе Пи

В: Что такое полное и точное число Пи?

Многие уравнения представляют Пи целиком, но, поскольку это иррациональное число, его десятичное представление, начинающееся с 3,14159… будет продолжаться вечно, по крайней мере, при вычислении.

В: Как вычислить Пи?

Существует много способов рассчитать число Пи, но стандартный метод заключается в измерении длины окружности ниткой или рулеткой, измерении диаметра линейкой и делении длины окружности на диаметр.