Минимизация булевых функций.
Минимизация булевых функций. <==BackБулевы Функции- Основные понятия.
- Аналитическое представление булевых функций.
- Функционально полные системы будевых функций.
- Минимизация булевых функций.
- Метод Квайна.
- Метод Квайна — Мак-Класки.
- Метод Блейка — Порецкого.
- Метод диаграмм Вейча.
- Минимизация коньюнктивных нормальных форм.
- Метод Петрика.
- Минимизация частично определенных булевых функций.
- Минимизация систем булевых функций.
Минимизация булевых функций.
» При проэктировании цифровых автоматов широко используются методы минимизации булевых функций, позволяющие получать рекомендации для построения экономичных схем цифровых автоматов. Общая задача минммизации булевых функций может быть сформулирована следующим образом: найти аналитическое выражение заданой булевой функции в форме, содержащей минимально возможное число букв.
Определение.
Элементарной конъюнкцией называется конъюнкция конечного числа различных между собой булевых переменных, каждая из которых может иметь или не иметь отрицания.
Определение.
Дизъюнктивной нормальной формой (ДНФ) называется дизъюнкция элементарных конъюкций.
Определение.
Минимальной дизъюнктивной нормальной формой булевой функции называется ДНФ, содержащая наименьшее число букв (по отношению ко всем другим ДНФ, представляющим заданную булеву функцию).
Определение.
Булева функция g(x1,…,xn) называется импликантой булевой функции f(x1,…,xn), если для любого набора переменных, на котором g=1, справедливо f=1.
| Таблица 4.1 | ||||||||
| x3x2x1 | f | g1 | g2 | g3 | g4 | g5 | g6 | g7 |
| 000 001 010 011 100 101 110 111 | 0 0 0 1 0 0 1 1 | 0 0 0 0 0 0 0 1 | 0 0 0 0 0 0 1 0 | 0 0 0 0 0 0 1 1 | 0 0 0 1 0 0 0 0 | 0 0 0 1 0 0 0 1 | 0 0 0 1 0 0 1 0 | 0 0 0 1 0 0 1 1 |
f = /x1x2x3 v x1x2/x3 v x1x2x3 = g
g1 = x1x2x3;
g2 = x1x2/x3;
g3 = x1x2x3 v x1x2/x3 = x1x2 (x3 v x3) = x1x2;
g4 = /x1x2x3;
g5 = /x1x2x3 v x1x2x3 = x2x3;
g6 = /x1x2x3 v x1x2/x3;
Определение.
Импликанта g булевой функции f, являющаяся элементарной конъюнкцией, называется простой, если никакая часть импликанты g не является импликантой функции f.
Из примера видно, что импликанты g3 = x1x2 и g5 = x2 x3 являются простыми импликантами функции f. Импликанты g1, g2, g4, g6 не являются простыми, так как их части являются импликантами функции f, например g3 является частью g1. Приведем без доказательства два утверждения, полезные при получении минимальной ДНФ.
- Дизъюнкция любого числа импликант булевой функции f также является импликантой этой функции.
- Любая булева функция f эквивалентна дизъюнкции всех своих простых импликант. Такая форма представления булевой функции называется сокращенной ДНФ.
 Следовательно, сокращенная ДНФ функции f имеет вид
Следовательно, сокращенная ДНФ функции f имеет видf = g3 v g5 = x
Как видно из табл. 4.1, импликанты g3, g5 в совокупности покрывают своими единицами все единицы функции f. Получение сокращенных ДНФ является первым этапом отыскания минимальных форм булевых функций. Как уже отмечалось, в сокращенную ДНФ входят все простые импликанты булевой функции. Иногда из сокращенной ДНФ можно убрать одну или несколько простых импликант, не нарушая эквивалентности исходной функции. Такие простые импликанты назовем лишними. Исключение лишних простых импликант из сокращенных ДНФ — второй этап минимизации.
Определение.
Сокращенная ДНФ булевой функции называется тупиковой, если в ней отсутствуют лишние простые импликанты.
Устранение лишних простых импликант из сокращенной ДНФ булевой функции не является однозначным процессом, т. е. булева функция может иметь несколько тупиковых ДНФ.
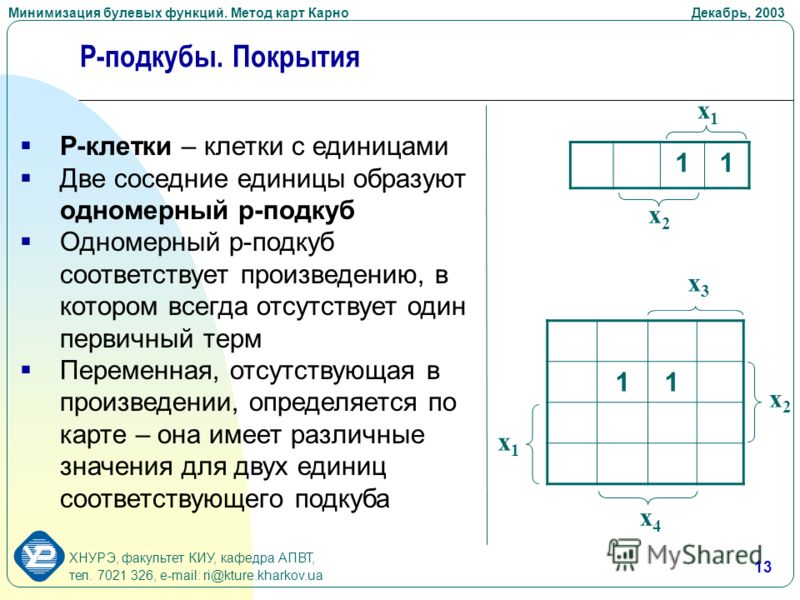
Утверждение.
Рассмотрим несколько методов минимизации. Все они практически различаются лишь на первом этапе — этапе получения сокращенной ДНФ. Следует отметить, что, к сожалению, поиск минимальной ДНФ всегда связан с некоторым перебором решений. Существуют методы уменьшения этого перебора, однако он всегда остается.»
Использованная литература:
1) «Прикладная теория цифровых автоматов» Киев «Вища Школа» 1987
К.Г. Самофалов, А.М. Романкевич, В.Н. Валуйский,
Ю.С. Каневский, М.М. Пиневич
страницы (195 — 197).
Прикладная теория цифровых автоматов
Прикладная теория цифровых автоматов
ОглавлениеПРЕДИСЛОВИЕГлава 1. ИНФОРМАЦИОННЫЕ ОСНОВЫ ЦИФРОВЫХ АВТОМАТОВ 1.1. ПОНЯТИЕ ИНФОРМАЦИИ 1.2. КОЛИЧЕСТВО ИНФОРМАЦИИ И ЭНТРОПИЯ 1.3. ДИСКРЕТИЗАЦИЯ ИНФОРМАЦИИ 1.4. АЛФАВИТНОЕ ПРЕДСТАВЛЕНИЕ И ПРЕОБРАЗОВАНИЕ ИНФОРМАЦИИ Глава 2. СИСТЕМЫ СЧИСЛЕНИЯ И ПРЕДСТАВЛЕНИЯ ИНФОРМАЦИИ В ЭВМ 2.1. НЕПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ 2.2. ПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ 2.  3. КОДИРОВАННЫЕ ПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ 3. КОДИРОВАННЫЕ ПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ2.4. СИСТЕМЫ СЧИСЛЕНИЯ СПЕЦИАЛЬНОГО НАЗНАЧЕНИЯ 2.5. ПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ С НЕПОСТОЯННЫМИ ВЕСАМИ РАЗРЯДОВ 2.6. СИМВОЛИЧЕСКИЕ СИСТЕМЫ СЧИСЛЕНИЯ 2.7. ПЕРЕВОД ЧИСЕЛ ИЗ ОДНОЙ СИСТЕМЫ СЧИСЛЕНИЯ В ДРУГУЮ 2.8. ВЫБОР СИСТЕМЫ СЧИСЛЕНИЯ ДЛЯ ПРИМЕНЕНИЯ ЭВМ 2.9. ДВОИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ 2.10. ПРЕДСТАВЛЕНИЕ ДВОИЧНЫХ ЧИСЕЛ В ЭВМ 2.11. ТОЧНОСТЬ ПРЕДСТАВЛЕНИЯ ЧИСЕЛ В ЭВМ Глава 3. ВЫПОЛНЕНИЕ ОПЕРАЦИЯ АЛГЕБРАИЧЕСКОГО СЛОЖЕНИЯ И СДВИГА В ЭВМ 3.2. ОПЕРАЦИЯ АЛГЕБРАИЧЕСКОГО СЛОЖЕНИЯ В ЭВМ 3.3. ОПЕРАЦИЯ СДВИГА 3.4. СЛОЖЕНИЕ ЧИСЕЛ В МАШИНАХ С ПЛАВАЮЩЕЙ ЗАПЯТОЙ 3.5. ОКРУГЛЕНИЕ ЧИСЕЛ В ЭВМ Особенности округления чисел, заданных инверсными кодами Погрешности выполнения арифметических операций 3.6. ТОЧНОСТЬ ВЫПОЛНЕНИЯ ОПЕРАЦИИ В МАШИНЕ С ПЛАВАЮЩЕЙ ЗАПЯТОЙ 3.7. ВЫЧИСЛЕНИЯ С ДВОЙНОЙ ТОЧНОСТЬЮ Глава 4. ВЫПОЛНЕНИЕ ОПЕРАЦИИ УМНОЖЕНИЯ И ДЕЛЕНИЯ В ЭВМ 4.  3. СРАВНЕНИЕ СХЕМ УМНОЖЕНИЯ МЕТОДОМ НАКОПЛЕНИЯ 3. СРАВНЕНИЕ СХЕМ УМНОЖЕНИЯ МЕТОДОМ НАКОПЛЕНИЯ4.4. МЕТОДЫ УСКОРЕНИЯ ОПЕРАЦИИ УМНОЖЕНИЯ Матричный метод умножения Быстрое умножение чисел большой разрядности 4.5. УМНОЖЕНИЕ ЧИСЕЛ, ЗАДАННЫХ В ДОПОЛНИТЕЛЬНОМ КОДЕ 4.6. УМНОЖЕНИЕ ЧИСЕЛ В МАШИНАХ С ПЛАВАЮЩЕЙ ЗАПЯТОЙ 4.7. ОСОБЕННОСТИ ВЫПОЛНЕНИЯ ОПЕРАЦИИ УМНОЖЕНИЯ В СОВРЕМЕННЫХ ЭВМ 4.8. ДЕЛЕНИЕ ЧИСЕЛ С ВОССТАНОВЛЕНИЕМ ОСТАТКОВ 4.9. ДЕЛЕНИЕ БЕЗ ВОССТАНОВЛЕНИЯ ОСТАТКОВ 4.10. МАШИННЫЕ СХЕМЫ ДЕЛЕНИЯ 4.11. ДЕЛЕНИЕ ЧИСЕЛ В ДОПОЛНИТЕЛЬНОМ КОДЕ 4.12. СПОСОБЫ УСКОРЕННОГО ДЕЛЕНИЯ 4.13. ДЕЛЕНИЕ ЧИСЕЛ В МАШИНАХ С ПЛАВАЮЩЕЙ ЗАПЯТОЙ 4.14. ДЕЛЕНИЕ ЧИСЕЛ В ЭВМ СОВРЕМЕННЫХ МОДЕЛЕЙ Глава 5. НЕОСНОВНЫЕ АРИФМЕТИЧЕСКИЕ ОПЕРАЦИИ 5.1. ОПЕРАЦИЯ ИЗВЛЕЧЕНИЯ КВАДРАТНОГО КОРНЯ 5.2. ВЫЧИСЛЕНИЕ СУММ ПАРНЫХ ПРОИЗВЕДЕНИИ 5.3. АРИФМЕТИКА КОМПЛЕКСНЫХ ЧИСЕЛ 5.4. МЕТОДЫ ВЫЧИСЛЕНИЯ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ Глава 6. ДВОИЧНО-ДЕСЯТИЧНАЯ АРИФМЕТИКА 6.2. СЛОЖЕНИЕ ЧИСЕЛ В ИНВЕРСНЫХ Д-КОДАХ 6.3. СДВИГ Д-КОДОВ 6.  4. УМНОЖЕНИЕ ЧИСЕЛ В Д-КОДАХ 4. УМНОЖЕНИЕ ЧИСЕЛ В Д-КОДАХ6.5. ДЕЛЕНИЕ ЧИСЕЛ В Д-КОДАХ 6.6. ПЕРЕВОД ЧИСЕЛ В Д-КОДАХ Глава 7. ВЫПОЛНЕНИЕ АРИФМЕТИЧЕСКИХ ОПЕРАЦИЙ В СИСТЕМАХ СПЕЦИАЛЬНОГО НАЗНАЧЕНИЯ 7.2. АРИФМЕТИЧЕСКИЕ ОПЕРАЦИИ В МИНУС-ДВОИЧНОЙ СИСТЕМЕ СЧИСЛЕНИЯ 7.3. АРИФМЕТИЧЕСКИЕ ОПЕРАЦИИ В СИСТЕМЕ ОСТАТОЧНЫХ КЛАССОВ Глава 8. КОНТРОЛЬ ВЫПОЛНЕНИЯ ОПЕРАЦИИ 8.2. ВЫБОР МОДУЛЯ ДЛЯ КОНТРОЛЯ 8.8. КОНТРОЛЬ ЛОГИЧЕСКИХ ОПЕРАЦИЙ 8.4. КОНТРОЛЬ АРИФМЕТИЧЕСКИХ ОПЕРАЦИЙ Глава 9. БУЛЕВЫ ФУНКЦИИ 9.2. АНАЛИТИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ БУЛЕВЫХ ФУНКЦИИ 9.3. ФУНКЦИОНАЛЬНО ПОЛНЫЕ СИСТЕМЫ БУЛЕВЫХ ФУНКЦИЙ 9.4. МИНИМИЗАЦИЯ БУЛЕВЫХ ФУНКЦИЙ 9.6. АБСОЛЮТНО МИНИМАЛЬНАЯ ФОРМА ПРЕДСТАВЛЕНИЯ БУЛЕВЫХ ФУНКЦИЙ 9.7. МНОГОЗНАЧНЫЕ ПЕРЕКЛЮЧАТЕЛЬНЫЕ ФУНКЦИИ Глава 10. АБСТРАКТНЫЕ ЦИФРОВЫЕ АВТОМАТЫ 10.2. ДЕКОМПОЗИЦИЯ АБСТРАКТНЫХ АВТОМАТОВ Глава 11. ПРОЕКТИРОВАНИЕ КОМБИНАЦИОННЫХ СХЕМ 11.2. ПРОЕКТИРОВАНИЕ КОМБИНАЦИОННЫХ СХЕМ В БУЛЕВОМ И МОНОФУНКЦИОНАЛЬНОМ БАЗИСАХ 11.  3. ПРОЕКТИРОВАНИЕ КОМБИНАЦИОННЫХ СХЕМ С УЧЕТОМ КОЭФФИЦИЕНТОВ ОБЪЕДИНЕНИЯ ПО ВХОДУ И ВЫХОДУ 3. ПРОЕКТИРОВАНИЕ КОМБИНАЦИОННЫХ СХЕМ С УЧЕТОМ КОЭФФИЦИЕНТОВ ОБЪЕДИНЕНИЯ ПО ВХОДУ И ВЫХОДУ11.4. ПРОЕКТИРОВАНИЕ КОМБИНАЦИОННЫХ СХЕМ НА ДЕШИФРАТОРАХ И МУЛЬТИПЛЕКСОРАХ 11.5. ПРОЕКТИРОВАНИЕ КОМБИНАЦИОННЫХ СХЕМ НА ПЗУ 11.6. ПРОЕКТИРОВАНИЕ КОМБИНАЦИОННЫХ СХЕМ НА ПЛМ 11.7. АСИМПТОТИЧЕСКИЕ МЕТОДЫ СИНТЕЗА ПЕРЕКЛЮЧАТЕЛЬНЫХ СХЕМ Глава 12. ПРОЕКТИРОВАНИЕ ЦИФРОВЫХ АВТОМАТОВ С ПАМЯТЬЮ 12.1. КАНОНИЧЕСКИЙ МЕТОД СТРУКТУРНОГО СИНТЕЗА АВТОМАТОВ С ПАМЯТЬЮ 12.2. ОБЕСПЕЧЕНИЕ УСТОЙЧИВОСТИ ФУНКЦИОНИРОВАНИЯ ЦИФРОВЫХ АВТОМАТОВ 12.8. СТРУКТУРНЫЙ СИНТЕЗ ЭКОНОМИЧНЫХ СХЕМ АВТОМАТОВ С ПАМЯТЬЮ 12.4. МИКРОПРОГРАММНЫЕ АВТОМАТЫ Глава 13. ЭЛЕМЕНТЫ ТЕОРИИ ПОМЕХОУСТОЙЧИВОГО КОДИРОВАНИЯ 13.2 ЛИНЕЙНЫЕ ГРУППОВЫЕ КОДЫ 13.3. ЦИКЛИЧЕСКИЕ КОДЫ Глава 14. КОНТРОЛЬ ЦИФРОВЫХ АВТОМАТОВ 14.2. ОБЩИЕ МЕТОДЫ ФУНКЦИОНАЛЬНОГО КОНТРОЛЯ ЦИФРОВЫХ АВТОМАТОВ 14.3. ФУНКЦИОНАЛЬНЫЙ КОНТРОЛЬ ЦИФРОВЫХ АВТОМАТОВ ПРИ ИСПОЛЬЗОВАНИИ ЛИНЕЙНЫХ ГРУППОВЫХ КОДОВ 14.4. ЭЛЕМЕНТЫ ТЕОРИИ САМОПРОВЕРЯЕМЫХ ЦИФРОВЫХ АВТОМАТОВ 14.  5. ТЕСТОВЫЙ КОНТРОЛЬ 5. ТЕСТОВЫЙ КОНТРОЛЬ14.6. САМОДИАГНОСТИРУЕМЫЕ ВЫЧИСЛИТЕЛЬНЫЕ СИСТЕМЫ СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ |
Минимизация булевых функций | Организация и архитектура компьютера
(подготовлено Тан Цзы Линг B031210024)
Формы логических уравнений
Булева алгебра — это комбинации переменных и операторов. Как правило, он имеет один или несколько входов и выдает результат в диапазоне от 0 до 1. Дополнение переменных показано чертой над буквой.
Все логические уравнения могут быть представлены в двух формах:
- Сумма произведений (СОП)
Ø Комбинация входных значений, которая дает 1 с, преобразуется в эквивалентные переменные, объединяется по И, а затем по ИЛИ с другими комбинированными переменными с тем же выходом.
Ø СОП легче вывести из таблицы истинности.
- Произведение сумм (POS)
Ø Комбинации входных данных, которые дают 0 в сумме (переменные, объединенные ИЛИ), объединяются вместе.
Ø Преобразуйте входные значения, которые производят 0, в эквивалентные переменные, объедините переменные по операции ИЛИ, а затем по И с другими формами по операции ИЛИ.
Ø Обычно используется, если функция вывода производит более 1 с.
Минимизация булевых функций
Минимизация означает более простой способ понимания и более легкую запись, они также менее подвержены ошибкам в интерпретации, но, что наиболее важно, упрощенные выражения обычно более эффективны и действенны при применении на практике.
Логическое выражение состоит из переменных и термов. Упрощение логических выражений может привести к более эффективным компьютерным программам, алгоритмам и схемам.
Есть три способа минимизировать логическое уравнение:
- Законы булевой алгебры
- Диаграммы Венна
- Карта Карно
1. Законы булевой алгебры
Логические выражения можно изменять или упрощать. Ниже показаны основные законы булевой алгебры, помогающие работать с логическими уравнениями: ( * ~X = не X )
| И Форма | ИЛИ Форма | |
| Закон о личности | Х. 1 = Х 1 = Х | Х + 0 = Х |
| Закон нуля и единицы | Х.0 = 0 | Х + 1 = 1 |
| Обратный закон | Х . ~Х = 0 | Х + ~Х = 1 |
| Закон идемпотента | Х.Х = Х | Х + Х = Х |
| Коммутативное право | XY = YX | Х + У = У + Х |
| Ассоциативное право | X.(Y.Z) = (X.Y).Z | Х+(У+Z) = (Х+У)+Z |
| Распределительное право | Х+(Y.Z) = (Х+Y).(X.Z) | X.(Y+Z) = (X.Y)+(X.Z) |
| Закон о поглощении | Х(Х+У) = Х | Х + Х.У = Х |
| Х + ~ХУ = Х +У | ||
| Закон Де Моргана | ~(X.Y) = ~X+~Y | ~(X+Y) = ~X.~Y |
| Закон двойного дополнения | ~~Х = Х | |
| Х.1 = Х | Х+1 = 1 | |
| Операции над константами | Х. 0 = 0 0 = 0 | Х+0 = 0 |
**************************************************** ******************************************************* *
- ~(XY) = ~X.~Y
- При разрыве строки изменить знак:
- Ø ~ (X.Y) = ~X + ~Y
- Ø ~ (X +Y) = ~X.~Y
2.Диаграмма Венна
i) ИЛИ Оператор
ИЛИ – Присутствует любой из терминов (могут присутствовать более одного термина).
Пример 1: фрукты ИЛИ овощи
Пример 2:
фрукты ИЛИ овощи ИЛИ злаки
ИЛИ – часто используется для расширения поиска путем связывания нескольких синонимов.
автомобили или автомобили / марихуана, травка или каннабис / эвтаназия или помощь в самоубийстве
ii) И Оператор
И – Все термины присутствуют. И — это лучший способ сузить область поиска, ограничив результаты только теми ресурсами (статьями или книгами), которые касаются выбранных вами слов.
Пример 3 : реки И соленость
Пример 4 : молочные продукты И экспорт И Европа
iii) НЕ Оператор
НЕ – Второй термин присутствует, но не первый.
Пример 5: фрукты НЕ яблоки
iv) Использование скобок для выражения правильной логики поиска
Порядок приоритета логических операторов: И, НЕ, ИЛИ. То есть операция И будет выполняться перед операцией ИЛИ, если обе операции включены в запрос, если только круглые скобки не используются для переопределения приоритета операторов поиска. Выражения в скобках обрабатываются первыми.
Пример 6 : (лисы ИЛИ кролики) И борьба с вредителями
Оператор в скобках — «лисы ИЛИ кролики» — обрабатывается первым.
Пример 7 :
Если скобки были опущены: лисы ИЛИ кролики И борьба с вредителями
Операция И – «кролики И борьба с вредителями» – обрабатывается первой.
3. Карты Карно
Карта Карно или К-карта является важным инструментом цифрового проектирования для упрощения логических выражений
или преобразования таблицы истинности в соответствующую логику 9Цепь 0206.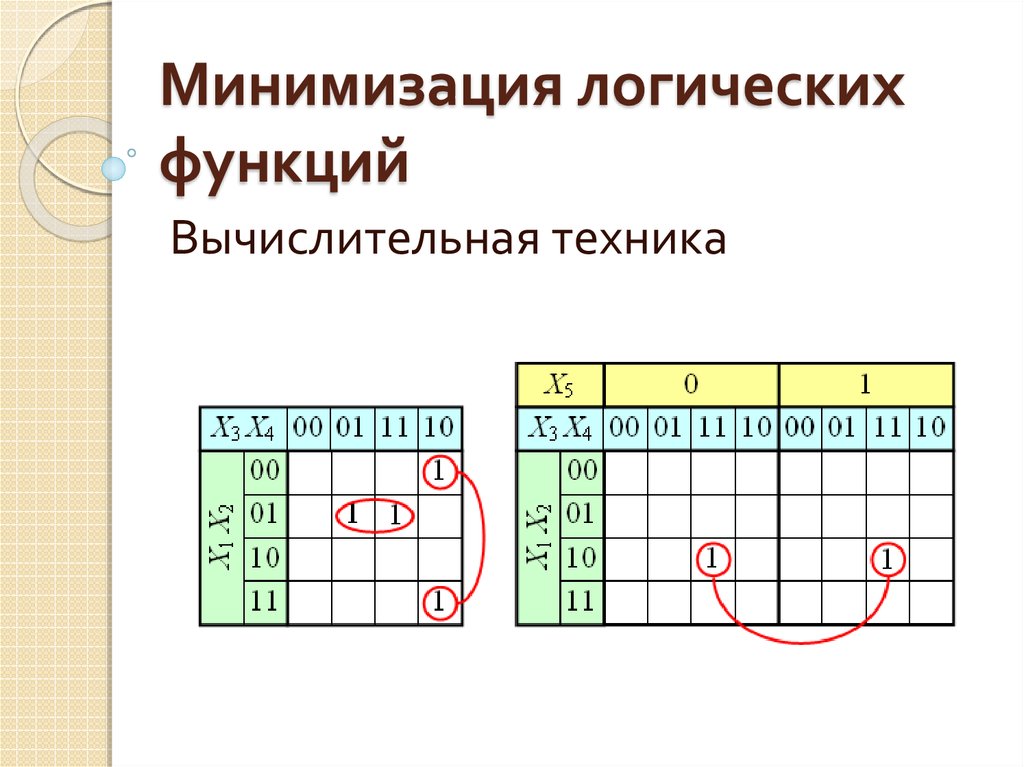 Процесс объединения пар, четверок или октетов единиц 90 206 упрощает логическое выражение для вывода, исключая переменные, которые 90 206 появляются как в дополненной, так и в недополненной форме.
Процесс объединения пар, четверок или октетов единиц 90 206 упрощает логическое выражение для вывода, исключая переменные, которые 90 206 появляются как в дополненной, так и в недополненной форме.
Пример 8: чтобы продемонстрировать, как процесс зацикливания упрощает выходное выражение. Таблица истинности0050
Карта Карно использует следующие правила для упрощения выражений
с помощью группировки вместе смежных ячеек, содержащих единицу:
1) Группы не могут включать ячейки, содержащие ноль.
2) Группы могут быть горизонтальными или вертикальными, но не диагональными.
3) Группы должны содержать 1, 2, 4, 8 или вообще 2 n ячеек.
То есть, если n = 1, группа будет содержать две единицы, так как 2 1 = 2,
Если n = 2, группа будет содержать четыре единицы, поскольку 2 2 = 4.
4) Каждая группа должна быть как можно больше.
5) Каждая ячейка, содержащая и , должна входить хотя бы в одну группу.
6) Группы могут пересекаться.
7) Группы могут располагаться вокруг стола. Крайняя левая ячейка в строке может быть сгруппирована с самой правой ячейкой, а верхняя ячейка в столбце может быть сгруппирована с нижней ячейкой
.
8) Групп должно быть как можно меньше, если это не противоречит
ни одному из предыдущих правил.
Резюме правила упрощения:
- Нули не допускаются.
- Без диагоналей.
- Только мощность 2-х ячеек в каждой группе.
- Группы должны быть как можно больше.
- Каждый должен быть хотя бы в одной группе.
- Перекрытие разрешено.
- Разрешен циклический перенос.
- Наименьшее возможное количество групп.
Ссылка:
http://staff.science.uva.nl/~jesshope/web-site-08123/Downloads/laws.pdf
http://hyperphysics.phy-astr.gsu.edu/ hbase/electronic/demorgan.html
http://www. ee.surrey.ac.uk/Projects/Labview/minimisation/index.html
ee.surrey.ac.uk/Projects/Labview/minimisation/index.html
http://users.cecs.anu.edu.au/~Matthew .James/engn2211-2002/doc/kmap/kmap.html
Нравится:
Нравится Загрузка…
Минимизация двухуровневой логики — Python EDA Documentation
В этой главе объясняется, как использовать PyEDA для минимизации двухуровневого Формы «сумма произведений» булевых функций.
Известно, что логическая минимизация является NP-полной задачей. Это эквивалентно нахождению множества с минимальной стоимостью подмножеств множества \(S\) что покрывает \(S\). Иногда это называют «проблемой мощения». потому что это концептуально похоже на поиск самой дешевой конфигурации плитка, покрывающая пол. В связи со сложностью этой операции PyEDA использует расширение C для известной библиотеки Berkeley Espresso [1].
Во всех примерах в этой главе предполагается, что интерактивные символы импортированы:
>>> из pyeda.inter import *
Минимизация логических выражений
Рассмотрим функцию с тремя входами \(f_{1} = a \cdot b’ \cdot c’ + a’ \cdot b’ \cdot c + a \cdot b’ \cdot c + a \cdot b \cdot c + a \cdot b \cdot c’\)
>>> a, b, c = map(exprvar, 'abc') >>> f1 = ~a & ~b & ~c | ~а и ~б и в | а и ~ б и в | а и б и в | а и б и ~ в
Чтобы использовать Espresso для минимизации:
>>> f1m, = espresso_exprs(f1.to_dnf()) >>> ф1м Или(И(~а, ~б), И(а, б), И(~б, в))
Обратите внимание, что функция espresso_exprs возвращает кортеж.
Причина в том, что эта функция может минимизировать несколько входных функций
одновременно.
Для демонстрации создадим вторую функцию
\(f_{2} = a’ \cdot b’ \cdot c + a \cdot b’ \cdot c\).
>>> f2 = ~a & ~b & c | а и ~ б и в >>> f1m, f2m = espresso_exprs(f1, f2) >>> ф1м Или(И(~а, ~б), И(а, б), И(~б, в)) >>> ф2м И(~б, в)
Легко проверить, что минимальные функции эквивалентны оригиналам:
>>> f1.equivalent(f1m) Истинный >>> f2.эквивалент(f2m) Истинный
Минимизация таблиц истинности
Выражение является полностью определенной функцией.
Иногда вместо минимизации существующего выражения
вместо этого вы начинаете только с таблицы истинности, которая отображает входные данные в \({0, 1}\)
к выводам в \({0, 1, *}\), где \(*\) означает «все равно».
Для этого типа не полностью заданная функция,
вы можете использовать функцию espresso_tts , чтобы найти недорогой, эквивалентный
Логическое выражение.
Рассмотрим следующую таблицу истинности с четырьмя входами и двумя выходами: Выходы x3 x2 х 1 х0 ф1 ф2 0 0 0 0 0 0 0 0 0 1 0 0 0 0 1 0 0 0 0 0 1 1 0 1 0 1 0 0 0 1 0 1 0 1 1 1 0 1 1 0 1 1 0 1 1 1 1 1 1 0 0 0 1 0 1 0 0 1 1 0 1 0 1 0 х х 1 0 1 1 х х 1 1 0 0 х х 1 1 0 1 х х 1 1 1 0 х х 1 1 1 1 х х
Функция espresso_tts принимает последовательность входных функций таблицы истинности,
и возвращает последовательность экземпляров выражений DNF.
>>> X = ttvars('x', 4)
>>> f1 = правдивость(X, "0000011111------")
>>> f2 = правдивость(X, "0001111100------")
>>> f1m, f2m = espresso_tts(f1, f2)
>>> ф1м
Или(х[3], И(х[0], х[2]), И(х[1], х[2]))
>>> ф2м
Или (х [2], И (х [0], х [1]))
Вы можете проверить, эквивалентны ли полученные выражения исходным таблицы истинности при визуальном осмотре (или более умном методе):
>>> expr2truthtable(f1m) х[3] х[2] х[1] х[0] 0 0 0 0 : 0 0 0 0 1 : 0 0 0 1 0 : 0 0 0 1 1 : 0 0 1 0 0 : 0 0 1 0 1 : 1 0 1 1 0 : 1 0 1 1 1 : 1 1 0 0 0 : 1 1 0 0 1 : 1 1 0 1 0 : 1 1 0 1 1 : 1 1 1 0 0 : 1 1 1 0 1 : 1 1 1 1 0 : 1 1 1 1 1 : 1 >>> expr2truthtable(f2m) х[2] х[1] х[0] 0 0 0 : 0 0 0 1 : 0 0 1 0 : 0 0 1 1 : 1 1 0 0 : 1 1 0 1 : 1 1 1 0 : 1 1 1 1 : 1
Espresso Script
Начиная с версии 0.20 , PyEDA включает скрипт, который реализует некоторые
функциональности оригинальной утилиты командной строки Espresso.
$ эспрессо -ч
использование: эспрессо [-h] [-e {быстрый, ness, nirr, nunwrap, начало, крепкий}] [--fast]
[--no-ess] [--no-irr] [--no-unwrap] [--onset] [--strong]
[файл]
Свернуть PLA-файл
позиционные аргументы:
файл PLA-файл (по умолчанию: стандартный ввод)
необязательные аргументы:
-h, --help показать это справочное сообщение и выйти
...
Вот пример простого файла PLA, который является частью набора тестов BOOM. Эта функция имеет 50 входных переменных, 5 выходных переменных и 50 условий продукта. Кроме того, 20% литералов в импликантах имеют значение «все равно».
$ расширение кота/эспрессо/тест/bb_all/bb_50x5x50_20%_0.pla .i 50 .о 5 .p 50 .ilb x0 x1 x2 x3 x4 x5 x6 x7 x8 x9 x10 x11 x12 x13 x14 x15 x16 x17 x18 x19 x20 x21 x22 x23 x24 x25 x26 x27 x28 x29 x30 x31 x32 x33 x34 x35 x36 x37 x38 x39 x40 x41 x44 x43 х48 х49.ob у0 у1 у2 у3 у4 .type фр. 001011110--00--0100-0010-10-01010101-010--01011111 00011 0-1-1010-01000100--11011-0110001010-10001010-1-1-0 00100 0111010111110110110-100101101010010001111----1-011 10000 01-0010011-001110--000-011--11--1-0100-01101--1000 00001 001011010-1100000001101--10100-010-001100111110010 00101 011-01010-10-1101110-00-1-11001-1-0000--1-1-00-000 00011 0000000011001-0000010-000110-11011001110--100-1-10 00110 00-111111-00100-100111101000-11101100--0-1110-1-10 10001 -1-10011011000011--00-0011011101-1-1101110--1-001- 11100 -0101100-110111-010-01110-0110011-1-1---1001011111 11000 0-111011101000-11-1--10-0001001101000010-11-111101 11001 11000000-1-01--1111-10111111----0010--1-0--1--0111 01010 00-101000011-1-10101101-1101011-0101000-111111011- 11011 1-00-11111-0010-0---000--0110-0010111--000001-0001 11011 -1-1100100001--00--00001000-1-1--100-0111-00011011 11000 0-0000-010-11-1100-101-00101000111-01--11-0010-011 10000 11-1-0001100101-10-0-1-0-1100010101111-1111000-101 11101 10-01--10011111-11011-001001101100110010010-000-0-01110 1-11010-00011101-010--101010--0111010101-11-101--1 00111 11--111-111-111-000-11000-101-1-011--1000--1111100 01111 0---0-10011101000--11001-1100-10-000011-0100011100 11110 -01--11-010-1001011-0-101000100000--10111---100-1- 11101 11-1-000010--00110-011101--11-10-1-0000110100-1101 11010 -0111110-100-11-110001001100001-100011110001001100 11110 11--00100-01--00-10---11-0001-00011101001011-01110 00000 1--010011-001-0000--0-11-001010001110-00-01-110-11 01101 100011--0101--1-1-0-101--001-0-101-1-1011101011-01 00111 0--0-01-10101-11-0100111111000-1-1011100-111-01111 10100 0-0110010--11101-0---1001-1001--001-110000---1011-00100 0-1000-0--00000010-0--1011-1001011-01-00-011001111 10000 111-1101111-01001101-111--00-01011111000001-001001 11100 0--100111-1010001-0111-0-000--00-0111101111-101100 11000 00001101100-001001-1010010010011-1101-110-10-110-1 01011 0101-01-0100101000010111--0011-0011011110-111100-0 00100 000-1--100-00-1001-10-000000100-001100-10101010001 10000 10001001-0001011-1-1-0-00101110-10100---0010001--- 10111 01011000000100100000---1--11-0001011111101-01-1011 01111 1--01--00100110001-110-0-00001011---01001000110--- 10010 0-0001--01--11101010100000000010011001000-01100001 00011 0-0100110-00111100-001--11--00-1001-00-0-11-1-0-1-00100 101-1-100-001001-010111-01--010-1-1011-01101001001 11000 0110-111011--1-010101-011-1-00100110-00-1111000-11 11001 011001011---010011-10-00-11-001000000101101101-0-1 00100 1001111-1-1111-1001-000111010-100--0111110011000-1 10111 1-1010-1-100111110010-101011-1001000111-0000--11-1 11000 -00110001000010000010100010010-0-0-100-1-0111011-1 00101 1110-01100111111-1-1-110-0-110--011--01-11-0000-01 00000 -01010101010-1-1-00-1111010100-1001111110110--0-00 11011 110-10000001--0-0-01001111-0011-0110110100010--111 11111 101-10111000011110000-1001-001-01111-011-0001-0100 00100 .е
После запуска входного файла через сценарий эспрессо ,
он минимизирует функцию до 26 импликантов со значительно меньшим количеством литералов.
$ расширение эспрессо/эспрессо/тест/bb_all/bb_50x5x50_20%_0.pla .i 50 .о 5 .ilb x0 x1 x2 x3 x4 x5 x6 x7 x8 x9 x10 x11 x12 x13 x14 x15 x16 x17 x18 x19 x20 x21 x22 x23 x24 x25 x26 x27 x28 x29 x30 x31 x32 x33 x34 x35 x36 x37 x38 x39 x40 x41 x44 x43 х48 х49 .ob у0 у1 у2 у3 у4 стр. 26 ----------------------0-----1---0------0---------- 01110 ------0--------------1-----1--0--0- 11100 ---------------------------1--------1---0------0-- 01011 -------------------------------------11-1---------1 10000 0-------------------------1----------1-1------------ 00110 --------0--------1----------0-------0------------- 00010 -------------0---------0-0-0------1- 10001 --------------0-00----0--------1----- 00101 --------------------------0-0---0----------0------- 00011 -----------0----0-----------0---0--- 10000 -------------------------1---0---1----------------1 10000 --------------------------01-----------------------------0---1--1 11000 ----------------------------00------------------------11--------- 11000 ----------------------------0-1----------0-0---1--- 11110 --------------------------1----1--0------------1-- 00100 -----1---------------1-1---1-------- 00111 ------1---------------0-------1--1---0------------ 11001 ------0----0----------------1-1-0--- 01000 -1---1---------1----------------------------------0 00001 ------------------1------------------------------------0-----0-1- 01010 --------------------0--------1----------1------0--- 00100 ---------------------------11-------------1-0-1--- 10010 --------------------------1-----0----10----------- 00100 ------0------0---------0---------0-----------0---- 00101 -------0----------0---1--1--0---0--- 11011 --------------------0-----------0-----------1-0--- 00100 .

 Г. Самофалов, А. М. Ромлинкевич, В. Н. Валуйский, Ю. С. Каневский, М. М. Пиневич.— К.: Вища шк. Головное изд-во, 1987. — 375 с.
Г. Самофалов, А. М. Ромлинкевич, В. Н. Валуйский, Ю. С. Каневский, М. М. Пиневич.— К.: Вища шк. Головное изд-во, 1987. — 375 с.
 to_dnf())
>>> ф1м
Или(И(~а, ~б), И(а, б), И(~б, в))
to_dnf())
>>> ф1м
Или(И(~а, ~б), И(а, б), И(~б, в))
 е
е
