| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | cos(pi/4) | ||
| 9 | Найти точное значение | sin(45 град. ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | ||
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| Найти точное значение | arcsin(0) | ||
| 95 | Найти точное значение | sin(120 град. ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
Как найти значения углов во всех 4 квадрантах?
ВведениеБольше примеров
Purplemath
На предыдущей странице мы видели, как мы можем расширить контекст тригонометрических соотношений от геометрических прямоугольных треугольников до алгебраических углов, основанных на начале координат и использующих углы любой меры .
Это отделяет триггерные соотношения от физических ограничений, позволяя использовать их во многих других областях исследования, таких как физика и инженерия.
Содержание продолжается ниже
MathHelp.com
Чтобы обновить:
Как найти коэффициенты триггера для углов более девяноста градусов?
Чтобы найти значения тригонометрических отношений, когда углы больше 90°, выполните следующие действия:
- В плоскости x , y нарисуйте конечную сторону угла.
- Нарисуйте линию от этой конечной линии до 9Ось 0022 x , перпендикулярная оси x .
- Внутри прямоугольного треугольника, образованного осью, конечной линией и перпендикуляром, обозначьте базовый угол (в начале координат) его размером в этом квадранте плоскости. Например, угол 120° становится треугольником во втором квадранте с мерой угла при основании 180° — 120° = 60°.
- Обозначьте длину оси и перпендикуляр с их значениями в квадранте . Например, для угла 60° во втором квадранте «противоположная» величина (высота y ) положительна, а «смежная» сторона (вдоль оси x ) отрицательна.
- Используйте теорему Пифагора, чтобы найти значение гипотенузы, если это необходимо. (Это значение всегда будет положительным.)
- После того, как все три стороны промаркированы, с их знаками , прочтите пропорции прямо с картинки.
Немного потренировавшись, описанный выше процесс станет довольно простым. Давайте посмотрим на пример.
- Найдите шесть тригонометрических соотношений для угла с точкой (4, −3) на конце.
Сначала я нарисую рисунок, показывающий две оси, заданную точку, линию от начала координат через точку (представляющую конечную сторону угла) и угол θ, образованный положительным x -ось и конечная точка:
Да, этот рисунок немного неаккуратный.
Но моя картина не должна быть точной или «в масштабе». Это просто заполнитель. Мне нужно только общее представление о том, в каком квадранте я нахожусь и где находится угол θ.
Теперь, когда я нарисовал угол в четвертом квадранте, я опустил перпендикуляр вниз от оси вниз к конечной точке:
Получился прямоугольный треугольник в четвертом квадранте. Я могу работать с этим.
От х — и y — значения точки, которую они мне дали, я могу обозначить две стороны моего прямоугольного треугольника:
Тогда теорема Пифагора дает мне длину r гипотенузы:
r 2 = 4 2 + (−3) 2
r 2 = 16 + 9 = 25
r = 5
Теперь я закончу свою картину, добавив длину гипотенузы к моему прямоугольному треугольнику:
И это даст мне все, что мне нужно для нахождения соотношений. Чтобы найти ответы, я могу просто прочитать числа с моей картинки:
Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в нахождении тригонометрических соотношений из точки на конечной стороне угла.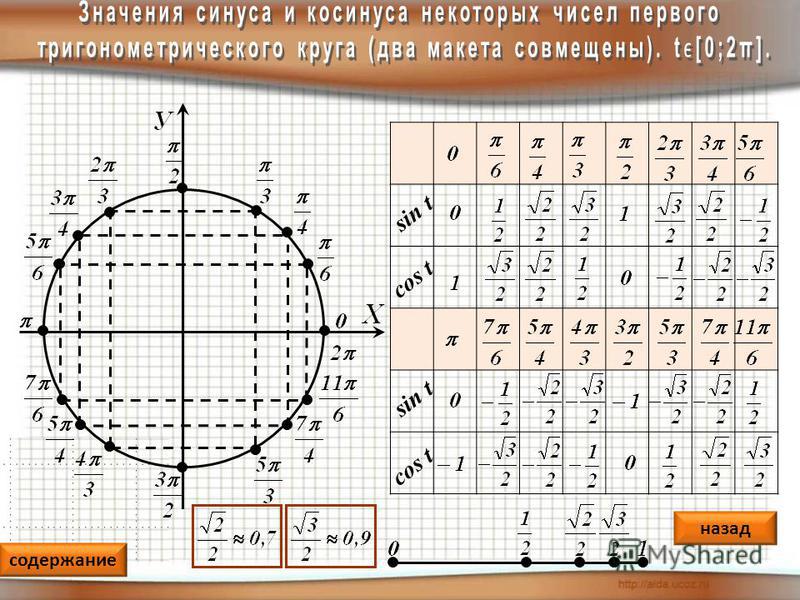
(Или пропустите виджет и продолжите урок.) Попробуйте введенное упражнение или введите свое собственное упражнение. Затем нажмите кнопку и выберите «Найти [коэффициент срабатывания]», чтобы сравнить свой ответ с ответом Mathway.
Пожалуйста, примите куки «предпочтения», чтобы включить этот виджет.
(Нажмите «Нажмите, чтобы просмотреть шаги», чтобы перейти непосредственно на сайт Mathway для платного обновления.)
Иногда вам будут давать фрагментарную информацию, из которой вас попросят вычислить квадрант для контекста.
- Определите квадрант, в котором лежит конечная сторона угла θ, учитывая, что tan(θ) < 0 и sin(θ) < 0.
В этом упражнении мне нужно рассмотреть значения x и y в различных квадрантах в контексте соотношений триггеров. Мне не нужно находить какие-либо фактические значения; Мне нужно работать только со знаками и с тем, что я знаю о соотношениях и квадрантах.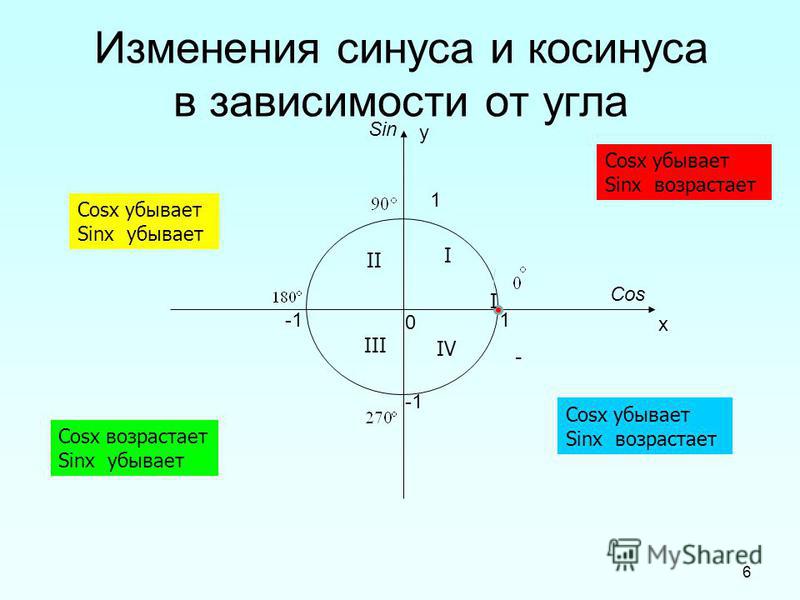
Тангенс равен y / x , поэтому тангенс будет отрицательным, когда x и y имеют противоположные знаки. Это происходит во втором квадранте (где x отрицательно, а y положительно) и в четвертом квадранте (где x положительно, а y отрицательно). Итак, знак касательной говорит мне, что конец угла находится в QII или в QIV.
Коэффициент синуса равен y / r , а гипотенуза r всегда положительный. Таким образом, синус будет отрицательным, когда y отрицательны, что происходит в третьем и четвертом квадрантах.
Таким образом, тангенс отрицателен в QII и QIV, а синус отрицателен в QIII и QIV. Перекрытие между двумя решениями равно QIV, поэтому:
конечная сторона θ: QIV
Мыслительный процесс в приведенном выше упражнении приводит к правилу запоминания знаков тригонометрических соотношений в каждом из квадрантов.
Каковы знаки синуса, косинуса и тангенса в четырех квадрантах?
Используя знаки x и y в каждом из четырех квадрантов, и учитывая тот факт, что гипотенуза r всегда положительна, находим следующее:
- В первом квадранте все значения ( x , y и r) положительны, поэтому все коэффициенты триггеров положительны.
- Во втором квадранте значения x отрицательные, поэтому x / r и y / x отрицательные; положительно только y / r , поэтому в QII положителен только синус.
- В третьем квадранте каждое из x и y отрицательно, поэтому x / r и y / r отрицательны; только y / x является положительным, поэтому в QIII положителен только тангенс.
- В четвертом квадранте значения и отрицательные, поэтому y / r и y / x отрицательные; положительно только x / r , поэтому в QIV положителен только косинус.
Вам, наверное, интересно, почему в предыдущем абзаце я написал триггерные коэффициенты и слово «Все» с большой буквы. Я сделал это, чтобы объяснить эту картинку:
Буквы в квадрантах обозначают начальные значения триггерных соотношений, которые в этом квадранте равны положительным .
Какие мнемоники помогут вам запомнить, где синус, косинус и тангенс положительны?
Некоторые люди запоминают буквы, обозначающие положительность, используя слово «ACTS», но это обратный нормальный (против часовой стрелки) тригонометрический порядок. Другие помнят буквы со словом «CAST», что является нормальным порядком вращения, но не начинается в обычном (первом квадранте) начальном месте.
Чтобы начать с обычного места и повернуться в обычном направлении, третьи используют мнемонику «Все ученики принимают исчисление» (что не соответствует действительности). Используйте тот метод, который лучше всего подходит для вас.
- Найдите значения остальных тригометрических отношений, учитывая, что cos(θ) = -8/17 и θ принадлежит QIII.
Из знака значения косинуса я знаю только, что угол находится в QII или QIII. Вот почему они должны были дать мне эту дополнительную спецификацию: чтобы я знал, в каком из этих двух квадрантов я работаю.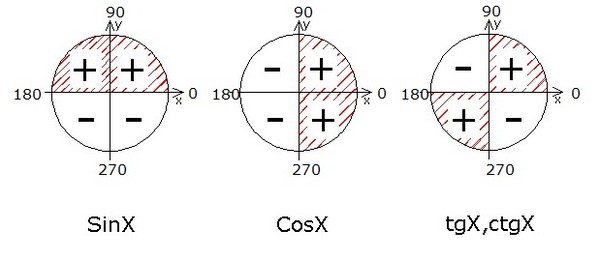
а именно, что конечная сторона θ находится в QIII, что «прилегающая» сторона (вдоль x ) имеет длину -8, а гипотенуза r имеет длину 17:
(Для длины по оси x я использую термин «длина» вольно, поскольку длина на самом деле не является отрицательной. Ожидайте, что в этом контексте слово «длина» будет часто использоваться в этом контексте.)
Теорема Пифагора дает мне длину оставшейся стороны:
17 2 = (−8) 2 + у 2
289 = 64 + у 2
225 = y 2
±15 = y
Поскольку я нахожусь в QIII, я ниже оси x , поэтому y отрицательно. Поэтому я возьму отрицательное решение уравнения и добавлю это к своей картинке:
Теперь я могу считать значения оставшихся пяти триггерных коэффициентов с моей картинки:
URL: https ://www.purplemath.com/modules/quadangs2.
htm
Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в нахождении тригонометрических отношений по значению одного из отношений вместе с квадрантом в игре. (Или пропустите виджет и перейдите на следующую страницу.) Попробуйте введенное упражнение или введите свое собственное упражнение. Затем нажмите кнопку и выберите «Найти значение триггера», чтобы сравнить свой ответ с ответом Mathway. (Вместо названия квадранта используйте диапазон градусов для этого квадранта.)
Пожалуйста, примите куки-файлы настроек, чтобы включить этот виджет.
(Нажмите «Нажмите, чтобы просмотреть шаги», чтобы перейти непосредственно на сайт Mathway для платного обновления.) Тригонометрия Мабела М. 3cos(8pi*x)-8sin(8pi*x) -3cos(8pi*x)-8sin(8pi*x) 8sin(8pi*x)-3cos(8pi*x) 3cos(8pi*x)+8sin(8pi*x) Подписаться
І
2 Подробнее Отчет Автор:
Лучшие новыеСамые старые Люк Дж. Репетитор 4.7
(26) Опытный репетитор STEM от старшей школы до колледжа Об этом репетиторе › Об этом репетиторе › Дано: 3 cos( 8πx ) — 8 sin( 8πx ) -3 cos( 8πx ) — 8 sin( 8πx ) 8 sin( 8πx ) — 3 cos( 8πx ) 8 π 3 cos) + 8 sin( 8πx ) Найти: A cos( 8πx + φ ) A = ? φ = ? Для всех 4 случаев Решение: Поскольку у меня нет времени на решение всех задач, я дам вам схему и первое решение, а остальные должны последовать Цель состоит в том, чтобы составить уравнение Я показал в разделе «Найти» эквивалент каждой суммы или разности синуса и косинуса следующим образом: A cos( 8πx + φ ) = 3 cos( 8πx ) — 8 sin( 8πx ) Что это позволяет нам сделать то, что мы можем расширить левую часть уравнения, используя формулу суммы косинуса угла: cos( F + G ) = cos F * cos G — sin F * sin G Итак, давайте сделаем это: cos( 8πx ) * A cos( φ ) — sin( 8πx ) * A sin ( φ ) = 3 cos( 8πx ) — 8 sin( 8πx ) Таким образом: A cos( φ ) = 3 A sin( φ ) = 8 , если бы правая часть была вместо «+ 8 sin( 8πx )», то A sin( φ ) было бы равно -8 вместо +8 [ A cos( φ ) ] 2 + [ A sin( φ ) ] 2 = 3 2 + 8 2 = A 2 = 73 ∴ A = √ (73) ≈ 8,544 A SIN) / A COS (φ) = 8 /3 /3 /3 / = Tan φ ∴ φ = TAN -1 (8/3) ≈ 1,212 рад SO, 1 ответ эксперта
Лучший
Новейшие
Самый старый
ответил 21.04.22
8
8
8
9038 9.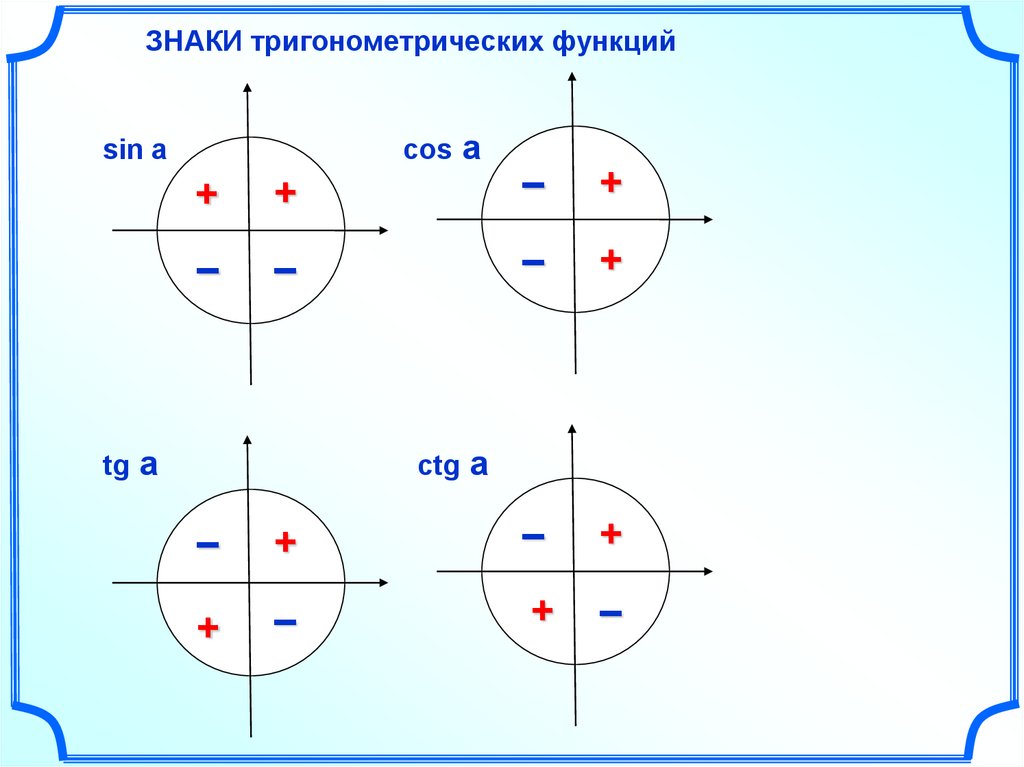
( 73 ) cos( 8πx + tan -1 ( 8/3 ) ) ≈ 8,544 cos( 8πx + 1,212 )
Надеюсь, это поможет! Извините, что я не смог опубликовать все решения проблем, я бы все равно достиг лимита символов на Wyzant! Напишите мне в комментариях, если у вас есть какие-либо вопросы, комментарии или опасения по поводу того, что и как я сделал выше!
Голосовать за 1 Понизить
Подробнее
Отчет
Все еще ищете помощь? Получите правильный ответ, быстро.
Задайте вопрос бесплатно
Получите бесплатный ответ на быстрый вопрос.
Ответы на большинство вопросов в течение 4 часов.
ИЛИ
Найдите онлайн-репетитора сейчас
Выберите эксперта и встретьтесь онлайн.