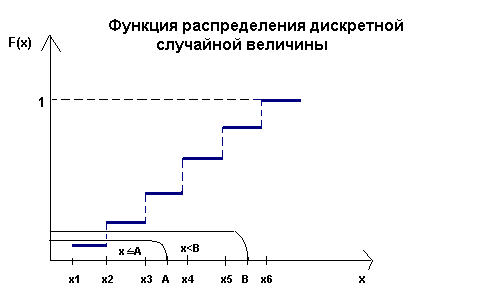
Функция распределения дискретной и непрерывной случайной величины
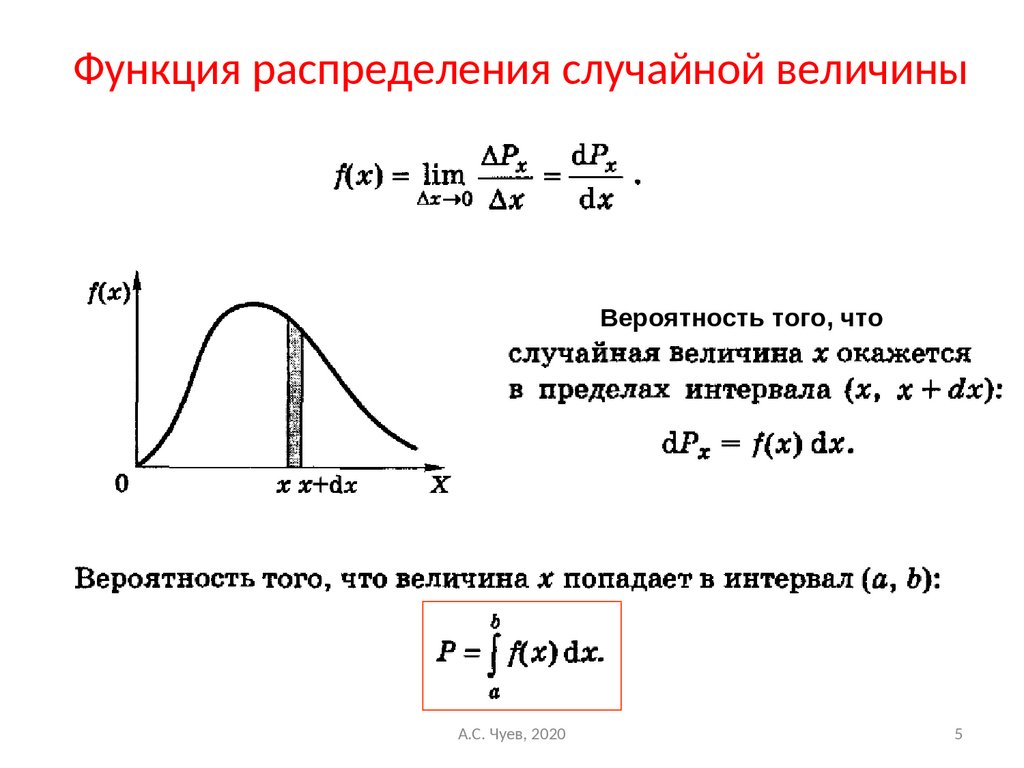
Функцией распределения случайной величины X называется функция F(x), задающая вероятность того, что случайная величина X принимает значение меньшее x, то есть
F(x) = р(Х<х)
Также функцию F(x) называют интегральной функцией распределения.
Плотность распределения вероятности (также называют дифференциальной функцией) функции распределения определяет непрерывную случайную величину.
Случайная величина X называется непрерывной, если её функция распределения непрерывна на всей числовой оси.
Обозначение: F(x)
1. Функция распределения есть неотрицательная функция, заключенная между нулем и единицей:
0≤F(x)≤1
2. Функция монотонно возрастающая, т. е. если xj > xi
3.
4. P(a≤X<b) = F(b) — F(a)
Пример 1 (Функция распределения дискретной случайной величины)
По заданному закону распределения случайной величины X, вычислить функцию распределения дискретной случайной величины.
| X | 0 | 1 | 2 | 3 | 4 |
| P | 0,2 | 0,1 | 0,25 | 0,15 | 0,3 |
Решение
Если x≤0, то F(x)=Р(Х<0)=0, следовательно событие при Р(Х<0) невозможно.
Если 0<x≤1, то F(x)=Р(Х<1)=Р(Х=0)=0.2
Если 1<x≤2, то F(x)=Р(Х<2)=Р(Х=0)+Р(Х=1)=0. 2+0.1=0.3
2+0.1=0.3
Если 2<x≤3, то F(x)=Р(Х<3)=Р(Х=0)+Р(Х=1)+Р(Х=2)=0.2+0.1+0.25=0.55
Если 3<x≤4, то F(x)=Р(Х<4)=Р(Х=0)+Р(Х=1)+Р(Х=2)+Р(Х=3)=
=0.2+0.1+0.25+0.15=0.7
Если x>4, то F(x)=Р(Х<4)=Р(Х=0)+Р(Х=1)+Р(Х=2)+Р(Х=)+Р(Х=4)=
=0.2+0.1+0.25+0.15+0.3=1
Получаем функцию распределения дискретной СВ в аналитическом виде:
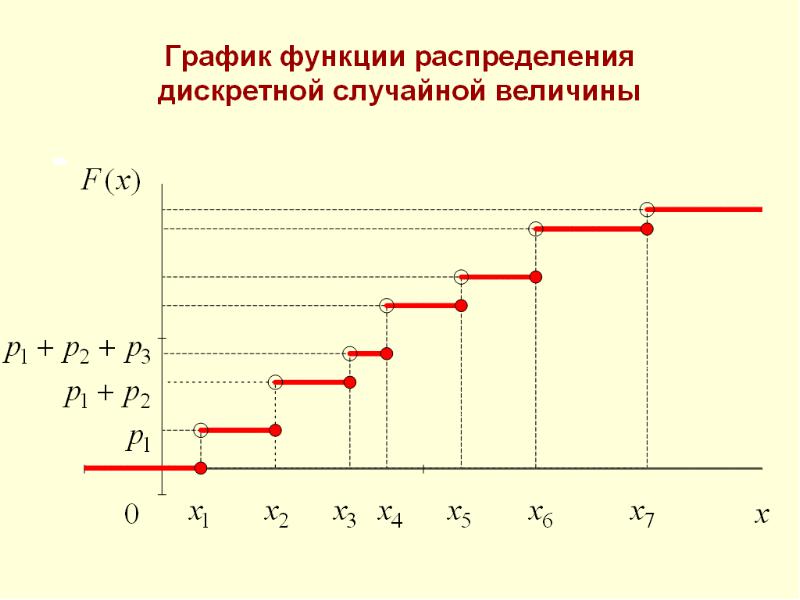
График функции распределения дискретной случайной величины имеет вид:
Пример 2 (Функция распределения непрерывной случайной величины)
Пример для непрерывной случайной величины X можно посмотреть здесь.
Показана функция распределения для показательного (экспоненциального) закона распределения
Дискретная случайная величина / Теория вероятности [Калинин В.
 М., Тихомиров С.Р.] / 3dstroyproekt.ru
М., Тихомиров С.Р.] / 3dstroyproekt.ruСлучайная величина. Закон распределения дискретной случайной величины
Опр Случайной величиной называют величину, которая в результате испытания примет одно из возможных значений, заранее неизвестное.
Например. Подбрасывается монета. Заранее не известен результат. Выпадения орла или решки — случайно. Случайные величины обозначают большими буквами Х, У:
$X( { x_1 ,x_2 ,\ldots x_n } )- значения\,x_1 \ldots x_n -$ возможные значения случайной величины.
Имеется три типа случайных величин: непрерывные, дискретные, смешанные.
Опр Дискретной { прерывной } называют случайную величину, которая принимает отдельные изолированные значения. Число случайных величин может быть конечным или бесконечным.
Опр Непрерывной — называют случайную величину, которая может принимать все значения из некоторого конечного промежутка.
Опр Законом распределения дискретной случайной величины называется соответствие между возможными значениями случайной величины и их вероятностями. Закон распределения можно задать в виде таблицы:
так как события $х_ { 1 } ,х_ { 2 } ,\ldots ,х_ { n } $ образуют полную группу то $р_ { 1 } + р_ { 2 } + \ldots + р_ { n } = 1 $
Пример. Написать закон распределения для суммы выпавших очков при подбрасывании двух игральных костей.
Пояснения к примеру: число благоприятных событий m :
$ 2) \left\{ { 1 } \right.\left. 1 \right\} -всего\,1\,, $
$ 3) \left\{ { \begin{array} { l } 2 1 \\ \,1 2 \\ \end{array} } \right\} \,-всего\,2\,, $
$4) \left\{ { \begin{array} { l } 2 2 \\ 3 1 \\ 1 3 \\ \end{array} } \right\} -всего\,3\,, $
$ 5) \left\{ { \begin{array} { l } 1 4 \\ 4 1 \\ 2 3 \\ 3 2 \\ \end{array} } \right\} -всего\,4, $
$ 6) \left\{ { \begin{array} { l } 1 5 \\ 5 1 \\ 2 4 \\ 4 2 \\ 3 3 \\ \end{array} }\right\} -всего\,5\,, $
$ 7) \left\{ { \begin{array} { l } 2 5 \\ 5 2 \\ 3 4 \\ 4 3 \\ 6 1 \\ 1 6 \\ \end{array} } \right\} -всего\,6\,, $
и так далее.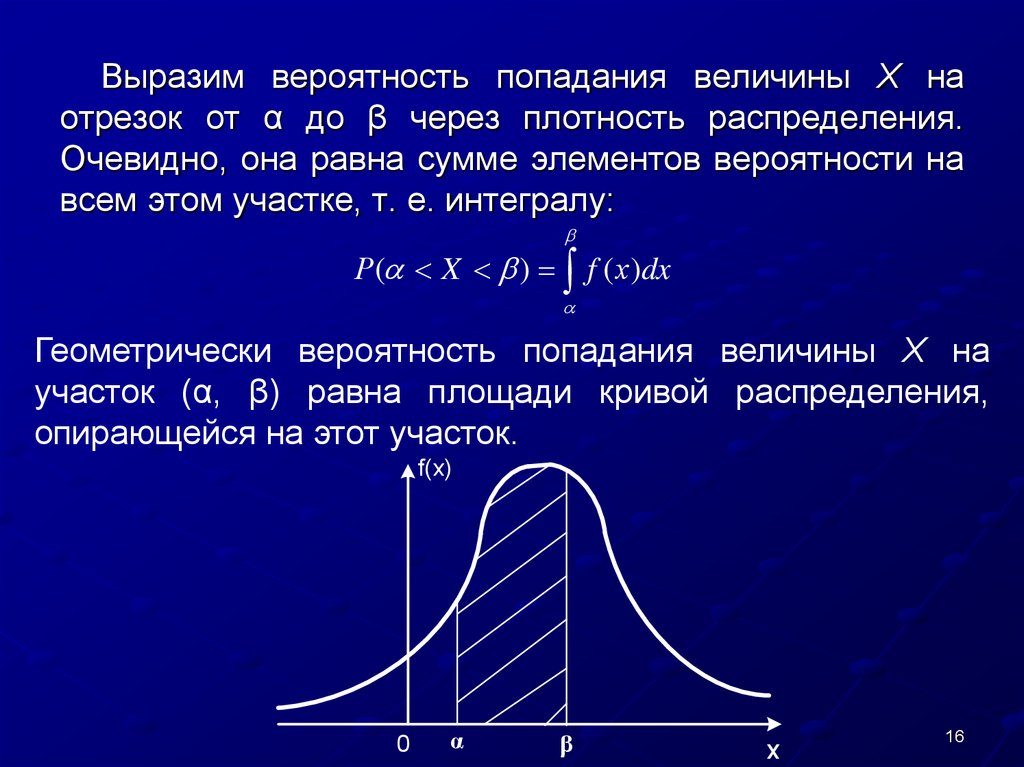 Закон распределения имеет вид:
Закон распределения имеет вид:
\begin{array} { |l|l|l|l|l|l|l|l|l|l|l|l| } \hline X& 2& 3& 4& 5& 6& 7& 8& 9& 10& 11& 12 \\ \hline p& \frac { 1 } { 36 } & \frac { 2 } { 36 } & \frac { 3 } { 36 } & \frac { 4 } { 36 } & \frac { 5 } { 36 } & \frac { 6 } { 36 } & \frac { 5 } { 36 } & \frac { 4 } { 36 } & \frac { 3 } { 36 } & \frac { 2 } { 36 } & \frac { 1 } { 36 } \\ \hline \end{array}
Пример 2. Охотник стреляет в цель до первого попадания, но делает 5-ть выстрелов. Вероятность попадания при одном выстреле 0,8. Построить закон распределения числа произведенных выстрелов.
Решение: Событие $A =$ { попал в цель } , тогда $\bar A =$ { промах } .
- $(\bar A ‘ A) =$ { попал со второго раза } ,
- $(\bar A ‘ \bar A ‘ A) =$ { попал с третьего раза } ,
- $(\bar A ‘ \bar A ‘ \bar A ‘ A) =$ { попал с четвертого раза } ,
- $(\bar A ‘ \bar A ‘ \bar A ‘ \bar A) =$ { попал с пятого раза } .
 { 4 } \\ \hline p& 0,8& 0,16& 0,032& 0,0064& 0,0016 \\ \hline \end{array}
{ 4 } \\ \hline p& 0,8& 0,16& 0,032& 0,0064& 0,0016 \\ \hline \end{array}Функция распределения дискретной случайной величины
Функцией распределения называют функцию $F(x)$, определяющую вероятность того, что случайная величина $X$ в результате испытания примет значение, меньшее $х$, т. е. $F(x)=p(X<x)$. функция распределения д. с. в. строится по ряду распределения. Воспользуемся рядом, полученным в предыдущем примере.
Построим график функции распределения д.с.в.
$ F(x_i )=\left\{ { \begin{array} { l } 0:x\in (-\infty , 1) \\ p_1 =0,8: x\in [\,1,\,2) \\ p_1 +p_2 =0,8+0,16=0,96: x\in [\,2,\,3) \\ p_1 +p_2 +p_3 =0,8+0,16+0,32=0,992: x\in [\,3,\,4) \\ p_1 +p_2 +p_3 +p_4 =0,8+0,16+0,32+0,064=0,9984: x\in [\,4,\,5) \\ p_1 +p_2 +p_3 +p_4 +p_5 =0,8+0,16+0,32+0,064+0,016=1, \\ \,x\in [\,5,\,\infty ] \\ \end{array} }\right. $
Функция распределения дискретной случайной величины — это ступенчатая разрывная функция.
 m } $
m } $Далее:
Вычисление двойного интеграла. Двукратный интеграл
Поток жидкости через поверхность
Класс $L$. Теорема о замкнyтости класса $L$
Вычисление криволинейного интеграла второго рода в случае выполнения условия независимости от формы
Решение задач с помощью алгебры высказываний
Определение тройного интеграла. Теорема существования тройного интеграла
Частные случаи векторных полей
Несобственные интегралы от неограниченной функции
Вычисление двойного интеграла
Примеры применения цилиндрических и сферических координат
Замыкание. Свойства замыкания. Теорема о сведении к заведомо полной системе
Нормальные формы
Огравление $\Rightarrow $
27 сентября 2016, 21:44 проектирование км, кмд, кж Теория вероятности [Калинин В.
 М., Тихомиров С.Р.] 0 3151 0
М., Тихомиров С.Р.] 0 3151 0Идея распределения вероятностей
Обзор
Случайная величина — это переменная, которая подвержена вариациям вследствие случайности. Можно представить себе случайную величину как результат случайного эксперимента, такого как бросание игральной кости, подбрасывание монеты, выбор числа из заданного интервала. Идея состоит в том, что каждый раз, когда вы проводите эксперимент, вы получаете выборку случайной величины. Поскольку переменная является случайной, вы ожидаете получить разные значения при получении нескольких выборок. (Некоторые значения могут быть более вероятными, чем другие, как в эксперименте с бросанием двух шестигранных костей и записью суммы двух полученных чисел, где получение значения 7 гораздо более вероятно, чем получение значения 12.) Вероятность распределение — это функция, описывающая вероятность того, что вы получите различные возможные значения случайной величины.
Оказывается, распределения вероятностей имеют совершенно разные формы в зависимости от того, принимает ли случайная величина дискретные значения (например, числа из множества $\{1,2,3,4,5,6\}$) или принимает любое значение из континуума (например, любое действительное число в интервале $[0,1]$).
 Несмотря на их различные формы, одни и те же манипуляции и вычисления можно выполнять как с дискретными, так и с непрерывными случайными величинами. Основное различие обычно заключается в том, используется ли сумма или интеграл.
Несмотря на их различные формы, одни и те же манипуляции и вычисления можно выполнять как с дискретными, так и с непрерывными случайными величинами. Основное различие обычно заключается в том, используется ли сумма или интеграл.Дискретное распределение вероятностей
Дискретная случайная величина — это случайная величина, которая может принимать любое значение из дискретного набора значений. Набор возможных значений может быть конечным, например, в случае броска шестигранного кубика, где значения лежат в множестве $\{1,2,3,4,5,6\}$. Однако множество возможных значений также может быть счетно бесконечным, например, множество целых чисел $\{0, 1, -1, 2, -2, 3, -3, \ldots \}$. Требование к дискретной случайной величине состоит в том, что мы можем перечислить все значения в наборе ее возможных значений, поскольку нам нужно будет просуммировать все эти возможности.
Для дискретной случайной величины $X$ мы формируем ее функцию распределения вероятностей, присваивая вероятность того, что $X$ равна каждому из ее возможных значений.
Например, для шестигранного кубика мы назначаем вероятность $1/6$ каждому из шести вариантов. В контексте дискретных случайных величин мы можем называть функцию распределения вероятности функцией массы вероятности . Функция массы вероятности $P(x)$ для случайной величины $X$ определяется так, что для любого числа $x$ значением $P(x)$ является вероятность того, что случайная величина $X$ равна заданному число $x$, т. е. \начать{выравнивать*} P(x) = \Pr(X = x). \конец{выравнивание*} Часто мы обозначаем случайную величину функции массы вероятности нижним индексом, поэтому можем написать \начать{выравнивать*} P_X(x) = \Pr(X = x). \конец{выравнивание*}
Чтобы функция $P(x)$ была допустимой функцией массы вероятности, $P(x)$ должна быть неотрицательной для каждого возможного значения $x$. Более того, случайная величина должна принимать некоторое значение из множества возможных значений с вероятностью единица, поэтому мы требуем, чтобы $P(x)$ в сумме равнялось единице.

Для примера броска шестигранного игрального кубика функция массы вероятности имеет вид \начать{собирать*} P(x) = \begin{случаи} \frac{1}{6} & \text{if $x \in \{1,2,3,4,5,6\}$}\\ 0 & \text{иначе.} \end{случаи} \end{собрать*}
Если бросить два шестигранных кубика, и пусть $X$ будет суммой, то $X$ может принимать любое значение из множества $\{2,3,4,5,6,7,8,9 ,10,11,12\}$. Функция массы вероятности для этого $X$ равна \начать{собирать*} P(x) = \begin{случаи} \frac{1}{36} & \text{if $x \in \{2,12\}$}\\ \frac{2}{36}=\frac{1}{18} & \text{if $x \in \{3,11\}$}\\ \frac{3}{36}=\frac{1}{12} & \text{if $x \in \{4,10\}$}\\ \frac{4}{36}=\frac{1}{9} & \text{if $x \in \{5,9\}$}\\ \frac{5}{36} & \text{if $x \in \{6,8\}$}\\ \frac{6}{36} =\frac{1}{6} & \text{if $x = 7$}\\ 0 & \text{иначе.
} \end{случаи} \end{собрать*} $P(x)$ представлен в виде гистограммы на следующем рисунке.
Непрерывное распределение вероятностей
Непрерывная случайная величина — это случайная величина, которая может принимать любое значение из континуума, такого как набор всех действительных чисел или интервал. Мы не можем составить сумму по такому набору чисел. (Их слишком много, поскольку такой континуум несчетен.) Вместо этого мы заменяем сумму, используемую для дискретных случайных величин, интегралом по множеству возможных значений.
Для непрерывной случайной величины $X$ мы не можем сформировать ее функцию распределения вероятностей, назначая вероятность того, что $X$ точно равна каждому значению. Функция распределения вероятностей, которую мы должны использовать в этом случае, называется функция плотности вероятности , которая по существу присваивает вероятность того, что $X$ находится рядом с каждым значением. Чтобы понять, почему мы должны использовать такую плотность, а не назначать отдельные вероятности, см.
 страницу, описывающую идею функции плотности вероятности.
страницу, описывающую идею функции плотности вероятности.Имея функцию плотности вероятности $\rho(x)$ для $X$, мы определяем вероятность того, что $X$ находится в любом множестве $A$ (т. е. что $X \in A$ (запутался?)) по формуле интегрируя $\rho(x)$ по множеству $A$, т.е. \начать{собирать*} \Pr(X \in A) = \int_A \rho(x)dx. \end{собрать*} Часто мы обозначаем случайную величину функции плотности вероятности нижним индексом, поэтому можем написать \начать{собирать*} \Pr(X \in A) = \int_A \rho_X(x)dx. \end{собрать*}
Определение этой вероятности с помощью интеграла дает одно важное следствие для непрерывных случайных величин. Если множество $A$ содержит только один элемент, то сразу видно, что вероятность того, что $X$ равно этому единственному значению, равна нулю, поскольку интеграл по одной точке равен нулю. Для непрерывной случайной величины $X$ вероятность того, что $X$ является любым единственным значением, всегда равна нулю.
В остальном функция плотности вероятности непрерывных случайных величин ведет себя точно так же, как функция массы вероятности для дискретной случайной величины, где нам просто нужно использовать интегралы, а не суммы.

Примеры непрерывных случайных величин и связанных с ними функций плотности вероятности см. на странице, посвященной идее функции плотности вероятности.
Объяснение урока: Дискретные случайные величины
В этом объяснении мы узнаем, как идентифицировать дискретную случайную величину и определить ее соответствующее распределение вероятностей.
Чтобы понять, что такое дискретная случайная величина, полезно сначала обсудить, что такое случайная величина.

Определение: Случайные величины
Случайная величина — это переменная, которая может принимать несколько различных значений (которые присваиваются случайным образом), каждое из которых имеет соответствующую вероятность.
Как и в случае вероятностей взаимоисключающих событий, вероятности, связанные со всеми значениями, которые может принимать случайная величина, должны в сумме давать 1. Более того, каждая вероятность должна лежать в интервале [0,1].
Случайная величина может быть либо дискретный или непрерывный . Для дискретной случайной величины значения случайного значения должны быть дискретными. Как правило, они принимают целочисленные значения, но это не обязательно так.
Определение: Дискретная случайная величина
Дискретная случайная величина — это случайная величина, которая может принимать несколько различных дискретных значений, каждое из которых имеет соответствующую вероятность.

Одним из примеров дискретной случайной величины являются результаты броска игральной кости. Дискретная случайная величина может принимать следующие значения: 1, 2, 3, 4, 5 и 6, где 16 — это соответствующая вероятность для каждого значения.
Мы можем представить дискретную случайную величину , используя функцию распределения вероятностей . Это функция, которая отображает значения дискретной случайной величины в связанные с ними вероятности.
Определение: Функция распределения вероятностей
Функция распределения вероятностей — это функция, которая генерирует вероятности со значением 𝑓(𝑥) при заданном результате со значением 𝑥 и должна обладать следующими свойствами:
- 𝑓(𝑥)=1 для всех значений 𝑥 в области функции распределения вероятностей
- каждое значение 𝑓(𝑥) должно лежать в интервале [0,1].
Точно так же, как мы можем по-разному представлять входы и выходы функции, мы можем также представлять функцию распределения вероятностей в разных форматах.
 В первых двух примерах рассмотрим вопросы, где функция распределения вероятностей представлена в виде таблицы. Первый демонстрирует, как проверить, является ли функция функцией распределения вероятностей, используя факты, связанные с вероятностью.
В первых двух примерах рассмотрим вопросы, где функция распределения вероятностей представлена в виде таблицы. Первый демонстрирует, как проверить, является ли функция функцией распределения вероятностей, используя факты, связанные с вероятностью.Пример 1. Проверка того, является ли функция в таблице функцией распределения вероятностей
Может ли функция в данной таблице быть функцией распределения вероятностей?
𝑥 0 1 4 5 𝑓(𝑥) 0.17 0.43 0.69 0.36 Answer
We know that for любая функция распределения вероятностей, 𝑓(𝑥)=1. Следовательно, если функция в таблице является функцией вероятности, то все вероятности в таблице будут в сумме равны 1: 0,17+0,43+0,69+0,36=1,65.
Поскольку это не так, так как они в сумме дают 1,65, то 𝑓(𝑥) не является функцией распределения вероятностей.

Обратите внимание, что даже если сумма всех вероятностей равна 1, нам также нужно будет проверить, что каждая вероятность находится в интервале [0,1].
Во втором примере также используется таблица для представления функции распределения вероятностей, но показано, как найти неизвестное значение в таблице, используя факты, связанные с вероятностью.
Пример 2. Поиск неизвестного значения функции распределения вероятностей в таблице
Функция в данной таблице является функцией распределения вероятностей дискретной случайной величины 𝑋. Найдите значение 𝑎.
𝑥 1 2 3 4 5 𝑓(𝑥) 15 110 310 110 𝑎 Answer
Мы знаем, что для любой функции распределения вероятностей 𝑓(𝑥)=1, поэтому мы можем использовать это, чтобы определить неизвестное значение 𝑎: 15+110+310+110+𝑎=1710+𝑎=1𝑎=310.

Поскольку значение 𝑎 находится в интервале [0,1], мы знаем, что 310 является подходящим значением.
Помимо представления функции распределения вероятностей в виде таблицы, мы можем представить каждое значение и связанную с ним вероятность, используя обозначение 𝑃(𝑋=𝑥)=𝑝, где 𝑥 представляет значение дискретной случайной величины 𝑋, а 𝑝 — ассоциированная вероятность этого значения. Используя это обозначение, мы можем сказать, что 𝑃(𝑋=𝑥)=1 и все значения 𝑝 должны лежать в интервале [0,1].
В следующем примере рассмотрим, как найти неизвестную вероятность, когда функция распределения вероятностей представлена в формате 𝑃(𝑋=𝑥)=𝑝.
Пример 3. Нахождение неизвестного значения при других значениях функции распределения вероятностей
Пусть 𝑋 обозначает дискретную случайную величину, которая может принимать значения 0, 1, 2 и 3. Учитывая, что 𝑃(𝑋=0)=19 , 𝑃(𝑋=1)=49, 𝑃(𝑋=2)=𝑎 и 𝑃(𝑋=3)=3𝑎, найдите значение 𝑎.
Ответ
Поскольку сумма всех вероятностей в функции распределения вероятностей равна 1, мы знаем, что 𝑃(𝑋=0)+𝑃(𝑋=1)+𝑃(𝑋=2)+𝑃(𝑋=3)=1.

Подставляя соответствующие вероятности, мы получаем 19+49+𝑎+3𝑎=1.
Тогда упрощение, перестановка и решение для 𝑎 дает нам 59+4𝑎=14𝑎=49𝑎=19.
Поскольку значение 𝑎 находится в интервале [0,1], то 19 является подходящим ответом.
Как мы видели в примере 2, функция распределения вероятностей может быть представлена как функция 𝑥, где 𝑥 — значение, которое может принимать дискретная случайная величина, а 𝑓(𝑥) — связанная с ней вероятность. Следовательно, мы знаем, что 𝑓(𝑥)=1 для всех значений 𝑥, которые может принимать случайная величина. Далее, каждое значение 𝑓(𝑥) должно лежать в интервале [0,1].
В следующем примере используются свойства 𝑓(𝑥)=1 и все значения 𝑓(𝑥), лежащие в интервале [0,1], чтобы определить, является ли функция распределения вероятностей допустимой или нет для данного набора значений 𝑥.
Пример 4. Определение того, какая функция распределения вероятностей может представлять дискретную случайную величину
Пусть 𝑋 обозначает дискретную случайную величину, которая может принимать значения 3, 5 и 6.
 Какая из следующих функций может представлять функцию вероятности 𝑋?
Какая из следующих функций может представлять функцию вероятности 𝑋?- 𝑓(𝑥)=𝑥+310
- 𝑓(𝑥)=𝑥−28
- 𝑓(𝑥)=45𝑥+2
- 𝑓(𝑥)=4𝑥+52
Answer
For a функция распределения вероятностей, чтобы можно было представить дискретную случайную величину 𝑋, которая может принимать значения 3, 5 и 6, 𝑓(𝑥)=1 и каждое значение 𝑓(𝑥) должно лежать в интервале [0,1 ]. Мы проверим каждую функцию по очереди.
Для 𝑓(𝑥)=𝑥+310 мы сначала вычислим соответствующие вероятности для каждого значения дискретной случайной величины, подставив 3, 5 и 6 в 𝑓(𝑥).
Когда 𝑥=3, 𝑓(3)=3+310=1210.
Поскольку 1210 находится за пределами интервала [0,1], мы уже можем сделать вывод, что 𝑓(𝑥)=𝑥+310 не может быть действительной функцией распределения вероятностей для дискретная случайная величина 𝑋.
Аналогично, для 𝑓(𝑥)=𝑥−28 мы сначала вычислим связанные вероятности для каждого значения дискретной случайной величины 3, 5 и 6, подставив в 𝑓(𝑥).

Когда 𝑥=3, 𝑓(3)=3−28=18.
Когда 𝑥=5, 𝑓(5)=5−28=38.
Когда 𝑥=6, 𝑓(6)=6−28=48.
Поскольку каждое значение лежит в интервале [0,1], то пока 𝑓(𝑥)=𝑥−28 является действительной функцией распределения вероятностей для дискретной случайной величины 𝑋.
Теперь проверим, является ли 𝑓(𝑥)=1: 𝑓(3)+𝑓(5)+𝑓(6)=18+38+48=1.
Поскольку 𝑓(𝑥)=1, то 𝑓(𝑥)=𝑥−28 является действительной функцией распределения вероятностей для дискретной случайной величины 𝑋.
Примечание:
Остальные функции можем проверить, но так как правильный ответ мы уже определили, то в этом нет необходимости.
В следующем примере мы можем использовать свойства 𝑓(𝑥)=1 и все значения 𝑓(𝑥), лежащие в интервале [0,1], чтобы определить неизвестный коэффициент в функции 𝑓(𝑥) заданы значения, которые может принимать случайная величина.
Пример 5. Нахождение неизвестного коэффициента в функции распределения вероятностей при заданных значениях, которые может принимать дискретная случайная величина
Пусть 𝑋 обозначает дискретную случайную величину, которая может принимать значения 1, 2, 3, 4, 5 и 6.
 Дано что 𝑋 имеет функцию распределения вероятностей 𝑓(𝑥)=𝑎𝑥5, найдите значение 𝑎.
Дано что 𝑋 имеет функцию распределения вероятностей 𝑓(𝑥)=𝑎𝑥5, найдите значение 𝑎.Ответ
Чтобы функция распределения вероятностей могла представлять дискретную случайную величину 𝑋, которая может принимать значения 1, 2, 3, 4, 5 и 6, 𝑓(𝑥)=1 и каждое значение 𝑓(𝑥) должно лежать в интервале [0,1].
Сначала нам нужно заменить 1, 2, 3, 4, 5 и 6 на 𝑓(𝑥)=𝑎𝑥5.
Для 𝑥=1, 𝑓(1)=𝑎×15=𝑎5.
Для 𝑥=2, 𝑓(2)=𝑎×25=2𝑎5.
Для 𝑥=3, 𝑓(3)=𝑎×35=3𝑎5.
Для 𝑥=4, 𝑓(4)=𝑎×45=4𝑎5.
Для 𝑥=5, 𝑓(5)=𝑎×55=5𝑎5.
Для 𝑥=6, 𝑓(6)=𝑎×65=6𝑎5.
Далее мы используем свойство 𝑓(𝑥)=1, чтобы составить уравнение относительно 𝑎: 𝑓(1)+𝑓(2)+𝑓(3)+𝑓(4)+𝑓(5)+𝑓(6)=1,𝑎5+2𝑎5+3𝑎5+4𝑎5+5𝑎5+6𝑎5=1.
Тогда упрощение, перестановка и решение для 𝑎 дает нам 21𝑎5=1𝑎=521.
Хотя мы нашли значение 𝑎, рекомендуется проверить, что для каждого значения случайной величины соответствующая вероятность находится в интервале [0,1]. Мы делаем это, подставляя 𝑎=521 в 𝑓(1), 𝑓(2) и так далее.

Для 𝑥=1, 𝑓(1)=×15=121.
Для 𝑥=2, 𝑓(2)=×25=221.
Для 𝑥=3, 𝑓(3)=×35=321.
Для 𝑥=4, 𝑓(4)=×45=421.
Для 𝑥=5, 𝑓(5)=×55=521.
Для 𝑥=6, 𝑓(6)=×65=621.
Поскольку каждое значение 𝑓(𝑥) для всех значений случайной величины лежит в интервале [0,1], то мы знаем, что 𝑓(𝑥)=𝑎𝑥5 , где 𝑎=521, является действительной функцией распределения вероятностей.
До сих пор мы рассматривали примеры без контекста. В заключительной части объяснения мы рассмотрим примеры, в которых дается контекст.
В следующем примере мы рассмотрим, как использовать информацию из распределения вероятностей, чтобы отвечать на вопросы в контексте.
Пример 6: Решение задач в контексте с дискретными случайными величинами, заданными функцией распределения вероятностей
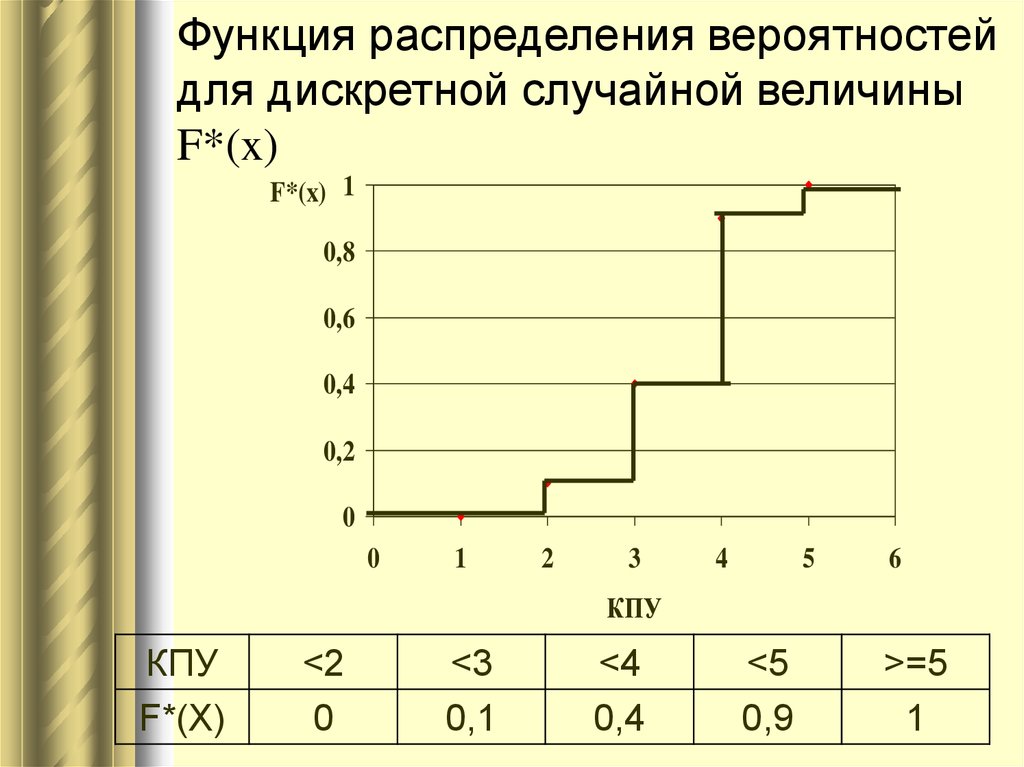
Пусть 𝑋 будет случайной величиной, которая представляет количество пациентов, посещающих стоматологическую клинику в час. Распределение вероятности 𝑋 показано в таблице ниже.

𝑥 10 11 12 13 14 15 𝑓(𝑥) 0.2 0.1 0.15 0.05 0.3 0.2 Find вероятность следующего.
- Ровно 13 пациентов посещают клинику в данный час
- Не менее 13 пациентов посещают клинику в данный час
- Максимум 13 пациентов посещают клинику в данный час
Ответ
Часть 1
Чтобы найти вероятность того, что ровно 13 пациентов посетят клинику в данный час, воспользуемся таблицей распределения вероятностей.
В данном случае 𝑋 представляет количество пациентов, посещающих стоматологическую клинику в час, поэтому 𝑥=13. Следовательно, вероятность 𝑥=13 определяется соответствующим значением 𝑓(𝑥) в таблице, которое равно 0,05.
Часть 2
Чтобы найти вероятность того, что не менее 13 пациентов посетят клинику в данный час, снова воспользуемся таблицей распределения вероятностей.

В этом случае 𝑥 может принимать несколько значений, так как мы находим вероятность того, что в данный час клинику посетило не менее 13 пациентов. Таким образом, 𝑥 может быть любым целым числом, большим или равным 13, или 𝑥≥13. Как видно из таблицы, 𝑋 может принимать только целые значения от 10 до 15, поэтому 𝑥 может быть 13, 14 или 15.
Чтобы найти вероятность того, что 𝑥 равно 13, 14 или 15, мы находим соответствующие значения для 𝑓(𝑥) в таблице и суммируйте их.
Для 𝑥=13, 𝑓(13)=0,05.
Для 𝑥=14, 𝑓(14)=0,3.
Для 𝑥=15, 𝑓(15)=0,2.
Следовательно, 𝑓(13)+𝑓(14)+𝑓(15)=0,05+0,3+0,2=0,55.
Значит, вероятность того, что в данный час клинику посетит не менее 13 пациентов, равна 0,55.
Часть 3
Чтобы найти вероятность того, что в данный час клинику посетит не более 13 пациентов, снова воспользуемся таблицей распределения вероятностей.
Как и в предыдущей части, 𝑥 может принимать несколько значений. Поскольку мы находим вероятность того, что в данный час клинику посетило не более 13 пациентов, то 𝑥 может быть любым целым числом, меньшим или равным 13, или 𝑥≤13.
 Как видно из таблицы, 𝑋 может принимать только целые значения от 10 до 15, поэтому 𝑥 может принимать значения 10, 11, 12 или 13.
Как видно из таблицы, 𝑋 может принимать только целые значения от 10 до 15, поэтому 𝑥 может принимать значения 10, 11, 12 или 13.Чтобы найти вероятность того, что 𝑥 равно 10, 11, 12 или 13, мы находим соответствующие значения для 𝑓(𝑥) в таблице и суммируем их.
Для 𝑥=10, 𝑓(10)=0,2.
Для 𝑥=11, 𝑓(14)=0,1.
Для 𝑥=12, 𝑓(15)=0,15.
Для 𝑥=13, 𝑓(13)=0,05.
Следовательно, 𝑓(10)+𝑓(11)+𝑓(12)+𝑓(13)=0,2+0,1+0,15+0,05=0,5.
Значит, вероятность того, что в данный час клинику посетит не более 13 пациентов, равна 0,5.
В последнем примере мы рассмотрим, какое распределение наиболее подходит для данного контекста.
Пример 7. Выбор распределения дискретной случайной величины с учетом контекста
В эксперименте, в котором правильная монета подбрасывается пять раз подряд, пусть 𝑋 будет дискретной случайной величиной, выражающей количество выпавших орлов минус количество решек. Найдите распределение вероятностей 𝑋.
𝑥 −5 −3 −1 1 3 5 𝑓(𝑥) 132 532 1032 1032 532 132 𝑥 −5 −3 −1 0 1 3 5 𝑓(𝑥) 132 532 932 232 932 532 132 𝑥 −3 −1 0 1 3 𝑓(𝑥) 532 1032 232 1032 532 𝑥 −4 −3 −1 1 3 4 𝑓(𝑥) 132 532 1032 1032 532 132 𝑥 −5 −3 −1 1 3 5 𝑓(𝑥) 132 1032 532 532 1032 132
Answer
Чтобы определить функцию распределения вероятностей 𝑓(𝑥) для дискретной случайной величины 𝑋, мы сначала определяем все возможные значения, которые может принимать 𝑋, а затем находим вероятность 𝑓(𝑥) для каждого значения 𝑋.

В вопросах говорится, что правильная монета подбрасывается 5 раз, а 𝑋 — это дискретная случайная величина, которая представляет собой количество выпавших орлов минус количество решек. Следовательно, возможные значения 𝑋 следующие:
- 5 орлов и 0 решек: 5−0=5,
- 4 орла и 1 решка: 4−1=3,
- 3 орла и 2 решки: 3−2=1,
- 2 орла и 3 решки : 2−3=−1,
- 1 орел и 4 решки: 1−4=−3,
- 0 орлов и 5 решек: 0−5=−5.
Итак, 𝑋 может принимать значения −5, −3, −1, 1, 3 и 5.
Далее мы вычислим вероятность 𝑓(𝑥) для каждого из значений 𝑋.
Чтобы рассчитать вероятность, полезно составить список возможных исходов для каждой дискретной случайной величины 𝑋, а затем определить вероятность после определения всех исходов.
Для 𝑥=5 есть 5 орлов и 0 решек. HHHHH — единственный результат.
При 𝑥=3 4 орла и 1 решка. HHHHT, HHHTH, HHTHH, HTHHH и THHHH — это 5 исходов.
Для 𝑥=1 есть 3 орла и 2 решки. HHHTT, HHTHT, HTHHT, THHHT, HHTTH, HTHTH, THHTH, HTTHH, THTHH и TTHHH — это 10 исходов.

Для 𝑥=−1 есть 2 орла и 3 решки. HHTTT, HTHTT, THHTT, HTTHT, THTHT, TTHHT, HTTTH, THTTH, TTHTH и TTTHH — это 10 исходов.
Для 𝑥=−3 есть 1 орел и 4 решки. HTTTT, THTTT, TTHTT, TTTHT и TTTTH — это 5 исходов.
Для 𝑥=−5 0 орлов и 5 решек. ТТТТ — единственный результат.
Складывая все исходы вместе, мы получаем 1+5+10+10+5+1=32, то есть всего 32 исхода.
Следовательно, чтобы найти вероятность каждого исхода, мы берем количество исходов для каждой дискретной случайной величины и делим его на общее число исходов следующим образом.
Для 𝑥=5, 𝑓(5)=132.
Для 𝑥=3, 𝑓(3)=532.
Для 𝑥=1, 𝑓(1)=1032.
Для 𝑥=−1, 𝑓(−1)=1032.
Для 𝑥=−3, 𝑓(−3)=532.
Для 𝑥=−5, 𝑓(−5)=132.
При отображении в таблице имеем следующее.
𝑥 −5 −3 −1 1 3 5 𝑓(𝑥) 132 532 1032 1032 532 132 В этом объяснении мы узнали о дискретных случайных величинах и их функциях распределения вероятностей.


 { 4 } \\ \hline p& 0,8& 0,16& 0,032& 0,0064& 0,0016 \\ \hline \end{array}
{ 4 } \\ \hline p& 0,8& 0,16& 0,032& 0,0064& 0,0016 \\ \hline \end{array} m } $
m } $ М., Тихомиров С.Р.] 0 3151 0
М., Тихомиров С.Р.] 0 3151 0 Несмотря на их различные формы, одни и те же манипуляции и вычисления можно выполнять как с дискретными, так и с непрерывными случайными величинами. Основное различие обычно заключается в том, используется ли сумма или интеграл.
Несмотря на их различные формы, одни и те же манипуляции и вычисления можно выполнять как с дискретными, так и с непрерывными случайными величинами. Основное различие обычно заключается в том, используется ли сумма или интеграл.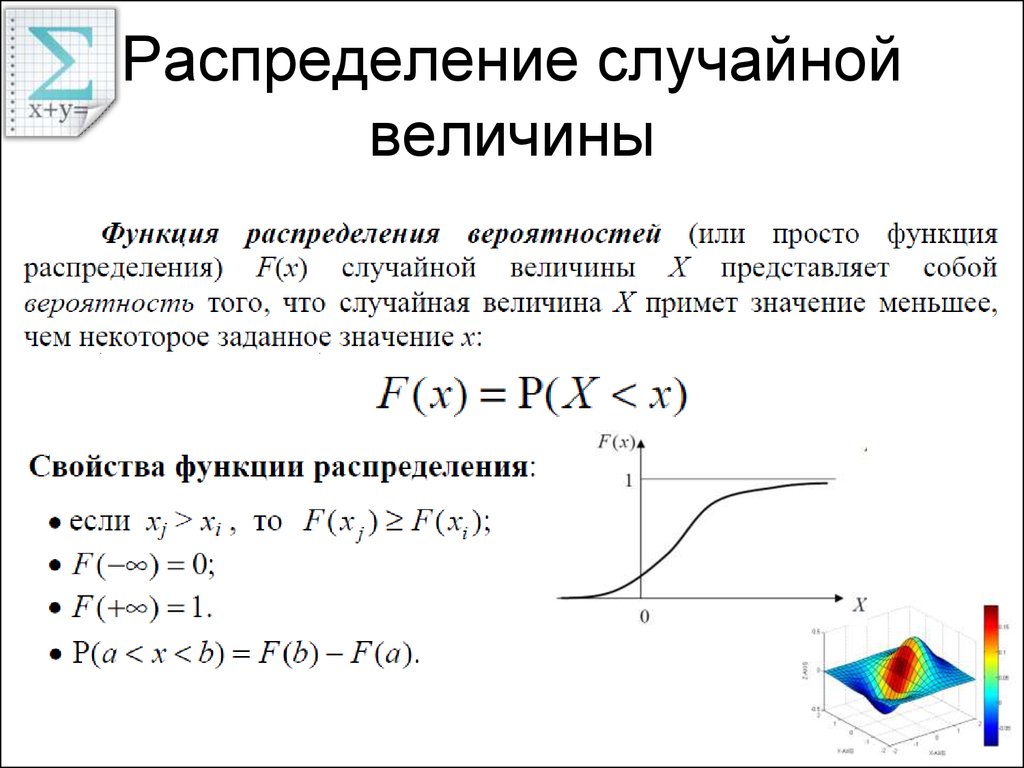


 страницу, описывающую идею функции плотности вероятности.
страницу, описывающую идею функции плотности вероятности.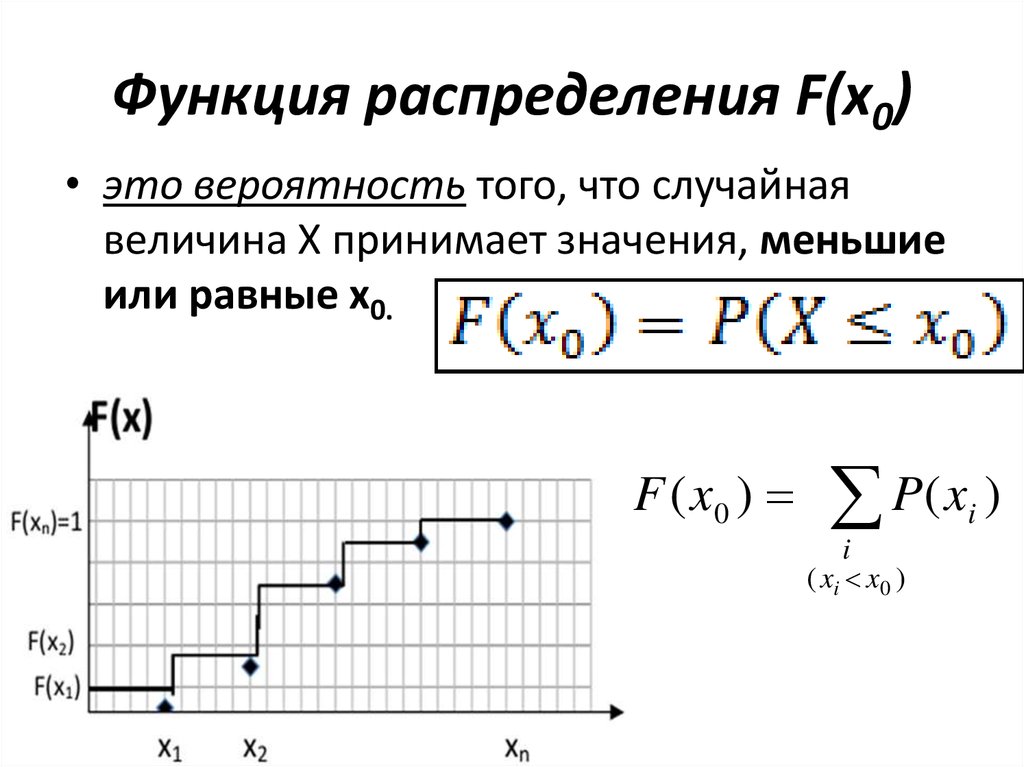

 В первых двух примерах рассмотрим вопросы, где функция распределения вероятностей представлена в виде таблицы. Первый демонстрирует, как проверить, является ли функция функцией распределения вероятностей, используя факты, связанные с вероятностью.
В первых двух примерах рассмотрим вопросы, где функция распределения вероятностей представлена в виде таблицы. Первый демонстрирует, как проверить, является ли функция функцией распределения вероятностей, используя факты, связанные с вероятностью.

 Какая из следующих функций может представлять функцию вероятности 𝑋?
Какая из следующих функций может представлять функцию вероятности 𝑋?
 Дано что 𝑋 имеет функцию распределения вероятностей 𝑓(𝑥)=𝑎𝑥5, найдите значение 𝑎.
Дано что 𝑋 имеет функцию распределения вероятностей 𝑓(𝑥)=𝑎𝑥5, найдите значение 𝑎.
 Как видно из таблицы, 𝑋 может принимать только целые значения от 10 до 15, поэтому 𝑥 может принимать значения 10, 11, 12 или 13.
Как видно из таблицы, 𝑋 может принимать только целые значения от 10 до 15, поэтому 𝑥 может принимать значения 10, 11, 12 или 13.