Возведение числа в отрицательную степень и отличие от возведения в положительную степень
Как известно, в математике существуют не только положительные числа, но и отрицательные. Если знакомство с положительными степенями начинается с определения площади квадрата, то с отрицательными всё несколько сложнее.
Содержание:
- Основные понятия и положения
- Возведение в отрицательную степень числа по модулю от нуля до единицы
- Значение больше нуля
- Значение меньше нуля
- Возведение в целую отрицательную степень если модуль больше единицы
- Возведение в случае отрицательного дробного показателя
- Заключение
- Видео
Основные понятия и положения
Это следует знать:
- Возведением числа в натуральную степень называется умножение числа (понятие число и цифра в статье будем считать эквивалентными) само на себя в таком количестве, каков показатель степени (в дальнейшем будем использовать параллельно и просто слово показатель).
 5 = 40*40*40*40*40/(-29)*(-29)*(-29)*(-29)*(-29) = 102400000/(-20511149) = -4,9924.
5 = 40*40*40*40*40/(-29)*(-29)*(-29)*(-29)*(-29) = 102400000/(-20511149) = -4,9924. - 6 целых 7/17 = 109/17;
- 2,54 = 254/100.
В данном случае, мы видим, что модуль продолжает расти, а вот знак зависит от чётности или нечётности показателя.
Следует заметить, если мы возводим единицу, то она всегда останется сама собой. В случае, если нужно возвести число минус один, то при чётном показателе степени она превратится в единицу, при нечётном останется минус единицей.
Возведение в целую отрицательную степень если модуль больше единицы
Для цифр, чей модуль больше единицы, есть свои особенности действий. Прежде всего, нужно целую часть дроби перевести в числитель, то есть перевести в неправильную дробь. Если у нас имеется десятичная дробь, то её необходимо перевести в обычную. Делается это следующим образом:
Теперь рассмотрим, как возвести число в отрицательную степень в данных условиях. 3) = 1/rad64 = 1/8.
3) = 1/rad64 = 1/8.
В этом случае, нужно иметь в виду, что извлечение корней высокого уровня возможно только в специально подобранном виде и, скорее всего, избавиться от знака радикала (корня квадратного, кубического и так далее) при точных вычислениях вам не удастся.
Все же, подробно изучив предыдущие главы, сложностей в школьных вычислениях ожидать не стоит.
Следует заметить, что под описание данной главы подходит и возведение с заведомо иррациональным показателем, например, если показатель равен минус ПИ. Действовать нужно по вышеописанным принципам. Однако, вычисления в подобных случаях становятся настолько сложными, что под силу только мощным электронно-вычислительным машинам.
Заключение
Действие, которое мы изучали, является одной из самых сложнейших задач в математике (особенно в случае дробно-рационального или иррационального его значения). Однако, подробно и пошагово изучив данную инструкцию, можно научиться без особых проблем проделывать это на полном автомате.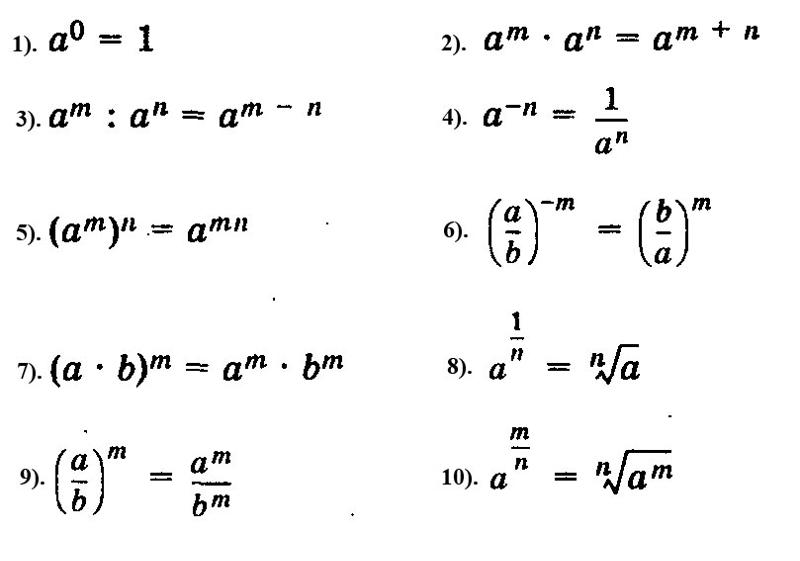
Видео
В видео подробно рассказывается о том, как производить вычисления, если степень с отрицательным показателем.
|
Заглавная страница
КАТЕГОРИИ: Археология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. |
⇐ ПредыдущаяСтр 8 из 13Следующая ⇒
Определение 10.1. Сравнением первой степени относительно неизвестного целого числа x называется сравнение вида , (10.1) где a , b и m – целые числа. Если сравнение верно, то число называется частным решением сравнения. Пусть – частное решение сравнения (10.1), тогда любое число вида , где , очевидно, также является частным решением данного сравнения, а множество частных решений вида , где , называется общим решением сравнения. Рассмотрим сначала частный случай сравнений первой степени, а именно случай, когда правая часть сравнения равна 1. Определение 10.2. Рассмотрим сравнение . Любое частное решение этого сравнения называется числом, обратным к числу a по модулю m. Пример. Число 3 обратно к числу 2 по модулю 5, так как . Число также является обратным к числу 2 по модулю 5 при любом целом t. Теорема 10.1. Для того, чтобы существовало число x, обратное к числу a по модулю m, необходимо и достаточно, чтобы . Доказательство. По теореме 5.1 (признаку взаимной простоты чисел) , для которых выполняется . Это равенство можно записать в виде: . Это и означает, что число u обратно к a по модулю m. Как было установлено ранее, числа u и v можно находить при помощи алгоритма Евклида. Значит, алгоритм Евклида можно использовать для нахождения числа, обратного к данному. Пример. Найти число, обратное к 26 по модулю 49. Решим сравнение . Поскольку , искомое число существует. Найдем НОД чисел 26 и 49, (который, как мы знаем, равен 1), по алгоритму Евклида. Последний, отличный от 0, остаток и равен 1. Найдем его линейное представление: Итак, получили, что . Тогда – частное решение сравнения . Общим решением этого сравнения будут числа вида . Все числа такого вида и будут числами, обратными к 26 по модулю 49. Вернемся теперь к общему случаю сравнения: (10.1) Теорема 10.2. Пусть . Для того, чтобы сравнение (10.1) имело решение, необходимо и достаточно, чтобы . Доказательство. 1) Необходимость. Пусть сравнение имеет решение . Тогда – верно. Это означает, , где где . Тогда . Поскольку – целое число, . 2) Достаточность. Пусть , тогда найдется такое целое число k , что . Поскольку по свойству НОД (теорема 3.3) , где . Рассмотрим линейное представление числа 1 как НОД чисел и : . Умножим обе части равенства на d, получим , затем умножим обе части полученного равенства на k, получим . Отсюда следует, что . Значит, сравнение имеет решение. Теорема 10.2 указывает путь к решению сравнений первой степени. Действительно, решение сравнения первой степени можно свести к решению неопределенного уравнения. Пример. Решить сравнение . Решение этого сравнения существует, поскольку и . Запишем сравнение в виде , где . Решим полученное неопределенное уравнение при помощи алгоритма Евклида, получим частное решение , где . Тогда решением исходного сравнения является множество чисел вида , где . Другой способ решения сравнений первой степени состоит в применении теоремы Эйлера. Рассмотрим сравнение . Не умаляя общности, можно считать, что . Действительно, если и , то по теореме 10.2 для существования решения сравнения необходимо и достаточно, чтобы . По свойству сравнений (следствие 1 к свойству 8) можно разделить обе части сравнения и модуль на их общий делитель . При этом частные от делений чисел a и m будут взаимно просты. Поэтому можно изначально предполагать, что . Тогда по теореме Эйлера . Умножим обе части сравнения на число b , получим . Запишем последнее сравнение в виде . Число , очевидно, является частным решением сравнения. Общее решение сравнения имеет вид: . Пример. Решить сравнение . Поскольку , по теореме Эйлера . Положим . Найденное значение является частным решением сравнения. Тогда общее решение сравнения имеет вид: . Заменим на число, сравнимое с ним по модулю 3 и запишем ответ в упрощенном виде: . Итак, мы рассмотрели два способа решения сравнений. Первый способ сводит решение сравнения к решению неопределенного уравнения. Используя второй способ, мы можем наоборот свести решение неопределенного уравнения к решению сравнения. Рассмотрим неопределенное уравнение . Предположим, что и . Тогда, как было установлено в § 6, данное уравнение имеет решение. Запишем уравнение в виде . Решив сравнение при помощи функции Эйлера, найдем частное решение . Подставив его в уравнение, найдем частное решение , а затем выпишем общее решение уравнения. Пример. Решить уравнение . Из уравнения получим сравнение . Поскольку , сравнение имеет решение. Тогда – частное решение сравнения. Упростим его, получим . Общее решение сравнения , . Подставим полученное частное решение в уравнение: . Тогда частное решение , а общее решение , . Таким образом, мы получили общее решение уравнения: , .
⇐ Предыдущая3456789101112Следующая ⇒ Читайте также: Где возникла философия и почему? Относительная высота сжатой зоны бетона Сущность проекции Гаусса-Крюгера и использование ее в геодезии Тарифы на перевозку пассажиров |
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 2230; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia. |
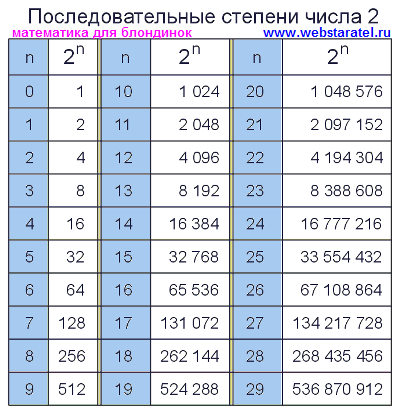
элементарная теория чисел — Какова первая степень двойки, в которой старшая цифра равна 7?
спросил
Изменено 11 лет, 2 месяца назад
Просмотрено 2к раз
$\begingroup$
Я как раз читал анекдот об ученице третьего класса, которую учитель математики попросил найти число, которое при возведении двойки в степень этого числа дает число, начинающееся с цифры 7 (в основании 10, как ясно из контекста).
Я смог быстро написать однострочник на Perl, который находил наименьшее такое число, 46, которое в итоге и было найдено студентом. Но в рассказе говорится, что вопрос был задан на уроке математики, и подразумевается, что ученик нашел ответ без помощи компьютера.
Но в рассказе говорится, что вопрос был задан на уроке математики, и подразумевается, что ученик нашел ответ без помощи компьютера.
Я не смог придумать пути решения этой задачи, который не зависел бы от компьютера, тем более способ, который мог бы открыть третьеклассник, даже на относительно продвинутом уровне математики. Итак, как это можно сделать? 96$, что составляет 64$. Нам нужно увеличить 64 доллара на чуть менее 10 процентов, умножить на 10 долларов. Но поскольку нас интересует только первая цифра, мы даже не видим в степени 10$, интуитивно мы просто хотим увеличить число с 6,4$ до 7$.
Легко видеть, что двукратного увеличения на $2,4% недостаточно, чтобы начать с $7$. То, что сделать это три раза недостаточно, менее очевидно, но немного пошалить, даже без калькулятора, помогает: хотя начисление процентов помогает, 2,4 доллара три раза не дают 10 долларов. Ясно, что увеличение 64 долларов на 2,4 процента в четыре раза приведет нас к 7 долларам и оставляет нас весьма далекими от того, чтобы начать с 8 долларов. Таким образом, требуемая мощность равна $6+(10)(4)$. 9{53} $ едва доставят нас туда. Это первый законный кандидат, но расчеты должны быть более точными, чем для цифры $7$, чтобы убедиться, что нам не нужно подниматься до $63$.
Таким образом, требуемая мощность равна $6+(10)(4)$. 9{53} $ едва доставят нас туда. Это первый законный кандидат, но расчеты должны быть более точными, чем для цифры $7$, чтобы убедиться, что нам не нужно подниматься до $63$.
$\endgroup$
$\begingroup$
Я не хочу отбрасывать возможность того, что какой-то третьеклассник достаточно разбирается в экспонентах, чтобы решить эту задачу, но я думаю, что более вероятно, что вопрос был представлен иначе, чем то, как он описан. В третьем классе ученики обычно изучают умножение, и это упражнение на самом деле просто умножение на 2:9.0005
Упражнение: Умножьте 2 x 2. Затем снова умножьте ответ на 2. Сколько раз вам нужно умножить на 2, пока первая цифра ответа не станет 7?
Это интересный способ попрактиковаться в умножении на 2 в ряде задач, и я не думаю, что 46 итераций займут неоправданно много времени, если делать это вручную. Если не считать того факта, что числа становятся длиннее по мере прохождения, это не более 2 страниц домашнего задания.
Если не считать того факта, что числа становятся длиннее по мере прохождения, это не более 2 страниц домашнего задания.
Конечно, не у всех третьеклассников хватило бы терпения, но я уверен, что некоторые дети любят усердно работать над повторяющейся задачей, подобной этой, потому что она большая (окончательное число состоит из 14 цифр!), но это все еще в их силах.
$\endgroup$
2
$\begingroup$
В логарифмах с основанием $10$ первая цифра $7$ совпадает с дробной частью логарифма между $\log_{10}(7)=0,845098040014257$ и $\log_{10}(8)=0,
9986991943$ . $46\;\log_{10}(2)=13,847379{46}=70368744177664$ — это первая степень числа двойки, старшая цифра которого равна $7$.
Однако, что касается выполнения метода без калькулятора, то это, похоже, не то. Если бы вы знали $\log_{10}(2)$ и $\log_{10}(7)$, вы могли бы сделать это повторным сложением, поскольку $\log_{10}(8)=3\;\log_{10 }(2)$. 6 = 64\:.$ Таким образом, для $\rm\:d = 64$ мы желаем $\rm\ 70 \le 64\ (1 + 0,024\ n) < 80\:,\ :$ так $\rm\: 6 \le 1.5\ n < 16\:,\:$ так $\rm\: 4\le n < 10\:.$ 9{46} = 70368744177664\:.\:$ Другие значения $\rm\:n\:$ также работают, хотя исключение $\rm\:n=10\:$ произошло по счастливой случайности, поскольку приближения т достаточно сильный.
6 = 64\:.$ Таким образом, для $\rm\:d = 64$ мы желаем $\rm\ 70 \le 64\ (1 + 0,024\ n) < 80\:,\ :$ так $\rm\: 6 \le 1.5\ n < 16\:,\:$ так $\rm\: 4\le n < 10\:.$ 9{46} = 70368744177664\:.\:$ Другие значения $\rm\:n\:$ также работают, хотя исключение $\rm\:n=10\:$ произошло по счастливой случайности, поскольку приближения т достаточно сильный.
$\endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя адрес электронной почты и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
Степени и степени
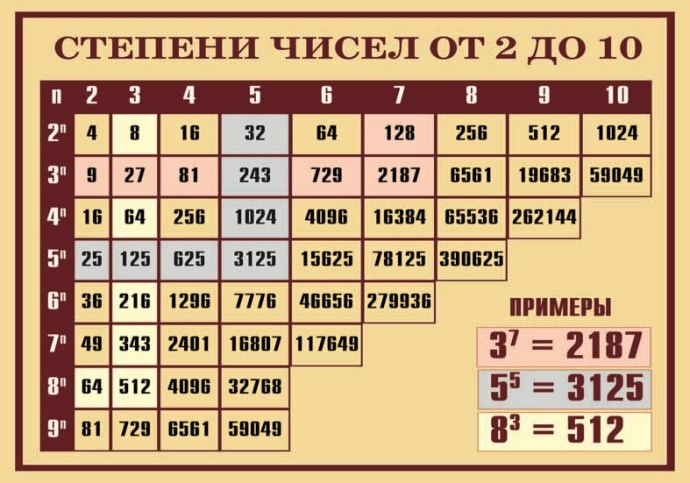
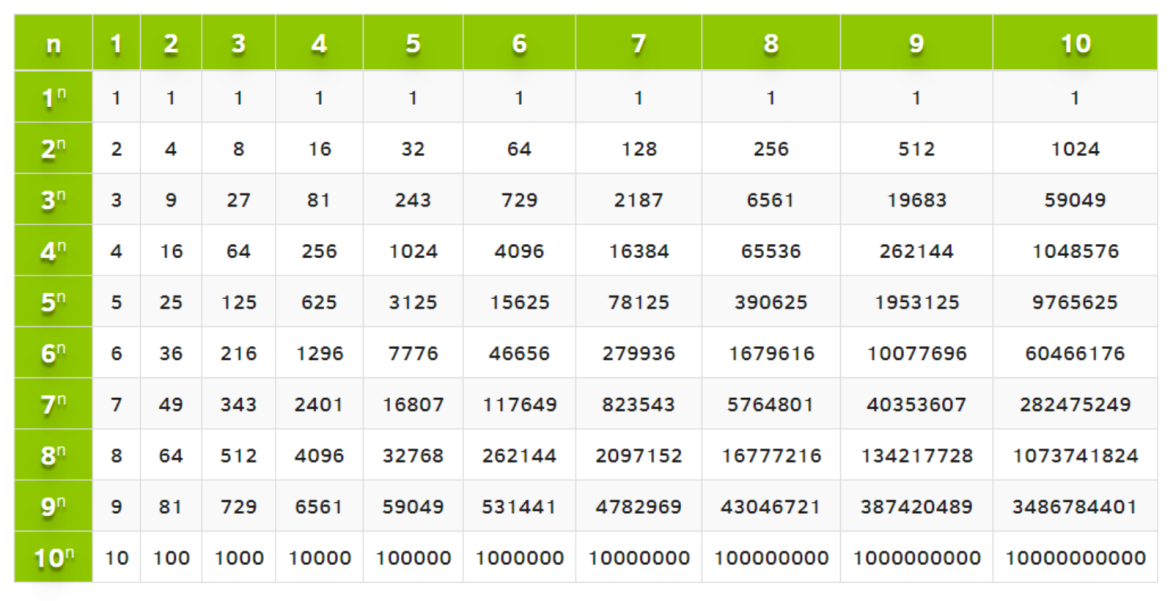
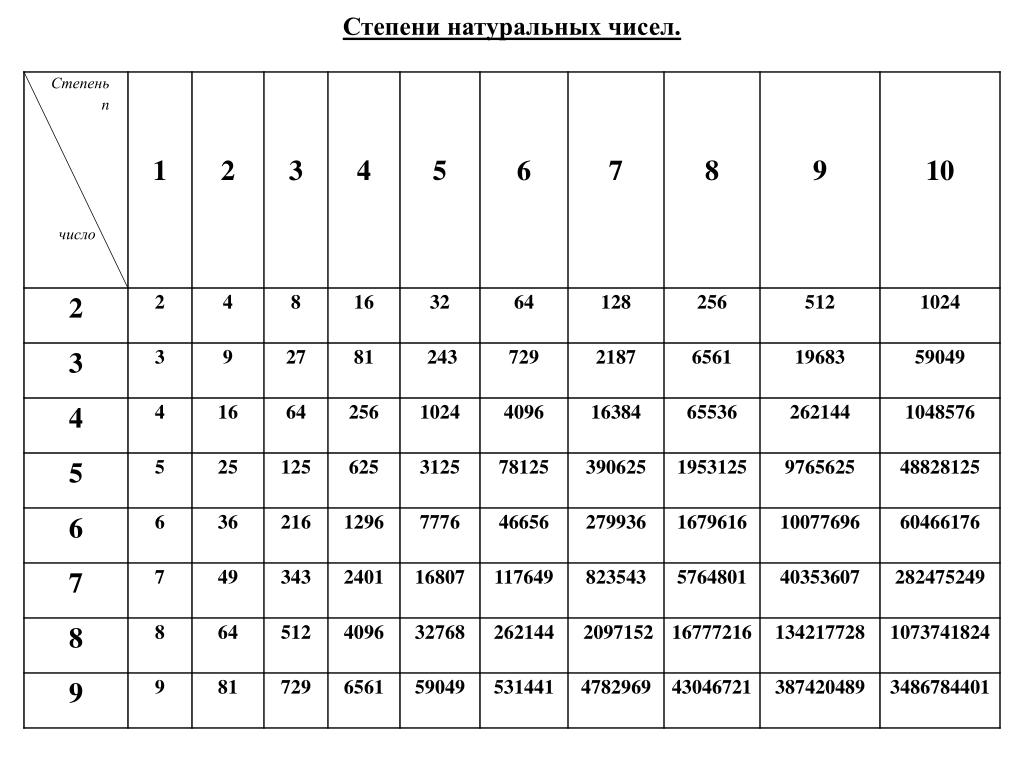
Степень есть результат многократного умножения одного и того же множителя.
Например, 125 — это 5 в 3-й степени. Потому что
125 = 5 ⋅ 5 ⋅ 5
Степень можно записать в форме, состоящей из двух частей.
Число, называемое основанием, и число, называемое показателем степени. Экспонента показывает, сколько раз основание использовалось как фактор.
Число в первой степени, например 13 1 , обычно записываются без показателя степени.
Мы можем читать и записывать полномочия, как указано ниже.
Power
In words
Value
15 1
15 to the first power
15 1 = 15
(0.4) 2
0.4 to the вторая степень, или 0,4 в квадрате
(0,4)(0,4) = 0,16
4 3
4 в третьей степени, или 4 в кубе
4 ⋅ 4 ⋅ 4 = 64
7 4
7 до четвертой мощности
7 ⋅ 7 ⋅ 7 ⋅ 7 = 2401
с использованием экспонентов
Пример 1:
Написать. с помощью экспоненты.
с помощью экспоненты.
а. 15 ⋅ 15 ⋅ 15 ⋅ 15
б. (0,5)(0,5)(0,5)
в. х ⋅ х ⋅ х ⋅ х ⋅ х ⋅ х
d. у ⋅ у ⋅ у ⋅ у ⋅ у
Решение:
а. 15 4 | Основание 15 используется как множитель 4 раза. |
б. (0,5) 3 | База 0,5 используется как множитель 3 раза. |
в. х 6 | Основание x используется как множитель 6 раз. |
д. у 5 | Основание y используется как множитель 5 раз. |
Пример 2:
Оцените выражение M 5 Когда M = 3.
Решение:
= M 5
.
= (3) 5
Используйте 3 в качестве коэффициента 5 раз.
= 3 ⋅ 3 ⋅ 3 ⋅ 3 ⋅ 3
Умножить.
= 243
Пример 3 :
Оцените выражение x 4 , когда x = 0,5.
Решение:
= x 4
Подставьте 0,5 вместо x.
= (0,5) 4
Используйте 0,5 в качестве коэффициента 4 раза.
= (0,5)(0,5)(0,5)(0,5)
Умножить.
= 0,0625
Использование степеней в формулах
Пример 4 :
Художник использует ледяной блок кубической формы, чтобы сделать ледяную скульптуру для конкурса. Найдите объем ледяной глыбы.
Решение:
Используйте формулу для объема куба:
V = s 3
Подставьте 15 вместо s.
= 15 3
Используйте 15 как множитель 3 раза.
= 15 ⋅ 15 ⋅ 15
Умножить.
= 3375
Объем глыбы льда составляет 3375 кубических дюймов.
Помимо всего вышеперечисленного, если вам нужны какие-либо другие материалы по математике, воспользуйтесь нашим пользовательским поиском Google здесь.

 5 = 40*40*40*40*40/(-29)*(-29)*(-29)*(-29)*(-29) = 102400000/(-20511149) = -4,9924.
5 = 40*40*40*40*40/(-29)*(-29)*(-29)*(-29)*(-29) = 102400000/(-20511149) = -4,9924.
 Определение реакций опор и моментов защемления
Определение реакций опор и моментов защемления
 Таким решением является, например, число .
Таким решением является, например, число .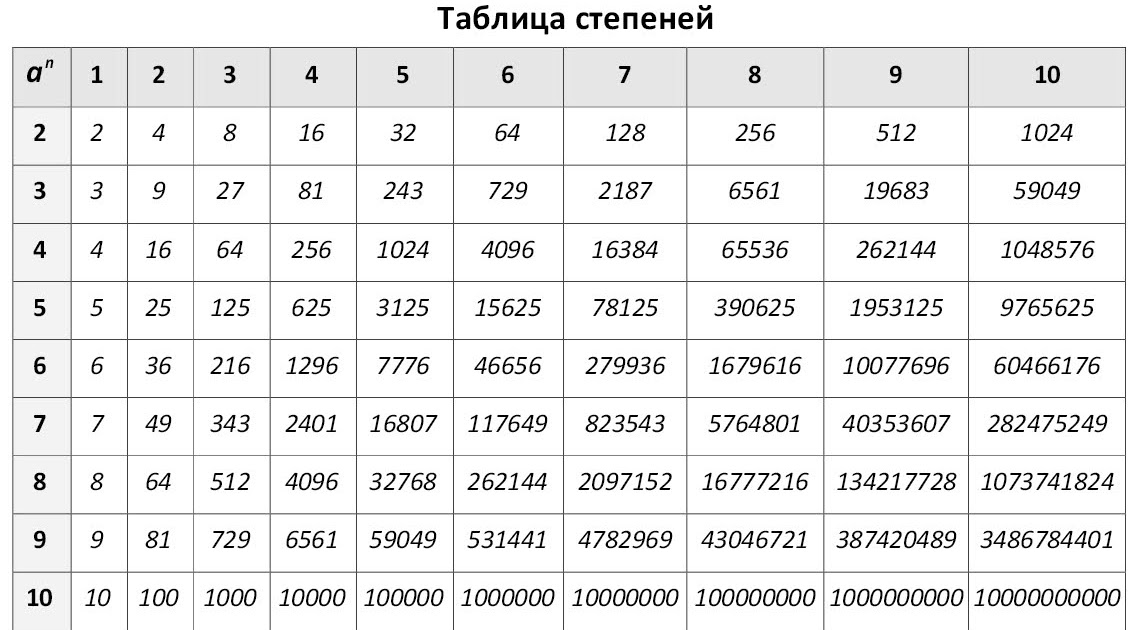
 su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.005 с.)
su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.005 с.)