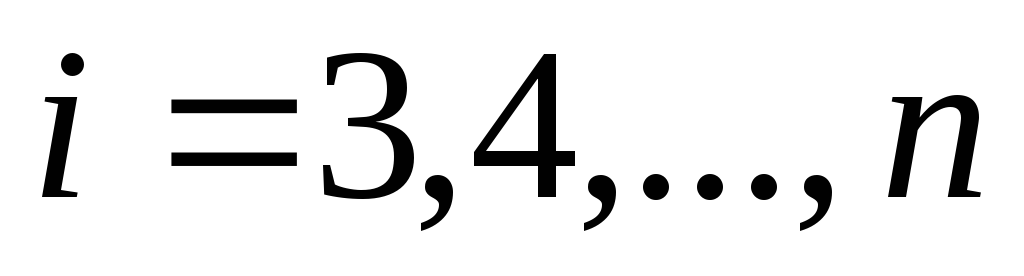Сообщество Экспонента
- вопрос
- 26.11.2022
Математика и статистика, Другое
Здравствуйте! Посмотрите пожалуйста код, почему не могу посчитать неизвестные a и b? очень срочно надо посчитать!! диплом горит(((
Здравствуйте! Посмотрите пожалуйста код, почему не могу посчитать неизвестные a и b? очень срочно надо посчитать!! диплом горит(((
2 Ответа
- Maple
- математика
- Программирование
26.11.2022
- вопрос
- 23.11.2022
Изображения и видео, Встраиваемые системы, Математика и статистика, Другое
Подскажите,может кто разбирался в методу главных компонент. Занимаюсь комплексированием 2-ух изображений методом главных компонент. По порядку использую функции cov, затем получаю собственные значения…
Подскажите,может кто разбирался в методу главных компонент.
- комплексирование
- матрица
- статистика
23.11.2022
- вопрос
- 23.11.2022
Системы связи, Цифровая обработка сигналов, Робототехника и беспилотники
Как запустить модели примеров с кнопкой ПОПРОБОВАТЬ В матлаб???
Как запустить модели примеров с кнопкой ПОПРОБОВАТЬ В матлаб???
19 Ответов
- вопрос
- 23.11.2022
Системы связи, Цифровая обработка сигналов, Другое
Какая создать модель в виде кода визуализируя спектральную эффективность в полном дуплексе?
Какая создать модель в виде кода визуализируя спектральную эффективность в полном дуплексе?
3 Ответа
- вопрос
- 22.
 11.2022
11.2022
Другое, Математика и статистика
Уважаемые форумчане, У кого есть опыт работы с функцией mesh? Написан код, посвященный решению задачи теплопроводности: рассматривается нагрев воды лазерным импульсом, решается задача теплопрово…
Уважаемые форумчане, У кого есть опыт работы с функцией mesh? Написан код, посвященный решению задачи теплопроводности: рассматривается нагрев воды лазерным импульсом, решается задача теплопрово…
6 Ответов
- pde
- mesh
22.11.2022
- Публикация
- 21.11.2022
Электропривод и силовая электроника
Какие опыты будут показаны? • Испытание устройств РЗиА в режиме жесткого реального времени с помощью КПМ РИТМ• Проверка протоколов цифровой подстанции (МЭК61850, С37.118, PRP, PTPv2) на киберустойчивость• Эксперименты с трансформатором и его циф…
Встретимся на форуме «ЭЛЕКТРИЧЕСКИЕ СЕТИ» (МФЭС) 22-25 ноября в Москве
Что будет представлено?
На стенде команда электроэнергетики представит отечественный программно-аппаратный комплекс реального времени на базе КПМ РИТМ.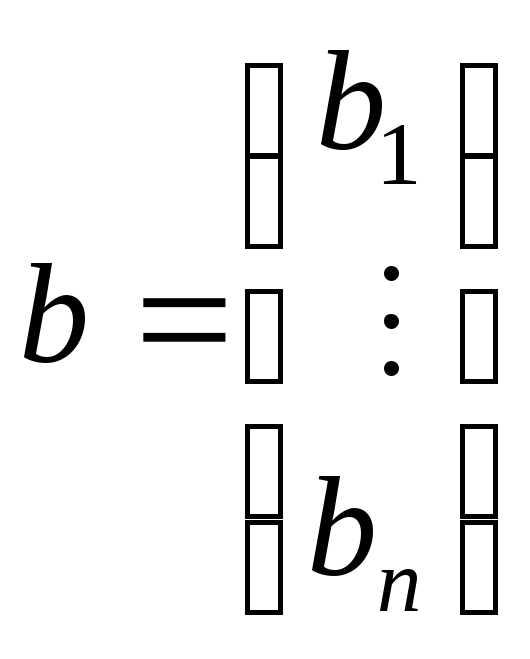
- Электропривод
- цифровая обработка сигналов
- РИТМ
21.11.2022
- вопрос
- 20.11.2022
Другое, Изображения и видео
Translator Подскажите как вычислить полигон ConvexHull, описывающий область на изображении используя функцию regionprops в Matlab
Translator Подскажите как вычислить полигон ConvexHull, описывающий область на изображении используя функцию regionprops в Matlab
1 Ответ
- MATLAB для студентов
20.11.2022
- Публикация
- 17.11.2022
Встраиваемые системы, ПЛИС и СнК
На вебинаре вы узнаете, как сократить временные и финансовые издержки при испытании встраиваемых систем управления с помощью технологии моделирования в реальном времени. В ходе вебинара будут затронуты следующие вопросы: Что такое тестирование в реальном врем…
Приглашаем вас на вебинар «Российские комплексы РИТМ для полунатурного моделирования и прототипирования встраиваемых систем», который пройдёт 29 ноября 2022 г. в 10:00 по московскому времени.
в 10:00 по московскому времени.
- MATLAB
- встраиваемые системы
- Simulink
- ПЛИС
- МОП
- Модельно ориентированное проектирование
17.11.2022
- Публикация
- 17.11.2022
Системы управления, Электропривод и силовая электроника
Интересно узнать еще больше об этом кейсе? Подробнее – тут.
Рассказываем, как инновационный центр «КАМАЗ» с помощью наших инженеров освоил современный рабочий процесс на базе модельно-ориентированного проектирования, который позволил небольшой команде разработчиков создать систему управления электрооборудования электробуса верхнего уровня в кратчайшие сроки.
- MATLAB
- системы управления
- САУ
- МОП
- Модельно ориентированное проектирование
17.11.2022
- вопрос
- 15.
 11.2022
11.2022
Системы связи, Математика и статистика, Цифровая обработка сигналов, Радиолокация, Робототехника и беспилотники
Создать с стандартными параметрами и хорошим его рисунком, спектром, автокореляцией! Спасибо за внимание!
Создать с стандартными параметрами и хорошим его рисунком, спектром, автокореляцией! Спасибо за внимание!
2 Ответа
Lu-разложение матрицы
LU-разложение матрицы
Предположим, что нам удалось привести данную матрицу A к виду
A=LU , (1)
где L – матрица вида , U – матрица вида .
Подставляя полученное разложение в исходную систему Ax=b, получим:
LUx=b. (2)
Пусть
Ux=y, (3)
тогда, подставляя (3) в (2), получаем:
Ly=b. (4)
Таким образом, решение данной системы сводится к трем этапам /2/:
-
нахождение элементов матриц L и U из матрицы A; -
решение системы (4) с матрицейL; -
решение системы (3) с матрицей U.
Учитывая равенство (1) и умножая последовательно столбцы матрицы L на строки матрицы U получаем систему из 9 уравнений и 9 неизвестных (элементы матриц L и U):
a11=l11;
a21=l21;a22=l22+l21*u12;a12=l11*u12;
a13=l11*u13;a23=l21*u13+l22*u23.
Находим элементы матриц L и U:
Решим систему (4). Ее решение сводится к решению следующей системы уравнений:
b1=l11*y1
b2=l21 *y1+ l22*y2
b3=l31*y1+ l32*y2+ l33*y3
Вектор y будет выглядеть следующим образом:y=
Следующий этап – решение системы Ux=y.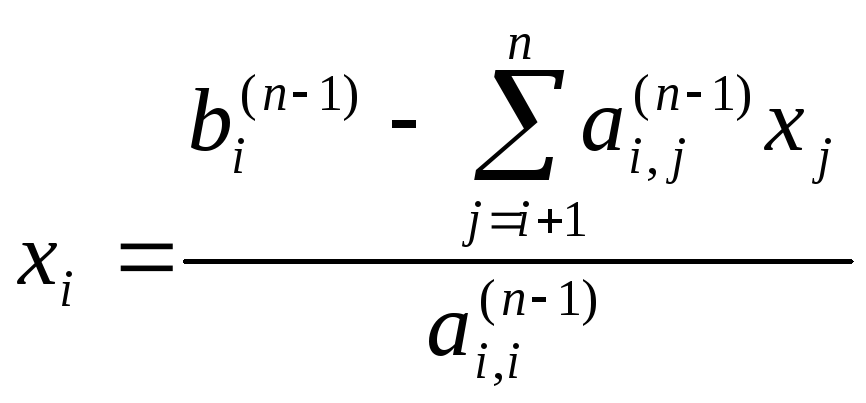 Решение сводится к решению следующей системы:
Решение сводится к решению следующей системы:
x1+u12*x2+u13*x3=y1
x2+u23*x3=y2
x3=y3
Находим вектор решения данной системы.x=
Чтобы найти определитель матрицы A, перемножим числа, стоящие на главной диагонали матрицы L.
detA=a11*a22*a33
Получение обратной матрицы
Имеем матрицу A=LU
где L – матрица вида , U – матрица вида .
Решим систему LU=E, где E – единичная матрица.
Представим единичную матрицу как набор вектор-столбцов:
e1=, e2=, e3=.
Решим последовательно системы Ly=e1, Ly=e2, Ly=e3 на основе формул, полученных в п. 2.2.
2.2.
Теперь решаем последовательно системы Ux=y1, Ux=y2, Ux=y3 .
СПИСОК ЛИТЕРАТУРЫ
-
Демидович Б.П., Марон И.А. Основы вычислительной математики. — М.: Наука, 1970. -
Вержбицкий В.М. Численные методы (линейная алгебра и нелинейные уравнения). — М.: Высшая школа, 2000.
ПРИМЕР РАБОТЫ ПРОГРАММЫ
Рис. 1. Результат работы программы. Вычисление корней
ВЫВОДЫ
Метод Гаусса решения систем линейных алгебраических уравнений позволяет с заданной точностью отыскать решение системы. К его преимуществам можно отнести простоту реализации на ЭВМ.
Метод LU-разложения при решении системы линейных алгебраических уравнений дает очевидные преимущества по сравнению с методом Гаусса. Во-первых, для решения систем с одинаковыми элементами A и разными элементами b, по методу Гаусса придется составлять схему с единственным делением столько раз, сколько подобных систем требуется решить. По методу
Во-первых, для решения систем с одинаковыми элементами A и разными элементами b, по методу Гаусса придется составлять схему с единственным делением столько раз, сколько подобных систем требуется решить. По методу
Математика | LU Разложение системы линейных уравнений
LU разложение матрицы – это разложение заданной квадратной матрицы на две треугольные матрицы, одну верхнюю треугольную матрицу и одну нижнюю треугольную матрицу, так что произведение этих двух матриц дает исходную матрицу . Он был введен Аланом Тьюрингом в 1948 году, который также создал машину Тьюринга.
Этот метод факторизации матрицы как произведения двух треугольных матриц имеет различные приложения, такие как решение системы уравнений, которое само по себе является неотъемлемой частью многих приложений, таких как определение тока в цепи и решение дискретной динамической системы проблемы; нахождение обратной матрицы и нахождение определителя матрицы.
В принципе, метод LU-разложения удобен, когда можно смоделировать решаемую задачу в матричной форме. Преобразование к матричной форме и решение с помощью треугольных матриц позволяет легко производить вычисления в процессе поиска решения.
Квадратная матрица A может быть разложена на две квадратные матрицы L и U так, что A = L U, где U — верхняя треугольная матрица, образованная в результате применения метода исключения Гаусса к A, а L — нижняя треугольная матрица с диагональю элементы, равные 1,
Для A = имеем L = и U = ; такое, что A = L U.
Здесь можно сравнить и найти значения l 21 , u 11 и т. д.
Метод исключения Гаусса
Согласно методу исключения Гаусса:
- Любая нулевая строка должна быть внизу матрицы.
- Первая ненулевая запись каждой строки должна быть справа от первой ненулевой записи предыдущей строки. Этот метод приводит матрицу к форме эшелона строк.

Шаги для разложения LU:
- Дан набор линейных уравнений, сначала преобразуйте их в матричную форму A X = C, где A — матрица коэффициентов, X — матрица переменных, а C — матрица чисел на правые части уравнений.
- Теперь приведите матрицу коэффициентов A, т. е. матрицу, полученную из коэффициентов переменных во всех заданных уравнениях, так что для «n» переменных у нас есть матрица nXn, к ступенчатой форме строки с использованием метода исключения Гаусса. Полученная таким образом матрица равна U.
- Чтобы найти L, у нас есть два метода. Первый состоит в том, чтобы принять оставшиеся элементы как некоторые искусственные переменные, составить уравнения, используя A = LU, и решить их, чтобы найти эти искусственные переменные.
Другой метод состоит в том, что оставшиеся элементы являются коэффициентами множителей, из-за которых соответствующие позиции стали равными нулю в матрице U. (Этот метод немного сложно понять словами, но он будет понятен в приведенном ниже примере) - Теперь у нас есть A (матрица коэффициентов nXn), L (нижняя треугольная матрица nXn), U (верхняя треугольная матрица nXn ), X (матрица переменных nX1) и C (матрица чисел nX1 в правой части уравнений).

- Данной системой уравнений является A X = C. Подставим A = L U. Таким образом, получим L U X = C.
Положим Z = U X, где Z — матрица или искусственные переменные, и решим сначала L Z = C, а затем решить для U X = Z, чтобы найти X или значения переменных, что и требовалось.
Пример:
Решите следующую систему уравнений, используя метод разложения LU:
Решение: Здесь у нас есть
A = и такое, что A X = C.
Теперь мы сначала рассмотрим и преобразуем его в форму эшелона строк, используя метод исключения Гаусса.
Таким образом, выполнив
(1)
(2)
Мы получаем
, сделав
(3)
Мы получаем
(помните, чтобы всегда сохранить между ними замените знак «+» на два знака «-» 3))
Теперь предположим Z и решим L Z = C.
Итак, имеем
Решая, получаем , и .
Теперь решим U X = Z
Следовательно, получим ,
Таким образом, решением данной системы линейных уравнений является , , а значит, матрица X =
Упражнение:
В LU разложение матрицы
| 2 2 | | 4 9 |
, если оба диагональных элемента U равны 1, то нижняя диагональная запись l22 L равна (GATE CS 2015)
(A) 4
(B) 5
(C) 6
(D) 7
Для решения см. https://www.geeksforgeeks.org/gate-gate-cs-2015-set-1-question-28 /
https://www.geeksforgeeks.org/gate-gate-cs-2015-set-1-question-28 /
Эта статья составлена Нишант Арора. Пожалуйста, пишите комментарии, если вы обнаружите что-то неправильное, или вы хотите поделиться дополнительной информацией по теме, обсуждаемой выше.
LU Разложение матрицы Примеры 1
Свернуть Содержание LU-разложение матрицы Примеры 1 Пример 1 Пример 2 |
Напомним со страницы LU Разложение матрицы, что если у нас есть $n \times n$ матрица $A$, то при условии, что при исключении по Гауссу верхняя треугольная матрица $U$ может быть получена без поворота, тогда существует существует другая нижнетреугольная матрица $L$ такая, что $A = LU$.
Теперь рассмотрим несколько конкретных примеров нахождения $LU$-разложения матрицы.
Пример 1
Найдите $LU$-разложение для матрицы $A = \begin{bmatrix} 3 & 1\\ 4 & 2 \end{bmatrix}$.
Мы начнем с применения метода исключения Гаусса, чтобы получить форму $A$, эквивалентную строке, которая является верхнетреугольной. Мы делаем это с помощью элементарной операции строки $R_2 — \frac{4}{3} R_1 \to R_2$, чтобы немедленно получить верхнюю треугольную матрицу, $U$:
Мы делаем это с помощью элементарной операции строки $R_2 — \frac{4}{3} R_1 \to R_2$, чтобы немедленно получить верхнюю треугольную матрицу, $U$:
(1)
\begin{align} U = \begin{bmatrix} 3 & 1\\ 0 & \frac{2}{3} \end{bmatrix} \end{align}
Теперь наша соответствующая нижняя треугольная матрица $L$ будет иметь $1$ на главной диагонали.
(2)
\begin{align} L = \begin{bmatrix} 1 & 0\\ * & 1 \end{bmatrix} \end{align}
Запись ниже главной диагонали получается как обратные операции со строками, примененные к $ долларов США. В этом случае у нас есть $R_2 + \frac{4}{3} R_1 \to R_2$, чтобы получить:
(3)
\begin{align} L = \begin{bmatrix} 1 & 0\\ \frac{4}{3} & 1 \end{bmatrix} \end{align}
Следовательно, наше разложение $A$ на $LU$:
(4)
\begin{align} \quad A = \begin{bmatrix} 3 & 1\\ 4 & 2 \end{bmatrix} = \begin{bmatrix} 1 & 0\\ \frac{4}{3} & 1 \end{bmatrix} \begin{bmatrix} 3 & 1\\ 0 & \frac{2}{3} \end{bmatrix} = LU \end{align}
Обратите внимание, что мы будем использовать только элементарную строку операции сложения/вычитания кратного одной строки в другую, поэтому обратные операции всегда будут отрицательными множителями, используемыми при выполнении исключения Гаусса для получения $A$ до $U$.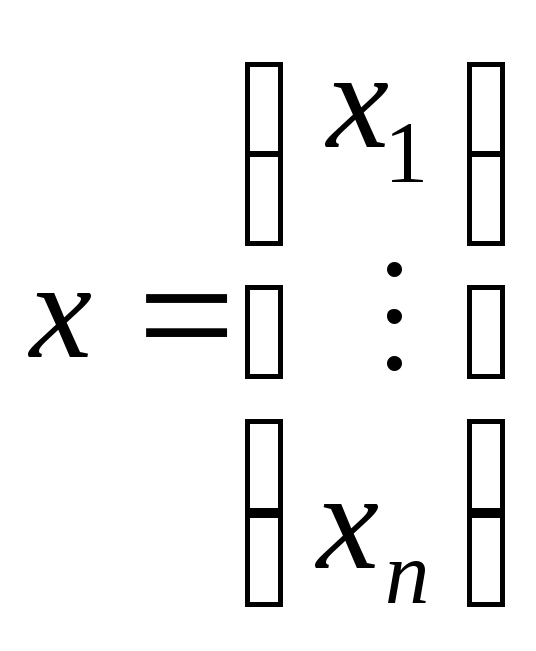
Пример 2
Найдите $LU$-разложение для матрицы $A = \begin{bmatrix} 1 & 2 & 3\\ 4 & 5 & 6\\ 7 & 8 & 9 \end{bmatrix}$ .
Опять же, мы начинаем с исключения Гаусса. Берем $R_2 — 4R_1\to R_2$, получаем:
(5)
\begin{bmatrix} 1 & 2 & 3\\ 0 & -3 & -6\\ 7 & 8 & 9 \end{bmatrix}
Теперь возьмем $R_3 — 7R_1 \to R_3$, чтобы получить:
(6)
\begin{bmatrix} 1 & 2 & 3\\ 0 & -3 & -6\\ 0 & -6 & -12 \end{bmatrix}
Наконец, мы берем $R_3 — 2R_2 \to R_3$, чтобы получить нашу верхнюю треугольную матрицу $U$:
(7)
\begin{align} U = \begin{bmatrix} 1 & 2 & 3\\ 0 & -3 & -6\\ 0 & 0 & 0 \end{bmatrix} \end{align}
Наш соответствующий нижний треугольная матрица $L$ снова будет иметь $1$ вдоль главной диагонали, а элементы под главной диагональю получаются из соответствующих обратных операций. Таким образом:
(8)
\begin{align} L = \begin{bmatrix} 1 & 0 & 0 \\ 4 & 1 & 0 \\ 7 & 2 & 1 \end{bmatrix} \end{align}
Следовательно, разложение $LU$ для $A$:
(9)
\begin{align} \quad A = \begin{bmatrix} 1 & 2 & 3\\ 4 & 5 & 6\\ 7 & 8 & 9 \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 \\ 4 & 1 & 0 \\ 7 & 2 & 1 \end{bmatrix} \begin{bmatrix} 1 & 2 & 3\\ 0 & -3 & -6\\ 0 & 0 & 0 \end{bmatrix } = LU \end{align}
Обратите внимание, что в этом конкретном примере третья строка $U$ состоит из нулей.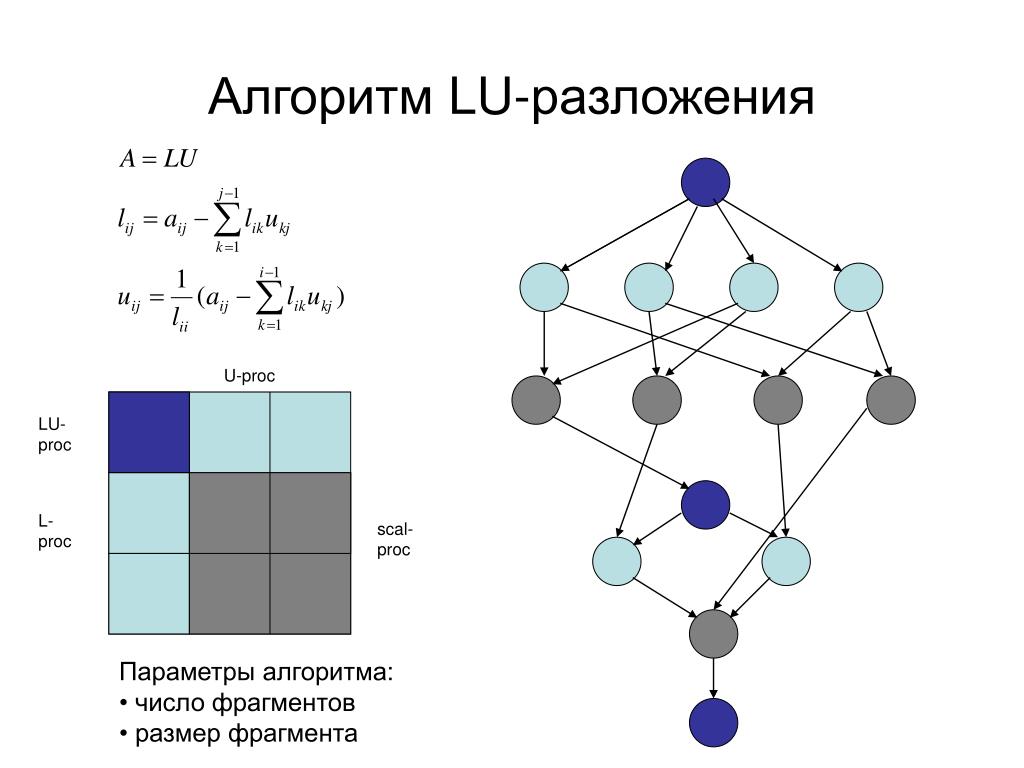

 11.2022
11.2022 11.2022
11.2022