Как правильно сравнивать дроби?
Поможем понять и полюбить математику
Начать учиться
Все познается в сравнении и особенно — дроби. Давайте узнаем, как и когда сравнивать дроби и чем это может быть полезно в жизни.
Сравнение дробей с одинаковыми знаменателями
Как и при любом другом сравнении, суть сравнения дробей — в том, чтобы определить меньшую и большую дроби.
Нет ситуации более благоприятной для сравнения, чем дроби с одинаковыми знаменателями. Если вся разница между дробями только в числителях, пользуемся следующим правилом:
Из двух дробей с одинаковыми знаменателями больше дробь с большим числителем. А меньше будет та дробь, числитель которой меньше. |
А теперь на примерах.
Пример 1.
Сравните дроби:
- Мы видим, что знаменатели дробей — равны. Значит сравниваем числители:
8 < 12
12 > 8 - Это значит, что < Изи!
Пример 2. Сравните дроби:
- Как и в прошлом примере, знаменатели дробей — равны. Сравниваем числители:
9 > 10
1 < 10 - Это значит, что >
Пример 3. Сравните дроби:
- Знаменатели дробей снова равны. Сравниваем числители:
3 > 1
1 < 3 - Это значит, что >
Как видите, нет ничего сложного в сравнении дробей, если знаменатели равны. Вся задача заключается в том, чтобы определить больший и меньший числитель.
Давайте разберем наглядный пример сравнения дробей.
Еще больше наглядных примеров — на курсах по математике в онлайн-школе Skysmart!
Допустим, в торте 6 кусков. Если от целого торта отрезать один кусок — в торте останется 5 кусков.
- Запишем в виде дробей: и
- А теперь сравним полученные дроби: знаменатели — равны, сравниваем числители:
6 > 5
5 < 6. - Это значит, что >
Понять, что целый торт больше, чем торт без одного куска, можно и без сравнения дробей. Но это же самое правило можно применить и при менее очевидных сравнениях, которые часто встречаются в повседневной жизни.
Реши домашку по математике на 5.
Подробные решения помогут разобраться в самой сложной теме.
Сравнение дробей с одинаковыми числителями
Вы уже разобрались со сравнением дробей с одинаковыми знаменателями. Теперь задача чуть усложняется — научимся сравнивать дроби с разными знаменателями, но с одинаковыми числителями.
Если у двух дробей одинаковые числители, то больше будет та дробь, чей знаменатель меньше. А меньше будет дробь с большим знаменателем. |
А теперь наши любимые примеры. Погнали!
Пример 1. Сравните дроби:
- У дробей разные знаменатели и одинаковые числители. Значит, согласно правилу, нужно сравнить знаменатели:
9 > 7
7 < 9 - Значит, дробь с меньшим знаменателем — больше:
Пример 2. Сравните дроби:
- У дробей разные знаменатели и одинаковые числители. Значит, согласно правилу, нужно сравнить знаменатели:
10 < 11
11 > 10 - Значит дробь с меньшим знаменателем — больше:
Пример 3.
Сравните дроби:
- У дробей разные знаменатели и одинаковые числители. Значит, согласно правилу, нужно сравнить знаменатели:
6 > 3
3 < 6 - Значит, дробь с меньшим знаменателем — больше.
Для наглядности представим ситуацию, в которой вам предстоит разделить торт между тремя друзьями. Это значит, что 6 кусков торта равномерно распределяются по 3 людям: каждому достается 6:3 = 2 по 2 кусочка.
А теперь представим более приятную ситуацию: кусков торта по-прежнему 6, а друзей уже только 2. Тогда каждому достанется по 3 вкуснейших кусочка:
Как видите, сравнение дробей может вам пригодиться в самых неожиданных ситуациях. Теперь, когда снова придется хорошенько задуматься о соотношении кусков торта и приглашенных гостях, изученная тема поможет вам принять верное решение😉.
Сравнение дробей с разными числителями и разными знаменателями
Нет ничего хитрого в сравнении дробей с одинаковыми числителями или знаменателями.
Чуть больше усилий потребуется при сравнении дробей, в которых нет ничего одинакового.
Запоминаем
Чтобы сравнить дроби с разными знаменателями, нужно привести дроби к общему знаменателю, а затем сравнить числители.
Сначала вспомним, как привести дроби к общему знаменателю.
Рассмотрим пример дробей с разными знаменателями.
- Нужно подобрать число, которое будет делиться на 7 и на 2, например, 14. Проверим:
14:7 = 2
14 : 2 = 7 - Первую дробь умножаем на дополнительный множитель 2:
- Вторую дробь умножаем на дополнительный множитель 7:
- Дроби приведены к общему знаменателю:
Давайте потренируемся в сравнении дробей.
Пример 1. Сравните дроби:
- Приведем дроби к общему знаменателю. 30 делится на 15 и на 2.
30 : 15 = 2
30 : 2 = 15 - Первую дробь умножаем на дополнительный множитель 2:
- Вторую дробь умножаем на дополнительный множитель 15:
- Дроби приведены к общему знаменателю:
- Если две дроби имеют одинаковые знаменатели, то, согласно правилу, больше та дробь, чей числитель больше:
При сравнении неправильных дробей с правильными помните, что неправильная дробь всегда больше правильной.
Пример 2: Сравните дроби:
- 6/5 — неправильная дробь.
- Выделим целую часть:
- Значит, что
Вычитание смешанных чисел
Вычитание проходит гладко, когда уменьшаемое больше вычитаемого.
- 12 — 7 = 6
12 — уменьшаемое
7 — вычитаемое
5 — разность
В случае, если вычитаемое больше уменьшаемого, разность оказывается отрицательной.
В этом нет ничего страшного. Но математика в 5 классе — «положительная», поэтому научимся находить разность смешанных чисел, не скатываясь «в минусы».
При вычитании дробей действует тот же самый принцип: вычитаемое должно быть меньше уменьшаемого. Вот здесь то вам и пригодится навык сравнивать дроби.
Пример 1. Вычислите:
Вычитаемая дробь меньше уменьшаемой
- Выполняем вычитание:
Пример 2.Найдите разность:
- Смешанные дроби превращаем в неправильные:
- Чтобы найти разность дробей с разными числителями и знаменателями, нужно привести их к общему знаменателю:
- Наименьшее общее кратное — 40
40 : 8 = 5
40 : 5 = 8 - Умножаем первую дробь на дополнительный множитель 5:
- Дроби приведены к общему знаменателю:
Примеры для самопроверки
Теория — это, конечно, хорошо.
Но без практики — никуда. Пора потренироваться в решении примеров и закрепить тему сравнения дробей.
Пример 1. Сравните дроби:
Ответ: по правилу сравнения дробей с одинаковыми знаменателями, больше та дробь, у которой числитель больше. Это значит, что
Пример 2. Сравните дроби:
Ответ: по правилу сравнения дробей с разными знаменателями и одинаковыми числителями, больше та дробь, чей знаменатель меньше. Это значит, что
Пример 3. Сравните дроби:
Как решаем:
Ответ:.
- По правилу сравнения дробей с разными числителями и знаменателями, сначала нужно привести дроби к общему знаменателю:
- Наименьшее общее кратное — 15:
15 : 15 = 1
15 : 5 = 3 - Умножаем первую дробь на дополнительный множитель 1:
- Умножаем вторую дробь на дополнительный множитель 3:
- Дроби приведены к общему знаменателю:
- Сравниваем числители получившихся дробей: 3 < 6
Пример 4.
Найдите разность:
Как решаем:
- Смешанные дроби превращаем в неправильные:
- Чтобы найти разность дробей с разными числителями и знаменателями, нужно привести их к общему знаменателю.
- Наименьшее общее кратное — 42:
42 : 7 = 6
42 : 6 = 7 - Умножаем первую дробь на дополнительный множитель 6:
- Умножаем вторую дробь на дополнительный множитель 7:
- Дроби приведены к общему знаменателю.
- Теперь можно вычитать:
Ответ:
Шпаргалки для родителей по математике
Все формулы по математике под рукой
Анастасия Белова
К предыдущей статье
117.9K
Основное тригонометрическое тождество
К следующей статье
Что такое пропорция
Получите план обучения, который поможет понять и полюбить математику
На вводном уроке с методистом
Выявим пробелы в знаниях и дадим советы по обучению
Расскажем, как проходят занятия
Подберём курс
1/6 Конвертер дробей и процентов, Дроби
1/6 — Одна шестая.
Конвертер величин. /
Конвертер дробей и процентов, ДробиEN ES PT RU FR
Ой… Javascript не найден.
Увы, в вашем браузере отключен или не поддерживается JavaScript.
К сожалению, без JavaScript этот сайт работать не сможет. Проверьте настройки браузера, может быть JavaScript выключен случайно?
1/6 — Одна шестая. Конвертер и таблица перевода величины.
Всё очень просто: Нужна помощь? x Этот конвертер величин очень простой. Правда.
|
| ||||||||||
?Настройки конвертера:
x
Объяснение настроек конвертера
Кстати, пользоваться настройками не обязательно. Вам вполне могут подойти настройки по умолчанию.
Количество значащих цифр
Для бытовых целей обычно не нужна высокая точность, удобнее получить округлённый результат. В таких случаях выберите 3 или 4 значащих цифры. Максимальная точность — 9 значащих цифр. Точность можно изменить в любой момент.
Разделитель групп разрядов
Выберите, в каком виде вам будет удобно получить результат:
| 1234567.89 | нет |
|---|---|
| 1 234 567.89 | пробел |
1,234,567. 89 | запятая |
| 1.234.567,89 | точка |
- Значащих цифр: 1 23456789
- Разделитель разрядов: нет пробел запятая точка
Укажите значение (одна шестая, 1/6):
» открыть »
» свернуть »
Единицы количества
| одна шестая → единица (1) | |
| одна шестая → пара | |
| одна шестая → тройка | |
| одна шестая → полдюжины | |
| одна шестая → декада | |
| одна шестая → дюжина | |
| одна шестая → чертова дюжина | |
| одна шестая → скор (англ.) | |
| одна шестая → флок (англ.) | |
| одна шестая → шок (англ.) | |
| одна шестая → сотня | |
| одна шестая → большая сотня (англ.) | |
| одна шестая → гросс | |
| одна шестая → тысяча | |
| одна шестая → большой гросс |
Единицы:
единица
(1)
/
пара
/
тройка
/
полдюжины
/
декада
/
дюжина
/
чертова дюжина
/
скор (англ.
)
/
флок (англ.)
/
шок (англ.)
/
сотня
/
большая сотня (англ.)
/
гросс
/
тысяча
/
большой гросс
» открыть »
» свернуть »
Проценты и доли
| одна шестая → процент (%) | |
| одна шестая → промилле (‰) | |
| одна шестая → частей на миллион (ppm) | |
| одна шестая → частей на миллиард (ppb) |
Единицы: процент (%) / промилле (‰) / частей на миллион (ppm) / частей на миллиард (ppb)
» открыть »
» свернуть »
Дроби
Внимание! Эта секция помогает ответить на вопросы такого типа: «Сколько 1/7-ых в одной половинке?» Чтобы получить ответ, введите 1 напротив 1/2 и посмотрите результат напротив 1/7. А теперь проверьте себя! Сможете при помощи нашего калькулятора быстро решить задачку: «Несколько одинаковых тортов разделили на 9 равных частей каждый, потом некоторые куски съели. Осталось 15 кусков. Если бы торты делили на 6 равных частей, и съели бы ровно такой же объём, сколько осталось бы кусков?».
Наш калькулятор позволяет получить ответ в одно действие.
| одна шестая → половина (1/2) | |
| одна шестая → треть (1/3) | |
| одна шестая → четверть (1/4) | |
| одна шестая → одна пятая (1/5) | |
| одна шестая → одна седьмая (1/7) | |
| одна шестая → одна восьмая (1/8) | |
| одна шестая → одна девятая (1/9) | |
| одна шестая → одна десятая (1/10) | |
| одна шестая → одна шестнадцатая (1/16) | |
| одна шестая → одна тридцать вторая (1/32) |
Единицы: половина (1/2) / треть (1/3) / четверть (1/4) / одна пятая (1/5) / / одна седьмая (1/7) / одна восьмая (1/8) / одна девятая (1/9) / одна десятая (1/10) / одна шестнадцатая (1/16) / одна тридцать вторая (1/32)
» открыть »
» свернуть »
Метрические префиксы
Эти префиксы широко используются в системе SI, могут применяться к любой единице.
Например, килояблоко — это 1000 яблок.
| одна шестая → кекто (q) | |
| одна шестая → ронто (r) | |
| одна шестая → йокто (y) | |
| одна шестая → цепто (z) | |
| одна шестая → атто (a) | |
| одна шестая → фемто (f) | |
| одна шестая → пико (p) | |
| одна шестая → нано (n) | |
| одна шестая → микро (µ, mc) | |
| одна шестая → милли (m) | |
| одна шестая → санти (c) | |
| одна шестая → деци (d) | |
| одна шестая → дека (da) | |
| одна шестая → гекто (h) | |
| одна шестая → кило (k) | |
| одна шестая → мега (M) | |
| одна шестая → гига (G) | |
| одна шестая → тера (T) | |
| одна шестая → пета (P) | |
| одна шестая → экза (E) | |
| одна шестая → зетта (Z) | |
| одна шестая → йотта (Y) | |
| одна шестая → ронна (R) | |
| одна шестая → кетта (Q) |
Единицы: кекто (q) / ронто (r) / йокто (y) / цепто (z) / атто (a) / фемто (f) / пико (p) / нано (n) / микро (µ, mc) / милли (m) / санти (c) / деци (d) / дека (da) / гекто (h) / кило (k) / мега (M) / гига (G) / тера (T) / пета (P) / экза (E) / зетта (Z) / йотта (Y) / ронна (R) / кетта (Q)
» открыть »
» свернуть »
Количество выступающих
| одна шестая → солист | |
| одна шестая → дуэт | |
| одна шестая → трио | |
| одна шестая → квартет | |
| одна шестая → квинтет | |
| одна шестая → сикстет | |
| одна шестая → септет | |
| одна шестая → октет |
Единицы: солист / дуэт / трио / квартет / квинтет / сикстет / септет / октет
Не можете найти нужную единицу?
Попробуйте поискать:
Другие варианты:
Посмотрите алфавитный список всех единиц
Задайте вопрос на нашей странице в facebook
< Вернитесь к списку всех конвертеров
Надеемся, Вы смогли перевести все ваши величины,
и Вам у нас на Convert-me.
Com понравилось. Приходите снова!
!
Значение единицы приблизительное.
Либо точного значения нет,
либо оно неизвестно. ?
Пожалуйста, введите число. (?)
Простите, неизвестное вещество. Пожалуйста, выберите что-то из списка. ***
Нужно выбрать вещество.
От этого зависит результат.
Совет: Не можете найти нужную единицу? Попробуйте поиск по сайту. Поле для поиска в верхней части страницы.
Нашли ошибку? Хотите предложить дополнительные величины? Свяжитесь с нами в Facebook.
Действительно ли наш сайт существует с 1996 года? Да, это так. Первая версия онлайнового конвертера была сделана ещё в 1995, но тогда ещё не было языка JavaScript, поэтому все вычисления делались на сервере — это было медленно. А в 1996г была запущена первая версия сайта с мгновенными вычислениями.
Для экономии места блоки единиц могут отображаться в свёрнутом виде. Кликните по заголовку любого блока, чтобы свернуть или развернуть его.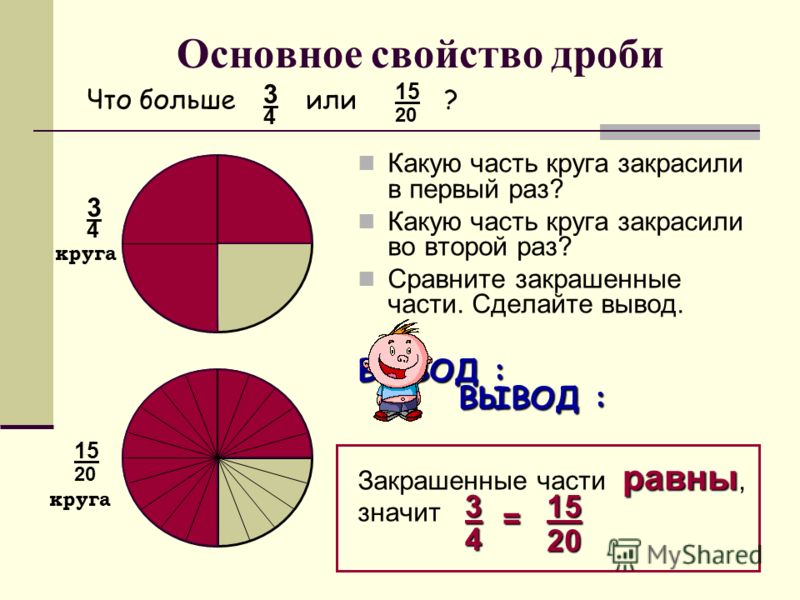
Слишком много единиц на странице? Сложно ориентироваться? Можно свернуть блок единиц — просто кликните по его заголовку. Второй клик развернёт блок обратно.
Наша цель — сделать перевод величин как можно более простой задачей. Есть идеи, как сделать наш сайт ещё удобнее? Поделитесь!
Минуточку, загружаем коэффициенты…
Какая дробь больше 1? Определение, типы, примеры
Что такое дроби?
Дроби представляют собой части целого или набора объектов. Когда целое или собрание делится на равные части, каждая часть составляет дробь. Например, если пицца разделена на шесть равных ломтиков, говорят, что каждый ломтик составляет 1/6 части пиццы. Это означает одну из шести равных частей. Его также можно прочитать как «одна шестая» или «1 на 6».
Если мы выберем два куска пиццы, это будет 2/6 пиццы. Точно так же, если мы выберем три куска этой пиццы, это будет 3/6 пиццы.
Число в верхней части строки называется числителем .
Он говорит нам, сколько равных частей целого взято. Число под чертой называется знаменателем . Он показывает общее количество равных частей, на которые делится целое.
В основном существует три типа фракций.
Правильные дроби: Если числитель дроби меньше ее знаменателя, то это правильная дробь. Например, ⅙, ⅜, ⅘ — правильные дроби.
Неправильные дроби: Когда числитель дроби больше или равен ее знаменателю, она называется неправильной дробью. Например, 4/3, 8/5, 6/4 — неправильные дроби.
Смешанные дроби : Смешанные дроби состоят из целого числа и правильной дроби. Например, $3\frac{4}{7}$, $4\frac{2}{5}$ — смешанные дроби.
Родственные игры
Что такое дробь больше 1?
В дроби знаменатель представляет собой общее количество равных частей, на которые делится целое. Можно сказать, что знаменатель представляет собой целое, а числитель представляет выбранную часть целого.
Если числитель дроби больше знаменателя, то дробь больше целого. Например,
Если каждый прямоугольник делится поровну на 3 части, то 5 частей больше, чем одно целое (или 3 части). Следовательно, 5/3 больше 1.
Когда числитель дроби больше ее знаменателя, значение дроби больше 1. Такие дроби также называют неправильными дробями.
Связанные рабочие листы
Как дроби больше 1 преобразуются в смешанные дроби?
Смешанные числа считаются простой формой неправильных дробей. Вот почему важно изучить преобразование между ними.
Чтобы преобразовать дробь больше 1 или неправильную дробь в смешанное число, мы должны выполнить шаги, указанные ниже:
- Шаг 1: Разделить числитель на знаменатель и получить частное и остаток.
- Шаг 2: Расположите значения частного, остатка и делителя следующим образом, чтобы получить смешанную дробь.
$Частное\фракция{Остаток}{Делитель}$
Знаменатель неправильной и смешанной дроби всегда один и тот же.
Например, смешанная дробная форма $\frac{7}{4}$ равна 1 ¾.
Дроби больше 1 на числовой прямой
Чтобы изобразить на числовой прямой дроби больше 1, нам нужно определить, между какими двумя целыми числами лежит дробь. Мы можем сделать это, преобразовав его в смешанное число.
Например, 5/3 = 1 ⅔
Глядя на число, мы знаем, что наша дробь больше 1. Значит, она будет между 1 и 2. Разделим интервал между 1 и 2 на 3 равные части.
Это будет смешанное число 1 ⅔ или дробь 5/3.
Преобразование дробей больше 1 в десятичные
Чтобы преобразовать дроби больше 1 в десятичные, разделите числитель на знаменатель. Например, $\frac{17}{10}$ = 1,7
Чтобы преобразовать смешанное число в десятичное, разделите числитель на знаменатель дробной части и прибавьте целую часть.
Например, $1\frac{3}{10}$ = 1 + 0,3 = 1,3
Примеры решения
Пример 1: $\frac{9}{7}$ больше 1?
Решение: В дробях больше 1 числитель больше числителя.
Таким образом, $\frac{9}{7}$ – это дробь, превышающая 1.
Пример 2. Преобразование $\frac{15}{7}$ в смешанные дроби.
Решение: При делении 15 на 7 мы получим 2 в частном и 1 в качестве напоминания.
Мы можем записать смешанную дробь $Частное\frac{Остаток}{Дивизор}$ или $2\frac{1}{7}$.
Пример 3. Является ли $\frac{14}{5}$ − $\frac{12}{5}$ больше 1?
Решение: $\frac{14}{5}$ − $\frac{12}{5}$ = $\frac{2}{5}$
Поскольку числитель меньше знаменателя, его значение меньше единицы.
Практические задачи
1
Какой из следующих ответов будет ответом, если мы преобразуем $\frac{14}{3}$ в смешанную дробь?
$4\frac{2}{3}$
$6\frac{3}{4}$
$7\frac{5}{6}$
$8\frac{5}{6}$
Правильный ответ: $4\frac{2}{3}$
При делении 14 на 3 мы получим 4 в частном и 2 в остатке.
2
Укажите, верны или нет приведенные ниже утверждения.
1. Дроби, большие единицы, называются правильными дробями.
2. Неправильные дроби можно преобразовать в смешанные дроби.
Верно только утверждение 1.
Верно только утверждение 2.
Ни одно из утверждений не верно.
Оба утверждения 1 и 2 верны.
Правильный ответ: Верно только утверждение 2.
Дроби больше 1 называются неправильными дробями.
Неправильные дроби можно преобразовать в смешанные дроби.
3
Между какими двумя числами будет дробь 9/4 на числовой прямой?
0 и 1
2 и 3
4 и 5
9 и 10
Правильный ответ: 2 и 3
9/4 равно 2 ¼. На числовой прямой эта дробь лежит между 2 и 3.
Часто задаваемые вопросы
В чем разница между дробями больше 1 и дробями меньше 1?
Если числитель дроби больше знаменателя, то дробь больше 1.
Такие дроби также называют неправильными. Эти дроби лежат справа от 1 на числовой прямой.
Если числитель дроби меньше ее знаменателя, то дробь меньше 1. Такие дроби еще называют правильными. Эти дроби лежат между 0 и 1 на числовой прямой.
Какое значение имеет сравнение дробей с одним целым?
Поскольку дроби являются частью целого, сравнение дробей с целым помогает нам определить различные типы дробей. Дроби меньше 1 являются правильными дробями. Дроби больше 1 могут быть записаны как неправильные дроби или смешанные числа.
Может ли смешанная дробь быть меньше 1?
Нет, смешанная дробь состоит из целого числа и правильной дроби. Следовательно, оно всегда больше 1,9.0005
Дроби: сравнение и сокращение дробей
Урок 2: сравнение и сокращение дробей
/en/fractions/introduction-to-fractions/content/
Сравнение дробей
показывая часть чего-то.
Дроби полезны, поскольку они позволяют нам точно сказать, сколько у нас чего-то есть. Некоторые дроби больше других. Например, что больше: 6/8 пиццы или 7/8 пиццы?
На этом изображении мы видим, что 7/8 больше. Иллюстрация позволяет легко сравнить этих дробей. Но как бы мы это сделали без картинок?
Щелкните слайд-шоу, чтобы узнать, как сравнивать дроби.
Ранее мы видели, что дроби состоят из двух частей.
Одна часть является старшим числом, или числитель .
Другим является нижнее число, или знаменатель .
Знаменатель говорит нам, сколько частей в целом.
Числитель говорит нам, сколько таких частей у нас есть.
Если дроби имеют одинаковый знаменатель, это означает, что они разделены на одинаковое количество частей.
Это означает, что мы можем сравнить этих дробей, просто взглянув на числитель.
Здесь 5 больше 4…
Здесь 5 больше 4… так что мы можем сказать, что 5/6 больше 4/6.
Давайте рассмотрим другой пример. Какой из них больше: 2/8 или 6/8?
Если вы думали, что 6/8 больше, вы были правы!
Обе дроби имеют одинаковый знаменатель.
Итак, мы сравнили числители. 6 больше 2, поэтому 6/8 больше 2/8.
Как вы видели, если две или более дроби имеют одинаковый знаменатель, вы можете сравнить их, взглянув на их числители. Как вы можете видеть ниже, 3/4 больше, чем 1/4. Чем больше числитель, тем больше дробь.
Сравнение дробей с разными знаменателями
На предыдущей странице мы сравнили дроби, имеющие одинаковые нижних чисел или знаменателей . Но вы знаете, что дроби могут иметь любое число в качестве знаменателя. Что происходит, когда вам нужно сравнить дроби с разными нижними числами?
Например, какой из них больше: 2/3 или 1/5? Трудно сказать, просто глядя на них.
В конце концов, 2 больше, чем 1, но знаменатели не совпадают.
Если вы посмотрите на картинку, то разница очевидна: 2/3 больше, чем 1/5. С иллюстрацией сравнить эти дроби было легко, но как это сделать без картинки?
Щелкните слайд-шоу, чтобы узнать, как сравнивать дроби с разными знаменателями.
Сравним эти дроби: 5/8 и 4/6.
Прежде чем мы их сравним, нам нужно изменить обе дроби так, чтобы они имели одинаковый знаменатель или нижний номер.
Сначала найдем наименьшее число, которое можно разделить на оба знаменателя. Мы называем это наименьшим общим знаменателем .
Наш первый шаг — найти числа, которые можно без остатка разделить на 8.
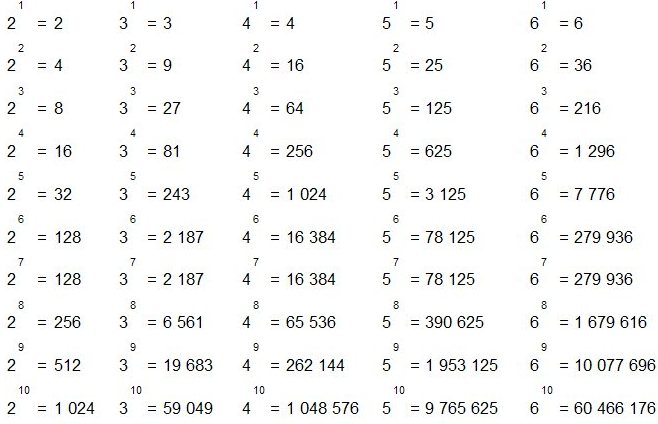
Использование таблицы умножения упрощает эту задачу. Все числа в 8-й строке можно разделить на 8 без остатка.
Теперь давайте посмотрим на наш второй знаменатель: 6.
Мы снова можем использовать таблицу умножения.
Все числа в 6-й строке можно разделить на 6 без остатка.Сравним две строки. Похоже, что есть несколько чисел, которые можно разделить на 6 и 8 без остатка.
24 — наименьшее число, встречающееся в обеих строках, поэтому это наименьший общий знаменатель .
Теперь мы изменим наши дроби так, чтобы они имели одинаковый знаменатель: 24.
Для этого нам нужно изменить числители так же, как мы изменили знаменатели.
Давайте еще раз посмотрим на 5/8. Чтобы изменить знаменатель на 24…
Давайте снова посмотрим на 5/8. Чтобы изменить знаменатель на 24… нам пришлось умножить 8 на 3.
Поскольку мы умножили знаменатель на 3, мы также умножим числитель, или верхнее число, на 3.
5 умножить на 3 равно 15. Таким образом, мы изменили 5/8 на 15/24.
Мы можем это сделать, потому что любое число равно 1.
Итак, когда мы умножаем 5/8 на 3/3.
..Итак, когда мы умножаем 5/8 на 3/ 3… на самом деле мы умножаем 5/8 на 1.
Поскольку любое число, умноженное на 1, равно самому себе…
Поскольку любое число, умноженное на 1, равно самому себе… мы можем сказать что 5/8 равно 15/24.
Теперь то же самое проделаем с другой дробью: 4/6. Мы также изменили его знаменатель на 24,9.0005
Наш старый знаменатель был 6. Чтобы получить 24, мы умножили 6 на 4.
Итак, мы также умножим числитель на 4. равно 16/24.
Теперь, когда знаменатели совпадают, мы можем сравнить две дроби, взглянув на их числители.
16/24 больше 15/24…
16/24 больше 15/24… поэтому 4/6 больше 5/8.
Все числа в 6-й строке можно разделить на 6 без остатка.
..Уменьшающие дроби
Какая из них больше: 4/8 или 1/2?
Если бы вы посчитали или просто посмотрели на картинку, то могли бы сказать, что они равны .
Другими словами, 4/8 и 1/2 означают одно и то же, хотя и пишутся по-разному.
Если 4/8 означает то же самое, что и 1/2, почему бы просто не назвать его так? Половина легче сказать, чем четыре восьмых , и для большинства людей это также легче понять. В конце концов, когда вы едите с другом, вы делите счет на 9.0009 половина , а не восьмых .
Если вы запишете 4/8 как 1/2, вы на уменьшите . Когда мы уменьшаем на дробь, мы записываем это в более простой форме. Сокращенные дроби всегда равны исходной дроби.
Мы уже уменьшили 4/8 до 1/2. Если вы посмотрите на приведенные ниже примеры, то увидите, что и другие числа можно уменьшить до 1/2. Все эти дроби равны .
5/10 = 1/2
11/22 = 1/2
36/72 = 1/2
Все эти дроби также были приведены к более простой форме.
4/12 = 1/3
14/21 = 2/3
35/50 = 7/10
Щелкните слайд-шоу, чтобы узнать, как уменьшить дроби на , разделив .
Попробуем уменьшить эту дробь: 16/20.
Так как числитель и знаменатель четные числа , вы можете разделить их на 2, чтобы уменьшить дробь.
Сначала мы разделим числитель на 2. 16 разделить на 2 будет 8.
Затем мы разделим знаменатель на 2. 20 разделить на 2 равно 10.
Мы’ ve уменьшил 16/20 до 8/10. Мы могли бы также сказать, что 16/20 равно 8/10.
Если числитель и знаменатель все еще можно разделить на 2, мы можем продолжить сокращение дроби.
8 разделить на 2 равно 4.
10 разделить на 2 равно 5.
Поскольку не существует числа, на которое можно разделить 4 и 5, мы не можем больше сокращать 4/5.
Это означает, что 4/5 является простейшей формой от 16/20.
Попробуем сократить другую дробь: 6/9.
Хотя числитель четный, знаменатель нечетное число , поэтому мы не можем уменьшить путем деления на 2.
Вместо этого нам нужно найти число, которое 6 и 9можно разделить на. Таблица умножения поможет найти это число.
Найдем 6 и 9 в той же строке . Как видите, 6 и 9 можно разделить на 1 и 3.
Деление на 1 не изменит эти дроби, поэтому мы будем использовать наибольшее число , на которое можно разделить 6 и 9.
Это 3. Это называется наибольшим общим делителем или НОД . (Вы также можете назвать это наибольший общий делитель или GCF .)
3 — это НОД чисел 6 и 9, потому что это наибольшее число , на которое они могут делиться.
Итак, мы разделим числитель на 3. 6 разделить на 3 равно 2.
Затем мы разделим знаменатель на 3. 9 разделить на 3 равно 3.
Теперь мы уменьшено 6/9 до 2/3, что является его простейшей формой.
Мы могли бы также сказать, что 6/9 равно 2/3.
Мы могли бы также сказать, что 6/9 равно 2/3.Несократимые дроби
Не все дроби можно сократить. Некоторые из них уже настолько просты, насколько это возможно. Например, вы не можете уменьшить 1/2, потому что нет другого числа, кроме 1, на которое можно разделить и 1, и 2. (По этой причине вы не можете уменьшить любую дробь , у которой числитель равен 1.)
Некоторые дроби с большими числами также не могут быть уменьшены. Например, 17/36 нельзя уменьшить, потому что нет числа, на которое можно разделить и 17, и 36. Если вы не можете найти общие кратные для чисел в дроби, скорее всего, это неприводимое .
Попробуй!
Приведите каждую дробь к простейшей форме.
Смешанные числа и неправильные дроби
На предыдущем уроке вы узнали о смешанных числах . Смешанное число имеет как дробь , так и целое число .
Например, 1 2/3. Вы бы прочитали 1 2/3 так: одна и две трети .
Другой способ записи: 5/3 или пять третей . Эти два числа выглядят по-разному, но на самом деле они одинаковы. 5/3 — неправильная дробь . Это просто означает, что числитель на больше , чем знаменатель.
Иногда вы можете предпочесть использовать неправильную дробь вместо смешанного числа. Смешанное число легко превратить в неправильную дробь. Давайте узнаем, как:
Преобразуем 1 1/4 в неправильную дробь.
Во-первых, нам нужно выяснить, сколько частей составляют целое число: 1 в этом примере.
Для этого умножим целое число , 1 на знаменатель, 4.
1 умножить на 4 равно 4.
Теперь добавим 4 к этому числу числитель 1.
4 плюс 1 равно 5.
Знаменатель остается прежним.
Наша неправильная дробь — 5/4, или пять четвертых. Таким образом, мы могли бы сказать, что 1 1/4 равно 5/4.
Это означает, что в 1 1/4 содержится пять 1/4.
Преобразуем другое смешанное число: 2 2/5.
Сначала умножим целое число на знаменатель. 2 умножить на 5 равно 10.
Далее мы добавим 10 к числителю. 10 плюс 2 равно 12.
Как всегда, знаменатель останется прежним.
Итак, 2 2/5 равно 12/5.
Попробуй!
Попробуйте преобразовать эти смешанные числа в неправильные дроби.
Преобразование неправильных дробей в смешанные числа
Неправильные дроби полезны для решения математических задач, в которых используются дроби, как вы узнаете позже. Однако их сложнее читать и понимать, чем смешанные числа . Например, гораздо легче представить себе 2 4/7, чем 18/7.
Просмотрите слайд-шоу, чтобы узнать, как преобразовать неправильную дробь в смешанное число.
Превратим 10/4 в смешанное число.
Любую дробь можно представить как деление задачу . Просто относитесь к линии между числами как к знаку деления (/).
Итак, разделим числитель, 10, на знаменатель, 4.
10 разделить на 4 равно 2… остаток от 2.
Ответ 2 станет нашим целым числом, потому что 10 можно разделить на 4 дважды .
И остаток , 2 станет числителем дроби, потому что у нас осталось 2 части.
Знаменатель остается прежним.
Итак, 10/4 равно 2 2/4.
Возьмем другой пример: 33/3.
Разделим числитель 33 на знаменатель 3.
33 разделить на 3…
33 разделить на 3… равно 11 без остатка.
