Что следует из подобия треугольников: Признаки подобия треугольников

Подобные треугольники | Математика

В двух треугольниках, имеющих равные углы, стороны, лежащие против одинаковых углов, называются сходственными (соответственными).

В треугольниках ABC и DEF (черт. 152), в которых

∠A = ∠D, ∠B = ∠E, ∠C = ∠F

стороны AB и DE, BC и EF, AC и DF, лежащие против равных углов C и F, A и D, B и E будут соответственными сторонами.

Определение подобных треугольников. Подобными называются такие два треугольника, у которых углы равны и сходственные стороны пропорциональны.

Если в двух треугольниках (черт. 152) ABC и DEF углы равны

∠A = ∠D, ∠B = ∠E, ∠C = ∠F

и соответственные стороны пропорциональны

AB/DE = AC/DF = BC/EF

то треугольники называются подобными.

Подобие обычно выражают знаком ∼.

Подобие двух треугольников изображают письменно:

ABC ∼ DEF.

Случаи подобия треугольников

Теорема 89. (Первый случай подобия.) Два треугольника подобны, если три угла одного равны трем углам другого треугольника.

Дано. В треугольниках ABC и DEF углы равны (черт. 153).

∠A = ∠D, ∠B = ∠E, ∠C = ∠F

Требуется доказать, что они подобны. Для этого нужно доказать, что их стороны пропорциональны, т. е. удовлетворяют отношениям:

AB/DE = AC/DF = BC/EF

Доказательство. Наложим треугольник DEF на ABC так, чтобы вершина E совпала с вершиной B, сторона ED со стороной AB. По равенству углов B и E сторона EF пойдет по стороне BC. Положим, точка D упадет в D’, а точка F в E’. Треугольник D’BE’ равен треугольнику DEF, следовательно,

∠D’ = ∠D, ∠D = ∠A

откуда

∠D’ = ∠A.

Если соответственные углы равны, то D’E || AC.

По теореме 86 имеют место равенства

AC/D’E’ = AB/BD’ = BC/BE’

Так как BD’ = ED, BE’ = EF, D’E’ = DF, то

AC/DF = AB/ED = BC/EF (ЧТД).

Теорема 90 (второй случай подобия). Два треугольника подобны, если они имеют по два равных угла.

Доказательство. Если в двух треугольниках ABC и DEF два угла равны (черт. 153).

A = D, B = E

то и третьи углы тоже равны, а в таком случае треугольники подобны (теорема 89).

Теорема 91 (третий случай подобия). Два треугольника подобны, если они имеют по равному углу, заключающемуся между пропорциональными сторонами.

Дано. В треугольниках ABC и DEF (черт. 153) углы B и E равны, и стороны, их содержащие, пропорциональны, т. е.

∠B = ∠E и AB/DE = BC/EF.

Требуется доказать, что треугольники подобны.

Доказательство. Совместим угол E с углом B, и отложим BD’ = ED, BE’ = EF, тогда ∆BD’E’ = ∆DEF, следовательно,

∠D’ = ∠D, ∠E’ = ∠F.

Так как имеет место пропорция

AB/BD’ = BC/BE’

то сторона D’E’ || AC (теорема 87).

Поэтому ∠D’ = ∠A, ∠C = ∠E’.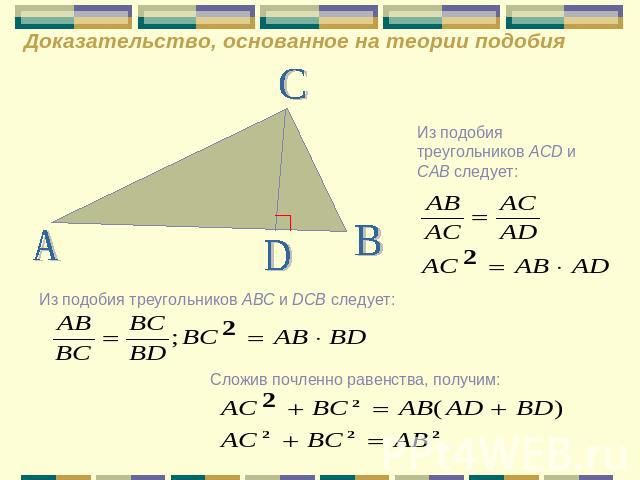

Следовательно,

∠A = ∠D, ∠C = ∠F, ∠B = ∠E

т. е. три угла одного равны трем углам другого треугольника.

В этом же случае треугольники ABC и DEF подобны (ЧТД).

Теорема 92 (четвертый случай подобия). Два треугольника подобны, если стороны одного пропорциональны сторонам другого.

Дано. В треугольниках ABC и abc (черт. 154) стороны пропорциональны:

AB/ab = BC/bc = AC/ac (1)

Требуется доказать, что у них углы равны, т. е.

A = a, B = b, C = c.

Доказательство. Отложим на стороне BA отрезок Ba’, равный ba, и проведем отрезок a’c’, параллельный AC, тогда будут иметь место отношения:

AB/Ba’ = BC/Bc’ = AC/a’c’

Так как Ba’ = ba, то рядом с этими имеют место отношения:

AB/ab = BC/Bc’ = AC/a’c’ (2)

Сопоставляя отношения (1) и (2), заключаем, что

Bc’ = bc, a’c’ = ac,

следовательно, два треугольника a’Bc’ и abc равны, откуда

∠B = ∠b, ∠Ba’c’ = ∠a, ∠Bc’a’ = ∠c

а так как

∠A = ∠a’, ∠C = ∠c’, то
B = b, A = a, C = c,

следовательно, углы двух треугольников ABC и abc равны (ЧТД).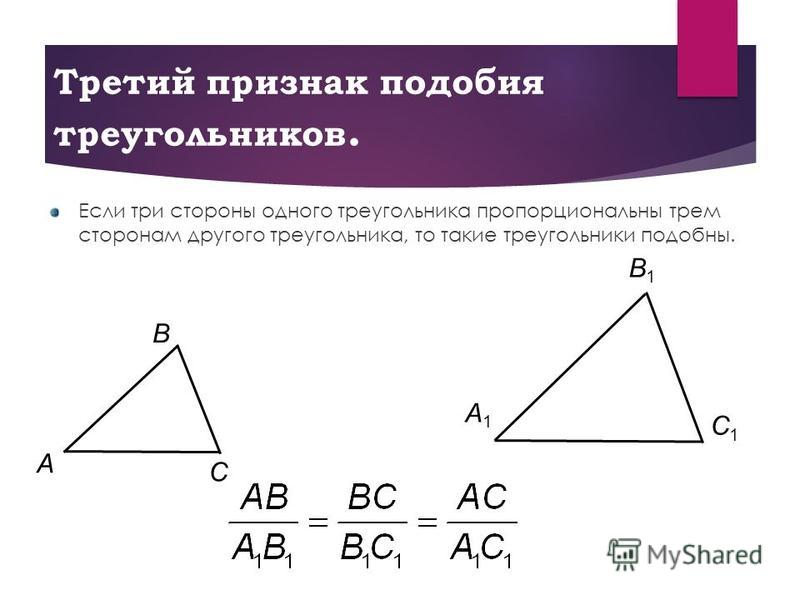

Теорема 93 (пятый случай подобия). Два треугольника подобны, если стороны одного параллельны сторонам другого.

Доказательство. Здесь могут быть два случая:

1-й случай. Если углы двух треугольников с параллельными сторонами обращены в одну сторону. В таком случае в двух таких треугольниках ABC и abc (черт. 155) все углы одного соответственно равны углам другого, и, следовательно, треугольники подобны.

2-й случай. Когда углы с параллельными сторонами обращены в разные стороны. Так в треугольниках ABC и a’b’c’ стороны параллельны.

AB || a’b’, AC || a’c’, BC || b’c’.

Углы же между параллельными сторонами обращены в разные стороны.

В таком случае, продолжив стороны a’c’ и a’b’, откладываем на продолжении их части a’b» = a’b’ и a’c» = a’c’.

Треугольники a’b»c» и a’b’c’ равны. Треугольник a’b»c» подобен треугольнику ABC, ибо у него стороны параллельны и углы, направленные в одну сторону, равны, следовательно,

∆ABC ~ a’b»c», следовательно, ∆ABC ~ a’b’c’ и
AB/a’b’ = AC/a’c’ = BC/b’c’

Теорема 94 (шестой случай подобия). Два треугольника подобны, если стороны одного перпендикулярны к сторонам другого.

Даны два треугольника ABC и abc (черт. 156), стороны которых перпендикулярны:

ab ⊥ AB, ac ⊥ AC, bc ⊥ BC

Требуется доказать, что треугольники подобны.

Доказательство. Продолжим стороны ac и bc до пересечения их со сторонами AC и BC в точках n и p. Тогда в двух треугольниках mcn и mCp все углы равны, ибо

n = p как прямые

Углы при точке m равны как вертикальные,

а следовательно, и третьи углы равны ∠pCm = ∠mcn.

Так как

∠pCm = ∠ACB, ∠mcn = ∠acb

следовательно,

∠ACB = ∠acb

Подобным же образом можно доказать, что A = a, B = b, следовательно, треугольники ABC и abc подобны и имеет место пропорция

AB/ab = AC/ac = BC/bc

Подобие прямоугольных треугольников

Теорема 95. Два прямоугольных треугольника подобны, если они имеют по равному острому углу.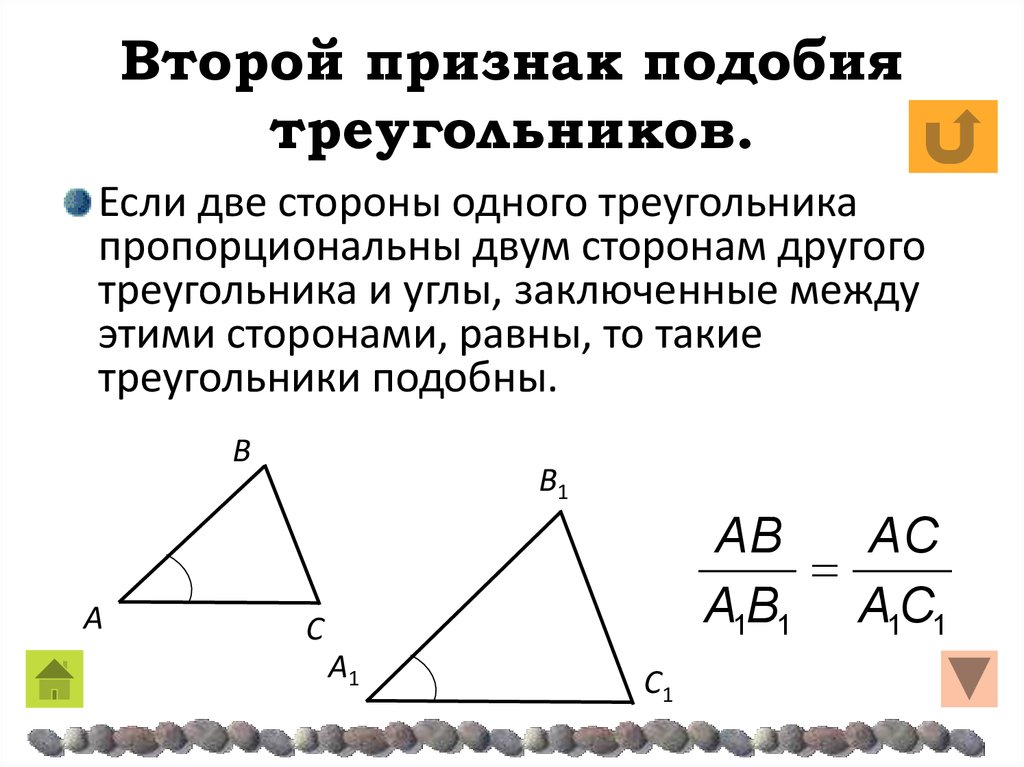

Дано. У прямоугольных треугольников ABC и abc (черт. 157) острые углы C и c равны.

Требуется доказать, что треугольники ABC и abc подобны.

Доказательство. Углы B и b равны как прямые, углы C и c равны по условию, следовательно, они подобны (теорема 90).

Теорема 96. Два прямоугольных треугольника подобны, если катет и гипотенуза одного пропорциональна катету и гипотенузе другого.

Дано. В прямоугольных треугольниках ABC и abc (черт. 157)

AC/ac = AB/ab (a)

Требуется доказать, что ∠A = ∠a, ∠C = ∠c.

Доказательство. Отложим на отрезке BA отрезок Bm, равный ba и из точки m проведем отрезок mn, параллельный ac, тогда имеет место пропорция:

AC/mn = AB/Bm (b)

Так как Bm = ab по построению, то, сравнивая две пропорции (a) и (b), заключаем, что ac = mn, следовательно, два прямоугольных треугольника Bmn и abc, имея по равному катету и равной гипотенузе, равны.

Действительно, у них Bm = ab, mn = ac.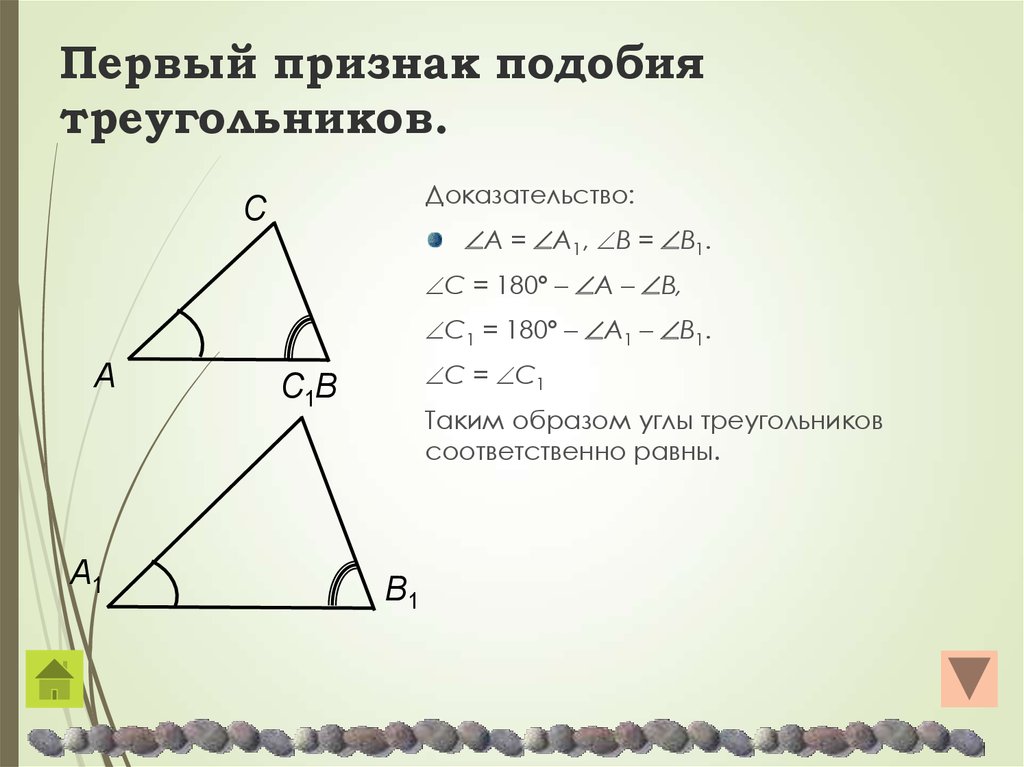 У равных треугольников и углы равны:

∠m = ∠a = ∠A и ∠n = ∠c = ∠C

следовательно, два треугольника ABC и abc подобны.

Теорема 97. В подобных треугольниках высоты пропорциональны сторонам.

Даны два подобных треугольника ABC и FED (черт. 158), следовательно,

∠A = ∠F, ∠B = ∠E, ∠C = ∠D и
AB/FE = BC/ED = AC/DF

и проведены высоты BH и Eh.

Требуется доказать, что AB/FE = BH/Eh.

Доказательство. Прямоугольные треугольники ABH и FEh подобны, ибо ∠A = ∠F по условию, ∠AHB = ∠FhE как прямые, следовательно,

AB/FE = BH/Eh (ЧТД).

Теорема 98. Прямая, разделяющая угол треугольника пополам, делит его противоположную сторону на части пропорциональные двум другим сторонам.

Дано. Отрезок BD делит угол B треугольника ABC пополам (черт. 159).

∠ABD = ∠DBC или ∠α = ∠β

Требуется доказать, что AB/BC = AD/DC.

Доказательство.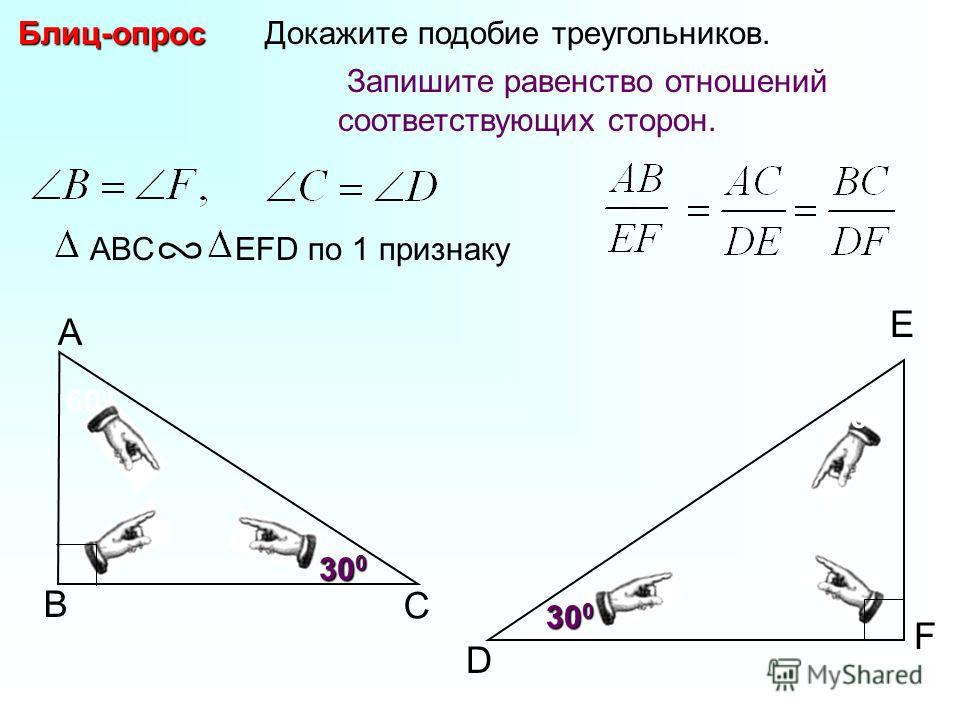 Проведем из точки A отрезок AF параллельный BD до пересечения его с прямой BC в точке F. В треугольнике FBA

∠AFB = ∠β как соответственные углы,
∠FAB = ∠α как внутренние накрест-лежащие углы от пересечения параллельных AF и BD третьей прямой AB.

Так как ∠α = ∠β по условию, то

∠AFB = ∠FAB, т. е. треугольник FAB равнобедренный, поэтому FB = AB.

Из того, что AF || BD вытекает пропорция:

FB/BC = AD/DC

Заменяя FB равным отрезком AB, получим пропорцию:

AB/BC = AD/DC (ЧТД).

Теорема 99 (обратная 98). Прямая, проведенная из вершины треугольника и делящая противоположную сторону на части, пропорциональные двум другим сторонам, делит угол при вершине пополам.

Дано. В треугольнике ABC (черт. 159) прямая BD рассекает противоположную сторону так, что имеет место пропорция:

AB/BC = AD/DC (a)

Требуется доказать, что ∠α = ∠β.

Доказательство. Проведем отрезок AF параллельно BD, тогда из треугольника AFC вытекает пропорция:

FB/BC = AD/DC (b)

Сравнивая две пропорции (a) и (b), заключаем, что FB = AB, следовательно,

∠AFB = ∠FAB.

Так как ∠α = ∠FAB, ∠β = ∠AFB, то и

∠α = ∠β (ЧТД).

Отношения в прямоугольном треугольнике

Теорема 100. Перпендикуляр, опущенный из вершины прямого угла на гипотенузу, среднепропорционален между частями гипотенузы.

Дано. В треугольнике ABC угол ABC прямой (черт. 160) и BD ⊥ AC.

Требуется доказать, что AD/BD = BD/DC.

Доказательство. Треугольники ABD и BDC подобны, ибо углы при точке D равны как прямые; кроме того из равенств ∠A + ∠α = d, ∠α +∠β = d вытекает

A + α = α + β, или A = β, следовательно и C = α.

Из подобия треугольников ABD и BDC вытекает пропорция

AD/BD = BD/DC (ЧТД).

Примечание. Если составляют одно отношение из сторон одного треугольника, то другое отношение составляется из соответственных сторон другого треугольника. При этом рассуждают следующим образом: против стороны AD лежит угол α, которому в подобном треугольнике BCD равен угол C, а против него лежит сходственная сторона BD треугольника BCD и т. д.

Теорема 101. Каждый катет среднепропорционален между целой гипотенузой и отрезком, прилежащим катету.

Доказательство. a) Треугольники ABC и ABD (черт. 160) подобны, ибо ∠ABC = ∠ADB как прямые, ∠A общий, следовательно,

∠C = ∠α

Из подобия треугольников вытекает пропорция:

AD/AB = AB/AC (a)

b) Треугольники ABC и BCD подобны, ибо ∠ABC = ∠BDC как прямые, ∠C общий, следовательно,

∠A = ∠β, откуда
DC/BC = BC/AC (b)

Теорема 102. Квадрат гипотенузы равен сумме квадратов катетов.

Из предыдущих пропорций (a) и (b) вытекают равенства:

AB² = AD · AC
BC² = DC · AC

Складывая их, получим:

AB² + BC² = AD · AC + DC · AC или
AB² + BC² = AC (AD + DC) = AC · AC = AC², т. е.
AC² = AB² + BC²

откуда

a) Гипотенуза равна корню квадратному из суммы квадратов катетов.

b) Катет равен корню квадратному из квадрата гипотенузы без квадрата другого катета.

Теорема 103. Диагональ квадрата несоизмерима с его стороной, или гипотенуза равнобедренного прямоугольного треугольника несоизмерима с катетом.

Дано. В квадрате ABCD проведена диагональ AC (черт. 161).

Требуется доказать, что отношение AC/AD есть величина несоизмеримая.

Доказательство. Станем сравнивать больший отрезок AC с меньшим BC по обыкновенным приемам нахождения общей меры, т. е. наложим меньший отрезок на больший, первый остаток на меньший и т. д.

a) Наложим отрезок BC на отрезок AC. Отложив отрезок AE, равный AB или BC, мы видим, что отрезок BC уложился один раз, ибо

AB + BC > AC.

Так как AB = BC, то 2BC > AC и BC > ½AC, следовательно, первый остаток EC < BC.

b) Наложим первый остаток EC на отрезок BC. Для этого из точки E восставим перпендикуляр EF и соединим точку F с A.

c) Треугольник FEC равнобедренный, ибо ∠EFC = ∠BAC как углы с перпендикулярными сторонами

∠BAC = ∠ECF, следовательно,
∠EFC = ∠ECF

На этом основании стороны EF и EC равны:

EF = EC (1)

Треугольники ABF и AEF равны, ибо они прямоугольны и у них

AF сторона общая
AB = AE по построению, следовательно,
BF = EF (2)

Таким образом из равенств (1) и (2) выходит, что

EC = EF = BF

Не трудно видеть, что первый остаток укладывается в отрезке BC не более двух раз.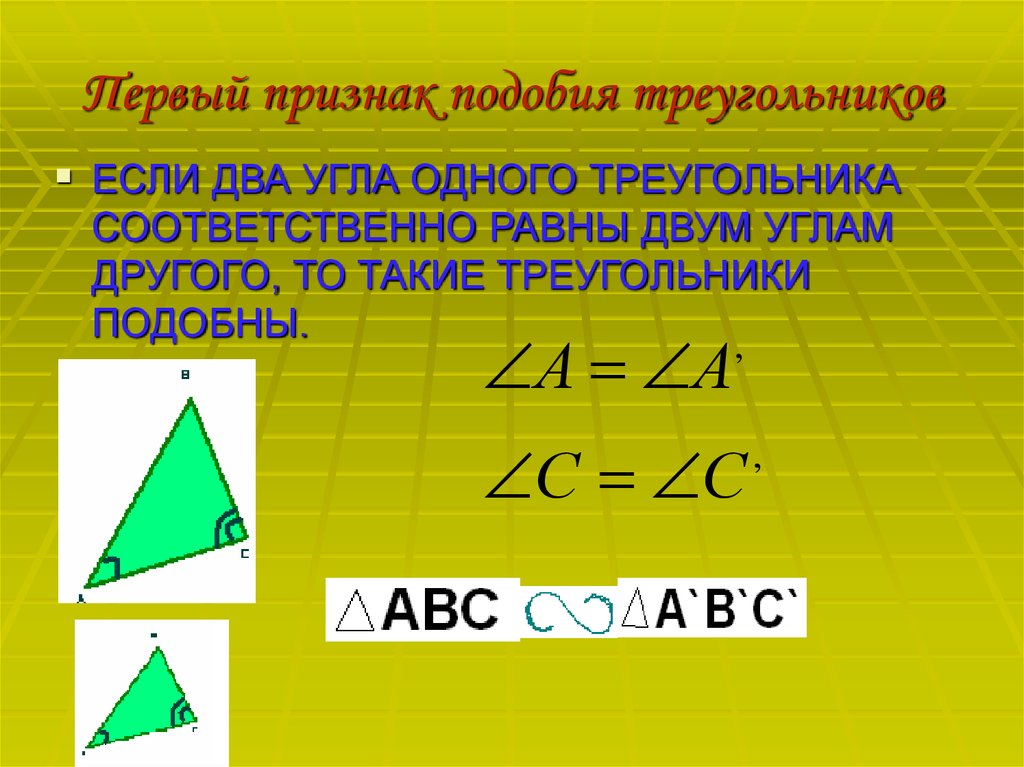 Отложив EC два раза на отрезке BC, найдем точку G и второй остаток GC. Таким образом, остаток после наложения сторон квадрата на диагональ укладывается в стороне квадрата не более двух раз.

d) Наложим второй остаток GC на первый EC.

В прямоугольном и равнобедренном треугольнике FEC соотношение между отрезками GC, FC и EC то же самое как и соотношение между данными отрезками EC, AC и BC в треугольнике ABC, ибо треугольник FEC прямоугольный и равнобедренный, следовательно, при дальнейшем наложении мы будем снова получать остаток. Продолжая так поступать, мы всегда будем получать остатки, поэтому общей меры мы никогда не получим, следовательно, отрезки AC и BC несоизмеримы.

Обозначив длину диагонали черед l, длину стороны квадрата через a, последовательные величины остатков через d₁, d₂ и т. д., т. е. положив

AC = l, BC = a, CE = d₁, GC = d₂ и т. д.

имеем равенства:

l = a + d₁, a = 2d₁ + d₂, d₁ = 2d₂ + d₃ и т.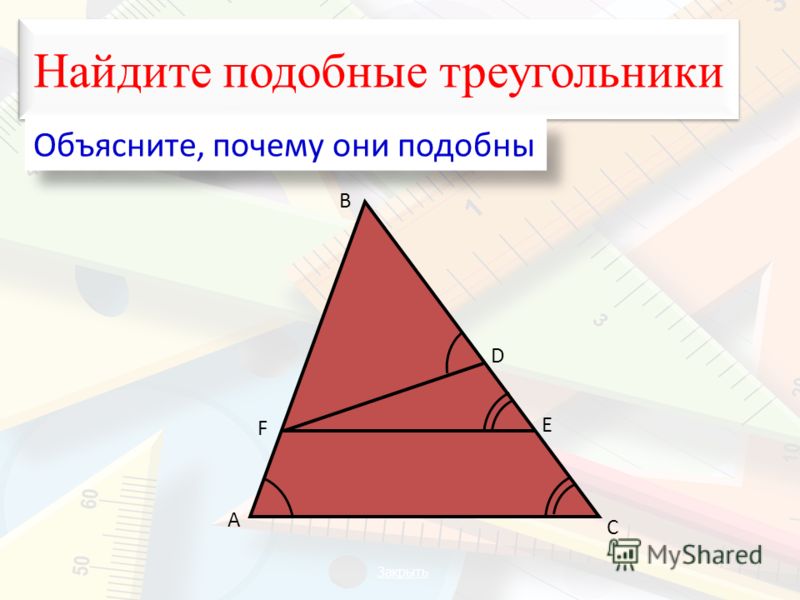 д.

откуда

l/a = 1 + d₁/a
a/d₁ = 2 + d₂/d₁ или d₁/a = ½ + d₂/d₁
d₁/d₂ = 2 + d₃/d₂ или d₂/d₁ = ½ + d₃/d₂

следовательно,

l/a = 1 + ½ + ½ + …

Отношение между длинами l и a выражается бесконечной непрерывной дробью. Несоизмеримость впрочем прямо вытекает из выражения диагонали квадрата по катетам.

Действительно,

AC² = AB² + BC².

Так как AB = BC, то AC² = 2AB², откуда AC = AB√2 и AC/AB = √2 величина несоизмеримая.

Соотношение между сторонами остроугольного и тупоугольного треугольника

Теорема 104. Квадрат стороны, лежащей против острого угла, равен сумме квадратов прочих двух сторон треугольника без удвоенного произведения основания на отрезок, заключающийся между вершиной острого угла и высотой.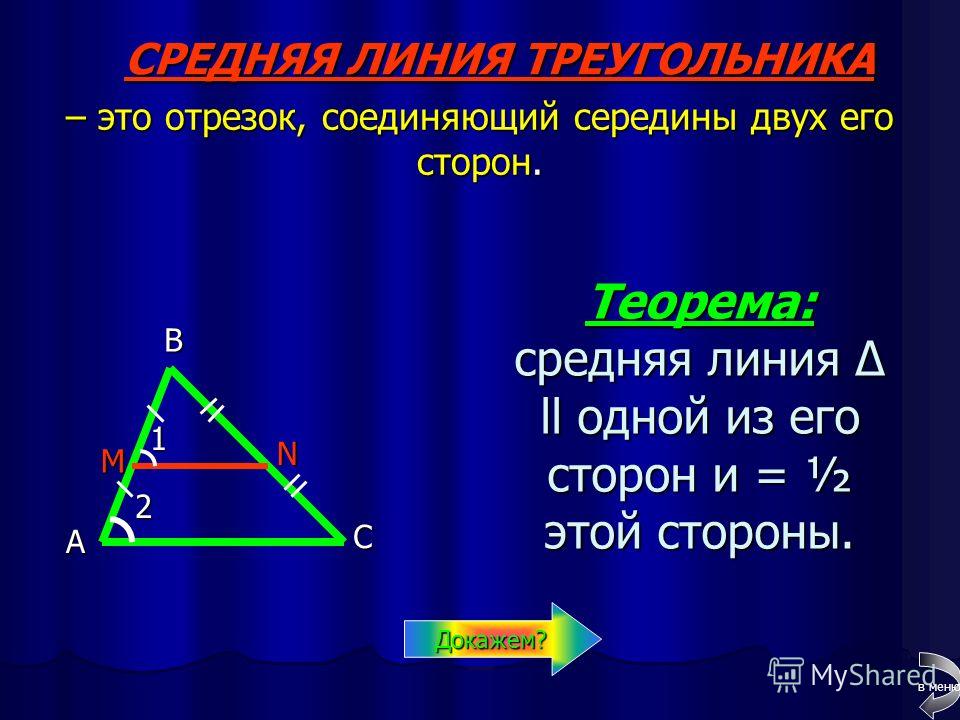

Здесь могут быть два случая: 1) когда перпендикуляр, выражающий высоту, пойдет внутри и 2) когда он пойдет вне треугольника.

Первый случай. Перпендикуляр BD (черт. 162), опущенный из вершины B на основание AC треугольника ABC, пойдет внутри треугольника.

Требуется доказать, что AB² = BC² + AC² — 2AC · DC.

Доказательство. Для прямоугольного треугольника ABD имеем равенство:

AB² = BD² + AD² (a)
AD = AC — DC, AD² = (AC — DC)² = AC² + DC² — 2AC · DC

Из прямоугольного треугольника BDC имеем:

BD² = BC² — DC²

Вставляя величины BD² и AD² в равенство (a), получим:

AB² = BC² — DC² + AC² + DC² — 2AC · DC, откуда
AB² = BC² + AC² — 2AC · DC (ЧТД).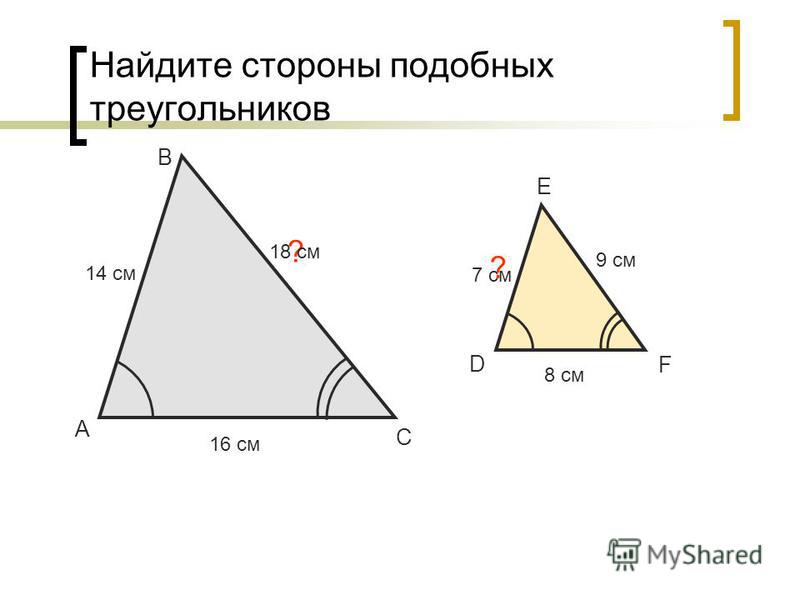

2-й случай. Перпендикуляр BD (черт. 163) лежит вне треугольника ABC.

Доказательство. Из прямоугольного треугольника ABD имеем:

AB² = BD² + DA²

Из прямоугольного треугольника BCD имеем:

BD² = BC² — CD²

следовательно,

AB² = BC² — CD² + DA².

Так как

DA = CD — AC
DA² = (CD — AC)² = CD² + AC² — 2CD · AC, то
AB² = BC² — CD² + CD² + AC² — 2CD · AC, откуда
AB² = BC² + AC² — 2CD · AC (ЧТД).

Теорема 105. Квадрат стороны, лежащей против тупого угла, равен сумме квадратов прочих двух сторон треугольника с удвоенным произведением основания на отрезок его от вершины тупого угла до высоты.

Дано.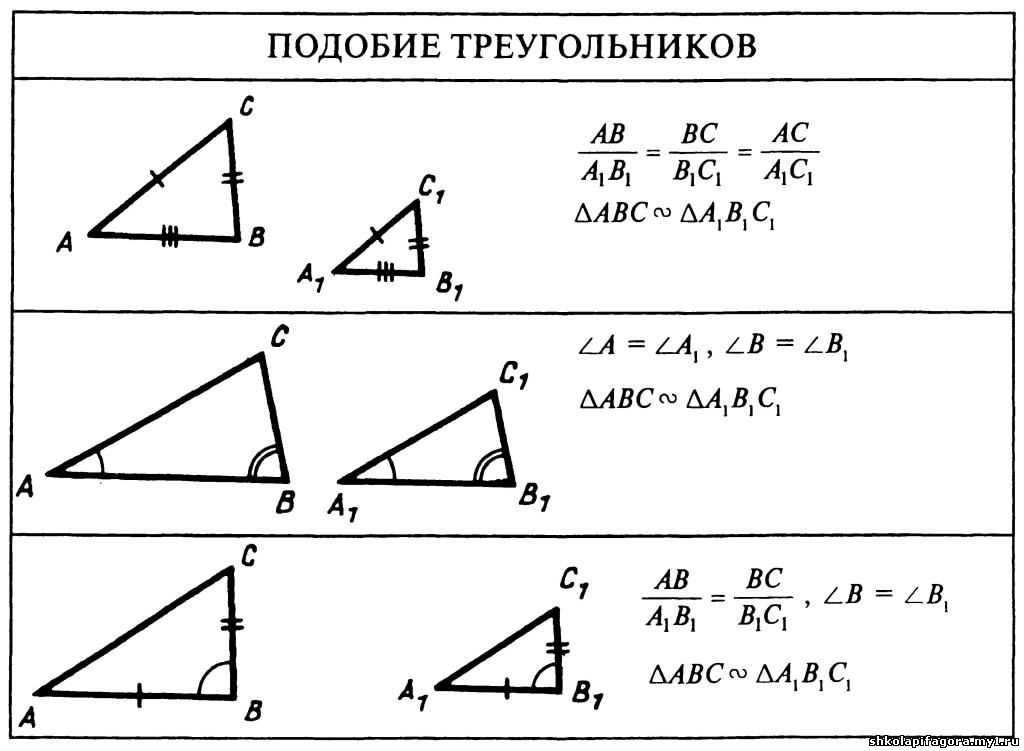 В тупоугольном треугольнике ABC отрезок CD (черт. 164) есть отрезок, лежащий между вершиной тупого угла и высотой.

Требуется доказать, что

AB² = AC² + BC² + 2AC · CD

Доказательство. Из тупоугольного треугольника ABC имеем:

AB² = BD² + AD² (a)
AD = AC + CD, AD² = AC² + CD² + 2AC · CD

Из прямоугольного треугольника BCD вытекает, что

BD² = BC² — CD²

Заменяя AD² и BD² в равенстве (a), получим:

AB² = BC² — CD² + AC² + CD² + 2AC · CD

откуда

AB² = BC² + AC² + 2AC · CD (ЧТД).

Теорема 106. Сумма квадратов диагоналей равна сумме квадратов всех четырех сторон параллелограмма.

Дан параллелограмм ABCD (черт.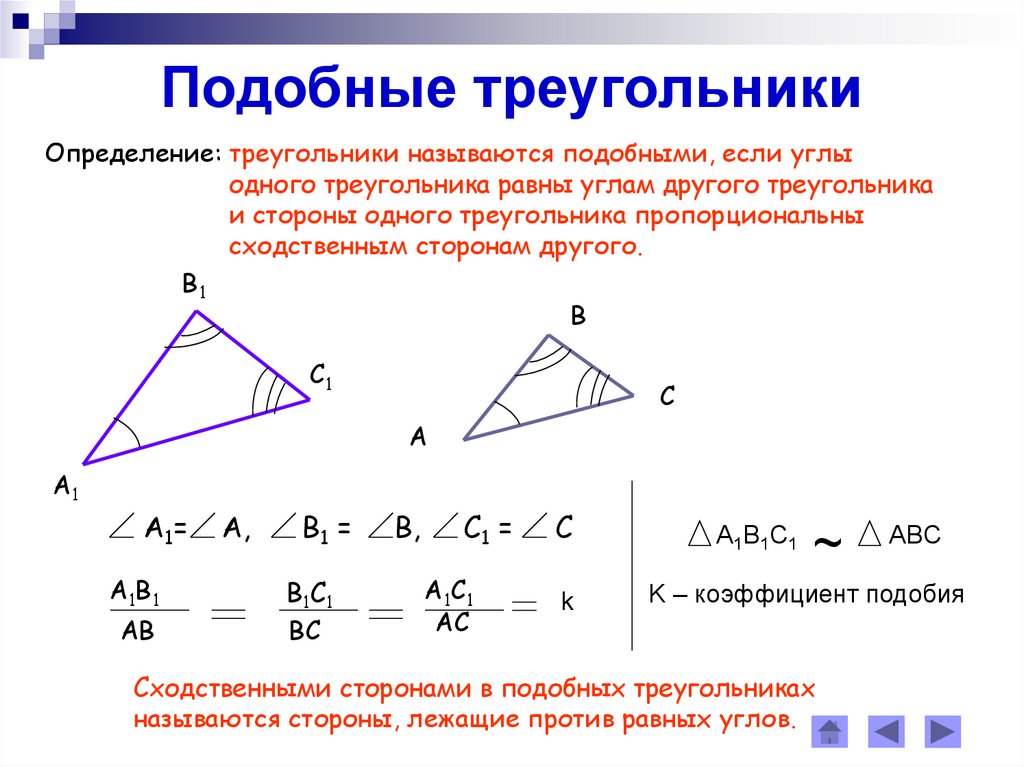 165) и проведены его диагонали AC и BD.

Требуется доказать, что

AC² + BD² = AB² + BC² + CD² + AD²

Доказательство. Опустив перпендикуляры BE и CF, имеем из косоугольного треугольника ABD равенство:

BD² = AB² + AD² — 2AD · AE (1)

Из тупоугольного треугольника ACD равенство:

AC² = CD² + AD² + 2AD · DF (2)

Отрезки AE и DF равны, ибо прямоугольные треугольники ABE и DCF равны, так как они имеют по равному катету и равной гипотенузе.

Сложив равенства (1) и (2), имеем:

BD² + AC² = AB² + AD² + CD² + AD²

Так как AD = BC, то

BD² + AC² = AB² + BC² + CD² + AD² (ЧТД).

Теорема 107.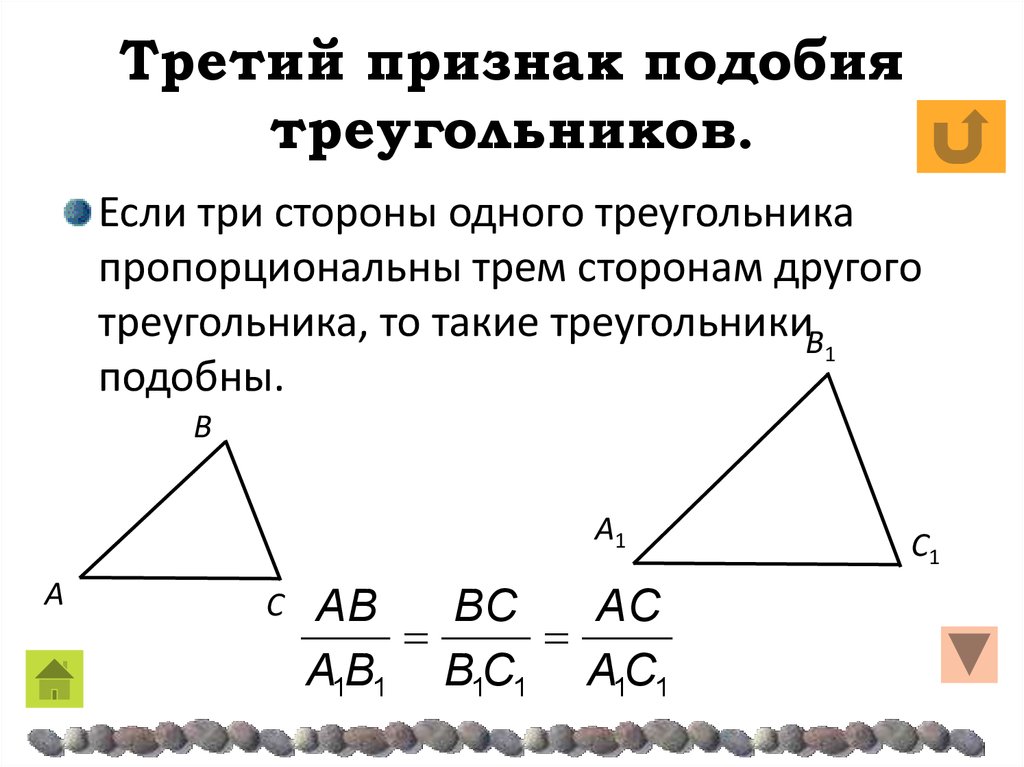 Сумма квадратов двух сторон треугольника равна сумме удвоенного квадрата отрезка, соединяющей вершину с серединой основания, с удвоенным квадратом половины основания.

Дано. Соединим вершину B с серединой основания D треугольника ABC так, что AD = DC (черт. 166).

Требуется доказать, что

AB² + BC² = 2AD² + 2BD²

Доказательство. Проведем высоту BE.

Из прямоугольных треугольников ABE и BCE вытекают равенства:

AB² = BE² + AE²
BC² = BE² + CE²

Сложив их, находим:

AB² + BC² = 2BE² + AE² + CE² (a)

Так как AE = AD + DE = CD + DE, CE = CD — DE, то

AE² = (CD + DE)² = CD² + DE² + 2CD · DE
CE² = (CD — DE)² = CD² + DE² — 2CD · DE

откуда

AE² + CE² = 2CD² + 2DE² (b)

Заменяя в равенстве (a) сумму AE² + CE² из равенства (b), имеем:

AB² + BC² = 2BE² + 2CD² + 2DE².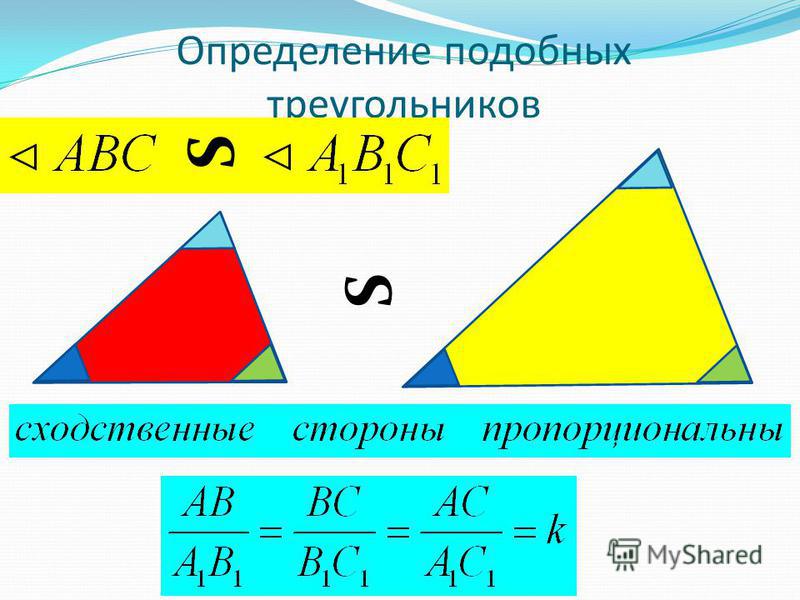

Из прямоугольного треугольника BDE видно, что

BE² = BD² — DE²

следовательно

AB² + BC² = 2BD² — 2DE² + 2CD² + 2DE²

откуда

AB² + BC² = 2BD² + 2CD² (ЧТД).

 

Третий признак подобия треугольников 8 класс онлайн-подготовка на Ростелеком Лицей

Подобные треугольники

 

Треугольники называются подобными, если углы соответственно равны, а сходственные стороны пропорциональны.

 

Имеем два треугольника ,  (см. Рис. 1).

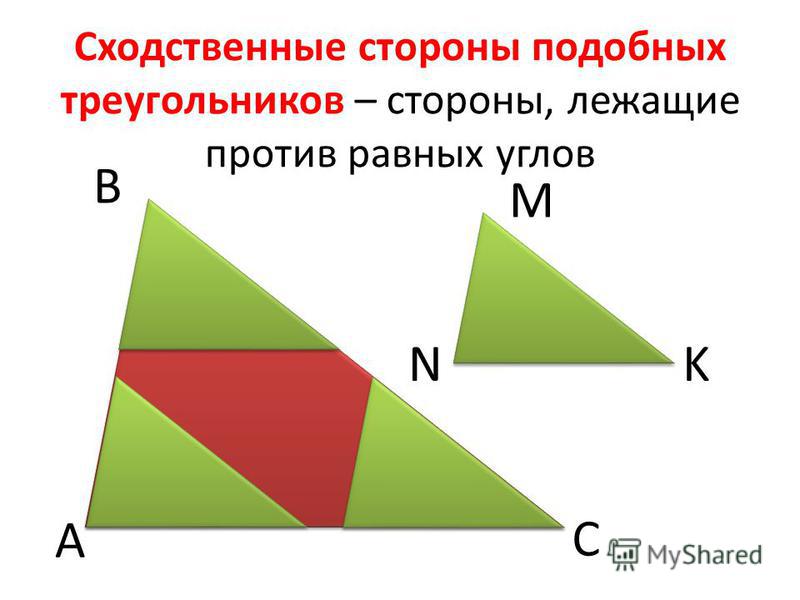
Сходственные стороны – те стороны, которые лежат против равных углов.

Рис. 1. Подобные треугольники

Определение:

:

Проверять все равенства не нужно, существуют признаки подобия.

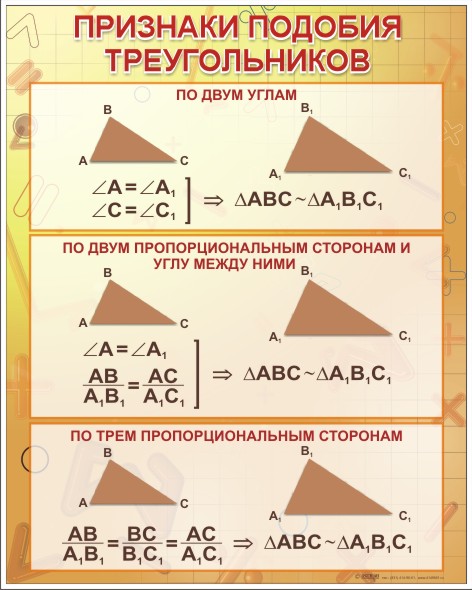
Первый признак подобия

Если хотя бы по два соответствующих угла треугольников равны, то эти треугольники подобны.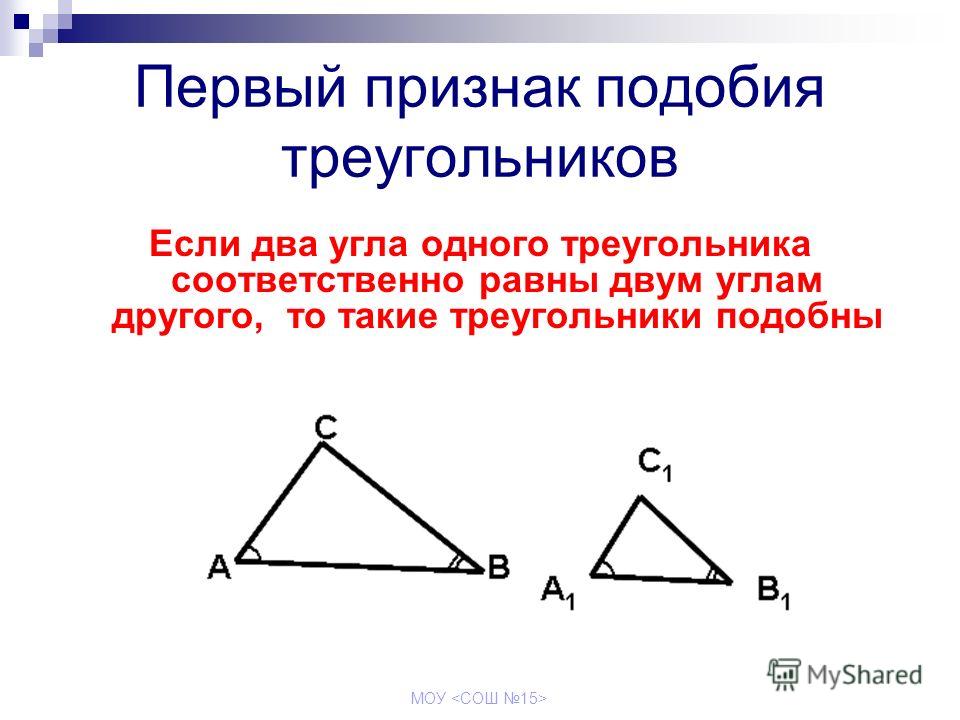

Второй признак подобия

По углу и пропорциональности прилежащих сторон.

 

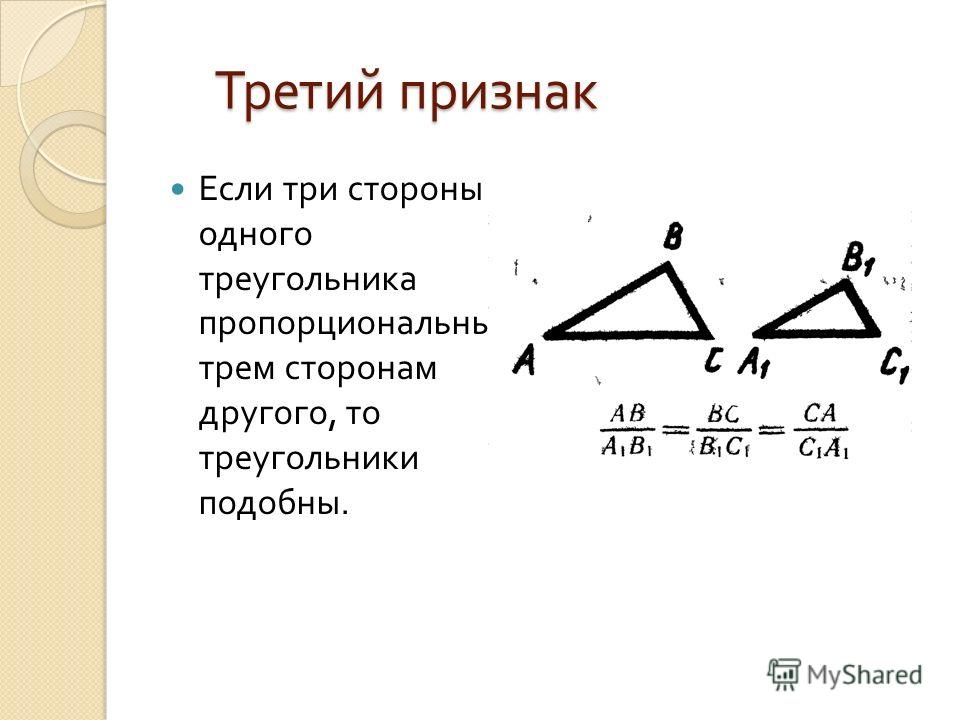
Третий признак подобия треугольников

 

 

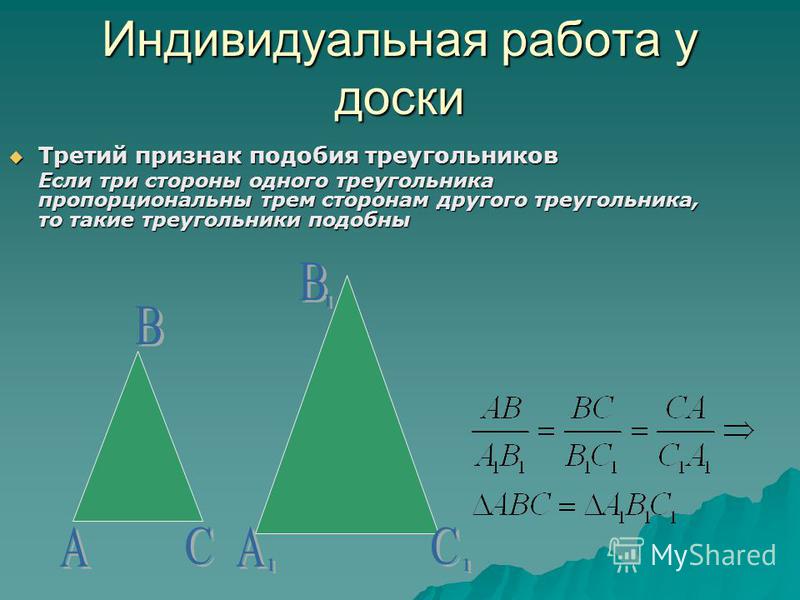
Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.

 

Дано:

Доказать:

Доказательство

Чтобы доказать третий признак, мы можем использовать второй признак, так как там есть пропорциональность сторон и нам останется доказать равенство угла, например, что . То есть мы докажем, что эти углы равны, сошлемся на второй признак, и третий признак будет доказан.

Вспомогательное построение: (см. Рис. 2).

Построим треугольник : – по первому признаку подобия.

Рис. 2. Доказательство третьего признака

Раз эти треугольники подобны, то можно выписать пропорциональность их сторон, сравнить с данной пропорциональностью и получить важные выводы.

Сравним с пропорциональностью сторон исходных треугольников.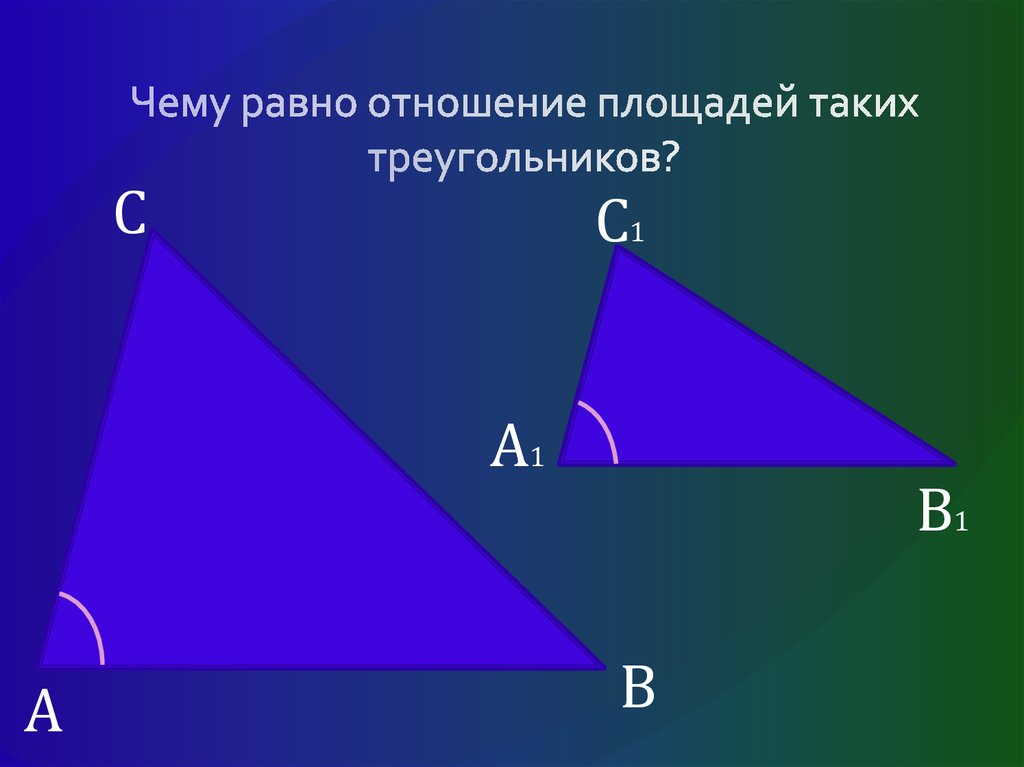

Значит,  и .

Из сравнения двух равенств следует, что треугольник  равен треугольнику  по трем сторонам.

Из равенства треугольников вытекает:

Итак, в двух исходных треугольниках имеем равные углы  и  и прилежащие стороны пропорциональны, значит, эти треугольники подобны по второму признаку подобия треугольников.

Что и требовалось доказать.

Специфика третьего признака подобия треугольников заключается в том, что в нем не фигурируют углы. Есть пропорциональность сходственных сторон. А как найти равные углы?

Перейдем к задачам.

 

Задача 1

 

 

По данным рисунка определите подобие треугольников, отметьте равные углы (см. Рис. 3).

 

Рис. 3. Условие задачи 1

Решение

Заметим пропорциональность сторон

 – по третьему признаку

Отметим равные углы (см. Рис. 4).

Рис. 4. Подобные углы треугольников

Ответ:  и  подобны.

 

Задача 2

 

 

По данным рисунка определить подобие треугольников (см.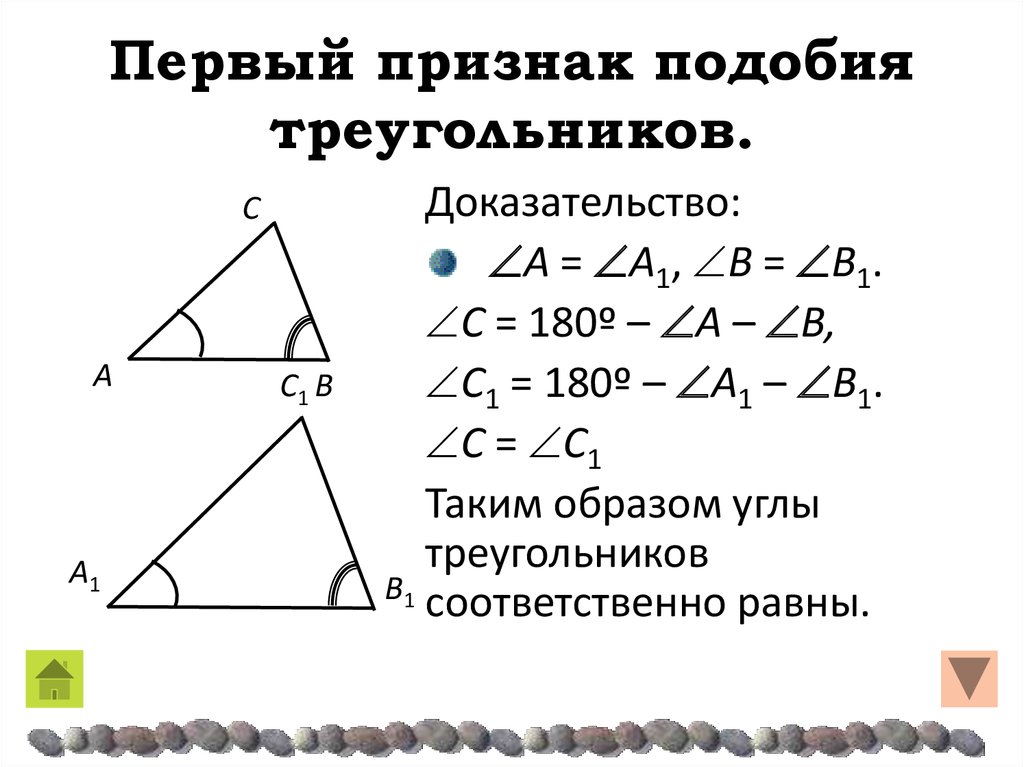 Рис. 5).

 

Решение

Рис. 5. Иллюстрация к задаче 2

Эти треугольники существуют, т. к. их самые большие стороны меньше, чем сумма двух других сторон:

Пропорциональности сторон не наблюдаем.

.

Ответ:  и  не подобны.

 

Задача 3

 

 

Стороны  равны 1; 3; 5. Стороны  равны 2; 6; 10. Определить подобие треугольников.

 

Решение

 – эти пары отрезков пропорциональны.

Однако треугольники с такими сторонами не существуют.

Ответ:  и  не существуют.

 

Задача 4

 

 

Дано: , ,  (см. Рис. 6).

 

Найти: ; .

Решение

Рис. 6. Иллюстрация к задаче 4

1.                   – по третьему признаку

Стороны одного треугольника выражены через стороны другого треугольника.

Отсюда важное свойство периметров подобных треугольников – их отношение равно коэффициенту подобия.

2.          Чтобы найти площадь, нужно найти высоту, поэтому проведем  – высоту в первом треугольнике: (см. Рис. 7).

Также проведем высоту во втором треугольнике:

Рис.7. Иллюстрация к задаче 4

Тогда имеем прямоугольные треугольники, которые подобны по первому признаку:

Найдем коэффициент их подобия :

Теперь мы готовы сравнить площади:

Итак, отношение площадей подобных треугольников равно квадрату коэффициенту их подобия.

Ответ: 1. ; 2. .

 

Задача 5

 

 

Дано: ; ; ; ; ; .

 

По данным рисунка 8 докажите, что .

Рис. 8. Условие задачи 5

Доказательство

Есть два треугольника с известными сторонами:  и .

Проверим пропорциональность или непропорциональность этих сторон.

Для подобия нужно, чтобы выполнялось равенство: .

 (по третьему признаку)

Мы видим, что сторона  лежит против угла , сторона  лежит против угла , значит, угол  равен углу , а значит, .

Что и требовалось доказать.

 

Заключение

 

 

Итак, мы доказали третий признак подобия треугольников, обсудили его, решили типовые задачи.

 

 

Список литературы

1. Геометрия, 7–9 классы, Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Позняк Э.Г., Юдина И.И. – 15-е изд. – М.: Просвещение, 2005.

2. Александров А.Д. и др. Геометрия, 8 класс. – М.: Просвещение, 2006.

3. Бутузов В.Ф., Кадомцев С.Б., Прасолов В.В. Геометрия, 8 класс. – М.: Просвещение, 2011.

4. Мерзляк А.Г., Полонский В.Б., Якир С.М. Геометрия, 8 класс. – М.: ВЕНТАНА-ГРАФ, 2009.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Интернет портал «Я Класс» (Источник)

2. Интернет портал «Уроки математики» (Источник)

3. Интернет портал «Учебно – методический кабинет» (Источник)

 

Домашнее задание

1. Дано:  – биссектриса угла ,  и .

а. По какому признаку подобны данные треугольники ?

б. Вычислите , если , , .

2. Определите, подобны ли треугольники со сторонами: 15, 12, 13 и 26, 24, 30.

3. На рисунке найдите подобные треугольники и докажите их подобие.

 

Подобие треугольников в курсе геометрии 8 класса.

Цели изучения:

· сформировать понятие подобных треугольников;

· изучить признаки подобия треугольников;

· рассмотреть применение подобия к доказательству теорем и решению задач.

Содержание учебного материала по учебнику Л.С. Атанасяна

«Геометрия. 7 — 9 классы».

Определение. Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого.

При этом если у треугольников АВС и А₁В₁С₁ углы соответственно равны: ÐА = ÐА₁, ÐВ = ÐВ₁, ÐС = ÐС₁, то стороны АВ и А₁В₁, ВС и В₁С₁, АС и А₁С₁ называют сходственными.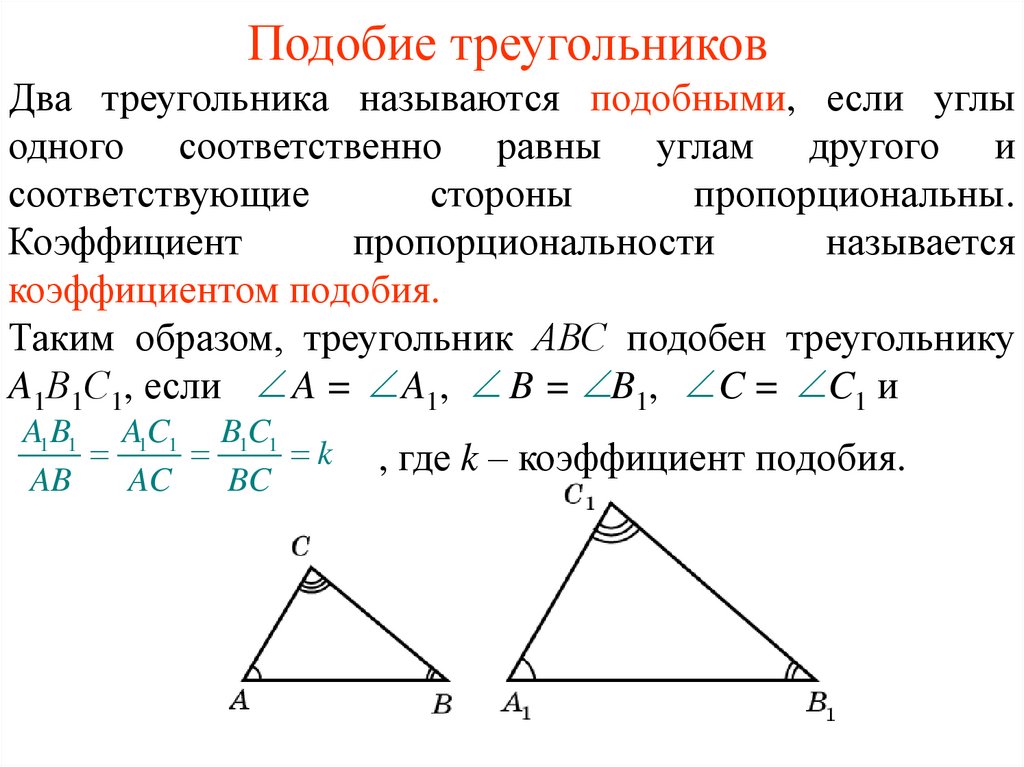

Другими словами, два треугольника подобны, если для них можно ввести обозначения АВС и А

1В₁С₁ так, что ÐА = ÐА₁, ÐВ = ÐВ₁, ÐС = ÐС₁ (1),

. Число k, равное отношению сходственных сторон, называется коэффициентом подобия.

Вводится обозначение DАВС ~ D А₁В₁С₁.

Далее изучаются признаки подобия треугольников.

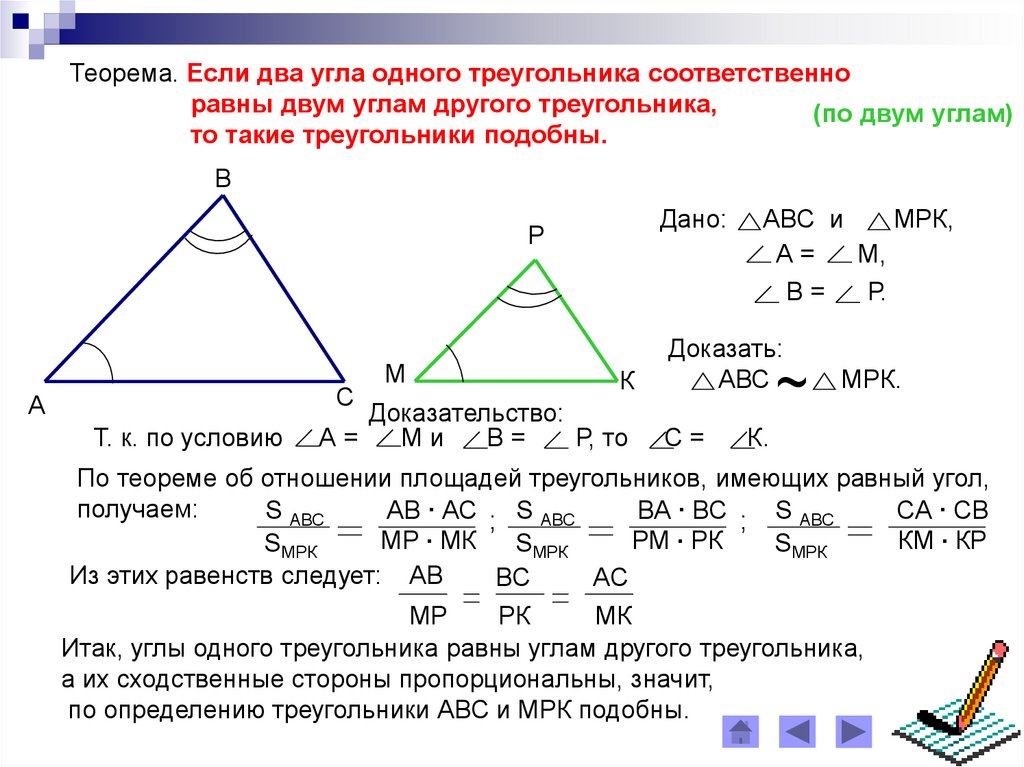
Первый признак подобия треугольников: если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.

Доказательство первого признака основывается на теореме, доказанной ранее: если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы (с. 126).

 

Дано: АВС и А₁В₁С₁

ÐА = ÐА₁, ÐВ = ÐВ

1

Доказать:

DАВС ~ D А₁В₁С₁

 

 

Доказательство.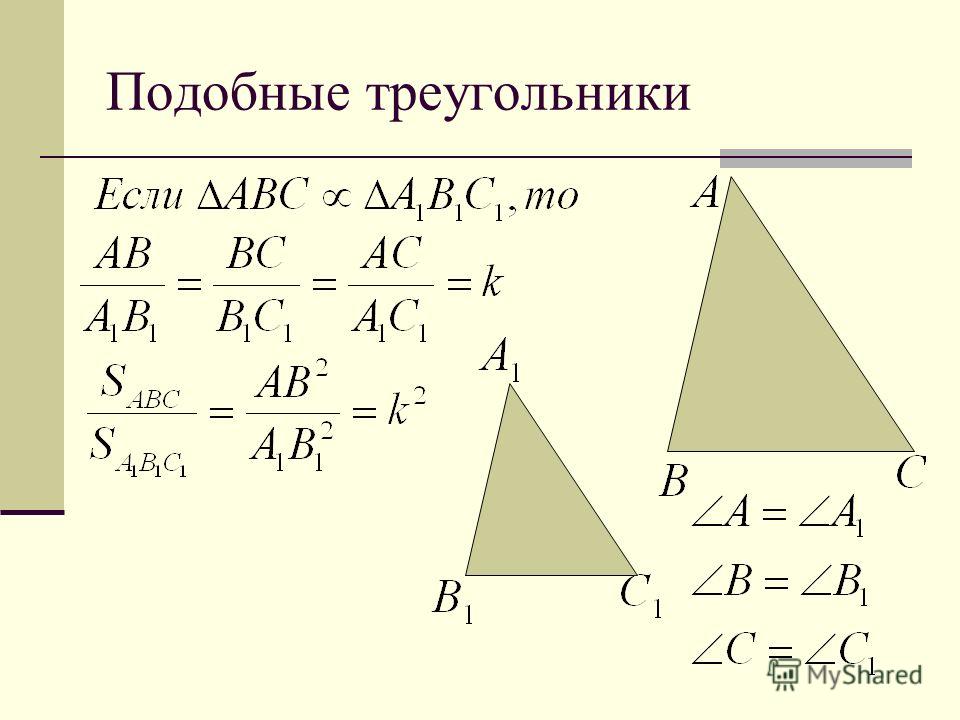

1. ÐС=180°-ÐА-ÐВ.

ÐС₁=180°-ÐА₁-ÐВ₁.

ÐС = ÐС₁, следовательно, углы треугольника АВС равны соответственно углам треугольника А₁В₁С₁.

2. Так как ÐА = ÐА₁, ÐС = ÐС₁, то и .

Из этих равенств следует, что . Аналогично, используя равенства

ÐА = ÐА₁ и ÐВ = ÐВ₁, получаем . Пропорциональность сходственных сторон треугольников доказана. Итак, DАВС ~ D А₁В₁С₁.

Второй признак подобия треугольников:если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключённые между этими сторонами равны, то такие треугольники подобны.

Дано: АВС и А₁В₁С₁

ÐА = ÐА₁, .

Доказать:

DАВС ~ D А₁В₁С₁

 

Доказательство

Доказательство второго признака сводится к первому признаку: достаточно доказать, что ÐВ = ÐВ₁.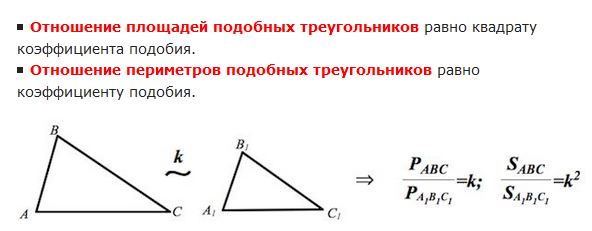

1. Рассмотрим треугольник АВС₂: Ð1 = ÐА₁, Ð2 = ÐВ₁.

 

DАВС₂ ~ DА₁В₁С₁ (по двум углам), поэтому . По условию , следовательно, АС=АС₂.

2. DАВС = DАВС₂ (по двум сторонам и углу между ними). Следовательно,

Ð2 =ÐВ и Ð2 =ÐВ₁: ÐВ = ÐВ_1. Тогда DАВС ~ D А

1В₁С₁ (по двум углам).

Третий признак подобия треугольников: если три стороны одного треугольника пропорциональны трём сторонам другого треугольника, то такие треугольники подобны.

Доказательство третьего признака сводится ко второму признаку и аналогично ему. Рассмотреть самостоятельно (с. 144).

В учебнике рассматриваются практические приложения подобия треугольников: при решении задач на построение методом подобия и при проведении различных измерительных работ на местности (определение высоты предмета и расстояния до недоступной точки).

Содержание учебного материала по учебнику А.В. Погорелова

«Геометрия. 7 — 11 классы».

Определение. Две фигуры называются подобными, если они переводятся друг в друга преобразованием подобия. Обозначение F~F¢.

Таким образом, два треугольника называются подобными, если они переводятся друг в друга преобразованием подобия.

Напомним, что преобразование фигуры F в фигуру F¢ называется преобразованием подобия, если при этом преобразовании расстояния между точками изменяются в одно и то же число раз. Это значит, что если произвольные точки X, Y фигуры F при преобразовании подобия переходят в точки Х¢, Y¢ фигуры F¢, то Х¢ Y¢ =k×X Y. Причём число k — одно и то же для всех точек X, Y. Число k называется коэффициентом подобия.

Рассматриваются свойства преобразования подобия, в частности, оно сохраняет углы между полупрямыми.

Рассматривается преобразование гомотетия, которое задаётся центром и коэффициентом гомотетии – положительным числом k.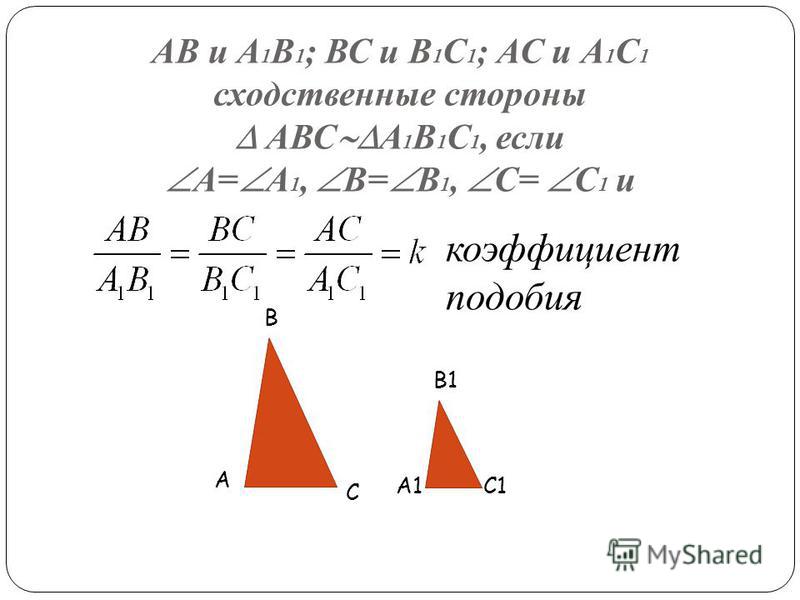

Построим точку Х¢, гомотетичную точке Х. Для этого проведем луч Ох и на нём отложим отрезок ОХ¢=2ОХ. Аналогично строится точка Y¢, гомотетичная точке Y.

Преобразование фигуры F, при котором каждая её точка Х переходит в точку Х¢, построенную указанным способом называется гомотетией относительно центра О. Фигуры F и F¢ называют гомотетичными.

Доказывается, что гомотетия есть преобразование подобия.

Из свойств преобразования подобия следует, что у подобных треугольников DАВС и D А₁В₁С₁ ÐА = ÐА₁, ÐВ = ÐВ₁, ÐС = ÐС₁ и .

---

Дата добавления: 2016-06-15; просмотров: 3295; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

---

«Первый признак подобия треугольников». 8-й класс

Тема урока: «Первый признак подобия треугольников». 8-й класс

• Бузецкая Татьяна Валерьевна, учитель математики

org/BreadcrumbList»> Разделы: Математика, Конкурс «Презентация к уроку»

Класс: 8

---

Презентация к уроку

Загрузить презентацию (647 кБ)

---

Цель урока:

• закрепление знаний, умений и навыков учащихся по теме «Определение подобных треугольников, отношение их площадей» в процессе решения задач;
•  ознакомление учащихся с первым признаком подобия  треугольников;
• формирование у учащихся навыков применения этого признака  при решении задач.

Задачи урока:

• Познакомить с  первым признаком подобия треугольников
• Повторить определение подобных треугольников, коэффициента подобия, теорему об отношении площадей и периметров подобных треугольников
• Провести первичное закрепление на задачах по готовым чертежам
• Развивать внимание, логику, наблюдательность.

Оборудование: мультимедийный проектор,  компьютер, интерактивная доска, презентация PowerPoint, учебник «Геометрия 7-9», автор Атанасян Л.С.

Этап урока	Деятельность учителя	Деятельность ученика	Результат совместной деятельности	Слайд в презентации
1. Организаци-онный этап	Приветствие учащихся	Приветствие учителя
2. Введение в тему урока	Формулирует тему урока, организует постановку учащимися цели урока	Обсуждают, что значит полученное выражение.	Постановка целей урока.	Слайд 2
3. Актуализация знаний	1) Подобные фигуры это? 2) Два треугольника подобны… 3) Определение подобных треугольников? 4) Что такое сходственные стороны треугольников? 5) Сформулировать теорему об отношении площадей подобных треугольников?	Вспоминают понятие подобных фигур, понятие двух подобных треугольников, понятие сходственных сторон треугольников, коэффициент подобия, теорема об отношении площадей подобных треугольников,	Вывод о том, что ребята уже знакомы с определением подобных треугольников. Но можно рассмотреть теоремы (по аналогии с равенством треугольников), которые помогут быстрее доказать, что треугольники подобны	Слайды 3,4,5
4. Изучение теоретического материала	Знакомит учеников  с формулировкой  первого признака подобия треугольников и его доказательством.	Слушают, делают записи в тетради. Отвечают на вопросы учителя: можно ли переформулировать теорему с использованием слов «достаточно» или «необходимо». Если да, то сформулируйте?	Знакомство с теоремой и способом его доказательства.	Слайды 6, 7
5. Первичная проверка понимания и закрепление изученного материала	Организует работу с готовыми чертежами	Работают по готовым чертежам, находят пары подобных треугольников, находят неизвестные элементы треугольников	Умение находить на чертеже пары подобных треугольников и обосновывать свой ответ.	Слайды 9-12
6. Расширение и углубление знаний. Закрепление полученных знаний	Решение задачи на применение первого признака	Слушают, записывая в тетрадь, отвечая на вопросы учителя по ходу решения задачи: Что такое параллелограмм? Какие свойства вы знаете? Почему углы равны? Почему треугольники подобны? Что следует из подобия треугольников? Почему? Как найти неизвестный член пропорции? Что запишем в ответ?	Совместное решение задачи.	Слайд 13
8. Домашнее задание	Знакомит учащихся с домашним заданием, поясняет выполнение задания	Записывают задание в дневник		Слайд 14-16
9. Итог урока (рефлексия)	Предлагает проанализировать свои действия на уроке, оценить себя	Анализируют свои действия и выставляют себя оценки (в виде смайликов)	Оценка действий учеников	Слайд 17-19

Домашнее задание выдается каждому ученику

1) Решите предложенные задачи, по готовым чертежам
2) Выясните, какие из чисел, записаны на конвертах, являются решениями в задачах. Закрасьте эти конверты, а из букв, изображенных на них составте название страны, в контуре которой расположены эти конверты. Запишите название столицы данного государства. Закрасьте флаг этой страны, если известно, что число 14 находится в синей полосе, а число 75 в красной, а остальная часть белая.

Приложение

3. 05.2014

Подобные треугольники | Образовательная социальная сеть

Краевой конкурс научных  проектов школьников   в рамках  краевой  научно-практической   конференции «Эврика» Малой академии наук учащихся Кубани

ПОДОБНЫЕ ТРЕУГОЛЬНИКИ

Секция: «Математика, компьютерные технологии»

Михайленко Яна Юрьевна

Россия, Краснодарский край

Каневской  район, ст. Каневская

МБОУ СОШ №6, 10 класс

Научный руководитель:

Михайленко Любовь Александровна,

учитель математики и физики  

МБОУ  СОШ №6

                                                               ст.  Каневской

ст. Каневская 2012 год

---

Михайленко Яна Юрьевна

Россия, Краснодарский край, Каневской район,

 станица Каневская МБОУ СОШ №6,10  класс

 Подобные треугольники

Научный руководитель: Михайленко Любовь Александровна,

учитель математики и физики МБОУ  СОШ №6

Аннотация

Представленная работа посвящена подобию треугольников.

Актуальность настоящей работы обусловлена тем, что зная, признаки подобия можно научиться рационально  решать задачи, как по математике, так и по физике.

Цель исследования: выявить геометрические теоремы, свойства и показать их применение в решениях задач, связанных с треугольниками. 

В работе использован поисково-исследовательский метод, способствующий нахождению более простых решений предложенных заданий.

В работе показано:

— применение дополнительных построений: использование в решении задач «выносного» чертежа, то есть фрагмента, имеющегося достаточно сложного чертежа, вынесенного отдельно для специального изучения;

— необходимость выработки умений и навыков по решению практических задач, так как, столкнувшись с реальными подобными ситуациями, они будут нужны в жизни;

—  быстрота и красота решений.

И что еще немало важно – эти задачи связывают несколько дисциплин – алгебру, геометрию и физику и показывают насколько целостный и взаимосвязанный мир наук.

ОГЛАВЛЕНИЕ

  ВВЕДЕНИЕ ………………………………………….……..………..4 стр

1.Из истории подобия……………………………………………….5 стр

2.Подобные треугольники…………………………………………………..6 стр

3.Применение подобия при доказательстве теорем и задач……..7 стр

4.Применение подобия при решении задач по математике…….11 стр

5.Применение подобия при решении задач по физике………….14 стр

  ЗАКЛЮЧЕНИЕ……………………………………………………. 19 стр

  СПИСОК  ЛИТЕРАТУРЫ………………………………………..  20 стр

Михайленко Яна Юрьевна

Россия, Краснодарский край, Каневской район,

 станица Каневская МБОУ СОШ №6,10  класс

 Подобные треугольники

Научный руководитель: Михайленко Любовь Александровна,

учитель математики и физики МБОУ  СОШ №6

ВВЕДЕНИЕ

Геометрия – это не просто наука о свойствах треугольников, параллелограммов, окружностей. Геометрия – это целый мир, который окружает нас с самого рождения. Ведь все, что мы видим вокруг, так или иначе относится к геометрии, ничто не ускользает от ее внимательного взгляда.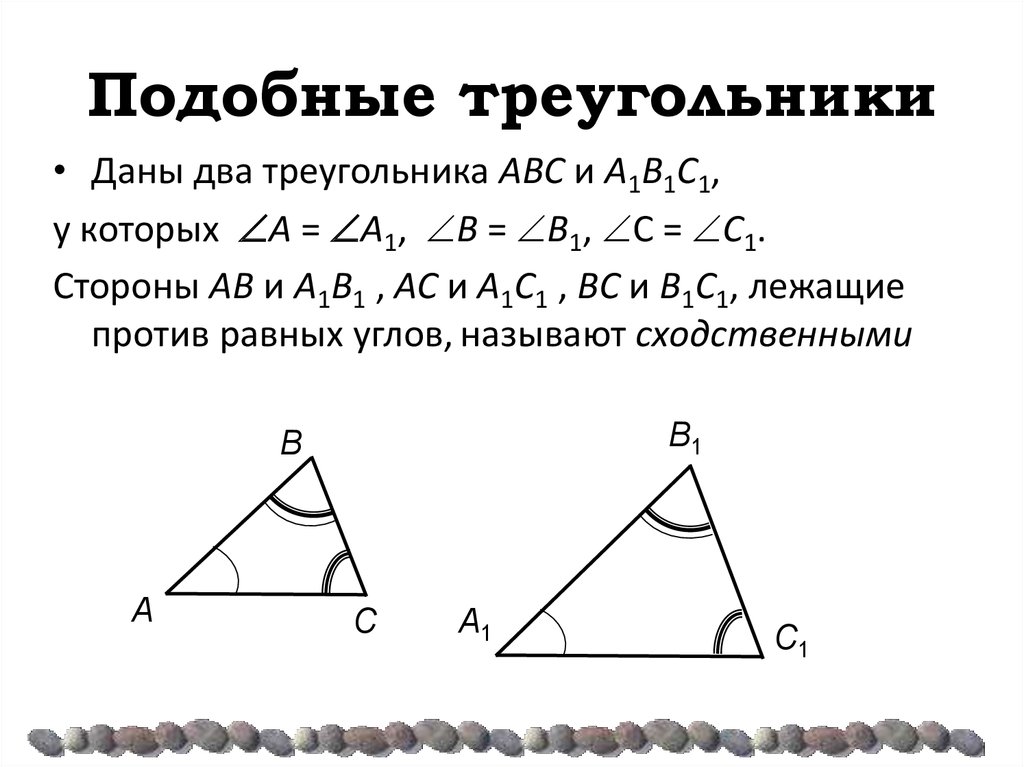 Геометрия помогает человеку идти по миру с широко открытыми глазами, учит внимательно смотреть вокруг и видеть красоту обычных вещей, смотреть и думать, думать и делать выводы.

Треугольник – самая простая геометрическая фигура, знакомая нам с детства. К треугольнику на уроках геометрии мы обращаемся чаще всего. Эта фигура таит в себе немало интересного и загадочного, как Бермудский треугольник, в котором бесследно исчезают корабли и самолеты. Один мудрец сказал: “Высшее проявление духа – это разум. Высшее проявление ума – это геометрия. Клетка геометрии – это треугольник. Он так же неисчерпаем, как и Вселенная”. 

Изучая геометрию, я поняла, что тема «Подобные треугольники» является одной из самых актуальных, обширных и распространенных в математике. Много теорем, следствий рассматривает этот раздел. Умение решать задачи на применение признаков подобия широко используется в геометрии, физике, астрономии.

Поэтому цель моей работы – выявить теоремы и показать их применение и рациональное использование в решении задач.

1. Из истории подобия

Идея отношения и пропорции зародилась в глубокой древности. Одинаковые по форме, но различные по величине фигуры встречаются в вавилонских и египетских памятниках. В сохранившейся погребальной камере отца фараона Рамсеса II имеется стена, покрытая сетью квадратиков, с помощью которой на стену перенесены в увеличенном виде рисунки меньших размеров. Особенности архитектуры, требования удобства, эстетики, техники и экономичности при возведении зданий и сооружений, вызвали возникновение и развитие понятий отношения и пропорциональности отрезков, площадей и других величин. До наших дней сохранилась клинописная табличка, в которой речь идет о построении пропорциональных отрезков путем проведения в прямоугольном треугольнике параллелей к одному из катетов.

Учение о подобии фигур на основе теории отношений и пропорции было создано в Древней Греции в V—IV вв. до н. э. трудами Гиппократа Хиосского, Архита Тарентского, Евдокса Книдского и др.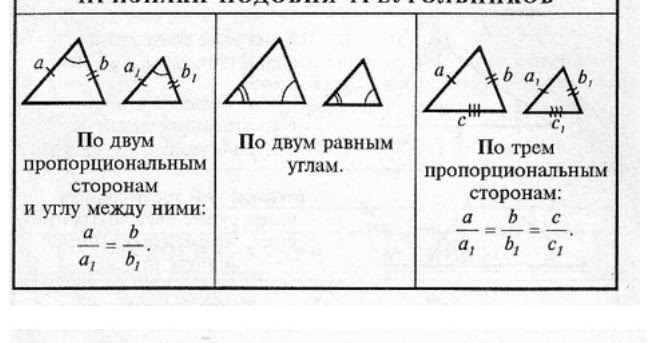 Оно изложено в VI книге «Начал» Евклида, начинающиеся следующим определением: «Подобные прямолинейные фигуры суть те, которые имеют соответственно  равные  углы  и  пропорциональные стороны». 

Задача [3]  

Греческий мудрец Фалес за шесть веков до нашей эры определил в Египте высоту пирамиды. Он воспользовался ее тенью. Жрецы и фараон, собравшиеся у подножия высочайшей пирамиды, озадаченно смотрели на северного пришельца, отгадывавшего высоту огромного сооружения.
Фалес,– говорит предание,– избрал день и час, когда длина собственной его тени равнялась его росту; в этот момент высота пирамиды должна так же равняться длине отбрасываемой ею тени. Конечно, длину тени надо было считать от средней точки квадратного основания пирамиды; ширину этого основания Фалес мог измерить непосредственно. Изменим, этот способ так, чтобы в солнечный день можно было воспользоваться любой тенью, какой бы длины она ни была. Пусть длина шеста 1м, а его тени 1,2м. Найти высоту дерева, если ее тень 6м.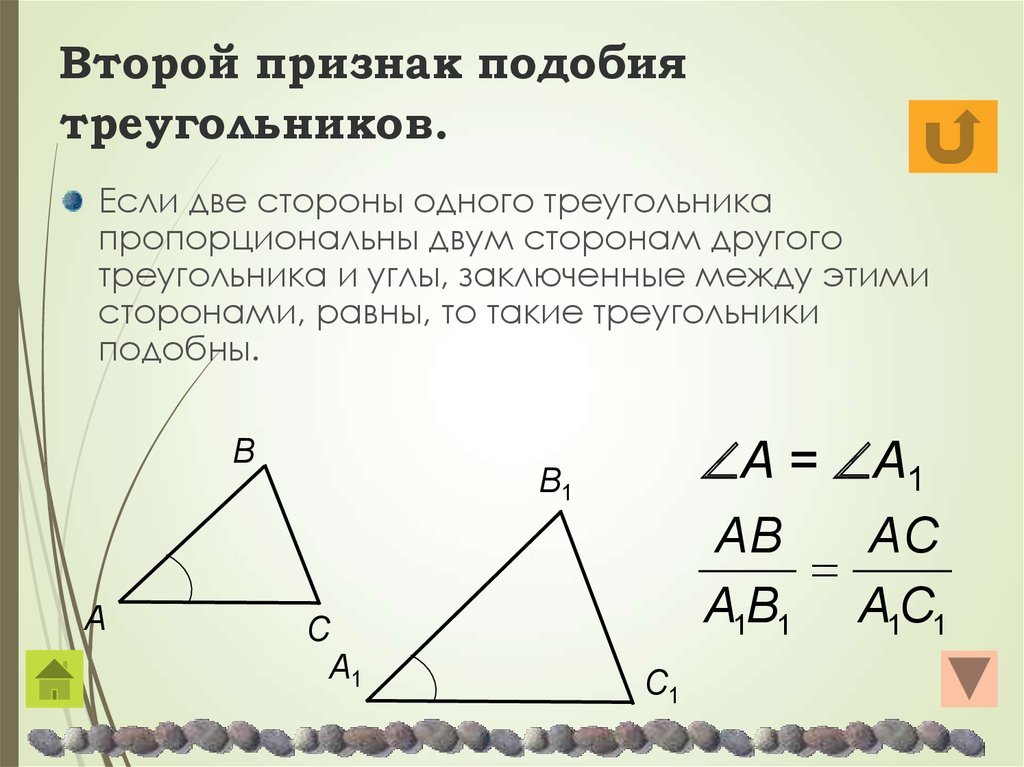

Таких красивых задач, которые решаются с применением признаков подобия, очень много.

2. Подобные треугольники [1]  

Определение

Два треугольника называют подобными, если их углы соответственно равны, и стороны одного треугольника пропорциональны сходственным сторонам другого треугольника.

∆А BC ~ ∆A1B1C1

        Признаки подобия треугольников

1) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.

2) Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, образованные этими сторонами, равны, то такие треугольники подобны.

3) Если стороны одного треугольника пропорциональны сторонам другого треугольника, то такие треугольники подобны.

Теорема о площадях двух подобных треугольников

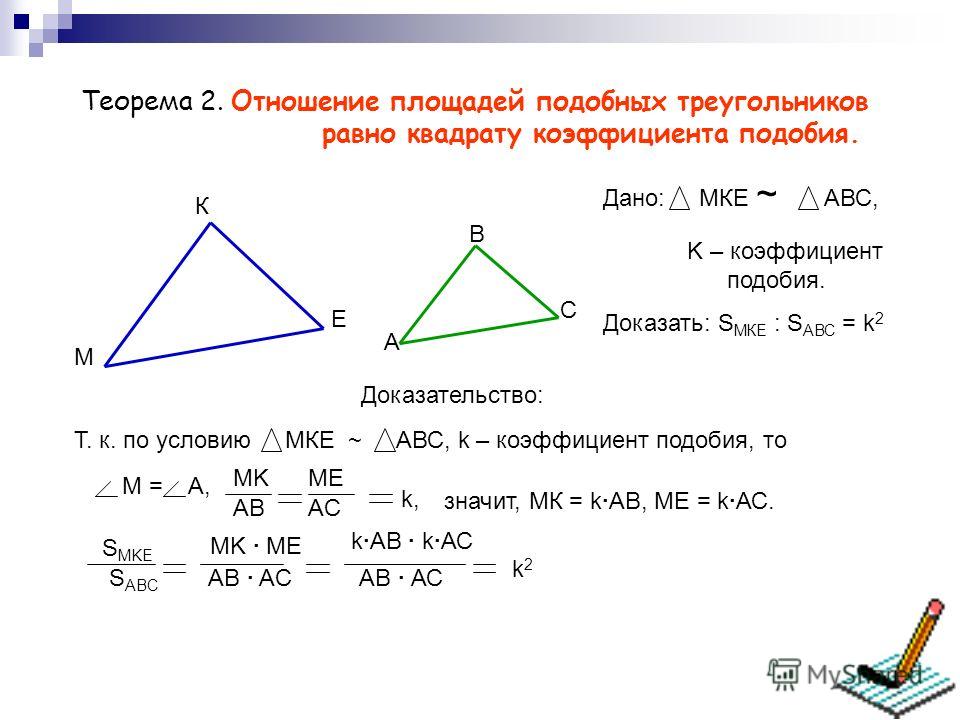
Отношение  площадей двух подобных треугольников равно квадрату коэффициента подобия.

---

3. Применение подобия при доказательстве теорем и задач [1]

Теорема.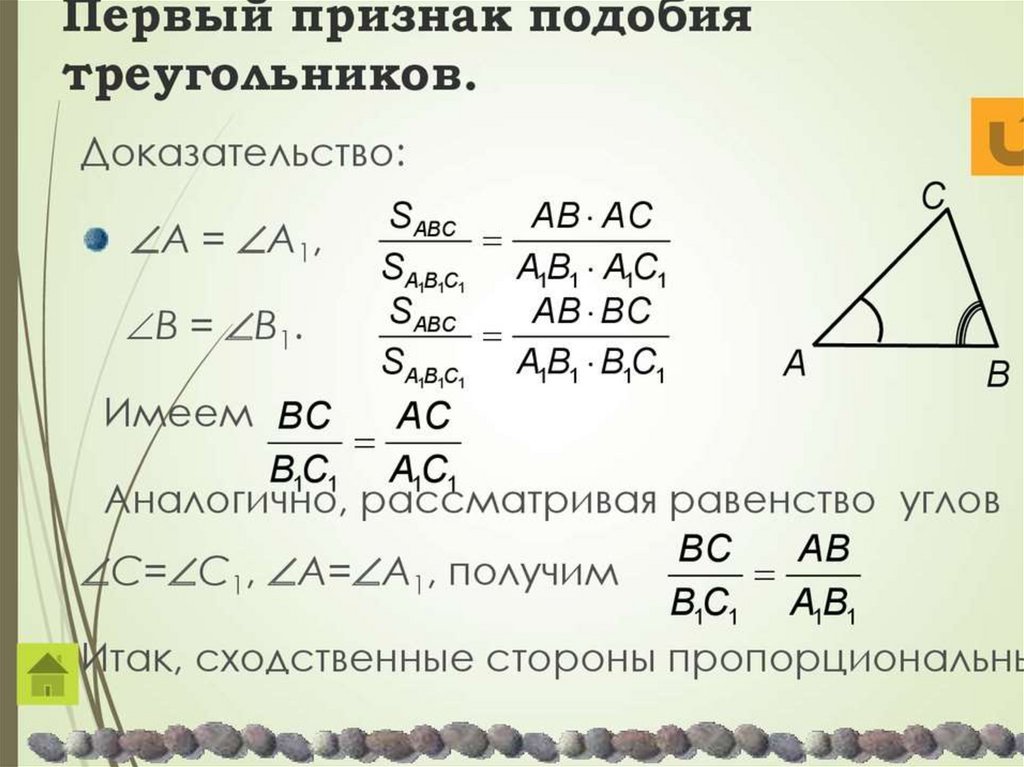 Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.

Доказательство. Пусть MN– средняя линия треугольника ABC. Докажем, что MN//AC и MN = ½ АС

Треугольники BMN и ВАС подобны по второму признаку подобия треугольников (угол B – общий) ВМ/ВА = BN/BC = ½ ), поэтому углы 1 и 2 равны и MN/AC = ½ . из равенства углов 1 и 2 следует, что MN//AC, а из второго равенства, что MN = ½ АС

Задача.  Доказать, что медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2:1, считая от вершины.

Решение. Рассмотрим произвольный треугольник ABC. Обозначим буквой О точку пересечения его медиан AA1 и BB1 и проведём среднюю линию A1B1 ,этого треугольника. Отрезок A1B1 параллелен стороне АВ, поэтому углы 1 и 2, 3 и 4 равны. Следовательно,
треугольники АОВ u A1OB1 подобны по двум углам, и, значит, их стороны пропорциональны: AO/A1O = BO/B1O = AB/A1B1. Но АВ = 2А1В1, поэтому АО = 2A1O и ВО = 2B1O. Таким образом, точка О пересечения медиан AA1 и BB1  делит каждую из них в отношении 2:1, считая от вершины.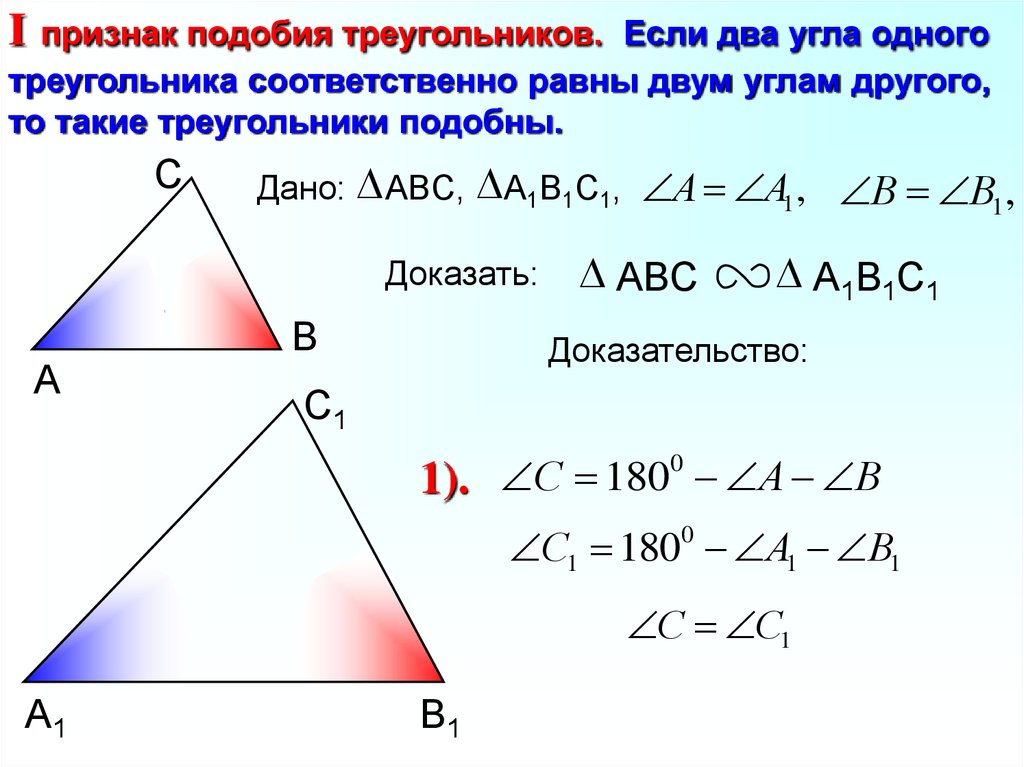

Аналогично доказывается, что точка пересечения медиан BB1 и СС1 делит каждую из них в отношении 2:1, считая от вершины, и, следовательно, совпадает с точкой О. Итак, все три медианы треугольника ABC пересекаются в точке О и делятся ею в отношении 2:1, считая от вершины.

Следующие утверждения также доказываются с помощью подобия

10 Высота прямоугольного треугольника, проведённая из вершины прямого угла, разделяет треугольник на два подобных прямоугольных треугольника, каждый из которых подобен данному треугольнику.

20 Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между проекциями катетов на гипотенузу.                                                    

 

30   Катет прямоугольного треугольника есть среднее пропорциональное между гипотенузой и проекцией этого катета на гипотенузу.

40 Если хорды АВ и CD окружности пересекаются в точке S, то AS ∙BS = CS∙DS, то есть DS/BS = AS/CS.

 

50 Если из точки Р к окружности проведены две секущие, пересекающие окружность в точках А, В и С, D соответственно, то АР/СР = DP/BP.

 

60 Биссектриса угла треугольника делит противолежащую сторону на отрезки, пропорциональные двум другим сторонам.

70 Середины оснований, точка пересечения диагоналей и точка пересечения продолжений боковых сторон трапеции лежат на одной прямой.

Теорема Чевы [ 2 ]

Пусть точки A1, B1 и С1 принадлежат сторонам BC, AC и AB треугольника ABC. Отрезки AA1, BB1 и CC1 пересекаются в одной точке тогда и только тогда, когда

 

Доказательство: Докажем сначала, что если отрезки пересекаются, то произведение отношений равно 1. Пусть O — точка пересечения отрезков AA1, BB1 и CC1. Проведём через точку A прямую q, параллельную прямой BC . Продолжим отрезки BB1 и CC1 за точки В1 и C1 до пересечения с прямой q в точках В2 и C2 соответственно. Тогда треугольники ВОА1 и В20А подобны по двум углам. Также подобны треугольники COA1 и C2OA. Следовательно, .  Также подобны треугольники BB1C и B2B1A, а значит, . Аналогично .  Перемножив три получившихся равенства, получим:

                                           

                 

          Докажем обратное утверждение. Пусть  отрезки AA1 и BB1 пересекаются в точке O. Проведем через точки C и O прямую. Пусть эта прямая пересекает сторону AB в точке K. В этом случае точки A1, B1 и K удовлетворяет данному соотношению по выше доказанному. Но точки A1, B1 и C1 также удовлетворяют данному соотношению. Значит, точки K и C1 делят сторону AB в равном соотношении, то есть они совпадают. Но CK проходит через точку O. Следовательно, отрезок CC1 также проходит через эту точку. Значит, отрезки AA1, BB1 и CC1 пересекаются в точке O. Что и требовалось доказать.

4. Применение подобия при решении задач по математике

1. Внутри треугольника ABC взята точка М, через которую проведена прямая, параллельная сторонам треугольника. При этом площади трёх образовавшихся треугольников с вершиной М равны S1, S2, S3. Найдите площадь треугольника ABC.

Решение. Т. к. ΔАВ С ~ ΔА1А2М, ΔАВС ~ ΔMB1B2,

ΔАВС ~ Δ С2МС1 , то их площади относятся как квадраты соответствующих элементов, а именно: . Тогда . Отсюда .

2. В трапеции MNPK (MK и NP — основания) О — точка пересечения диагоналей. Площади Δ MOK и Δ NOP равны S1 и S2 соответственно. Найдите площадь трапеции.

Решение. Проведём OO1┴NР, OO2┴MK, тогда O€O1O2, и O1O2┴NP, O1O2┴MK. ΔMOK~ΔPON по двум углам, отсюда , т.е. ;

Ответ:

3.        Расстояния от точки пересечения диагоналей равнобокой трапеции до середин её сторон равны  2 см, 1 см и 2 см соответственно. Найдите радиус окружности, описанной около трапеции.

Решение. Радиус окружности, описанной около трапеции, найдём как радиус окружности, описанной около ΔACD. Точки F, N, М — середины отрезков ВС, CD, AD соответственно. Тогда по условию, FO=1, ON=OM=2. Треугольники ВОС и AOD подобны, а потому, АO=2OС. Построим DK // ON, тогда АК .= КО = ОС и KD = 4. KD — медиана ΔAOD, ОМ — серединный перпендикуляр к AD и медиана ΔAOD. Точка Т — точка пересечения медиан ΔAОD делит медиану DK на отрезки: 8/3 и 4/3, делит медиану ОМ на отрезки: 4/3 и 2/3.

Пусть L — середина ОК, тогда L — середина АС.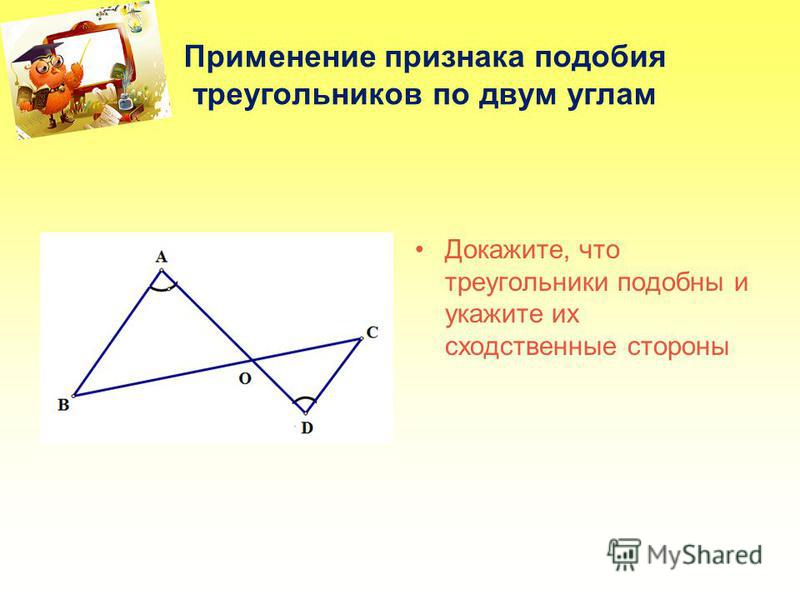 ΔКТО — равнобедренный, т. к. ОТ = КТ =4/3 и TL — является серединным  перпендикуляром к отрезку АС. Следовательно, точка Т является центром окружности, описанной около ΔACD, радиус которой равен 8/3.

Ответ: 8/3.

4.        На сторонах  АВ и АС треугольника ABC взяты соответственно точки М и N так, что ВМ = MN = NC. Отрезки ММ1 и NN1 — биссектрисы треугольника AMN. Докажите, что M1N1// ВС.

Решение. Угол MNA — внешний для равнобедренного треугольника MNC, поэтому угол MNA = NMC + NCM = 2NCM. Так как NN1 — биссектриса, то угол ANN1 = 1/2MNA = NCM. Получим, что ΔANN1 подобен ΔАСМ по двум углам (угол А — общий). Следовательно,

 AN1/AN = AM/AC.                        (1)

 Проводя аналогичные рассуждения, из подобия треугольников АММ1 и ABN получим

AM1/AN =АМ/АВ.        (2)

Поделив равенство (1) на (2) получим AN1/AM1 = АВ/АС, и так как угол А — общий для треугольников AN1M1 и ABC, то они подобны. Значит, угол AN1M1 =АВС. Следовательно, M1N1 // СВ

5. Дан правильный тетраэдр SABC, объем которого равен  V. На ребрах SA и SB взяты их середины D и E, а на ребре SC взята точка F такая, что SF:FC=1:3. Найдите объем пятигранника DEFABC.

Решение.

Пусть G – середина ребра SC. Тогда  F – середина отрезка SG и поэтому  EF – средняя линия в треугольнике  SBG. Аналогично, DF – средняя линия в треугольнике SAG и по условию DE – средняя линия в треугольнике SAB. Значит, при гомотетии с центром S и коэффициентом 2 пирамида SDEF перейдет в пирамиду SABG, то есть эти пирамиды подобны с коэффициентом 2. Следовательно, объем пирамиды SDEF в 8 раз меньше объема пирамиды SABG.

Но последний объем составляет половину всего объема V. Действительно, отрезок SG перпендикулярен отрезкам AG и BG, так как они являются высотами в соответствующих гранях. Значит, прямая SC перпендикулярна плоскости ABG, и поэтому при симметрии относительно этой плоскости пирамида SABG перейдет в пирамиду CABG. Поэтому их объемы равны, в сумме они составляют V и, значит объем каждой из них равен половине V.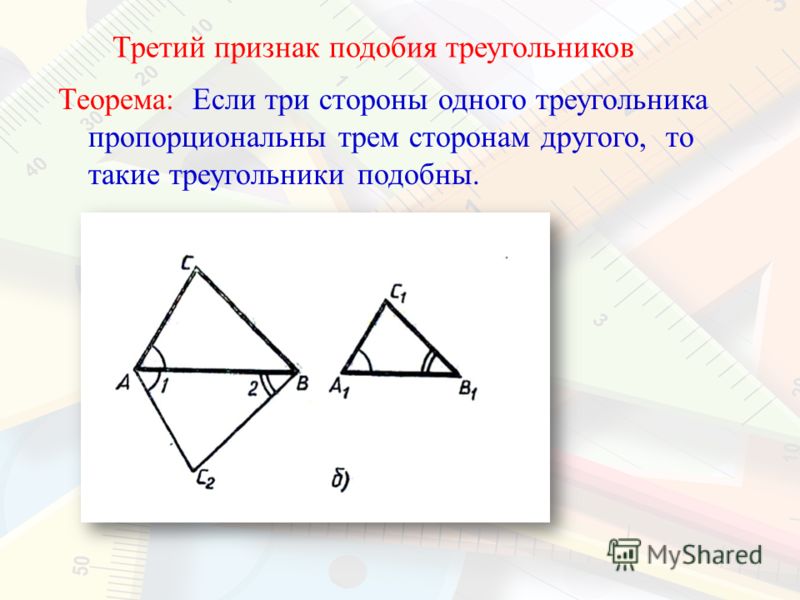

В итоге, VSDEF=1/8 VSABG = 1/8*1/2 V=1/16 V и поэтому VDEFABC=15/16 V.

Ответ: 15/16 V.

---

5. Применение подобия при решении задач по физике                                       

1. Найти высоту предмета, к основанию которого можно подойти с помощью подобия треугольников?

Решение:

Берем два кола BD и CE и устанавливаем их так, чтобы точки А, В и C находились на одной прямой.

Измеряем BD и СЕ, а также DG и DE. Если провести прямую CH ║ EG, то ∆ACH~∆BCF , следовательно, , откуда ;

2. Лодочник, направляясь из пункта  А в пункт В, всё время направляет лодку под углом α к берегу. Найти скорость лодки  относительно воды, если скорость течения реки равна  u, а лодку снесло ниже пункта В на расстояние l.

В основу решения положен факт подобия треугольников сложения скоростей и сложения перемещений.

Решение

НСО – неподвижная система отсчёта (берег), ПСО – подвижная система отсчёта (вода).

Из условия задачи следует, что АС – перемещение лодки относительно берега – . Вектор скорости   направлен вдоль .

 

Однако величина этого вектора неизвестна. Достроим треугольник скоростей, используя закон сложения скоростей

,

для чего через конец вектора  проведём линию, параллельную берегу, до пересечения с АС. Получившийся отрезок не что иное, как , а точка пересечения линии, вдоль которой он направлен, и АС – конец вектора . Треугольник скоростей готов.

Теперь достроим треугольник перемещений. Продлив линию, вдоль которой направлен вектор , до пересечения с противоположным берегом, получим вектор – перемещение лодки в ПСО. Вектор, соединяющий концы векторов   и , есть не что иное, как вектор перемещения ПСО относительно НСО – . Треугольник перемещений готов.

Треугольники скоростей и перемещений подобны по определению.

Составим отношение подобия

.

Откуда

Из чертежа

,  

После подстановки и сокращений получаем конечную формулу.

---

3. Фонарь весом 43 Н укреплён на подвесе. Определите силу упругости бруска АВ и проволоки ВС [ 4 ]

 

Решение. Запишем условие равновесия точки В

         (1)

Расставить эти силы на чертеже сразу невозможно. Не определены направления и величины действующих на точку В сил упругости  и .

Преобразуем формулу (1).

                (1.1)

Используя формулу (1.1), построим силы, начиная с . От точки В в сторону, противоположную , построим –

Разложим вектор –на направления действия сил  и .  

Треугольник BKL, образованный силами, подобен треугольнику АВС по построению.

Составим отношения подобия

,      ,

откуда

,       .

4. Два заряда по 10 -8 Кл находятся в воздухе на расстоянии 8 м друг от друга. Найдите

напряженность на расстоянии 5 м от обоих зарядов. [4]

Решение. Как видно из рисунка, таких точек две (D и Е). Решение проводят для одной из них, например для D. Заряды в точках  А и В обозначают соответственно qA и qB, ЕА и Ев — модули напряженностей в точке D, созданные зарядами qA и qB. По условию задачи qA = qB. Общая напряженность электрического поля в точке D: ED = ЕА + Ев, которую находят как диагональ параллелограмма со сторонами векторов напряженности ЕА и Ев.

Модули напряженностей ЕА = Ев = k,   а   модуль   напряженности ED определяют

из подобия  ∆ ACD и ∆ DMF: DF = DM         

Подставляя числовые данные, получим ED = 4,3 Н/Кл.

 

Приведённые примеры показывают, что использование способа, основанного на подобии треугольников, позволяет существенно упростить и сократить решение задачи. Особенно примечательно, что он не требует знакомства с дополнительным математическим материалом и основывается на часто используемых в геометрии подходах к решению стандартных геометрических задач.

---

 ЗАКЛЮЧЕНИЕ  

Как найти расстояние до недоступной точки? Как путём построения подобных треугольников найти расстояние между двумя недоступными пунктами  А и В? Как найти высоту предмета, к основанию которого можно подойти?

Решение подобных задач способствует развитию логического мышления, умению анализировать ситуацию, а использование метода подобия треугольников в их решении, повышает тем самым математическую культуру,  развивая математические способности. Использовать рассмотренный мною геометрический материал можно как на уроках геометрии и физики, так и при подготовке к  Единому государственному экзамену, а также на элективных курсах математического и физического направления. 

---

СПИСОК ЛИТЕРАТУРЫ

1. Атанасян Л.С., Бутузов В.Ф. и др. Геометрия. 7-9 классы: учебник для общеобразовательных учреждений – М.: «Просвещение», 2010
2. Атанасян Л.С., Бутузов В.Ф. и др. Геометрия. 10-11 классы: учебник для общеобразовательных учреждений – М.: «Просвещение», 2010
3. Дениз Сечеи. Геометрия. Шаг за шагом- М.: Аст: Астрель, 2006
4. Каменецкий С.Е., Орехов В.П. Методика решения задач по физике в средней школе. — М.: «Просвещение, 1987

Признаки подобия треугольников, подобие прямоугольных треугольников.

Тема урока: Глава2 Признаки подобия треугольников, подобие прямоугольных треугольников.

Цели урока:

Оценка: на уроке оценивают результаты своей работы, проводят коррекцию знаний Синтез: развивают навыки решения задач на использование признаков подобия треугольников, прямоугольных треугольников Анализ: доказывают признаки подобия треугольников, работают с чертежами. Применение: используют признаки подобия треугольников в решении задач, выполняют чертежи Понимание: обсуждают доказательство признаков подобия треугольников и их следствия Знание: называют признаки подобия треугольников

Учебно-воспитательные задачи: Образовательная:

Продолжать формирование признаков подобия треугольников, подобия прямоугольных треугольников, научить доказывать, работать с чертежами.

Развивающая: развитие способности выражать мысли, познавательных способностей, логического мышления, развитие умений рассуждать, проводить доказательство теорем.

Воспитательная: способствовать выявлению, раскрытию способностей учащихся, побуждать их к применению полученных знаний, воспитывать учащихся к проявлению инициативы, к продуктивному мышлению

Результаты обучения: Учащиеся знают: признаки подобия треугольников

Учащиеся умеют: решать задачи на применение признаков подобия треугольников, выполнять чертежи

Тип урока: совершенствование знаний

Форма проведения урока: беседа

Методы обучения:

По источнику получения знаний: словесные, наглядные, практические.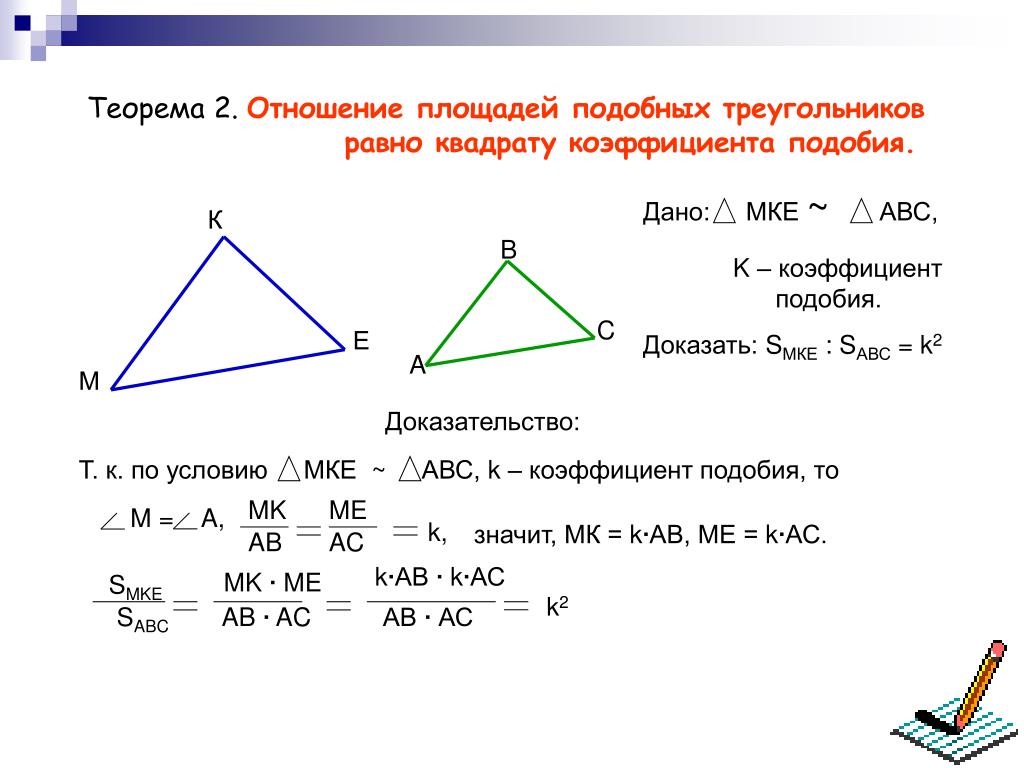

По способу организации познавательной деятельности: объяснительно-иллюстративные, репродуктивные.

Методы воспитания: Организация деятельности, формирование мировоззрения, стимулирование деятельности, осуществление контроля, взаимоконтроля, самоконтроля.

Формы обучения: коллективные, индивидуальные, групповые

Основные понятия темы:

Задание на дом: № 346-347(1), гл.2 § 5

Оборудование, ресурсы, наглядные пособия:

учебник, рабочая тетрадь, дидактический материал

Учитель: Шуринова Е.К.

Ход урока

Этапы урока	Содержание этапа
Оргмомент. Задачи: обеспечить нормальную внешнюю обстановку на уроке, психологически подготовить детей к общению	Приветствие Проверка подготовленности к уроку Организация внимания школьников Ознакомление с планом проведения урока
Проверка домашнего задания. Задачи: установить правильность, полноту и осознанность выполнения всеми учащимися домашнего задания, выявить пробелы в знаниях, устранить в ходе проверки обнаруженные пробелы	Выявление степени усвоения заданного учебного материала Устный опрос. Индивидуальный опрос. Ликвидация обнаруженных недостатков. 3 учащихся у доски: доказательство теорем 1-3
Вызов. Задачи: обеспечить включение школьников в совместную деятельность по определению целей учебного занятия.	Сообщение темы урока Какие треугольники называются подобными? (Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого). — Определите сходственные стороны подобных треугольников, назовите их(3 слайд) — Что такое коэффициент подобия? (число k, равное отношению сходственных сторон подобных треугольников, называется коэффициентом подобия). — Чему равно отношение площадей двух подобных треугольников?(Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия). — Цель нашего урока предполагает решения задач на применение признаков подобия, нам необходимо знать эти признаки. — Сколько признаков подобия существует? Вспомним и назовем все три признака (ответы детей). — Это те теоретические знания, которые нам сегодня пригодятся при решении задач.
Актуализация знаний и умений Задачи: психологическая подготовка ученика: сосредоточение внимания, осознание значимости предстоящей деятельности, возбуждение интереса к уроку; учащиеся воспроизводят известные им знания, осознают их, обобщают факты, связывают старые знания с новыми условиями, с новыми данными и т.д.	Актуализация знаний и умений.
Применение знаний на практике. Задачи: установить правильность и осознанность учащимися изученного материала, выявить пробелы при выполнении практических заданий.	№ 345 -347 работа по учебнику Дан четырехугольник, по рисунку необходимо сформулировать задачу. Найти: BAD. Сформулируйте задачу.  — Назовите, что дано. Что требуется найти. — Начертите рисунок в тетрадь и запишите, что дано, что требуется найти. Дано: ABCD – четырехугольник, АС – диагональ, ВС = 10, СD = 15, AD = 21, AC = 14, АВ = , В = 80º, D = 55º. Найти: BAD. — Прочитайте, что у вас получилось. Поиск решения задачи: — Что нам надо найти? BAD — Что достаточно знать, чтобы найти этот угол? ВАС САD — Откуда мы найдем эти углы? ∆ АВС ∆ ACD — Если в треугольнике мы знаем один угол, что поможет нам найти другие углы? Для чего даны стороны? (устанавливаем отношение между сторонами, покажем, что треугольники подобны) — Чему равен коэффициент подобия?  — Что из этого следует? ∆ АВС подобен ∆ ACD — По какому признаку? (по 3 признаку) — Что следует из подобия? равенство углов — Какие углы сможем найти? ВАС САD — А зная их, найдем… BAD — План решения понятен? Повторите. План решения задачи: — устанавливаем подобие треугольников ∆ АВС и ∆ ACD; — доказательство подобия, через соотношение сторон; — устанавливаем равенство соответствующих углов в подобных треугольниках; — по свойству суммы углов треугольника находим углы ВАС и САD; — находим угол BAD.
Контроль знаний. Задачи: установить качество усвоения учащимися знаний, определить недостатки в знаниях и их причины
Коррекция знаний. Задачи: скорректировать выявленные проблемы	Организация деятельности учащихся по коррекции выявленных недостатков Повторное разъяснение учителя. Помощь эксперта.
Подведение итогов. Рефлексия. Задачи: инициировать рефлексию учащихся по поводу своего эмоционального состояния, дать оценку работе отдельных учащихся и всего класса	Мобилизация учащихся на рефлексию. Листок рефлексии В занятии для меня было: самым полезным ___________________________________________________________ самым приятным ___________________________________________________________ самым интересным ______________________________________________ ___________ Я бы хотел еще узнать _______________________________________________________ Выставление оценок.

Рефлексия учителя о проведенном уроке:

Объяснение урока: Подобие треугольников

В этом объяснении мы научимся определять и доказывать, подобны ли два треугольника, используя равенство соответствующих углов или пропорциональность соответствующих сторон и как использовать подобие для нахождения неизвестных длин и углов.

Начнем с определения подобных треугольников.

Определение: Подобные треугольники

Подобные треугольники имеют конгруэнтные соответствующие углы и пропорциональные соответствующие стороны.

Мы можем доказать, что два треугольника подобны, если

• соответствующих углов равны или
• соответствующих сторон пропорциональны.

Обратите внимание, что определение конгруэнтных треугольников отличается, поскольку в конгруэнтных треугольниках соответствующие углы конгруэнтны и соответствующие стороны равны .

Мы можем видеть пример сходства с треугольниками 𝐴𝐵𝐶 и 𝐷𝐸𝐹 ниже.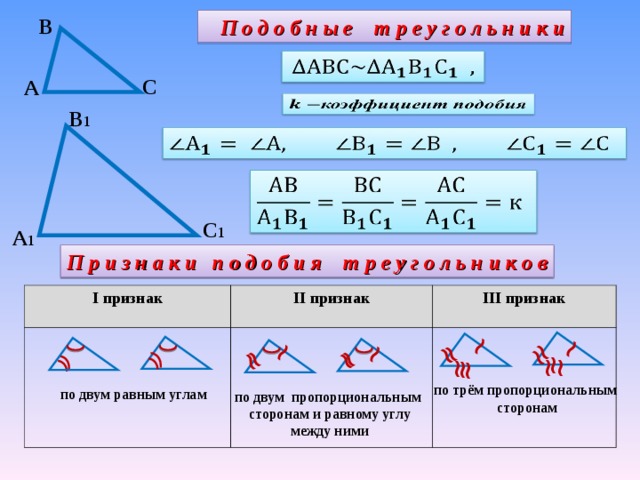

Существуют 3 пары соответствующих угловых мер, конгруэнтных: 𝑚∠𝐴=𝑚∠𝐷,𝑚∠𝐵=𝑚∠𝐸,𝑚∠𝐶=𝑚∠𝐹.

Мы также можем написать, что стороны пропорциональны, так как у нас есть 𝐴𝐵𝐷𝐸=𝐴𝐶𝐷𝐹=𝐵𝐶𝐸𝐹714=36=510=12.

Также было бы допустимо записать соотношение сторон в треугольниках со всеми сторонами △𝐷𝐸𝐹 в качестве числителей и все стороны △𝐴𝐵𝐶 в качестве знаменателей (то есть все дроби перевернуты), так что 𝐷𝐸𝐴𝐵=𝐷𝐹𝐴𝐶=𝐸𝐹𝐵𝐶147=63=105.

В этом случае все отношения сторон были бы равны 2.

Любого утверждения пропорции было бы достаточно, чтобы доказать, что △𝐴𝐵𝐶∼△𝐷𝐸𝐹.

При доказательстве того, что два треугольника подобны, достаточно показать, что углы равны или что стороны пропорциональны, чтобы доказать, что треугольники подобны. Это потому, что если нам даны 3 угловых измерения, мы можем нарисовать только подобных треугольников с такими же угловыми измерениями. а не непохожий треугольник, так как все стороны были бы пропорциональны исходному треугольнику. Или, учитывая 3 длины сторон, если мы нарисуем другой треугольник со сторонами в той же пропорции, все меры угла будут конгруэнтны углам исходного треугольника.

Обозначения, которые мы используем при записи отношений подобия, важны. Подобные формы могут быть связаны символом ∼. Однако, порядок, в котором мы записываем вершины фигур, очень важен, поскольку само отношение подобия указывает на соответствующие вершины (и стороны).

Например, на рисунке выше мы могли бы написать, что △𝐴𝐵𝐶∼△𝐷𝐸𝐹. Если бы мы написали, например, что △𝐴𝐵𝐶∼△𝐸𝐷𝐹, это было бы неверно, так как вершина 𝐴 соответствует вершине 𝐷, а не 𝐸. Однако мы могли бы написать ряд различных правильных утверждений подобия, например, △𝐵𝐶𝐴∼△𝐸𝐹𝐷,△𝐶𝐴𝐵∼△𝐹𝐷𝐸,△𝐵𝐴𝐶∼△𝐸𝐷𝐹.

В первых примерах мы увидим, как можно доказать, что два треугольника подобны, начиная с примера, где мы используем длины сторон треугольников.

Пример 1. Определение сходства треугольников путем рассмотрения их сторон

Похож ли треугольник 𝑀𝑁𝐿 на треугольник 𝑋𝑍𝑌?

Ответ

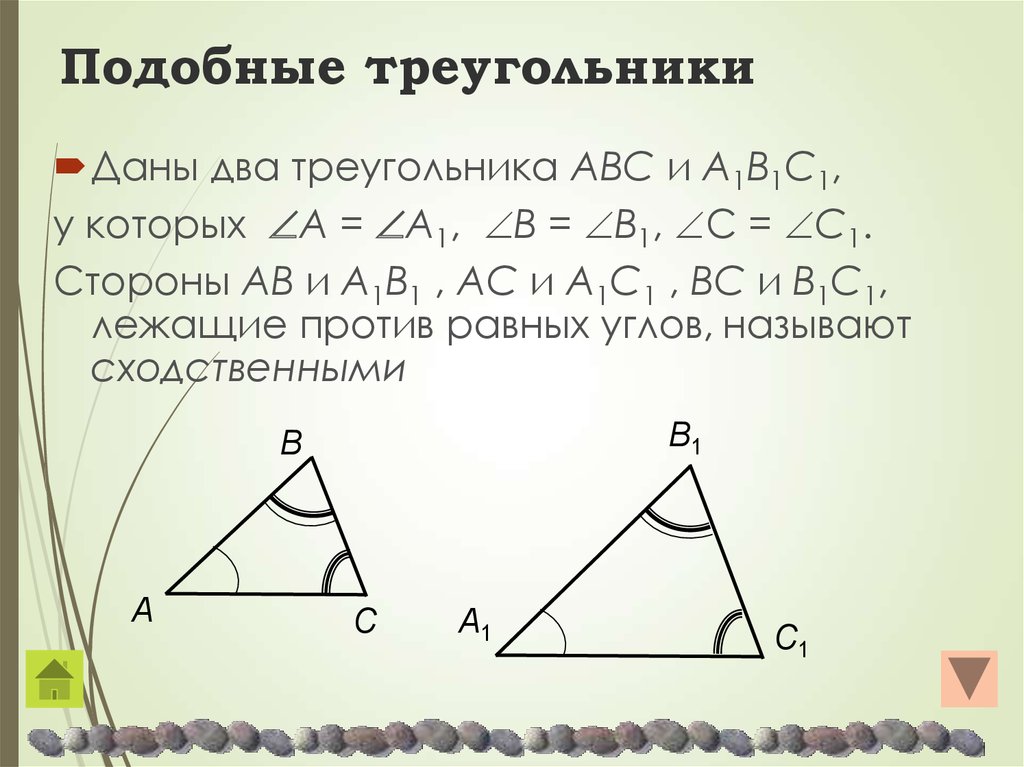В подобных треугольниках соответствующие углы равны, а соответствующие стороны пропорциональны. Поскольку одно из этих свойств ведет к другому, мы можем доказать, что треугольники подобны, если у них либо соответствующие углы конгруэнтны, либо соответствующие стороны пропорциональны.

Учитывая, что у нас есть длины сторон на этом рисунке, давайте определим отношение между каждой из соответствующих длин сторон.

Заметим, что оба треугольника равносторонние, поскольку длины сторон каждого треугольника равны по трем сторонам. Используя соответствующие пары сторон, 𝑀𝑁=12см и 𝑋𝑍=18см, 𝑀𝐿=12см и 𝑋𝑌=18см, и 𝑁𝐿=12см и 𝑍𝑌=18см, мы можем написать это 𝑀𝑁𝑋𝑍=𝑀𝐿𝑋𝑌=𝑁𝐿𝑍𝑌 поскольку все они равны отношению 1218, или 23,9.0003

Следовательно, мы можем ответить, что треугольник 𝑀𝑁𝐿 подобен треугольнику 𝑋𝑍𝑌.

Обратите внимание, мы могли бы также продемонстрировать, что треугольники подобны, записав соотношения, поменяв местами все числители и знаменатели. То есть, 𝑋𝑍𝑀𝑁=𝑋𝑌𝑀𝐿=𝑍𝑌𝑁𝐿.

В этом случае все эти отношения по-прежнему будут равны, но на этот раз 1812, или 32.

В предыдущем примере мы использовали тот факт, что стороны пропорциональны друг другу, чтобы доказать, что треугольники подобны. Однако мы могли бы использовать альтернативный метод. Установив, что оба треугольника равносторонние, мы могли бы вспомнить, что у равносторонних треугольников все три угловые меры равны. до 60∘. Так как соответствующие меры углов в каждом треугольнике конгруэнтны, то треугольники подобны.

Попутно отметим, что все правильные многоугольники будут похожи. Например, все квадраты подобны, все правильные пятиугольники подобны, все правильные шестиугольники подобны и так далее. Равносторонний треугольник, будучи правильным треугольником, всегда похож на любой другой равносторонний треугольник.

Теперь мы рассмотрим другой пример, в котором мы будем использовать угловые меры для построения пары подобных треугольников.

Пример 2. Определение сходства треугольников путем рассмотрения их углов

Какой из следующих треугольников подобен показанному на данном рисунке?

Ответ

Напомним, что два треугольника подобны, если у них соответствующие меры углов конгруэнтны, а соответствующие стороны пропорциональны. Один из способов, которым мы можем доказать, что треугольники подобны, если соответствующие меры их углов равны.

Когда мы рассматриваем 5 различных вариантов, мы видим, что ни один из доступных треугольников не имеет углов, которые имеют ту же меру, что и данный треугольник, 100∘ и 30∘. Поэтому будет полезно вычислить мера третьего угла в этом треугольнике, который мы можем определить как 𝑥∘. Используя свойство, что сумма внутренних углов в треугольнике равна 180 ∘, мы имеем, что 𝑥+100+30=180𝑥+130=180𝑥=180−130=50.∘∘∘∘∘∘∘∘∘∘∘

Если мы посмотрим на доступные варианты, то увидим, что единственным треугольником, у которого две конгруэнтные меры угла, является вариант E. Мы можем вычислить недостающий угол, определяется как 𝑦∘, в выборе E с использованием того факта, что сумма угловых мер в треугольнике 180∘: 𝑦+50+30=180𝑦+80=180𝑦=180−80=100.∘∘∘∘∘∘∘∘∘∘∘

Таким образом, все 3 соответствующие угловые меры данного треугольника конгруэнтны тем, которые указаны в выборе E.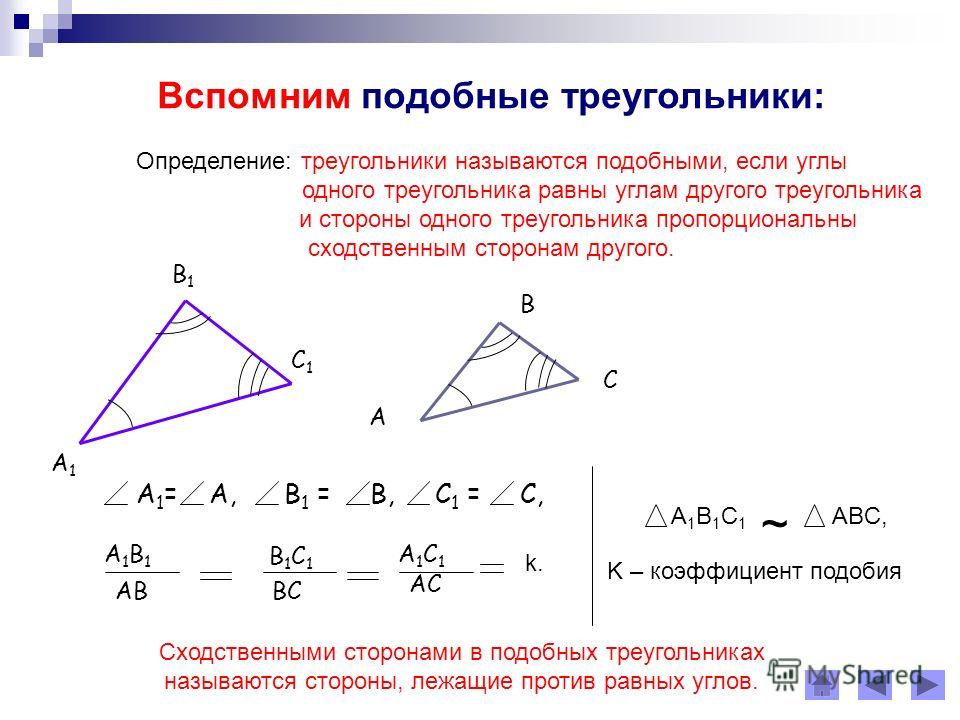

Следовательно, треугольник, подобный данной фигуре, является треугольником выбора E.

В предыдущем примере мы вычислили меру третьего угла на данной фигуре, а затем вычислили меру третьего угла в выборе E для установить, что его мера равна 100∘. Однако, если мы знаем, что две пары соответствующих углов в два треугольника равны, то третья пара углов в треугольниках также должна быть равна. Это вытекает непосредственно из того факта, что внутренний угол измеряет в сумме треугольника 180∘.

На рисунке ниже, если нам даны две пары конгруэнтных угловых мер, 𝑎∘ и 𝑏∘, то третий угол, 𝑐∘, в каждом треугольнике будет равно 𝑐=180−(𝑎+𝑏)∘∘∘∘.

Теперь мы рассмотрим другой пример.

Пример 3. Определение подобных треугольников с помощью свойства угла равнобедренных треугольников

Какие два из этих треугольников подобны?

Ответ

Напомним, что два треугольника подобны, если у них соответствующие углы конгруэнтны, а соответствующие стороны пропорциональны. Мы можем доказать, что два треугольника подобны, либо определяя, равны ли соответствующие углы, либо определяя, пропорциональны ли соответствующие стороны.

В этом вопросе нам не дают никакой информации о длинах сторон этих треугольников. Итак, давайте посмотрим, можем ли мы вычислить меры углов в треугольниках. Мы можем заметить, что все 4 треугольника должны быть равнобедренными, так как у каждого треугольника отмечена пара конгруэнтных сторон. В равнобедренном треугольнике два угла при основании равны равной меры. Мы также знаем, что внутренний угол в треугольнике равен 180∘.

Начиная с треугольника 1, мы знаем, что, поскольку угол при основании равен 40∘, другой угол при основании также равен 40∘. Вычитая их из 180∘, мы можем найти мера третьего угла, определяемая как 𝑎∘, как 𝑎+40+40=180𝑎+80=180𝑎=180−80=100.∘∘∘∘∘∘∘∘∘∘∘

Мы могли бы продолжить вычисление всех недостающих углов на других рисунках; однако полезно заметить, что единственный другой заданный треугольник, который также имеет угол при вершине 100 ∘ — это треугольник 4.

Определив 2 конгруэнтных угла при основании в треугольнике 4 как 𝑏∘, мы могли бы вычислить их меру, используя угол при вершине 100 ∘, как 𝑏+𝑏+100=1802𝑏+100=1802𝑏=180−1002𝑏=80𝑏=802=40.∘∘∘∘∘∘∘∘∘∘∘∘∘∘∘

подобны.

Для полноты картины мы могли бы установить все недостающие углы в каждом треугольнике, как показано ниже.

Даже не вычисляя эти углы, мы можем заметить, что треугольники 2 и 3 имеют две неконгруэнтные меры угла вершины 40° и 90°; поэтому они не будут похожи друг к другу или к треугольникам 1 и 4.

Следовательно, два треугольника подобны 1 и 4.

В следующем примере мы увидим, как мы можем найти неизвестную длину стороны, сначала установив, являются ли два треугольника похожий.

Пример 4. Поиск недостающей длины по сходству

Определите длину 𝐴𝐶.

Ответ

На данном рисунке у нас есть два треугольника с разными длинами сторон. Это означает, что треугольники не равны. Однако мы можем проверить, похожи ли они. Напомним, что два треугольника подобны, если у них соответствующие углы равны, а соответствующие стороны пропорциональны. Мы можем доказать, что два треугольника подобны либо определяя, равны ли соответствующие углы, либо определяя, пропорциональны ли соответствующие стороны.

У нас недостаточно информации для сравнения длин всех сторон, поэтому мы проверяем размеры углов. Так как в каждом треугольнике даны 2 угловые меры, мы можем использовать свойство, что внутренний угол измеряется в сумме треугольника до 180 ∘, чтобы помочь нам вычислить третий угол каждого треугольника.

В △𝑋𝑌𝑍 нам дано, что 𝑚∠𝑋𝑍𝑌=61∘ и 𝑚∠𝑋𝑌𝑍=60∘; таким образом, мы можем вычислить 𝑚∠𝑍𝑋𝑌 в качестве 𝑚 Хорошо+𝑚 Хорошо 𝑋𝑌𝑍 𝑚 Ворт = 18061+60+𝑚 Ворта.∘∘∘∘∘∘∘∘∘

Поскольку мы установили, что 61+60+59=180∘∘∘∘, то 𝑚∠𝐴𝐵𝐶 можно определить как 60∘.

Теперь у нас есть это 𝑚∠𝑋=𝑚∠𝐴,𝑚∠𝑌=𝑚∠𝐵,𝑚∠𝑍=𝑚∠𝐶.

Поскольку существуют 3 пары соответствующих угловых мер, мы доказали, что △𝑋𝑌𝑍∼△𝐴𝐵𝐶.

Затем мы можем использовать эту информацию для определения длины 𝐴𝐶. Сторона 𝐴𝐶 в △𝐴𝐵𝐶 соответствует стороне 𝑋𝑍 в △𝑋𝑌𝑍.

Чтобы найти длину 𝐴𝐶, мы ищем другую пару соответствующих сторон, для которых нам даны измерения длины. Заметим, что нам дано, что соответствующие стороны 𝐵𝐶 и 𝑌𝑍 равны 22,8 см и 12 см соответственно.

Итак, мы можем написать оператор пропорции, а затем подставить значения длины. Это дает нам 𝐴𝐶𝑋𝑍=𝐵𝐶𝑌𝑍𝐴𝐶12,1=22,812.

Умножив обе части на 12,1, получим 𝐴𝐶=12,1×22,812=22,99 см

Следовательно, мы можем дать ответ, что длина 𝐴𝐶 равна 22,99 см.

В предыдущем примере мы сначала доказали, что два треугольника подобны, и использовали это, чтобы найти длину стороны. В следующем примере мы выйдем за рамки этого к нахождению длин сторон для выполнения дальнейшего вычисления: нахождения периметра треугольника. Напомним, что периметр многоугольника – это расстояние вокруг его внешний край.

Чтобы сделать это, нам нужно понять коэффициент сходства (часто называемый коэффициентом масштабирования) между двумя похожими формами. Рассмотрим подобные треугольники 𝐴𝐵𝐶 и 𝐴′𝐵′𝐶′ ниже.

Мы можем подтвердить, что △𝐴𝐵𝐶∼△𝐴′𝐵′𝐶′, так как все соответствующие длины сторон находятся в такая же пропорция. То есть мы можем написать, что 𝐴′𝐵′𝐴𝐵=𝐵′𝐶′𝐵𝐶=𝐶′𝐴′𝐶𝐴.

Подставляя длины любых двух соответствующих сторон, мы можем установить отношение подобия. При условии 𝐴𝐵=4см и 𝐴′𝐵′=8см, мы имеем, что отношение подобия от △𝐴𝐵𝐶 к △𝐴′𝐵′𝐶′ может быть определено как отношение сходства=𝐴′𝐵′𝐴𝐵=84=2.

Кроме того, поскольку периметр также является мерой длины, то периметры двух подобных треугольников (да и любых двух подобных многоугольников) будут равны в том же отношении, что и отношение подобия между ними.

Мы можем продемонстрировать это, вычислив периметры △𝐴𝐵𝐶 и △𝐴′𝐵′𝐶′ на рисунке выше следующим образом: периметрсмпериметрсм△𝐴𝐵𝐶=4+6+5=15,△𝐴′𝐵′𝐶′=8+12+10=30.

Тогда мы можем записать отношение периметров как периметр периметра△𝐴′𝐵′𝐶′△𝐴𝐵𝐶=3015=2.

Поскольку мы знаем, что коэффициент сходства между △𝐴𝐵𝐶 и △𝐴′𝐵′𝐶′ также равен 2, то мы подтвердили, что периметрпериметротношения подобия△𝐴′𝐵′𝐶′△𝐴𝐵𝐶=.

Теперь посмотрим, как это можно применить на следующем примере.

Пример 5. Нахождение периметра треугольника по сходству двух треугольников

𝐴𝐵𝐶𝐷 — прямоугольник, в котором 𝐴𝐷=21см, 𝐴𝑋=9см, а 𝑋𝑀=12см. Вычислите периметр △𝑌𝑀𝐶.

Ответ

Часто бывает полезно начать такой вопрос, записав на диаграмме любые заданные измерения длины и установив, что именно нас просят рассчитать.

Нам известно, что 𝐴𝐵𝐶𝐷 — прямоугольник, поэтому противоположные стороны параллельны и равны. Из схемы имеем, что 𝑋𝑌∥𝐴𝐵, поэтому мы знаем, что все 3 вертикальных отрезка параллельны: 𝑋𝑌∥𝐴𝐵∥𝐷𝐶. Поскольку 𝐴𝐵𝐶𝐷 — прямоугольник, тогда все 3 вертикальных отрезка перпендикулярны 𝐴𝐷 и 𝐵𝐶.

Посмотрим, есть ли у нас подобные треугольники на этом рисунке. Напомним, что два треугольника подобны, если у них соответствующие углы равны и соответствующие стороны в той же пропорции. Один из способов доказать, что два треугольника подобны, — показать, что соответствующие углы конгруэнтны. Давайте посмотрим, сможем ли мы использовать параллельные линии для определения дальнейших мер конгруэнтного угла.

Используя трансверсаль 𝐴𝐶, мы получаем, что ∠𝑋𝐴𝑀 альтернативно ∠𝑌𝐶𝑀; следовательно, 𝑚∠𝑋𝐴𝑀=𝑚∠𝑌𝐶𝑀.

Кроме того, у нас также есть пара вертикально противоположных углов: ∠𝑋𝑀𝐴 и ∠𝑌𝑀𝐶; следовательно, 𝑚∠𝑋𝑀𝐴=𝑚∠𝑌𝑀𝐶.

Как 𝑋𝑌∥𝐷𝐶 и тем, что мы знаем, что прямоугольник имеет прямой угол при ∠𝐴𝐷𝐶 соответствующий угол при ∠𝐴𝑋𝑀 будет конгруэнтным. Сходным образом, 𝑚∠𝐶𝐵𝐴=𝑚∠𝐶𝑌𝑀=90∘. Таким образом, у нас есть третья пара соответствующих углов в треугольниках: 𝑚∠𝐴𝑋𝑀=𝑚∠𝐶𝑌𝑀(=90).∘

Следовательно, поскольку у нас есть 3 пары равных углов, мы можем написать, что △𝑋𝑀𝐴∼△𝑌𝑀𝐶.

Мы можем использовать подобие этих треугольников, чтобы найти периметр △𝑌𝑀𝐶. Соотношение между периметрами двух подобных треугольников равно отношению любых двух соответствующих сторон (коэффициент подобия). Поскольку периметр — это расстояние вокруг внешнего края, мы можем вычислить периметр △𝑋𝑀𝐴, а затем применить коэффициент подобия из △𝑋𝑀𝐴 к △𝑌𝑀𝐶, чтобы определить периметр △𝑌𝑀𝐶.

Заметим, что у нас есть одна неизвестная длина стороны, 𝐴𝑀, в △𝑋𝑀𝐴. Однако, учитывая, что это прямоугольный треугольник, мы можем применить теорему Пифагора. Теорема Пифагора утверждает, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов двух других сторон.

Таким образом, если 𝑋𝑀=12 см и 𝐴𝑋=9 см, длину гипотенузы 𝐴𝑀 можно рассчитать как (𝐴𝑀)=(𝑋𝑀)+(𝐴𝑋)(𝐴𝑀)=12+9(𝐴𝑀)=144+81(𝐴𝑀)=225.

Затем мы можем извлечь квадратный корень из обоих сторон, а поскольку 𝐴𝑀 — это длина, мы рассматриваем только положительное значение. Следовательно, 𝐴𝑀=√225=15 см

Затем можно рассчитать периметр △𝑋𝑀𝐴, учитывая 𝐴𝑋=9 см, 𝑋𝑀=12см, а 𝐴𝑀=15см, в качестве периметрсм△𝑋𝑀𝐴=𝐴𝑋+𝑋𝑀+𝐴𝑀=9+12+15=36.

Затем мы определяем отношение подобия между двумя треугольниками, определяя длины пары соответствующих длин сторон. Хотя не появляется что у нас есть какие-либо измерения в △𝑌𝑀𝐶, мы используем свойство, что в прямоугольнике противоположные стороны конгруэнтны; таким образом, 𝐵𝐶=𝐴𝐷=21см. Кроме того, поскольку 𝐴𝑋𝑌𝐵 также образует прямоугольник, тогда 𝐵𝑌=𝐴𝑋=9см. Таким образом, мы можем вычислить длину 𝐶𝑌 как 𝐶𝑌=𝐵𝐶−𝐵𝑌=21−9=12.cm

Обратите внимание, что в подобных треугольниках 𝑋𝑀𝐴 и 𝑌𝑀𝐶 стороны 𝐶𝑌 (12 см) и 𝐴𝑋 (9см) соответствуют.

Мы можем определить коэффициент подобия от △𝑋𝑀𝐴 до △𝑌𝑀𝐶, используя эти соответствующие длины сторон как коэффициент сходства с△𝑋𝑀𝐴△𝑌𝑀𝐶=𝐶𝑌𝐴𝑋=129=43.

Как упоминалось ранее, отношение между периметрами двух подобных треугольников равно отношению между любыми двумя соответствующими сторонами. Учитывая, что периметр △𝑋𝑀𝐴 равен 36 см, мы умножаем это на отношение подобия от △𝑋𝑀𝐴 к △𝑌𝑀𝐶. Это дает периметрсм△𝑌𝑀𝐶=36×43=1443=48.

Таким образом, сначала доказав, что два треугольника подобны, и применив отношение подобия между треугольниками, мы определили, что периметр △𝑌𝑀𝐶 равен 48 см.

В предыдущем примере мы видели, что пара подобных треугольников образована параллельными прямыми и секущей внутри прямоугольника. В целом, у нас всегда есть подобные треугольники, созданные следующими двумя геометрическими расположениями, включающими параллельные линии, поскольку мы можем доказать, что альтернативные, соответствующие, а вертикально противоположные углы равны.

Таким образом, при решении задач, связанных с подобными треугольниками, очень важно уметь использовать и запоминать самые разнообразные свойства углов, такие как параллельные прямые, вертикально противоположные углы, сумма углов на прямой и сумма углов треугольника. В зависимости от решаемой проблемы, некоторые из этих свойств могут позволить нам доказать, что два треугольника подобны.

Подведем итоги.

Ключевые моменты

• У подобных треугольников соответствующие углы конгруэнтны, а соответствующие стороны пропорциональны.
• Мы можем доказать, что два треугольника подобны, если
  • соответствующих углов равны или
  • соответствующих сторон пропорциональны.
• При записи отношения подобия между двумя треугольниками важен порядок вершин. Соответствующие вершины должны быть в той же позиции в утверждении подобия.
• Отношение периметров двух подобных треугольников равно отношению любых двух соответствующих сторон.

Применение сходства треугольников — SAT Mathematics

Все ресурсы SAT по математике

137 Практические тесты Вопрос дня Карточки Learn by Concept

SAT Mathematics Help » Треугольники, линии и углы » Применение подобия треугольника

На приведенном выше рисунке длина отрезка AB равна 10, отрезка AC равна 8, отрезка BD равна 10, а отрезка DE равна 12. Каков периметр трапеции BCDE?

Возможные ответы:

36

28

32

24

Правильный ответ:

36

Объяснение:

Когда вы распаковываете данную информацию, несколько вещей должны выделяться:

1. Треугольники ABC и ADE подобны. Каждый из них имеет прямой угол, и каждый из них имеет общий угол в точке A, а это означает, что их нижние левые углы (в точках B и D) также будут одинаковыми, поскольку сумма всех углов в треугольнике должна равняться 180.  

2. Сторона BC должна быть равна 6, так как вам даны одна сторона (AC = 8) и гипотенуза (AB = 10) прямоугольного треугольника. Вы можете использовать для решения теорему Пифагора или распознать соотношение сторон 3-4-5 (которое здесь составляет треугольник 6-8-10).

3. Затем это позволяет использовать сходство треугольников для определения длин сторон большого треугольника. Поскольку гипотенуза равна 20 (отрезки AB и BD, каждая по 10, вместе образуют сторону, равную 20), и вы знаете, что это 3-4-5, как и меньший треугольник, вы можете заполнить сторону DE как 12 (удвоенная длина BC) и сегмент CE как 8.

Итак, теперь вы знаете размеры параллелограмма: BD — 10, BC — 6, CE — 8, DE — 12. Сумма этих четырех сторон равна 36.

 

Сообщить об ошибке

На рисунке выше треугольник ABC подобен треугольнику XYZ. Если сторона XZ равна 10, какова площадь треугольника XYZ?

Возможные ответы:

48

32

40

24

Правильный ответ: 309003 240002 Пояснение:

Поскольку треугольники подобны, вы можете сказать, что если гипотенуза большего треугольника равна 15, а гипотенуза меньшего треугольника равна 10, то отношение сторон треугольников равно 3:2. Это позволяет заполнить стороны XYZ: сторона XY равна 6 (что составляет 2/3 соответствующей стороны AB, равной 9) и поскольку YZ равно 8 (что составляет 2/3 его противоположной стороны, BC, равной 12).

Поскольку площадь треугольника равна  Основание * Высота, если вы знаете, что у вас есть основание 8 и высота 6, это означает, что площадь равна .

Сообщить об ошибке

В приведенном выше треугольнике отрезок BC равен 2, а отрезок CD равен 8. Если площадь треугольника ABD равна 25, то какова длина отрезка EC?

Возможные ответы:

Правильный ответ:

4

Пояснение:

В этой задаче важно понимать, что треугольники ABD и ECD подобны. У каждого есть прямой угол, и они имеют один и тот же угол в точке D, а это означает, что их третьи углы (BAD и CED, углы в верхнем левом углу каждого треугольника) также должны иметь одинаковую меру.

Зная это, вы можете использовать заданные длины сторон, чтобы установить соотношение между длинами сторон треугольников. Если BC равно 2, а CD равно 8, это означает, что нижние стороны треугольников равны 10 для большого треугольника и 8 для меньшего, или отношение 5:4.

Затем вам сообщают площадь большего треугольника. Зная, что площадь равна 25 и что площадь = Основание x Высота, вы можете подставить 10 в качестве основания и определить, что высота, сторона AB, должна быть равна 5.

Поскольку вы знаете, что высота меньшего треугольника будет равна длине 5, вы можете заключить, что сторона EC равна 4, и это ваш правильный ответ.

Сообщить об ошибке

Линии AD и BE пересекаются в точке C, как показано на рисунке. Какое из следующих отношений равно отношению длины отрезка АВ к длине отрезка АС?

Возможные ответы:

Длина стороны CD к длине стороны CE

Длина стороны CE к длине стороны ED

Длина стороны ED к длине стороны CD

Длина стороны ED к длине стороны CE

2 Правильный ответ 4:

Длина стороны от ED до длины стороны CD

Объяснение:

Приступая к этой задаче, важно отметить, что два изображенных треугольника, ABC и CED, подобны. У каждого из них прямой угол, и они имеют общий вертикальный угол в точке C, а это означает, что углы в A и D также должны быть равны, и поэтому треугольники подобны.

Это означает, что длины их сторон будут пропорциональны, что позволит вам ответить на этот вопрос. Вас просят сопоставить отношение AB к AC, которые представляют собой сторону, противоположную углу C, и гипотенузу соответственно. В треугольнике CED они отображаются на сторону ED и сторону CD, поэтому нужное соотношение равно ED:CD.

Сообщить об ошибке

Треугольник ABC подобен треугольнику DEF. Если периметр треугольника ABC в два раза больше длины периметра треугольника DEF, каково отношение площади треугольника ABC к площади треугольника DEF?

Возможные ответы:

1:2

3:1

4:1

1:4

Правильный ответ:

2 3 3

4 90 Пояснение:

Если периметр треугольника ABC в два раза длиннее периметра треугольника DEF, и вы знаете, что эти треугольники подобны, то это означает, что длина каждой стороны треугольника ABC в два раза больше соответствующей стороны в треугольнике DEF . Это также означает, что высоты имеют одинаковое соотношение 2:1: высота ABC в два раза больше длины высоты DEF.

Поскольку формула площади треугольника – основание x высота, вы можете выразить площадь треугольника DEF как bh, а площадь ABC – как . Затем вы увидите, что площади от ABC до DEF равны  и bh, что соответствует отношению 4:1.

ПРИМЕЧАНИЕ. Может показаться удивительным, что отношение не равно 2:1, если каждая длина одного треугольника вдвое превышает соответствующую длину другого треугольника. Но имейте в виду, что для площади вы умножаете две длины вместе и переходите от единицы, такой как «дюймы», к единице, такой как «квадратные дюймы». Поскольку каждая длина умножается на 2, эффект усугубляется.

Сообщить об ошибке

На приведенном выше рисунке линии DG, CF и BE параллельны. Если отрезок AB = 6, отрезок AE = 9, отрезок EF = 10 и отрезок FG = 11, какова длина отрезка AD?

Возможные ответы:

22

20

23

21

Правильный ответ: 30

209002 Объяснение:

Ключом к решению этой проблемы является осознание того, что вы имеете дело с подобными треугольниками. Поскольку прямые BE, CF и DG параллельны, это означает, что верхний треугольник ABE подобен двум большим треугольникам, ACF и ADG. Вы знаете это, потому что все они имеют один и тот же угол A, и тогда, если все горизонтальные линии параллельны, то два нижних угла каждого треугольника также будут конгруэнтны. Вы установили сходство через угол-угол-угол.

Это означает, что соотношение сторон будет одинаковым для каждого треугольника. А для верхнего треугольника ABE вы знаете, что отношение левой стороны (AB) к правой стороне (AE) составляет 6 к 9 или отношение 2 к 3. Обратите внимание, что остальная часть данной информации дает вам длина всей правой стороны, прямой AG, большего треугольника ADG. Если AE равно 9, EF равно 10, а FG равно 11, то сторона AG равна 30. А поскольку вы знаете, что отношение левой стороны к правой составляет 2:3, то отрезок AD должен быть равен 20.

Сообщить об ошибке

На приведенном выше рисунке отрезок AC параллелен отрезку BD. Если отрезок AC = 15, отрезок BD = 10 и отрезок CE = 30, какова длина отрезка CD?

Возможные ответы:

25

10

20

15

Правильный ответ: 30

109002 Пояснение:

Эта задача проверяет концепцию подобных треугольников. Во-первых, вы должны признать, что треугольник ACE и треугольник BDE подобны. Вы знаете это, потому что все они имеют одинаковую угловую меру: они делят угол, созданный в точке E, и каждая из них имеет 9Угол 0 градусов, поэтому угол CAE должен соответствовать углу DBE (верхний левый угол в каждом треугольнике).

Поскольку эти треугольники подобны, их размеры будут пропорциональны. Поскольку стороны, AC и BD пропорциональны сторонам, поскольку они оба напротив того же угла, E — делите соотношение 3 : 2, и вы знаете, что каждая сторона меньшего треугольника (BDE) будет такой же длины, как и ее аналог в большем треугольнике (ACE). Следовательно, если нижняя сторона CE в сторона большего треугольника равна 30, то пропорциональная сторона меньшего треугольника (сторона DE) будет такой же длинной, как и 20,

Так как вопрос касается длины CD, вы можете принять сторону CE (30) и вычесть DE (20), чтобы получить правильный ответ, 10.

Сообщить об ошибке

AD и BE пересекаются в точке C. Какова длина отрезка BE?

Возможные ответы:

25

20

28

18

Правильный ответ: 309003 25002 Объяснение:

Эта задача зависит от вашей способности распознавать две важные темы: во-первых, треугольник ABC является особым прямоугольным треугольником с соотношением сторон 6-8-10, что позволяет подставить 8 вместо стороны AB. А во-вторых, треугольники ABC и CDE — подобные треугольники. Вы знаете это, потому что каждый треугольник помечен как прямоугольный, а углы ACB и ECD являются вертикальными углами, что означает, что они конгруэнтны. Поскольку сумма всех углов треугольника должна быть равна 180, если два угла одинаковы, то и третий тоже должен быть равен, так что у вас здесь похожие треугольники.

Зная это, вы знаете, что треугольник ECD соответствует соотношению 3-4-5 (упрощенная версия 6-8-10), поэтому, если сторона, противоположная углу C в ABC, равна 8, а в CDE равна 12, то вы знаете, что у вас есть треугольник 9-12-15. Зная, что сторона CE равна 15, вы можете прибавить ее к стороне BC, равной 10, и вы получите ответ 25.

Сообщить об ошибке

На диаграмме выше линия JX параллельна линии KY. Если длина JX равна 16, KY равна 8, а площадь треугольника JXZ равна 80, какова длина отрезка XY?

Возможные ответы:

Правильный ответ:

5

Пояснение:

Важным моментом в этой задаче является то, что треугольники JXZ и KYZ подобны. У каждого есть прямой угол, и каждый имеет общий угол в точке Z, поэтому третьи углы (XJZ и YKZ, каждый в верхнем левом углу своего треугольника) также должны быть одинаковыми.

Учитывая, что, если вы знаете, что размер JX равен 16, а размер KY равен 8, вы знаете, что каждая сторона большего треугольника в два раза длиннее противоположной стороны меньшего треугольника.

У вас также достаточно информации для вычисления стороны XZ, поскольку вам дана площадь треугольника JXZ и линия JX, которая может служить его высотой (помните, что для использования уравнения основания x высоты для площади треугольника , вам нужно, чтобы основание и высота были перпендикулярны; линии JX и XZ перпендикулярны). Поскольку , вы можете видеть, что XZ должно быть равно 10. А так как XZ будет в два раза длиннее YZ по коэффициенту сходства, YZ = 5, а это означает, что XY также должно быть равно 5.

Сообщить об ошибке

Для изображенных треугольников ABC и XYZ, какое из следующих чисел равно отношению ?

Возможные ответы:

Правильный ответ:

Объяснение:

Первое, что важно отметить в этой задаче, это то, что для каждого треугольника вам даны два угла: прямой угол и еще один угол. Поскольку сумма всех углов треугольника должна составлять 180 градусов, это означает, что вы можете найти недостающие углы.

В ABC у вас есть углы 36 и 90, что означает, что для суммы 180 недостающий угол ACB должен быть 54. А в XYZ у вас есть углы 90 и 54, что означает, что недостающий угол XZY должен быть 36.

Далее , вы можете заметить, что оба треугольника имеют одинаковые углы: 36, 54 и 90.  Это означает, что треугольники подобны, а значит, и отношения их сторон будут одинаковыми. Вам просто нужно убедиться, что вы сопоставляете стороны на основе углов, под которыми они находятся.

Вам дано отношение AC к BC, которое в треугольнике ABC равно отношению стороны, противоположной прямому углу (AC), к стороне, противоположной углу 54 градуса (BC). В треугольнике XYZ эти стороны равны XZ и XY, поэтому искомое соотношение равно .

 

Сообщить об ошибке

Уведомление об авторских правах

Все ресурсы по математике SAT

137 Практические тесты Вопрос дня Карточки Learn by Concept

4.

2: Подобные треугольники — Математика LibreTexts

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

34136

• Генри Африк
• Нью-Йоркский технологический колледж CUNY через Нью-Йоркский городской технологический колледж в CUNY Academic1 Works4 Works

  Два треугольника называются подобными, если у них равные множества углов. На рисунке \(\PageIndex{1}\) \(\треугольник ABC\) подобен \(\треугольнику DEF.\) Углы, которые равны, называются соответствующие углы . На рисунке \(\PageIndex{1}\) \(\угол A\) соответствует \(\угол D\), \(\угол B\) соответствует \(\угол E\) и \(\ угол C\) соответствует \(\угол F\). Стороны, соединяющие соответствующие вершины, называются соответствующими сторонами . На рисунке \(\PageIndex{1}\) \(AB\) соответствует \(DE\), \(BC\) соответствует \(EF\), а \(AC\) соответствует \(DF\ ). Символом подобного является \(\sim\). Оператор подобия \(\triangle ABC \sim \triangle DEF\) всегда будет записываться так, чтобы соответствующие вершины отображались в одном и том же порядке.

  Для треугольников на рисунке \(\PageIndex{1}\) мы могли бы также написать \(\triangle BAC \sim \triangle BDF\) или \(\triangle ACB \sim \triangle DFE\), но никогда \(\ треугольник ABC \sim \треугольник EDF\) или \(\треугольник ACB \sim \треугольник DEF\).

  Рисунок \(\PageIndex{1}\): \(\треугольник ABC\) похож на \(\треугольник DEF\).

  Мы можем сказать, какие стороны соответствуют из заявления подобия. Например, если \(\треугольник ABC \sim \треугольник DEF\), то сторона \(AB\) соответствует стороне \(DE\), поскольку обе являются первыми двумя буквами. \(BC\) соответствует \(EF\), потому что оба являются двумя последними буквами, \(AC\) соответствует \(DF\), потому что оба состоят из первой и последней букв. 9{\circ} \nonumber\]

  Следовательно, оба треугольника имеют одинаковые углы и \(\треугольник ABC \sim \треугольник EFD\).

  Ответ : \(\треугольник ABC \sim \треугольник EFD\).

  Пример А предполагает, что для доказательства подобия нужно только знать, что два соответствующих угла равны:

  Теорема \(\PageIndex{1}\)

  Два треугольника подобны, если два угла одного равны двум углам другого \((AA = AA)\).

  На рисунке \(\PageIndex{2}\), \(\треугольник ABC \sim \треугольник DEF\), поскольку \(\угол A = \угол D\) и \(\угол B = \угол E\) . 9{\circ} — (\угол D + \угол E) = \угол F\).

  Пример \(\PageIndex{2}\)

  Определите, какие треугольники подобны, и напишите утверждение о сходстве: параллельные линии. \(\угол C = \угол C\) из-за тождества. Поэтому \(\треугольник ABC \sim \треугольник DEC\) через \(AA = AA\).

  Ответ : \(\треугольник ABC \sim \треугольник DEC\). 9{\circ}\). Поэтому

  Ответ: \(\треугольник ABC \sim \треугольник ACD \sim \треугольник CBD\).

  Подобные треугольники важны из-за следующей теоремы:

  Теорема \(\PageIndex{2}\)

  Соответствующие стороны подобных треугольников пропорциональны. Это означает, что если \(\triangle ABC \sim \triangle DEF\), то

  \(\dfrac{AB}{DE} = \dfrac{BC}{EF} = \dfrac{AC}{DF}\).

  То есть первые две буквы \(\треугольник ABC\) относятся к первым двум буквам \(\треугольник DEF\), а последние две буквы \(\треугольник ABC\) относятся к последним двум буквам в \(\треугольник DEF\) как первая и последняя буквы \(\треугольник ABC\) к первой и последней буквам \(\треугольник DEF\).

  Прежде чем пытаться доказать теорему \(\PageIndex{2}\), мы приведем несколько примеров ее использования:

  Пример \(\PageIndex{4}\)

  Найти \(x\):

  Решение

  \(\угол A = \угол D\) и \(\угол B = \угол E \) так что \(\треугольник ABC \sim \треугольник DEF\). По теореме \(\PageIndex{2}\),

  \(\dfrac{AB}{DE} = \dfrac{BC}{EF} = \dfrac{AC}{DF}\).

  Здесь мы проигнорируем \(\dfrac{AB}{DE}\), поскольку мы не знаем и не должны находить ни \(AB\), ни \(DE\).

  \[\begin{array} {rcl} {\dfrac{BC}{EF}} & = & {\dfrac{AC}{DF}} \\ {\dfrac{8}{x}} & = & {\dfrac{2}{3}} \\ {24} & = & {2x} \\ {12} & = & {x} \end{массив}\]

  Проверить:

  Ответ: \ (х = 12\).

  Пример \(\PageIndex{5}\)

  Найти \(x\):

  Решение

  \(\угол A = \угол A, \угол ADE = \угол ABC\), поэтому \(\треугольник ADE \sim \треугольник ABC\) на \(AA = AA\).

  \(\dfrac{AD}{AB} = \dfrac{DE}{BC} = \dfrac{AE}{AC}\).

  Мы игнорируем \(\dfrac{AD}{AB}\).

  \[\begin{array} {rcl} {\dfrac{DE}{BC}} & = & {\dfrac{AE}{AC}} \\ {\dfrac{5}{15}} & = & {\ dfrac {10} {10 + x}} \\ {5 (10 + x)} & = & {15 (10)} \\ {50 + 5x} & = & {150} \\ {5x} & = & {150 — 50} \\ {5x} & = & {100} \\ {x} & = & {20} \end{массив}\]

  Проверка:

  Ответ: \(x = 20\).

  Пример \(\PageIndex{6}\)

  Найдите \(x\):

  Решение

  \(\угол A = \угол CDE\), так как они являются соответствующими углами параллельных прямых. \(\угол C = \угол C\) из-за тождества. Поэтому \(\треугольник ABC \sim \треугольник DEC\) через \(AA = AA\).

  \(\dfrac{AB}{DE} = \dfrac{BC}{EC} = \dfrac{AC}{DC}\)

  Мы игнорируем \(\dfrac{BC}{EC}\):

  \[\ begin {массив} {rcl} {\ dfrac {AB} {DE}} & = & {\ dfrac {AC} {DC}} \\ {\ dfrac {x + 5} {4}} & = & {\dfrac{x + 3}{3}} \\ {(x + 5)(3)} & = & {(4)(x + 3)} \\ {3x + 15} & = & {4x + 12} \\ {15 — 12} & = & {4x — 3x} \\ {3} & = & {x} \end{массив}\] 92 + 12x — 64} & = & {0} \\ {(x — 4)(x + 16)} & = & {0} \\ {x = 4\ \ \ \ \ \ \ \ x} & = & {-16} \end{array}\]

  Мы отвергаем ответ \(x = -16\), потому что \(AD = x\) не может быть отрицательным.

  Проверка, \(x = 4\)

  Ответ: \(x = 4\).

  Пример \(\PageIndex{8}\)

  Дерево отбрасывает тень длиной 12 футов, в то время как 6-футовый человек отбрасывает тень длиной 4 фута. Какова высота дерева?

  9{\circ}\), мы имеем \(\треугольник ABC \sim \треугольник DEF\) через \(AA = AA\).

  \[\begin{array} {rcl} {\dfrac{AC}{DF}} & = & {\dfrac{BC}{EF}} \\ {\dfrac{4}{12}} & = & {\dfrac{6}{x}} \\ {4x} & = & {72} \\ {x} & = & {18} \end{массив}\]

  Ответ: \(x = 18\) ноги.

  Доказательство теоремы \(\PageIndex{2}\) («Соответствующие стороны подобных треугольников пропорциональны»):

  Проиллюстрируем доказательство треугольниками из примера \(\PageIndex{4}\) (рисунок \(\PageIndex{3}\)). Доказательство для других подобных треугольников следует той же схеме. Здесь мы докажем, что \(x = 12\), так что \(\dfrac{2}{3} = \dfrac{8}{x}\).

  Рисунок \(\PageIndex{3}\). Треугольники из примера \(\PageIndex{4}\).Рисунок \(\PageIndex{4}\): нарисуйте линии, параллельные сторонам \(\треугольника ABC\) и \(\треугольника DEF\).

  Сначала нарисуйте линии, параллельные сторонам \(\треугольника ABC\) и \(\треугольника DEF\), как показано на рисунке \(\PageIndex{4}\). Соответствующие углы этих параллельных прямых равны, и каждый из параллелограммов со стороной, равной 1, имеет и противоположную сторону, равную 1. Следовательно, все маленькие треугольники со стороной, равной 1, конгруэнтны по формуле \(AAS = AAS \). Соответствующие стороны этих треугольников образуют сторону \(BC = 8\) треугольника \(\треугольник ABC\) (см. рисунок \(\PageIndex{5}\)). Следовательно, каждая из этих сторон должна быть равна 4 и \(x = EF = 4 + 4 + 4 = 12\) (рисунок \(\PageIndex{6}\)).

  Рисунок \(\PageIndex{5}\). Маленькие треугольники конгруэнтны, поэтому каждая из соответствующих сторон, лежащих на \(BC\), должна быть равна 4.Рисунок \(\PageIndex{6}\). Маленькие треугольники \(\треугольник DEF\) конгруэнтны малым треугольникам \(\треугольник ABC\), следовательно \(x = EF = 4 + 4 + 4 = 12\).

  (Примечание для инструктора: это доказательство можно провести, когда длины сторон треугольников являются рациональными числами. Однако, поскольку иррациональные числа могут быть сколь угодно точно приближены рациональными числами, доказательство распространяется и на этот случай. )

  Историческая справка

  Фалес (ок. 600 г. до н.э.) использовал пропорциональность сторон подобных треугольников для измерения высоты пирамид в Египте. Его метод был очень похож на тот, который мы использовали в примере \(\PageIndex{8}\) для измерения высоты деревьев.

  Рисунок \(\PageIndex{7}\). Использование подобных треугольников для измерения высоты пирамиды.

  На рисунке \(\PageIndex{7}\) \(DE\) представляют высоту пирамиды, а \(CE\) — длину ее тени. \(BC\) представляет собой вертикальную палку, а \(AC\) — длину ее тени. У нас есть \(\треугольник ABC\sim\треугольник CDE\). Фалес смог непосредственно измерить длины \(AC, BC\) и \(CE\). Подставив эти значения в пропорцию \(\dfrac{BC}{DE} = \dfrac{AC}{CE}\), он смог найти высоту \(DE\).

  1 — 6. Определите, какие треугольники аналогичны, и напишите заявление об сходстве:

  1.

  2.

  3.

  4.

  5.

  6.

  7 — 22. Для каждого из следующих

  (1) напишите определение подобия

  (2) напишите соотношение между соответствующими сторонами

  (3) найдите \(x\) или \(x\) и \(у\).

  7.

  8.

  9.

  10.

  11.

  12.

  13.

  14.

  15.

  16.

  17.

  18.

  19.

  20.

  21.

  22.

  23. А. 80 футов в длину, в то же время 5-футовый мальчик отбрасывает тень длиной 4 фута. Насколько высок флагшток?

  24. Найдите ширину \(AB\) реки:

  ---

  Эта страница под названием 4.2: Similar Triangles публикуется в соответствии с лицензией CC BY-NC-SA 4.0 и была создана, изменена и/или курирована Генри Африком (Нью-Йоркский технологический колледж в CUNY Academic Works) через исходный контент, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.

  1. Наверх
  • Была ли эта статья полезной?

  1. Тип изделия

     Раздел или страница

     Автор

     Генри Африк

     Лицензия

     СС BY-NC-SA

     Версия лицензии

     4,0

     Показать страницу Содержание

     нет

  2. Метки

     1. соответствующие стороны
     2. подобных треугольников
     3. источник@https://academicworks. cuny.edu/ny_oers/44

  Калькулятор похожих треугольников

  Этот калькулятор подобных треугольников поможет вам найти подобный треугольник путем масштабирования известного треугольника . Вы также можете использовать этот калькулятор, чтобы найти недостающую длину подобного треугольника!

  Пролистайте эту статью, пока мы обсуждаем законы подобных треугольников и изучаем некоторые основы:

  • Что такое подобные треугольники?
  • Нахождение подобных треугольников: как определить, подобны ли два треугольника?
  • Как найти недостающую сторону подобного треугольника?
  • Как найти площадь подобного треугольника?

  Что такое подобные треугольники?

  Два треугольника подобны , если их соответствующие стороны находятся в одинаковом отношении , что означает, что один треугольник является масштабированной версией другого. Естественно, что соответствующих углов подобных треугольников равны . Например, рассмотрим следующие два треугольника:

  Стороны △ABC\треугольника \text{ABC}△ABC и △DEF\треугольника \text{DEF}△DEF пропорциональны.

  Обратите внимание, что соответствующие стороны пропорциональны:

  DEAB=EFBC=DFAC=2\frac{\text{DE}}{\text{AB}} = \frac{\text{EF}}{\text{BC }} =\frac{\text{DF}}{\text{AC}} = 2ABDE​=BCEF​=ACDF​=2

  Следовательно, мы можем сказать △ABC\треугольник \text{ABC}△ABC ∼\ sim∼ △DEF\треугольник \text{DEF}△DEF. Здесь символ ∼\sim∼ указывает на то, что треугольники подобны.

  Мы называем долю сходства масштабным коэффициентом (k)(k)(k). В приведенном выше примере коэффициент масштабирования k=2k = 2k=2. Если вам нужна помощь в поиске коэффициентов, воспользуйтесь нашим калькулятором коэффициентов.

  Нахождение подобных треугольников: закон подобных треугольников

  Мы знаем, что два треугольника подобны, если верно любое из следующих утверждений:

  • соответствующие стороны треугольника находятся в пропорции ; или
  • соответствующие углы равны.

  Отсюда мы можем вывести специальные правила для определения того, подобны ли любые два треугольника:

  1. Сторона-сторона-сторона (SSS) : Если все три соответствующие стороны из двух треугольников составляют пропорцию , они подобны. Это правило является самым простым и требует, чтобы вы знали все стороны треугольников.
  Все стороны треугольников △ABC\треугольник \text{ABC}△ABC и △DEF\треугольник \text{DEF}△DEF должны быть известны и пропорциональны друг другу.

  Мы можем выразить это, используя аналогичную формулу треугольника:

  DEAB=EFBC=DFAC=k\qquad \frac{\text{DE}}{\text{AB}} = \frac{\text{EF}}{\ text{BC}} =\frac{\text{DF}}{\text{AC}} = kABDE​=BCEF​=ACDF​=k

  где kkk — масштабный коэффициент .

  2. Сторона-Угол-Сторона (SAS): Если любые две соответствующие стороны двух треугольников находятся в пропорции и их углы равны равны , то треугольники подобны. Мы можем использовать это правило всякий раз, когда нам известны только две стороны каждого треугольника и прилежащие к ним углы.
  Любые две пары сторон должны быть пропорциональны, а их вписанные углы должны быть равны.

  Треугольники на изображении выше подобны, если:

  DEAB=DFAC=k,and∠BAC=∠EDF\qquad \begin{align*} &\frac{\text{DE}}{\text{AB}} = \frac{\text{DF}}{\text{AC}} = k, \text{and}\\\\ & \угол\текст{BAC} = \угол\текст{EDF} \end{align*}​ABDE​=ACDF​=k,and∠BAC=∠EDF​

  Это правило удобно в случаях, как на изображении ниже, где треугольники имеют общий угол:

  Треугольники △ABC\triangle \text{ABC}△ABC и △PBQ\треугольник \text{PBQ}△PBQ имеют общий угол. В таких случаях проще проверить критерий SAS.

  Вы можете многое сделать, зная только сторону-угол-сторону треугольника. Узнайте больше, используя наш калькулятор треугольников SAS.

  3. Угол-Сторона-Угол (ASA) : Если любые два соответствующих угла двух треугольников равны и соответствующие стороны между ними пропорциональны, треугольники подобны.
  Два треугольника с двумя парами равных углов подобны. Знание соответствующих сторон поможет определить их масштабный коэффициент.

  Треугольники на изображении выше подобны, если:

  ∠BAC=∠EDF, ∠ABC=∠DEF и DEAB=k\qquad \begin{align*} & \угол\текст{BAC} = \угол\текст{EDF}, \\ & \angle\text{ABC} = \angle\text{DEF}, \text{ и}\\\\ &\frac{\text{DE}}{\text{AB}} = k \end{align*}​∠BAC=∠EDF,∠ABC=∠DEF и ABDE​=k​

  Вы можете найти третий угол , если знаете любые два угла в треугольнике, используя наш калькулятор углов треугольника. Мы знаем, что если любые два соответствующих угла в треугольниках равны, то треугольники подобны, а это означает, что в Правило соответствия ASA , нам не нужно знать сторону, пока известны углы. Однако без сторон мы не можем определить масштабный коэффициент ккк.

  Как найти недостающую сторону подобного треугольника?

  Чтобы найти отсутствующую сторону треугольника , используя соответствующую сторону подобного треугольника , выполните следующие действия: отношение любой известной стороны большего треугольника и соответствующей ей стороны меньшего.

• Определите , является ли треугольник с отсутствующей стороной меньшим или большим .
• Если треугольник на меньше , разделите его соответствующую сторону в большем треугольнике на k , чтобы получить недостающую сторону . В противном случае умножьте на соответствующую сторону меньшего треугольника на 9.1107 k , чтобы найти недостающую сторону .

Например, рассмотрим следующие два подобных треугольника.

Два подобных треугольника △ABC\треугольник \text{ABC}△ABC и △DEF\треугольник \text{DEF}△DEF, где сторона AC\text{AC}AC неизвестна.

Чтобы найти недостающую сторону, мы сначала вычисляем их масштабный коэффициент .

k=DEAB=84=2k = \frac{\text{DE}}{\text{AB}} = \frac{8}{4} = 2k=ABDE​=48​=2

Далее используйте отношение коэффициента масштабирования между отсутствует сторона AC и ее соответствующая сторона DF :

DFAC=k=2AC=DF2=62AC=3\begin{align*} \frac{\text{DF}}{\text{AC}} &= k=2\\[1em] \text{AC} &= \frac{\text{DF}}{2} = \frac{6}{2}\\[1em] \текст{АС} &= 3 \end{align*}ACDF​ACAC​=k=2=2DF​=26​=3​

Как найти площадь подобного треугольника?

Чтобы найти площадь треугольника A1 по площади подобного ему треугольника A2 , выполните следующие действия:

1. Найдите масштабный коэффициент k подобных треугольников, взяв отношение любой известной стороны большего треугольника и соответствующей ему стороны меньшего треугольника.
2. Определите , является ли треугольник с неизвестной площадью на меньше или на больше .
3. Если треугольник меньше, разделите A2 на квадрат масштабного коэффициента k , чтобы получить А1 = А2/к ² . В противном случае умножьте A2 на k ² , чтобы получить A1 = A2 × k ² .

Как пользоваться этим калькулятором подобных треугольников

Теперь, когда вы узнали, как найти длину подобного треугольника, формулу для подобных треугольников и многое другое, вы можете быстро понять, как работает этот калькулятор подобных треугольников.

Чтобы проверить, подобны ли два известных треугольника, используйте этот калькулятор следующим образом:

1. Выберите проверьте сходство в поле Введите .
2. Выберите критерий сходства, который вы хотите использовать. Вы можете выбрать между Side-Side-Side, Side-Angle-Side и Angle-Side-Angle .
3. Введите размеры двух треугольников. Калькулятор оценит, похожи они или нет.

Чтобы использовать этот калькулятор для расчета стороны или периметра подобных треугольников, выполните следующие действия:

1. Выберите найдите недостающую сторону в поле Введите .
2. Введите известные размеры, площадь, периметр и масштабный коэффициент треугольников. Калькулятор подобных треугольников найдет неизвестные значения.

Часто задаваемые вопросы

Все равносторонние треугольники подобны?

Да , если соответствующие углы двух треугольников равны, треугольники подобны. Так как каждый угол равностороннего треугольника равен 60° , все равносторонние треугольники подобны.

Найдите масштабный коэффициент подобных треугольников, площади которых равны 10 см² и 20 см²?

1,414 . Чтобы определить этот коэффициент масштабирования на основе двух площадей, выполните следующие действия:

1. Разделите большую площадь на меньшую, чтобы получить 20/10 = 2 .
2. Найдите квадратный корень из этого значения, чтобы получить масштабный коэффициент , k = √2 = 1,414 .
3. Проверьте этот результат с помощью калькулятора подобных треугольников Omni.

Подобные треугольники на GRE | GRE Geometry

Последнее обновление 30 ноября 2021 г.

Существует множество способов проверки треугольников на GRE. Например, вам может понадобиться найти площадь или периметр треугольника или использовать теорему Пифагора, чтобы найти длину стороны. В этой статье мы обсудим подобные треугольники, которые представлены в некоторых сложных вопросах GRE. Наше обсуждение будет включать в себя свойства подобных треугольников и некоторые из наиболее распространенных способов появления этих треугольников в GRE.

Начнем с изучения подобных треугольников.

• Что такое подобные треугольники?
• Properties of Similar Triangles
• Similar Triangles Examples
  • Similar Triangles – Example 1
  • Similar Triangles – Example 2
  • Similar Triangles – Example 3
• Similar Triangles Problems
  • Question 1
  • Question 2

Получите более высокий балл GRE Начните учиться в TTP сегодня! ПОПРОБУЙТЕ НАШ КУРС GRE ЗА 199 ДОЛЛАРОВ США0003

Что такое re Подобные треугольники?

Подобные треугольники — это треугольники, которые имеют одинаковую форму, но не обязательно одинаковый размер. Это происходит, когда их соответствующие углы равны. Подобные треугольники, имеющие одинаковую форму и размер, называются конгруэнтными треугольниками.

КЛЮЧЕВОЙ ФАКТ:

Подобные треугольники имеют одинаковую форму, но не обязательно одинаковый размер.

Теперь обсудим свойства подобных треугольников.

Свойства подобных треугольников

Хотя нам может казаться, что мы можем «на глаз» определить сходство треугольников, этот метод не рекомендуется, так как многие геометрические фигуры в GRE нарисованы не в масштабе. Давайте вместо этого обратимся к следующим критериям, которые помогут нам решить, действительно ли треугольники подобны. Мы будем знать, что два треугольника подобны, если верно любое из следующих утверждений:

1. Две пары соответствующих углов равны. Если два угла равны, то должен быть равен и третий угол.
2. Три пары соответствующих сторон пропорциональны. Если все три стороны пропорциональны попарно, мы знаем, что все три угла должны быть равны и попарно.
3. Две пары соответствующих длин сторон пропорциональны И угол между этими сторонами одинаков.

КЛЮЧЕВОЙ ФАКТ:

Треугольники подобны, если: (1) Две пары соответствующих углов равны; или (2) три пары соответствующих сторон равны; или (3) длины двух соответствующих сторон равны, и угол между этими сторонами одинаков.

Давайте теперь рассмотрим некоторые распространенные типы подобных треугольников, которые вы можете увидеть в GRE.

Примеры подобных треугольников

Примеры подобных треугольников 1:

Глядя на рисунок выше, мы можем определить, что два вертикальных угла, ACB и ECD, должны быть равны. Пока мы знаем, что любые другие пары соответствующих углов равны, мы можем определить, что у нас есть подобные треугольники. Например, если нам известно, что угол BAC равен углу CDE, то мы знаем, что углы ABC и DEC также должны быть равны, и, следовательно, эти два треугольника подобны.

Получите более высокий балл GRE Начните учиться в TTP сегодня! ПОПРОБУЙТЕ НАШ КУРС GRE ЗА $1

Подобные треугольники – Пример 2:

Треугольники AED и ABC подобны, если сторона ED параллельна стороне BC. Имея эту информацию, мы знаем, что соответствующие углы AED и ABC равны, а соответствующие углы ADE и ACB равны. Так как у нас есть две пары равных углов, у нас есть подобные треугольники. (Обратите внимание, что углы BAC и EAD на самом деле являются одним и тем же углом, и поэтому, конечно, они также равны.)

Подобные треугольники – пример 3:

В приведенном выше примере у нас есть три подобных треугольника: ABC, ABD и ACD. Эти три треугольника подобны, потому что каждый из них имеет прямой угол, а каждый из двух меньших треугольников имеет общий угол с большим треугольником ABC. Угол B является общим как для треугольника ABC, так и для треугольника ADB, а угол C является общим как для треугольника ABC, так и для треугольника ACD. Еще раз, поскольку мы видим, что каждый треугольник имеет два равных угла, мы знаем, что эти три треугольника подобны. Если это трудно увидеть, мы можем проиллюстрировать это, положив x = углу C, а затем мы можем заполнить остальные углы треугольников.

Таким образом, упрощенные углы выглядят следующим образом:

Мы видим, что каждый треугольник имеет углы x, 90 и 90 – x.

СОВЕТ TTP PRO:

Запомните схемы, на которых представлены подобные треугольники на GRE.

Теперь давайте потренируемся с двумя примерами вопросов.

Получите более высокий балл GRE Начните учиться в TTP сегодня! ПОПРОБУЙТЕ НАШ КУРС GRE ЗА $1

Похожие задачи на треугольники

Вопрос 1

На рисунке выше указаны меры некоторых внутренних углов и сторон треугольников ABC и DEF. Какова длина стороны DE?

1. 5
2. 6
3. 7
4. 8
5. 9

Решение. Точно так же угол DEF равен 180 – (60 + 64) = 56 градусов. Мы видим, что оба треугольника имеют внутренние углы 56°, 60° и 64°. Напомним, что когда все три внутренних угла треугольника равны внутренним углам другого треугольника, эти два треугольника подобны. Напомним также, что стороны подобных треугольников пропорциональны.

В треугольнике ABC длина стороны, противоположной углу 56°, равна 3. В треугольнике DEF сторона, противоположная углу 56°, имеет длину 6. Так как одна сторона треугольника DEF в два раза длиннее соответствующей стороны треугольника ABC, а так как эти треугольники подобны, то все стороны треугольника DEF в два раза длиннее соответствующих сторон треугольника ABC. Обратите внимание, что стороны BC и DE противолежащие друг другу под углом 60°, а значит, эти стороны равны. Отсюда следует, что длина DE должна быть вдвое больше длины BC. Таким образом, длина стороны DE равна 2 ⨉ 4 = 8,

Ответ: D

Вопрос 2

На приведенном выше рисунке отрезок DE параллелен отрезку BC, длина AD равна 5, длина DB равна 10, а длина BC равна 18.

Количество A
Длина отрезка DE

Количество B
6

Решение:

Угол DE равен углу ABCDE, и угол DE параллелен углу ABCDE. угол AED равен углу ACB. Таким образом, треугольник ADE и треугольник ABC подобны. Обратите внимание, что сторона AD треугольника ADE соответствует стороне AB треугольника ABC, а сторона DE треугольника ADE соответствует стороне BC треугольника ABC. Напомним, что отношения соответствующих сторон двух подобных треугольников равны. Следовательно, должно быть верно следующее:

Длина стороны AD/длина стороны AB = длина стороны DE/длина стороны BC

Обратите внимание, что сторона AB представляет собой комбинацию отрезков AD и DB, поэтому длина стороны AB равна 5 + 10 = 15. Мы теперь можно положить длину стороны DE = n, и мы получим следующее:

5/15 = n/18

Перемножив, мы получим следующее:

15n = 18 × 5

15n = 90

n = 6

Длина стороны DE = 6

Мы видим, что количество A равно количеству B.

Ответ: C

В этой статье мы рассмотрели лишь небольшую часть темы геометрии путем сближения подобных треугольников. Если вы хотите узнать больше о вопросах по геометрии GRE, вы можете посетить курс подготовки к целевому тесту GRE с самым высоким рейтингом.

Получите более высокий балл GRE Начните учиться в TTP сегодня! ПОПРОБУЙТЕ НАШ КУРС GRE ЗА $1

Подобные приложения Треугольники | Мир математики Пасси


Источник изображения: http://www.howitworksdaily.com

Мощный зум-объектив для 35-мм камеры может быть очень дорогим, потому что на самом деле он содержит несколько высокоточных стеклянных линз, которые необходимо перемещать с помощью крошечного мотора в очень точное положение, когда камера автоматически фокусируется.

Геометрия и математика этих линз очень сложны, и их нельзя просто массово производить и тестировать с помощью компьютерных роботов.

Для изготовления этих линз требуется много усилий, что приводит к их очень высокой цене.

Вот диаграмма, показывающая, как меняется внутреннее расположение зум-объектива при увеличении от 18 мм широкоугольного до 200 мм при полном увеличении:


Источник изображения: http://www.canon.com

 


Изображение Copyright 2013 by Passy’s World of Mathematics

Выше показаны некоторые фотографии группы, сделанные Пасси специальной камерой для слабого освещения.

К сожалению, эта камера не оснащена зум-объективом, поэтому для получения качественных снимков необходимо находиться в непосредственной близости от сцены.

Специальный зум-объектив с апертурой 1,4 для слабого освещения, предназначенный для фотографирования групп, имеет цену, немного превышающую текущую доступность Passy.

Световые лучи, проходящие через объектив камеры, связаны с некоторыми подобными математическими вычислениями треугольников.

Мы проделаем часть этой математики в примерах «Галстук-бабочка» позже в этом уроке.

Подобные треугольники также можно использовать для измерения высоты очень высоких объектов, таких как деревья, здания и вышки мобильной связи.

В этом уроке также рассматривается измерение высоты высоких объектов.

Очень важно, чтобы вы выполнили наш основной урок по подобным треугольникам, прежде чем приступать к следующему уроку.

Если вам нужно вернуться и посмотреть на Основные подобные треугольники, нажмите на ссылку ниже:

Подобные фигуры и подобные треугольники

 
 

Треугольники с галстуком-бабочкой приведенная выше установка для объектива камеры, у нас есть пара подобных треугольников в форме «галстука-бабочки».

Обратите внимание, что когда свет проходит через объектив камеры, исходное изображение оказывается перевернутым или «инвертированным».

Вот почему в камерах есть зеркало, чтобы поместить изображение прямо вверх, чтобы мы могли видеть его во время фотосъемки.

Очень важно, чтобы это зеркало содержалось в безупречной чистоте при замене объективов на 35-мм камере, и мы должны быть осторожны, чтобы никогда не касаться его пальцами.

 
 

Галстук-бабочка, пример 1A

На приведенной ниже диаграмме показаны треугольники из диаграммы объектива нашей камеры с нанесенными на них некоторыми измеренными значениями.

Мы использовали два измерения для определения «Масштабного коэффициента».

Как только мы получим S.F. тогда мы можем легко вычислить недостающее значение.


Image Copyright 2013 by Passy’s World of Mathematics

Нам не нужно использовать метод масштабного коэффициента, чтобы решить этот вопрос.

Вместо этого мы можем использовать метод перекрестного умножения отношений, как показано в «Примере 1B» ниже.

Вам решать, какой метод вы хотите использовать. Оба метода дают один и тот же правильный ответ.

 
 

Галстук-бабочка Пример 1B

В этом примере мы сначала размещаем две пары совпадающих сторон на приведенной ниже диаграмме.

Затем мы устанавливаем их как коэффициенты соответствия и используем метод перекрестного умножения коэффициентов, чтобы получить наш ответ.


Image Copyright 2013 by Passy’s World of Mathematics

 
 

Галстук-бабочка Пример 2

Вот еще один пример, где мы работаем с подобными треугольниками «Галстук-бабочка».


Изображение Copyright 2013 by Passy’s World of Mathematics

В приведенном выше примере мы использовали метод масштабного коэффициента.

Этот вопрос также можно решить с помощью перемноженных коэффициентов, если вы предпочитаете использовать этот метод.

 
 

Видео о вопросах на галстук-бабочку

В следующем видео показано, как ответить на несколько примеров вопросов на галстук-бабочку и треугольник с лестницей.

 
 

Использование треугольников для определения высоты

Подобные треугольники также можно использовать для определения высоты высоких объектов, таких как деревья, здания и башни, на которые нам слишком сложно взобраться и измерить их с помощью рулетки. .


Image Copyright 2013 by Passy’s World of Mathematics

Поскольку солнце светит издалека, оно падает под одним и тем же углом на оба объекта (человека и дерево).

От обоих этих объектов образуются тени, потому что солнце светит на них под углом.
Напр. Дама ростом 2 м отбрасывает тень длиной 12 м, а тень пальмы — 84 м.

В результате образуется пара подобных треугольников.

Сравнивая длины двух теней с двумя высотами, используя подобные треугольники, мы можем вычислить неизвестную высоту дерева.

В следующих двух примерах мы показываем, как эти типы вопросов о росте рисуются в виде треугольника внутри треугольника.

Затем мы используем метод масштабного коэффициента, чтобы получить ответ для «Примера 1А».

После этого мы задаем тот же вопрос, используя метод перекрестного умножения коэффициентов в «Примере 1B».

 
 

Вывод высоты — Пример 1A


Изображение Copyright 2013 от Passy World of Mathematics


Изображение Copyright 2013 By World of Passy’s World of Matematic математики

 
 

Нахождение высоты – пример 2

Вот еще один пример нахождения высоты по теням, но на этот раз у нас есть башня мобильного телефона и более низкий человек с меньшей тенью.


Image Copyright 2013 by Passy’s World of Mathematics

 


Image Copyright 2013 by Passy’s World of Mathematics

 

В приведенном выше примере мы использовали метод масштабного коэффициента.

Этот вопрос также можно решить с помощью перемноженных коэффициентов, если вы предпочитаете использовать этот метод.

 
 

Видео о нахождении высоты

Три с половиной минуты видео об использовании теней для определения высоты дерева:




Десятиминутное видео, показывающее, что парень действительно находит высоту стены с использованием теней:




Видео, показывающая некоторую алгебру X и Y. Зеркало

Мы также можем определить высоту высокого объекта, используя линию взгляда и зеркало, а не измеряя тени.

Это дает вопрос типа «Галстук-бабочка», который нам нужно решить.

Видео по следующей ссылке показывает пример того, как это сделать.

Нажмите здесь, чтобы посмотреть видео об определении высоты с помощью зеркала

 
 

Пример ширины реки

Подобные треугольники очень полезны для косвенного определения размеров предметов, которые трудно измерить вручную.

Типичные примеры включают высоту зданий, высоту деревьев и высоту башни.

Подобные треугольники также можно использовать для измерения ширины реки или озера.


Image Copyright 2013 by Passy’s World of Mathematics

Теперь инструкторы могут бросить монету, чтобы увидеть, кто привязывает к себе веревку, а затем переплывает ледяную воду, чтобы определить ширину реки.

Тем не менее, следующий метод, показанный здесь, намного проще, и никто не должен намокать!

При этом каждый человек движется дальше по реке и точно измеряет, насколько далеко он продвинулся от своих начальных точек в точках A и B.

Это показано на следующей диаграмме:


Image Copyright 2013 by Passy’s World of Mathematics

Мы можем нарисовать линию прямой видимости от дамы в точке «E» до парня на другом берегу реки в точке «C». », который затем создает пару подобных треугольников.

Мы можем решить эти треугольники с галстуком-бабочкой и вычислить ширину реки, как показано ниже.


Image Copyright 2013 by Passy’s World of Mathematics

 

(Обратите внимание, что некоторые клипарты из Интернета были использованы для приведенных выше диаграмм рек, и Passy’s World не претендует на право собственности на эти клипарты, а только на математические компоненты. содержится в этих примерах.)




Связанные предметы

высокие здания и большие плотины
Подобные формы и аналогичные треугольники
Геометрия в животном Королевстве
Математика акул
Классифицирующие треугольники
Угол и угол А. А. Англи
и треугольные угловые
.
Пифагор и прямоугольные треугольники
Конгруэнтные треугольники

 
 

Подписаться

Если вам понравился этот урок, почему бы не получить бесплатную подписку на наш сайт.
: После этого вы сможете получать уведомления о новых страницах прямо на свой адрес электронной почты.

Перейдите в область подписки на правой боковой панели, введите свой адрес электронной почты и нажмите кнопку «Подписаться».

Чтобы точно узнать, как работает бесплатная подписка, нажмите на следующую ссылку:

Как работает бесплатная подписка

Если вы хотите предложить идею для статьи или стать приглашенным автором на нашем веб-сайте, напишите нам по адресу адрес горячей почты, показанный в правой части этой страницы.

Если вы являетесь подписчиком Passy’s World of Mathematics и хотели бы получить бесплатную версию этого урока в PowerPoint, которая на 100 % бесплатна для вас как подписчика, напишите нам по следующему адресу:

Пожалуйста, укажите в своем электронном письме, что вы хотите получить бесплатную подписную копию «Similar Triangle Applications» Powerpoint.

 

Не стесняйтесь размещать ссылки на любые наши уроки, делиться ими в социальных сетях или использовать их в системах управления обучением в школах.

 

Отметьте нас на Facebook

 

Помогите Passy’s World расти

Каждый день Passy’s World предоставляет сотням людей бесплатные уроки математики.

Помогите нам поддерживать этот бесплатный сервис и поддерживать его рост.

Пожертвуйте любую сумму от $2 и выше через PayPal, щелкнув изображение PayPal ниже. Благодарю вас!







PayPal принимает кредитные карты, но вам нужно будет указать адрес электронной почты и пароль, чтобы PayPal мог создать для вас учетную запись PayPal для обработки транзакции. За это действие с вас не будет взиматься плата за обработку, так как PayPal вычитает комиссию из вашего пожертвования до того, как оно попадет в Passy’s World.

 
 

Наслаждайтесь,
Passy

Эта запись была размещена в Геометрия, Математика в реальном мире, Треугольники и помечены треугольники с галстуком-бабочкой, треугольники с галстуком-бабочкой, математика камеры, определение высоты высоких зданий, определение высоты с помощью зеркал, нахождение высоты с помощью пропорций, нахождение высоты с помощью теней, нахождение высоты с помощью треугольников, геометрические соотношения, геометрия, как вычислить ширину реки с помощью треугольников, геометрия линзы, соотношения, треугольники в реальной жизни, треугольники, подобные ширине реки, треугольники ширины реки, подобные треугольники в реальный мир, подобные треугольники, приложения подобных треугольников, решение отношений, решение отношений треугольников, треугольники, для чего используются подобные треугольники.

No related posts.