Что такое единичный угол: Виды углов. Измерение углов

Виды углов. Измерение углов

На каждом из рисунков 82, a − г изображены два луча. На каком из рисунков пара лучей образует угол, сторонами которого являются эти лучи?

Поскольку на рисунках 82, а − в начала лучей не совпадают, то они не могут служить сторонами угла. Лучи на рисунке 82, г образуют прямую. При этом начала лучей совпадают, а следовательно, они образуют угол. Такой угол называт развернутым.

Угол, стороны которого образуют прямую, нахывают развернутым.

Углы, как и отрезки, можно измерять. Напомним, что для измерения отрезков мы использовали единичный отрезок (1 мм, 1 см и т.п.).

Однако для измерения углов мы пока не имеем такого единичного угла.

Создать его можно, например, так. Разделим развернутый угол на 180 равных углов (рис. 83). Угол, образованный двумя соседними лучами, выбирают за единицу измерения. Его величину называют градусом (от лат. gradus − «шаг», «ступенька») и записывают 1°.

Измерить угол − значит подсчитать, сколько единичных углов в нем помещается.

Тогда величина или, как еще принято говорить, градусная мера развернутого угла равна 180°.

Для измерения углов используют специальный прибор − транспортир (рис. 84). Он состоит, как правило, из полукольца, соединенного с линейкой. Его шкала содержит 180 делений.

Чтобы измерить угол, совместим его вершину с центром транспортира таким образом, чтобы одна из сторон угла прошла по линейке (рис. 85).

Тогда штрих на шкале, через который пройдет вторая сторона, укажет градусная (величину) этого угла.

Так, на рисунке 85 градусная мера угла AOB равна 55°. Пишут: ∠AOB = 55°. На рисунке 86 имеем: ∠MON = 134°.

Равные углы имеют равные градусные меры. Из двух неравных углов бОльшим будем считать тот, градусная мера которого больше. Например, из трех углов, изображенных на рисунке 87, ∠MON − наибольший. В этом легко убедиться, измерив углы транспортиром.

Величина угла обладает следующим свойством.

Если между сторонами угла ABC провести луч BD, то градусная мера угла ABC равна сумме градусных мер углов ABD и DBC (рис. 88), т.е.

∠ABC = ∠ABD + ∠DBC.

Угол, градусная мера которого меньше 90°, называют острым (рис. 89, a).

Угол, градусная мера которого равна 90°, называют прямым (рис. 89, б).

На рисунке прямой угол обозначает так: ∟.

Угол, градусная мера которого больше 90°, но меньше 180° называют тупым (рис. 89, в).

Отметим, что биссектриса развернутого угла делит его на два угла, градусная мера каждого из которых равна 90°. Следовательно, биссектриса развернутого угла делит его на два прямых угла (рис. 90).

Пример 1. Дан луч OA. Постройте угол BOA, равный 72°.

Решение.

Совместим центр транспортира с точкой O так, чтобы луч OA прошел по линейке. Выберем на кольце транспортира штрих, который соответствует 72°. Возле этого штриха отметим точку B (рис. 91). Проведем луч OB. Угол BOA − искомый.

Если дан луч OA и построен угол BOA, то говорят, что от луча OA отложен угол BOA.

Пример 2. Из вершины угла ABC проведены два луча BK и BM так, что ∠ABK = 48°, ∠CBM = 72° (рис. 92).

Вычислите величину угла ABC, если ∠MBK = 16°.

Решение.

Имеем: ∠ABM = ∠ABK − ∠MBK, ∠ABM = 48° − 16° = 32°;

∠ABC = ∠ABM + ∠СBM, ∠ABC = 32° + 72° = 104°.

Ответ: 104°.

УГЛЫ НА ПЛОСКОСТИ И ИХ ИЗМЕРЕНИЕ

УГЛЫ НА ПЛОСКОСТИ И ИХ ИЗМЕРЕНИЕ. Фигура на плоскости, образованная двумя лучами, исходящими из одной точки O, называется углом. Лучи OA и OB называются сторонами угла, а точка O вершиной. Угол со сторонами OA и OB обозначается РAOB.

Углы сравнивают, складывают, измеряют. Они равны, если их можно совместить перемещением. Два угла называются смежными (рис. 1), если у них общие вершина и одна сторона, а две другие образуют прямую. Вообще, углы, имеющие общую вершину и одну общую сторону, называются прилежащими (рис. 2). Углы называются вертикальными (рис. 3), если стороны одного являются продолжениями за вершину сторон другого. Вертикальные углы равны между собой. Угол, у которого стороны образуют прямую, называется развернутым (рис. 4). Угол, равный своему смежному, называется прямым. Угол меньший прямого – острый, больший прямого, но меньший развернутого – тупой.

При пересечении двух прямых, лежащих в одной плоскости, третьей прямой образуются углы (рис. 5). 1 и 5, 2 и 6, 4 и 8, 3 и 7 называются соответственными; 2 и 5, 3 и 8 – внутренними односторонними; 1 и 6, 4 и 7 – внешними односторонними; 3 и 5, 2 и 8 – внутренними накрест лежащими; 1 и 7, 4 и 6 – внешними накрест лежащими.

Если луч OC проходит внутри угла AOB (рис. 6), то, по определению, считают, что угол AOC, как и угол COB, меньше угла AOB и что угол AOB равен сумме углов AOC и COB. Взяв за единицу измерения какой-либо конкретный угол, определяют величину любого угла, т.е. находят, сколько раз укладывается в нем данный единичный угол. При измерении угла исходят из двух его свойств, аналогичных свойствам длины отрезка: 1) величины равных углов равны, 2) величина суммы двух углов равна сумме их величин.

Если рассмотреть углы, вершиной которых является центр окружности, а сторонами – радиусы, то можно отметить, что равные углы высекают на окружности равные дуги, и сумме углов будет соответствовать сумма стягиваемых ими дуг. Поэтому величина угла пропорциональна длине высекаемой им дуги, и единицы измерения можно задавать, указывая, какую часть окружности составляет соответствующая дуга.

Обычно пользуются двумя системами измерения углов: градусной и радианной.

В градусной системе за единицу измерения принимают дугу размером в 1/360 окружности (обозначают °). Градус делится на 60 минут (обозначают ‘), минута на 60 секунд (обозначают »).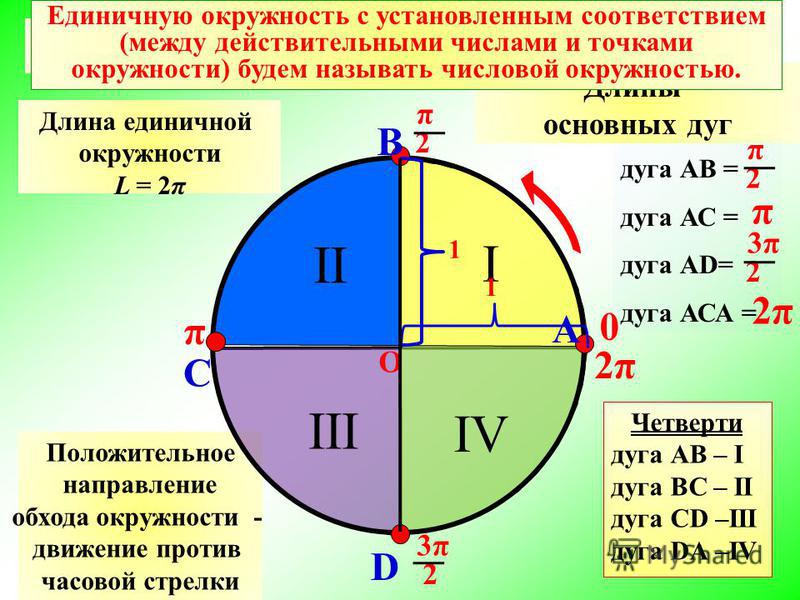 Шестидесятиричность измерений напоминает о Вавилоне, но был в истории еще один градус. Во времена Великой французской революции (1793) во Франции вместе с десятичной (метрической) системой мер была введена сотенная (центезимальная) система измерения углов. В ней прямой угол делится на 100 градусов («градов»), градус на 100 минут, минута на 100 секунд. Эта система наиболее часто применяется в геодезических измерениях.

Математики предпочитают пользоваться радианной мерой – за единицу измерения принимается угол, под которым видна из центра окружности ее дуга, равная радиусу. Величина такого угла и есть радиан. Она не зависит от радиуса окружности и от положения дуги на окружности. Т.к. полуокружность видна из центра под углом 180°, а ее длина равна 241 радиусам, то радиан в 241 раз меньше, чем угол 180°, т.е. один радиан равен 180°/241:

1 радиан » 57,2958° » 57°17’45»

И в радианной и в градусной системе угол измеряется единицей угла. То, что наименование в одном случае (для градуса) проставляется, а в другом (для радиана) подразумевается, не играет никакой роли.

Радианная мера, выражающаяся отношением длины дуги, описанной произвольным радиусом из центра и заключенной между сторонами угла, к радиусу этой дуги, не зависит от выбора единицы длины. Так же не зависит и градусная мера, т.к. она тоже является отношением двух длин, а именно длины дуги, описанной из вершины угла и заключенной между ее сторонами, к длине дуги равной 1/360 части окружности того же радиуса.

Таким образом, никакой принципиальной разницы между градусной и радианной мерой угла нет, однако введение радианной меры позволяет придать многим формулам более простой вид.

Соотношение градусной и радианной мер наиболее часто встречающихся углов приведено в следующей таблице

Соотношение градусной и радианной мер углов

Углы в градусах	360°	180°	90°	60°	45°	30°
Углы в радианах	2π	π	π/2	π/3	π/4	π/6

Прямой угол содержит в себе 90° или 241/2 радиан. Острый лежит в пределах от 0 до 90° или от 0 до 241/2 радиан, тупой – от 90 до 180° или от 241/2 до 241. Прямые линии, образующие прямой угол, называются перпендикулярными одна другой.

Часто важно указать, в каком направлении измеряется угол. Если рассматривать в качестве меры угла поворот вокруг вершины О, переводящий луч OA в положение OB, то положительной мера угла считается, если поворот происходит против часовой стрелки, в противном случае угол считается отрицательным. Таким образом, угол может иметь своей величиной любое действительное число. В тригонометрии такое рассмотрение позволяет изучать тригонометрические функции для любых значений аргумента.

Под углом между двумя кривыми, выходящими из общей точки, в которой каждая из кривых имеет определенную касательную, понимают угол, образованный этими касательными. Понятие угла обобщается и на различные объекты в пространстве (двугранные, телесные и многогранные углы.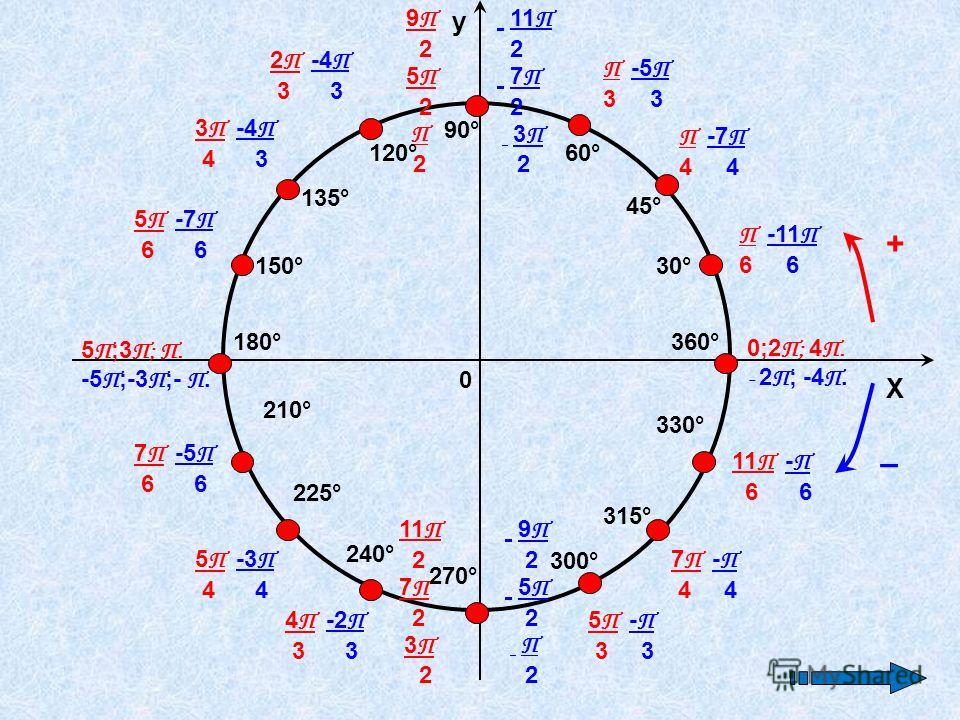

Проверь себя!
Ответь на вопросы викторины «Математика»

Как звали математика, который в 19 лет решил задачу, не поддававшуюся усилиям лучших геометров со времен Евклида?

Пройти тест

Угол — Единицы измерения угла — Значение, поворот, градусы и оборот

Углу обычно присваивается арифметическое значение, которое описывает его размер. Чтобы указать это значение, угол рисуется в стандартном положении в системе координат с вершиной в центре и одной стороной, называемой начальной стороной, вдоль оси x. Затем значение угла представляет собой величину поворота, необходимого для перехода от начальной стороны к другой стороне, называемой конечной стороной. Направление вращения указывает знак угла. Традиционно вращение против часовой стрелки дает положительное значение, а вращение по часовой стрелке дает отрицательное значение . Три термина, которые обычно используются для выражения значения угла, включают обороты, градусы или радианы.

Оборот — самая естественная единица измерения угла. Он определяется как величина поворота, необходимая для перехода от начальной стороны угла обратно к исходной стороне. Один из способов визуализировать революцию — представить, что колесо вращается один раз. Путь, пройденный любой точкой колеса, равен одному обороту. Затем углу можно присвоить значение, основанное на доле расстояния, пройденного точкой, деленной на расстояние, пройденное за один оборот. Например, угол, представленный четвертью оборота колеса, равен 0,25 оборота.

Более распространенной единицей измерения угла является градус. Эта единица использовалась вавилонянами еще в 1000 B . С . В то время они использовали систему счисления, основанную на числе 60, поэтому для математиков того времени было естественным делить углы равностороннего треугольника на 60 отдельных единиц. Эти единицы стали известны как градусы. Так как шесть равносторонних треугольников могут быть равномерно расположены в окружности , число градусов в одном обороте стало 6 × 60 = 360.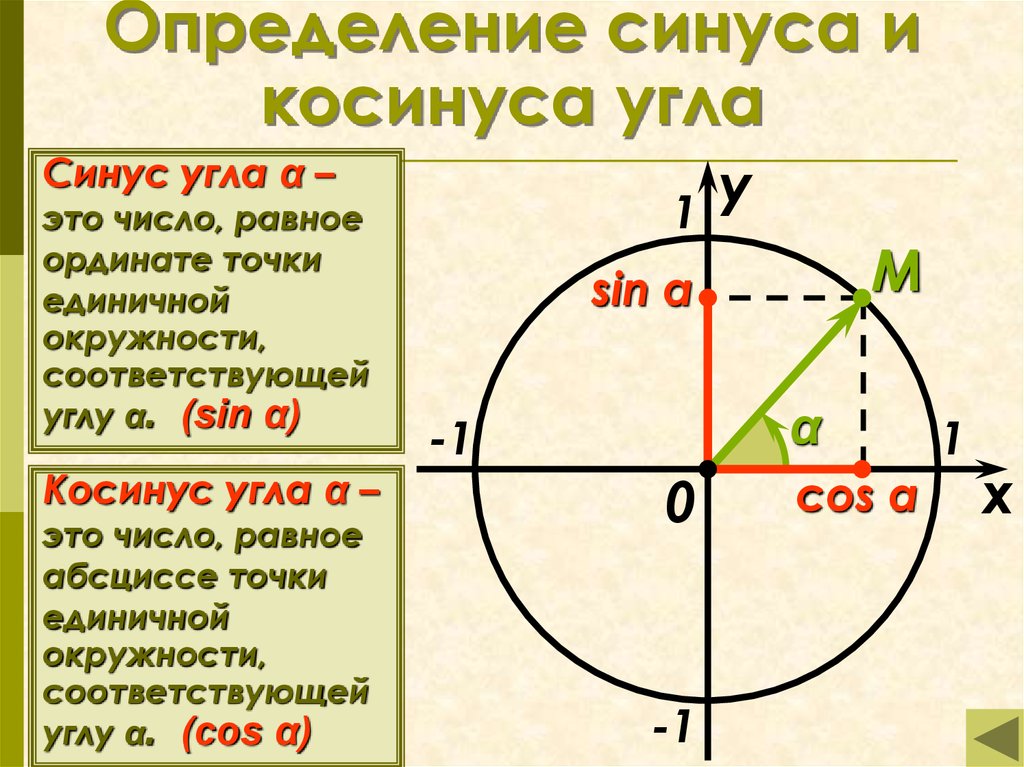 Единица градусов была разделена на 60 меньших единиц, называемых минутами, а эти минуты, в свою очередь, подразделялись на 60 более мелкие единицы, называемые секундами. Следовательно, обозначение угла, имеющего значение 44 градуса, 15 минут и 25 секунд, будет 44° 15′ 25″.

Угол можно измерить транспортиром, который представляет собой плоский инструмент в форме полукруга. На его внешних краях есть отметки, которые делят его на 180 равномерно расположенных единиц, или градусов. Измерения производятся путем размещения средней точки плоской кромки над вершиной угла и совмещения отметки 0° с начальной стороной. Число градусов можно считать в точке, где конечная сторона пересекает кривую транспортира.

Другая единица измерения угла, широко используемая в тригонометрия , это радиан. Эта единица связывает уникальный угол с каждым действительным числом. Рассмотрим круг с центром в начале графика и радиусом по оси x. Один радиан определяется как угол, создаваемый вращением радиуса вокруг окружности против часовой стрелки, так что длина пройденной дуги равна длине радиуса.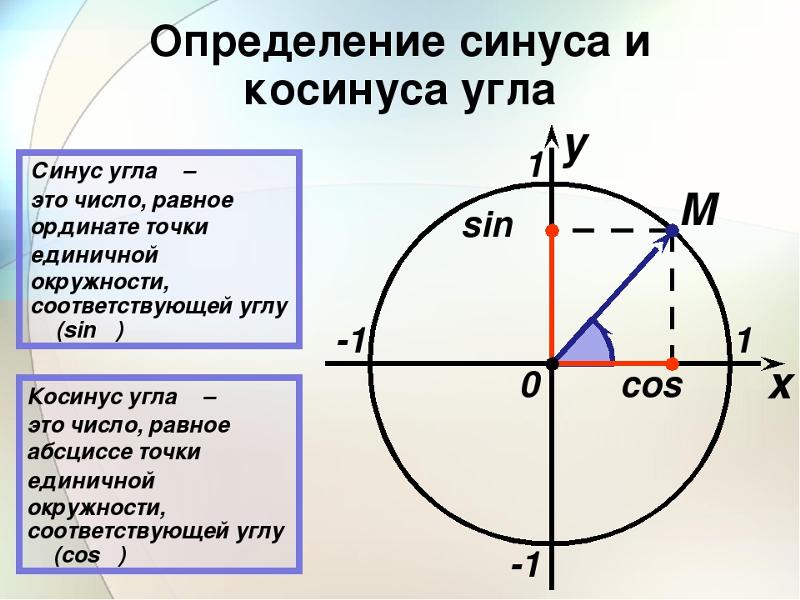 Используя формулу длины окружности, можно показать, что общее количество радианов при полном обороте на 360° равно 2π. Учитывая эту взаимосвязь, можно преобразовать градус в радиан.

Градус (угол) — New World Encyclopedia

Из New World Encyclopedia

Перейти к:навигация, поиск

Предыдущее (Дегенеративное искусство)

Следующее (Деизм)

Один градус (отмечено красным) ).

В этой статье описывается единица измерения угла.

A градуса (полностью градуса дуги , градуса дуги или градуса дуги ), обычно обозначаемый как ° (символ градуса), является измерением плоского угла, представляющий ¹ ⁄ ₃₆₀ полного оборота; один градус равен π/180 радиан. Когда этот угол относится к опорному меридиану, он указывает на положение вдоль большого круга сферы, такой как Земля (см. Географическая система координат), Марс или небесная сфера.

Содержание

• 1 История
  • 1.1 Индия
• 2 подразделения
• 3 Альтернативные устройства
• 4 См. также
• 5 Примечания
• 6 Каталожные номера
• 7 Внешние ссылки
• 8 кредитов

История

Окружность с равносторонней хордой (геометрия) (красный). Одна шестидесятая (1/60) этой дуги является градусом. Шесть таких аккордов замыкают круг.

Выбор числа 360 в качестве числа градусов (, т. е. наименьших практических субдуг) в окружности, вероятно, был основан на том факте, что 360 — это приблизительное количество дней в году. Часто говорят, что его использование восходит к методам древних вавилонян. ^[1] Древние астрономы заметили, что звезды на небе, которые каждый день вращаются вокруг небесного полюса, перемещаются по этому кругу примерно на одну 360-ю окружности, , т. е. на один градус, каждый день. (Примитивные календари, такие как персидский, использовали 360 дней в году.) Его применение для измерения углов в геометрии, возможно, можно проследить до Фалеса, который популяризировал геометрию среди греков и жил в Анатолии (современная западная Турция) среди людей, которые отношения с Египтом и Вавилоном.

Самая ранняя тригонометрия, использовавшаяся вавилонскими астрономами и их греческими последователями, основывалась на хордах окружности. Хорда длины, равной радиусу, составляет натуральную базовую величину. Одна шестидесятая из них, если использовать их стандартное шестидесятеричное деление, составляла градус; а шесть таких аккордов замыкали полный круг.

Другая причина выбора числа 360 заключается в том, что оно легко делится: 360 имеет 24 делителя (включая 1 и 360), включая все числа от 1 до 10, кроме 7. Чтобы количество степеней в окружности делилось на все число от 1 до 10, в окружности должно быть 2520 градусов, что является гораздо менее удобным числом.

Делителями числа 360 являются 1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 18, 20, 24, 30, 36, 40, 45, 60, 72, 90, 120 , 180 и 360.

Индия

Деление круга на 360 частей происходило и в Древней Индии, о чем свидетельствует Ригведа:

Двенадцать спиц, одно колесо, три пупка.

Кто может это понять?

На нем размещаются вместе

триста шестьдесят подобных колышков.

Они ничуть не трясутся.

( Диргхатама, Ригведа 1.164.48)

Подразделения

Для многих практических целей градус представляет собой достаточно малый угол, чтобы целые градусы обеспечивали достаточную точность. Когда это не так, как в астрономии или для широты и долготы на Земле, градусы могут быть записаны с десятичными знаками, но обычно используется традиционное шестидесятеричное деление. Один градус делится на 60 угловых минуты, , а одна минута на 60 секунды (угловой). Эти единицы измерения, также называемые угловыми минутами и угловыми секундами, , представлены соответственно одинарным и двойным штрихом или, при необходимости, одинарными и двойными кавычками: например, 40,1875° = 40° 11′ 15″ (или 40° 11′ 15″).

Если требуется еще большая точность, обычно используются десятичные доли секунды, а не трети из ¹ ⁄ ₆₀ секунды, четверти из ¹ ⁄ ₆₀ трети и так далее. Эти (редко используемые) подразделения были отмечены написанием римской цифры для числа шестидесятых в верхнем индексе: 1 ^I для «штриха» (минуты дуги), 1 ^II для секунды, 1 ^III для третья, 1 ^IV для четвертой и т. д. Отсюда и современные обозначения минуты и секунды дуги.

Альтернативные единицы

В большинстве математических работ, выходящих за рамки практической геометрии, углы обычно измеряются в радианах, а не в градусах. Это происходит по разным причинам; например, тригонометрические функции имеют более простые и «естественные» свойства, когда их аргументы выражены в радианах. Эти соображения перевешивают удобную делимость числа 360. Один полный круг (360°) равен 2 π радиан, поэтому 180° равно π радианам, или, что то же самое, градус является математической константой ° = ^π ⁄ ₁₈₀ .

С изобретением метрической системы, основанной на десятичных степенях, была предпринята попытка определить «десятичный градус» ( град или град ), чтобы количество десятичных градусов в прямом углу было 100 угольник, и будет 400 угольник по кругу. Однако эта идея не получила большого распространения.

Угловой мил, который чаще всего используется в военных целях, имеет как минимум три конкретных варианта.

В компьютерных играх, изображающих трехмерный виртуальный мир, потребность в очень быстрых вычислениях привела к принятию двоичной системы с 256 градусами. В этой системе прямой угол равен 64 градусам, углы могут быть представлены одним байтом, а все тригонометрические функции реализованы в виде небольших интерполяционных таблиц. Эти единицы иногда называют «бинарными радианами» («брадами») или «бинарными градусами».

См. также

• Компас
• Геометрия

Примечания

1. ↑ Степень, MathWorld

Ссылки

Ссылки ISBN поддерживают NWE за счет реферальных сборов

• Бекманн П. История Пи. St. Martin’s Griffin, 1976. ISBN 0312381859

Внешние ссылки

Все ссылки получены 26 июля 2022 г.

• Градусы как мера угла, с интерактивной анимацией
• Степень MathWorld

Кредиты

Энциклопедия Нового Света автора и редактора переписали и дополнили статьи Википедии в соответствии со стандартами New World Encyclopedia . Эта статья соответствует условиям лицензии Creative Commons CC-by-sa 3.0 (CC-by-sa), которая может использоваться и распространяться с надлежащим указанием авторства. Кредит должен быть указан в соответствии с условиями этой лицензии, которая может ссылаться как на New World Encyclopedia участников и самоотверженных волонтеров Фонда Викимедиа. Чтобы процитировать эту статью, щелкните здесь, чтобы просмотреть список допустимых форматов цитирования. История более ранних вкладов википедистов доступна исследователям здесь:

• Градус (угол)  ^{история}

История этой статьи с момента ее импорта в New World Encyclopedia :

• История «Градуса (угла)»

Примечание.