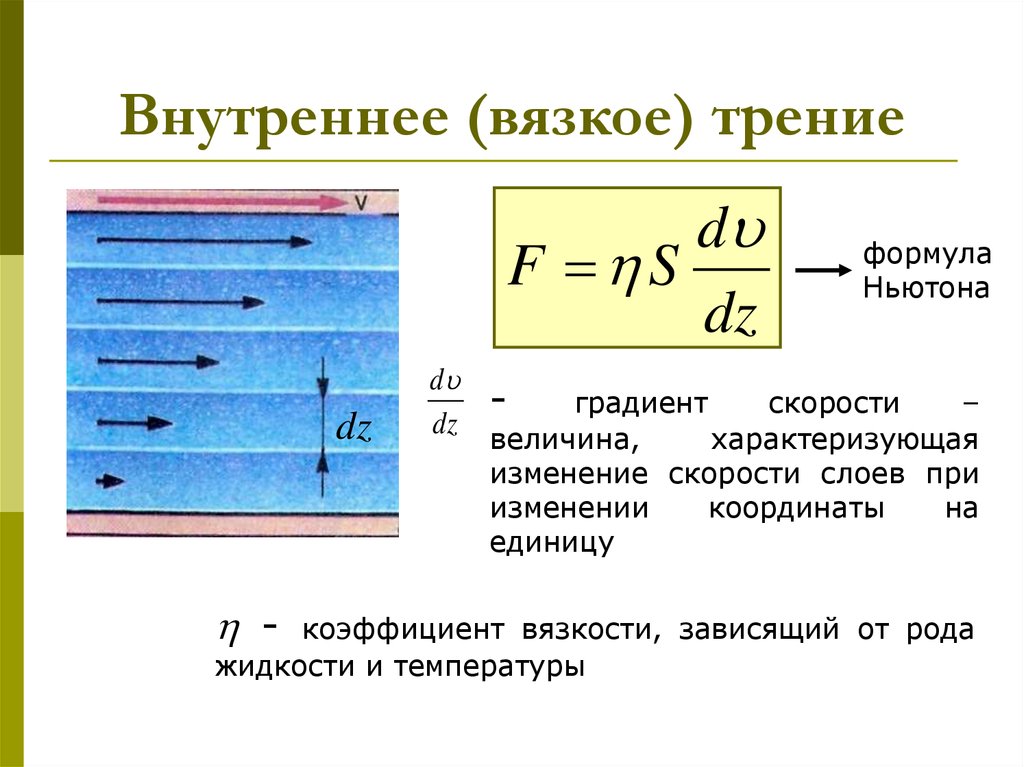
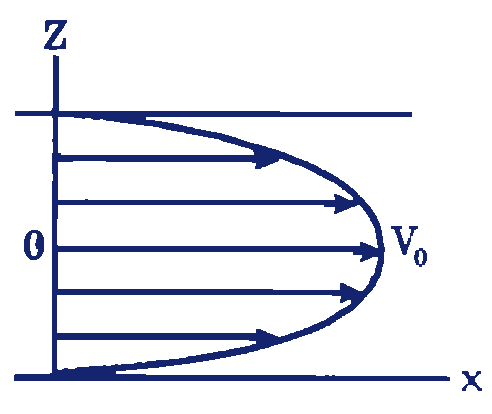
Градиент скорости — определение термина
интенсивность изменения скорости по заданному направлению, обычно по нормали к направлению скорости.
Научные статьи на тему «Градиент скорости»
Он первым сформулировал закон, по которому скорость фильтрации прямо пропорциональна градиенту давления…
Такое поведение потока проявляется в виде отклонения связи касательного напряжения и градиента скорости…
Существует три класса неньютоновских жидкостей, напряжение в которых зависит от градиента скорости, от…
градиента скорости и времени действия напряжения, а также жидкости, где зависимость градиента скорости…
от напряжения включает в себя производные по времени напряжений и градиента скорости.
Статья от экспертов
Представлены результаты исследования вязкости воды при малых градиентах скорости течения.
Creative Commons
Научный журнал
При плоскопараллельном потоке векторы скоростей параллельны по отношению к друг другу….
В каждом поперечном сечении скорость, давление, направление одинаковы, но при этом они отличаются от…
При плоскорадиальном потоке в каждой горизонтальной плоскости продолжения векторов скорости сходятся…
r • h$
где, r – радиус; h – толщина пласта;
При радиально-сферическом потоке продолжение векторов скоростей…
фильтрации нефти переменной вязкости заложены данные о характере изменения вязкости нефти, а также скорости
Статья от экспертов
Получена двучленная асимптотика угла гашения в сдвиговом ламинарном потоке суспензии жестких эллипсоидальных частиц при больших градиентах скорости потока.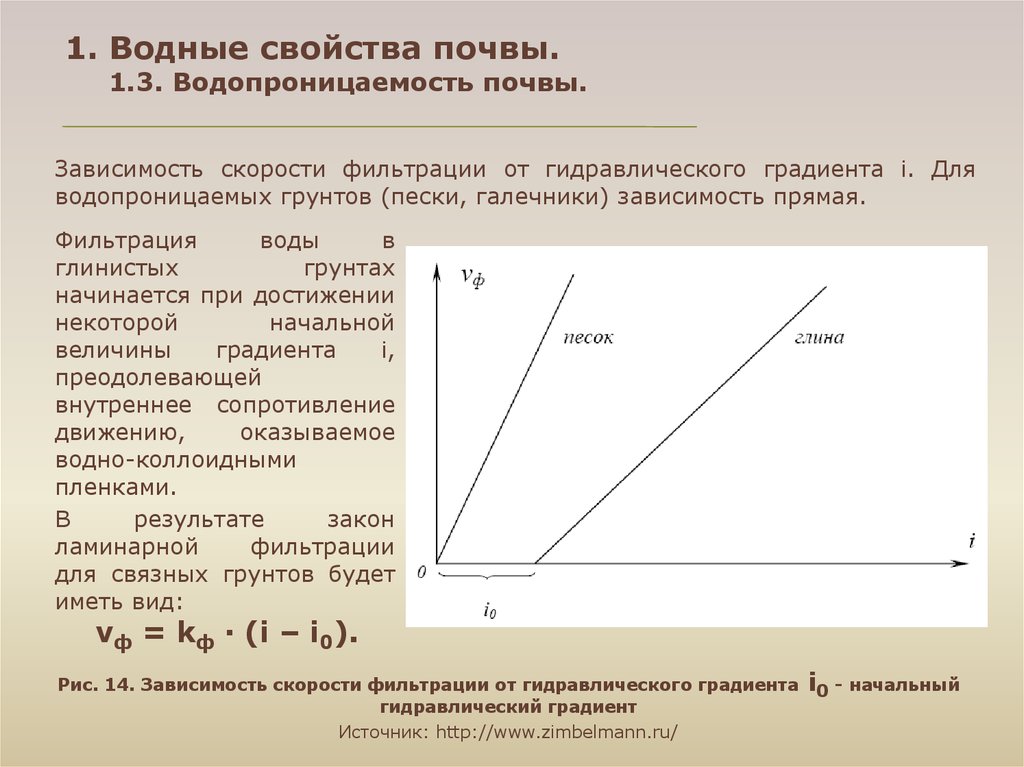 Указано условие применимости ее старшего члена. Развит метод определения размеров коллоидных частиц (макромолекул полимеров) по значениям угла гашения, измеренным при малых и больших градиентах скорости потока. Метод продемонстрирован на примере определения размеров частиц анизалдазина в растворах по экспериментальным кривым зависимости угла гашения от градиента скорости.
Указано условие применимости ее старшего члена. Развит метод определения размеров коллоидных частиц (макромолекул полимеров) по значениям угла гашения, измеренным при малых и больших градиентах скорости потока. Метод продемонстрирован на примере определения размеров частиц анизалдазина в растворах по экспериментальным кривым зависимости угла гашения от градиента скорости.
Creative Commons
Научный журнал
Еще термины по предмету «Гидравлика»
Абсолютная шероховатость
средняя высота выступов (бугров) шероховатости.
Гарантийная точка
эксплуатационные параметры насоса, которые гарантирует поставщик при точных условиях, установленных техническими требованиями; гарантийная точка может быть определена как: — полный напор или давление при точно определенной подаче; — подача при точно указанном полном напоре или давлении; — входная мощность насоса или привода; — эффективность насоса или агрегата;другие точки на кривой характеристики динамического насоса.
Гидропривод (пневмопривод) с управлением
объемный гидропривод (пневмопривод) с изменяющимися параметрами движения выходного звена объемного гидродвигателя (пневмодвигателя).
- Градиент
- Поперечный градиент скорости dV/dr
- Градиент неровноты
- Геометрический градиент
- Градиент осадков
- Градиент потенциала
- Климатологический градиент
- Автоконвективный градиент
- Барический градиент
- Вертикальный градиент
- Температурный градиент
- Градиент концентрации
- Градиент напряжения
- Градиент температуры
- Градиент цели
- Градиент эффекта
- Избежания градиент
- Приближения градиент
- Электрохимический градиент
- Градиент давления
Смотреть больше терминов
Повышай знания с онлайн-тренажером от Автор24!
- Напиши термин
- Выбери определение из предложенных или загрузи свое
- Тренажер от Автор24 поможет тебе выучить термины с помощью удобных и приятных карточек
Лекция 4 — Физико-теоретические основы элементов и систем управления движением и навигации
Лекция 4.
План:
1. Силы, действующие на жидкий объем;
2. Вязкость или внутреннее трение в жидкостях.
§2.4.1. Силы, действующие на жидкий объем.
Внешние силы, действующие на жидкий объем и определяющие его движение, разделяются на массовые (объемные) и поверхностные.
Массовые силы приложены ко всем жидким частицам, составляющим жидкий объем. К ним относятся силы тяжести и силы инерции. Кроме того, к массовым силам относятся силы взаимодействия частиц токопроводящей жидкости с электромагнитными полями. Наука, изучающая эти течения, называется магнитной гидрогазодинамикой.
Напряжением массовой силы (м/с2, Н/кг) называется отношение вектора массовой силы к массе жидкой частицы, на которую она действует:
(2.5)
В соответствии со вторым законом Ньютона, массовая сила равна произведению массы на ее ускорение, вызванное этой силой. Поэтому напряжение массовой силы равно ускорению центра массы частицы, проходящей в данный момент времени через данную точку, и характеризует распределение массовых сил в пространстве, занятом жидкостью. Проекции напряжения массовой силы на оси координат обозначим , тогда
Проекции напряжения массовой силы на оси координат обозначим , тогда
(2.6)
где — орты.
Поверхностные силы представляют воздействие внешней среды на поверхность выделенного объема. Это воздействие распределено по поверхности непрерывно. Выберем на плоскости , рассекающей некоторую массу жидкости на части 1 и 2 (рис. 1), элементарную площадку, на которой лежит точка . Отбросим часть 2 и заменим ее действие на площадку части 1 равнодействующей поверхностных сил . В общем случае величина зависит от ориентировки площадки и направлена к ней под острым углом . Ориентация площадки определяется единичным вектором внешней нормали .
Нормальная составляющая поверхностной силы действует по нормали к поверхности , противоположно .
Сила трения или тангенциальная составляющая действует в плоскости .
Напряжения поверхностных сил в точке —это пределы отношений соответствующих сил к площадке при стягивании ее в точку.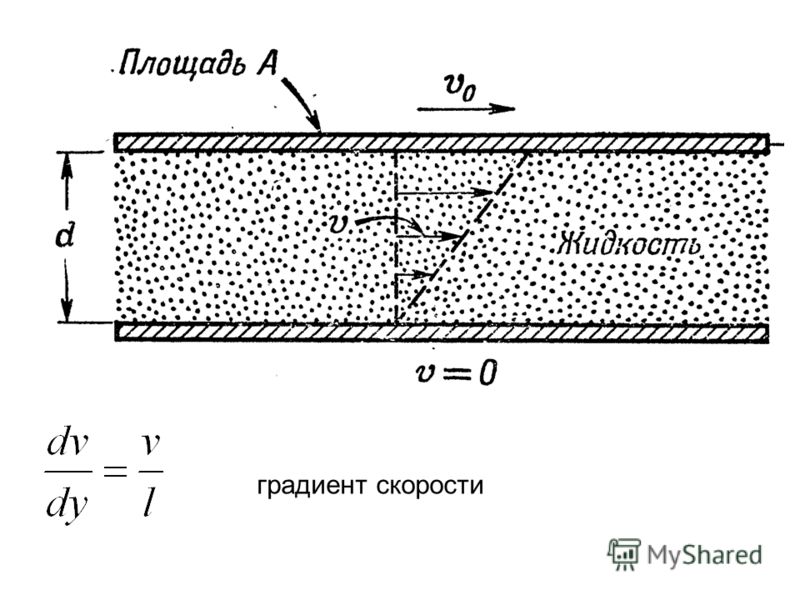 Различают следующие напряжения.
Различают следующие напряжения.
Напряжение равнодействующей поверхностной силы, Н/м2
(2.7)
Нормальное напряжение, Н/м2
(2.8)
Знак минус показывает, что за положительное принято растягивающее нормальное напряжение.
Напряжение трения или касательное напряжение, Н/м2
(2.9)
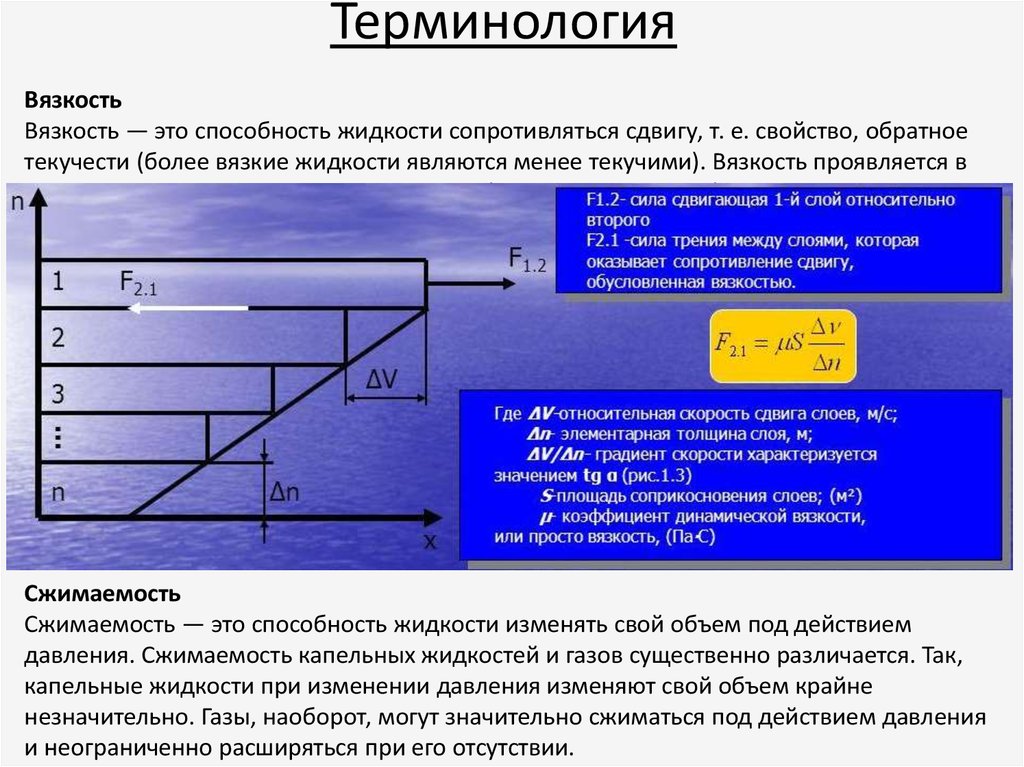
§2.4.2. Вязкость или внутреннее трение в жидкостях.
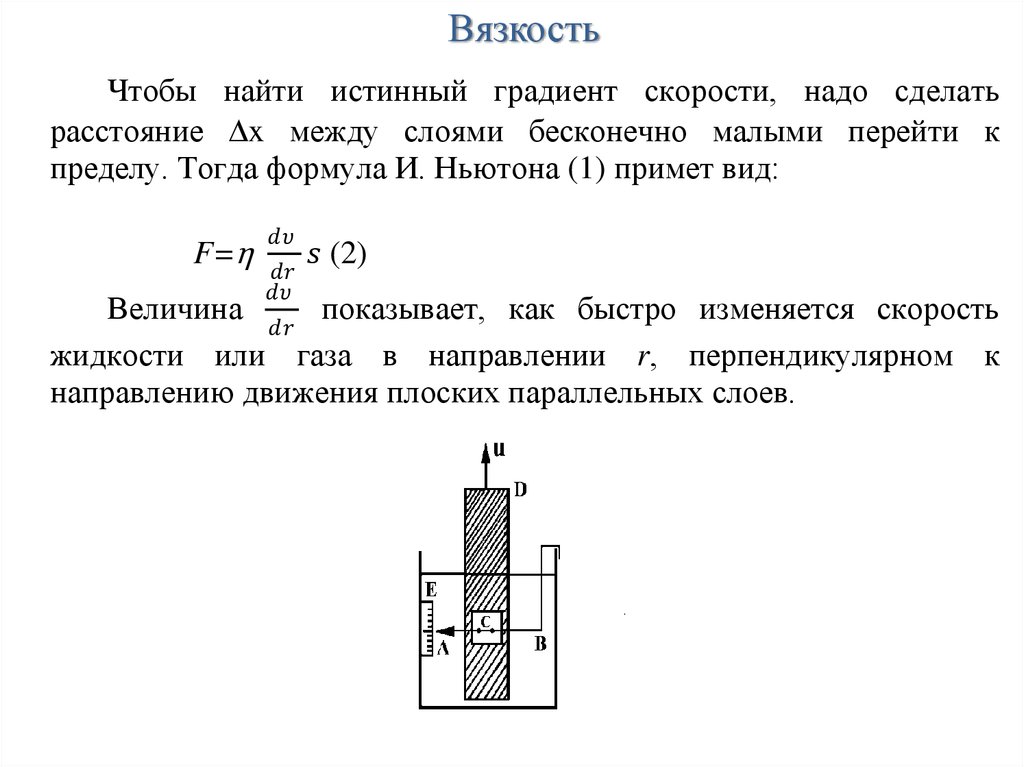
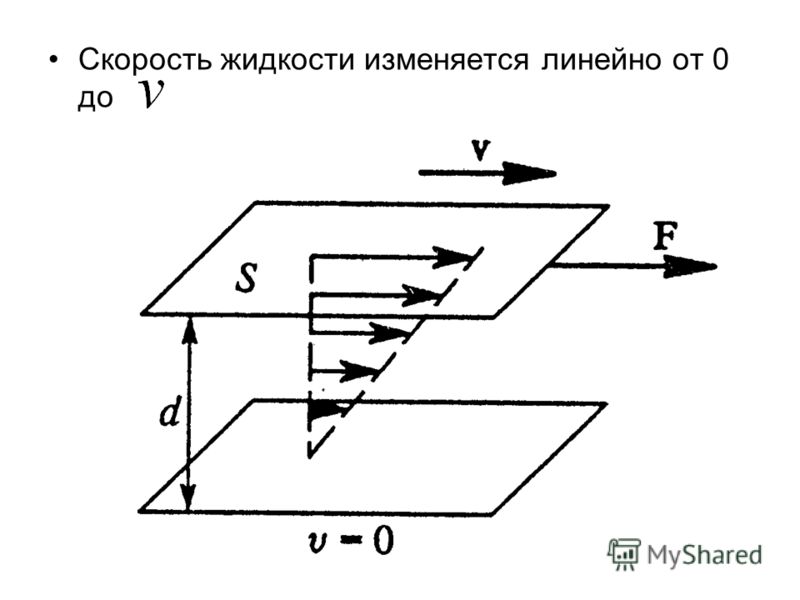
Вязкостью называется свойство всех реальных жидкостей оказывать сопротивление относительному сдвигу частиц, т. е. изменению их формы (но не объема). Для выяснения сущности вязкости рассмотрим течение жидкости между нижней неподвижной пластиной и верхней, движущейся параллельно нижней с постоянной скоростью (рис. 2).
Опыт показывает, что скорость жидкости у нижней пластины равна нулю, у верхней— (жидкость прилипает к твердым поверхностям), а скорость между пластинами распределена линейно: , давление постоянно во всей области. Такое течение называют течением чистого сдвига. Для его осуществления к жидкости со стороны верхней пластины должна быть приложена сила , уравновешивающая силу вязкости (трения) жидкости, а для удержания на месте нижней пластины — сила (). Измерения показывают, что напряжение трения пропорционально отношению скорости к расстоянию между пластинами и не зависит от абсолютной величины скорости (имеет значение лишь относительное движение слоев жидкости). Отношение называется градиентом скорости по нормали к плоскости скольжения слоев или кратко — поперечным градиентом скорости
Такое течение называют течением чистого сдвига. Для его осуществления к жидкости со стороны верхней пластины должна быть приложена сила , уравновешивающая силу вязкости (трения) жидкости, а для удержания на месте нижней пластины — сила (). Измерения показывают, что напряжение трения пропорционально отношению скорости к расстоянию между пластинами и не зависит от абсолютной величины скорости (имеет значение лишь относительное движение слоев жидкости). Отношение называется градиентом скорости по нормали к плоскости скольжения слоев или кратко — поперечным градиентом скорости
(2.10)
Формула (2.10) выражает закон Ньютона о молекулярном трении в жидкости — напряжение трения, пропорционально поперечному градиенту скорости. Этот закон был установлен Ньютоном экспериментальным путем. Жидкости, удовлетворяющие уравнению (2.10), называются ньютоновскими. Для неньютоновских жидкостей (смолы, коллоидальные растворы) напряжение трения определяется по более сложным формулам. Наука, изучающая движение неньютоновских жидкостей, называется реологией.
Наука, изучающая движение неньютоновских жидкостей, называется реологией.
Коэффициент пропорциональности , Н*с/м2 называется динамическим коэффициентом вязкости или просто вязкостью жидкости. Величина зависит от природы жидкости, ее агрегатного состояния, температуры и практически не зависит от давления в широком диапазоне его изменения. Чем больше , тем больше вязкость жидкости.
При исследовании течений, в которых действуют силы трения и силы инерции, используется кинематический коэффициент вязкости , м2/с
(2.11)
Из рис.3 следует, что с увеличением температуры вязкость капельных жидкостей уменьшается, а газов увеличивается. Это объясняется различием в механизмах молекулярного трения в них. Трение в капельных жидкостях заключается, главным образом, в преодолении сил взаимодействия между молекулами слоев, смещающихся относительно друг друга. С увеличением температуры капельной жидкости увеличиваются частота колебаний молекул и силы взаимодействия между ними уменьшаются, а вместе с ними уменьшается и вязкость.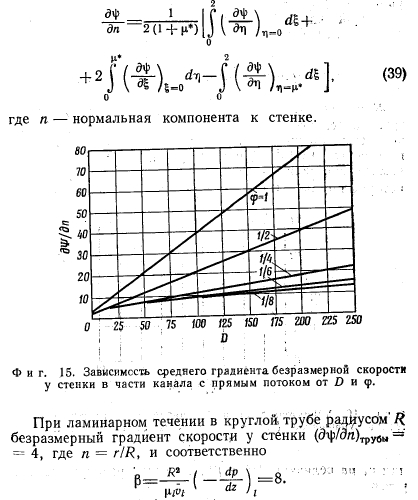 Величина для капельных жидкостей определяется экспериментальным путем.
Величина для капельных жидкостей определяется экспериментальным путем.
Трение в газах обусловлено переносом направленного количества движения молекул при их тепловом хаотическом движении. Пусть два соседних слоя газа движутся в одну сторону с различными скоростями («быстрый» и «медленный» слои). Молекулы «быстрого» слоя, переходя в «медленный», ускоряют его молекулы, а сами подтормаживаются и наоборот. С увеличением температуры газа скорость хаотического движения молекул и число соударений возрастают, а вместе с этим — перенос количества движения и вязкость газа.
В кинетической теории были найдены теоретическое обоснование закона Ньютона о молекулярном трении для газов и формулы для коэффициентов вязкости
, (2.12)
, (2.13)
где и — длина свободного пробега и скорость теплового хаотического движения молекул.
Зависимость газа от температуры обычно определяется с достаточной степенью точности по эмпирической формуле
(2. 14)
14)
Зная, что и , получим
(2.15)
и — значения, коэффициентов при и . Величина показателя уменьшается с увеличением температуры. Для воздуха при , а при . В дальнейшем для воздуха будем полагать .
Поперечный градиент скорости характеризует изменение скорости в направлении нормали к ней и является важнейшей величиной, так как закон Ньютона утверждает, что вязкость жидкости может проявиться только при . Если , то и вязкость жидкости не проявляется.
Физический смысл градиента скорости. Деформация сдвига кубической жидкой частицы в неравномерном поле скоростей за время равна . Отсюда поперечный градиент скорости
(2.16)
представляет собой скорость относительной деформации сдвига. Следовательно, в жидкостях касательные напряжения пропорциональны скорости относительной деформации сдвига. Одно из основных отличительных свойств жидкостей — их легкоподвижность — в том и состоит, что даже при значительной вязкости , при малой скорости относительной деформации сдвига () напряжение трения также исчезающе мало () и при неограниченном времени действия может вызвать деформацию сколь угодно большой величины (крохотные катера буксируют корабли в сотни тысяч тонн водоизмещением с малой скоростью).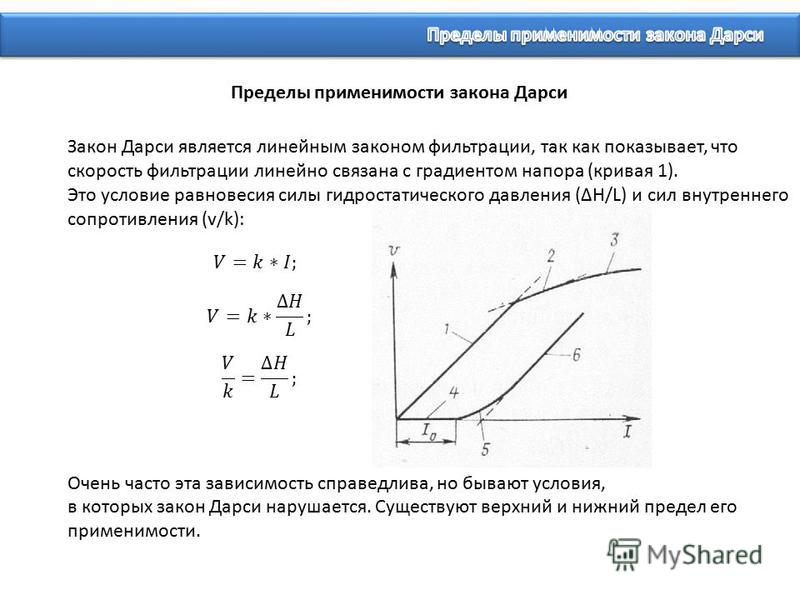 С другой стороны, даже в очень маловязких жидкостях, таких, как воздух, при больших скоростях относительной деформации () силы трения приобретают большое значение. Если величина напряжения трения постоянна для всей площади соприкосновения слоев, как это имеет место в случае чистого сдвига, то сила трения рассчитывается по формуле
С другой стороны, даже в очень маловязких жидкостях, таких, как воздух, при больших скоростях относительной деформации () силы трения приобретают большое значение. Если величина напряжения трения постоянна для всей площади соприкосновения слоев, как это имеет место в случае чистого сдвига, то сила трения рассчитывается по формуле
(2.17)
В противном случае необходимо интегрировать по площади.
Сила трения между твердыми телами пропорциональна силе нормального давления и не зависит ни от скорости относительного движения тел, ни от площади их соприкосновения. Сила трения покоя больше, чем сила трения при относительном движении. Сила трения покоя в жидкостях равна нулю так же как и при движении с равномерным полем скоростей, когда .
Обобщенный закон Ньютона или закон Стокса. Любое напряжение в жидкостях пропорционально соответствующей скорости относительной деформации. Например нормальное напряжение пропорционально относительным скоростям линейной и объемной деформаций.
Гидростатическое давление. Во всех случаях, когда в данной точке отсутствуют тангенциальные напряжения, т. е. при покое, при движении с равномерным полем скоростей, независимо от ориентации площадки, на нее действует только нормальное напряжение. Анализируя равновесие жидкой частицы можно доказать, что величина этого нормального напряжения не зависит от ориентации площадки. Это напряжение с обратным знаком называется гидростатическим давлением , т. е.
(2.18)
где — нормальные напряжения, действующие на грани частицы перпендикулярные осям произвольной системы координат.
Знак минус учитывает, что давление всегда направлено внутрь выделенного объема жидкости. В общем случае течения вязкость жидкостей проявляется не только в появлении касательных напряжений, но и во влиянии на величину нормальных. При этом величина нормальных напряжений в данной точке зависит от ориентации площадки, т. е. . Однако среднее арифметическое трех взаимно перпендикулярных нормальных напряжений в вязкой жидкости не зависит от ориентации площадки и для несжимаемой жидкости, равно давлению с обратным знаком
(2. 19)
19)
В гидродинамике сжимаемой вязкой жидкости принимается второе обобщение гипотезы Ньютона, согласно которому среднее нормальное напряжение равно сумме давления (со знаком минус) и произведения коэффициента второй вязкости на скорость относительной объемной деформации
(2.20)
Коэффициент второй вязкости учитывает диссипацию энергии в самопроизвольных процессах установления равновесия. Для одноатомных газов . Для многоатомных принимает существенное значение, сопоставимое с коэффициентом вязкости , в тех процессах, скорость протекания которых значительно выше скорости установления термодинамического равновесия. Это имеет место, например, при взрывах. Таким образом, учет вязкости существенно усложняет анализ законов движения жидкостей, так как вязкость приводит к появлению тангенциальных напряжений и сложным образом влияет на нормальные напряжения.
Идеальная жидкость — это жидкость, лишенная вязкости (). Эту модель используют для упрощения расчетов в случае, когда силами вязкости можно пренебречь. Нормальное напряжение в данной точке идеальной жидкости не зависит от ориентации площадки и равно гидростатическому давлению с обратным знаком.
Нормальное напряжение в данной точке идеальной жидкости не зависит от ориентации площадки и равно гидростатическому давлению с обратным знаком.
Динамический пограничный слой. С вязкостью связано возникновение пограничного слоя при обтекании жидкостями твердых тел. Пусть поток жидкости с равномерным полем скоростей набегает на поверхность плоской пластины и течет параллельно ей. Молекулы жидкости, непосредственно прилегающие к поверхности твердого тела, прилипают к этой поверхности под действием сил притяжения их к молекулам твердого тела. Прилипшие молекулы из-за вязкости жидкости взаимодействуют с близтекущими слоями, подтормаживая их. Теоретически такое тормозящее действие слоев друг на друга может простираться по направлению нормали к пластине в бесконечность, т. е. скорость вдоль нормали должна постепенно изменяться в таких пределах: . Поэтому пограничный слой называется асимптотическим. Однако в большинстве интересующих нас случаев (маловязкие жидкости и достаточно большие скорости) значительное влияние прилипших молекул и, следовательно, существенное изменение скорости наблюдается лишь в относительно тонком пристеночном слое . Здесь толщина пограничного слоя на расстоянии х от начала пластины, возрастающая вдоль пластины (подтормаживаются все новые слои жидкости).
Здесь толщина пограничного слоя на расстоянии х от начала пластины, возрастающая вдоль пластины (подтормаживаются все новые слои жидкости).
Граничные условия пограничного слоя. Вследствие асимптотичности пограничного слоя его условная толщина определяется общепринятыми граничными условиями:
внутренняя граница (условия прилипания) :
Если Вам понравилась эта лекция, то понравится и эта — Лекция №13 Пожарная безопасность.
внешняя граница (условная)
(2.21)
Формулировка теории пограничного слоя. Всю область течения жидкости около твердого тела можно разбить на две качественно отличные зоны:
а) пограничный слой толщиной . Это относительно тонкий слой , примыкающий к поверхности твердого тела. В этом слое существенно изменяется скорость от uw = 0 до и =0,99 и ди/ду>>0. Поэтому только внутри пограничного слоя проявляется вязкость жидкости и ее необходимо учитывать в расчетах. Однако для пограничного слоя учет вязкости существенно упрощается;
Однако для пограничного слоя учет вязкости существенно упрощается;
б) набегающий невозмущенный поток и область, лежащая над пограничным слоем, в которых . Поэтому жидкость, текущую над пограничным слоем, можно считать идеальной () и анализировать ее движение по более простым законам движения идеальной жидкости.
Теория пограничного слоя разделяет решение общей сложной задачи об обтекании твердого тела потоком вязкой жидкости на две более простые: обтекание твердого тела лишь тонким слоем вязкой жидкости и обтекание твердого тела несколько увеличенного в размерах (на величину пропорциональную толщине пограничного слоя) идеальной жидкостью.
Детали, связанные с градиентом скорости
При изучении гидромеханики важно также знать о градиентах скорости. Гидромеханика — это раздел физики, изучающий механику жидкостей, газов и действующих на них сил. Два свойства, связанные с поведением жидкостей, — это плотность и вязкость.
Вязкость не видна, если жидкость не приведена в движение. Он также устанавливает применение градиента скорости во всех слоях жидкости. Мы обсудим все аспекты, связанные с вязкостью, градиентом скорости и его размерами.
Он также устанавливает применение градиента скорости во всех слоях жидкости. Мы обсудим все аспекты, связанные с вязкостью, градиентом скорости и его размерами.
Согласно определению градиента скорости, разница скоростей между слоями жидкости называется градиентом скорости. Он представлен как v/x, где v обозначает скорость, а x обозначает расстояние между соседними слоями жидкости.
Пример
Когда вода течет по трубе или любому твердому предмету, слой воды, соприкасающийся с трубой твердой поверхности, находится в том же состоянии движения. Однако слой в центре находится в другом состоянии движения. Эта разница между слоями жидкости, протекающей через объект, определяется как градиент скорости.
Другой пример: кто-то красит стену. Вся сила краски должна быть нанесена с помощью кисти, чтобы распределить по стене. Нижний слой краски прилипает к твердой поверхности, тогда как поверхностные слои краски прилипают к кисти. Сила, прикладываемая кистью, влияет на разные слои краски.
Сила, прикладываемая кистью, влияет на разные слои краски.
Молекулы краски при контакте с поверхностью находятся в неподвижной фазе. Но движение увеличивается через слои, когда оно достигает слоя, находящегося в контакте с кистью. Это показывает, что градиент скорости наложен на слои краски.
Уравнение градиента скоростиГрадиент скорости пропорционален величине силы, приложенной к слоям жидкости на единицу.
T α dV/dx
Где
- T обозначает силу.
- В — это скорость.
- x — расстояние перпендикулярно поверхности.
Для установления связи в уравнение вводится константа пропорциональности,
T = η dV/dx,
Здесь η называется коэффициентом вязкости.
Это уравнение применимо к большинству существующих жидкостей; они называются ньютоновскими жидкостями. Жидкости, которые не подчиняются этому уравнению, называются неньютоновскими жидкостями.
Размерность градиента скоростиРазмерная формула градиента скорости [M0 L0 T-1], где
- M = масса
- L = длина
- 9 T = время 9003
Градиент скорости = скорость x расстояние-1 _____ (1)
Размерная формула градиента скорости : [M0 L0 T-1] _____ (2)
Размерная формула расстояния: [M0L1T0] _____ (3)
Размещение (2) и (3) в (1) получаем
V = [M0 L1 T-1] × [M0 L1 T0]-1 = [M0 L0 T-1].
Факторы, влияющие на вязкость жидкостей
Температура в значительной степени влияет на вязкость. Проще говоря, вязкость некоторых жидкостей уменьшается с повышением температуры.
Медовые и сахарные сиропы становятся легкими и легко текучими при нагревании. С другой стороны, моторные масла и другие типы гидравлических жидкостей загустевают в холодные дни и влияют на работу транспортных средств и машин в зимнее время.
С повышением температуры средняя скорость молекул, находящихся в жидкости, увеличивается, а средние межмолекулярные силы также уменьшаются. Связь между скоростью и температурой нелинейна. Она резко меняется, когда жидкость меняет фазу.
Обычно вязкость не зависит от давления, но жидкости, находящиеся под экстремальным давлением, могут испытывать увеличение вязкости, поскольку жидкости естественным образом несжимаемы. Увеличение давления на самом деле не сближает молекулы.
Жидкости текут быстрее, когда они горячие, с другой стороны, газы становятся гуще.
 Следовательно, вязкость газов увеличивается с повышением температуры и пропорциональна квадратному корню из температуры. Это происходит потому, что увеличивается частота межмолекулярных столкновений при повышенном уровне температуры.
Следовательно, вязкость газов увеличивается с повышением температуры и пропорциональна квадратному корню из температуры. Это происходит потому, что увеличивается частота межмолекулярных столкновений при повышенном уровне температуры.Вязкость жидкостей зависит от размера, формы и химической природы их молекул. Вязкость лиофильного коллоидного раствора высокая. На вязкость воды также влияют электролиты. Небольшие количества электролитов уменьшают вязкость, тогда как большое количество растворенных твердых веществ увеличивает вязкость.
Взвешенные частицы в растворе или жидкости увеличивают вязкость. На вязкость крови влияет существующая в плазме эмульсионно-коллоидная система, а также количество взвешенных форменных элементов.
ЗаключениеДля изучения гидромеханики важно знать, что такое градиент скорости. Градиент скорости – это разница скоростей между различными слоями жидкости. Это можно объяснить явлением течения воды по трубе. Слои воды, соприкасающиеся со стенками трубы, движутся иначе, чем слои в центре.

Помимо знания того, что такое градиент скорости, полезно также изучить вопросы о градиенте скорости. Они помогают понять более глубокие аспекты темы и решать задачи.
Градиенты скорости
Введение
Градиенты скорости абсолютно необходимы для анализа пути. зависимых материалов, таких как пластическая деформация металлов. Конечно, резину обычно можно рассматривать как гиперэластичную, что подразумевает нет зависимости от пути. Хотя вязкостное демпфирование резины можно решить с градиентами скорости. Несмотря на это, градиенты скорости полезны для лучшего понимания деформаций и особенно полезно для определения энергетически сопряженные напряжения и деформации, что важно для всех материалов.
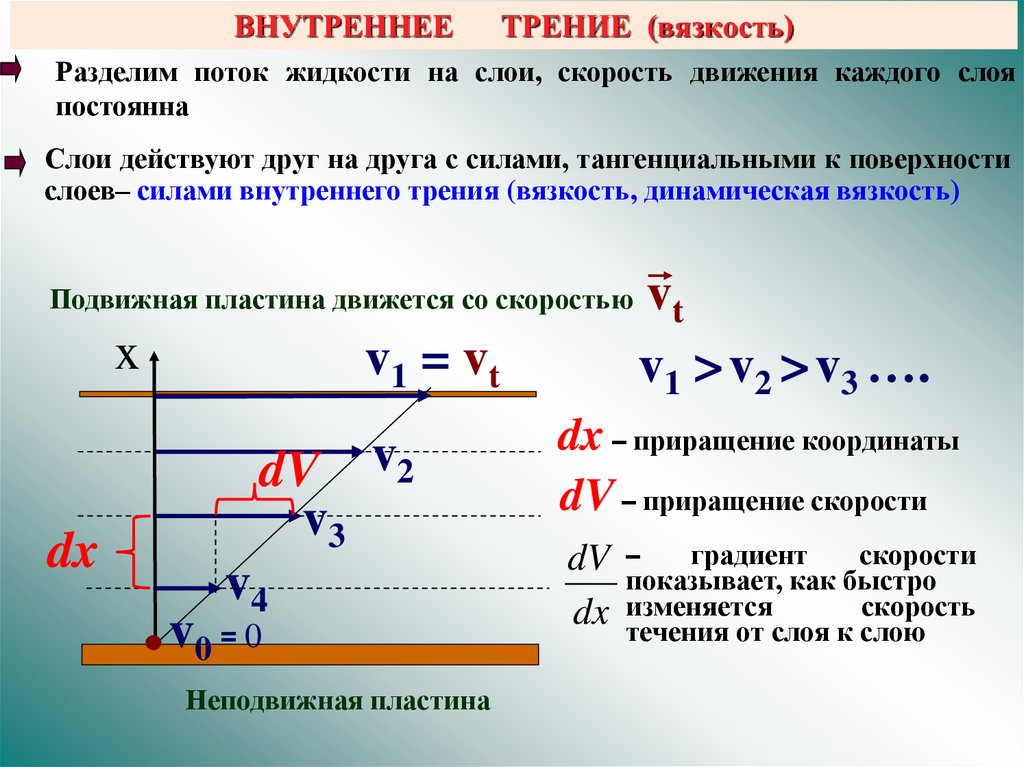
Градиент скорости
Градиент скорости относится к скоростям, что градиент деформации перемещения. Градиент скорости представлен \({\bf L}\) и определяется
\[ {\ bf L} знак равно {\ парциальное {\ bf v} \ над \ парциальное {\ bf х}} = \слева[ \матрица{ {\ парциальное v_x \ над \ парциальное х} & {\ парциальное v_x \ над \ парциальное у} & {\ парциальное v_x \ над \ парциальное z} \\ \\ {\ парциальное v_y \ над \ парциальное х} & {\ парциальное v_y \ над \ парциальное у} & {\ парциальное v_y \ над \ парциальное z} \\ \\ {\ парциальное v_z \ над \ парциальное х} & {\ парциальное v_z \ над \ парциальное у} & {\ парциальное v_z \ над \ парциальное г} } \верно] \]
 Этот
означает, что это эйлерова величина , а не лагранжева величина .
Градиент скорости также может быть записан как
Этот
означает, что это эйлерова величина , а не лагранжева величина .
Градиент скорости также может быть записан как\[ L_ {ij} знак равно {\ парциальное v_i \ над \ парциальное x_j} \] или как
\[ L_{ij} = v_{i,j} \]
Хотя это обозначение зависит от читателя зная, что «\(j\)» представляет \(x_j\) вместо \(X_j\).Пример градиента скорости
Градиент скорости идеально подходит для приложений, связанных с жидкостями. Для жидкостей невозможно указать \({\bf X}\). Это оставляет \({\bf x}\) как единственные практические координаты для описания поле скоростей в.
Предположим, что поле скоростей
\[ {\bf v} = ({1 \более 5-x}, {-y \; \более 10}, 0) \]
Это дает скорость любой частицы в жидкости как функцию положение частицы в этот момент. 92} & 0 & & 0 \\ 0 & {-1 \; \больше 100 \\ \\ 0 & 0 & & 0 } \верно] \]По-прежнему желательно найти способ выразить \({\bf L}\) в терминах из \({\bf F}\), чтобы можно было преобразовать из Моды от Лагранжа к Эйлеру.
 {-1}\) получается уравнение
для \({\bf L}\) через \({\bf F}\).
9{-1}
\]
{-1}\) получается уравнение
для \({\bf L}\) через \({\bf F}\).
9{-1}
\]
Приведенные выше два уравнения невероятно полезны, хотя, вероятно, это не так. очевидно в этот момент. С тем, что непосредственно выше, можно вычислить эйлерову величину \({\bf L}\), используя только лагранжиан количество, \({\bf F}\).Пример градиента скорости растяжения
Вспомните пример штамма Almansi в в котором смещения выражались через \({\bf X}\), а затем \({\bf х}\). На этот раз, чтобы вычислить градиенты скорости, мы должны сначала имеют скорости.
Итак, на этот раз пусть
\[ x = \left( {X \over L_o} \right) L_F \]
Если объект растягивается так, что\[ L_F = L_o + A\,t \]
, где \(A\) — любая положительная константа, то\[ x = \left( {X \over L_o} \right) (L_o + A\,t) \]
и \(v_x\) равно \({dx \over dt}\), поэтому это дает\[ v_x = \left( {X \over L_o} \right) A \]
Это хорошо, но не поможет градиенту скорости, потому что скорость не выражается как функция \(x\). Но это можно преодолеть, объединив
два приведенных выше уравнения, чтобы получить
Но это можно преодолеть, объединив
два приведенных выше уравнения, чтобы получить\[ v_x = {A x \над L_o + A\,t} \]
Теперь можно оценить градиент скорости.\[ L_ {11} знак равно {\ partial v_x \ over \ partial x} = {A \ over L_o + A \, t} = {A \ over L_F} \]
и\[ {\ бф L} = \слева[ \матрица{ A/L_F & 0 \;\; & 0 \\ 0 & 0 \;\; & 0 \\ 0 & 0 \;\; & 0 } \верно] \]
Этот результат подчеркивает, что градиент скорости является эйлеровой величиной, потому что \(L_{11} = {A \over L_F}\), а не \({A \over L_o}\). По мере того, как объект растягивается, \(L_F\) со временем увеличивается, а \(L_{11}\) уменьшается. 9{-1} = \слева[ \матрица{ {L_o \над L_o+A\,t} & 0 & \;\;0 \\ \\ 0 & 1 & \;\;0 \\ \\ 0 & 0 & \;\;1 } \верно] «=» \слева[ \матрица{ {L_o \over L_F} & 0 & \;\;0 \\ \\ 0 & 1 & \;\;0 \\ \\ 0 & 0 & \;\;1 } \верно] \]
Нам также понадобится \(\dot {\bf F}\). Это\[ \ точка {\ bf F} = \слева[ \матрица{ {А\над L_о} & 0 & \;\;0 \\ \\ 0 & 0 & \;\;0 \\ \\ 0 & 0 & \;\;0 } \верно] \]
Таким образом, произведение \(\dot {\bf F}\) и \({\bf F}^{-1}\) дает 9{-1} = \слева[ \матрица{ {А\над L_о} & 0 & \;\;0 \\ \\ 0 & 0 & \;\;0 \\ \\ 0 & 0 & \;\;0 } \верно] \слева[ \матрица{ {L_o \over L_F} & 0 & \;\;0 \\ \\ 0 & 1 & \;\;0 \\ \\ 0 & 0 & \;\;1 } \верно] «=» \слева[ \матрица{ {A \над L_F} & 0 & \;\;0 \\ \\ 0 & 0 & \;\;0 \\ \\ 0 & 0 & \;\;0 } \верно] \]
Идентичен предыдущему примеру.
Градиенты скорости и Abaqus UMATS
Абак В пакете конечных элементов есть функция, называемая «UMAT». для подпрограммы USER MATERIAL. Эта подпрограмма дает пользователю возможность написать подпрограмма, которая рассчитывает напряженное состояние в материале с учетом градиентов деформации в начале \({\bf F}_t\) и в конце \({\bf F}_{t+\Delta t}\) временного шага. (Документация Abaqus здесь.)
Можно рассматривать каучук как сверхэластичный и рассчитать напряжение исключительно на основе \({\bf F}_{t+\Delta t}\). Или можно было бы использовать обе деформации градиенты для вычисления градиента скорости и использования его для включения вязкоупругого или гистерезисное демпфирование при расчете напряжения.
Например, предположим, что Abaqus выполняет временной шаг во время моделирования переходного процесса то есть \(\Delta t = 0,1 \text{sec}\). В начале временного шага (который был как раз конец предыдущего шага), градиент деформации равен
\[ {\ бф F} _t = \слева[ \матрица{ 1.
 30 и 0 и 0 \\
0 и 0,90 и 0 \\
0 и 0 и 0,90
} \верно]
\]
30 и 0 и 0 \\
0 и 0,90 и 0 \\
0 и 0 и 0,90
} \верно]
\]
И в конце шага\[ {\bf F}_{t+\Delta t} = \слева[ \матрица{ 1,40 и 0 и 0 \\ 0 и 0,85 и 0 \\ 0 и 0 и 0,85 } \верно] \]
Итак, \(\dot {\bf F}\) равно\[ \begin{выравнивание} \dot {\bf F} & = & {1 \over \Delta t} \left( {\bf F}_{t+\Delta t} — {\bf F}_t \right) \\ \\ \\ & = & {1 \более 0,1} \влево( \слева[ \матрица{ 1,40 и 0 и 0 \\ 0 и 0,85 и 0 \\ 0 и 0 и 0,85 } \верно] — \слева[ \матрица{ 1.30 и 0 и 0 \\ 0 и 0,9{-1} = \слева[ \матрица{ 1,0 и 0 и 0 \\ 0 и -0,5 и 0 \\ 0 и 0 и -0,5 } \верно] \слева[ \матрица{ 0,714&0&0\ 0 и 1,177 и 0 \\ 0 и 0 и 1,177 } \верно] «=» \слева[ \матрица{ 0,714 & \;\;\;0 & \;\;\;0 \\ 0&-0,588&\;\;\;0\ 0 & \;\;\;0 & -0,588 } \верно] \]
Тензоры скорости деформации и вращения
Градиент скорости можно разложить на симметричную и антисимметричную части. следующее. 9T ) / 2\), симметричен и выглядит и ведет себя очень похоже на тензор малых деформаций обсуждалось ранее, за исключением, конечно, того, что это касается скорости, а не перемещения.
 T \вправо)
\]
9Т \ справа)
\]
T \вправо)
\]
9Т \ справа)
\]
Таким образом, уравнение градиента скорости может быть записано как\[ {\ bf L} = {\ bf D} + {\ bf W} \]
Компоненты тензора скорости деформации \({\bf D}\) равны\[ {\ бф D} = \слева[ \матрица{ L_{11} & {L_{12} + L_{21} \более 2} & {L_{13} + L_{31} \более 2} \\ \\ {L_{21} + L_{12} \более 2} & L_{22} & {L_{23} + L_{32} \более 2} \\ \\ {L_{31} + L_{13} \более 2} и {L_{32} + L_{23} \более 2} и L_{33} } \верно] \]
Компоненты тензора спина \({\bf W}\) равны\[ {\ бф W} = \слева[ \матрица{ 0 & {L_{12} — L_{21} \более 2} & {L_{13} — L_{31} \более 2} \\ \\ {L_{21} — L_{12} \более 2} & 0 & {L_{23} — L_{32} \более 2} \\ \\ {L_{31} — L_{13} \более 2} и {L_{32} — L_{23} \более 2} & 0 } \верно] \]
С точки зрения парциалов тензор скорости деформации равен\[ {\ бф D} = \слева[ \матрица{ {\ парциальное v_x \ над \ парциальное х} & {1 \ над 2} \ влево ( {\ парциальное v_x \ над \ парциальное у} + {\ парциальное v_y \ над \ парциальное х} \ справа) & {1 \ над 2} \ влево ( {\ парциальное v_x \ над \ парциальное г} + {\ парциальное v_z \ над \ парциальное х} \ справа) \\ \\ {1 \ над 2} \ влево ( {\ парциальное v_y \ над \ парциальное х} + {\ парциальное v_x \ над \ парциальное у} \ справа) & {\ парциальное v_y \ над \ парциальное у} & {1 \ над 2} \ влево ( {\ парциальное v_y \ над \ парциальное г} + {\ парциальное v_z \ над \ парциальное у} \ справа) \\ \\ {1 \ над 2} \ влево ( {\ парциальное v_z \ над \ парциальное х} + {\ парциальное v_x \ над \ парциальное г} \ справа) & {1 \ над 2} \ влево ( {\ парциальное v_z \ над \ парциальное у} + {\ парциальное v_y \ над \ парциальное г} \ справа) & {\ парциальное v_z \ над \ парциальное г} } \верно] \]
и тензор спина
\[ {\ бф W} = \слева[ \матрица{ 0 & {1 \ над 2} \ влево ( {\ парциальное v_x \ над \ парциальное у} — {\ парциальное v_y \ над \ парциальное х} \ справа) & {1 \ над 2} \ влево ( {\ парциальное v_x \ над \ парциальное г} — {\ парциальное v_z \ над \ парциальное х} \ справа) \\ \\ {1 \ над 2} \ влево ( {\ парциальное v_y \ над \ парциальное х} — {\ парциальное v_x \ над \ парциальное у} \ справа) & 0 & {1 \ над 2} \ влево ( {\ парциальное v_y \ над \ парциальное г} — {\ парциальное v_z \ над \ парциальное у} \ справа) \\ \\ {1 \ над 2} \ влево ( {\ парциальное v_z \ над \ парциальное х} — {\ парциальное v_x \ над \ парциальное г} \ вправо) & {1 \ над 2} \ влево ( {\ парциальное v_z \ над \ парциальное у} — {\ парциальное v_y \ над \ парциальное г} \ справа) & 0 } \верно] \]
Тензор вращения и вектор угловой скорости
Рассмотрим объект на рисунке, вращающийся против часовой стрелки вокруг оси \(z\) со скоростью угловая скорость, \(\omega_z\).
 Вычислите компонент \(W_{21}\) спинового тензора.
Вычислите компонент \(W_{21}\) спинового тензора.Следующие уравнения описывают вращение.
\[ \begin{выравнивание} x & = & X \cos \omega_z t & — & Y \sin \omega_z t \\ y & = & X \sin \omega_z t & + & Y \cos \omega_z t \end{эквнаррай} \]
Возьмите производную по времени от уравнений, чтобы получить \(v_x\) и \(v_y\).\[ \begin{выравнивание} v_x & = & — \omega_z X \sin \omega_z t & — & \omega_z Y \cos \omega_z t \\ v_y & = & \;\;\,\omega_z X \cos \omega_z t & — & \omega_z Y \sin \omega_z t \end{эквнаррай} \]
Это дает нам \(v_x\) и \(v_y\) через \(X\) и \(Y\). Но мы вместо этого нужны \(v_x\) и \(v_y\) с точки зрения \(x\) и \(y\), чтобы вычислить компоненты тензора спина. Этого можно добиться, сначала обратив первая пара уравнений для получения \(X\) и \(Y\) через \(x\) и \(y\), и подставив их во вторую пару уравнений. 9{-1}} \cdot {\bf x}\}}Подставив эти инвертированные уравнения во вторую пару, содержащую компоненты скорости дают удивительно простой результат.

\[ \begin{выравнивание} v_x&=&-\omega_z\,y\ v_y & = & \;\;\,\omega_z \, х \end{эквнаррай} \]
Теперь можно легко вычислить \(W_{21}\) компонент тензора спина.\[ \begin{выравнивание} W_{21} \quad = \quad {1 \over 2} \left( {\partial v_y \over \partial x} — {\partial v_x \over \partial y} \right) \ quad = \ quad {1 \ более 2} \ влево ( {\ парциальное (\ omega_z \, x) \ более \ парциальное х} — {\ парциальное (- \ omega_z \, у) \ более \ парциальное у} \ право ) \quad = \quad \omega_z \end{эквнаррай} \]
Этот простой двумерный пример демонстрирует, как тензор спина может содержать компоненты вектор угловой скорости.Трехмерный тензор спина можно резюмировать как
\[ {\ бф W} = \слева[ \матрица{ \;\;0 & -\omega_z & \;\;\;\omega_y \\ \;\;\;\omega_z & \;\;0 & -\omega_x \\ -\omega_y & \;\;\;\omega_x & \;\;0 } \верно] \]
, где \(\boldsymbol{\omega}\) — вектор угловой скорости. Это напрямую связано к вращению вокруг оси обсуждаемому вращению страница матрицы. Напомним, что он содержал угол поворота \(\alpha\) относительно
ось, \({\bf p} = (p_x, p_y, p_z)\). Отношения
Напомним, что он содержал угол поворота \(\alpha\) относительно
ось, \({\bf p} = (p_x, p_y, p_z)\). Отношения\[ \omega_x \, = \, \dot \alpha \, p_x = {1 \over 2} \left( {\partial v_z \over \partial y} — {\partial v_y \over \partial z} \right) \qquad \qquad \omega_y \, = \, \dot \alpha \, p_y = {1 \over 2} \left( {\partial v_x \over \partial z} — {\partial v_z \over \partial x} \right) \]
\[ \ omega_z \, = \, \ точка \ альфа \, p_z = {1 \ над 2} \ влево ( {\ парциальное v_y \ над \ парциальное х} — {\ парциальное v_x \ над \ парциальное у} \ справа) \]Скорость деформации и вращение Пример
Если градиент скорости
\[ {\ бф L} = \слева[ \матрица{ \;\;\;0,5 & \;\;\;0,4 & \;\;\;0,3 \\ \;\;\;0,2 и -0,1 и -0,2 \\ -0,3 и \;\;\;0,4 и -0,1 } \верно] \]
Тогда тензор скорости деформации равен\[ {\ бф D} = \слева[ \матрица{ 0,5 & \;\;\;0,3 & \;\;\;0,0 \\ 0,3&-0,1&\;\;\;0,1\ 0,0 и \;\;\;0,1 и -0,1 } \верно] \]
, а тензор спина равен\[ {\ бф W} = \слева[ \матрица{ \;\;\;0,0 & \;\;0,1 & \;\;\;0,3 \\ -0,1&\;\;0,0&-0,3\ -0,3 & \;\;0,3 & \;\;\;0,0 } \верно] \] 9\text{Истина}_{\text{Объем}} \]
И это применимо независимо от уровня деформации или ориентации. T\), чтобы повернуть его в
текущая ориентация точно так же, как
9Т
«=»
\омега
\слева[ \матрица{
-\sin\theta & -\cos\theta\\
\;\;\;\cos \тета & -\грех \тета}
\верно]
\слева[ \матрица{
\;\;\;\cos\тета и \sin\тета\\
-\sin\тета и \cos\тета}
\верно]
\\
\\
\\
«=»
\омега
\слева[ \матрица{
0 и -1 \\
1 & \;\;\;0 }
\верно]
\end{эквнаррай}
\]
T\), чтобы повернуть его в
текущая ориентация точно так же, как
9Т
«=»
\омега
\слева[ \матрица{
-\sin\theta & -\cos\theta\\
\;\;\;\cos \тета & -\грех \тета}
\верно]
\слева[ \матрица{
\;\;\;\cos\тета и \sin\тета\\
-\sin\тета и \cos\тета}
\верно]
\\
\\
\\
«=»
\омега
\слева[ \матрица{
0 и -1 \\
1 & \;\;\;0 }
\верно]
\end{эквнаррай}
\]
Таким образом, результатом является антисимметричный спиновый тензор.Градиент скорости и зеленая деформация
Последнее соотношение, которое нужно развить, — это соотношение между градиентом скорости и производная по времени от тензора деформации Грина. Начните с определения штамма Грина. 9{-1} \]
Эти уравнения, связывающие \(\dot {\bf E}\) и \({\bf D}\), будут использоваться для определения пары энергетически сопряженных тензоров напряжений и деформаций.Ограничения
В заключение стоит отметить, что обычные ограничения небольшие деформации и/или небольшие повороты, которые усложняют большинство расчетов деформации, не применяются к градиентам скорости.



 Следовательно, вязкость газов увеличивается с повышением температуры и пропорциональна квадратному корню из температуры. Это происходит потому, что увеличивается частота межмолекулярных столкновений при повышенном уровне температуры.
Следовательно, вязкость газов увеличивается с повышением температуры и пропорциональна квадратному корню из температуры. Это происходит потому, что увеличивается частота межмолекулярных столкновений при повышенном уровне температуры.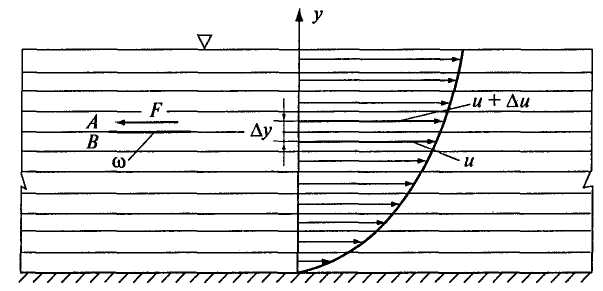
 Этот
означает, что это эйлерова величина , а не лагранжева величина .
Градиент скорости также может быть записан как
Этот
означает, что это эйлерова величина , а не лагранжева величина .
Градиент скорости также может быть записан как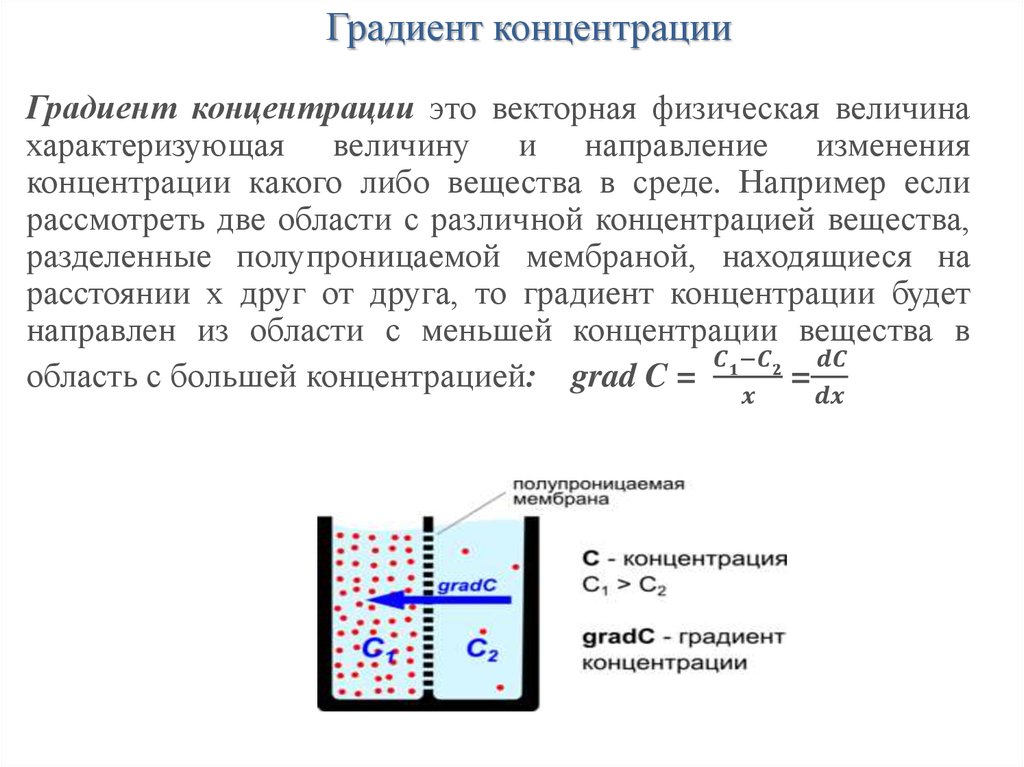 {-1}\) получается уравнение
для \({\bf L}\) через \({\bf F}\).
9{-1}
\]
{-1}\) получается уравнение
для \({\bf L}\) через \({\bf F}\).
9{-1}
\]  Но это можно преодолеть, объединив
два приведенных выше уравнения, чтобы получить
Но это можно преодолеть, объединив
два приведенных выше уравнения, чтобы получить
 30 и 0 и 0 \\
0 и 0,90 и 0 \\
0 и 0 и 0,90
} \верно]
\]
30 и 0 и 0 \\
0 и 0,90 и 0 \\
0 и 0 и 0,90
} \верно]
\]  T \вправо)
\]
9Т \ справа)
\]
T \вправо)
\]
9Т \ справа)
\]  Вычислите компонент \(W_{21}\) спинового тензора.
Вычислите компонент \(W_{21}\) спинового тензора.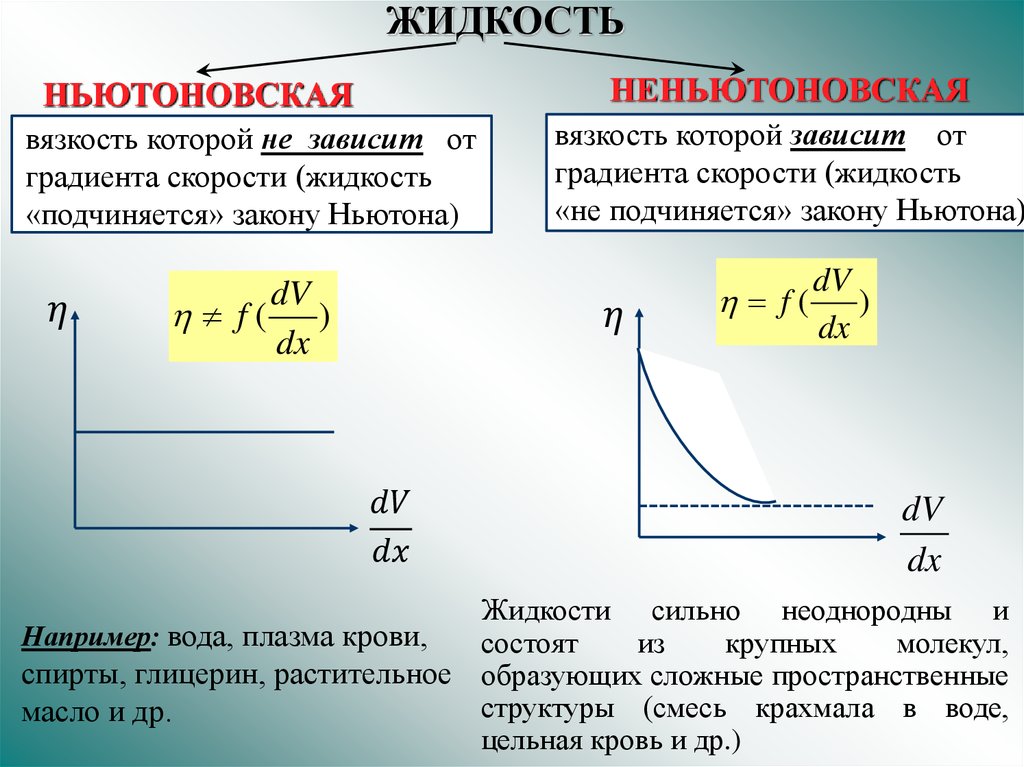
 Напомним, что он содержал угол поворота \(\alpha\) относительно
ось, \({\bf p} = (p_x, p_y, p_z)\). Отношения
Напомним, что он содержал угол поворота \(\alpha\) относительно
ось, \({\bf p} = (p_x, p_y, p_z)\). Отношения T\), чтобы повернуть его в
текущая ориентация точно так же, как
9Т
«=»
\омега
\слева[ \матрица{
-\sin\theta & -\cos\theta\\
\;\;\;\cos \тета & -\грех \тета}
\верно]
\слева[ \матрица{
\;\;\;\cos\тета и \sin\тета\\
-\sin\тета и \cos\тета}
\верно]
\\
\\
\\
«=»
\омега
\слева[ \матрица{
0 и -1 \\
1 & \;\;\;0 }
\верно]
\end{эквнаррай}
\]
T\), чтобы повернуть его в
текущая ориентация точно так же, как
9Т
«=»
\омега
\слева[ \матрица{
-\sin\theta & -\cos\theta\\
\;\;\;\cos \тета & -\грех \тета}
\верно]
\слева[ \матрица{
\;\;\;\cos\тета и \sin\тета\\
-\sin\тета и \cos\тета}
\верно]
\\
\\
\\
«=»
\омега
\слева[ \матрица{
0 и -1 \\
1 & \;\;\;0 }
\верно]
\end{эквнаррай}
\]