Урок геометрии в 7-м классе по теме: «Медиана, биссектриса, высота»
- Сафронова Вера Николаевна
Разделы: Математика
Цели урока.
Ход урока и примерная дозировка по времени.

5 минут.
33 минуты.
5 минут.
2 минуты.
Оборудование и наглядность урока.
- Рисунок 1.
- Модели треугольников, изготовленные из плотного цветного картона, с закреплёнными в вершинах цветными тесёмками (для каждого ученика и учителя).
- Чертёж прямоугольного треугольника с изображением 3-х его высот, которые пересекаются в вершине прямого угла.
- Магнитофон, кассета с записью песни “Когда я стану кошкой” (Музыка Фадеева М., слова Секачёвой И.) для проведения физминутки.
- Весёлые рисунки геометрических
зверят: биссектриса – крыса, медиана – обезьяна,
высота похожа на кота.

- У каждого ученика тетрадь с печатной основой “Геометрия – 7. Проверочные работы с элементами тестирования”. Альхова З.Н. Издательство “Лицей”, 2000 г.
- Портреты Архимеда и Л. Эйлера.
- На каждой парте 3 треугольника из цветного картона с изображением на них высот, медиан, биссектрис (аппликация).
- Физическая карта Америки.
I. Сообщение темы урока и постановка задач урока.
Какую геометрическую фигуру изобразила Коптилова Рита на своём весёлом рисунке? (Треугольник). Рис. 1.
А что называется треугольником? (Треугольником называется геометрическая фигура, состоящая из трёх точек, не лежащих на одной прямой и соединённых попарно отрезками).
Сколько у него элементов? (6) Назовите
элементы треугольника. (Три стороны и три угла).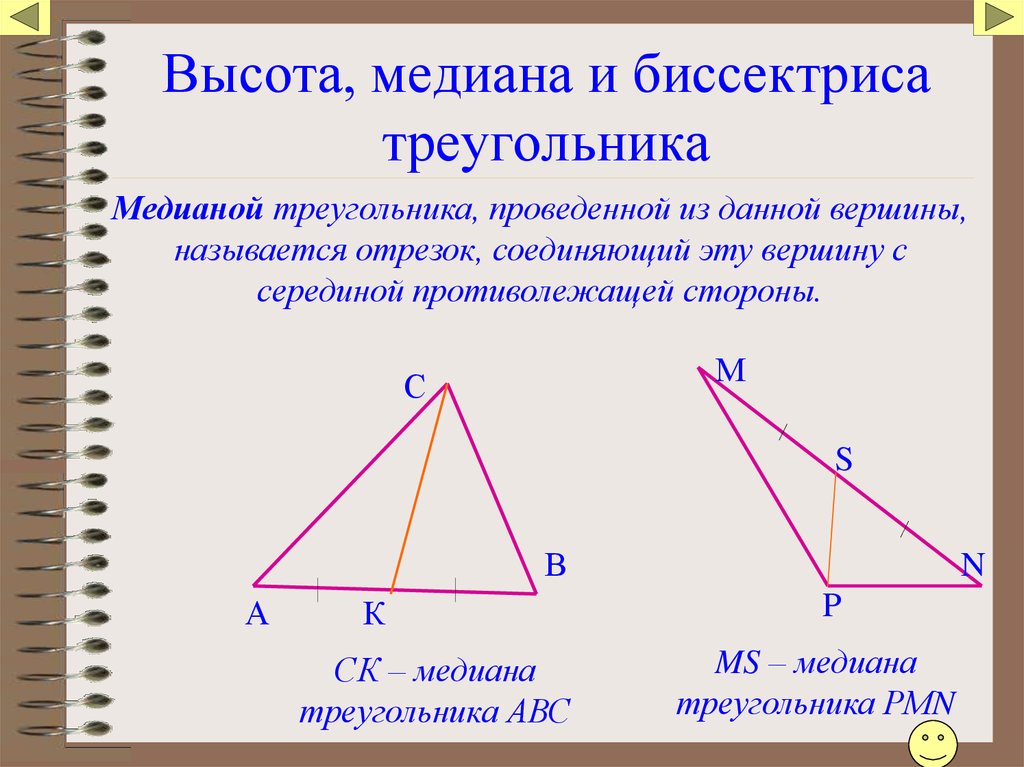
Кто из вас не слышал о загадочном Бермудском треугольнике, в котором бесследно исчезают корабли и самолёты? (Он находится в Атлантическом океане между Бермудскими островами, государством Пуэрто-Рико и полуостровом Флорида).
А ведь знакомый всем нам треугольник также таит в себе немало интересного и загадочного.
Зовётся он треугольник,
И с ним хлопот не оберётся школьник!
Тема сегодняшнего урока: “Медиана, биссектриса и высота треугольника”.
Преодолеть хлопоты – трудности, связанные с новыми понятиями – медиана, биссектриса и высота треугольника – нам сегодня помогут три мои ассистентки: Емельянова Катя, Грязнова Маша и Гамаюнова Оля (одноклассницы, подготовленные учителем заранее).
II. Объяснение нового материала.
1. Медиана.
Начертите треугольник АВС и найдите середину стороны ВС – точку М.
Что называется серединой отрезка? (Серединой отрезка называется точка отрезка, которая делит его пополам, то есть на два равных отрезка).
Запись на доске: АМ=МС. Рис. 2.
Соедините точку М с вершиной В. Отрезок ВМ называется медианой треугольника.
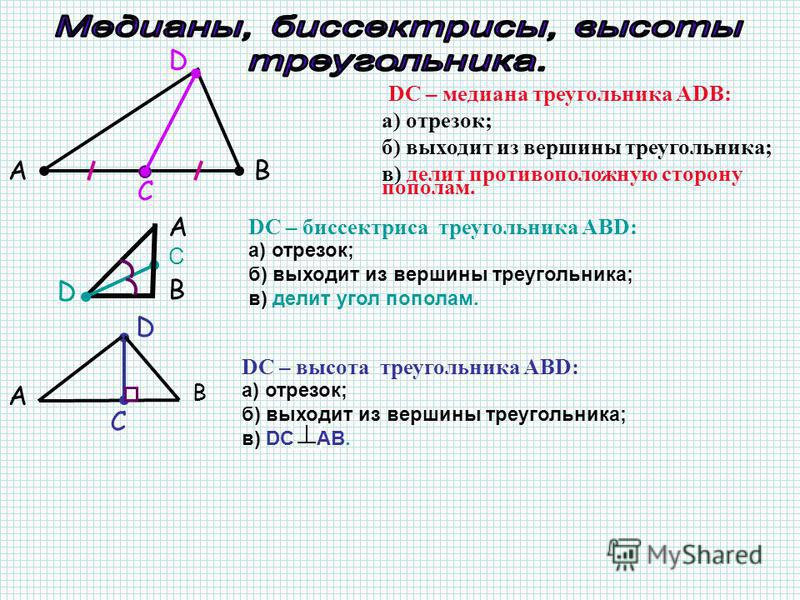
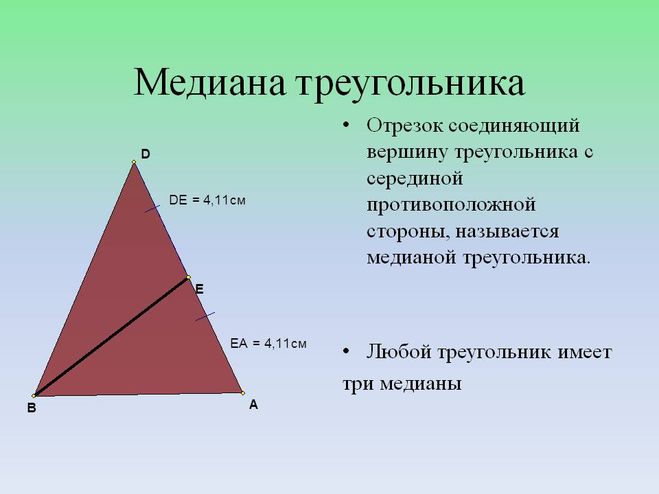
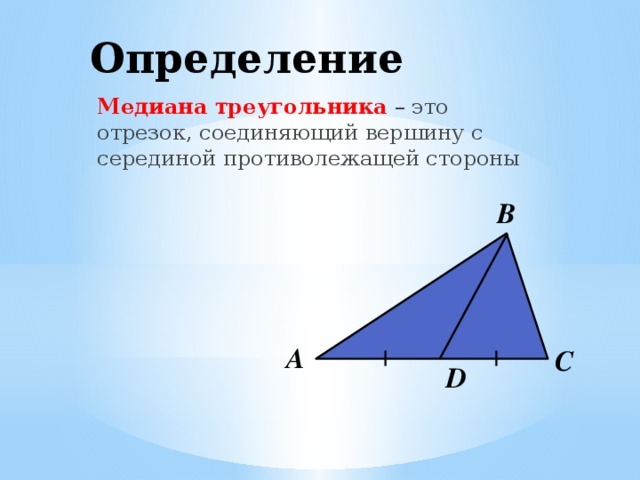
Определение. Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника.
Сколько вершин у треугольника?
(3). Сколько у него сторон? (3).
Сколько медиан можно провести в треугольнике?(3).
“Проведите” три медианы на моделях треугольников. (Ассистентки контролируют правильность выполнения задания, помогают в случае необходимости).
Какое свойство медиан вы заметили?
В любом треугольнике все медианы пересекаются в одной точке.
Эта точка называется центром тяжести треугольника.
[1].
№ 114 (стр. 37) [4] — у доски.
Докажите, что в равных треугольниках медианы, проведённые к равным сторонам, равны. Рис. 3.
Дано:
АВС, А1В1С1,
М1=М1С1.
АС=А1С1,
АМ=МС,
А1Доказать:
ВМ=В1М1.
Доказательство:
2. Высота.
Запись на доске: ВН АС, Н АС. Рис. 4.
С помощью чертёжного угольника из вершины В треугольника АВС проведём перпендикуляр ВН к прямой АС. Он называется высотой треугольника.
Определение. Высотой треугольника называется перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противолежащую сторону.
Сколько высот имеет треугольник? (3).
“Постройте” все три высоты на модели вашего треугольника. (Ассистенты проверяют).Обладают ли высоты аналогичным свойством, что и медианы? (Да).
У некоторых из вас модели прямоугольных треугольников. Где пересеклись их высоты? (В вершине прямого угла).Учащимся показывается ответ на рисунке (плакат на доске). Рис. 5.
№ 103 (стр. 36) [4] – у доски.
Начертите треугольник АВС, у которого угол В – тупой. С помощью чертёжного угольника проведите его высоты.
Решение.
ВН1 АС, АН2 ВС, СН3 АВ. Рис. 6.
Вывод. Высоты или их продолжения пересекаются в одной точке.
Эта точка называется ортоцентром. [1]
Физминутка.
(Её проводит Емельянова Катя в образе кошки под запись песни “Когда я стану кошкой”).
Для физминутки Катя не зря выбрала образ кошки. Он поможет нам в запоминании нового понятия – высота.
Катя (первая ассистентка).
Высота похожа на кота,
Который, выгнув спину,
И под прямым углом
Соединит вершину
И сторону хвостом. [2] Рис. 7.(Стихи иллюстрируются весёлым рисунком).
Конечно, геометрия – наука серьёзная, и учить её надо серьёзно и вдумчиво. Но и забавные стихи и весёлые “геометрические” зверята помогают учению.
Ольга (вторая ассистентка).
Медиана-обезьяна,
У которой зоркий глаз,
Прыгнет точно в середину
Стороны против вершины,
Где находится сейчас. [2] Рис. 8.Маша (третья ассистентка).
Биссектриса – это крыса,
Которая бегает по углам
И делит угол пополам. Рис.9.
(Строки сопровождаются показом рисунков).
3. Биссектриса.
Вспомните определение биссектрисы угла.
Луч, исходящий из вершины угла и делящий его на два равных угла, называется биссектрисой угла.
Запись на доске: АВК = СВК
К АС. Рис. 10.
Постройте биссектрису ВК угла В с помощью транспортира. Она пересечёт отрезок АС в точке К. Отрезок ВК называется биссектрисой угла В треугольника АВС.
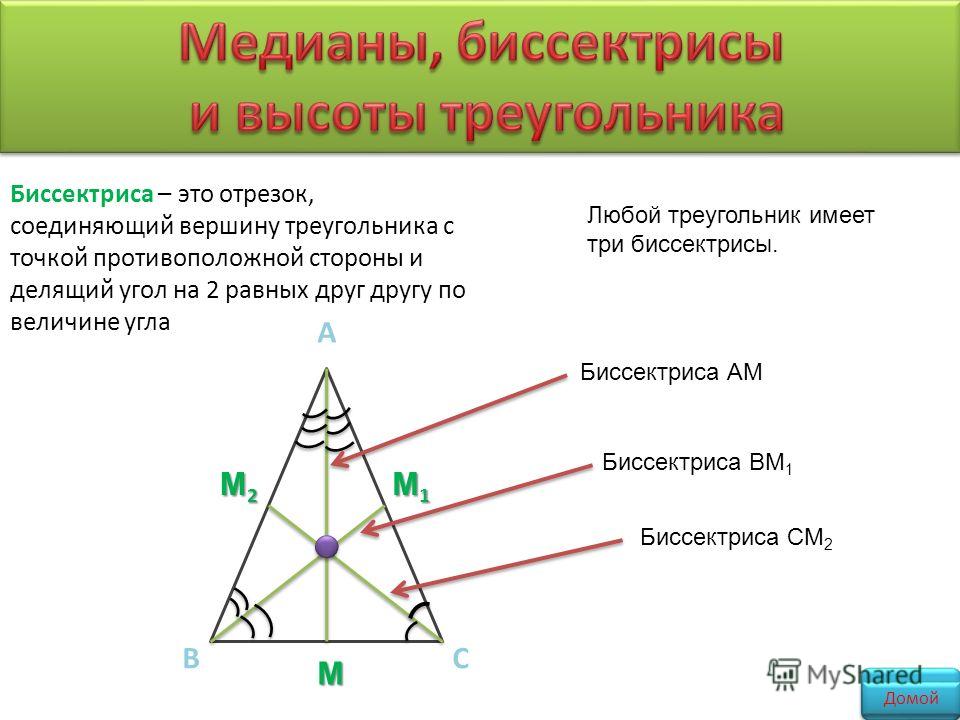
Определение. Биссектрисой треугольника называется отрезок биссектрисы угла треугольника, соединяющий вершину угла треугольника с точкой противоположной стороны треугольника.
Покажите все три биссектрисы на вашей модели треугольника. (Контроль со стороны учителя и ассистенток).
Сформулируйте свойство биссектрис треугольника.
В любом треугольнике биссектрисы пересекаются в одной точке.
Тест – 6, В – 1 (стр. 22). [3]
№ 5 (с комментированием). Рис. 11.
Дано:
АВK,
АС – биссектриса угла А.Доказать:
АВС= АКС.
Доказательство:
III. Закрепление.
1.
Тест – 6, В –1 (стр. 21) [3] – с комментированием.№ 1, 2.
1. Заполните пропуски в формулировках элементов треугольника и свойств геометрических фигур.
а) Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника.
б) Из точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притомединственный. 2. Верны ли следующие утверждения? (В случае “нет” напишите верный ответ).
а) В любом треугольнике можно провести три медианы. (Да).
2. Работа в парах.
б) Точка пересечения высот любого треугольника лежит внутри треугольника. (Не всегда).
в) Все биссектрисы треугольника пересекаются в одной точке. (Да).На каждой парте лежат три треугольника, разносторонние, разных цветов. На одном из них изображены три медианы, на другом – высоты, на третьем – биссектрисы.
- Покажите треугольник с изображением высот. ( Фиолетовые и красные).
- Поднимите треугольник, на котором изображены медианы. (Синие, жёлтые и оранжевые).
- Покажите треугольник с изображением биссектрис. (Зелёные, чёрные).
(Учащиеся поднимают треугольники).
Центр тяжести треугольника, его ортоцентр и точка пересечения биссектрис треугольника называются (особыми) замечательными точками треугольника.
Замечательные точки есть у треугольника.
Точка первая – она
Чувством гордости полна:
Медианы в ней пересекаются,
Центром тяжести та точка называется.
Ортоцентр – вторая точка,
Архимед её открыл,
Все высоты в ней встречаются,
Удивив учёный мир.
Третья точка – тоже важная
Биссектрисы всех углов,
Бросив вызов свой отважный,
В ней “сошлись”, не тратя слов.
Эйлер точки все заметил,
Свойства новые открыл, —
Так на радость школьникам
Возникла новая ветвь математики —
Геометрия треугольника.Тригонометрию вы будете изучать в старших классах.
С какими новыми геометрическими понятиями вы сегодня познакомились? (Медиана, биссектриса, высота).
IV.
Стр. 33- 34, № 101, 102, 106.Домашнее задание.
V. Выставление оценок и их комментирование.
Литература.
- Глейзер Г.И. История математики в школе 7 – 8 классы. М., Просвещение, 1985 г.
- Народное образование. № 9 – 10, 1993 г. “Ребятам о зверятах”. Елизарова С.
- Проверочные работы с элементами тестирования по геометрии. 7 класс. Альхова З.Н., Саратов, Лицей, 2000 г.
- Атанасян Л.С., Бутузов В.Ф. и др. Геометрия 7 – 9. М., Просвещение, 2003 г.
Урок геометрии для 7 класса на тему «Медиана, биссектриса и высота треугольника»
Шангина Ирина Евгеньевна, учитель математики ОУ СОШ № 11 г.Октябрьска Самарской области
Урок геометрии в 7 классе
Тема: Медиана, биссектриса и высота треугольника.
Цель: ввести новые понятия высоты, медианы и биссектрисы треугольника, показать их применение при решении задач.
Задачи:
Ввести новые понятия высоты, медианы и биссектрисы треугольника.
Способствовать формированию устойчивого познавательного интереса к изучению геометрии.
Развивать логическое мышление учащихся.
Тип урока: урок изучения нового материала.
Формы организации учебной деятельности: коллективная, индивидуальная, работа в парах.
Оборудование и наглядность урока: магнитофон, кассета с записью музыки для проведения музыкальной паузы, рисунок 1, модели треугольников, изготовленные из плотного цветного картона, с закреплёнными в вершинах цветными тесёмками (для каждого ученика и учителя), чертёж прямоугольного треугольника с изображением 3-х его высот, которые пересекаются в вершине прямого угла, весёлые рисунки геометрических зверят: биссектриса – крыса, медиана – обезьяна, высота похожа на кота, портреты Л. Эйлера и Архимеда, на каждой парте 3 треугольника из цветного картона с изображением на них высот, медиан, биссектрис (аппликация).
Эйлера и Архимеда, на каждой парте 3 треугольника из цветного картона с изображением на них высот, медиан, биссектрис (аппликация).
Ход урока
Организационный момент.
Сообщение темы урока и постановка задач урока.
Рисунок 1
А что называется треугольником? (Треугольником называется геометрическая фигура, состоящая из трёх точек, не лежащих на одной прямой и соединённых попарно отрезками).
Сколько у него элементов? (6)
Назовите элементы треугольника. (Три стороны и три угла).
Кто из вас не слышал о загадочном Бермудском треугольнике, в котором бесследно исчезают корабли и самолёты? {Он находится в Атлантическом океане между Бермудскими островами, государством Пуэрто – Рико и полуостровом Флорида}.
А ведь знакомый всем нам треугольник также таит в себе немало интересного и загадочного.

Зовётся он треугольник,
И с ним хлопот не оберётся школьник!
Преодолеть хлопоты – трудности, связанные с новыми понятиями – медиана, биссектриса и высота треугольника – нам сегодня помогут три мои ассистентки (ученицы этого класса, подготовленные учителем заранее).
III. Объяснение нового материала.
1. Медиана.
Начертите треугольник АВС и найдите середину стороны ВС – точку М. Рис.2
Что называется серединой отрезка? (Серединой отрезка называется точка отрезка, которая делит его пополам, то есть на два равных отрезка).
Запись на доске: АМ = МС.
Рисунок 2
Определение. Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника.
Сколько вершин у треугольника? (3).
Сколько у него сторон? (3).

Сколько медиан можно провести в треугольнике?(3).
“Проведите” три медианы на моделях треугольников. (Ассистентки контролируют правильность выполнения задания, помогают в случае необходимости).
Какое свойство медиан вы заметили? (В любом треугольнике все медианы пересекаются в одной точке).
Эта точка называется центром тяжести треугольника.
Решим номер 114 из учебника (стр. 37) у доски.
№114. Докажите, что в равных треугольниках медианы, проведённые к равным сторонам, равны. Рис. 3.
Дано:
АВС, А1В1С1,
АС=А1С1,
АМ=МС,
А1М1=М1С1.
Доказать:
ВМ=В1М1.
Рисунок 3
Доказательство:
АВ = А1В1,
1. АВС = А1В1С1 А = А1,
АС = А1С1.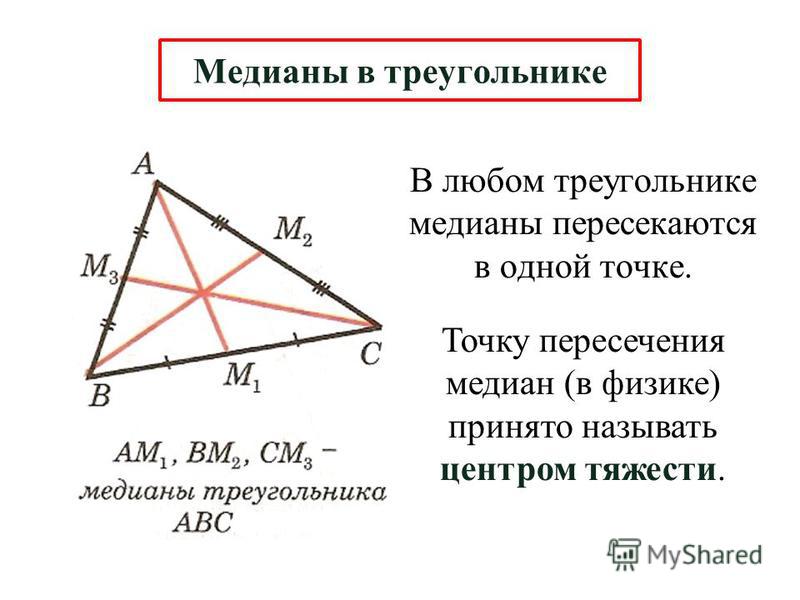
2. АС = А1С1,
АМ = МС, АМ = А1М1.
А1М1 = М1С1
3. А = А1,
АВ = А1В1, АВМ = А1В1М1 ВМ = В1М1, ч.т.д.
АМ = А1М1
2. Высота.
Запись на доске: ВН АС, Н АС. Рис. 4.
Рисунок 4
Определение. Высотой треугольника называется перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противолежащую сторону.
Сколько высот имеет треугольник? (3).
“Постройте” все три высоты на модели вашего треугольника. (Ассистенты проверяют).
Обладают ли высоты аналогичным свойством, что и медианы? (Да).
У некоторых из вас модели прямоугольных треугольников. Где пересеклись их высоты? (В вершине прямого угла).

Учащимся показывается ответ на рисунке (плакат на доске). Рис. 5.
Рисунок 5
№.103. Начертите треугольник АВС, у которого угол В – тупой. С помощью чертёжного угольника проведите его высоты.
Решение.
ВН1 АС, АН2 ВС, СН3 АВ. Рис. 6.
Рисунок 6
Конечно, геометрия – наука серьёзная, и учить её надо серьёзно и вдумчиво. Но и забавные стихи и весёлые “геометрические” зверята помогают учению.
Для музыкальной паузы девочки выбрали различные образы, которые помогут нам в запоминании новых понятий – медиана, биссектриса и высота
Первая ассистентка.
Высота похожа на кота,
Который, выгнув спину,
И под прямым углом
Соединит вершину
И сторону хвостом. Рис. 7.
Рисунок 7
(Стихи иллюстрируются весёлым рисунком).
Вторая ассистентка.
Медиана-обезьяна,
У которой зоркий глаз,
Прыгнет точно в середину
Стороны против вершины,
Где находится сейчас. Рис. 8.
Рисунок 8
Третья ассистентка.
Биссектриса – это крыса,
Которая бегает по углам
И делит угол пополам. Рис. 9.
Рисунок 9
3. Биссектриса.
Определение. Луч, исходящий из вершины угла и делящий его на два равных угла, называется биссектрисой угла.
Запись на доске: АВК = СВК, К АС. Рис. 10.
Определение. Биссектрисой треугольника называется отрезок биссектрисы угла треугольника, соединяющий вершину угла треугольника с точкой противоположной стороны треугольника.
Рисунок 10
Дано:
АВK,
АС – биссектриса угла А.
Доказать:
АВС = АКС.
Рисунок 11
Доказательство:
АС – биссектриса А ВАС = КАС
АВ = АК (по условию) АВС = АКС, ч.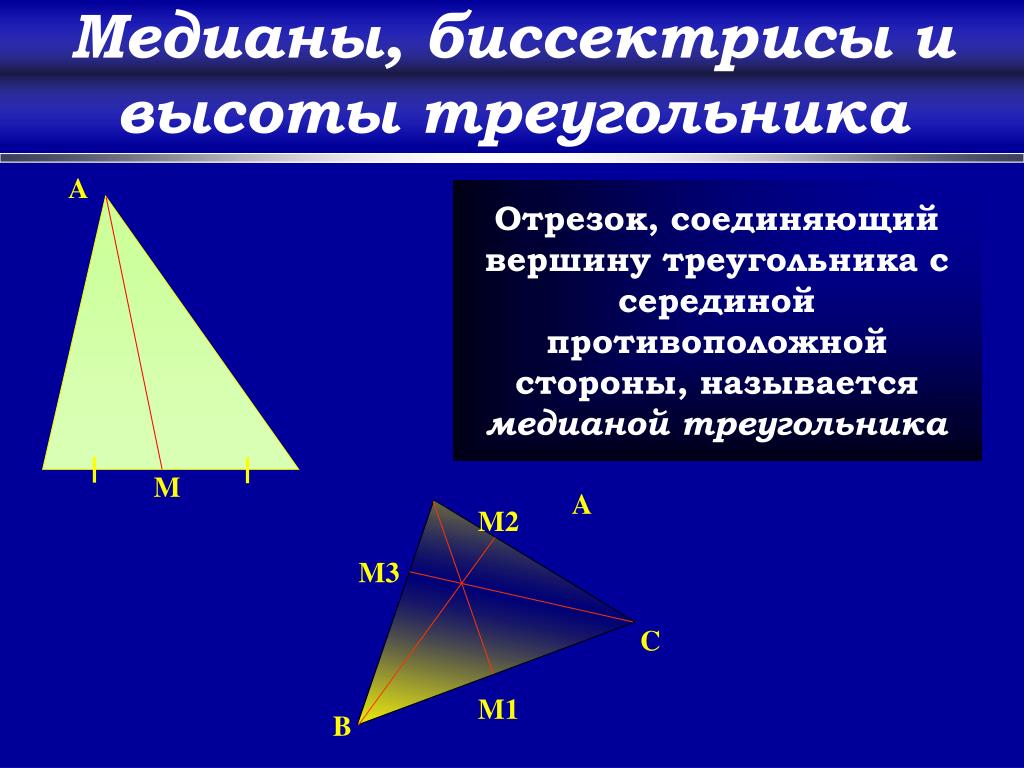 т.д.
т.д.
АС – общая сторона
IV. Контроль усвоения учащимися нового материала.
1. Заполните пропуски в формулировках элементов треугольника и свойств геометрических фигур.
а) Отрезок, соединяющий вершину треугольника с серединой ______________, называется ___________ треугольника.
(Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника).
б) Из точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом _____________.
(Из точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом единственный).
2. Верны ли следующие утверждения? (В случае “нет” напишите верный ответ).
а) В любом треугольнике можно провести три медианы. (Да).
б) Точка пересечения высот любого треугольника лежит внутри треугольника. (Не всегда).
в) Все биссектрисы треугольника пересекаются в одной точке. (Да).
(Да).
Работа в парах. На каждой парте лежат три треугольника, разносторонние, разных цветов. На одном из них изображены три медианы, на другом – высоты, на третьем – биссектрисы.
Покажите треугольник с изображением высот. (Фиолетовые и красные).
Поднимите треугольник, на котором изображены медианы. (Синие, жёлтые и оранжевые).
Покажите треугольник с изображением биссектрис. (Зелёные, чёрные).
(Учащиеся поднимают треугольники).
Замечательные точки есть у треугольника.
Точка первая – она
Чувством гордости полна:
Медианы в ней пересекаются,
Центром тяжести та точка называется.
Ортоцентр – вторая точка,
Архимед её открыл,
Все высоты в ней встречаются,
Удивив учёный мир.
Третья точка – тоже важная
Биссектрисы всех углов,
Бросив вызов свой отважный,
В ней “сошлись”, не тратя слов.
Эйлер точки все заметил,
Свойства новые открыл, —
Так на радость школьникам
Возникла новая ветвь математики —
Геометрия треугольника.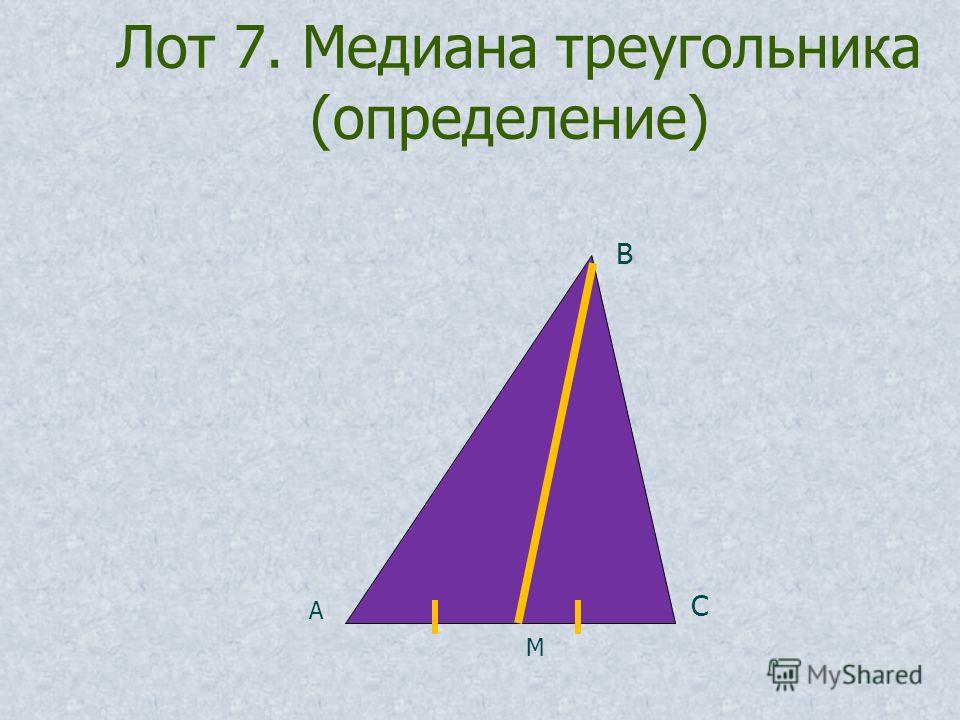
V. Подведение итогов урока.
1. Домашнее задание. Стр. 33 – 34, № 101, 102, 106.
2. Выставление оценок и их комментирование.
Литература.
Глейзер Г.И. История математики в школе 7 – 8 классы. М., Просвещение, 1985 г.
Проверочные работы с элементами тестирования по геометрии. 7 класс. Альхова З.Н., Саратов, Лицей, 2000 г.
http://www.etudes.ru/ru/forums/topic.php?post=84&
Медиана прямоугольного треугольника
Примечание. В данном уроке изложены теоретические материалы и решение задач по геометрии на тему «медиана в прямоугольном треугольнике». Если Вам необходимо решить задачу по геометрии, которой здесь нет — пишите об этом в форуме. Почти наверняка курс будет дополнен.
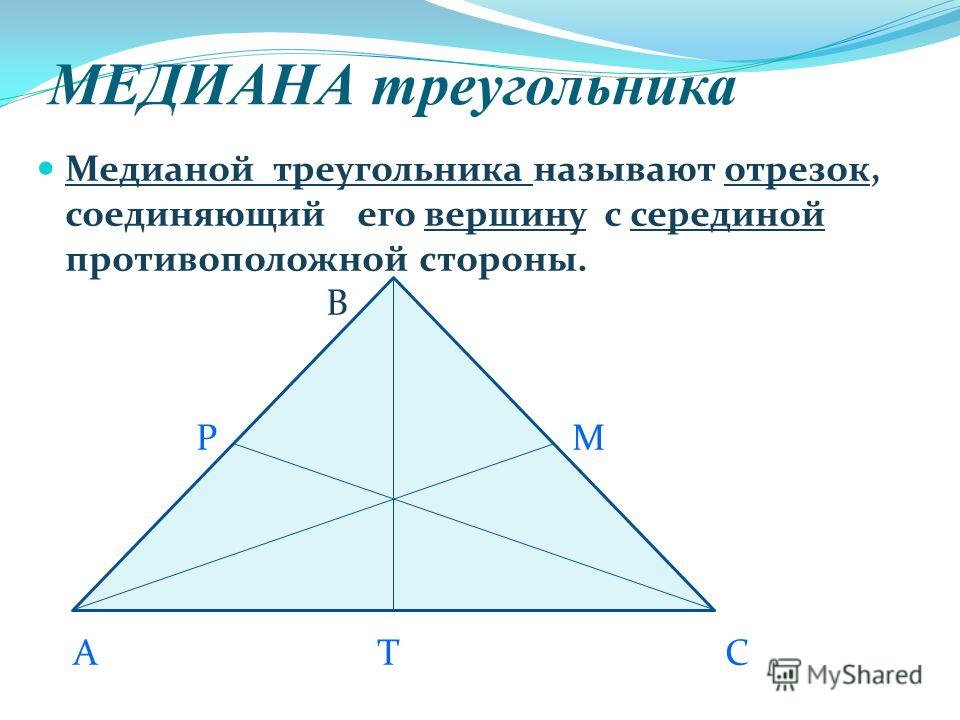
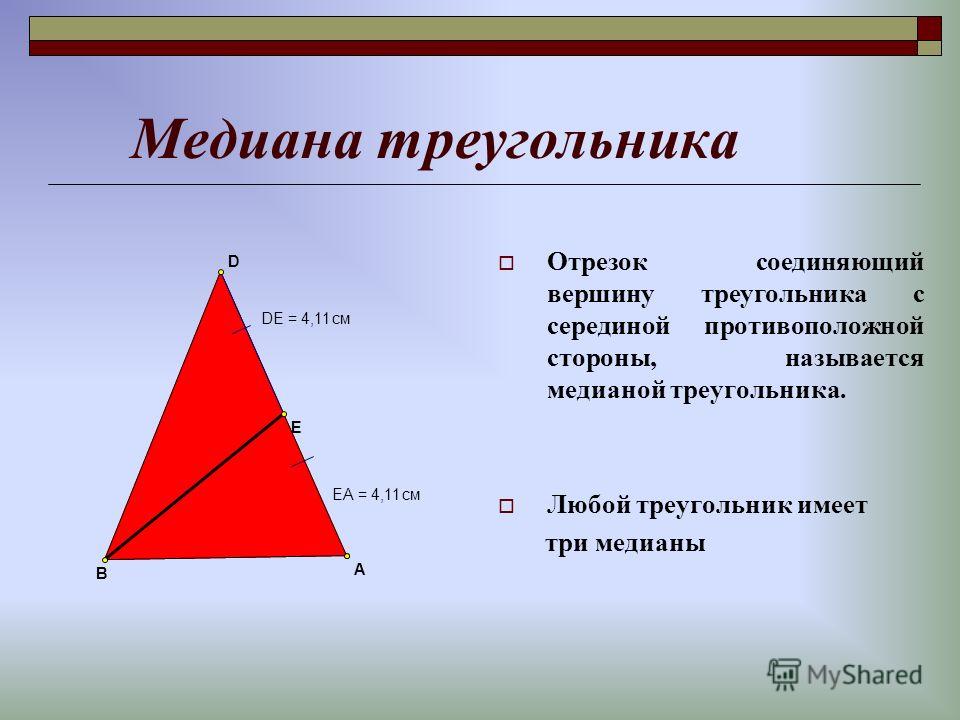
Определение медианы
|
Медианой треугольника называется отрезок, соединяющий один из углов треугольника с серединой противолежащей ему стороны. (медианой также называют прямую, содержащую данный отрезок) |
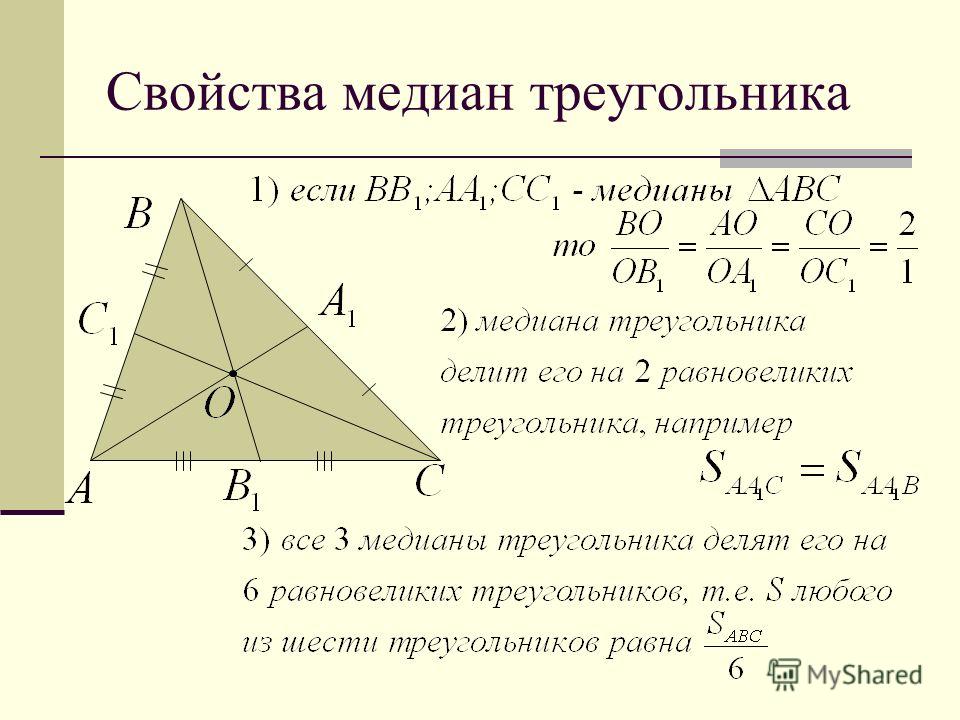
- Медианы треугольника пересекаются в одной точке и делятся этой точкой на две части в отношении 2:1, считая от вершины угла. Точка их пересечения называется центром тяжести треугольника (относительно редко в задачах для обозначения этой точки используется термин «центроид»),
- Медиана разбивает треугольник на два равновеликих треугольника.
- Треугольник делится тремя медианами на шесть равновеликих треугольников.
- Большей стороне треугольника соответствует меньшая медиана.
Задачи по геометрии, предлагаемые для решения, в основном, используют следующие свойства медианы прямоугольного треугольника.
- Сумма квадратов медиан, опущенных на катеты прямоугольного треугольника равна пяти квадратам медианы, опущенной на гипотенузу (Формула 1)
- Медиана, опущенная на гипотенузу прямоугольного треугольника равна половине гипотенузы (Формула 2)
- Медиана, опущенная на гипотенузу прямоугольного треугольника, равна радиусу окружности, описанной вокруг данного прямоугольного треугольника (Формула 2)
- Медиана, опущенная на гипотенузу, равна половине корня квадратного из суммы квадратов катетов (Формула 3)
- Медиана, опущенная на гипотенузу, равна частному от деления длины катета на два синуса противолежащего катету острого угла (Формула 4)
- Медиана, опущенная на гипотенузу, равна частному от деления длины катета на два косинуса прилежащего катету острого угла (Формула 4)
- Сумма квадратов сторон прямоугольного треугольника равна восьми квадратам медианы, опущенной на его гипотенузу (Формула 5)
Обозначения в формулах:
a, b — катеты прямоугольного треугольника
c — гипотенуза прямоугольного треугольника
Если обозначить треугольник, как ABC, то
ВС = а
AC = b
AB = c
(то есть стороны a,b,c — являются противолежащими соответствующим углам)
ma — медиана, проведенная к катету а
mb — медиана, проведенная к катету b
mc — медиана прямоугольного треугольника, проведенная к гипотенузе с
α (альфа) — угол CAB, противолежащий стороне а
Задача про медиану в прямоугольном треугольнике
Медианы прямоугольного треугольника, проведенные к катетам, равны, соответственно, 3 см и 4 см.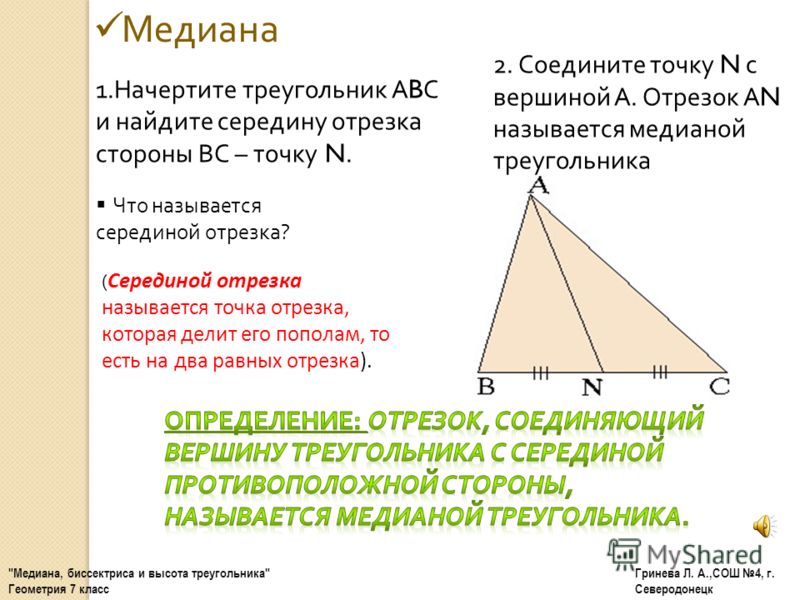 Найдите гипотенузу треугольника
Найдите гипотенузу треугольника
Решение
Прежде чем начать решение задачи, обратим внимание на соотношение длины гипотенузы прямоугольного треугольника и медианы, которая опущена на нее. Для этого обратимся к формулам 2, 4, 5 свойств медианы в прямоугольном треугольнике. В этих формулах явно указано соотношение гипотенузы и медианы, которая на нее опущена как 1 к 2. Поэтому,для удобства будущих вычислений (что никак не повлияет на правильность решения, но сделает его более удобным), обозначим длины катетов AC и BC через переменные x и y как 2x и 2y (а не x и y).
Рассмотрим прямоугольный треугольник ADC. Угол C у него прямой по условию задачи, катет AC — общий с треугольником ABC, а катет CD равен половине BC согласно свойствам медианы. Тогда, по теореме Пифагора
AC2 + CD2 = AD2
Поскольку AC = 2x, CD = y (так как медиана делит катет на две равные части), то
4x2 + y2 = 9
Одновременно, рассмотрим прямоугольный треугольник EBC. У него также угол С прямой по условию задачи, катет BC является общим с катетом BC исходного треугольника ABC, а катет EC по свойству медианы равен половине катета AC исходного треугольника ABC.
У него также угол С прямой по условию задачи, катет BC является общим с катетом BC исходного треугольника ABC, а катет EC по свойству медианы равен половине катета AC исходного треугольника ABC.
По теореме Пифагора:
EC2 + BC2 = BE2
Поскольку EC = x (медиана делит катет пополам), BC = 2y, то
x2 + 4y2 = 16
Так как треугольники ABC, EBC и ADC связаны между собой общими сторонами, то оба полученных уравнения также связаны между собой.
Решим полученную систему уравнений.
4x2 + y2 = 9
x2 + 4y2 = 16
Сложим оба уравнения (впрочем, можно было выбрать и любой другой способ решения).
5x2 + 5y2 = 25
5( x2 + y2 ) = 25
x2 + y2 = 5
Обратимся к исходному треугольнику ABC. По теореме Пифагора
По теореме Пифагора
AC2 + BC2 = AB2
Так как длина каждого из катетов нам «известна», мы приняли, что их длина равна 2x и 2y, то есть
4x2 + 4y2 = AB2
Так как оба слагаемых имеют общий множитель 4, вынесем его за скобки
4 ( x2 + y2 ) = AB2
Чему равно x2 + y2 мы уже знаем (см. выше x2 + y2 = 5), поэтому просто подставим значения вместо x2 + y2
AB2 = 4 х 5
AB2 = 20
AB = √20 = 2√5
Ответ: длина гипотенузы равна 2√5
0
Угол между высотой и медианой треугольника | Описание курса | Медіана прямокутного трикутника
TOP 10 что такое медиана в геометрии ЛУЧШИЕ и НОВЕЙШИЕ
Вы задаетесь вопросом что такое медиана в геометрии но в настоящее время нет ответа, поэтому давайте kienthuctudonghoa. com подведем итоги и перечислим лучшие статьи с вопросом. ответьте на вопрос, что такое медиана в геометрии, что поможет вам получить наиболее точный ответ. Следующая статья призвана помочь вам сделать правильный выбор и получить больше полезной информации.
com подведем итоги и перечислим лучшие статьи с вопросом. ответьте на вопрос, что такое медиана в геометрии, что поможет вам получить наиболее точный ответ. Следующая статья призвана помочь вам сделать правильный выбор и получить больше полезной информации.
Mục lục
- 1 1. Медиана (геометрия) – Википедия
- 2 2. Медиана определения треугольника (Иллюстрированный математический словарь)
- 3 3. Медиана треугольника – формула, определения, свойства, примеры – MathHelp.com – Справка по геометрии – YouTube
- 5 5.Что такое медиана треугольника? – YouTube
- 6 6. Медиана формулы треугольника, примеры задач, свойства…
- 7 7. Медиана треугольника | Определение и формула – Study.com
- 8 8. Медианы (чтение) | Геометрия | CK-12 Foundation
- 9 9. Высота и медиана треугольника (определение и свойства) – Byju’s
- 10 10. Медианы треугольника – университетские наставники
:
en.wikipedia. org
orgСм. Подробности
2. Медиан определения треугольника (иллюстрированный словарь математики)
- Автор: www.mathsisfun.com
- Пост Дата: 24 вчера
- Рейтинг: 27.
- Высший рейтинг: 5
- Низкий рейтинг: 3
- Сводка: Иллюстрированное определение медианы треугольника: отрезок прямой от вершины (угловой точки) до середины противоположной стороны. Треугольник имеет три медианы …
Подробнее
3. Медиана треугольника – формула, определения, свойства, примеры
- Автор: www.
 cuemath.com
cuemath.com - 1 1 Дата публикации: 2 вчера Рейтинг: 4(1135 отзывов)
- Высшая оценка: 3
- Низкая оценка: 3
- Итог: В геометрии медиана треугольника относится к отрезку, соединяющему вершину треугольника с серединой противоположной стороны, таким образом
Подробнее
0012
See 9007
5.WHAT AS AS AS ARIAT IS AS AS AS AS AS AS AS AS ARIAT IS AS AS AS ARIAT IS AS AS AS ARIATIIAN? — YouTube
- Автор: www.youtube.com
- Пост Дата: 22 вчера
- Рейтинг: 1 (883 Обзоры)
- Высокий рейтинг: 3
- .0037 2
- РЕЗЮМЕ:
См. Подробная информация
Подробная информация
6. Медиан формулы треугольника, пример проблем, свойства…
- Автор: www.youtube.com
- Пост.
- Рейтинг: 1 (738 Обзоры)
- Высокий рейтинг: 5
- Низкий рейтинг: 2
- РЕЗЮМЕ:
См. Детали
7.Median at Ariangle | TRIANGLIN | Определение и формула – Study.com
- Автор: Исследование. :
Подробнее
8. Медианы (прочитано) | Геометрия | CK-12 Foundation
- Автор: www.ck12.org
- Дата публикации: 11 вчера
- Рейтинг: 2 (332 Обзоры)
- Высокий рейтинг: 3
- Низкий рейтинг: 3
- Суммируют:
См. Подробности
9.alt
- Автор: byjus.
 com
com - Пост Дата: 28 Вчера
- Рейтинг: 3 (1548 Обзоры)
- Высокий рейтинг: 4
- Low Rate0037 3
- Summary:
See Details
10.Medians of a Triangle – Varsity Tutors
- Author: www.varsitytutors.com
- Post date: 5 yesterday
- Rating: 1(733 отзыва)
- Высшая оценка: 4
- Низкая оценка: 2
- Резюме: Медиана треугольника – это отрезок, проведенный из вершины к середине противоположной стороны треугольника. вершина.
См. подробности
Приведенная выше информация о вопросе что такое медиана в геометрии , безусловно, помогла вам получить нужный ответ, пожалуйста, поделитесь этой статьей со всеми. так что каждый может знать эту полезную информацию. Желаю тебе хорошего дня!
Желаю тебе хорошего дня!
Учебное пособие по геометрии PinkMonkey.com — 2.4 Высота, медиана и биссектриса угла
Учебное пособие по геометрии PinkMonkey.com — 2.4 Высота, медиана и биссектриса углаПолучите бесплатный месяц Amazon Prime по запросу! | Получайте деньги за участие в опросах! 5-75 долларов США за опрос | Техасское безопасное вождение онлайн — всего 25 долларов | Услуга выезда на место, Решения для перевозки грузовиков. | Бесплатная аренда видеоигр через Gamefly! |
| |
|
Все содержание Авторские права
Все права защищены.
Дальнейшее распространение строго запрещено.
Высота и медиана треугольника – свойства, примеры и решенные примеры
Медиана треугольника – это отрезок прямой линии, проведенный от вершины треугольника к средней точке противоположной стороны. Он делит противоположную сторону треугольника на два равных отрезка. Это означает, что мы знаем, что это медиана, если у нас есть эти равные отрезки. Итак, на приведенной ниже диаграмме линия «AB» называется «медианой».
Давайте узнаем еще о двух терминах «высота и медиана треугольника» в следующей статье. Мы надеемся, что доступный контент поможет вам лучше понять медианы главы и высоты треугольников.
(Изображение будет загружено в ближайшее время)
Свойства медианы треугольника
В треугольнике может быть до трех медиан, по одной из каждой вершины. Обратитесь к следующему изображению.
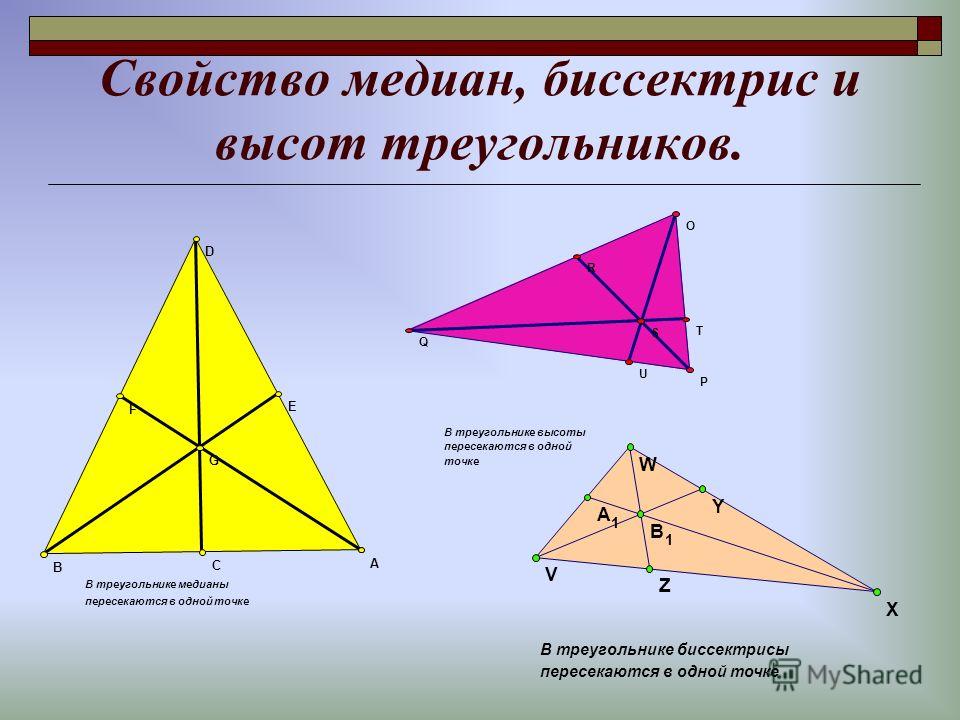
Однако, когда мы рисуем три медианы, они всегда пересекаются в одной точке.
 И эта единственная точка известна как центр тяжести треугольника.
И эта единственная точка известна как центр тяжести треугольника.Медианы делят треугольники пополам. На самом деле два новых треугольника, образованные добавлением медианы, имеют равные площади.
Эти шесть (6) треугольников, образованных тремя (3) медианами, также состоят из равных площадей.
(Изображение будет загружено в ближайшее время)
Что такое высота треугольника?
Высота — это отрезок перпендикулярной линии, проведенный из вершины треугольника к противоположной стороне. В нашем треугольнике на приведенной выше диаграмме, если мы проведем линию из вершины А перпендикулярно противоположной стороне, она будет известна как высота. Однако мы могли бы сделать это из любой вершины, но чаще всего мы видим это сверху. Как и в случае с медианой, у нас также есть отношение к свойствам треугольника.
(Изображение будет загружено в ближайшее время)
Свойства высоты треугольника
Каждый треугольник может иметь 3 высоты, т. е. по одной из каждой вершины, как вы можете ясно видеть на изображении ниже.
Все 3 высоты треугольника всегда встречаются в одной точке, независимо от формы треугольника.
На приведенной выше диаграмме также видно, что высота — это кратчайшее расстояние от вершины до ее противоположной стороны.
Разница между медианой и высотой треугольника
Если вы запутались между двумя этими терминами: медианой и высотой треугольника и думаете, являются ли они одинаковыми или нет, то позвольте мне разъяснить вам здесь.
Ответ: Нет. Высота и медиана в треугольнике не совпадают.
Высота и медиана в треугольнике не совпадают.
Высота — это биссектриса, лежащая на любой стороне треугольника, и она измеряет расстояние между вершиной и линией, являющейся противоположной стороной, тогда как медиана — это отрезок, соединяющий вершину с центральной точкой треугольника. Обратная сторона. Следовательно, медиана не обязательно должна быть перпендикулярна каждый раз. Однако в случае равностороннего треугольника медиана и высота всегда одинаковы.
Решенные примеры
Пример:
Данные углы треугольника PQR относятся как 3 : 2 : 1. Вычислите все углы ΔPQR.
Решение:
Пусть первый угол P равен x.
Следовательно, ∠B = 2x и ∠C = 3x
Мы знаем, что сумма всех углов треугольника = 180°
x + 2x + 3x = 180°
6x = 180°
x = 30
Итак, ∠P = 30°
∠Q = 2 × 30° = 60°,
∠R = 3 × 30° = 90°.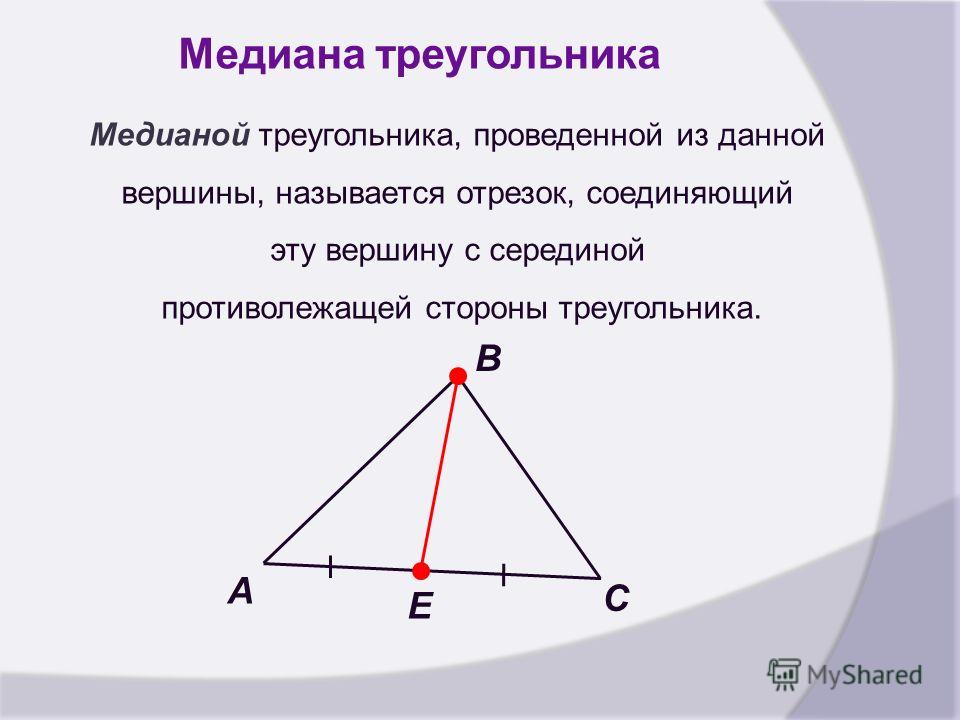
Таким образом, треугольник является разносторонним с тремя различными углами
Построение медианы треугольника с помощью компаса
Построение медианы треугольника с помощью компаса имеет очень простой метод. В этом методе ученики должны иметь весы, карандаш и циркуль. Во-первых, вы должны снять мерку с компаса и нарисовать дуги одинакового размера вверх с каждой стороны.
В точку, образованную пересечением дуг, проведите отрезок перпендикулярной линии к основанию треугольника. И так вы делаете медиану треугольника. Нарисовав отрезок с серединой, основание уже разделено на равные размеры.
Уникальные сведения о медиане и высоте
Во многих случаях высота и медиана треугольника могут совпадать. Хотя единственное различие между медианой и высотой, которое учащиеся могут заметить, заключается в том, как они нарисованы. Медиана проводится от вершины треугольника к середине основания.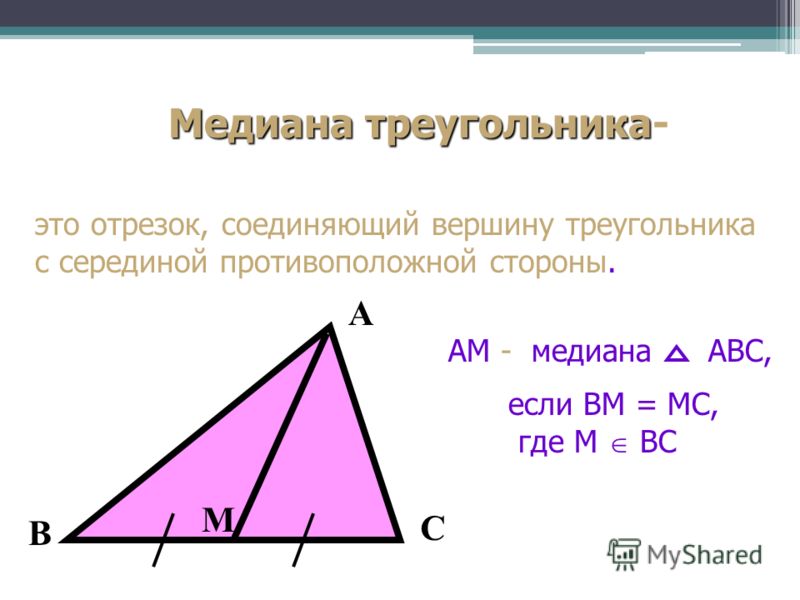 При этом высота проводится от любой вершины треугольника к противоположной стороне, перпендикулярной ей. Количество высот и медианы, которые может иметь треугольник, равно трем для обоих.
При этом высота проводится от любой вершины треугольника к противоположной стороне, перпендикулярной ей. Количество высот и медианы, которые может иметь треугольник, равно трем для обоих.
В равностороннем треугольнике медиана и высота равны. Это связано с тем, что перпендикулярная линия, проведенная из вершины треугольника к основанию, пересекает его одинаково. Также в равнобедренном треугольнике высота и медиана одинаковы. В этом случае высотный и срединный треугольники могут иметь три биссектрисы угла. И они всегда встречаются в одной и той же точке.
Как мы уже знаем о случае равносторонних треугольников и равнобедренных треугольников, высоты могут также находиться вне треугольника. Это происходит в основном для тупоугольных треугольников.
Параллелизм в медиане
Медианы в треугольниках не подчиняются правилу всегда быть перпендикулярными биссектрисами. Это не похоже на то, что каждая медиана не перпендикулярна.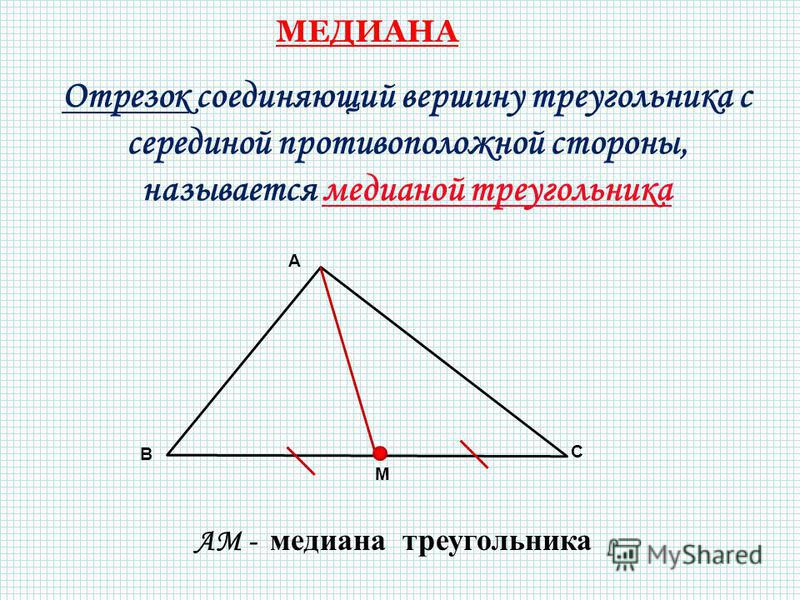



 [1].
[1].



 Домашнее задание.
Домашнее задание.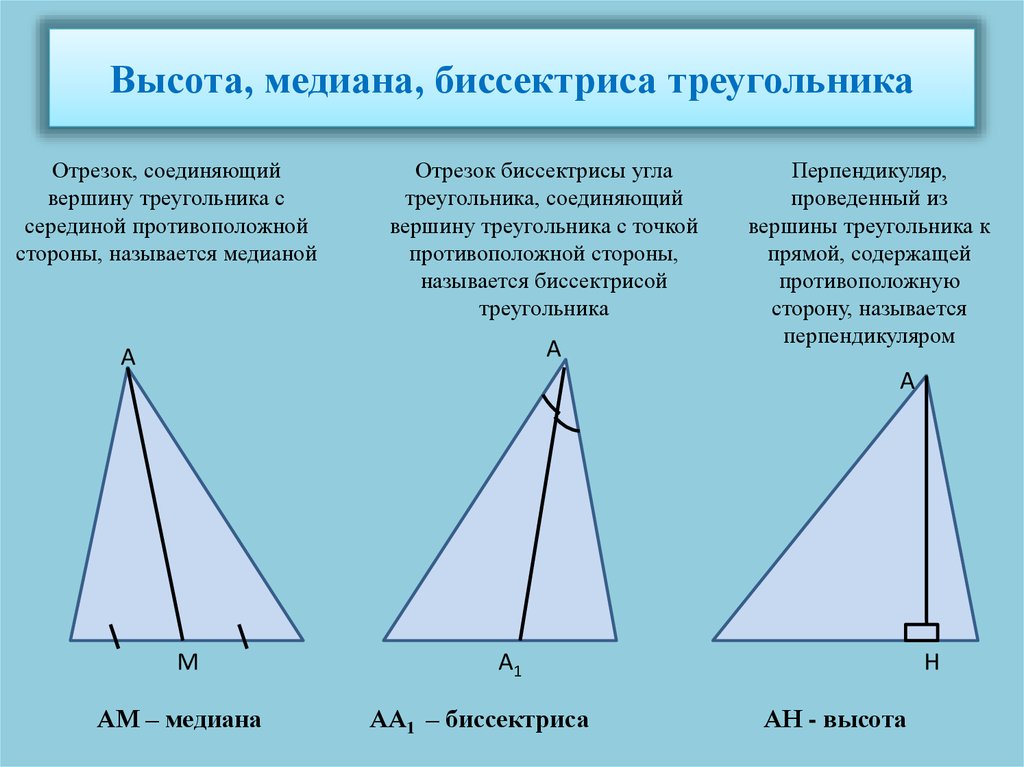

 cuemath.com
cuemath.com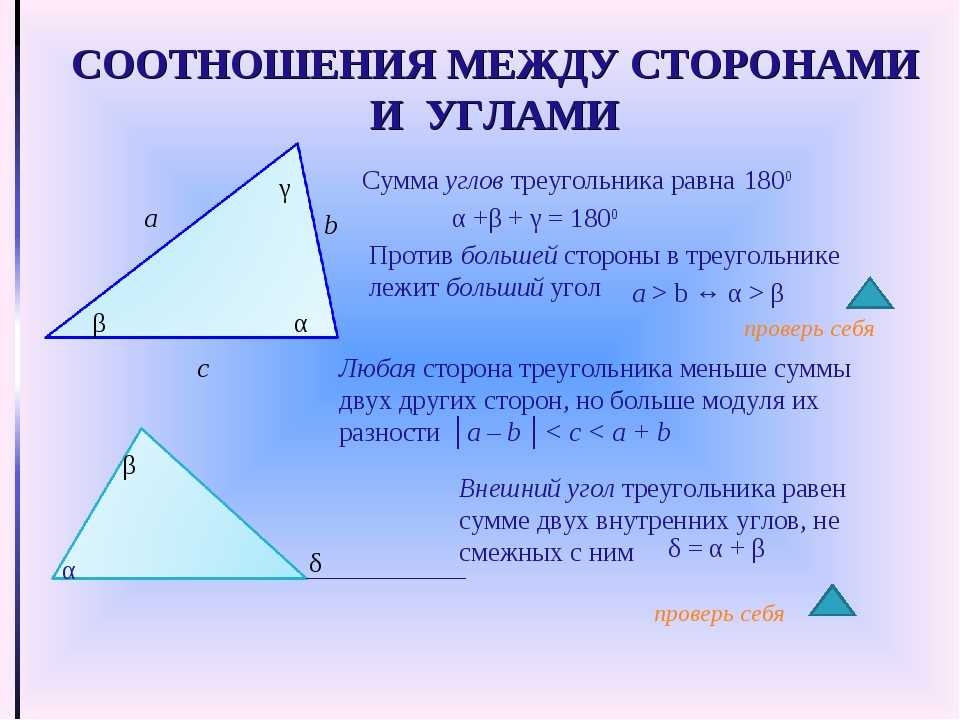 com
com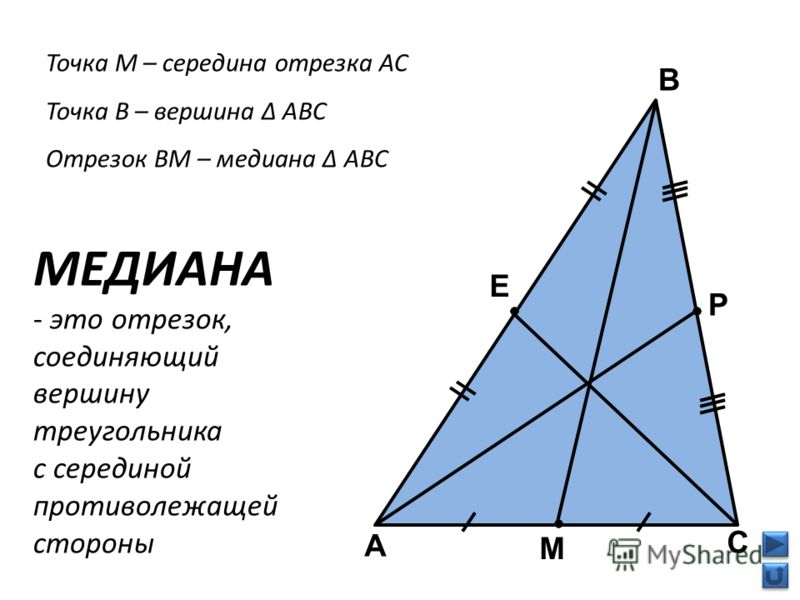
 10 все высоты
присутствуют в треугольнике.
10 все высоты
присутствуют в треугольнике. Высота
из A встречается со строкой, содержащей seg.BC, в D. Следовательно, seg. ОБЪЯВЛЕНИЕ
это высота. Точно так же seg.CE — это высота до AB и BF.
высота на сегменте. переменного тока. Из трех высот только
один присутствует внутри треугольника. Два других находятся на
продолжение линии, содержащей противоположную сторону. Эти три
высоты пересекаются в точке Р, которая находится вне треугольника.
Высота
из A встречается со строкой, содержащей seg.BC, в D. Следовательно, seg. ОБЪЯВЛЕНИЕ
это высота. Точно так же seg.CE — это высота до AB и BF.
высота на сегменте. переменного тока. Из трех высот только
один присутствует внутри треугольника. Два других находятся на
продолжение линии, содержащей противоположную сторону. Эти три
высоты пересекаются в точке Р, которая находится вне треугольника.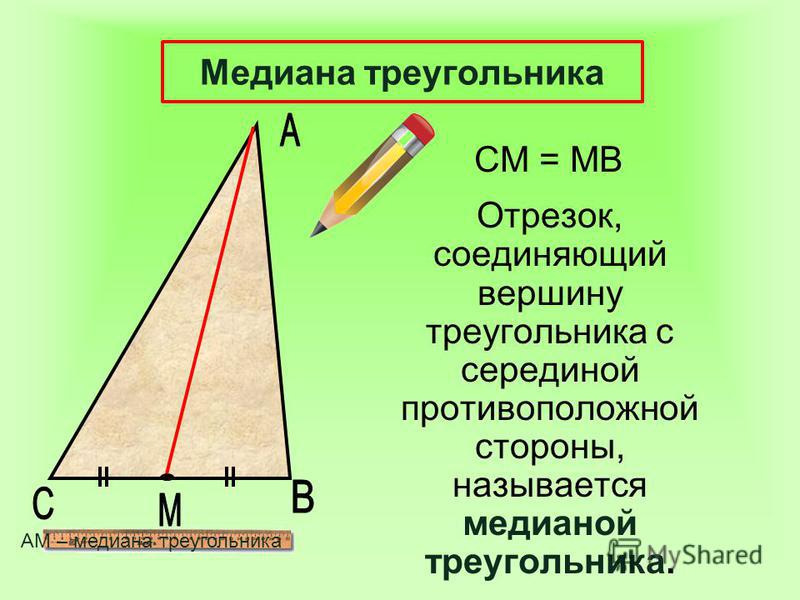
 И эта единственная точка известна как центр тяжести треугольника.
И эта единственная точка известна как центр тяжести треугольника.