Что такое натуральный логарифм ln: Натуральный логарифм | это… Что такое Натуральный логарифм?

Натуральный логарифм | это… Что такое Натуральный логарифм?

График функции натурального логарифма. Функция медленно приближается к положительной бесконечности при увеличении x и быстро приближается к отрицательной бесконечности, когда x стремится к 0 («медленно» и «быстро» по сравнению с любой степенной функцией от x).

Натуральный логарифм — это логарифм по основанию e, где e — иррациональная константа, равная приблизительно 2,718281828. Натуральный логарифм обычно обозначают как ln(x), log_e(x) или иногда просто log(x), если основание e подразумевается.^[1]

Натуральный логарифм числа x (записывается как ln(x)) — это показатель степени, в которую нужно возвести число e, чтобы получить x. Например, ln(7,389…) равен 2, потому что e²=7,389…. Натуральный логарифм самого числа e (ln(e)) равен 1, потому что e¹

= e, а натуральный логарифм 1 (ln(1)) равен 0, поскольку e⁰ = 1.

Натуральный логарифм может быть определён для любого положительного вещественного числа a как площадь под кривой y = 1/x от 1 до a. Простота этого определения, которое согласуется со многими другими формулами, в которых применяется натуральный логарифм, привела к появлению названия «натуральный». Это определение можно расширить на комплексные числа, о чём будет сказано ниже.

Если рассматривать натуральный логарифм как вещественную функцию действительной переменной, то она является обратной функцией к экспоненциальной функции, что приводит к тождествам:

Подобно всем логарифмам, натуральный логарифм отображает умножение в сложение:

Таким образом, логарифмическая функция представляет собой изоморфизм группы положительных действительных чисел относительно умножения на группу вещественных чисел по сложению, который можно представить в виде функции:

Логарифм может быть определён для любого положительного основания, отличного от 1, а не только для e, но логарифмы для других оснований отличаются от натурального логарифма только постоянным множителем, и, как правило, определяются в терминах натурального логарифма. Логарифмы полезны для решения уравнений, в которых неизвестные присутствуют в качестве показателя степени. Например, логарифмы используются для нахождения постоянной распада для известного периода полураспада, или для нахождения времени распада в решении проблем радиоактивности. Они играют важную роль во многих областях математики и прикладных наук, применяются в сфере финансов для решения многих задач, включая нахождение сложных процентов.

Содержание 1 История 2 Конвенции об обозначениях 2.1 Русская (и советская в целом) система 2.2 Англо-американская система 2.3 Техника 3 Происхождение термина натуральный логарифм 4 Определение 5 Свойства 6 Производная, ряд Тейлора 7 Натуральный логарифм в интегрировании 8 Численное значение 8.1 Высокая точность 8.2 Вычислительная сложность 9 Непрерывные дроби 10 Комплексные логарифмы 11 См. также 12 Примечания 13 Ссылки

История

Первое упоминание натурального логарифма сделал Николас Меркатор в работе Logarithmotechnia, опубликованной в 1668 году^[2], хотя учитель математики Джон Спайделл ещё в 1619 году составил таблицу натуральных логарифмов.^[3] Ранее его называли гиперболическим логарифмом,^[4] поскольку он соответствует площади под гиперболой. Иногда его называют логарифмом Непера, хотя первоначальный смысл этого термина был несколько другой.

Конвенции об обозначениях

Русская (и советская в целом) система

Натуральный логарифм принято обозначать через «ln(x)», логарифм по основанию 10 — через «lg(x)», а прочие основания принято указывать явно при символе «log».

Во многих работах по дискретной математике, кибернетике, информатике авторы используют обозначение «log(x)» для логарифмов по основанию 2, но это соглашение не является общепринятым и требует разъяснения либо в списке использованных обозначений, либо (при отсутствии такого списка) сноской или комментарием при первом использовании.

Скобки вокруг аргумента логарифмов (если это не приводит к ошибочному чтению формулы) обычно опускают, а при возведении логарифма в степень показатель приписывают непосредственно к знаку логарифма: ln² ln³ 4x⁵ = [ln([ln(4x⁵)]³)]².

Англо-американская система

Математики, статистики и часть инженеров обычно используют для обозначения натурального логарифма либо «log(x)», либо «ln(x)» , а для обозначения логарифма по основанию 10 — «log₁₀(x)».

Некоторые инженеры, биологи и другие специалисты всегда пишут «ln(x)» (или изредка «log_e(x)»), когда они имеют в виду натуральный логарифм, а запись «log(x)» у них означает log₁₀(x).

В теоретической информатике, теории информации и криптографии «log(x)» обычно означает логарифм по основанию 2 «log₂(x)» (хотя часто вместо этого пишется просто lg(x)).

Техника

В наиболее часто используемых языках программирования и пакетах прикладных программ, включая C, C++, SAS, MATLAB, Фортран и BASIC функция «log» или «LOG» относится к натуральному логарифму.

В ручных калькуляторах натуральный логарифм обозначается ln, тогда как log служит для обозначения логарифма по основанию 10.

Происхождение термина

натуральный логарифм

Сначала может показаться, что поскольку наша система счисления имеет основание 10, то это основание является более «натуральным», чем основание e. Но математически число 10 не является особо значимым. Его использование скорее связано с культурой, оно является общим для многих систем счисления, и связано это, вероятно, с числом пальцев у людей.

[5] Некоторые культуры основывали свои системы счисления на других основаниях: 5, 8, 12, 20 и 60.^[6][7][8]

log_e является «натуральным» логарифмом, поскольку он возникает автоматически и появляется в математике очень часто. Например, рассмотрим проблему производной логарифмической функции:^[9]

Если основание b равно e, то производная равна просто 1/x, а при x = 1 эта производная равна 1. Другим обоснованием, по которому основание e логарифма является наиболее натуральным, является то, что он может быть довольно просто определён в терминах простого интеграла или ряда Тейлора, чего нельзя сказать о других логарифмах.

Дальнейшие обоснования натуральности не связаны со счислением. Так, например, есть несколько простых рядов с натуральными логарифмами. Пьетро Менголи и Николай Меркатор называли их

логарифмус натуралис несколько десятилетий до тех пор, пока Ньютон и Лейбниц не разработали дифференциальное и интегральное исчисление.^[10]

Определение

ln(a) определяется как площадь под кривой f(x) = 1/x от 1 до a.

Формально ln(a) может быть определён как площадь под кривой графика 1/x от 1 до a, т. е. как интеграл:

Это действительно логарифм, поскольку он удовлетворяет фундаментальному свойству логарифма:

Это можно продемонстрировать, допуская следующим образом:

Число e может быть определено как единственное действительное число a такое, что ln(

a) = 1.

Или же, если показательная функция была определена раньше с использованием бесконечных рядов, натуральный логарифм может быть определён как обратная к ней функция, т. е. ln — это функция, такая что . Так как диапазон значений экспоненциальной функции от реальных аргументов есть все положительные вещественные числа, а экспоненциальная функция строго возрастает, то это хорошо определённая функция для всех положительных x.

Свойства

(комплексный логарифм)

Производная, ряд Тейлора

Полиномы Тейлор дают точную аппроксимацию для только в диапазоне -1 < x ≤ 1. Заметим, что для x > 1 полиномы Тейлора более высокой степени дают аппроксимацию хуже.

Производная натурального логарифма равна

На основании этого можно выполнить разложение в ряд Тейлора около 0, называемого иногда рядом Меркатора:

Справа дано изображение и некоторых её полиномов Тейлора около 0. Эти аппроксимации сходятся к функции только в области -1 < x ≤ 1, а за её пределами полиномы Тейлора высших степеней дают аппроксимацию менее точную.

Подставляя x-1 для x, получим альтернативную форму для ln(x), а именно:

^[11]

С помощью преобразования Эйлера ряда Меркатор можно получить следующее выражение, которое справедливо для любого х больше 1 по абсолютной величине:

Этот ряд похож на формулу Бэйли—Боруэйна—Плаффа.

Также заметим, что — это её собственная инверная функция, поэтому для получения натурального логарифма определенного числа y нужно просто для x присвоить значение .

Натуральный логарифм в интегрировании

Натуральный логарифм даёт простую интегральную функцию вида g(x) = f ‘(x)/f(x): первообразная функции g(x) имеет вид ln(|f(x)|). Это подтверждается цепным правилом и следующим фактом:

В другом виде:

и

Ниже дан пример для g(x) = tan(x):

Пусть f(x) = cos(x) и f’(x)= — sin(x):

где C — произвольная константа.

Натуральный логарифм можно проинтегрировать с помощью интегрирования по частям:

Численное значение

Для расчета численного значения натурального логарифма числа можно использовать разложение его в ряд Тейлора в виде:

Чтобы получить лучшую скорость сходимости, можно воспользоваться следующим тождеством:

при условии, что y = (x−1)/(x+1) и x > 0.

Для ln(x), где x > 1, чем ближе значение x к 1, тем быстрее скорость сходимости. Тождества, связанные с логарифмом, можно использовать для достижения цели:

Эти методы применялись ещё до появления калькуляторов, для чего использовались числовые таблицы и выполнялись манипуляции, аналогичные вышеописанным.

Высокая точность

Для вычисления натурального логарифма с большим количеством цифр точности ряд Тейлора не является эффективным, поскольку его сходимость медленная. Альтернативой является использование метода Ньютона, чтобы инвертировать в экспоненциальную функцию, ряд которой сходится быстрее.

Альтернативой для очень высокой точности расчёта является формула:^[12]

[13]

где M обозначает арифметико-геометрическое среднее 1 и 4/s, и

m выбрано так, что p знаков точности достигается. (В большинстве случаев значение 8 для m вполне достаточно. ) В самом деле, если используется этот метод, может быть применена инверсия Ньютона натурального логарифма для эффективного вычисления экспоненциальной функции. (Константы ln 2 и пи могут быть предварительно вычислены до желаемой точности, используя любой из известных быстро сходящихся рядов.)

Вычислительная сложность

Вычислительная сложность натуральных логарифмов (с помощью арифметико-геометрического среднего) равна O(M(n) ln n). Здесь n — число цифр точности, для которой натуральный логарифм должен быть оценен, а M(n) — вычислительная сложность умножения двух n-значных чисел.

Непрерывные дроби

Хотя для представления логарифма отсутствуют простые непрерывные дроби, но можно использовать несколько обобщённых непрерывных дробей, в том числе:

Комплексные логарифмы

Основная статья: Комплексный логарифм

Экспоненциальная функция может быть расширена до функции, которая даёт комплексное число вида e^x для любого произвольного комплексного числа x, при этом используется бесконечный ряд с комплексным x. Эта показательная функция может быть инвертирована с образованием комплексного логарифма, который будет обладать большей частью свойств обычных логарифмов. Есть, однако, две трудности: не существует x, для которого e^x = 0, и оказывается, что e^2πi = 1 = e⁰. Поскольку свойство мультипликативности действительно для комплексной экспоненциальной функции, то e^z = e^z+2nπi для всех комплексных z и целых n.

Логарифм не может быть определён на всей комплексной плоскости, и даже при этом он является многозначным — любой комплексный логарифм может быть заменён на «эквивалентный» логарифм, добавив любое целое число, кратное 2πi. Комплексный логарифм может быть однозначным только на срезе комплексной плоскости. Например, ln i = 1/2 πi или 5/2 πi или −3/2 πi, и т.д., и хотя i⁴ = 1, 4 log i может быть определена как 2πi, или 10πi или −6 πi, и так далее.

См. также

• Джон Непер — изобретатель логарифмов
• Интегральный логарифм
• Число e
• Леонард Эйлер

Примечания

1. ↑ Mathematics for physical chemistry. — 3rd. — Academic Press, 2005. — P. 9. — ISBN 0-125-08347-5, Extract of page 9
2. ↑ J J O’Connor and E F Robertson The number e. The MacTutor History of Mathematics archive (сентябрь 2001). Архивировано из первоисточника 12 февраля 2012.
3. ↑ Cajori Florian A History of Mathematics, 5th ed. — AMS Bookstore, 1991. — P. 152. — ISBN 0821821024
4. ↑ Flashman, Martin Estimating Integrals using Polynomials. Архивировано из первоисточника 12 февраля 2012.
5. ↑ Boyers Carl A History of Mathematics. — John Wiley & Sons, 1968.
6. ↑ Harris, John (1987). «Australian Aboriginal and Islander mathematics» (PDF). Australian Aboriginal Studies 2: 29–37.
7. ↑ Large, J.J. (1902). «The vigesimal system of enumeration». Journal of the Polynesian Society 11 (4): 260–261.
8. ↑ Cajori first=Florian (1922). «Sexagesimal fractions among the Babylonians». American Mathematical Monthly 29 (1): 8–10. DOI:10.2307/2972914.
9. ↑ Larson Ron Calculus: An Applied Approach. — 8th. — Cengage Learning, 2007. — P. 331. — ISBN 0-618-95825-8
10. ↑ Ballew, Pat Math Words, and Some Other Words, of Interest. Архивировано из первоисточника 12 февраля 2012.
11. ↑ «Logarithmic Expansions» at Math3.org
12. ↑ (1982) «Practically fast multiple-precision evaluation of log(x)». Journal of Information Processing 5 (4): 247–250. Проверено 30 March 2011.
13. ↑ (1999) «Fast computations of the exponential function» 1564: 302–312. DOI:10.1007/3-540-49116-3_28.

Ссылки

• Demystifying the Natural Logarithm (ln) | BetterExplained

Натуральный логарифм | это… Что такое Натуральный логарифм?

График функции натурального логарифма. Функция медленно приближается к положительной бесконечности при увеличении x и быстро приближается к отрицательной бесконечности, когда x стремится к 0 («медленно» и «быстро» по сравнению с любой степенной функцией от x).

Натуральный логарифм — это логарифм по основанию e, где e — иррациональная константа, равная приблизительно 2,718281828. Натуральный логарифм обычно обозначают как ln(x), log_e(x) или иногда просто log(x), если основание e подразумевается.^[1]

Натуральный логарифм числа x (записывается как ln(x)) — это показатель степени, в которую нужно возвести число e, чтобы получить x.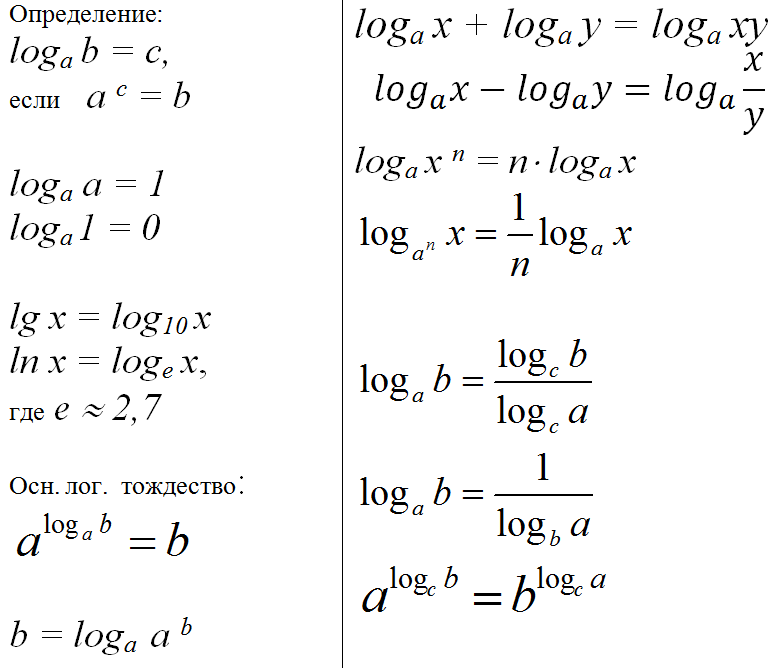 Например, ln(7,389…) равен 2, потому что e²=7,389…. Натуральный логарифм самого числа e (ln(e)) равен 1, потому что e¹ = e, а натуральный логарифм 1 (ln(1)) равен 0, поскольку e⁰ = 1.

Натуральный логарифм может быть определён для любого положительного вещественного числа a как площадь под кривой y = 1/x от 1 до a. Простота этого определения, которое согласуется со многими другими формулами, в которых применяется натуральный логарифм, привела к появлению названия «натуральный». Это определение можно расширить на комплексные числа, о чём будет сказано ниже.

Если рассматривать натуральный логарифм как вещественную функцию действительной переменной, то она является обратной функцией к экспоненциальной функции, что приводит к тождествам:

Подобно всем логарифмам, натуральный логарифм отображает умножение в сложение:

Таким образом, логарифмическая функция представляет собой изоморфизм группы положительных действительных чисел относительно умножения на группу вещественных чисел по сложению, который можно представить в виде функции:

Логарифм может быть определён для любого положительного основания, отличного от 1, а не только для e, но логарифмы для других оснований отличаются от натурального логарифма только постоянным множителем, и, как правило, определяются в терминах натурального логарифма. Логарифмы полезны для решения уравнений, в которых неизвестные присутствуют в качестве показателя степени. Например, логарифмы используются для нахождения постоянной распада для известного периода полураспада, или для нахождения времени распада в решении проблем радиоактивности. Они играют важную роль во многих областях математики и прикладных наук, применяются в сфере финансов для решения многих задач, включая нахождение сложных процентов.

Содержание 1 История 2 Конвенции об обозначениях 2.1 Русская (и советская в целом) система 2.2 Англо-американская система 2.3 Техника 3 Происхождение термина натуральный логарифм 4 Определение 5 Свойства 6 Производная, ряд Тейлора 7 Натуральный логарифм в интегрировании 8 Численное значение 8.1 Высокая точность 8.2 Вычислительная сложность 9 Непрерывные дроби 10 Комплексные логарифмы 11 См. также 12 Примечания 13 Ссылки

История

Первое упоминание натурального логарифма сделал Николас Меркатор в работе Logarithmotechnia, опубликованной в 1668 году^[2], хотя учитель математики Джон Спайделл ещё в 1619 году составил таблицу натуральных логарифмов.^[3] Ранее его называли гиперболическим логарифмом,^[4] поскольку он соответствует площади под гиперболой. Иногда его называют логарифмом Непера, хотя первоначальный смысл этого термина был несколько другой.

Конвенции об обозначениях

Русская (и советская в целом) система

Натуральный логарифм принято обозначать через «ln(x)», логарифм по основанию 10 — через «lg(x)», а прочие основания принято указывать явно при символе «log».

Во многих работах по дискретной математике, кибернетике, информатике авторы используют обозначение «log(x)» для логарифмов по основанию 2, но это соглашение не является общепринятым и требует разъяснения либо в списке использованных обозначений, либо (при отсутствии такого списка) сноской или комментарием при первом использовании.

Скобки вокруг аргумента логарифмов (если это не приводит к ошибочному чтению формулы) обычно опускают, а при возведении логарифма в степень показатель приписывают непосредственно к знаку логарифма: ln² ln³ 4x⁵ = [ln([ln(4x⁵)]³)]².

Англо-американская система

Математики, статистики и часть инженеров обычно используют для обозначения натурального логарифма либо «log(x)», либо «ln(x)» , а для обозначения логарифма по основанию 10 — «log₁₀(x)».

Некоторые инженеры, биологи и другие специалисты всегда пишут «ln(x)» (или изредка «log_e(x)»), когда они имеют в виду натуральный логарифм, а запись «log(x)» у них означает log₁₀(x).

В теоретической информатике, теории информации и криптографии «log(x)» обычно означает логарифм по основанию 2 «log₂(x)» (хотя часто вместо этого пишется просто lg(x)).

Техника

В наиболее часто используемых языках программирования и пакетах прикладных программ, включая C, C++, SAS, MATLAB, Фортран и BASIC функция «log» или «LOG» относится к натуральному логарифму.

В ручных калькуляторах натуральный логарифм обозначается ln, тогда как log служит для обозначения логарифма по основанию 10.

Происхождение термина

натуральный логарифм

Сначала может показаться, что поскольку наша система счисления имеет основание 10, то это основание является более «натуральным», чем основание e. Но математически число 10 не является особо значимым. Его использование скорее связано с культурой, оно является общим для многих систем счисления, и связано это, вероятно, с числом пальцев у людей.^[5] Некоторые культуры основывали свои системы счисления на других основаниях: 5, 8, 12, 20 и 60.^[6][7][8]

log_e является «натуральным» логарифмом, поскольку он возникает автоматически и появляется в математике очень часто. Например, рассмотрим проблему производной логарифмической функции:^[9]

Если основание b равно e, то производная равна просто 1/x, а при x = 1 эта производная равна 1. Другим обоснованием, по которому основание e логарифма является наиболее натуральным, является то, что он может быть довольно просто определён в терминах простого интеграла или ряда Тейлора, чего нельзя сказать о других логарифмах.

Дальнейшие обоснования натуральности не связаны со счислением. Так, например, есть несколько простых рядов с натуральными логарифмами. Пьетро Менголи и Николай Меркатор называли их логарифмус натуралис несколько десятилетий до тех пор, пока Ньютон и Лейбниц не разработали дифференциальное и интегральное исчисление.^[10]

Определение

ln(a) определяется как площадь под кривой f(x) = 1/x от 1 до a.

Формально ln(a) может быть определён как площадь под кривой графика 1/x от 1 до a, т. е. как интеграл:

Это действительно логарифм, поскольку он удовлетворяет фундаментальному свойству логарифма:

Это можно продемонстрировать, допуская следующим образом:

Число e может быть определено как единственное действительное число a такое, что ln(a) = 1.

Или же, если показательная функция была определена раньше с использованием бесконечных рядов, натуральный логарифм может быть определён как обратная к ней функция, т. е. ln — это функция, такая что . Так как диапазон значений экспоненциальной функции от реальных аргументов есть все положительные вещественные числа, а экспоненциальная функция строго возрастает, то это хорошо определённая функция для всех положительных x.

Свойства

(комплексный логарифм)

Производная, ряд Тейлора

Полиномы Тейлор дают точную аппроксимацию для только в диапазоне -1 < x ≤ 1. Заметим, что для x > 1 полиномы Тейлора более высокой степени дают аппроксимацию хуже.

Производная натурального логарифма равна

На основании этого можно выполнить разложение в ряд Тейлора около 0, называемого иногда рядом Меркатора:

Справа дано изображение и некоторых её полиномов Тейлора около 0. Эти аппроксимации сходятся к функции только в области -1 < x ≤ 1, а за её пределами полиномы Тейлора высших степеней дают аппроксимацию менее точную.

Подставляя x-1 для x, получим альтернативную форму для ln(x), а именно:

^[11]

С помощью преобразования Эйлера ряда Меркатор можно получить следующее выражение, которое справедливо для любого х больше 1 по абсолютной величине:

Этот ряд похож на формулу Бэйли—Боруэйна—Плаффа.

Также заметим, что — это её собственная инверная функция, поэтому для получения натурального логарифма определенного числа y нужно просто для x присвоить значение .

Натуральный логарифм в интегрировании

Натуральный логарифм даёт простую интегральную функцию вида g(x) = f ‘(x)/f(x): первообразная функции g(x) имеет вид ln(|f(x)|). Это подтверждается цепным правилом и следующим фактом:

В другом виде:

и

Ниже дан пример для g(x) = tan(x):

Пусть f(x) = cos(x) и f’(x)= — sin(x):

где C — произвольная константа.

Натуральный логарифм можно проинтегрировать с помощью интегрирования по частям:

Численное значение

Для расчета численного значения натурального логарифма числа можно использовать разложение его в ряд Тейлора в виде:

Чтобы получить лучшую скорость сходимости, можно воспользоваться следующим тождеством:

при условии, что y = (x−1)/(x+1) и x > 0.

Для ln(x), где x > 1, чем ближе значение x к 1, тем быстрее скорость сходимости. Тождества, связанные с логарифмом, можно использовать для достижения цели:

Эти методы применялись ещё до появления калькуляторов, для чего использовались числовые таблицы и выполнялись манипуляции, аналогичные вышеописанным.

Высокая точность

Для вычисления натурального логарифма с большим количеством цифр точности ряд Тейлора не является эффективным, поскольку его сходимость медленная. Альтернативой является использование метода Ньютона, чтобы инвертировать в экспоненциальную функцию, ряд которой сходится быстрее.

Альтернативой для очень высокой точности расчёта является формула:^[12][13]

где M обозначает арифметико-геометрическое среднее 1 и 4/s, и

m выбрано так, что p знаков точности достигается. (В большинстве случаев значение 8 для m вполне достаточно. ) В самом деле, если используется этот метод, может быть применена инверсия Ньютона натурального логарифма для эффективного вычисления экспоненциальной функции. (Константы ln 2 и пи могут быть предварительно вычислены до желаемой точности, используя любой из известных быстро сходящихся рядов.)

Вычислительная сложность

Вычислительная сложность натуральных логарифмов (с помощью арифметико-геометрического среднего) равна O(M(n) ln n). Здесь n — число цифр точности, для которой натуральный логарифм должен быть оценен, а M(n) — вычислительная сложность умножения двух n-значных чисел.

Непрерывные дроби

Хотя для представления логарифма отсутствуют простые непрерывные дроби, но можно использовать несколько обобщённых непрерывных дробей, в том числе:

Комплексные логарифмы

Основная статья: Комплексный логарифм

Экспоненциальная функция может быть расширена до функции, которая даёт комплексное число вида e^x для любого произвольного комплексного числа x, при этом используется бесконечный ряд с комплексным x. Эта показательная функция может быть инвертирована с образованием комплексного логарифма, который будет обладать большей частью свойств обычных логарифмов. Есть, однако, две трудности: не существует x, для которого e^x = 0, и оказывается, что e^2πi = 1 = e⁰. Поскольку свойство мультипликативности действительно для комплексной экспоненциальной функции, то e^z = e^z+2nπi для всех комплексных z и целых n.

Логарифм не может быть определён на всей комплексной плоскости, и даже при этом он является многозначным — любой комплексный логарифм может быть заменён на «эквивалентный» логарифм, добавив любое целое число, кратное 2πi. Комплексный логарифм может быть однозначным только на срезе комплексной плоскости. Например, ln i = 1/2 πi или 5/2 πi или −3/2 πi, и т.д., и хотя i⁴ = 1, 4 log i может быть определена как 2πi, или 10πi или −6 πi, и так далее.

См. также

• Джон Непер — изобретатель логарифмов
• Интегральный логарифм
• Число e
• Леонард Эйлер

Примечания

1. ↑ Mathematics for physical chemistry. — 3rd. — Academic Press, 2005. — P. 9. — ISBN 0-125-08347-5, Extract of page 9
2. ↑ J J O’Connor and E F Robertson The number e. The MacTutor History of Mathematics archive (сентябрь 2001). Архивировано из первоисточника 12 февраля 2012.
3. ↑ Cajori Florian A History of Mathematics, 5th ed. — AMS Bookstore, 1991. — P. 152. — ISBN 0821821024
4. ↑ Flashman, Martin Estimating Integrals using Polynomials. Архивировано из первоисточника 12 февраля 2012.
5. ↑ Boyers Carl A History of Mathematics. — John Wiley & Sons, 1968.
6. ↑ Harris, John (1987). «Australian Aboriginal and Islander mathematics» (PDF). Australian Aboriginal Studies 2: 29–37.
7. ↑ Large, J.J. (1902). «The vigesimal system of enumeration». Journal of the Polynesian Society 11 (4): 260–261.
8. ↑ Cajori first=Florian (1922). «Sexagesimal fractions among the Babylonians». American Mathematical Monthly 29 (1): 8–10. DOI:10.2307/2972914.
9. ↑ Larson Ron Calculus: An Applied Approach. — 8th. — Cengage Learning, 2007. — P. 331. — ISBN 0-618-95825-8
10. ↑ Ballew, Pat Math Words, and Some Other Words, of Interest. Архивировано из первоисточника 12 февраля 2012.
11. ↑ «Logarithmic Expansions» at Math3.org
12. ↑ (1982) «Practically fast multiple-precision evaluation of log(x)». Journal of Information Processing 5 (4): 247–250. Проверено 30 March 2011.
13. ↑ (1999) «Fast computations of the exponential function» 1564: 302–312. DOI:10.1007/3-540-49116-3_28.

Ссылки

• Demystifying the Natural Logarithm (ln) | BetterExplained

математика — Почему натуральный логарифм представлен $\ln$?

спросил 7 лет, 3 месяца назад

Изменено 2 года, 10 месяцев назад

Просмотрено 3к раз

$\begingroup$

Натуральный логарифм часто представляется несколькими различными обозначениями:

• $\log_e x$
• $\log x$ (хотя это также используется для логарифмов с основанием 10)
• $\ln x$

Это третье обозначение, которое меня интересует. Почему используется $\ln$, а не, скажем, $\text{nl}$? Две мои теории по этому поводу:

1. . Это сокращение от «натуральный логарифм» на неанглийском языке
.
2. Предполагается, что он соответствует «$l$» в типичной логарифмической записи.

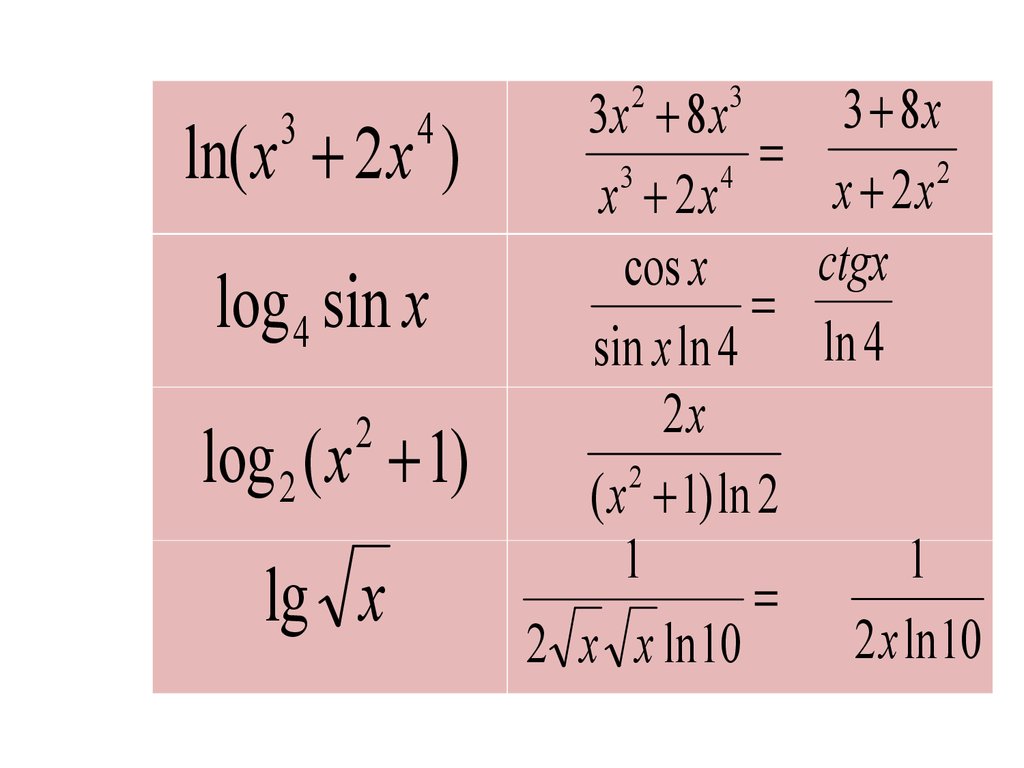
Почему обозначение $\ln$?

• математика
• нотация

$\endgroup$

6

$\begingroup$

Насколько мне известно, математический оператор, обычно обозначаемый как $\ln$, является сокращением от латинского термина l ogarithmus n āturalis .

Я не уверен, кто первым использовал эту аббревиатуру, но я предполагаю, что это вполне мог быть Нейпир.

Я помню, что видел ln , написанное как сокращение из двух слов в форме $l.n.$

$\endgroup$

1

$\begingroup$

В соответствии с первым использованием функциональных символов:

$\ln$ (для натурального логарифма) использовалось в 1893 г. Ирвингом Стрингемом (1847-1909) в Uniplanar Algebra (Cajori vol. 2, page 107).

Спасибо за ссылку KCd в его комментарии, у нас есть более раннее появление:

• Антон Штайнхаузер, Lehrbuch der Mathematik für höhere Gewerbeschulen (1875), стр. 277.

$\endgroup$

1

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя адрес электронной почты и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

Натуральный логарифм

Натуральный логарифм — это логарифм по основанию e, где e — иррациональная константа, приблизительно равная 2,718281828. Натуральный логарифм обычно записывается как ln(x), loge(x) или иногда, если основание e неявно, как просто log(x).

Натуральный логарифм числа x (записывается как ln(x)) — это степень, в которую нужно возвести e, чтобы оно равнялось x. Например, ln(7,389…) равно 2, поскольку e ² = 7,389…. Натуральный логарифм самого e (ln(e)) равен 1, поскольку e ¹ = e, а натуральный логарифм 1 (ln(1 )) равен 0, так как e0 = 1.

Натуральный логарифм можно определить для всех положительных действительных чисел x как площадь под кривой y = 1/t от 1 до x. Простота этого определения, которая совпадает со многими другими формулами, включающими натуральный логарифм, приводит к термину «натуральный». Определение можно распространить на ненулевые комплексные числа, как объяснено ниже.

Функция натурального логарифма, если рассматривать ее как вещественную функцию действительной переменной, является обратной функцией экспоненциальной функции, что приводит к тождествам:

сложение:

Таким образом, логарифмическая функция является изоморфизмом группы положительных действительных чисел при умножении в группу действительных чисел при сложении, представленной в виде функции:

Логарифмы могут быть определены с любым положительным основанием, кроме 1, а не только с e; однако логарифмы по другим основаниям отличаются от натурального логарифма только постоянным множителем и обычно определяются в терминах последнего. Логарифмы полезны для решения уравнений, в которых неизвестное выступает как показатель степени некоторой другой величины. Например, логарифмы используются для решения периода полураспада, постоянной распада или неизвестного времени в задачах экспоненциального распада. Они важны во многих областях математики и естественных наук и используются в финансах для решения задач, связанных со сложными процентами.

История

Первое упоминание о натуральном логарифме было Николасом Меркатором в его работе Logarithmotechnia, опубликованной в 1668 году[1], хотя учитель математики Джон Спейделл уже в 1619 году составил таблицу натурального логарифма[2]. Раньше его также называли гиперболическим логарифмом[3]. Его также иногда называют логарифмом Напьера, хотя первоначальное значение этого термина немного отличается.

Условные обозначения

Математики, статистики и некоторые инженеры обычно понимают под «log(x)» или «ln(x)» значение loge(x), т. е. натуральный логарифм x, и пишут «log10(x)», если логарифм x по основанию 10.

Некоторые инженеры, биологи и некоторые другие обычно пишут «ln(x)» (или иногда «loge(x)»), когда имеют в виду натуральный логарифм x, и принимают «log(x)» как log10(x). ).

В наиболее часто используемых языках программирования, включая C, C++, SAS, MATLAB, Fortran и BASIC, «log» или «LOG» относится к натуральному логарифму.

В портативных калькуляторах натуральный логарифм обозначается как ln, тогда как log — это логарифм по основанию 10.

В теоретической информатике, теории информации и криптографии «log(x)» обычно означает «log2(x)» (хотя вместо этого часто записывается как lg(x)).

Происхождение термина натуральный логарифм

Сначала может показаться, что, поскольку наша система счисления основана на 10, это основание будет более «естественным», чем основание e. Но математически число 10 не имеет особого значения. Его использование в культуре — в качестве основы для систем нумерации многих обществ — вероятно, связано с типичным для людей количеством пальцев. [4] Другие культуры основывали свои системы счета на таких вариантах, как 5, 8, 12, 20 и 60.[5][6][7]

loge является «естественным» журналом, потому что он автоматически возникает из математики и так часто встречается в ней. Например, рассмотрим задачу дифференцирования логарифмической функции:

Если основание b равно e, то производная просто 1/x, и при x = 1 эта производная равна 1. Другой смысл, в котором основание e логарифма наиболее естественным является то, что его можно довольно легко определить в терминах простого интеграла или ряда Тейлора, чего нельзя сказать о других логарифмах.

Дальнейшее понимание этой естественности не требует исчисления. Например, есть ряд простых рядов с натуральным логарифмом. Пьетро Менголи и Николас Меркатор назвали его естественным логарифмом за несколько десятилетий до того, как Ньютон и Лейбниц разработали исчисление.

Определения

ln(x) определяется как площадь под кривой f(x) = 1/x от 1 до x.

Формально ln(a) можно определить как площадь под графиком 1/x от 1 до a, то есть как интеграл,

Это определяет логарифм, потому что он удовлетворяет основному свойству логарифма:

Это можно продемонстрировать следующим образом: ln(a) = 1,

В качестве альтернативы, если экспоненциальная функция была определена сначала с использованием бесконечного ряда, натуральный логарифм может быть определен как ее обратная функция, т. е. ln является такой функцией, что . Поскольку диапазоном экспоненциальной функции для действительных аргументов являются все положительные действительные числа, а экспоненциальная функция строго возрастает, это хорошо определено для всех положительных x.

Свойства

(см. комплексный логарифм)

Производная, ряд Тейлора

Полиномы Тейлора для обеспечивают точные приближения только в диапазоне -1 < x ≤ 1. Обратите внимание, что для x > 1 полиномы Тейлора более высокой степени являются худшими приближениями.

Производная натурального логарифма равна

Это приводит к ряду Тейлора примерно для 0; также известный как ряд Меркатора. за пределами этой области полиномы Тейлора более высокой степени являются худшими приближениями для функции.

Подставляя x-1 вместо x, мы получаем альтернативную форму самого ln(x), а именно

.[9]

Используя преобразование Эйлера в рядах Меркатора, можно получить следующее, которое справедливо для любого x с абсолютным значением больше 1:

.

Эта серия аналогична формуле типа BBP.

Также обратите внимание, что это собственная обратная функция, поэтому, чтобы получить натуральный логарифм определенного числа y, просто подставьте вместо x.

Натуральный логарифм при интегрировании

Натуральный логарифм позволяет просто интегрировать функции вида g(x) = f ‘(x)/f(x): первообразная g(x) определяется выражением ln(| f(x)|). Это происходит из-за цепного правила и следующего факта:

.

Другими словами,

.

и

.

Вот пример для случая g(x) = tan(x):

.
.

Пусть f(x) = cos(x) и f'(x)= — sin(x):

.

где C — произвольная постоянная интегрирования.

Натуральный логарифм можно проинтегрировать с помощью интегрирования по частям:

Числовое значение

Чтобы вычислить числовое значение натурального логарифма числа, разложение в ряд Тейлора можно переписать как:

Чтобы получить лучшую скорость сходимости, можно использовать следующее тождество.

при условии, что y = (x−1)/(x+1) и x > 0.

Для ln(x), где x > 1, чем ближе значение x к 1, тем быстрее скорость сходимости. Для этого можно использовать тождества, связанные с логарифмом:

Такие методы использовались до появления калькуляторов путем обращения к числовым таблицам и выполнения манипуляций, подобных приведенным выше.

Высокая точность

Для вычисления натурального логарифма с точностью до многих цифр метод ряда Тейлора неэффективен, так как сходимость медленная. Альтернативой является использование метода Ньютона для обращения экспоненциальной функции, ряд которой сходится быстрее.

Альтернативой для вычисления с чрезвычайно высокой точностью является формула [10] [11]

, где M обозначает среднее арифметико-геометрическое, а

с m выбрано таким образом, чтобы было достигнуто p бит точности. (Для большинства целей достаточно значения 8 для m.) Фактически, если используется этот метод, ньютоновское обращение натурального логарифма может, наоборот, использоваться для эффективного вычисления экспоненциальной функции. (Константы ln 2 и π можно предварительно вычислить с нужной точностью, используя любой из нескольких известных быстро сходящихся рядов.)

Вычислительная сложность
Основная статья: Вычислительная сложность математических операций

Вычислительная сложность вычисления натурального логарифма (с использованием среднего арифметико-геометрического) составляет O(M(n) ln n). Здесь n — число цифр точности, с которой должен быть оценен натуральный логарифм, а M(n) — вычислительная сложность умножения двух n-значных чисел.

Непрерывные дроби

Хотя простых непрерывных дробей нет, существует несколько обобщенных непрерывных дробей, в том числе:

Комплексные логарифмы
Основная статья: Комплексный логарифм

Показательная функция может быть расширена до функции, которая дает комплексное число как ex для любого произвольного комплексного числа x; просто используйте бесконечный ряд с комплексом x. Эту экспоненциальную функцию можно инвертировать, чтобы получить комплексный логарифм, обладающий большинством свойств обыкновенного логарифма. Здесь возникают две трудности: ни один x не имеет ex = 0; и оказывается, что e2πi = 1 = e0. Поскольку свойство мультипликативности по-прежнему работает для комплексной экспоненциальной функции, ez = ez+2nπi для всех комплексных z и целых чисел n.

Таким образом, логарифм не может быть определен для всей комплексной плоскости, да и то он многозначен – любой комплексный логарифм можно превратить в «эквивалентный» логарифм, добавив любое целое число, кратное 2πi по желанию.