Парабола и гипербола
Свежий выпуск
Помните гениальное произведение Алексея Толстого «Гиперболоид инженера Гарина»? Его иногда называют авантюрно-фантастическим. Конечно, сегодня с высоты прожитых человечеством лет вполне очевидна абсурдность сюжетной линии романа, согласно которой в капстране происходит народное восстание, организованное советским агентом. Но и удивляться такому сценарию не приходится, в те времена многие мечтали о мировой революции. Однако фантастичность романа не в этом, а в другом – автор описал новое оружие, настолько мощное и результативное, что читателя было трудно оторвать от чтения, а фильм просто произвел фурор.
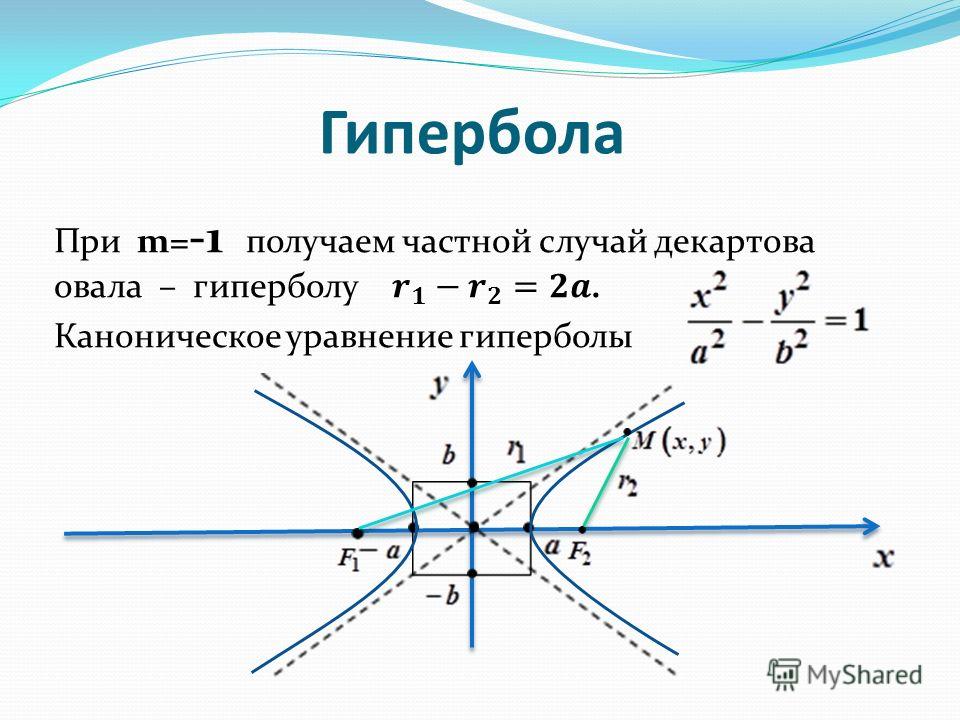
Где же взял такое экзотическое слово автор трилогии «Хождение по мукам»? Термин «гипербола» означает геометрическое место точек евклидовой плоскости, для которых абсолютное значение разности расстояний до двух точек, называемых фокусами, постоянно.
Поэтому более правильным было назвать аппарат Гарина параболоидом. Алексей Толстой об этом знал, однако слово «гиперболоид» ему больше пришлось по душе. Вспомним, что есть второе значение гиперболы – стилистическая фигура явного и намеренного преувеличения для усиления выразительности мысли.
Но не так уж и прост был автор исторического романа «Петр I». Вогнутое зеркало гиперболической формы действительно не фокусирует, а рассеивает свет. Однако инженер Гарин волею писателя применил в своем аппарате два гиперболических зеркала – главное вогнутое и малое выпуклое. Такая конструкция очень напоминает систему телескопа Ричи – Кретьена, предложенную в 1924 году. Инженеры включили в нее два гиперболических зеркала, и система теперь используется в большинстве крупных телескопов и в резонаторах мощных лазеров.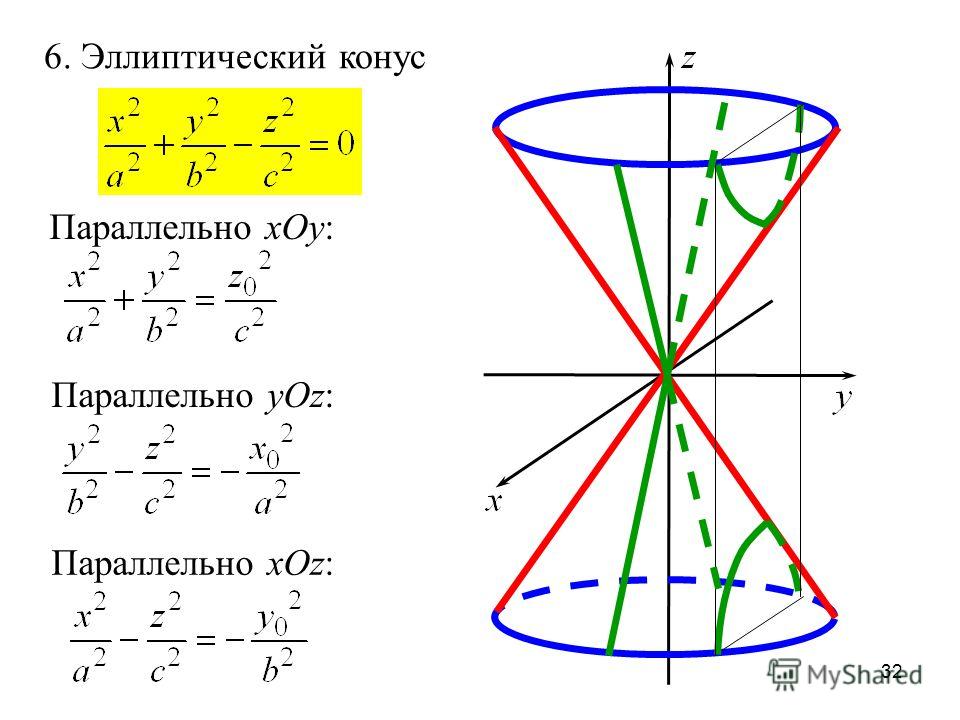
Выходит, самая фантастическая деталь романа стала наиболее реалистичным элементом сюжета, ведь лазерами сегодня никого не удивишь. К тому же сама идея гиперболоида для научной фантастики предвоенной эпохи была просто замечательная. Ведь мысль о таком изобретении уже витала в воздухе.
Гениальному изобретателю того времени Николе Тесле принадлежат слова: «Если не будет возможности успешно напасть ни на одно государство, войны прекратятся». С этой идеей он обратился к правительствам самых сильных в военном отношении государств, предложив свой проект создания первой в мире электронной пушки.
Это сверхмощное оружие очень напоминало так называемый «тепловой луч», использованный фантастом Гербертом Уэллсом в его романе «Война миров». Сочинил он его еще в 1897 году. Великий же серб «смертоносными лучами» предлагал уничтожать самолеты авиации противника.
Говорят, что Никола Тесла был большим идеалистом, уверенным в том, что как только его сверхмощное оружие поступит на вооружение армий самых крупных государств нашей планеты, ведение войн станет бессмысленным, ведь каждая страна сможет окружить свою территорию «валом Адриана», как это сделали древние римляне в Британии, только невидимым.
Не случайно изобретенный «смертоносный луч» Никола Тесла называл «умиротворяющим лучом»…
- За сутки
- За неделю
- За месяц
Почти год прошел после трагических январских событий. Они оставили неизгладимый след в истории Казахстана и жизни людей, которые в те дни были на передовой
Водители обращают внимание на участившиеся остановки автомобилей полицией, иногда без объяснения причин
Новая ТЭЦ появится в Семее лишь к 2027 году. Пока же в правобережной части областного центра наблюдается дефицит теплоэнергии
Начало нового пути
Представители миссии Тюркской парламентской ассамблеи (ТюркПА) о выборах Президента.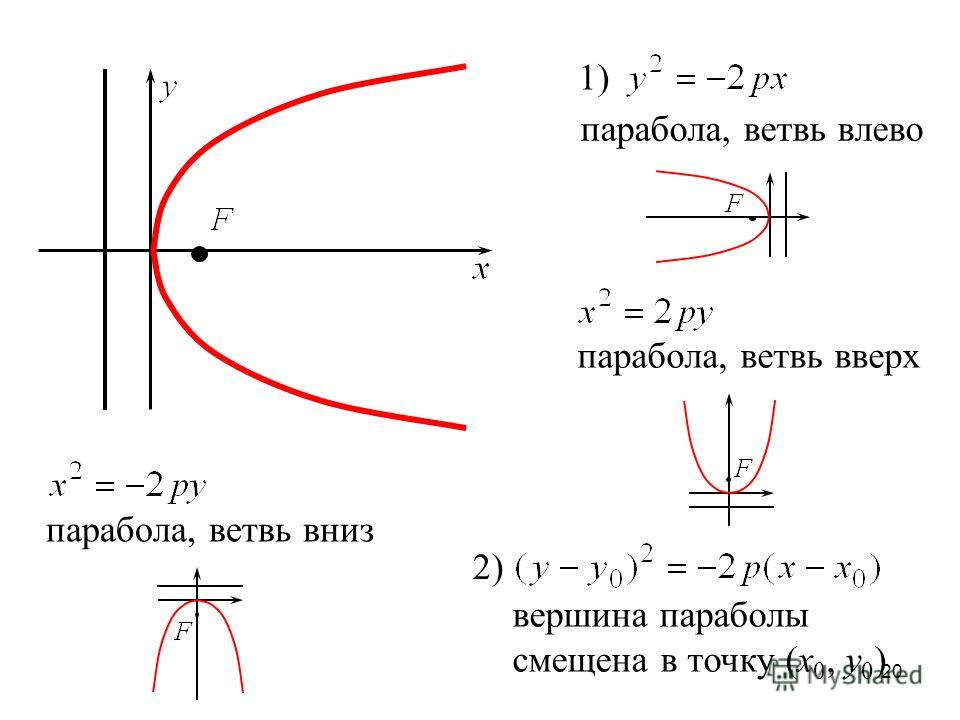
Рубрика Политика
Век тюркского мира
Предвзятая оценка
Мнениями о состоявшихся выборах Президента РК продолжили делиться в Астане 21 ноября международные наблюдатели
Блестящая организация, прозрачность, открытость, свобода
Осознанный выбор на пути к демократии
Свои мнения об уровне и качестве внеочередных президентских выборов озвучили на пресс-конференции в Астане представители миссии Организации тюркских государств
«Фишка» от многодетной мамы
Куда привела история
Лаиб приглашает на праздник
Важные шаги строительства Справедливого Казахстана
Казахстанцев ждут перемены
Историю делают люди!
Мамуля, где ваша дочка?
Системная трансформация страны
Безопасность – важнейшая составляющая
Токаев запустил строительство мультибрендового автомобильного завода в Алматы
Бабушка попросила полицию забрать у нее 3-месячную внучку в СКО
Жамаубаев отказался раскрывать размер зарплаты премьер-министра без его разрешения
Ильин навестил в больнице огнеборцев, пострадавших при пожаре в Астане
Видео о сдаче военных касок на металлолом прокомментировали в Минобороны РК
Касым-Жомарт Токаев прилетел в Алматы
Педофил через соцсети выкупал у детей их обнаженные фото
Взрыв котла в акмолинской школе: стало известно о состоянии пострадавших
Видео с избивающей малыша матерью шокировало Казнет
Снял боевую одежду и вошел в огонь: стали известны подробности подвига столичного пожарного
Семье героя-пожарного из Астаны подарят 3-комнатную квартиру, второму – погасят ипотеку
Подозреваемого в нападении на 12-летнюю девочку задержали в Талдыкоргане
Токаев наградил орденами двух столичных пожарных
Дети не пострадали при взрыве в школьной котельной в Акмолинской области
Токаев: В казахстанском обществе должен укорениться культ знаний, а не диплома
Беглого иностранного преступника нашли через 17 лет в Казахстане
О цифровизации торговли высказался Жумангарин
Котел взорвался во дворе школы в Акмолинской области, есть пострадавшие
Бахтияра Байсеитова объявили в розыск за хищение 320 миллионов тенге
Полицейские задержали мужчину, который гулял с пистолетом в Талдыкоргане
Астана попала в Книгу рекордов Гиннесса
Казахстанский боксер нокаутировал мексиканца на профессиональном ринге
Водитель выпрыгнул из машины на полном ходу в Павлодарской области
Иманбек Зейкенов женился
Новый праздник появился в Казахстане
Водителям «скорой помощи» запретили проезжать на красный и выезжать на встречную полосу
Закон Республики Казахстан Об амнистии
Акимат Алматинской области сделал заявление после гибели мужчины в массовой драке
Ипотеку без первоначального взноса запускают в Алматинской области
Двое рабочих упали с 14-го этажа в Астане, один погиб
Российский блогер снимал на видео свои нарушения на дорогах Алматы
Избранница Иманбека из родного Аксу
В Актобе несовершеннолетний устроил поножовщину в торгово-развлекательном центре
Дайрабаев высказался о внешней политике Казахстана
Жительница Балхаша убила свою мать за замечание
В Российском городе Иркутск военный самолет упал на жилой дом
Ребенок под защитой государства – Кошанов о позиции Токаева
Казахстан и Узбекистан подписали Дорожную карту
Ауесбаев ответил на критику оппонентами его партии
«12-летнюю внучку развращал дедушка» – в полиции Алматы прокомментировали публикацию
Новости СМИ2
Новости СМИ2
Свежий выпуск
Дрожала от страха и боли
Свежий выпуск
Дружелюбно, мирно и без провокаций
Свежий выпуск
Голосовали за будущее
Свежий выпуск
Наши в США
- [[year]]
- [[month.label]]
- [[day]]
Парабола и гипербола, решение задач, урок и презентация в 8 классе
Дата публикации: .
2, x
Решение.
График нашей функции строится кусочками, на одном и той же координатной плоскости нам надо построить две части (кусочка) графика. В нашем случае, при $х
График функции мы построили, осталось его прочитать.
1. Область определения: $хϵ(-∞;+∞)$.
2. $y=0$ при $x=0$, $y>0$ при $xϵ(-1;0)U(0;+∞)$, $y
3. У функции есть точка разрыва с абсциссой $х=-1$.
4. Функция возрастает на отрезках $(-∞;-1)U(0;+∞)$. Функция убывает на отрезке $(-1;0)$.
5. Функция не ограничена.
6. Наименьшего и наибольшего значения нет.
7. Область значений: $yϵ(-∞;-2)U(0;+∞)$.
Пример 5.
Решить уравнение: $-\frac{5}{x}=-x+4$.
Решение.
Решим графически. В этот раз нам предстоит построить график гиперболы и линейной функции и найти точки пересечения этих графиков. Графики наших функций пересекаются в двух точках с координатами $(-1;5)$ и $(5;-1)$. Для решения уравнения нам нужны абсциссы этих точек.
Ответ: $х=-1$ и $х=5$.
Ребята, не забывайте проверять корни уравнений! Лучше проверить и быть уверенным в правильности, чем полениться потратить минутку и остаться без правильного решения!
Пример 6.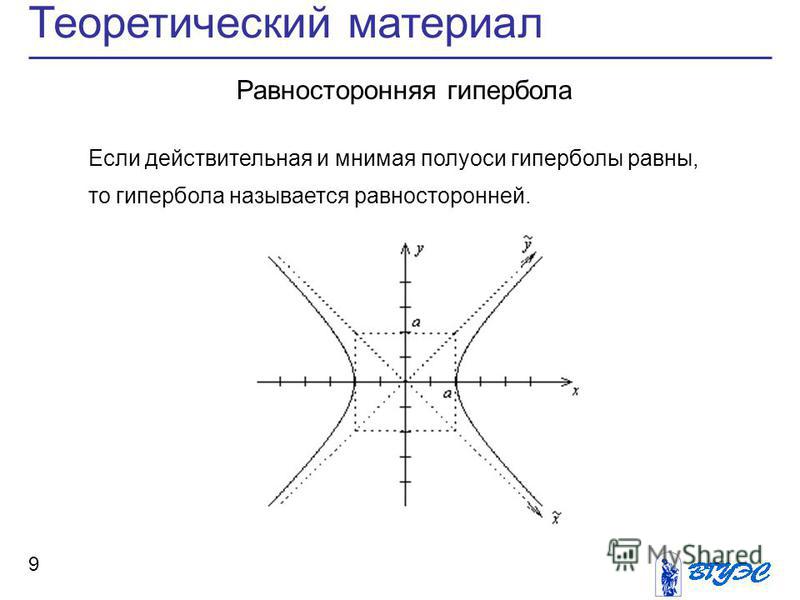
2,x≤1, \\ -\frac{4}{x}, x>1. \end {cases}$.
Разница между параболой и гиперболой
Ключевая разница: Парабола — это коническое сечение, которое получается, когда плоскость пересекает коническую поверхность, параллельную стороне конуса. Гипербола образуется, когда плоскость пересекает коническую поверхность параллельно оси.Парабола и гипербола — это два разных слова, сечения и уравнения, которые используются в математике для описания двух разных сечений конуса. Они различаются по форме, размеру и различным другим факторам, включая формулы, которые используются для его расчета. Чтобы понять их, давайте сначала разберемся с конусом и различными коническими сечениями.
Коническое сечение — это кривая, полученная при пересечении плоскости с конусом разными способами. Разрезы, полученные в результате пересечения, включают эллипс, окружность, параболу и гиперболу. Согласно аналитической геометрии, коника определяется как «плоская алгебраическая кривая степени 2».
Популярное определение конического сечения включает точку фокусировки, направляющую линию и эксцентриситет. Ожидается, что точка фокусировки и линии директрисы будут находиться в фиксированном соотношении в конике. Отношение известно как эксцентриситет конического сечения. Эксцентриситет эллипсов, парабол и гипербол различается; эллипсы имеют эксцентриситет меньше 1, параболы имеют эксцентриситет, равный 1, а гиперболы имеют эксцентриситет больше 1. Самая ранняя известная работа по коническим сечениям может быть датирована четвертым веком до нашей эры Менехмом, который открыл способ решить задачу удвоения куба с помощью параболы. 92.
Линия, проходящая через середину параболы, называется осью симметрии; эта линия также перпендикулярна директрисе и проходит через фокус. Точки, которые находятся на оси симметрии, пересекающей параболу, называются вершинами. Расстояние между вершиной и фокусом известно как «фокусное расстояние». Параболы могут открываться в любом направлении, включая вверх, вниз, вправо или влево.
Также главной особенностью парабол является то, что они все одинаковые, отличаются только размером. Их можно перемещать и масштабировать точно так, чтобы они соответствовали любой другой параболе. Параболы используются в различных приложениях, таких как отражатели автомобильных фар, конструкция баллистических ракет и т. д. Они также играют важную роль в физике, технике, математике и т. д.
Гипербола — это гладкая кривая, возникающая при пересечении плоскости с конусом, параллельным оси Y, что создает разрез вдоль стороны конуса. Гипербола определяется своими геометрическими свойствами или уравнениями, для которых она является набором решений. Термин «гипербола» происходит от греческого слова, означающего «заброшенный» или «чрезмерный». Считается, что этот термин был введен Аполлонием Пергским, который внес большой вклад в изучение конических сечений.
Известно, что гипербола имеет ответвления, которые являются зеркальным отображением друг друга и напоминают две бесконечные дуги.
Точки на двух ветвях, которые находятся ближе всего друг к другу, называются вершинами. Линия, соединяющая вершины, называется поперечной осью или большой осью, что соответствует большому диаметру эллипса. Середина поперечной оси известна как центр гиперболы. Уравнение гиперболы записывается как x2/a2-y2/b2= 1. Гиперболы используются в различных приложениях в современном мире, включая путь, по которому следует тень кончика солнечных часов, форму открытой орбиты; используется как арка во многих строящихся зданиях, как уравнения в математике и геометрии, физике и т. д.
Гиперболы и параболы являются незамкнутыми кривыми, что означает, что они не заканчиваются и продолжаются до бесконечности, чего не могут сделать эллипсы и окружности.
Разница между параболой и гиперболой
Коническое сечение — это кривая, полученная при пересечении плоскости с конусом под определенным углом. Существует три типа конических сечений: эллипс, парабола и гипербола.
Содержание
Эллипс — это плоская кривая с двумя фокусными точками, которая чем-то напоминает круг.
Однако парабола и гипербола путают сечения.
Разница между параболой и гиперболой заключается в том, что парабола представляет собой одну незамкнутую кривую с эксцентриситетом, равным единице, тогда как гипербола имеет две кривые с эксцентриситетом больше единицы.
Парабола — это одиночная незамкнутая кривая, уходящая в бесконечность. Он имеет U-образную форму и имеет один фокус и одну директрису.
Гипербола — это незамкнутая кривая, имеющая две несоединенные ветви. Имеет два фокуса и две директрисы, по одной на каждую ветвь.
Сравнение Таблица
| Параметр сравнения | Parabola | Hyperbola |
|---|---|---|
| Определение | ||
| . . | Гипербола — это геометрическое место точек, имеющих постоянную разность между двумя фокусами. | |
| Форма | Парабола — это незамкнутая кривая, имеющая один фокус и одну направляющую.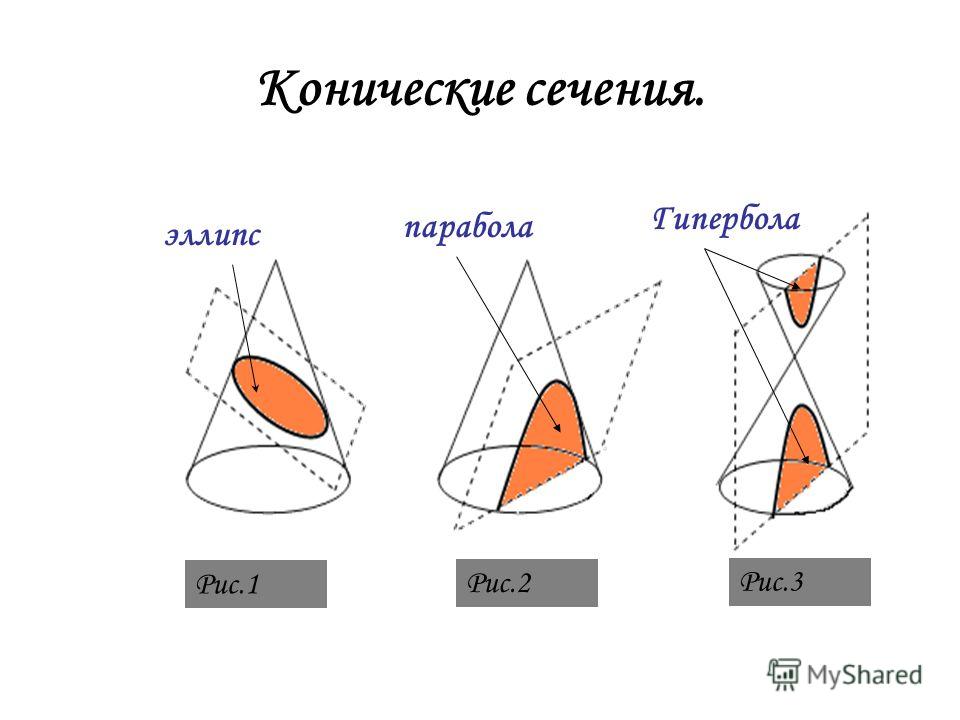 | Гипербола представляет собой незамкнутую кривую с двумя ветвями, которая имеет два фокуса и две директрисы. |
| Эксцентриситет | Неотрицательный эксцентриситет параболы равен единице. | Неотрицательный эксцентриситет e гиперболы больше единицы. |
| Пересечение плоскости | Пересечение плоскости параллельно (идеальный случай) наклонной высоте конуса. | Пересечение плоскости параллельно (идеальный случай) перпендикулярной высоте двойного конуса. |
| General Equation | The general equation of the parabola is y = ax² , a ≠ 0 | The general equation of the hyperbola is x²/a² – y²/b² = 1 |
What Парабола?
Парабола — это геометрическое место всех точек, равноудаленных от точки и прямой. Эта точка называется фокусом, а эта линия – директрисой.
Парабола образуется, когда плоскость пересекает конус в направлении, параллельном (идеальный случай) его наклонной высоте.
Общее уравнение параболы задается как
y = ax² , a ≠ 0
Значение a определяет форму кривой.
Если a > 0, устье параболы открывается вверх.
Если a < 0, устье параболы открывается вниз.
Фокус этой параболы находится в (0, 1/4a). Директриса (-1/4a).
Однако, когда a=1, парабола называется единичной параболой.
Эксцентриситет параболы равен единице.
Парабола симметрична относительно своей оси. На бесконечном расстоянии кривые выглядят как параллельные линии.
Что такое гипербола?
Гипербола — это геометрическое место всех точек, которые имеют постоянную разность от двух различных точек. Эти точки называются фокусами гиперболы.
Гипербола образуется, когда сплошная плоскость пересекает конус в направлении, параллельном его перпендикулярной высоте.
Общее уравнение гиперболы имеет вид
(x-α) ²/a² – (y-β)²/b² = 1
Фокусы приведенной выше гиперболы равны ( α ± sqrt(a²+b²), β).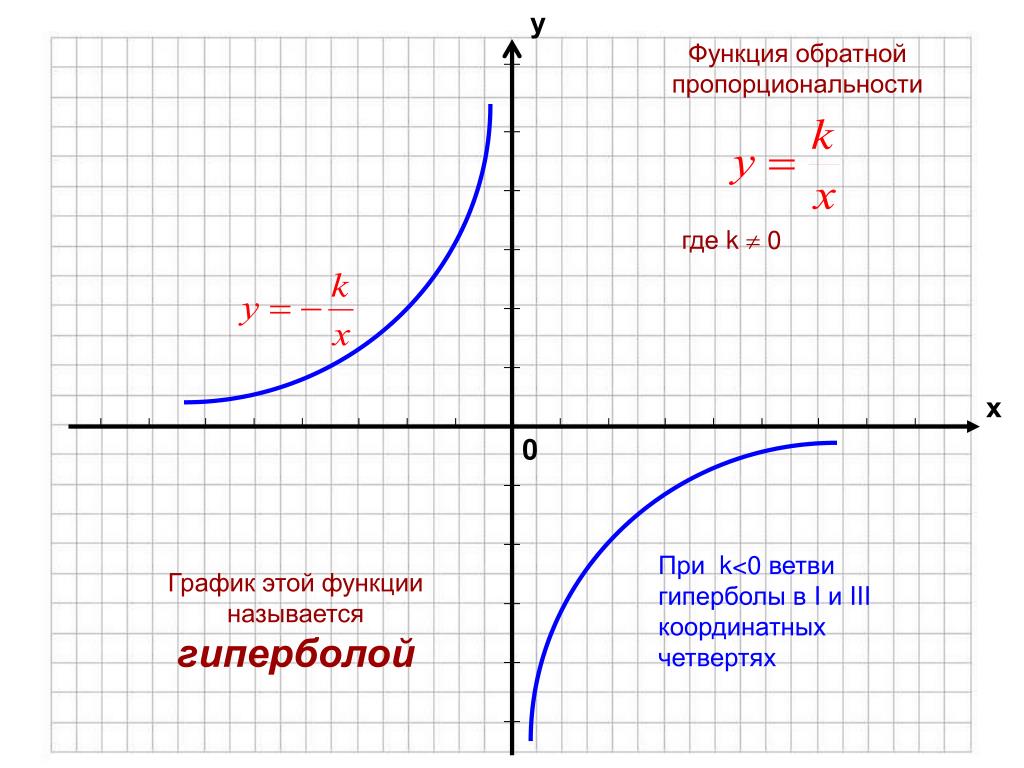
Вершины (±a, β).
Эксцентриситет гиперболы больше единицы.
Гипербола имеет две оси симметрии. Это поперечная ось и сопряженная ось.
Основные различия между параболой и гиперболой
Парабола и гипербола являются коническими сечениями. Они имеют разные формы и свойства.
Основные различия между ними:
- Парабола — это геометрическое место всех точек, находящихся на равном расстоянии от фокуса и директрисы. С другой стороны, гипербола — это геометрическое место всех точек, для которых разница в расстоянии между двумя фокусами постоянна.
- Парабола — это незамкнутая кривая, имеющая один фокус и директрису, тогда как гипербола — это незамкнутая кривая с двумя ответвлениями, имеющими два фокуса и директрисы.
- Эксцентриситет параболы равен единице, тогда как эксцентриситет гиперболы больше единицы.
- Парабола образуется, когда плоскость пересекает конус по его наклонной высоте.
