Что такое периметр квадрата 2 класс: Периметр — урок. Математика, 2 класс.

Урок математики на тему: «Периметр квадрата» (2 класс)

Откройте учебник на странице 59-й.

На прошлых уроках вы знакомились с понятием периметр, сегодня мы продолжим его изучение.

Учитель повторяет определение периметра, показывая это на наглядном пособии. (наглядное пособие состоит из картона 1 фигура в форме квадрата, 2 фигура в форме прямоугольника)

Показываю прямоугольник.

— Что это за фигура? (прямоугольник)

— Почему вы так решили?

Показываю квадрат.

— Что это за фигура? (квадрат)

— Почему? (все стороны равны)

— Показывая фигуру прямоугольника. Давайте вспомним что такое периметр? (периметр сумма длин всех сторон многоугольника)

-посмотрите в учебнике на страницу 59-ю, у вас даны две записи, с помощью которых мы можем найти периметр прямоугольника и квадрата.

— Как вы думаете с помощью какой записи мы найдём периметр прямоугольника? (первой)

— Почему?

— а с помощью какой периметр квадрата? (второй)

— Почему?

— Что в этой записи означает — а, а что, — b.

-Начертите квадрат со стороной 5см у себя в тетрадях.

— Вспомните последовательность построения фигуры с прямыми углами.

— Какой записью мы будем пользоваться? (Р= а x 4)

— Найдите сумму длин сторон квадрата с помощью действия сложения. (5+5+5+5=20(см))

— Найдите сумму длин сторон квадрата с помощью действия умножения. (5 х 4=20(см))

— Выражение «сумма длин сторон» помним называется одним словом «ПЕРИМЕТР» и обозначаем латинской буквой «Р» (пэ).

Вывод:

Давайте вспомним что такое периметр? (сумма длин всех сторон многоугольника)

По дорожке, по дорожке

Скачем мы на правой ножке.

И по этой же дорожке

Скачем мы на левой ножке.

По тропинке побежим

До лужайки добежим.

На лужайке, на лужайке

Мы попрыгаем как зайки.

Стоп. Немного отдохнем

И домой пешком пойдем.

-Постройте у себя в тетрадях прямоугольник со сторонами 3 см и 2 см, найдите периметр прямоугольника разными способами.

Взаимопроверка по построению прямоугольника. Дети предлагают свои способы нахождения периметра прямоугольника и записывают на доске варианты.

Р= 3+2+3+2= (10 см)

Р= 3 x 2 + 2 x 2

P= (2+3) x 2

— Кто решил иначе? ( Если нет других вариантов решения, то учитель сам объясняет другие способы нахождения периметра у прямоугольника)

Посмотрите на номер 392-й.

Внимательно послушайте задачу.

Элли и её друзья отправились в изумрудный город в среду и были в пути 2 недели и ещё двое суток. Определи день недели, в который они пришли в Изумрудный город.

1. Чтение задачи

2. Давайте прочитаем условие задачи

3. Давайте прочитаем требование к задаче

— В какой день недели вышли Элли и её друзья?

На доске учитель записывает схему.

С. + + +

Ч. + + +

П. + + В пятницу придут Элли и её друзья.

С. + +

В. + +

П. + +

В. + +

— Первая неделя со среды, по среду, вторая неделя со среды по среду, да ещё двое суток- в пятницу они пришли в Изумрудный город.

— каков ответ задачи? (Элли и её друзья пришли в изумрудный город в пятницу)

Посмотрите внимательно на экран, прочитайте задачу.

Для покрытия пола купили плитку квадратной формы, сторона которой 25 см. Чему равна сумма длин сторон одной такой плитки?

-Прочитайте условие задачи.

— Прочитайте вопрос задачи.

— Какой формы плитка? (квадратной)

— Сторона плитки 25 см.

— Как одним словом мы называем сумму длин всех сторон? (периметр)

— Как мы ищем периметр квадрата? (Р = a x 4)

Сторона- 25 см.

Р- ? см

Решение.

Запиши на доске ту запись которая нам понадобиться для нахождения периметра квадрата.

Р = a x 4

25 x 4 =25 + 25 + 25 + 25= 100 (см)

Ответ: Р = 100 см.

А сейчас я проверю вашу внимательность.

На странице 58-й, посмотрите на номер 394

Давайте выполним действие двигаясь по стрелкам.

9+7…: 2 … — 3… x 4 … + 12 … x 1 …

— На 59 странице учебника. Посмотрите 396 задание. Прочитайте.

— Определи закономерность в расположении чисел в разных столбцах таблицы и заполни пустые клетки.

15	27	39	51	63	75
12	19	26	33	40	47
3	8	13	18	23	28

— Есть ли закономерность в расположении чисел? (действия во всех столбцах выполняются на такое действие, как вычитание)

В строчке проговорить

1строчка каждое последующее число увеличивается на 12

2 строчка каждое последующее число увеличивается на 7

3 строчка каждое последующее число увеличивается на 5.

ГДЗ по математике 2 класс учебник Моро, Волкова 2 часть

---

• Тип: ГДЗ, Решебник.
• Автор: Моро М. И., Волкова С. И., Бельтюкова Г. В.
• Год: 2020.
• Серия: Школа России (ФГОС).
• Издательство: Просвещение.

Решебник — страница 70Готовое домашнее задание

Номер 45.

На сколько сантиметров длина одного отрезка меньше длины другого?

Ответ:

Длина красного отрезка 11 см, а синего 8 см. 11 − 8 = 3 (см) Ответ: на 3 см длина синего отрезка, меньше длины красного отрезка.

Номер 46.

Начерти три отрезка: длина первого 5 см, длина второго на 2 см больше длины первого, а длина третьего на 4 см меньше длины второго. Запиши, чему равна длина третьего отрезка?

Ответ:

Номер 47.

1) Найди в данных треугольниках прямые и острые углы.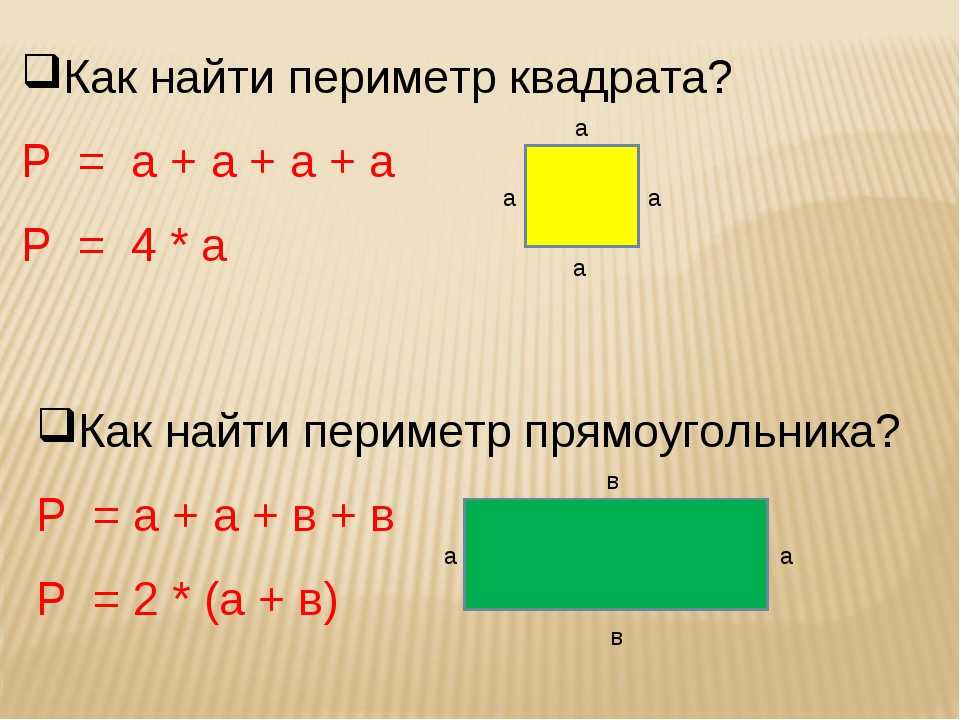

Выпиши их номера.
2) Измерь стороны этих треугольников и найди их периметр.

Ответ:

1) Красный треугольник: 1 – прямой угол; 2 и 3 – острые.     Синий треугольник: 4, 5, 6 – острые.     Зеленый треугольник: 8 – прямой угол; 7 и 9 – острые.
2) Периметр красного треугольника: 20 + 30 + 36 = 86 мм.     Периметр синего треугольника: 4 см + 3 см 1 мм + 3 см 1 мм = 10 см 2 мм.     Периметр зеленого треугольника: 3 см + 4 см + 5 см = 12 см.

Номер 48.

1) Начерти прямоугольник, длины сторон которого 2 см и 3 см.
2) Начерти отрезок, длина которого равна периметру этого прямоугольника.

Ответ:

1)

2) Периметр прямоугольника:     2 + 3 + 2 + 3 = (2 + 3) ∙ 2 = 10 см

Номер 49.

Начерти квадрат, длина стороны которого 4 см, и найди его периметр.

Ответ:

Периметр квадрата: 4 + 4 + 4 + 4 = 4 ∙ 4 = 16 см

Номер 50.

Начерти ломаную линию, состоящую из 4 равных по длине звеньев. Найди ее длину.

Ответ:

Берем любую длину звена, например, 4 см. Тогда длина ломаной будет 4 + 4 + 4 + 4 = 16 см.
При длине звена 5 см, длина ломаной будет 5 + 5 + 5 + 5 = 20 см. При длине звена 6 см, длина ломаной будет 6 + 6 + 6 + 6 = 24 см.

Номер 51.

Ответ:

3 см 5 мм < 38 мм, потому что 35 мм < 38 мм 73 см = 7 дм 3 см, потому что 73 см = 73 см

24 см = 2 дм 4 см, потому что 24 см = 24 см 5 см 8 мм < 6 см 1 мм, потому что 58 мм < 61 мм

Номер 52.

Какие многоугольники ты видишь на чертеже?
Сколько фигур каждого вида?
Из каких фигур составлены прямоугольники?

Ответ:

На чертеже есть треугольники, прямоугольники и четырёхугольники.
Треугольники 8 шт. Четырёхугольников 7 шт. Прямоугольников 3 шт.
Один прямоугольник состоит из синего и желтого треугольников. Второй прямоугольник состоит из трёх треугольников – розового, зеленого, оранжевого. Третий прямоугольник состоит из пяти треугольников – синего, жёлтого, зеленого, оранжевого, розового.

Рейтинг

Выберите другую страницу

1 часть

Учебник Моро	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36	37	38	39	40	41	42	43	44	45	46	47	48	49	50	51	52	53	54	55	56	57	58	59	60	61	62	63	64	65	66	67	68	69	70	71	72	73	74	75	76	77	78	79	80	81	82	83	84	85	86	87	88	89	90	91	92	93	94	95

2 часть

4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36	37	38	39	40	41	42	43	44	45	46	47	48	49	50	51	52	53	54	55	56	57	58	59	60	61	62	63	64	65	66	67	68	69	70	71	72	73	74	75	76	77	78	79	80	81	82	83	84	85	86	87	88	89	90	91	92	93	94	95	96	97	98	99	100	101	102	103	104	105	106	107	108	109	110	111

Ваше сообщение отправлено!

+

Что такое квадрат? (Определение, свойства и видео)

Написано

Малкольм МакКинси

11 января 2023

Проверка по фактам

Paul Mazzola

Определение квадратного.

у которого все стороны одинаковой длины и все углы прямые, равные 90 градусам. Чтобы быть квадратом, форма должна быть всем этим:

• Плоская фигура

• Замкнутая фигура

• Правильный многоугольник

• Четырехугольник

Вот квадрат. Сначала это может показаться немного скучным, но как только вы узнаете больше о квадрате, вы увидите, что это интересно и очень полезно. Вокруг вас появляются квадраты. Они отлично подходят для строительства, украшения и создания трехмерных фигур. И, хотите верьте, хотите нет, но квадраты обладают множеством интересных отличительных свойств.

Квадрат должен  иметь следующие две вещи:

1. Четыре конгруэнтных (равной длины) стороны

2. Четыре конгруэнтных (равных размера) внутренних угла

Квадрат

Что такое квадрат?

Семейство четырехугольников включает множество форм, и квадрат может быть одним из них. Квадрат   – это разновидность параллелограмма, прямоугольника и ромба. Это параллелограмм, потому что у него две пары параллельных конгруэнтных сторон. Это прямоугольник, потому что у него две пары параллельных конгруэнтных сторон с четырьмя конгруэнтными внутренними углами. Это ромб, потому что у него четыре равные стороны.

Все квадраты являются параллелограммами, прямоугольниками и ромбами, но не все параллелограммы, прямоугольники и ромбы являются квадратами.

Квадрат с маркировкой

Квадрат является правильным многоугольником, потому что он имеет стороны одинаковой длины (равносторонние) и равные углы ( равноугольный ). Сравните его с правильным многоугольником только с тремя сторонами, равносторонним треугольником или правильным восьмиугольником, как вы можете видеть на знаках остановки на перекрестках улиц.

Как построить квадрат

Вы можете построить квадрат, используя четыре прямых (линейных) объекта одинаковой длины. Положите четыре прямых предмета (ручки, линейки, шнурки) так, чтобы все восемь конечных точек касались ровно одной другой конечной точки. Работайте с объектами, пока все четыре внутренних угла не станут одинаковыми.

Вы построили квадрат, потому что четыре стороны равны (равносторонние) и четыре внутренних угла равны (равноугольные). Каждый внутренний угол равен 90° .

Как нарисовать квадрат

Вы можете нарисовать квадрат с помощью линейки, карандаша и транспортира. Нарисуйте горизонтальный отрезок на листе бумаги рядом с центром бумаги. Назовите его YN , чтобы конечная точка Y находилась слева от вас, а конечная точка N — справа.

С помощью транспортира нарисуйте отрезок линии, поднимающийся вверх от конечной точки Y , перпендикулярный отрезку линии YN  и такой же длины, как YN . Пометьте его конечную точку Z .

Повторите этот процесс, чтобы создать отрезок, восходящий от конечная точка N . Пометьте его конечную точку  A .

Как построить квадрат

Если вы все нарисовали правильно, соединение конечной точки Z с конечной точкой A даст вам квадрат ZANY .

Если соединить конечных точек Z и N , получится диагональ квадрата. Соедините A и Y , и вы получите другую диагональ.

Посмотрите внимательно на эти диагонали. Они одинаковой длины и делят друг друга пополам (делят друг друга пополам).

Квадраты в реальной жизни

Квадрат — это форма, которую легко сделать, вырезать или построить из повседневных материалов. Он также может покрыть плоскость, когда вы неоднократно ставите квадраты друг против друга.

Когда вы покрываете поверхность так, чтобы ничего не выглядывало, вы создаете мозаику поверхности. Только несколько правильных многоугольников могут создать мозаичную поверхность, и квадрат — один из них. Это делает квадрат очень удобным для строительства, украшения и производства произведений искусства. Вы можете найти квадраты повсюду.

Многие напольные плитки и потолочные панели имеют квадратную форму. Керамическая плитка для ванной часто имеет квадратную форму. Художники и архитекторы часто используют квадраты.

Основание квадратной пирамиды, трехмерного тела, представляет собой квадрат. Грани кубов и игральных костей (также трехмерных или трехмерных тел) представляют собой квадраты.

Квадраты в реальной жизни

Квадраты можно найти на картинках, в рамках для картин, в коробках с кроссвордами, на сторонах маленьких детских кубиков, на плитках Эрудит и на доске Эрудит, и даже на клавишах на многих компьютерных клавиатурах.

В Соединенных Штатах большая часть бумаги для письма и печати имеет прямоугольную, а не квадратную форму, но в Японии квадратная бумага используется для складывания в искусстве оригами. Вы можете сделать замечательных животных и другие фигурки в оригами, начиная с квадрата бумаги.

Свойства квадрата

Квадраты обладают тремя отличительными свойствами, связанными с их диагоналями, сторонами и внутренними углами.

Свойства квадратов

Диагонали

Все квадраты имеют ровно две конгруэнтные диагонали, которые пересекаются под прямым углом и делят друг друга пополам. Диагонали квадрата также делят его внутренние углы пополам.

Никакая другая форма не обладает таким отличительным свойством!

Стороны

Все четыре стороны квадрата равны. Это означает, что они равны друг другу по длине. Для равенства противоположные стороны квадрата должны быть параллельны. Ромб разделяет это идентифицирующее свойство, поэтому квадраты являются ромбами.

Внутренние углы

Все четыре внутренних угла квадрата равны. Поскольку внутренние углы любого четырехугольника должны складываться с 360° , быстрое деление показывает, что каждый угол равен 90°.

Таким образом, все квадраты имеют четыре прямых угла. Прямоугольник разделяет это идентифицирующее свойство, поэтому квадраты — это прямоугольники.

Как найти периметр квадрата

Поскольку квадрат имеет четыре конгруэнтные (равносторонние или равные по длине) стороны, найти расстояние вокруг фигуры очень просто. Отметьте длину любой стороны a , а затем умножьте 4 :

Формула периметра квадрата

Итак, для нашего квадрата ZANY одна из сторон равна 37 ярдов .

Периметр квадрата

Пример #2

Попробуйте сами. Допустим, квадрат ZANY имеет одну сторону 1000 метров . Что такое периметр?

Как найти площадь квадрата

Площадь всегда выражается в квадратных единицах линейного измерения. Обычно мы говорим, что площадь равна длине, умноженной на ширину, но в квадрате длина равна ширине. Это облегчает вашу работу.

Чтобы найти площадь квадрата, умножьте длину любой стороны на себя (возведите во вторую степень):

Формула площади квадрата

Найдем площадь квадрата со стороной 37 дворы.

Площадь квадрата

Пример #3

Попробуйте сами. Возьмем тот же квадрат ZANY со сторонами 1000 метров . Какова его площадь в квадратных метрах?

Краткое содержание урока

Посмотрев видео и прочитав эти инструкции, вы узнали все о геометрической фигуре, квадрате. Вы знаете, как построить квадрат. Вы можете идентифицировать квадраты вокруг себя, вы можете сказать, как квадрат вписывается в семейство четырехугольников, и вы можете определить три отличительных свойства квадрата. 9{2}A=a2, в квадратных единицах.

Периметр квадрата: определение, формула и примеры

Периметр квадрата

Периметр квадрата: Периметр любой геометрической фигуры равен сумме всех сторон. Концепция периметра обычно встречается в младших классах, и понимание становится очень важным, чтобы иметь хорошую основу в математике. Периметр имеет свое применение в повседневной жизни, предположим, вы отправились на прогулку в парк, а позже вас попросили рассчитать периметр парка. Теперь угадайте, как вы будете рассчитывать периметр парка. Так форма парка квадратная, тогда периметр парка будет суммой всех сторон парка.

Что такое периметр квадрата?

Периметр квадрата определяется как сумма всех сторон квадрата. Он рассчитывается путем прохождения всего пути геометрической формы. Как известно, квадрат – это четырехугольник. У квадрата все четыре стороны равны, поэтому периметр в четыре раза больше длины каждой стороны квадрата.

Формула периметра квадрата

Математически формула периметра квадрата выглядит следующим образом:

Как мы знаем, стороны квадрата равны,

Тогда Периметр квадрата = 4 × Сторона

Вычисление периметра квадрата 

У квадрата все четыре стороны равны, поэтому периметр в четыре раза больше длины каждой стороны квадрата.

Периметр (P) = длина всех сторон замкнутой фигуры

Периметр квадрата = сторона + сторона + сторона + сторона

Периметр квадрата = 4(S)

Где «S» означает сторону квадрат.

Расчет периметра квадрата

Периметр квадрата рассчитывается по-разному на основе разных параметров. Ниже приведена таблица, которая дает вам формулу для расчета периметра квадрата.

Calculation of Perimeter of Square
Parameters	Formula
Using Side Length	Perimeter = 4 × Side
Using Diagonal	Perimeter = (√ 2 × диагональ/2) × 4 = (2√2 × диагональ) единиц.
Использование площади квадрата	Периметр = (√площадь) × 4 = 4√единицы площади.

Примеры периметра квадрата

Q1.

Если периметр квадрата равен 72 ед. Тогда какой будет сторона квадрата?

Решение: Периметр квадрата = 72 Единицы,

Как мы знаем, Периметр = 4 × Сторона

72 = 4 × Сторона0004 Q2. Если сторону квадрата увеличить на 8 м, его площадь увеличится на 120 кв.м. Найдите сторону квадрата и его периметр.

Решение: Пусть длина каждой стороны квадратного парка равна x метров.

Как мы знаем, площадь квадрата = (Сторона × Сторона)

Согласно вопросу, Сторона = (x + 8)

, а площадь равна, Площадь = x² + 120

Следовательно, Площадь = ( сторона)² 

x² + 120 = (x + 8)² 

x² + 120 = x² + 16x + 64

120 = x² + 16x + 64 — x²

120 = 16x + 64

16x = 120-64

16x = 56

x = 56/16

x = 4

. составляет 4 метра

Периметр = 4 стороны

Периметр = 16 единиц

Q3. Площадь квадрата равна 289 квадратных единиц.

No related posts.