Знаки синуса, косинуса и тангенса угла
Дата проведения:
Группа:
Тема урока: Знаки синуса, косинуса и тангенса угла
Преподаватель: Касымова У.Ш.
Тип урока: систематизация знаний.
Цели урока:
1) образовательная: обобщить и проверить знания учащихся о понятиях «синус», «косинус», «тангенс», определении знаков и табличных значений и умения находить значения тригонометрических функций;
2) воспитательная: воспитывать интерес к предмету;
3) развивающая: развивать память, логическое мышление.
Литература: Алгебра и начала математического анализа А.Н.Колмогоров
Ход урока:
I. Организационный момент.
Учитель сообщает тему, цели и задачи урока.
II. Повторение (фронтальная работа с классом).
Устные упражнения
1) Выразить угол в радианах с помощью π.
45°, 150°, 90°, 360°, 30°, 270°, 135°, 60°, 180°, -720°.
3. Новая тема
Число (пи) – математическая константа, которая выражает отношение длины окружности к её диаметру. Равна приблизительно 3,14.
Какие знаки имеют координаты точки в зависимости от их положения в системе координат?
У точек первой четверти
у точек второй четверти
у точек третьей четверти
у точек четвёртой четверти
В какой координатной четверти находятся точки с указанными координатами
Ответ:
A | B | C | D | E | F |
2 | 4 | 2 | 3 | 1 | 4 |
А если точка находится на тригонометрической окружности, то как узнать зависимость знака координат точки от угла поворота вокруг начала координат?
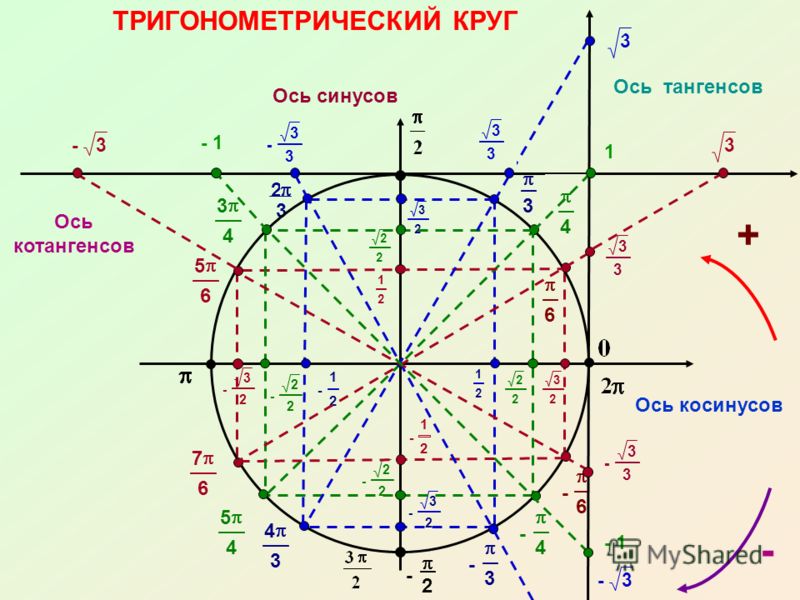
Сегодня на уроке мы узнаем знаки синуса, косинуса, тангенса и котангенса, научимся определять положение точки на тригонометрической окружности в зависимости от комбинации знаков синуса и косинуса, тангенса и котангенса.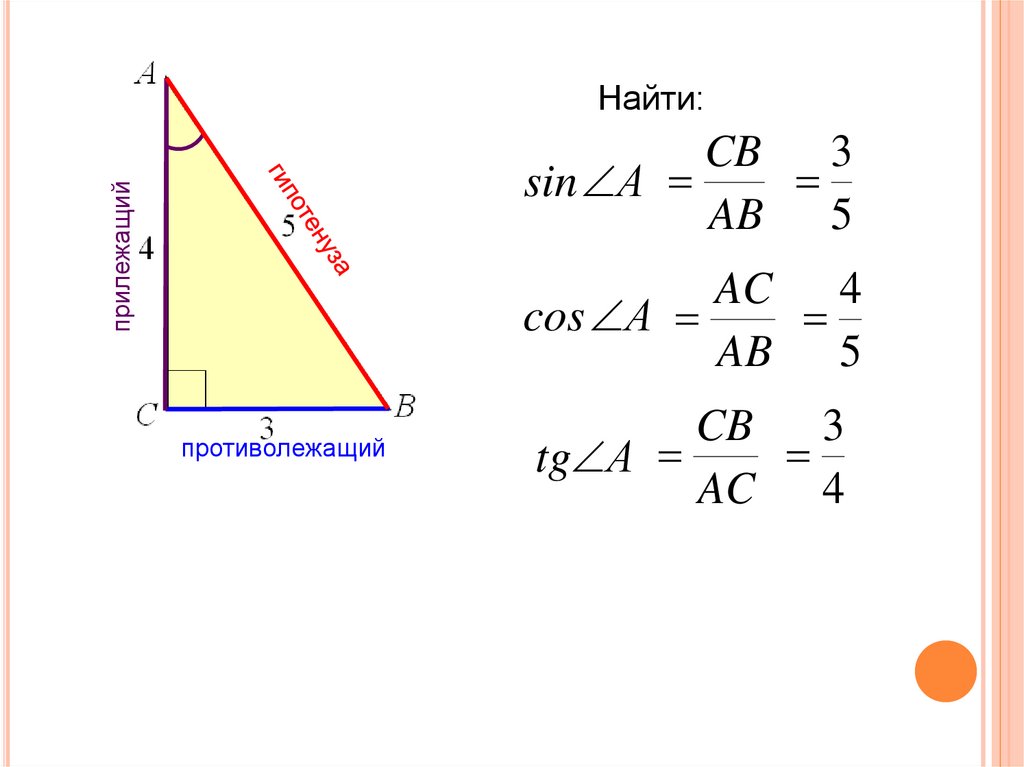
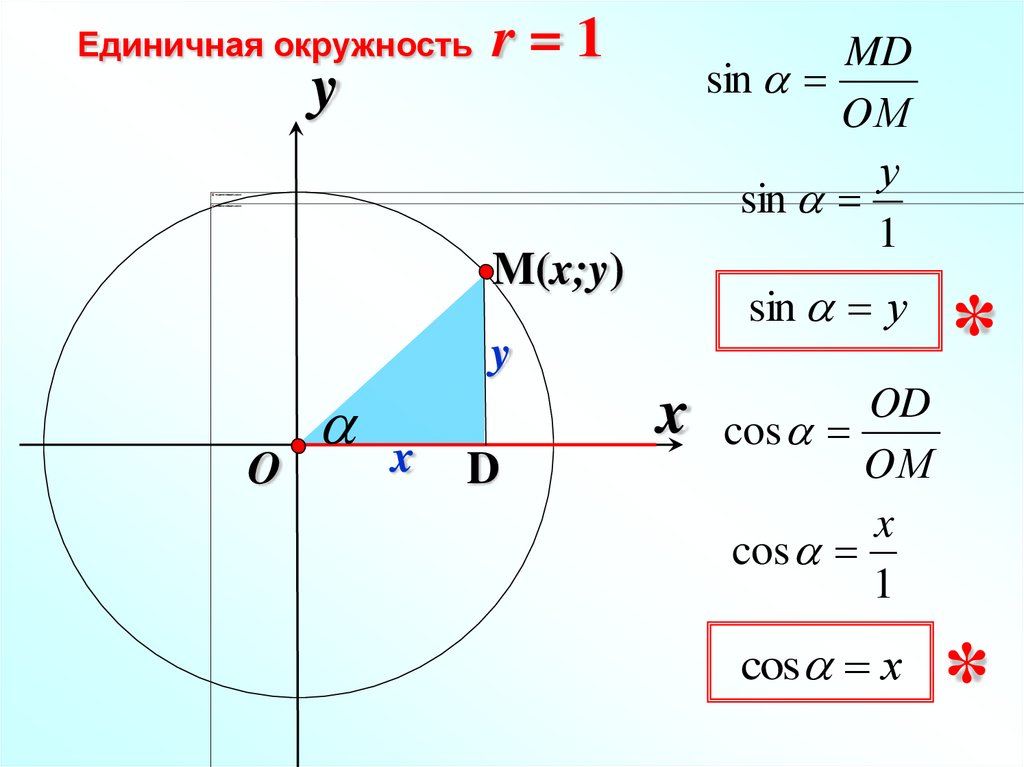
1.Рассмотрим единичную окружность в прямоугольной системе координат хОу.
Точка Р(1;0) при повороте вокруг начала координат на угол переместилась в точку Рₐ. Определим её координаты.
Синусом угла является ордината точки, полученной поворотом точки (1;0) вокруг начала координат на угол .
Косинусом угла является абсцисса точки, полученной поворотом точки (1;0) вокруг начала координат на угол .
Если угол , то точка Рₐ находится во второй четверти, здесь , , значит , .
Если угол , то точка Рₐ находится в третьей четверти, здесь , , значит
Если угол , то точка Рₐ находится в четвертой четверти, здесь , , значит ,
На рисунке видно какие знаки имеет синус, а какие косинус.
3.Закрепление Пример1. Определить знаки синуса и косинуса угла .
Решение: Выясним, в какой четверти находится точка, полученная поворотом на угол .
во второй четверти синусы положительны, косинусы отрицательны.
Ответ:
Пример 2. Определить знаки синуса и косинуса угла .
Решение: Полный угол, при котором точка «обойдёт» всю окружность, равен .
а это значит, что точка после 2 оборотов окажется в первой четверти, где синус и косинус положительны.
Ответ:
Пример 3.Определить знаки синуса и косинуса угла .
Решение: Угол отрицательный, значит точка получена поворотом по часовой стрелке.
в 4 четверти синусы отрицательны, косинусы положительны.
Ответ: синус отрицательный, косинус положительный.
Пример 4. Определить знаки .
Решение: Знаем, что , а . Значит, . Точка во второй четверти.
Ответ:
2.Знаки тангенса и котангенса.
Тангенс это отношение синуса угла к его косинусу:
Котангенс это отношение косинуса угла к его синусу: .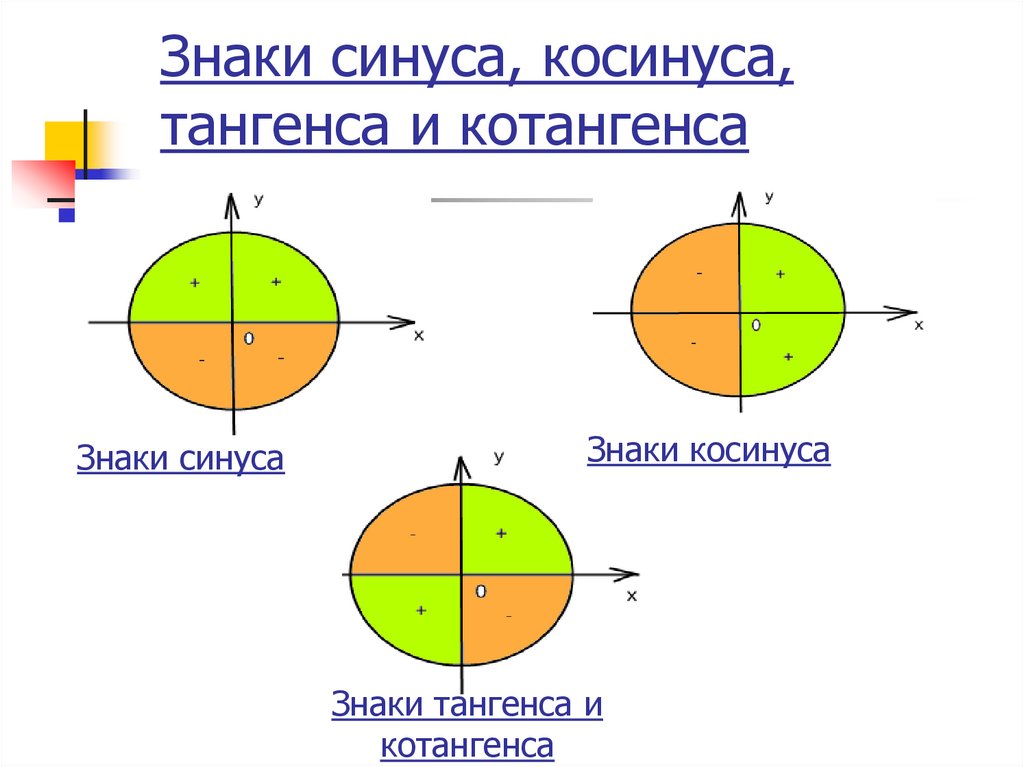
Тангенс и котангенс будут положительными там, где синус и косинус имеют одинаковые знаки. Это первая и третья четверти. Синус и косинус имеют разные знаки во второй и четвёртой четвертях, здесь тангенс и котангенс будут отрицательны. На рисунке изображены знаки тангенса и котангенса.
Пример 5.
Определить знак тангенса угла
Решение , угол второй четверти
Ответ: tg> 0
Пример 6
Вывод: чтобы определить знаки синуса, косинуса, тангенса и котангенса, нужно:
- выяснить в какой координатной четверти находится угол;
- знак синусов такой же, как ордината точки (у).
- знак косинусов такой же, как абсцисса точки (х).
- тангенсы и котангенсы положительны там, где синус и косинус имеют одинаковые знаки(1ч. и 4ч.), отрицательны, где синус и косинус имеют противоположные знаки (2ч. и 3ч.).
5.Итог урока
Оценивание
6. Дом/задание. Определить знак тангенса угла .
Дом/задание. Определить знак тангенса угла .
Просмотр содержимого документа
«Знаки синуса, косинуса и тангенса угла»
Дата проведения:
Группа:
Тема урока: Знаки синуса, косинуса и тангенса угла
Преподаватель: Касымова У.Ш.
Тип урока: систематизация знаний.
Цели урока:
1) образовательная: обобщить и проверить знания учащихся о понятиях «синус», «косинус», «тангенс», определении знаков и табличных значений и умения находить значения тригонометрических функций;
2) воспитательная: воспитывать интерес к предмету;
3) развивающая: развивать память, логическое мышление.
Литература: Алгебра и начала математического анализа А.Н.Колмогоров
Ход урока:
I. Организационный момент.
Организационный момент.
Учитель сообщает тему, цели и задачи урока.
II. Повторение (фронтальная работа с классом).
Устные упражнения
1) Выразить угол в радианах с помощью π.
45°, 150°, 90°, 360°, 30°, 270°, 135°, 60°, 180°, -720°.
3. Новая тема
Число (пи) – математическая константа, которая выражает отношение длины окружности к её диаметру. Равна приблизительно 3,14.
Какие знаки имеют координаты точки в зависимости от их положения в системе координат?
У точек первой четверти
у точек второй четверти
у точек третьей четверти
у точек четвёртой четверти
В какой координатной четверти находятся точки с указанными координатами
Ответ:
A | B | C | D | E | F |
2 | 4 | 2 | 3 | 1 | 4 |
А если точка находится на тригонометрической окружности, то как узнать зависимость знака координат точки от угла поворота вокруг начала координат?
Сегодня на уроке мы узнаем знаки синуса, косинуса, тангенса и котангенса, научимся определять положение точки на тригонометрической окружности в зависимости от комбинации знаков синуса и косинуса, тангенса и котангенса.
1.Рассмотрим единичную окружность в прямоугольной системе координат хОу.
Точка Р(1;0) при повороте вокруг начала координат на угол переместилась в точку Рₐ. Определим её координаты.
Синусом угла является ордината точки, полученной поворотом точки (1;0) вокруг начала координат на угол .
Косинусом угла является абсцисса точки, полученной поворотом точки (1;0) вокруг начала координат на угол .
Если угол то точка Рₐ находится в первой четверти, здесь , значит
Если угол , то точка Рₐ находится во второй четверти, здесь , , значит , .
Если угол , то точка Рₐ находится в третьей четверти, здесь , , значит
Если угол , то точка Рₐ находится в четвертой четверти, здесь , , значит ,
На рисунке видно какие знаки имеет синус, а какие косинус.
3.Закрепление Пример1. Определить знаки синуса и косинуса угла .
Решение: Выясним, в какой четверти находится точка, полученная поворотом на угол .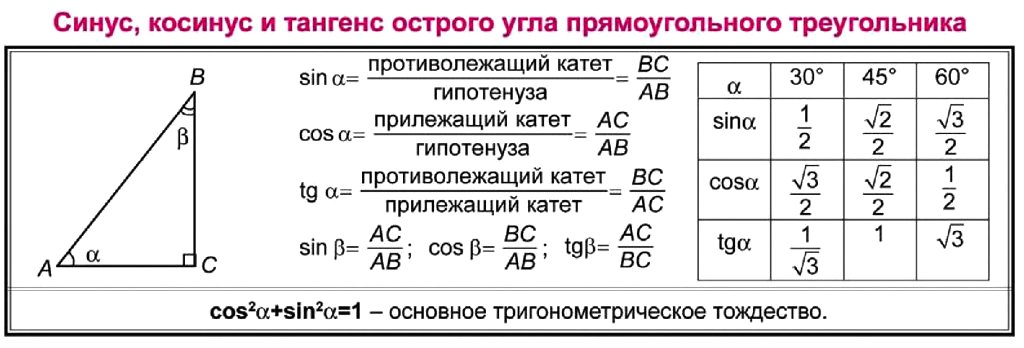
во второй четверти синусы положительны, косинусы отрицательны.
Ответ:
Пример 2. Определить знаки синуса и косинуса угла .
Решение: Полный угол, при котором точка «обойдёт» всю окружность, равен .
а это значит, что точка после 2 оборотов окажется в первой четверти, где синус и косинус положительны.
Ответ:
Пример 3.Определить знаки синуса и косинуса угла .
Решение: Угол отрицательный, значит точка получена поворотом по часовой стрелке.
в 4 четверти синусы отрицательны, косинусы положительны.
Ответ: синус отрицательный, косинус положительный.
Пример 4. Определить знаки .
Решение: Знаем, что , а . Значит, . Точка во второй четверти.
Ответ:
2.Знаки тангенса и котангенса.
Тангенс это отношение синуса угла к его косинусу:
Котангенс это отношение косинуса угла к его синусу: .
Тангенс и котангенс будут положительными там, где синус и косинус имеют одинаковые знаки.
Пример 5.
Определить знак тангенса угла
Решение , угол второй четверти
Ответ: tg 0
Пример 6
Вывод: чтобы определить знаки синуса, косинуса, тангенса и котангенса, нужно:
выяснить в какой координатной четверти находится угол;
знак синусов такой же, как ордината точки (у).
знак косинусов такой же, как абсцисса точки (х).
тангенсы и котангенсы положительны там, где синус и косинус имеют одинаковые знаки(1ч. и 4ч.), отрицательны, где синус и косинус имеют противоположные знаки (2ч. и 3ч.).
5.Итог урока
Оценивание
6.Дом/задание. Определить знак тангенса угла .
Ответы присылайте на почту.
Укажите Ф.И и группу.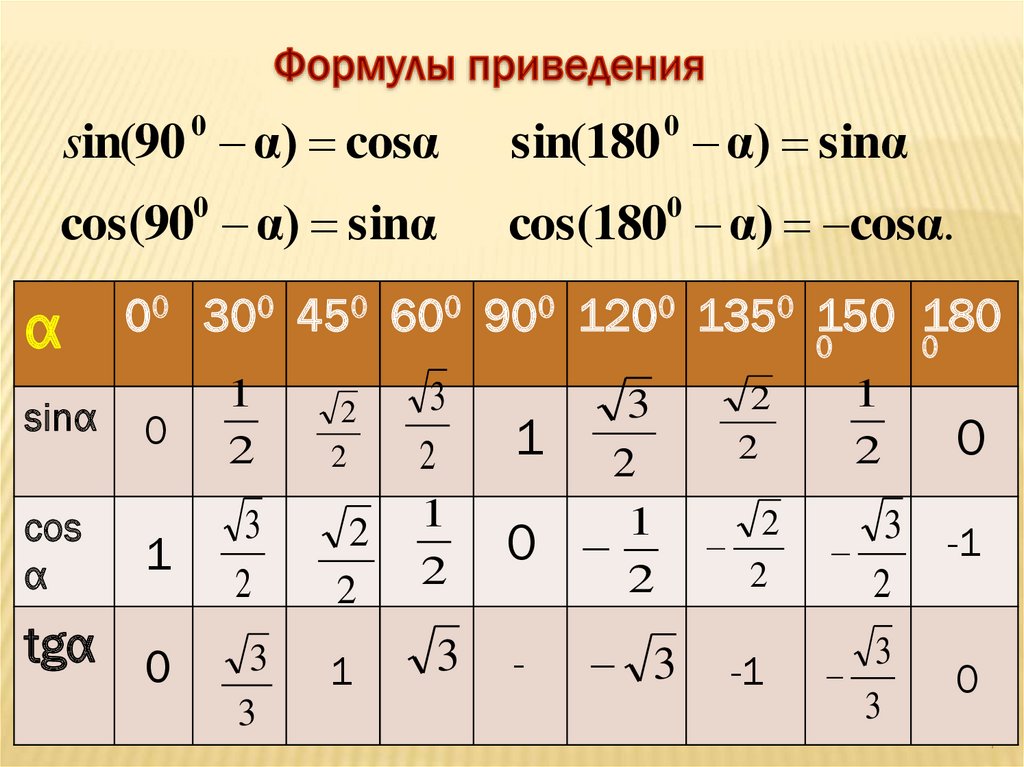
[email protected]
|
Деятельность учителя |
Деятельность учеников |
||||
1. |
Организационный этап Занятие сопровождается компьютерной Презентацией. Задачи: подготовка учащихся к работе на уроке, психологический настрой учащихся, организация внимания; — взаимное приветствие; |
Готовятся к уроку, приветствуют учителя. |
||||
2. |
Этап проверки домашнего задания Задача: проверить правильность, полноту и сознательность выполнения домашнего задания всем классом. |
Учащиеся сдают домашние задания, выполненные по карточкам. (Приложение 1) |
||||
3. |
Этап всесторонней проверки знаний Задача: проверить знания учащихся по теме «Угол поворота», «Измерение углов поворота в радианах»; закрепление, уточнение и систематизация знаний учащихся. |
Фронтальная устная работа по слайдам презентации. |
||||
Слайд 2: Выразить угол в радианах с помощью π. |
Выражают градусную меру углов в радианах с помощью π: 45°, 150°, 90°,360°, 30°, 270°,135°, 60°, 180°, -210°, -720° |
|||||
Слайд 3: Найти градусную меру угла по заданной радианной. |
Находят градусную меру угла по заданной радианной: ; ; 3π; ; . |
|||||
Слайд 4: Определить, какой координатной четверти принадлежит угол. |
Определяют, какой координатной четверти принадлежит угол: 45°; -80°; 150°; -120°; 250°; -200°; 400°; 820°; -460°; 450°. |
|||||
4. |
Этап усвоения новых знаний Задача: изучение понятий синуса, косинуса, тангенса и котангенса произвольного угла α; нахождение области определения и области значений выражений sin α, cos α, tg α, ctg α. |
|
||||
Слайд: Тема нового материала: «Определение косинуса, синуса, тангенса и котангенса». В курсе геометрии были определены косинус, синус и тангенс угла α при 0° ≤ α ≤ 180°. Распространим эти определения на случай произвольного угла α. Кроме того, введем понятие котангенса угла α. |
|
|||||
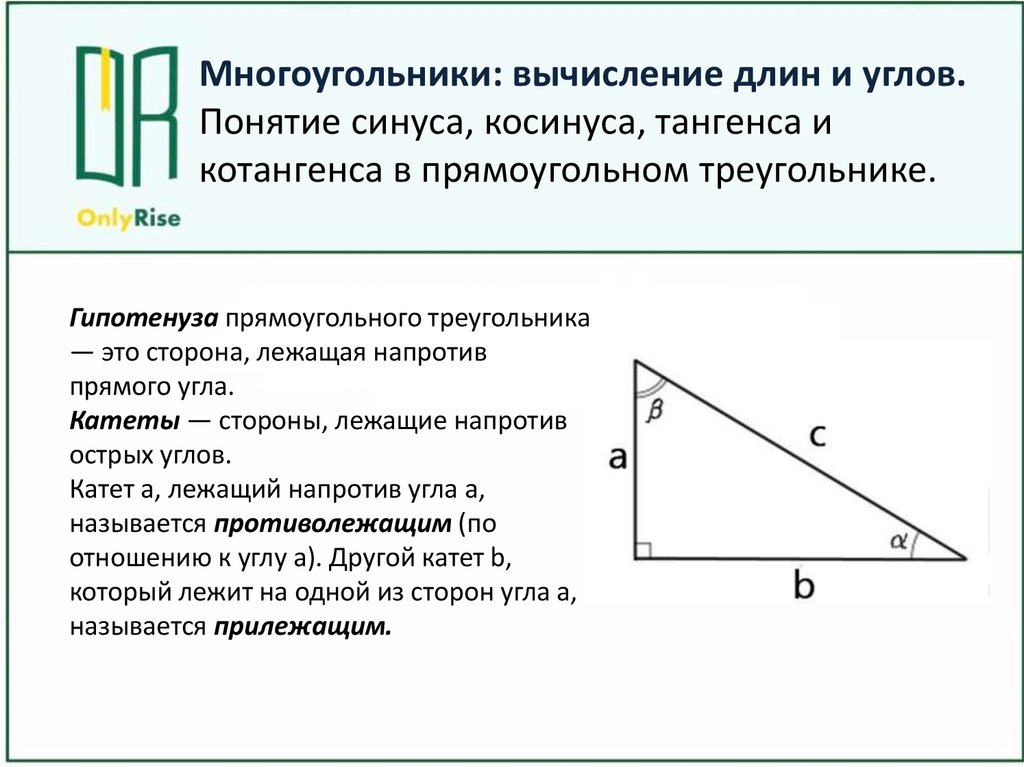
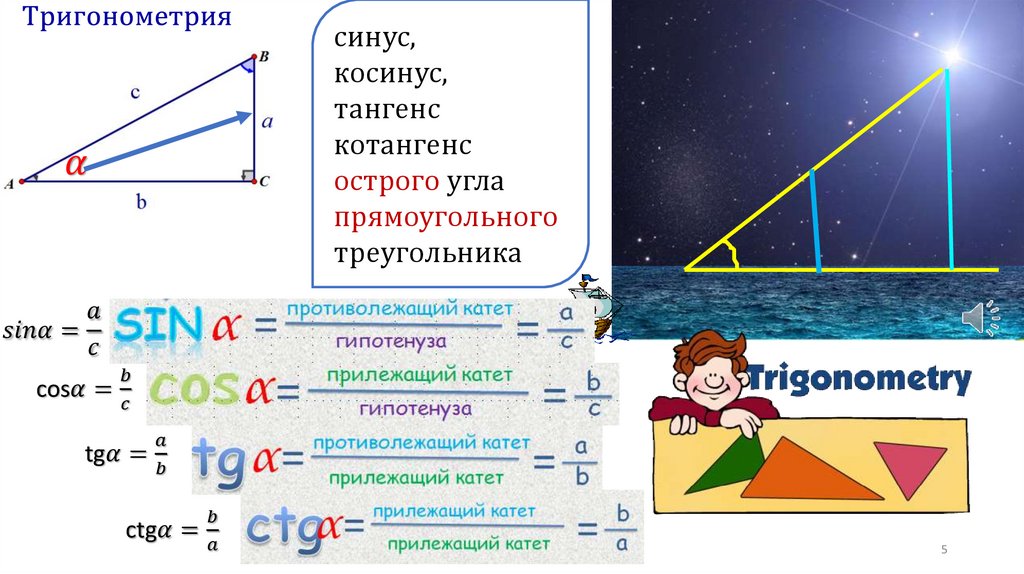
Слайд 6: Пусть при повороте около точки О на угол α начальный радиус ОА переходит в конечный радиус ОВ. Косинусом угла α называется отношение абсциссы точки В к длине радиуса. |
Записывают определение на лист с печатной основой. (Приложение 2) |
|||||
Слайд 7: Синусом угла α называется отношение ординаты точки В к длине радиуса. |
Записывают определение на лист с печатной основой. |
|||||
Слайд 8: Тангенсом угла α называется отношение ординаты точки В к ее абсциссе. |
Записывают определение на лист с печатной основой. |
|||||
Слайд 9: Котангенсом угла α называется отношение абсциссы точки В к ее ординате. |
Записывают определение на лист с печатной основой. |
|||||
Слайд 10: Докажем, что sin α, cos α, tg α, ctg α зависят только от угла α и не зависят от радиуса. Рассмотрим на примере sin α и cos α. Докажем, что для любого угла α отношение и не зависят от длины радиуса, а зависят только от угла α. |
Принимают участие в доказательстве (проводится в форме беседы). |
|||||
Слайд 11: 1. Возьмем два начальных радиуса ОА1 = R1, ОА2 = R2. 2. Повернем их около точки О на один и тот же угол α. 3. Получим радиусы ОВ1 и ОВ2, В1(х1; у1), В2 (х2; у2). 4. Построим прямоугольные треугольники ОВ1С1 и ОВ2С2 5. |
1. Сколько окружностей надо построить? (Две.) 2. Что можно сказать о длине радиусов ОВ1 и ОВ2? (ОВ1= R1, ОВ2 = R2) 3. Найдите длины сторон В1С1 и В2С2, ОС1 и ОС2(х2 и х1; у2 и у1) 4. Что можно сказать о прямоугольных треугольниках ОВ1С1 и ОВ2С2? (Они подобны.) 5. По какому признаку? (По двум углам.) |
|||||
Слайд 12: 6. Из подобия треугольников (с учетом знака координат точек В1 и В2) следует, что и . 7. Таким образом, для любого угла α отношение и не зависят от длины радиуса, а зависят только от угла α. |
6. Равенство каких отношений следует из подобия треугольников ОВ1С1 и ОВ2С2? ( и ) |
|||||
Слайд 13: Область определения выражений sin α, cos α, tg α, ctg α. 1. Выражения sin α и cos α определены при любом α, так как для любого угла поворота можно найти соответствующие значения дробей и . То есть областью определения этих выражений является промежуток (-∞; +∞). |
Отвечают на вопросы учителя, делают выводы, заполняют таблицу на листе с печатной основой. 1. Всегда ли определена дробь (Да, т.к. R≠0.) 3. Вывод? (Выражение cosα определено при любом α.) 4. Всегда ли определена дробь (Да, т.к. R≠0.) 5. Что можно сказать о выражении sin α? (Тоже всегда определено.) 6. Вывод? (Выражение sin α определено при любом α.) 7. То есть областью определения этих выражений является промежуток? (-∞; +∞) |
|||||
2. Выражение tg α имеет смысл при любом α , кроме углов поворота вида α = где n – целое число, т. |
1. Всегда ли определена дробь ? (Нет, не определена для углов поворота, у которых координата х равна 0.) 2. Какие это углы? (Углы вида α = где n – целое число.) 3. При каких значениях α имеет смысл выражение tg α ? (При любом α , кроме углов поворота вида α = n – целое.) |
|||||
3. Выражение сtg α имеет смысл при любом α , кроме углов поворота вида α = , где n – целое число, т.к. для этих углов не имеет смысла дробь . |
1. Всегда ли определена дробь ? (Нет, не определена для углов поворота, у которых координата у равна 0.) 2. Какие это углы? (Углы вида α = , где n – целое число.) 3. При каких значениях α имеет смысл выражение сtg α ? (При любом α , кроме углов поворота вида α = , где n – целое. |
|||||
Область значений выражений sin α, cos α, tg α, ctg α 1. Областью значений синуса и косинуса является промежуток , т.к. при изменении угла поворота координаты х и у изменяются в пределах от –R до R, а значит, отношения и изменяются в пределах от -1 до 1. |
1. В каких пределах изменяются координаты х и у при изменении угла поворота? (Координаты х и у изменяются в пределах от –R до R.) 2. В каких пределах изменяются отношения и ? (От -1 до 1.) 3. Значит, областью значений выражений sin α и cos α является промежуток? () |
|||||
2. Областью значений тангенса и котангенса является промежуток (-∞; +∞) |
|
|||||
5. |
Этап закрепления новых знаний: Задача: закрепить в памяти учащихся знания и умения, необходимые им для самостоятельной работы по новому материалу; сформировать умения и навыки нахождения значений выражений, содержащих синусы, косинусы, тангенсы и котангенсы углов 0°, 30°, 45°, 60°, 90°, 180°, 270°, 360°. 1. Рассмотрим примеры вычисления значений выражений sin α, cos α, tg α, ctg α для некоторых углов поворота. — для углов 30°, 45°, 60° знакомы нам из курса геометрии. Слайд 14 — при повороте на угол α =180° точка В имеет координаты( -R; 0). Значит, 2. Заполнить таблицу на раздаточном листе. Проверка ответов по слайду презентации. Слайд 15 Резервные номера: № 1028 |
Отвечают на вопросы учителя, вместе разбирают пример при α = 180° , заполняют таблицу значений sin α, cos α, tg α, ctg α на листе с печатной основой. Проверяют ответы по слайду презентации. 1. Назовите координаты точки в при повороте на угол α = 180°? (Точка В имеет координаты(-R; 0).) Проверка правильности заполнения таблицы по слайду презентации. Для учеников, быстро справившихся с заданием: № 1028.
|
||||
Задание на листе с печатной основой. Проверка по слайду презентации. Слайд 16 |
Весь класс выполняет задание на листе с печатной основой. (Приложение 3) Проверка по слайду презентации. |
|||||
6. |
Этап подведения итогов урока, информации учащихся о домашнем задании, инструктаж по его выполнению Задачи: — подвести итоги урока; выставить оценки за работу на уроке; — сообщить учащимся о домашнем задании; разъяснить методику его выполнения; мотивировать необходимость его выполнения. Слайд 17 Подводим итог урока, предлагая учащимся вопросы: 1. Сформулировать определение синуса, косинуса, тангенса, котангенса. Задание на дом Пункт 45, № 1026, 1027. |
Ученики отвечают на вопросы учителя. Записывают домашнее задание в дневники: пункт 45, № 1026, 1027. |
Trigonometric Functions: Sine, Cosine, Tangent, Cosecant, Secant,…
Recent Channels
- Trigonometry
Chemistry
- General Chemistry
- Organic Chemistry
- Analytical Chemistry
- GOB Chemistry
- Биохимия
Биология
- Общая биология
- Микробиология
- Анатомия и физиология
- Генетика
- Клеточная биология
Math
- College Algebra
- Trigonometry
- Precalculus
Physics
- Physics
Business
- Microeconomics
- Macroeconomics
- Financial Accounting
Social Sciences
- Psychology
Начните вводить текст, затем используйте стрелки вверх и вниз, чтобы выбрать вариант из списка.
- Углы и тригонометрические функции
- Правой треугольник Тригонометрия
- Используйте правые треугольники для оценки тригонометрических функций
Связанные видео
Связанные практики
Тригонометрические функции на поиск неизвестных сторон правых треугольников
By PatrickJMT 9005
7070707070707070707070707070707070707070707070707070707070707070707070707070707070707070707. Тоа?
Тэмми Григсби
298 просмотров
Тригонометрические функции: синус, косинус, тангенс, косеканс, секанс и котангенс
профессор Дэйв объясняет
155 просмотров
Все тригонометрические значения, приведенные правым треугольником
от Patrickjmt
186 Просмотров
Нахождение высоты объекта с использованием тригонометрии
от Patrickjmt
168 Просмотров
Тригмонт!
by patrickJMT
209 просмотров
Поиск значений тригонометрических функций по одному значению триггера в прямоугольном треугольнике
by patrickJMT
72 просмотров
Введение в тригонометрические функции с использованием треугольников
по Mathispower4u
184 Просмотры
Нахождение угла с учетом значения тригонометрической функции — Пример 2
от Patrickjmt
102 Views
Право -Англ Triangle TRIGONGONTER TRIGONGTET TRIGONGTER TRIGONTYTRITYTINGTYTRITYTINGETINGETINGETINGETINGETINGETINGETIONTINGTIONTINGTYTRITYTINGETION
от Eddie Woo
128 просмотров
Тригонометрические функции для нахождения неизвестных сторон прямоугольных треугольников, Ex 3
от patrickJMT
53 просмотров
Правые треугольники и тригонометрические функции
от Patrickjmt
29 Просмотров
Нахождение шести тригонометрических функций из Triangle
Bian McLogan
39 видов
Нахождение Trigonycration Fecund by patrickJMT
130 просмотров
«Генетический контекст для понимания тригонометрических функций» Дэнни Отеро
- < Предыдущий
Тип документа
Материалы курса
Дата публикации
Spring 3-2017
Аннотация
В этом проекте мы исследуем геносию Тригонометской функции: SAINE, COOTENGENT, COTENGENT, COTINGENT, COTENGENT, COOTENGENTENGENT, COOTENGENT, COTINGENTENTING, COOTENGENT, COTINGENT, COOTENGENT, COOTENGENTINGE, SACENENGENTING, SACENTENGENTING. и косеканс. Цель состоит в том, чтобы предоставить типичному учащемуся в курсе предварительного исчисления некоторый контекст для понимания этих понятий, который обычно отсутствует в стандартных разработках учебников. Тригонометрия возникла в древнегреческом мире (и, как предполагается, независимо также в Китае и Индии) из геометрического анализа, необходимого для решения основных астрономических задач относительно относительного положения и движения небесных объектов. В то время как греки (Гиппарх, Птолемей) признавали полезность составления таблиц хорд центральных углов окружности для решения задач сферической геометрии, индийские математики, такие как Варахамахира (505–587), сочли более целесообразным табулирование полухорд. , откуда стало популярным использование синуса и косинуса. Мы рассмотрим отрывок из этой работы, в котором Варахамахира описывает несколько стандартных современных соотношений между синусом и косинусом в ходе создания таблицы синусов. В XI веке арабский ученый и знаток индуистской науки Абу л-Райхан Мухаммад ал-Бируни (973—1055) опубликовал «Исчерпывающий трактат о тенях» (ок.
и косеканс. Цель состоит в том, чтобы предоставить типичному учащемуся в курсе предварительного исчисления некоторый контекст для понимания этих понятий, который обычно отсутствует в стандартных разработках учебников. Тригонометрия возникла в древнегреческом мире (и, как предполагается, независимо также в Китае и Индии) из геометрического анализа, необходимого для решения основных астрономических задач относительно относительного положения и движения небесных объектов. В то время как греки (Гиппарх, Птолемей) признавали полезность составления таблиц хорд центральных углов окружности для решения задач сферической геометрии, индийские математики, такие как Варахамахира (505–587), сочли более целесообразным табулирование полухорд. , откуда стало популярным использование синуса и косинуса. Мы рассмотрим отрывок из этой работы, в котором Варахамахира описывает несколько стандартных современных соотношений между синусом и косинусом в ходе создания таблицы синусов. В XI веке арабский ученый и знаток индуистской науки Абу л-Райхан Мухаммад ал-Бируни (973—1055) опубликовал «Исчерпывающий трактат о тенях» (ок. ~1021). В этой работе мы видим, как Бируни представляет геометрические методы использования солнечных часов; отношения внутри прямоугольных треугольников, создаваемые гномоном солнечных часов и тенью, отбрасываемой на их циферблат, приводят к изучению и табулированию значений тангенса и котангенса, секанса и косеканса. Бируни также определяет отношения этих величин к синусам и косинусам углов. Однако современная терминология для стандартных тригонометрических величин не была установлена до европейского Возрождения. Важнейшим в этом развитии является ориентир « О треугольниках» (1463 г.) Региомонтана (Иоганнес Мюллер). Региомонтан излагает тригонометрию в чисто геометрической форме, а затем применяет идеи к задачам круговой и сферической геометрии. Мы рассмотрим несколько теорем, которые исследуют тригонометрические отношения и которые используются для решения задач треугольника.
~1021). В этой работе мы видим, как Бируни представляет геометрические методы использования солнечных часов; отношения внутри прямоугольных треугольников, создаваемые гномоном солнечных часов и тенью, отбрасываемой на их циферблат, приводят к изучению и табулированию значений тангенса и котангенса, секанса и косеканса. Бируни также определяет отношения этих величин к синусам и косинусам углов. Однако современная терминология для стандартных тригонометрических величин не была установлена до европейского Возрождения. Важнейшим в этом развитии является ориентир « О треугольниках» (1463 г.) Региомонтана (Иоганнес Мюллер). Региомонтан излагает тригонометрию в чисто геометрической форме, а затем применяет идеи к задачам круговой и сферической геометрии. Мы рассмотрим несколько теорем, которые исследуют тригонометрические отношения и которые используются для решения задач треугольника.
Применимые курсы по математике
Pre-Calculus, тригонометрия
Академический дивизион
Редьер-дивизион
.




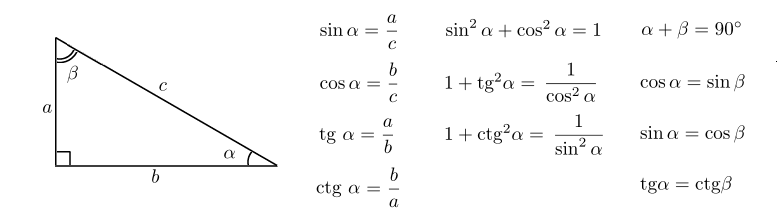
 Треугольники ОВ1С1 и ОВ2С2 подобны по двум углам.
Треугольники ОВ1С1 и ОВ2С2 подобны по двум углам. Эти равенства верны и тогда, когда точки В1 и В2 попадают на какую-либо из осей.
Эти равенства верны и тогда, когда точки В1 и В2 попадают на какую-либо из осей.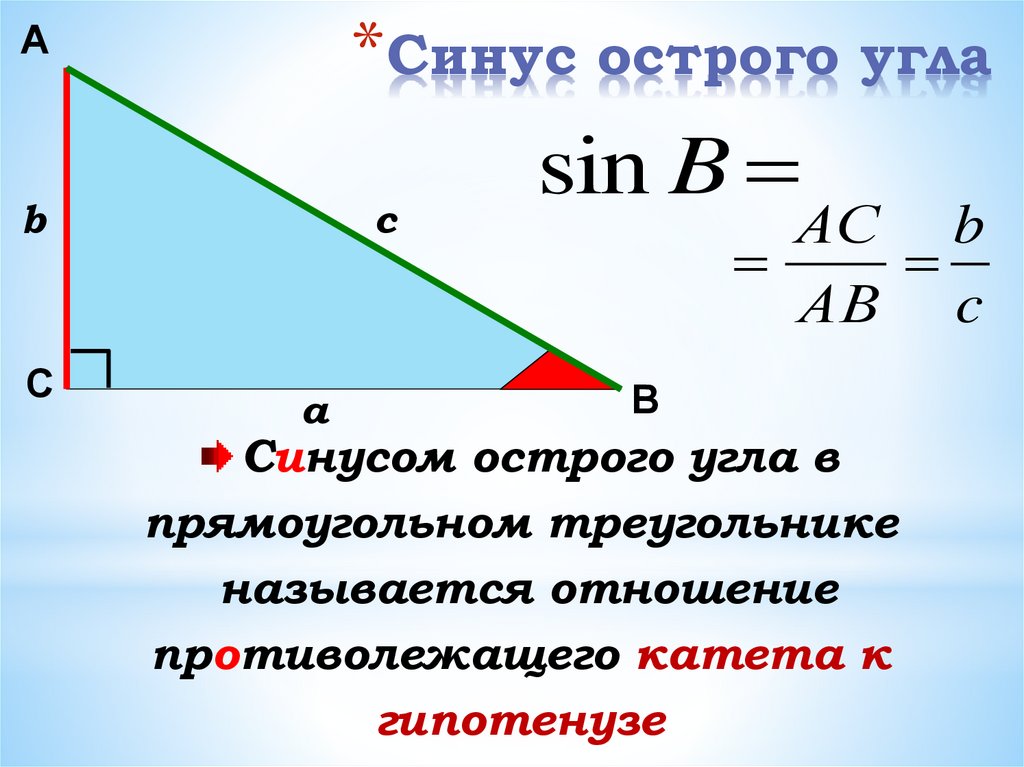
 к. для этих углов не имеет смысла дробь .
к. для этих углов не имеет смысла дробь . )
)
 (Приложение 3)
(Приложение 3)