Признаки средней линии трапеции. Средняя линия трапеции
Понятие средней линии трапеции
Для начала вспомним, какую фигуру называют трапецией.
Определение 1
Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие не параллельны.
При этом параллельные стороны называются основаниями трапеции, а не параллельные — боковыми сторонами трапеции.
Определение 2
Средняя линия трапеции — это отрезок, соединяющий середины боковых сторон трапеции.
Теорема о средней линии трапеции
Теперь введем теорему о средней линии трапеции и докажем её вектор ным методом.
Теорема 1
Средняя линия трапеции параллельна основаниям и равна их полусумме.
Доказательство.
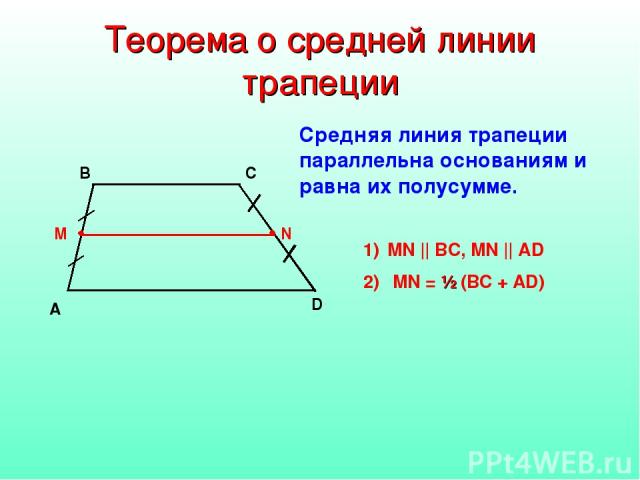
Пусть нам дана трапеция $ABCD$ с основаниями $AD\ и\ BC$. И пусть $MN$ — средняя линия этой трапеции (рис. 1).
Рисунок 1. Средняя линия трапеции
Докажем, что $MN||AD\ и\ MN=\frac{AD+BC}{2}$.
Рассмотрим вектор $\overrightarrow{MN}$.
Используем далее правило многоугольника для сложения векторов. С одной стороны получим, что
С другой стороны
Сложим два последних равенства, получим
Так как $M$ и $N$ — середины боковых сторон трапеции, то будем иметь
Получаем:
Следовательно
Из этого же равенства (так как $\overrightarrow{BC}$ и $\overrightarrow{AD}$ сонаправлены, а, следовательно, коллинеарны) получаем, что $MN||AD$.
Теорема доказана.
Примеры задач на понятие средней линии трапеции
Пример 1
Боковые стороны трапеции равны $15\ см$ и $17\ см$ соответственно. Периметр трапеции равен $52\ см$. Найти длину средней линии трапеции.
Решение.
Обозначим среднюю линию трапеции через $n$.
Сумма боковых сторон равна
Следовательно, так как периметр равен $52\ см$, сумма оснований равна
Значит, по теореме 1, получаем
Ответ: $10\ см$.
Пример 2
Концы диаметра окружности удалены от его касательной соответственно на $9$ см и $5$ см.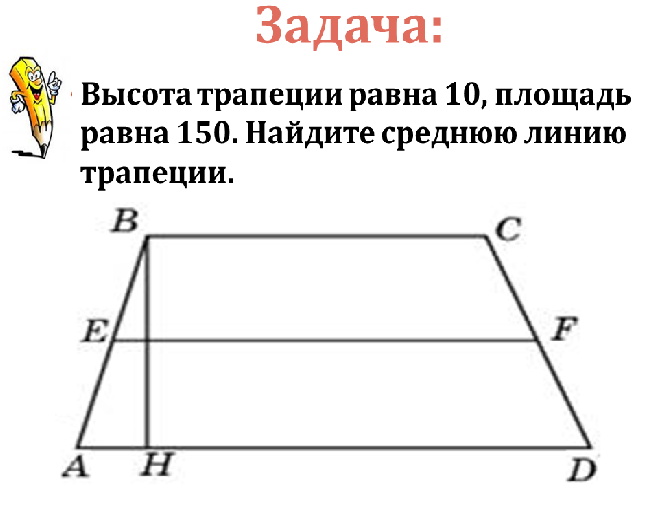
Решение.
Пусть нам дана окружность с центром в точке $O$ и диаметром $AB$. Проведем касательную $l$ и построим расстояния $AD=9\ см$ и $BC=5\ см$. Проведем радиус $OH$ (рис. 2).
Рисунок 2.
Так как $AD$ и $BC$ — расстояния до касательной, то $AD\bot l$ и $BC\bot l$ и так как $OH$ — радиус, то $OH\bot l$, следовательно, $OH|\left|AD\right||BC$. Из этого всего получаем, что $ABCD$ — трапеция, а $OH$ — ее средняя линия. По теореме 1, получаем
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.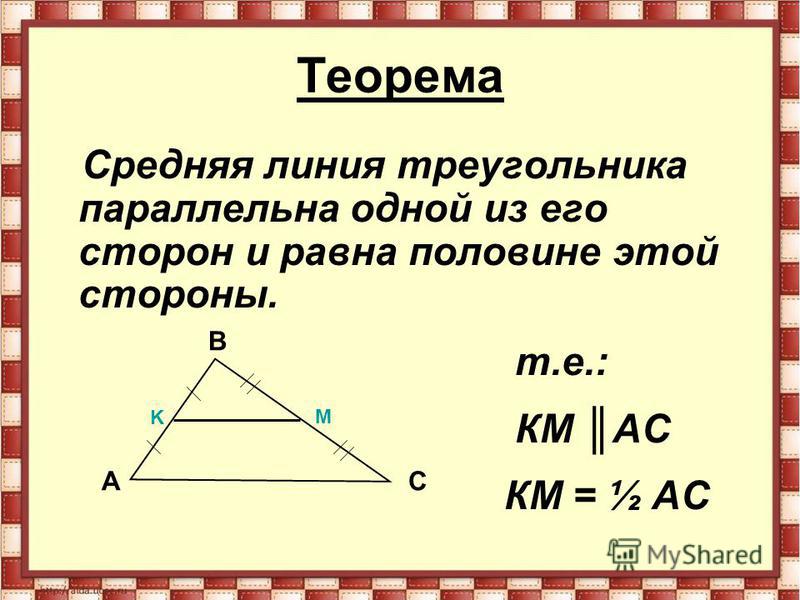
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.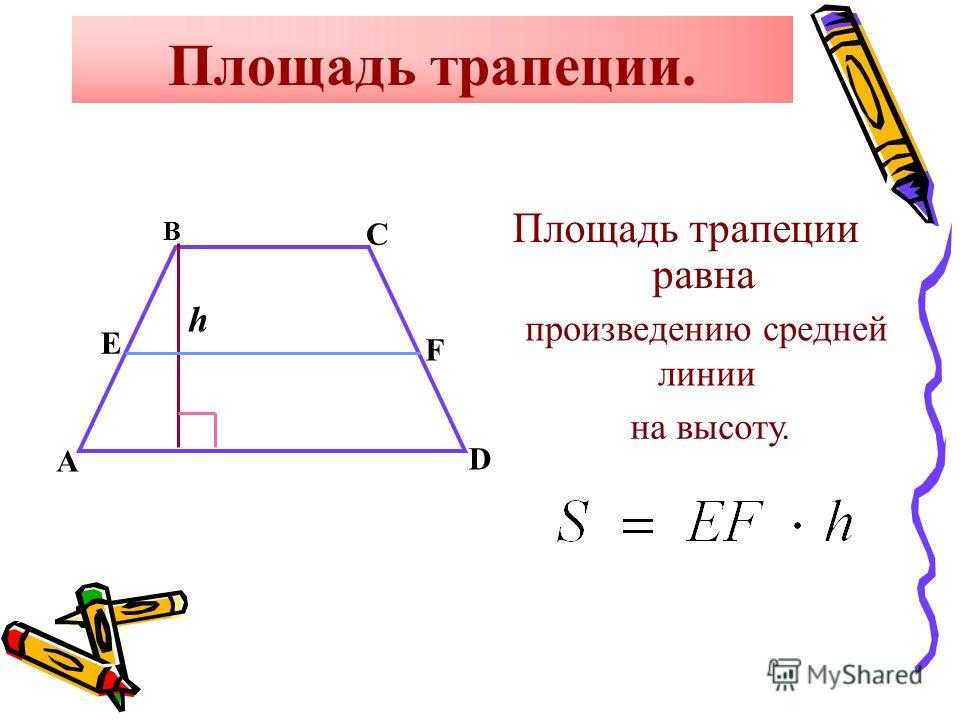
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.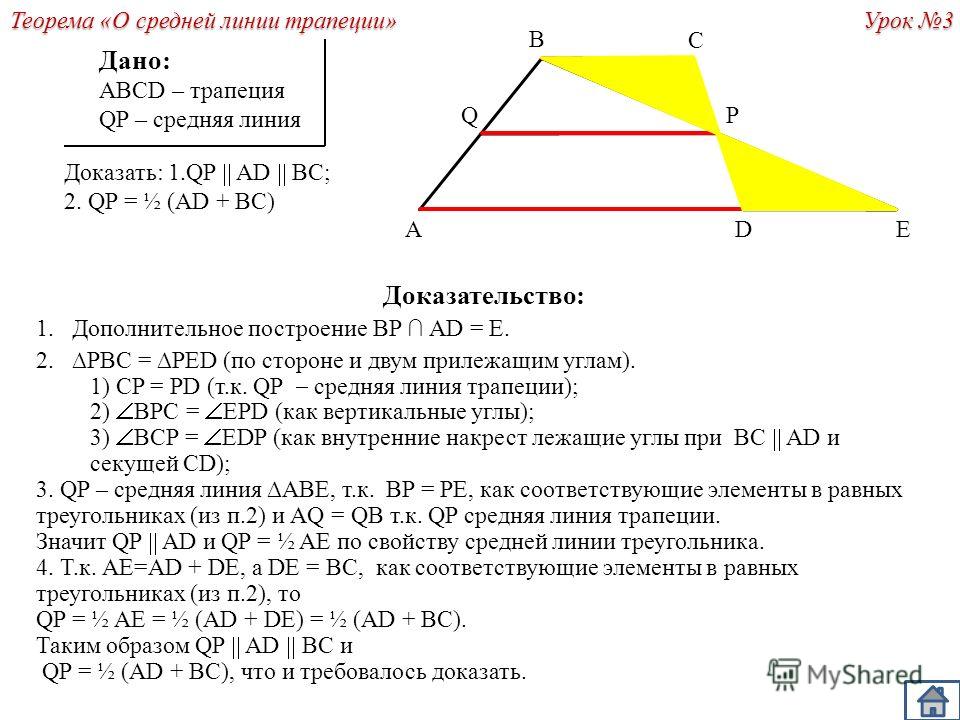
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Площадь трапеции. Приветствую вас! В этой публикации мы рассмотрим указанную формулу. Почему она именно такая и как её понять. Если будет понимание, то и учить её вам нет необходимости. Если же вы просто хотите посмотреть эту формулу и при чём срочно, то сразу можете прокрутить страницу вниз))
Теперь подробно и по порядку.
Трапеция это четырёхугольник, две стороны этого четырёхугольника параллельны, две другие нет. Те, что не параллельны – это основания трапеции. Две другие называются боковыми сторонами.
Если боковые стороны равны, то трапеция называется равнобедренной. Если одна из боковых сторон перпендикулярна основаниям, то такая трапеция называется прямоугольной.
В классическом виде трапецию изображают следующим образом – большее основание находится внизу, соответственно меньшее вверху. Но никто не запрещает изображать её и наоборот. Вот эскизы:
Следующее важное понятие.
Средняя линия трапеции это отрезок, который соединяет середины боковых сторон. Средняя линия параллельна основаниям трапеции и равна их полусумме.
Теперь давайте вникнем глубже. Почему именно так?
Рассмотрим трапецию с основаниями a и b и со средней линией l , и выполним некоторые дополнительные построения: через основания проведём прямые, а через концы средней линии перпендикуляры до пересечения с основаниями:
*Буквенные обозначения вершин и других точек не введены умышленно, чтобы избежать лишних обозначений.
Посмотрите, треугольники 1 и 2 равны по второму признаку равенства треугольников, треугольники 3 и 4 тоже самое. Из равенства треугольников следует равенство элементов, а именно катетов (они обозначены соответственно синим и красным цветом).
Теперь внимание! Если мы мысленно «отрежем» от нижнего основания синий и красный отрезок, то у нас останется отрезок (это сторона прямоугольника) равный средней линии. Далее, если мы «приклеим» отрезанные синий и красный отрезок к верхнему основанию трапеции, то у нас получится также отрезок (это тоже сторона прямоугольника) равный средней линии трапеции.
Уловили? Получается, что сумма оснований будет равна двум средним линиям трапеции:
Посмотреть ещё одно объяснение
Сделаем следующее – построим прямую проходящую через нижнее основание трапеции и прямую, которая пройдёт через точки А и В:
Получим треугольники 1 и 2, они равны по стороне и прилегающим к ней углам (второй признак равенства треугольников). Это означает что полученный отрезок (на эскизе он обозначен синим) равен верхнему основанию трапеции.
Теперь рассмотрим треугольник:
*Средняя линия данной трапеции и средняя линия треугольника совпадают.
Известно, что треугольника равна половине параллельного ей основания, то есть:
Хорошо, разобрались.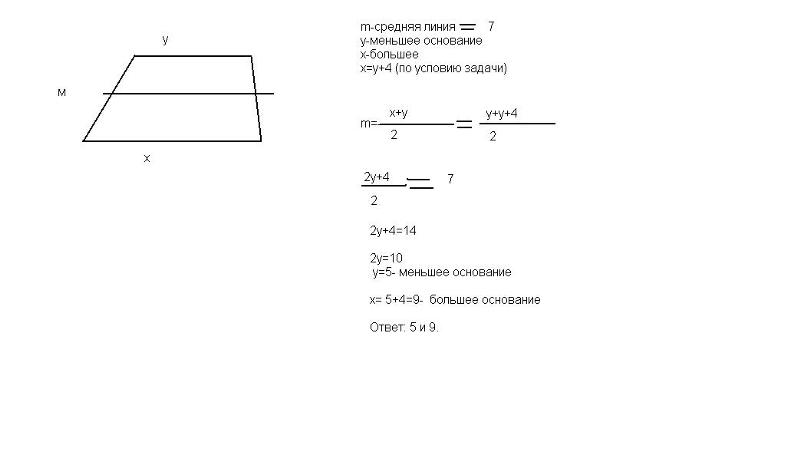
Теперь о площади трапеции.
Площадь трапеции формула:
Говорят: площадь трапеции равна произведению полусуммы её оснований и высоты.
То есть, получается, что она равна произведению средней линии и высоты:
Вы, наверное, уже заметили, что это очевидно. Геометрически это можно выразить так: если мы мысленно отрежем от трапеции треугольники 2 и 4 и положим их соответственно на треугольники 1 и 3:
То у нас получится прямоугольник по площади равный площади нашей трапеции. Площадь этого прямоугольника будет равна произведению средней линии и высоты, то есть можем записать:
Но дело тут не в записи, конечно, а в понимании.
Скачать (посмотреть) материал статьи в формате *pdf
На этом всё. Успеха вам!
С уважением, Александр.
Четырёхугольник, у которого только две стороны параллельны называются трапецией .
Параллельные стороны трапеции называются её основаниями , а те стороны, которые не параллельны, называются боковыми сторонами .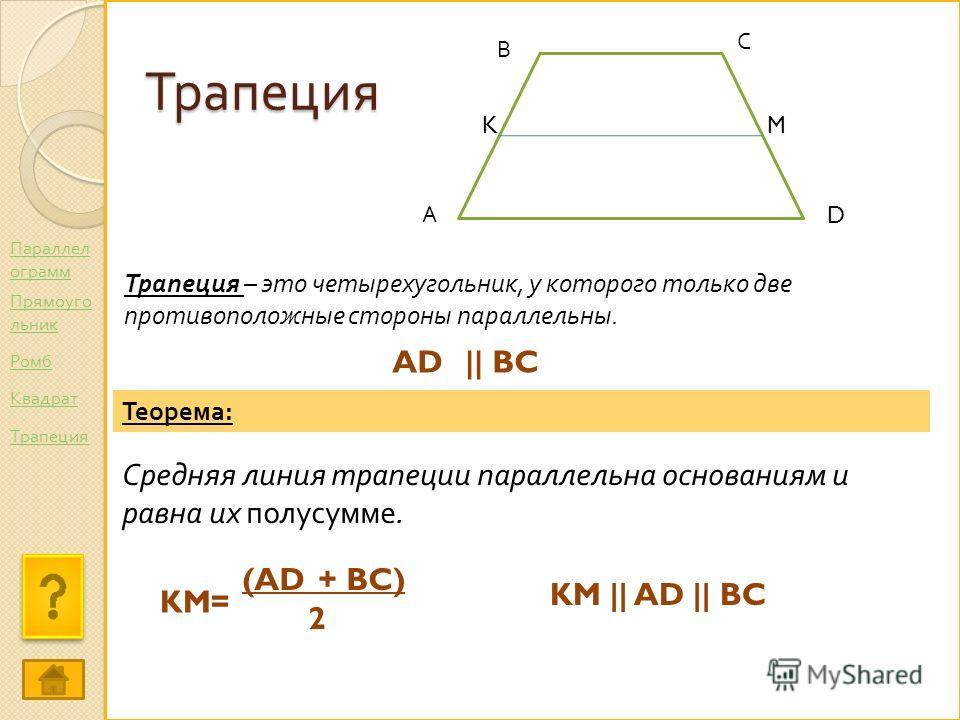
Если боковые стороны равны, то такая трапеция является равнобедренной. Расстояние между основаниями называется высотой трапеции.
Средняя Линия Трапеции
Средняя линия — это отрезок, соединяющий середины боковых сторон трапеции. Средняя линия трапеции параллельна её основаниям.
Теорема:
Если прямая, пересекающая середину одной боковой стороны, параллельна основаниям трапеции, то она делит пополам вторую боковую сторону трапеции.
Теорема:
Длина средней линии равна среднему арифметическому длин её оснований
MN || AB || DC
AM = MD; BN = NC
MN средняя линия, AB и CD — основания, AD и BC — боковые стороны
MN = (AB + DC)/2
Теорема:
Длина средней линии трапеции равна среднему арифметическому длин её оснований.
Основная задача : Доказать, что средняя линия трапеции делит пополам отрезок, концы которого лежат в середине оснований трапеции.
Средняя Линия Треугольника
Отрезок, соединяющий середины двух сторон треугольника, называется средней линией треугольника.
Она параллельна третьей стороне и её длина равна половине длины третьей стороны.
Теорема : Если прямая, пересекающая середину одной стороны треугольника, параллельна другой стороне данного треугольника, то она делит третью сторону пополам.
AM = MC and BN = NC
=>
Применение свойств средней линии треугольника и трапеции
Деление отрезка на определённое количество равных частей.
Задача: Разделить отрезок AB на 5 равных частей.
Решение:
Пусть p это случайный луч, у которого начало это точка А, и который не лежит на прямой AB. Мы последовательно откладываем 5 равных сегментов на p AA 1 = A 1 A 2 = A 2 A 3 = A 3 A 4 = A 4 A 5
Мы соединяем A 5 с B и проводим такие прямые через A 4 , A 3 , A 2 и A 1 , которые параллельны A 5 B. Они пересекают AB соответственно в точках B 4 , B 3 , B 2 и B 1 . Эти точки делят отрезок AB на 5 равных частей. Действительно, из трапеции BB 3 A 3 A 5 мы видим, что BB 4 = B 4 B 3 . Таким же образом, из трапеции B 4 B 2 A 2 A 4 получаем B 4 B 3 = B 3 B 2
В то время как из трапеции B 3 B 1 A 1 A 3 , B 3 B 2 = B 2 B 1 .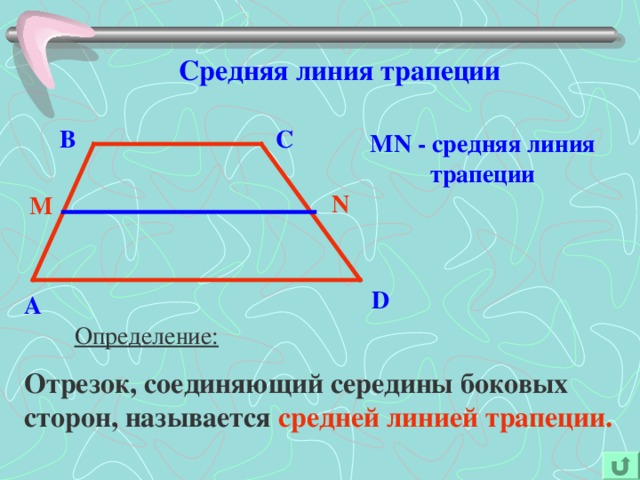
Тогда из B 2 AA 2 следует, что B 2 B 1 = B 1 A. В заключении получаем:
AB 1 = B 1 B 2 = B 2 B 3 = B 3 B 4 = B 4 B
Ясно, что для разделения отрезка AB на другое количество равных частей, нам нужно проецировать то же самое количество равных сегментов на луч p. И далее продолжать вышеописанным способом.
Трапеция, средняя линия трапеции, треугольник. Средняя линия треугольника
Четырёхугольник, у которого только две стороны параллельны называются трапецией .
Параллельные стороны трапеции называются её основаниями , а те стороны, которые не параллельны, называются боковыми сторонами . Если боковые стороны равны, то такая трапеция является равнобедренной. Расстояние между основаниями называется высотой трапеции.
Средняя Линия Трапеции
Средняя линия — это отрезок, соединяющий середины боковых сторон трапеции. Средняя линия трапеции параллельна её основаниям.
Теорема:
Если прямая, пересекающая середину одной боковой стороны, параллельна основаниям трапеции, то она делит пополам вторую боковую сторону трапеции.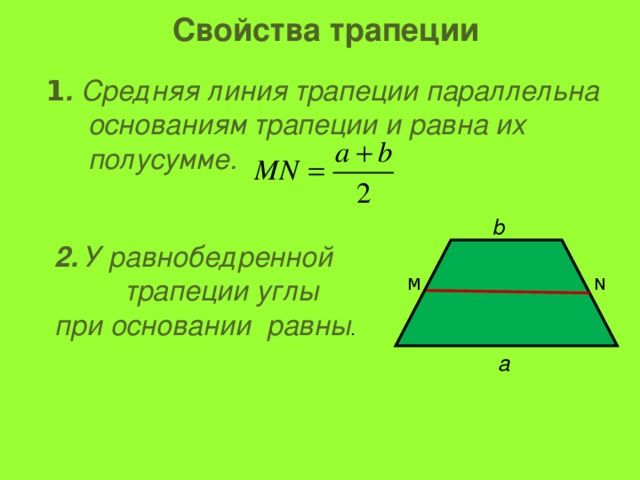
Теорема:
Длина средней линии равна среднему арифметическому длин её оснований
MN || AB || DC
AM = MD; BN = NC
MN средняя линия, AB и CD — основания, AD и BC — боковые стороны
MN = (AB + DC)/2
Теорема:
Длина средней линии трапеции равна среднему арифметическому длин её оснований.
Основная задача : Доказать, что средняя линия трапеции делит пополам отрезок, концы которого лежат в середине оснований трапеции.
Средняя Линия Треугольника
Отрезок, соединяющий середины двух сторон треугольника, называется средней линией треугольника. Она параллельна третьей стороне и её длина равна половине длины третьей стороны.
Теорема : Если прямая, пересекающая середину одной стороны треугольника, параллельна другой стороне данного треугольника, то она делит третью сторону пополам.
AM = MC and BN = NC
=>
Применение свойств средней линии треугольника и трапеции
Деление отрезка на определённое количество равных частей.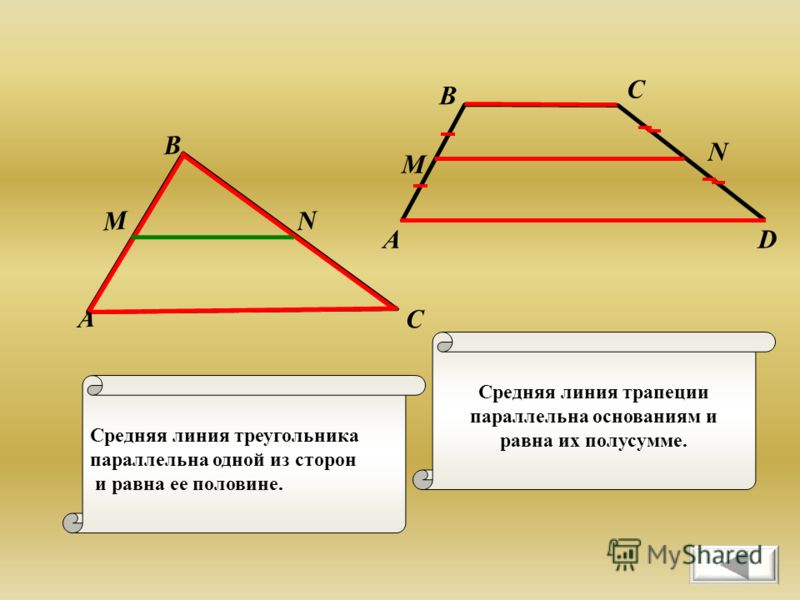
Задача: Разделить отрезок AB на 5 равных частей.
Решение:
Пусть p это случайный луч, у которого начало это точка А, и который не лежит на прямой AB. Мы последовательно откладываем 5 равных сегментов на p AA 1 = A 1 A 2 = A 2 A 3 = A 3 A 4 = A 4 A 5
Мы соединяем A 5 с B и проводим такие прямые через A 4 , A 3 , A 2 и A 1 , которые параллельны A 5 B. Они пересекают AB соответственно в точках B 4 , B 3 , B 2 и B 1 . Эти точки делят отрезок AB на 5 равных частей. Действительно, из трапеции BB 3 A 3 A 5 мы видим, что BB 4 = B 4 B 3 . Таким же образом, из трапеции B 4 B 2 A 2 A 4 получаем B 4 B 3 = B 3 B 2
В то время как из трапеции B 3 B 1 A 1 A 3 , B 3 B 2 = B 2 B 1 .
Тогда из B 2 AA 2 следует, что B 2 B 1 = B 1 A. В заключении получаем:
AB 1 = B 1 B 2 = B 2 B 3 = B 3 B 4 = B 4 B
Ясно, что для разделения отрезка AB на другое количество равных частей, нам нужно проецировать то же самое количество равных сегментов на луч p. И далее продолжать вышеописанным способом.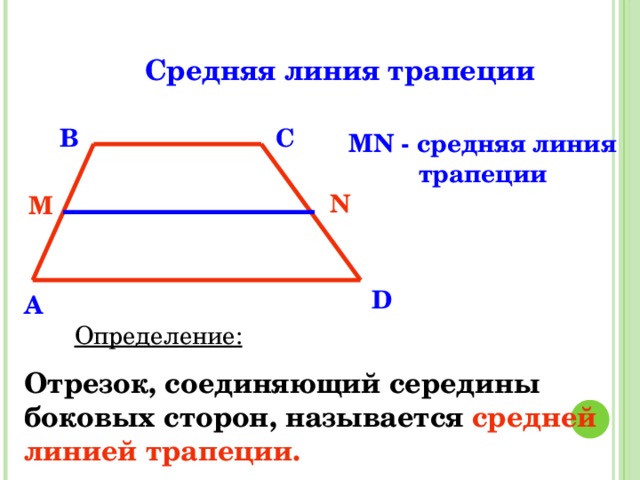
Средняя линия треугольника. Здравствуйте, друзья! Сегодня теоретический материал, связан он с треугольником. В составе экзамена имеется группа заданий, в которых используется свойство его средней линии. Причём не только в задачах с треугольниками, но и с трапециями. Была , в которой сии факты я предлагал просто запомнить, теперь подробнее…
Что такое средняя линия треугольника и каковы её свойства?
Определение. Средняя линия треугольника – это отрезок, соединяющий середины сторон треугольника.
Понятно, что средних линий в треугольнике три. Покажем их:
Без всяких доказательств вы уже, наверное, заметили, что все четыре образованные треугольника равны. Это так, но подробнее об этом поговорим далее.
Теорема . Средняя линия треугольника, соединяющая середины двух данных сторон, параллельна третьей стороне и равна ее половине.
Доказательство:
1.
Давайте рассмотрим треугольники BMN и BAC. По условию у нас BM=MA, BN=NC. Можем записать:
Следовательно треугольники подобны по двум пропорциональным сторонам и углу между ними (второй признак подобия). Что из этого следует? А то что:
По признаку параллельности прямых MN||AC.
2. Также из подобия треугольников следует, что
То есть MN в два раза меньше. Доказано!
Решим типичную задачу.
В треугольнике ABC точки M, N, K – середины сторон AB, BC, AC. Найти периметр треугольника ABC, если MN=12, MK=10, KN=8.
Решение. Конечно, прежде всего следует проверить существование треугольника MNK (а значит и существование треугольника АВС). Сумма двух меньших сторон должна быть более третьей стороны, записываем 10+8>12. Выполнятся, следовательно треугольник существует.
Построим эскиз:
Таким образом периметр треугольника АВС равен 24+20+16=60.
*Теперь подробнее о треугольниках полученных при построении всех трёх средних линий.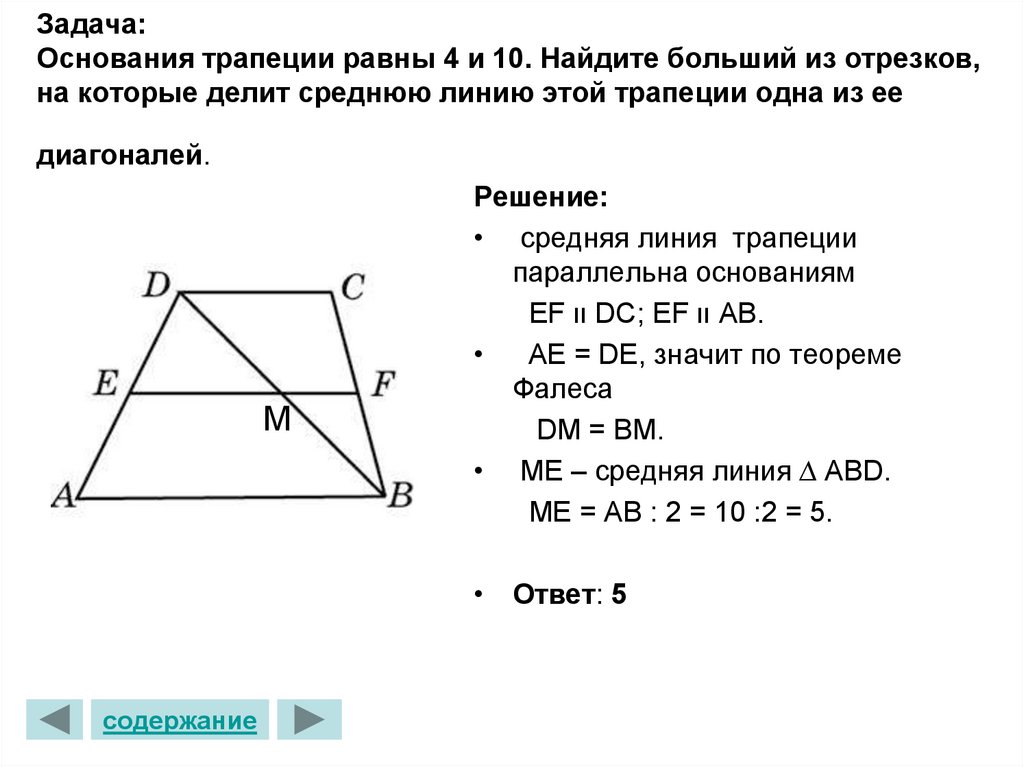
Их равенство легко доказывается. Посмотрите:
Равны они по трём сторонам. Конечно, и другие признаки здесь применимы. Получаем, что
Как это свойство используется в заданиях включённых в состав экзамена? Особо хочется заострить внимание на задачах по стереометрии. Есть такие типы, в которых речь идет о треугольной призме.
Например, сказано что плоскость проходит через середины сторон основания и она параллельна третьему ребру основания. Ставятся вопросы о изменении площади поверхности призмы, её объёма и другие.
Так вот. Зная и понимая информацию изложенную выше вы сразу же определите, что эта плоскость отсекает от основания указанной призмы одну четвёртую часть и задачу решите устно. Вот с такими задачами.
На этом всё! Всего доброго!
Скачать материал статьи
С уважением, Александр Крутицких.
Понятие средней линии треугольника
Введем понятие средней линии треугольника.
Определение 1
Это отрезок, соединяющий середины двух сторон треугольника (Рис.
1).
Рисунок 1. Средняя линия треугольника
Теорема о средней линии треугольника
Теорема 1
Средняя линия треугольника параллельна одной из его сторон и равна её половине.
Доказательство.
Пусть нам дан треугольник $ABC$. $MN$ — средняя линия (как на рисунке 2).
Рисунок 2. Иллюстрация теоремы 1
Так как $\frac{AM}{AB}=\frac{BN}{BC}=\frac{1}{2}$, то треугольники $ABC$ и $MBN$ подобны по второму признаку подобия треугольников. Значит
Также, отсюда следует, что $\angle A=\angle BMN$, значит $MN||AC$.
Теорема доказана.
Следствия из теоремы о средней линии треугольника
Следствие 1: Медианы треугольника пересекаются в одной точке и делятся точкой пересечения в отношении $2:1$ начиная с вершины.
Доказательство.
Рассмотрим треугольник $ABC$, где ${AA}_1,\ {BB}_1,\ {CC}_1$ его медианы. Так как медианы делят стороны пополам. Рассмотрим среднюю линию $A_1B_1$ (Рис. 3).
Рисунок 3.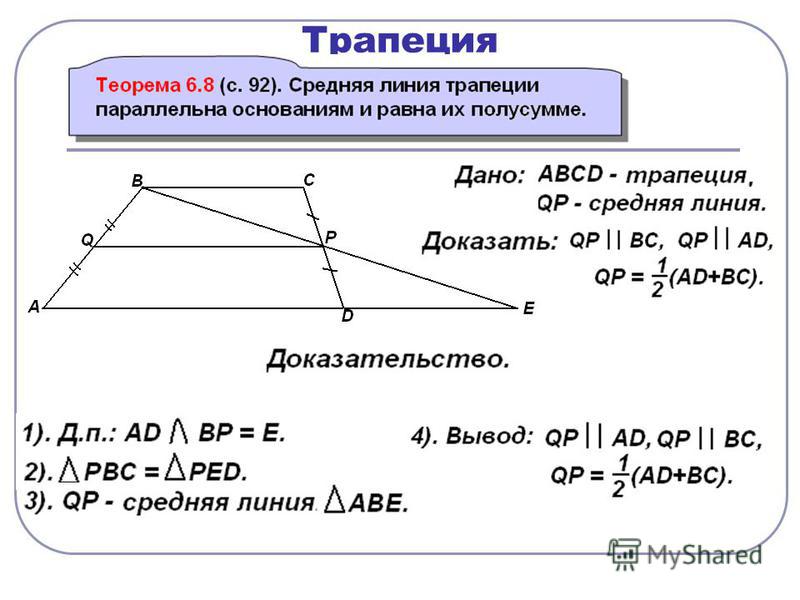
Иллюстрация следствия 1
По теореме 1, $AB||A_1B_1$ и $AB=2A_1B_1$, следовательно, $\angle ABB_1=\angle BB_1A_1,\ \angle BAA_1=\angle AA_1B_1$. Значит треугольники $ABM$ и $A_1B_1M$ подобны по первому признаку подобия треугольников. Тогда
Аналогично доказывается, что
Теорема доказана.
Следствие 2: Три средние линии треугольника делят его на 4 треугольника, подобных исходному треугольнику с коэффициентом подобия $k=\frac{1}{2}$.
Доказательство.
Рассмотрим треугольник $ABC$ со средними линиями $A_1B_1,\ {\ A}_1C_1,\ B_1C_1$ (рис. 4)
Рисунок 4. Иллюстрация следствия 2
Рассмотрим треугольник $A_1B_1C$. Так как $A_1B_1$ — средняя линия, то
Угол $C$ — общий угол этих треугольников. Следовательно, треугольники $A_1B_1C$ и $ABC$ подобны по второму признаку подобия треугольников с коэффициентом подобия $k=\frac{1}{2}$.
Аналогично доказывается, что треугольники $A_1C_1B$ и $ABC$, и треугольники $C_1B_1A$ и $ABC$ подобны с коэффициентом подобия $k=\frac{1}{2}$.
Рассмотрим треугольник $A_1B_1C_1$. Так как $A_1B_1,\ {\ A}_1C_1,\ B_1C_1$ — средние линии треугольника, то
Следовательно, по третьему признаку подобия треугольников, треугольники $A_1B_1C_1$ и $ABC$ подобны с коэффициентом подобия $k=\frac{1}{2}$.
Теорема доказана.
Примеры задачи на понятие средней линии треугольника
Пример 1
Дан треугольник со сторонами $16$ см, $10$ см и $14$ см. Найти периметр треугольника , вершины которого лежат в серединах сторон данного треугольника.
Решение.
Так как вершины искомого треугольника лежат в серединах сторон данного треугольника, то его стороны — средние линии исходного треугольника. По следствию 2, получим, что стороны искомого треугольника равны $8$ см, $5$ см и $7$ см.
Ответ: $20$ см.
Пример 2
Дан треугольник $ABC$. Точки $N\ и\ M$ — середины сторон $BC$ и $AB$ соответственно (Рис. 5).
Рисунок 5.
Периметр треугольника $BMN=14$ см.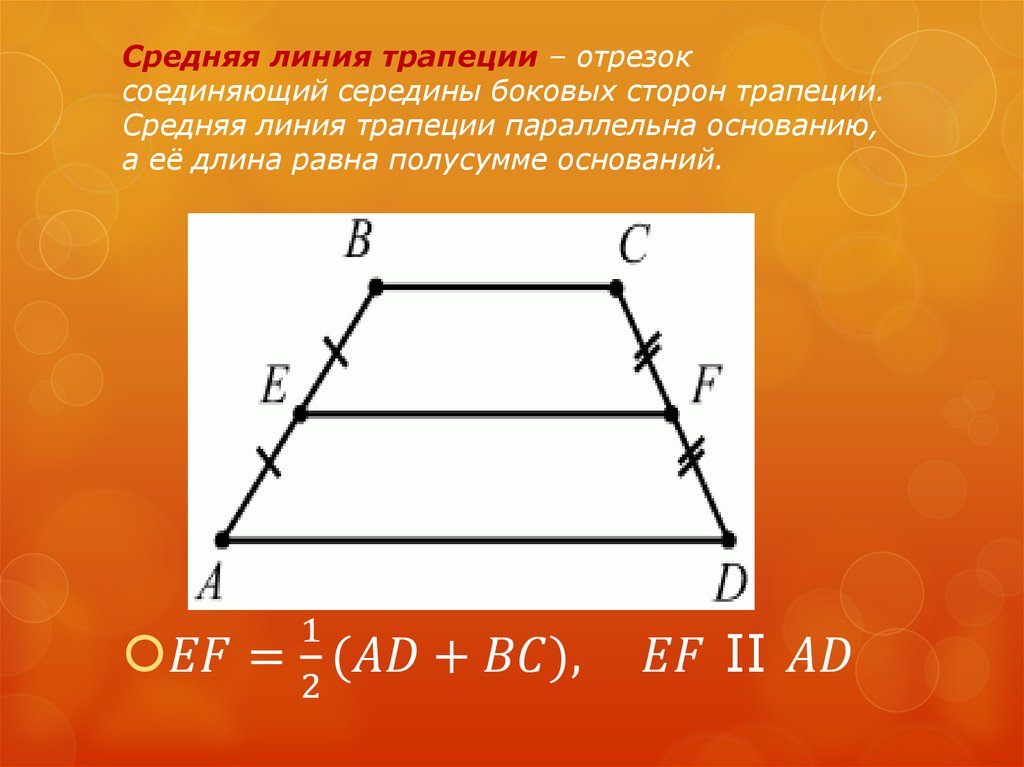
Найти периметр треугольника $ABC$.
Решение.
Так как $N\ и\ M$ — середины сторон $BC$ и $AB$, то $MN$ — средняя линия. Значит
По теореме 1, $AC=2MN$. Получаем:
определение, как найти, свойства, формулы, задачи
Содержание:
- Средняя линия трапеции – что это?
- Свойства
-
Как вычислить, основные формулы
- Через основания
- Через основание, высоту и углы при нижнем основании
- Через диагонали, высоту и угол между диагоналями
- Через площадь и высоту
- Примеры задач
Содержание
- Средняя линия трапеции – что это?
- Свойства
-
Как вычислить, основные формулы
- Через основания
- Через основание, высоту и углы при нижнем основании
- Через диагонали, высоту и угол между диагоналями
- Через площадь и высоту
- Примеры задач
Средняя линия трапеции – что это?
Средняя линия трапеции – отрезок, соединяющий середины боковых сторон трапеции.
Свойства
- Параллельна обоим основаниям трапеции.
- Вычисляется как половина суммы оснований.
- Разбивает трапецию на две, площади которых соотносятся как \(\frac{S_1}{S_2}=\frac{3\,BC+AD}{BC+3\,AD}\)
Как вычислить, основные формулы
Через основания
Источник: formula.ru\(m=\frac{a+b}2\)
Где \(a\) – нижнее основание, \(b\) – верхнее, \(m\) – средняя линия.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Через основание, высоту и углы при нижнем основании
Источник: formula.ru\(m=a-h\times\frac{ctg\alpha+ctg\beta}2\)
\(m=b+h\times\frac{ctg\alpha+ctg\beta}2\)
Где \(a\) – нижнее основание, \(b\) – верхнее, \(m\) – средняя линия, \(h\) – высота, \(\alpha,\beta\) – углы при нижнем основании.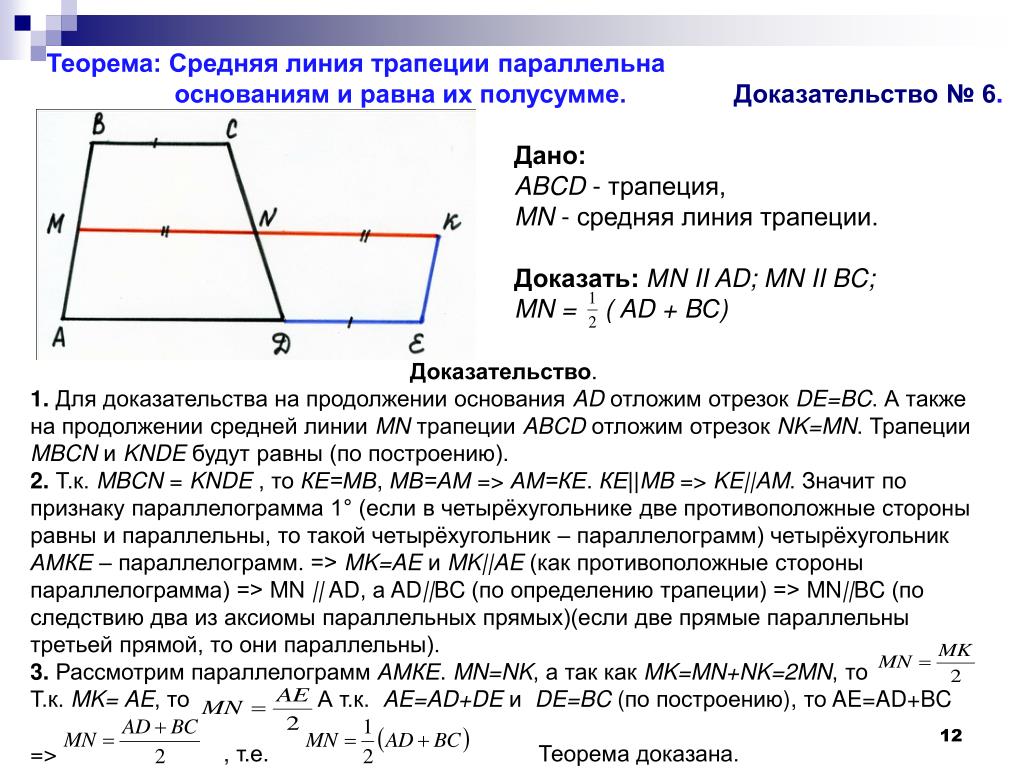
\circ\)
Рассмотрим \(\angle ABH\)
\(BH=\frac12AB=3,5\)
\(S_{ABCD}=\frac{AD+BC}2\times BH=\frac{6+18}2\times3,5=42\)
Ответ: 42
Задача 2
Основания трапеции равны 4 и 10. Чему равен больший из отрезков, на которые делит среднюю линию этой трапеции одна из ее диагоналей?
Источник: ege-study.ruСредняя линия трапеции ABCD так же является средней линией треугольников ABC и ACD т.к. проходит через середину одной стороны и параллельна основанию. Значит, из треугольника ACD x = 5.
Ответ: 5
Задача 3
ABCD – трапеция, BC = 2, AD = 3, PQ – средняя линия, BD и AC – диагонали. Найти MN.
Источник: ege-study.ru\(PQ=\frac{BC+AD}2=2,5\)
Отрезок MN лежит на средней линии трапеции. Докажем: PM и NQ средние линии треугольников ABC и BCD, значит M и N середины соответственно AC и BD. Из треугольника ABC находим длину PM = 1, из треугольника BCD находим NQ = 1, следовательно MN = 2,5 — 1 — 1 = 0,5
Ответ: 0,5
Насколько полезной была для вас статья?
У этой статьи пока нет оценок.
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Поиск по содержимому
Как найти большую сторону средней линии трапеции. Трапеция
Понятие средней линии трапеции
Для начала вспомним, какая фигура называется трапецией.
Определение 1
Трапеция – это четырехугольник, у которого две стороны параллельны, а две другие не параллельны.
При этом параллельные стороны называются основаниями трапеции, а не параллельные — сторонами трапеции.
Определение 2
Средняя линия трапеции — отрезок, соединяющий середины сторон трапеции.
Теорема о средней линии трапеции
Теперь введем теорему о средней линии трапеции и докажем ее векторным методом.
Теорема 1
Средняя линия трапеции параллельна основаниям и равна их полусумме.
Доказательства.
Пусть дана трапеция $ABCD$ с основаниями $AD\ и \BC$. И пусть $MN$ будет средней линией этой трапеции (рис.
1).
Рис. 1. Средняя линия трапеции
Докажем, что $ MN || AD\и \MN=\frac(AD+BC)(2)$.
Рассмотрим вектор $\overrightarrow(MN)$. Затем мы используем правило многоугольника для добавления векторов. С одной стороны получаем, что
С другой стороны
Складываем два последних равенства, получаем
Так как $M$ и $N$ — середины сторон трапеции, то будем иметь
Получаем:
Отсюда
Из того же равенства (поскольку $\overrightarrow(BC)$ и $\overrightarrow(AD)$ сонаправлены, а значит коллинеарны), получаем, что $MN || АД $.
Теорема доказана.
Примеры заданий на понятие средней линии трапеции
Пример 1
Стороны трапеции равны $15\см$ и $17\см$ соответственно. Периметр трапеции равен 52$\см$. Найдите длину средней линии трапеции.
Решение.
Обозначим среднюю линию трапеции через $n$.
Сумма сторон равна
Следовательно, так как периметр равен 52$\см$, сумма оснований равна
Отсюда по теореме 1 получаем
Ответ: $ 10 \см $.
Пример 2
Концы диаметра окружности удалены от ее касательной на $9$ см и $5$ см соответственно. Найдите диаметр этого круга.
Решение.
Дана окружность с центром в точке $O$ и диаметром $AB$. Проведите касательную $l$ и постройте расстояния $AD=9\см$ и $BC=5\см$. Нарисуйте радиус $OH$ (рис. 2).
Рисунок 2
Так как $AD$ и $BC$ — расстояния до касательной, то $AD\bot l$ и $BC\bot l$ и так как $OH$ — радиус, то $ ОН \bot l$, следовательно, $ОН | \\ слева | AD \ справа || БК $. Из всего этого получаем, что $ABCD$ — это трапеция, а $OH$ — ее средняя линия. По теореме 1 получаем
Ваша конфиденциальность важна для нас. По этой причине мы разработали Политику конфиденциальности, в которой описывается, как мы используем и храним вашу информацию. Пожалуйста, ознакомьтесь с нашей политикой конфиденциальности и сообщите нам, если у вас есть какие-либо вопросы.
Сбор и использование личной информации
Личная информация относится к данным, которые могут быть использованы для идентификации конкретного лица или для связи с ним.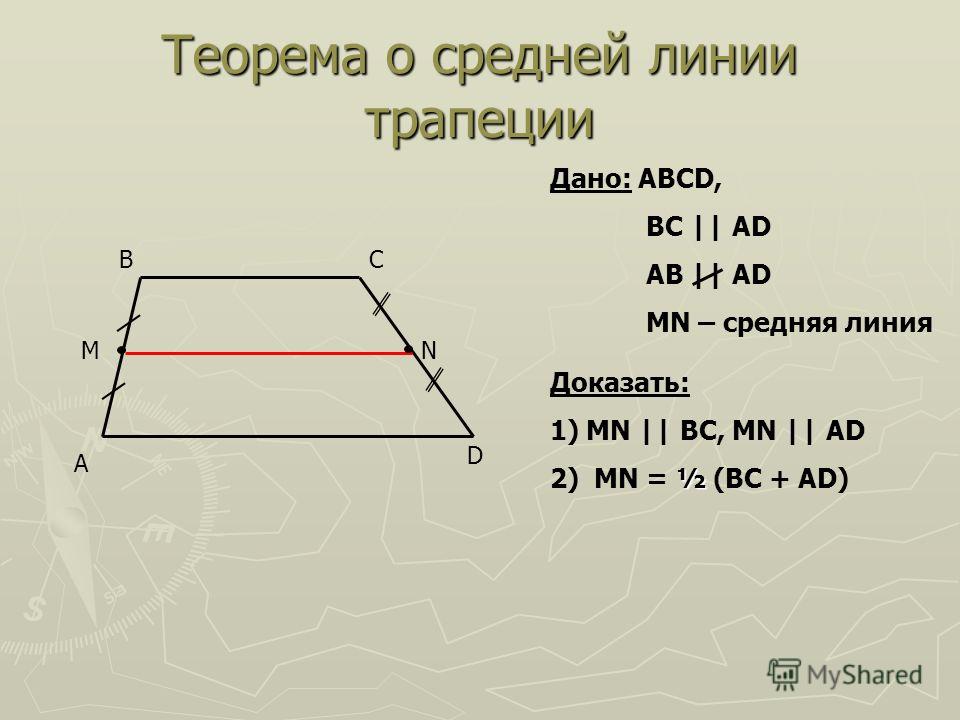
Вас могут попросить предоставить личную информацию в любое время, когда вы свяжетесь с нами.
Ниже приведены некоторые примеры типов личной информации, которую мы можем собирать, и того, как мы можем использовать такую информацию.
Какую личную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваше имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу личную информацию:
- Личная информация, которую мы собираем, позволяет нам связываться с вами и сообщать об уникальных предложениях, рекламных акциях и других событиях и предстоящих событиях.
- Время от времени мы можем использовать вашу личную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать личную информацию для внутренних целей, таких как проведение аудита, анализа данных и различных исследований, чтобы улучшить предоставляемые нами услуги и предоставить вам рекомендации относительно наших услуг.
- Если вы участвуете в розыгрыше призов, конкурсе или аналогичном рекламном мероприятии, мы можем использовать предоставленную вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от вас информацию третьим лицам.
Исключения:
- В случае необходимости — в соответствии с законодательством, судебной системой, в судебном порядке и/или на основании публичных запросов или запросов государственных органов в Российской Федерации — раскрыть вашу личную информацию. Мы также можем раскрыть информацию о вас, если решим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка или других общественно важных случаях.
- В случае реорганизации, слияния или продажи мы можем передать личную информацию, которую мы собираем, соответствующему третьему лицу, правопреемнику.
Защита личной информации
Мы принимаем меры предосторожности, в том числе административные, технические и физические, для защиты вашей личной информации от потери, кражи и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.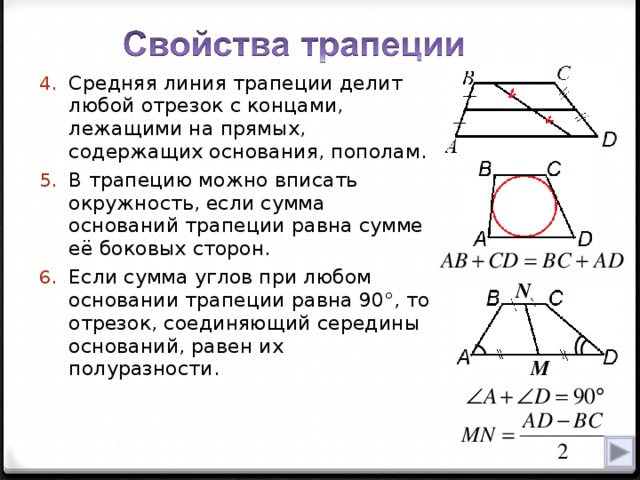
Уважайте вашу конфиденциальность на уровне компании
В целях обеспечения сохранности вашей личной информации мы доводим до сведения наших сотрудников правила конфиденциальности и безопасности, и строго следим за выполнением мер по обеспечению конфиденциальности.
В этой статье для вас сделана очередная подборка заданий с трапецией. Условия так или иначе связаны с его средней линией. Типы задач взяты из открытого банка типовых задач. При желании вы можете освежить свои теоретические знания. В блоге уже были рассмотрены задачи, с которыми также связаны условия. Кратко о средней линии:
Средняя линия трапеции соединяет середины сторон. Он параллелен основаниям и равен их полусумме.
Перед решением задач рассмотрим теоретический пример.
Дана трапеция ABCD. Диагональ AC, пересекающаяся со средней линией, образует точку K, диагональ BD — точку L. Докажите, что отрезок KL равен половине разности оснований.
Прежде всего отметим тот факт, что средняя линия трапеции делит пополам любой отрезок, концы которого лежат на ее основаниях. Этот вывод напрашивается сам собой. Представьте себе отрезок, соединяющий две точки основания, он разорвет эту трапецию на две другие. Получается, что отрезок, параллельный основаниям трапеции и проходящий через середину стороны другой стороны, пройдет через ее середину.
Основан также на теореме Фалеса:
Если на одной из двух прямых отложить последовательно несколько равных отрезков и провести через их концы параллельные прямые, пересекающие вторую прямую, то они будут отсекать равные отрезки на второй линии.
То есть в данном случае К — середина АС, а L — середина BD. Следовательно, ЕК — средняя линия треугольника ABC, LF — средняя линия треугольника DCB. По свойству средней линии треугольника:
Теперь мы можем выразить отрезок KL по основаниям:
Доказано!
Этот пример приведен не просто так.
В задачах для самостоятельного решения есть именно такая задача. Только не сказано, что отрезок, соединяющий середины диагоналей, лежит на средней линии. Рассмотрим задачи:
27819. Найдите среднюю линию трапеции, если ее основания равны 30 и 16.
Рассчитывается по формуле:
27820. Средняя линия трапеции равна 2, а меньшее основание равно 2 равно 18. Найдите большее основание трапеции.
Выразим большее основание:
Таким образом:
27836. Перпендикуляр, опущенный из вершины тупого угла к большему основанию равнобедренной трапеции, делит ее на части, имеющие длины 10 и 4. Найдите среднюю линию этой трапеции.
Чтобы найти среднюю линию нужно знать основания. Основание АВ найти легко: 10+4=14. Найдите DC.
Построить второй перпендикуляр DF:
Сегменты AF, FE и EB будут иметь номера 4, 6 и 4 соответственно. Почему?
В равнобедренной трапеции перпендикуляры, опущенные к большему основанию, разбивают ее на три отрезка.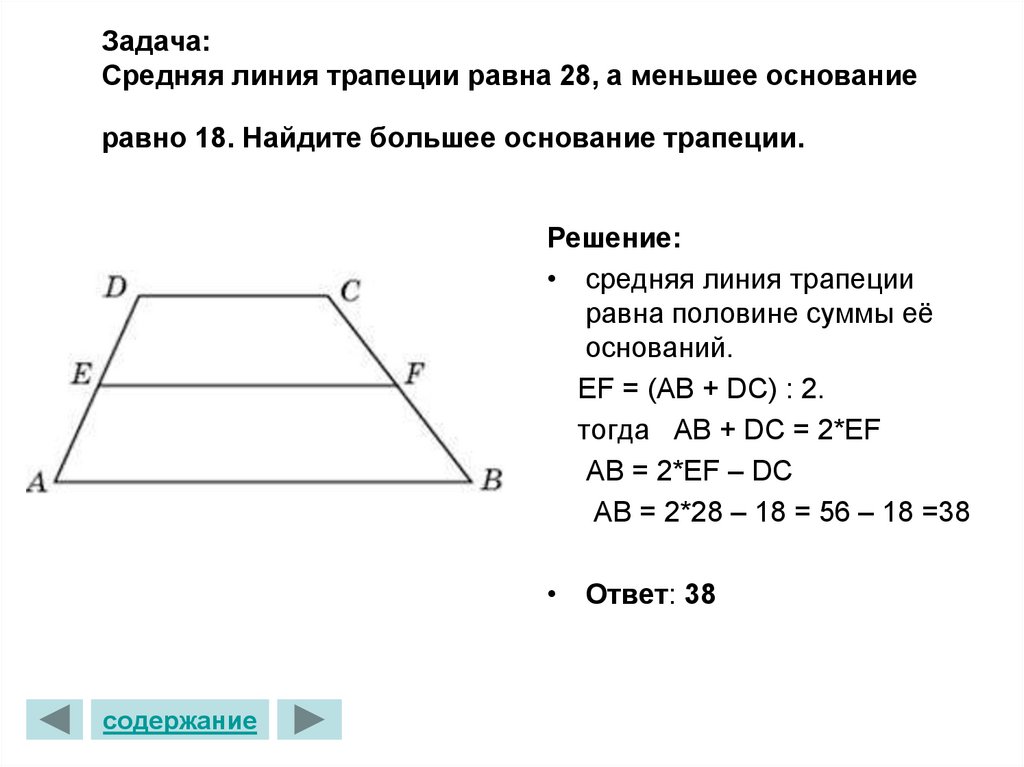
Два из них, являющиеся катетами отсеченных прямоугольных треугольников, равны между собой. Третий отрезок равен меньшему основанию, так как при построении указанных высот образуется прямоугольник, а у прямоугольника противоположные стороны равны. В этой задаче:
Значит DC = 6. Вычисляем:
27839. Основание трапеции 2:3, а центральная линия 5. Найдите меньшее основание.
Введем коэффициент пропорциональности x. Тогда АВ = 3х, ДС = 2х. Мы можем написать:
Следовательно, меньшее основание равно 2∙2 = 4.
27840. Периметр равнобедренной трапеции равен 80, ее средняя линия равна стороне. Найдите сторону трапеции.
Исходя из условия можно написать:
Если обозначить среднюю линию через значение x, то получим:
Второе уравнение уже можно записать так:
27841. Средняя линия трапеции равна 7, а одно из ее оснований больше другого на 4. Найдите большее основание трапеции.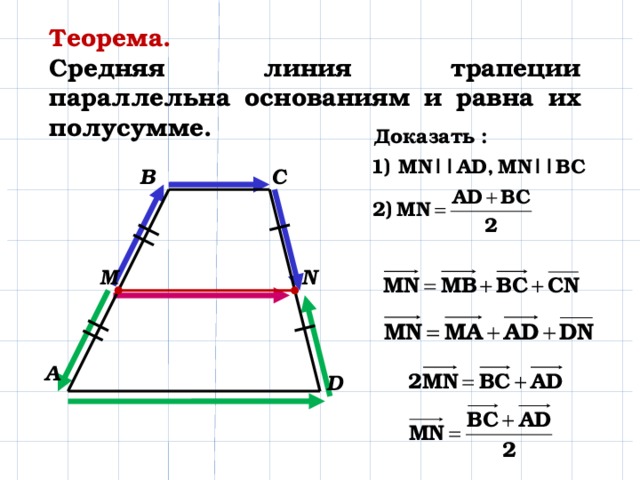
Обозначим меньшее основание (DC) как x, тогда большее (AB) будет x + 4. Мы можем записать
Мы получили, что меньшее основание равно пяти, поэтому большее равно 9.
27842. Средняя линия трапеции равна 12. Одна из диагоналей делит ее на два отрезка, разница которых равна 2. Найдите большее основание трапеции.
Мы можем легко найти большее основание трапеции, если рассчитаем сегмент EO. Это средняя линия в треугольнике ADB, а AB = 2∙EO.
Что у нас есть? Говорят, что средняя линия равна 12, а разница между отрезками EO и OF равна 2. Мы можем написать два уравнения и решить систему:
Понятно, что в данном случае без вычислений можно выбрать пару чисел, это 5 и 7. Но, тем не менее, решим систему:
Значит ЕО = 12–5 = 7. Таким образом, большее основание равно AB = 2 ∙ EO = 14.
27844. В равнобедренной трапеции диагонали перпендикулярны. Высота трапеции равна 12. Найдите ее среднюю линию.
Сразу отметим, что высота, проведенная через пересечение диагоналей в равнобедренной трапеции, лежит на оси симметрии и делит трапецию на две равные прямоугольные трапеции, то есть основания этой высоты делятся пополам .
Казалось бы, для вычисления средней линии надо найти основу. Тут возникает небольшой тупик… Как, зная высоту, в таком случае вычислить основания? Но ни как! Таких трапеций с фиксированной высотой и диагоналями, пересекающимися под углом 90 градусов, много. Как быть
Посмотрите на формулу средней линии трапеции. Ведь нам не обязательно знать сами основания, достаточно узнать их сумму (или полусумму). Мы можем сделать это.
Поскольку диагонали пересекаются под прямым углом, образуются равнобедренные прямоугольные треугольники с высотой EF:
Из вышеизложенного следует, что FO = DF = FC, а OE = AE = EB. Теперь запишем, чему равна высота, выраженная через отрезки DF и AE:
Значит средняя линия 12.
* В общем, это задача, как вы понимаете, для устного счета .
Но я уверен, что представленное подробное объяснение необходимо. И так… Если посмотреть на рисунок (при условии соблюдения угла между диагоналями при построении), сразу бросаются в глаза равенства FO=DF=FC и OE=AE=EB.
В составе прототипов также есть виды заданий с трапециями. Строится на листе в клеточку и нужно найти среднюю линию, сторона клеточки обычно равна 1, но может быть и другое значение.
27848. Найдите среднюю линию трапеции Abcd , если стороны квадратных клеток равны 1.
Все просто, вычисляем основания по ячейкам и используем формулу: (2+4)/2\ u003d 3
Если базы строятся под углом к ячейке сетки, то есть два пути. Например!
Трапеция — это частный случай четырехугольника, у которого одна пара сторон параллельна. Термин «трапеция» происходит от греческого слова τράπεζα, означающего «стол», «стол». В этой статье мы рассмотрим виды трапеций и их свойства. Кроме того, мы разберемся, как рассчитать отдельные элементы данного примера, диагональ равнобедренной трапеции, среднюю линию, площадь и т.
д. Материал изложен в стиле элементарной популярной геометрии, то есть в легкодоступной форме. доступная форма.
Общая информация
Сначала разберемся, что такое четырехугольник. Эта фигура является частным случаем многоугольника, содержащего четыре стороны и четыре вершины. Две вершины четырехугольника, не являющиеся смежными, называются противоположными. То же самое можно сказать и о двух несмежных сторонах. Основные виды четырехугольников – параллелограмм, прямоугольник, ромб, квадрат, трапеция и дельтовидная форма.
Итак, вернемся к трапеции. Как мы уже говорили, на этой фигуре две стороны параллельны. Они называются базами. Две другие (непараллельные) — стороны. В материалах экзаменов и различных контрольных очень часто можно встретить задачи, связанные с трапециями, решение которых часто требует от студента знаний, не предусмотренных программой. Школьный курс геометрии знакомит учащихся со свойствами углов и диагоналей, а также со средней линией равнобедренной трапеции.
Но, помимо этого, упомянутая геометрическая фигура имеет и другие особенности. Но о них чуть позже…
Типы трапеций
Есть много типов этой фигуры. Однако чаще всего принято рассматривать две из них – равнобедренную и прямоугольную.
1. Прямоугольной трапецией называется фигура, у которой одна из сторон перпендикулярна основаниям. У нее два угла всегда равны девяноста градусам.
2. Равнобедренная трапеция – геометрическая фигура, у которой стороны равны. Это означает, что углы при основаниях также попарно равны.
Основные принципы исследования свойств трапеций
Основным принципом является использование так называемого задачного подхода. На самом деле нет необходимости вводить в теоретический курс геометрии новые свойства этой фигуры. Их можно обнаружить и сформулировать в процессе решения различных задач (лучше системных). При этом очень важно, чтобы преподаватель знал, какие задачи необходимо ставить перед учащимися в тот или иной момент в процессе обучения.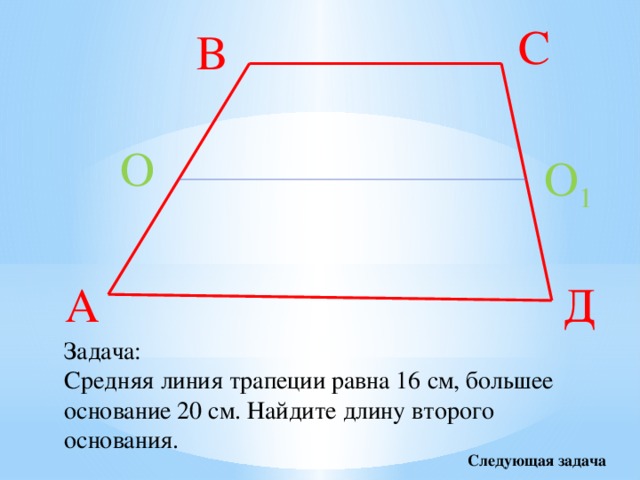
При этом каждое свойство трапеции может быть представлено как ключевая задача в системе задач.
Второй принцип – так называемая спиральная организация изучения «замечательных» свойств трапеции. Это предполагает возврат в процессе обучения к отдельным признакам данной геометрической фигуры. Это облегчает запоминание учащимися. Например, свойство четырех точек. Это можно доказать как при изучении подобия, так и впоследствии с помощью векторов. А равноудаленность треугольников, прилегающих к боковым сторонам фигуры, можно доказать, применяя не только свойства треугольников с равными высотами, проведенных к сторонам, лежащим на одной прямой, но и используя формулу S = 1/2 ( аб*сина). Кроме того, можно работать на вписанной трапеции или прямоугольном треугольнике на описанной трапеции и т. д.
Использование «внеклассных» особенностей геометрической фигуры в содержании школьного курса – задача технологии их обучения. Постоянное обращение к изучаемым свойствам при прохождении других тем позволяет учащимся больше узнать о трапеции и обеспечивает успешность решения поставленных задач.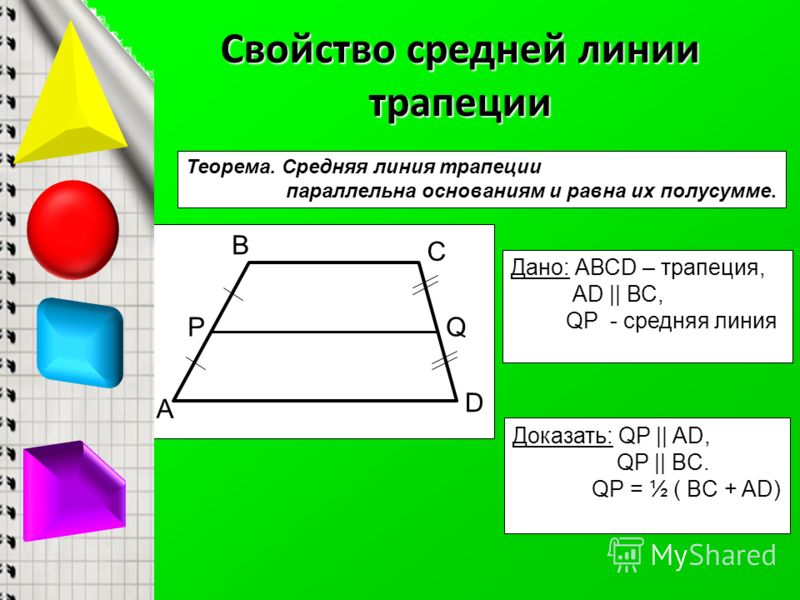
Итак, приступим к изучению этой замечательной фигуры.
Элементы и свойства равнобедренной трапеции
Как мы уже отмечали, в этой геометрической фигуре стороны равны. Его также называют правильной трапецией. Но чем он так примечателен и почему получил такое название? К особенностям этой фигуры можно отнести то, что у нее равны стороны и углы при основаниях, а также диагонали. Кроме того, сумма углов равнобедренной трапеции равна 360 градусов. Но это еще не все! Из всех известных трапеций только вокруг равнобедренной можно описать окружность. Это связано с тем, что сумма противоположных углов этой фигуры равна 180 градусам, и только при этом условии мы можем описать окружность вокруг четырехугольника. Следующее свойство рассматриваемой геометрической фигуры состоит в том, что расстояние от вершины основания до проекции противоположной вершины на линию, содержащую это основание, будет равно средней линии.
Теперь разберемся, как найти углы равнобедренной трапеции.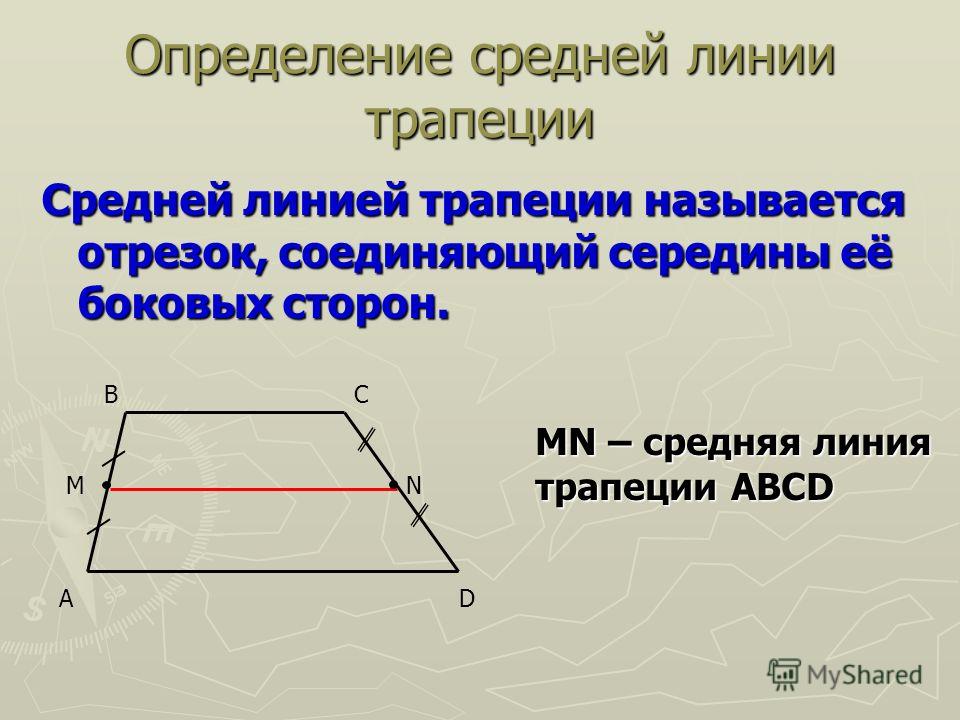
Рассмотрим решение этой задачи при условии, что известны размеры сторон фигуры.
Решение
Обычно четырехугольник принято обозначать буквами A, B, C, D, где BS и AD — основания. У равнобедренной трапеции стороны равны. Будем считать, что их размер равен X, а размеры оснований равны Y и Z (меньше и больше соответственно). Для проведения расчета необходимо из угла В провести высоту N. В результате получится прямоугольный треугольник ABN, где AB — гипотенуза, а BN и AN — катеты. Вычисляем размер катета AN: из большего основания вычитаем меньшее, а результат делим на 2. Записываем в виде формулы: (Z-Y)/2 = F. Теперь используем функцию cos для расчета острый угол треугольника. Получаем следующую запись: cos(β) = X/F. Теперь вычисляем угол: β = arcos(X/F). Далее, зная один угол, мы можем определить второй, для этого производим элементарное арифметическое действие: 180 — β. Все углы определены.
Есть второе решение этой проблемы. Вначале опускаем Н. из угла В на высоту.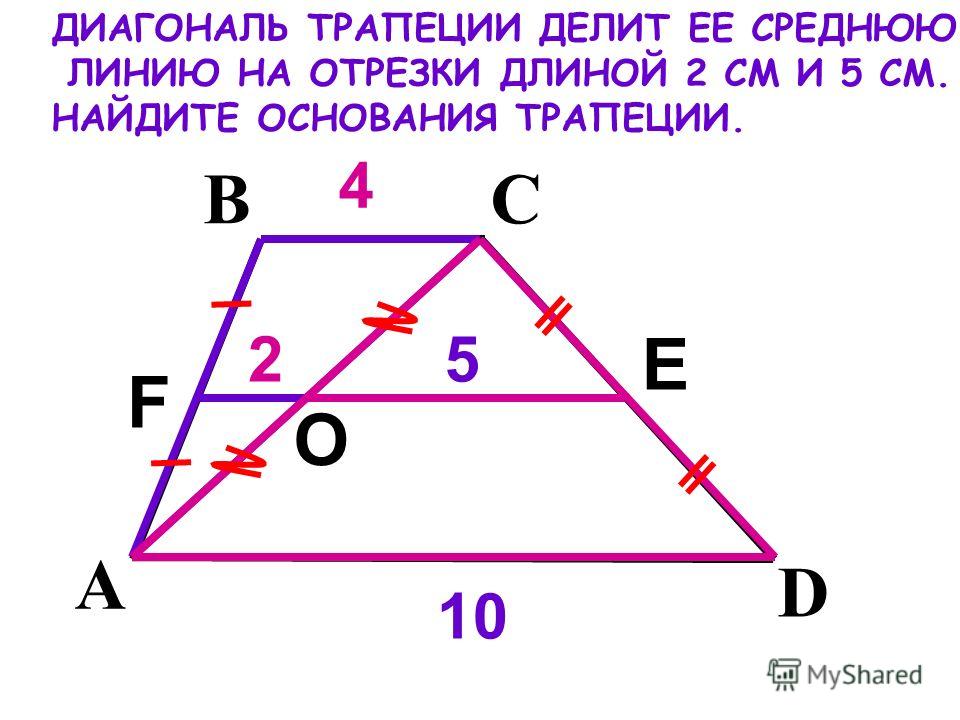
Рассчитываем стоимость ножки BN. Мы знаем, что квадрат гипотенузы прямоугольного треугольника равен сумме квадратов катетов. Получаем: БН = √(X2-F2). Далее воспользуемся тригонометрической функцией tg. В итоге имеем: β = arctan(BN/F). Острый угол найден. Далее определяем аналогично первому способу.
Свойство диагональной равнобедренной трапеции
Сначала запишем четыре правила. Если диагонали в равнобедренной трапеции перпендикулярны, то:
Высота фигуры будет равна сумме оснований, деленной на два;
Его высота и средняя линия равны;
Центром круга является точка их пересечения;
Если сторона делится точкой касания на отрезки Н и М, то она равна корню квадратному из произведения этих отрезков;
Четырехугольник, образованный точками касания, вершиной трапеции и центром вписанной окружности, представляет собой квадрат, сторона которого равна радиусу;
Площадь фигуры равна произведению оснований и произведению половины суммы оснований на ее высоту.
Аналогичная трапеция
Эта тема очень удобна для изучения свойств этой. Например, диагонали делят трапецию на четыре треугольника, причем прилежащие к основаниям подобны, а к сторонам — равны. Это утверждение можно назвать свойством треугольников, на которые трапеция делится своими диагоналями. Первая часть этого утверждения доказывается через признак подобия двух углов. Для доказательства второй части лучше использовать способ, описанный ниже.
Доказательство теоремы
Примем, что фигура АБСД (АД и БС — основание трапеции) делится диагоналями ВД и АС. Точка их пересечения — О. Получаем четыре треугольника: АОС — у нижнего основания, БОС — у верхнего основания, АВО и СОД у боковых сторон. Треугольники SOD и BOS имеют общую высоту, если их основаниями являются отрезки BO и OD. Получаем, что разность их площадей (Р) равна разнице этих отрезков: СВЕ/ПСОД=БО/ОД=К. Следовательно, ПСОД=СВЭ/К. Аналогично треугольники БОС и АОВ имеют общая высота. Примем за их основу сегменты СО и ОА.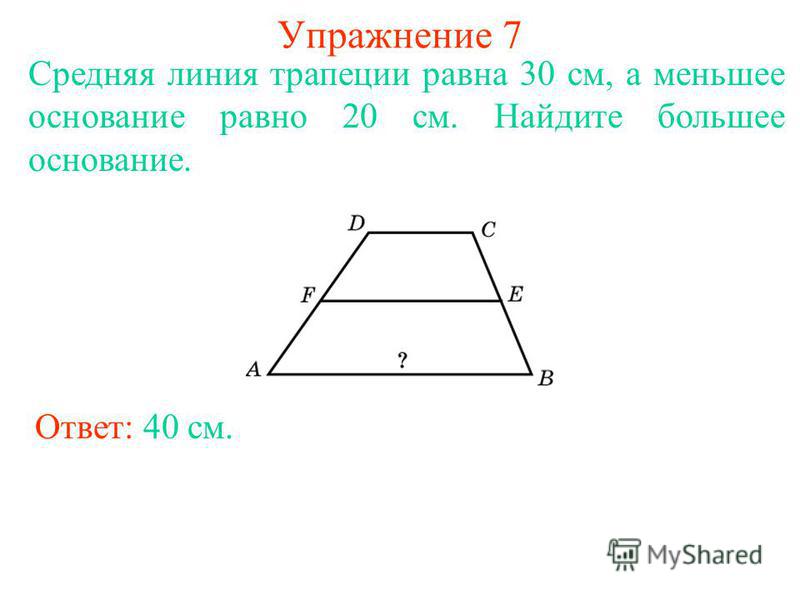
Получаем СВЭ/ПАОВ=СО/ОА=К и ПАОВ=СВЭ/К. Отсюда следует, что ПСОД=ПАОВ.
Для закрепления материала учащимся рекомендуется найти связь между площадями полученных треугольников, на которые делится трапеция своими диагоналями, решив следующую задачу. Известно, что площади треугольников BOS и AOD равны, необходимо найти площадь трапеции. Поскольку ПСОД = PAOB, значит, PABSD = CBE + PAOD + 2 * PSOD. Из подобия треугольников BOS и AOD следует, что BO/OD = √(TBC/PAOD). Следовательно, СВЭ/ПСОД = БО/ОД = √(СВЭ/ПАОД). Получаем PSOD=√(CBOS*PAOD). Тогда PABSD = TBC + PAOD + 2 * √ (TBC * PAOD) = (√ CBED + √ PAOD) 2.
Свойства подобия
Продолжая развивать эту тему, можно доказать и другие интересные свойства трапеции. Итак, используя подобие, можно доказать свойство отрезка, проходящего через точку, образованную пересечением диагоналей этой геометрической фигуры, параллельно основаниям. Для этого решим следующую задачу: необходимо найти длину отрезка РК, проходящего через точку О.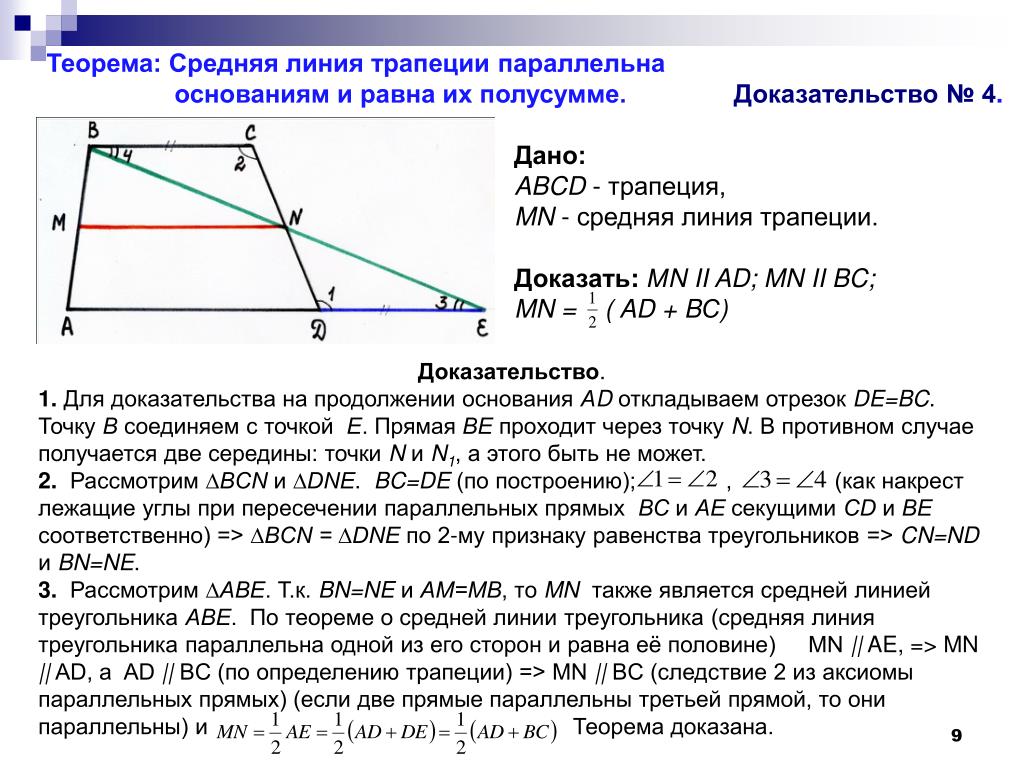
Из подобия треугольников АОД и БОС следует, что АО/ОС = AD/ БС. Из подобия треугольников АОР и АСБ следует, что АО/АС = РО/БС = АД/(БС + АД). Отсюда получаем, что РО = БС*АД/(БС+АД). Аналогично, из подобия треугольников ДОК и ДБС следует, что ОК = БС*АД/(БС+АД). Отсюда получаем, что ПО=ОК и ПК=2*БС*АД/(БС+АД). Прямая, проходящая через точку пересечения диагоналей параллельно основаниям и соединяющая две стороны, делится точкой пересечения пополам. Его длина есть среднее гармоническое основания фигуры.
Рассмотрим следующее качество трапеции, которое называется свойством четырех точек. Точки пересечения диагоналей (О), пересечения продолжения сторон (Е), а также середины оснований (Т и Г) всегда лежат на одной прямой. Это легко доказывается методом подобия. Получившиеся треугольники BES и AED подобны, и в каждом из них медианы ET и EJ делят угол при вершине E на равные части. Следовательно, точки Е, Т и М лежат на одной прямой. Точно так же точки T, O и G расположены на одной прямой.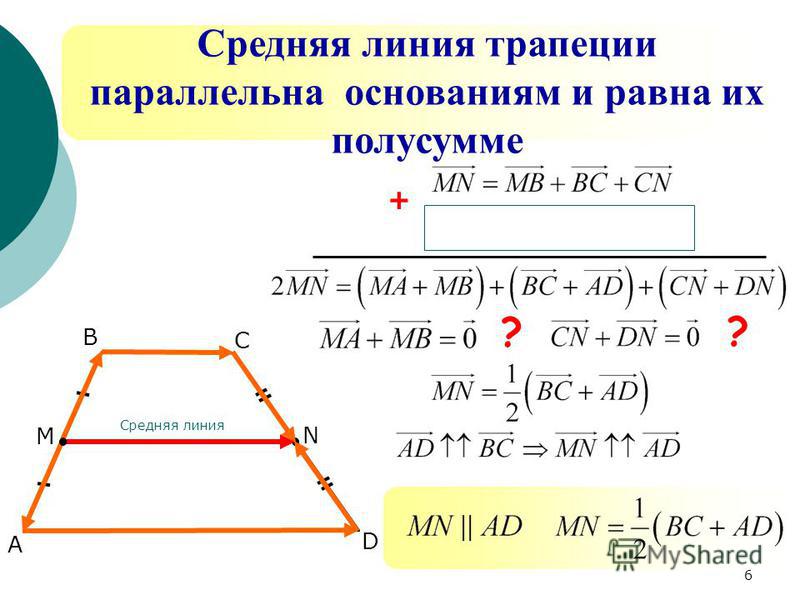
Все это следует из подобия треугольников BOS и AOD. Отсюда делаем вывод, что все четыре точки — Е, Т, О и W — будут лежать на одной прямой.
Используя подобные трапеции, учащимся можно предложить найти длину отрезка (LF), который делит фигуру на две подобные. Этот отрезок должен быть параллелен основаниям. Так как получившиеся трапеции ALPD и LBSF подобны, то BS/LF = LF/AD. Отсюда следует, что ЛФ = √(БС*АД). Получаем, что отрезок, делящий трапецию на две подобные, имеет длину, равную среднему геометрическому длин оснований фигуры.
Рассмотрим следующее свойство сходства. В его основе лежит отрезок, который делит трапецию на две равные фигуры. Примем, что трапеция ABSD делится отрезком EN на два подобных. От вершины B опускается высота, которая делится отрезком EH на две части — B1 и B2. Получаем: ПАБСД/2=(БС+ЕН)*В1/2=(АД+ЕН)*В2/2 и ПАБСД=(БС+АД)*(В1+В2)/2. Далее составляем система, первое уравнение которой (БС+ЭН)*В1=(АД+ЭН)*В2 и второе (БС+ЭН)*В1=(БС+АД)*(В1+В2)/2. Отсюда следует что В2/В1=(БС+ЭН)/(АД+ЭН) и БС+ЭН=((БС+АД)/2)*(1+В2/В1).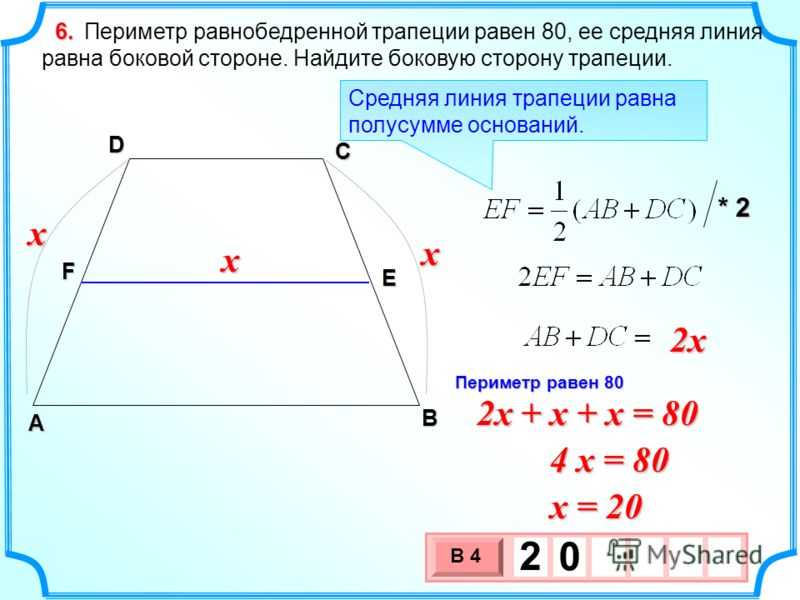
Получаем, что длина отрезка, делящего трапецию на две равные, равна среднему квадрату длин оснований: √ ((BS2 + AD2)/2).
Выводы подобия
Таким образом, мы доказали, что:
1. Отрезок, соединяющий середины сторон у трапеции, параллелен АД и БС и равен среднему арифметическому между БС и АД (длина основания трапеции) .
2. Прямая, проходящая через точку О пересечения диагоналей, параллельных АД и БС, будет равна среднему гармоническому чисел АД и БС (2*БС*АД/(БС+АД)).
3. Отрезок, делящий трапецию на подобные, имеет длину среднего геометрического оснований БС и АД.
4. Элемент, делящий фигуру на две равные, имеет длину средних квадратов чисел AD и BS.
Для закрепления материала и понимания связи между рассматриваемыми отрезками учащемуся необходимо построить их для конкретной трапеции. Он легко может отобразить среднюю линию и отрезок, проходящий через точку О — пересечение диагоналей фигуры — параллельно основаниям. Но где будут третья и четвертая? Этот ответ приведет студента к обнаружению желаемого соотношения между средними значениями.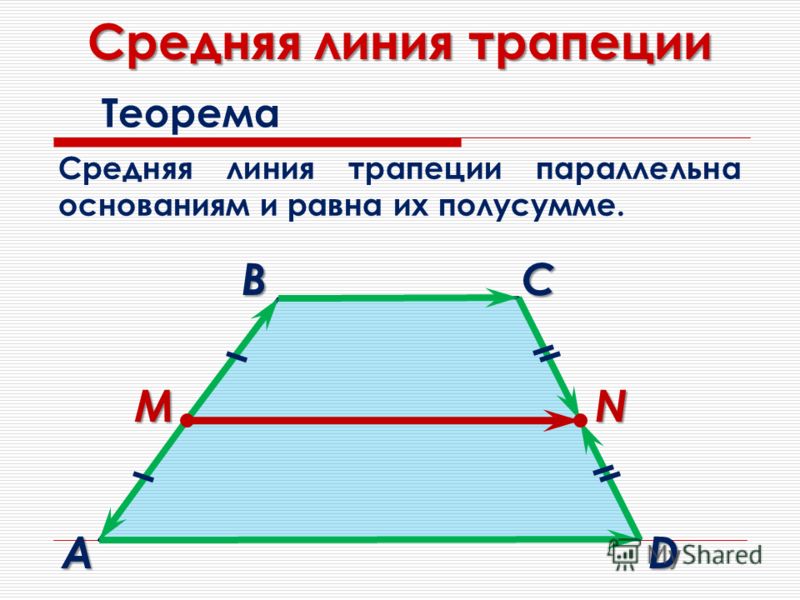
Прямая, соединяющая середины диагоналей трапеции
Рассмотрим следующее свойство этой фигуры. Примем, что отрезок MN параллелен основаниям и делит диагонали пополам. Точки пересечения называются W и U. Этот отрезок будет равен полуразности оснований. Мы проанализируем это более подробно. МС — средняя линия треугольника АБС, она равна БС/2. МСК — средняя линия треугольника АБД, она равна АД/2. Тогда получаем, что ШШ = МЩ-МШ, следовательно , ШЩ = АД / 2-БС / 2 = (АД + ВС) / 2.
Центр тяжести
Посмотрим, как определяется этот элемент для данной геометрической фигуры. Для этого вытяните основания в противоположные стороны. Что это значит? К верхнему необходимо добавить нижнее основание — в любую сторону, например, вправо. А нижний удлиняется на длину верхнего левого. Далее соедините их диагональю. Точка пересечения этого отрезка со средней линией фигуры является центром тяжести трапеции.
Трапеция вписанная и описанная
Перечислим признаки таких фигур:
1.
Трапецию можно вписать в окружность, только если она равнобедренная.
2. Трапецию можно описать по окружности при условии, что сумма длин их оснований равна сумме длин сторон.
Следствия вписанной окружности:
1. Высота описываемой трапеции всегда равна двум радиусам.
2. Боковая сторона описанной трапеции наблюдается из центра окружности под прямым углом.
Первое следствие очевидно, но для доказательства второго требуется установить прямой угол СОД, что, собственно, не составит труда. Но знание этого свойства позволит нам использовать прямоугольный треугольник при решении задач.
Уточним теперь эти следствия для равнобедренной трапеции, вписанной в окружность. Получаем, что высота есть среднее геометрическое основания фигуры: Н = 2R = √(БС*АД). Отрабатывая основной способ решения задач на трапеции (принцип удержания двух высот), учащийся должен решить следующую задачу. Примем, что ВТ есть высота равнобедренной фигуры АБС. Необходимо найти отрезки AT и TD.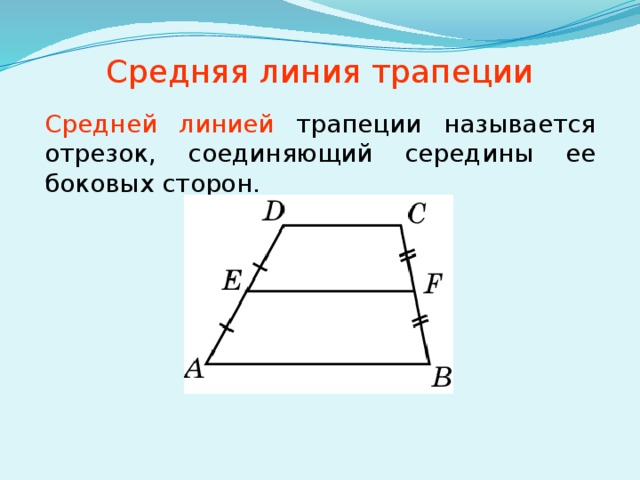
Применив формулу, описанную выше, это не составит труда.
Теперь разберемся, как определить радиус окружности, используя площадь описываемой трапеции. Опустите высоту от вершины Б до основания АД. Так как окружность вписана в трапецию, то БС+АД=2АВ или АВ=(БС+АД)/2. Из треугольника АБН находим sinα=ВН/АВ=2*БН/(БС+АД ). ПАБСД=(БС+АД)*БН/2, БН=2Р. Получаем ПАБСД=(БС+АД)*R, отсюда следует, что R=ПАБСД/(БС+АД).
Все формулы средней линии трапеции
Теперь пришло время перейти к последнему элементу этой геометрической фигуры. Разберемся, чему равна средняя линия трапеции (М):
1. Через основания: М = (А+В)/2.
2. Через высоту, основание и углы:
М = А-Н*(ctgα + ctgβ)/2;
М = В + Н * (ctgα + ctgβ) / 2.
3. Через высоту, диагонали и угол между ними. Например, D1 и D2 — диагонали трапеции; α, β – углы между ними:
М = D1 * D2 * sinα / 2H = D1 * D2 * sinβ / 2H.
4. Через площадь и высоту: M = P/N.
Площадь трапеции.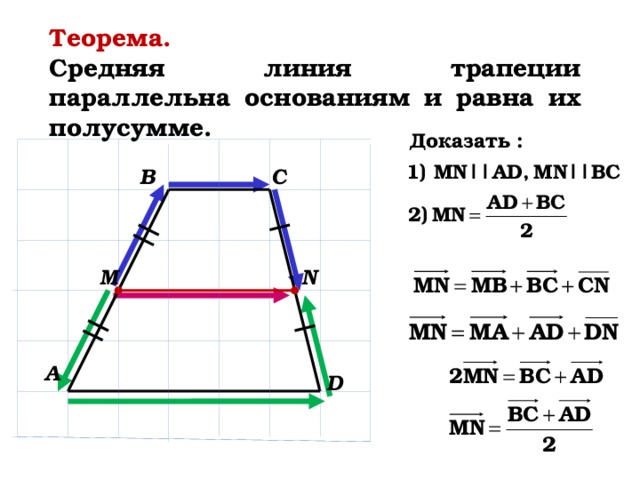
Привет! В данной публикации мы рассмотрим указанную формулу. Почему она такая и как ее понять. Если есть понимание, то не нужно его учить. Если просто хотите посмотреть эту формулу и что срочно, то можете сразу листать страницу вниз))
Теперь подробно и по порядку.
Трапеция — это четырехугольник, две стороны которого параллельны, а две другие — нет. Те, что не параллельны, являются основаниями трапеции. Два других называются сторонами.
Если стороны равны, то трапеция называется равнобедренной. Если одна из сторон перпендикулярна основаниям, то такая трапеция называется прямоугольной.
В классическом виде трапецию изображают так — большее основание внизу, соответственно меньшее вверху. Но никто не запрещает изображать ее и наоборот. Вот миниатюры:
Следующее важное понятие.
Средняя линия трапеции – это отрезок, соединяющий середины сторон. Средняя линия параллельна основаниям трапеции и равна их полусумме.
Теперь давайте углубимся.
Почему так?
Рассмотрим трапецию с основаниями a и b и со средней линией l , и проведем дополнительные построения: через основания проведем прямые, а через концы средней линии перпендикуляры до пересечения с основаниями:
* Алфавитные обозначения вершин и других точек намеренно не вводятся во избежание ненужных обозначений.
Смотрите, треугольники 1 и 2 равны по второму признаку равенства треугольников, треугольники 3 и 4 равны. Равенство треугольников подразумевает равенство элементов, а именно катетов (они обозначены синим и красным соответственно).
Внимание! Если мы мысленно «отрежем» синюю и красную линию от нижнего основания, то у нас получится линия (это сторона прямоугольника), равная средней линии. Далее, если «приклеить» отрезанную синюю и красную линию к верхнему основанию трапеции, то также получится линия (это и есть сторона прямоугольника), равная средней линии трапеции.
Поймал? Получается, что сумма оснований будет равна двум средним линиям трапеции:
См.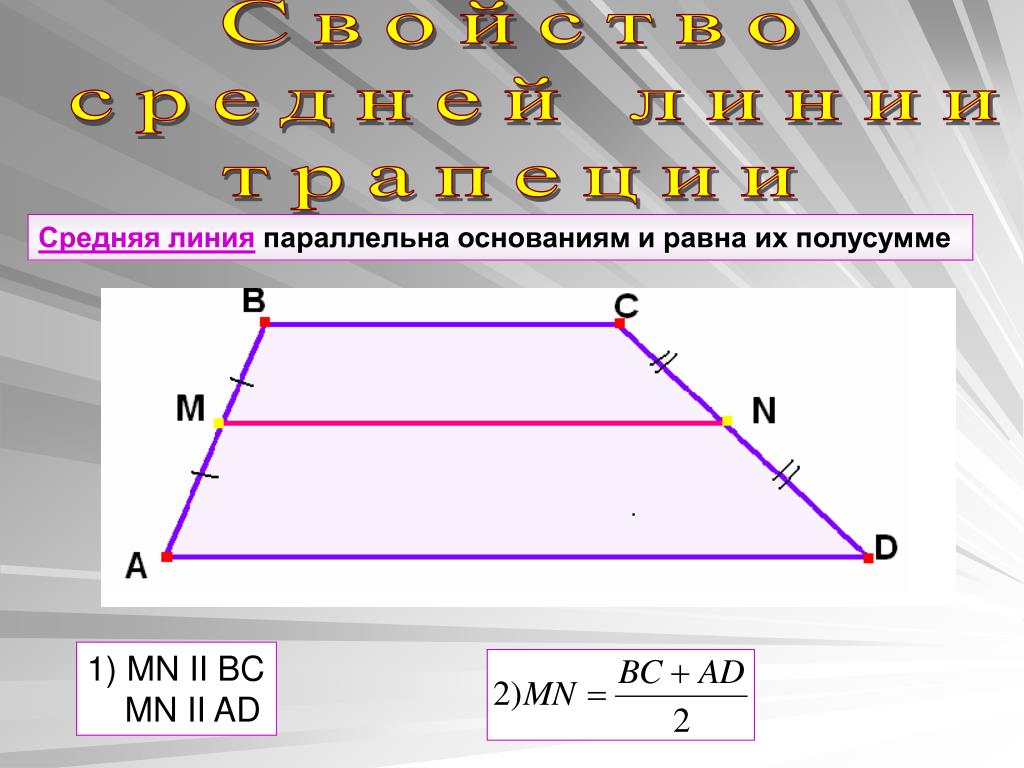
другое объяснение
Поступим следующим образом — построим прямую, проходящую через нижнее основание трапеции. трапеция и прямая, проходящая через точки А и В:
Получаем треугольники 1 и 2, они равны по стороне и прилежащим к ней углам (второй признак равенства треугольников). Это означает, что полученный отрезок (обозначенный на эскизе синим цветом) равен верхнему основанию трапеции.
Теперь рассмотрим треугольник:
* Средняя линия этой трапеции и средняя линия треугольника совпадают.
Известно, что треугольник равен половине параллельного ему основания, то есть:
Хорошо, разобрались. Теперь о площади трапеции.
Формула площади трапеции:
Говорят: площадь трапеции равна произведению половины суммы ее оснований и высоты.
То есть получается, что он равен произведению средней линии на высоту:
Вы наверное уже заметили, что это очевидно. Геометрически это можно выразить так: если мысленно вырезать из трапеции треугольники 2 и 4 и положить их на треугольники 1 и 3 соответственно:
Тогда получится прямоугольник по площади равной площади наша трапеция.
Площадь этого прямоугольника будет равна произведению средней линии на высоту, то есть мы можем написать:
Но тут дело не в записи, конечно, а в понимании.
Скачать (просмотреть) материал статьи в формате *pdf
Вот и все. Успехов вам!
С уважением, Александр.
Как найти среднюю линию трапеции
Понятие средней линии трапеции
Для начала вспомним, какая фигура называется трапецией.
Определение 1
Трапеция – это четырехугольник, у которого две стороны параллельны, а две другие не параллельны.
При этом параллельные стороны называются основаниями трапеции, а не параллельные — сторонами трапеции.
Определение 2
Средняя линия трапеции — это отрезок, соединяющий середины сторон трапеции.
Теорема о средней линии трапеции
Теперь введем теорему о средней линии трапеции и докажем ее векторным методом.
Теорема 1
Средняя линия трапеции параллельна основаниям и равна их полусумме.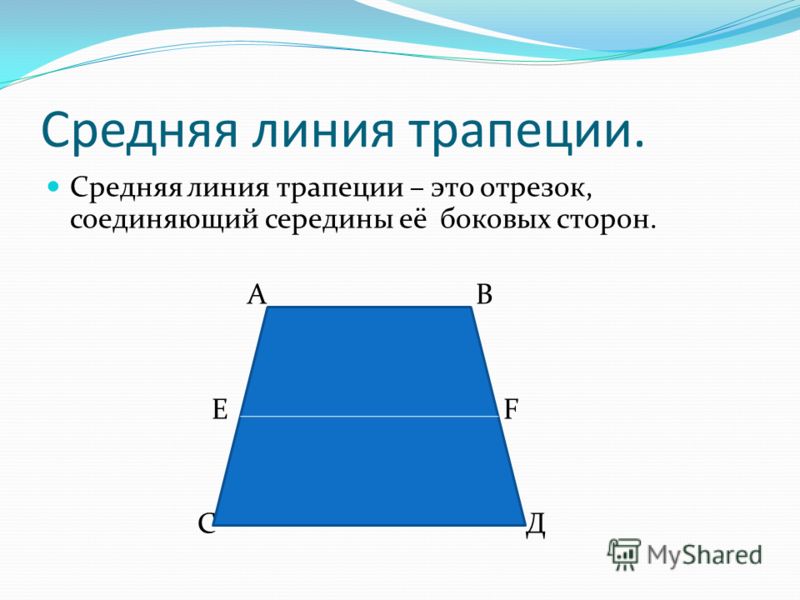
Доказательство.
Дана трапеция $ABCD$ с основаниями $AD\ и \BC$. И пусть $MN$ — средняя линия этой трапеции (рис. 1).
Рис. 1. Средняя линия трапеции
Докажем, что $ MN || AD\ и \MN = \frac(AD+BC)(2)$.
Рассмотрим вектор $\overrightarrow(MN)$. Затем мы используем правило многоугольника для добавления векторов. С одной стороны получаем что
С другой стороны
Сложим два последних равенства, получим
Так как $M$ и $N$ являются серединами боковых сторон трапеции, то будем иметь
Получаем:
Отсюда
Из того же равенства (так как $\overrightarrow(BC)$ и $\ (AD) $ сонаправлены и, следовательно, коллинеарны) получаем $ MN || АД $.
Теорема доказана.
Примеры заданий на понятие средней линии трапеции
Пример 1
Стороны трапеции равны $15\см$ и $17\см$ соответственно. Периметр трапеции равен 52$\см$. Найдите длину средней линии трапеции.
Решение.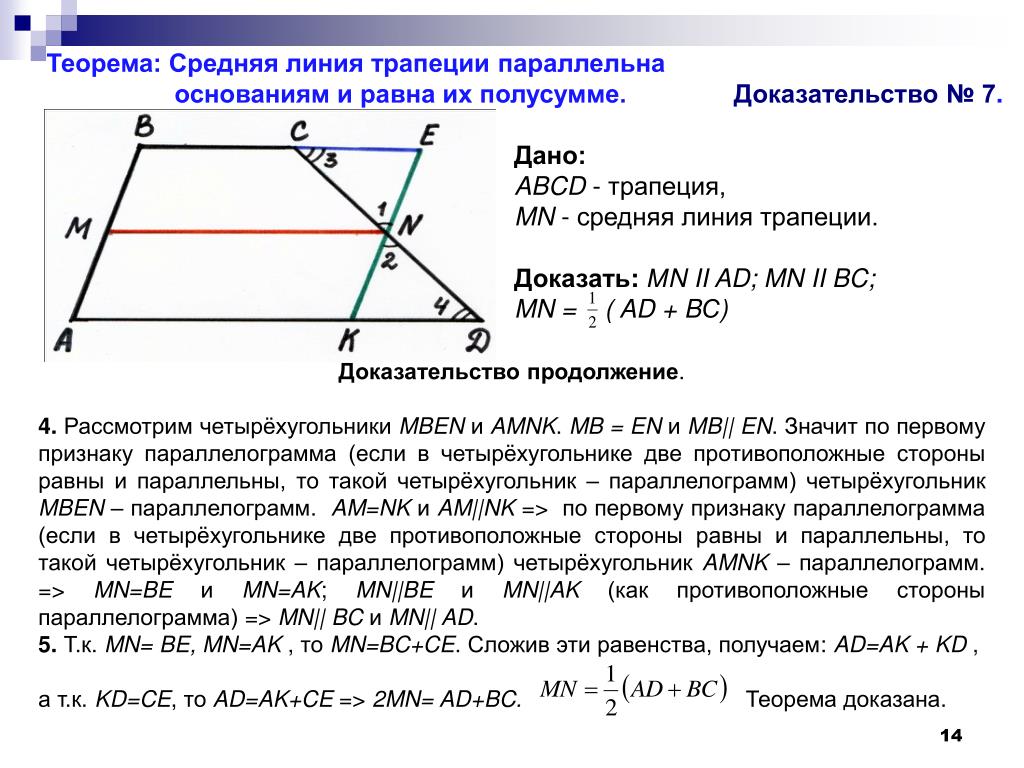
Обозначим среднюю линию трапеции через $n$.
Сумма сторон равна
Следовательно, так как периметр равен 52$\см$, то сумма оснований равна
Отсюда по теореме 1 получаем
Ответ: $10\см$.
Пример 2
Концы диаметра окружности удалены от ее касательной на $9$ см и $5$ см соответственно. Найдите диаметр этого круга.
Решение.
Дана окружность с центром $O$ и диаметром $AB$. Проведите касательную $l$ и постройте расстояния $AD=9\см$ и $BC=5\см$. Проведем радиус $ОН$ (рис. 2).
Рис. 2.
Так как $AD$ и $BC$ — расстояния до касательной, то $AD\bot l$ и $BC\bot l$ и так как $OH$ — радиус, то $OH \bot l $, следовательно, $OH | \ слева | AD \ вправо || БК $. Из всего этого получаем, что $ABCD$ — это трапеция, а $OH$ — ее средняя линия. По теореме 1 получаем
Отрезок прямой, соединяющий середины сторон трапеции, называется средней линией трапеции. Как найти среднюю линию трапеции и как она соотносится с другими элементами этой фигуры, мы обсудим ниже.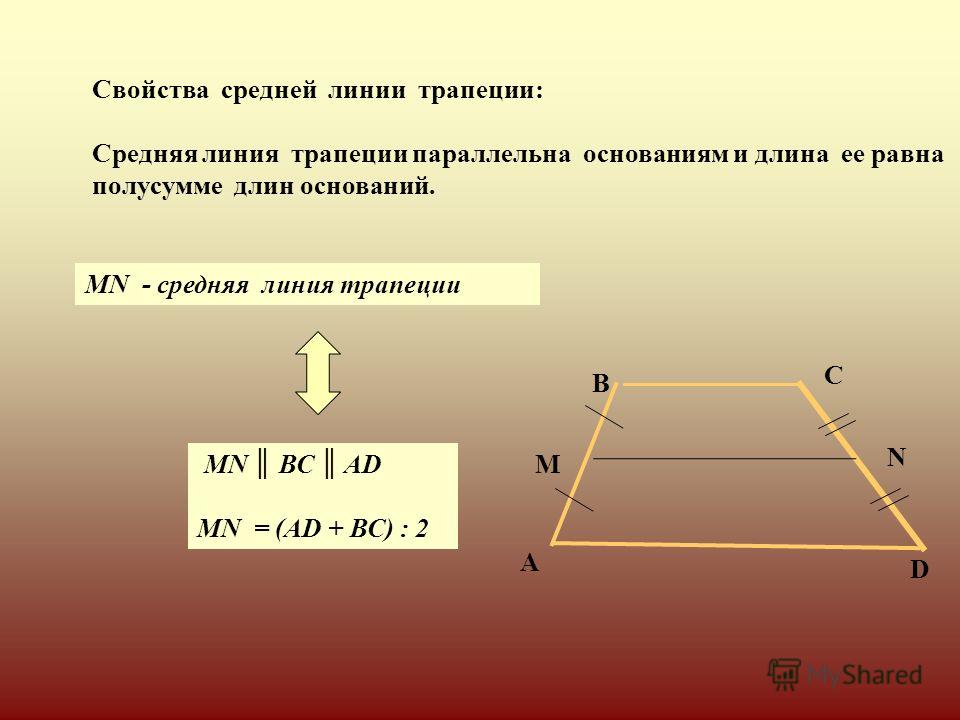
Теорема о центральной линии
Нарисуем трапецию, в которой AD — большее основание, BC — меньшее основание, EF — средняя линия. Продлить основание AD за точку D. Провести линию BF и продолжить ее до пересечения с продолжением основания AD в точке O. Рассмотрим треугольники ∆BCF и ∆DFO. Углы ∟BCF = ∟DFO как вертикальные. CF = DF, ∟BCF = ∟FDО, т.к. VS // АО. Следовательно, треугольники ∆BCF = ∆DFO. Следовательно, стороны BF = FO.
Теперь рассмотрим ∆ABO и ∆EBF. ∟ABO является общим для обоих треугольников. BE/AB = ½ по условию, BF/BO = ½, так как ∆BCF = ∆DFO. Следовательно, треугольники ABO и EFB подобны. Отсюда отношение сторон ЭФ/АО = ½, как и отношение остальных сторон.
Находим EF = ½ AO. На чертеже видно, что АО = AD + DO. DO = BC как стороны равнобедренных треугольников, поэтому AO = AD + BC. Следовательно, EF = ½ AO = ½ (AD + BC). Те. длина средней линии трапеции равна половине суммы оснований.
Всегда ли средняя линия трапеции равна половине суммы оснований?
Предположим, что существует особый случай, когда EF ≠ ½ (AD + BC).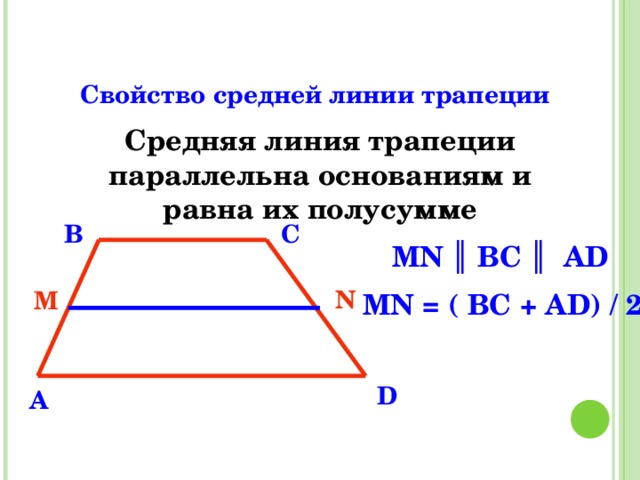
Тогда ВС ≠ DO, следовательно, ∆BCF ≠ ∆DCF. Но это невозможно, так как между ними равны два угла и стороны. Следовательно, теорема верна при всех условиях.
Задача о средней линии
Предположим, что в нашей трапеции ABCD AD // BC, ∟A = 90°, ∟C = 135°, AB = 2 см, диагональ AC перпендикулярна боковой стороне. Найдите среднюю линию трапеции EF.
Если ∟А = 90°, то ∟В = 90°, значит, ∆ABS прямоугольная.
∟BCA = ∟BCD — ∟ACD. ∟ACD = 90° по условию, поэтому ∟BCA = ∟BCD — ∟ACD = 135° — 90° = 45°.
Если в прямоугольном треугольнике ∆ABS один угол равен 45°, то катеты в нем равны: AB = BC = 2 см.
Гипотенуза AC = √ (AB² + BC²) = √8 см.
Учитывать ∆ACD. ∟ACD = 90° по условию. ∟CAD = ∟BCA = 45° как углы, образованные секущей параллельных оснований трапеции. Следовательно, ноги AC = CD = √8.
Гипотенуза AD = √ (AC² + CD²) = √ (8 + 8) = √16 = 4 см.
Средняя линия трапеции EF = ½ (AD + BC) = ½ (2 + 4) = 3 см.
Трапеция — частный случай четырехугольника, у которого одна пара сторон параллельна.
Термин «трапеция» происходит от греческого слова τράπεζα, означающего «стол», «стол». В этой статье мы рассмотрим виды трапеций и их свойства. Кроме того, мы разберемся, как рассчитать отдельные элементы этой, например, диагонали равнобедренной трапеции, центральной линии, площади и т. д. Материал представлен в стиле элементарной популярной геометрии, т. е. в легкодоступная форма.
Общие сведения
Для начала разберемся, что такое четырехугольник. Эта фигура представляет собой частный случай многоугольника с четырьмя сторонами и четырьмя вершинами. Две несмежные вершины четырехугольника называются противоположными. То же самое можно сказать и о двух несмежных сторонах. Основные виды четырехугольников – параллелограмм, прямоугольник, ромб, квадрат, трапеция и дельтовидная форма.
Итак, вернемся к трапециям. Как мы уже говорили, у этой фигуры две стороны параллельны. Они называются базами. Две другие (непараллельные) — стороны. В экзаменационных материалах и различных контрольных работах очень часто можно встретить задачи, связанные с трапециями, решение которых часто требует от студента знаний, не предусмотренных программой.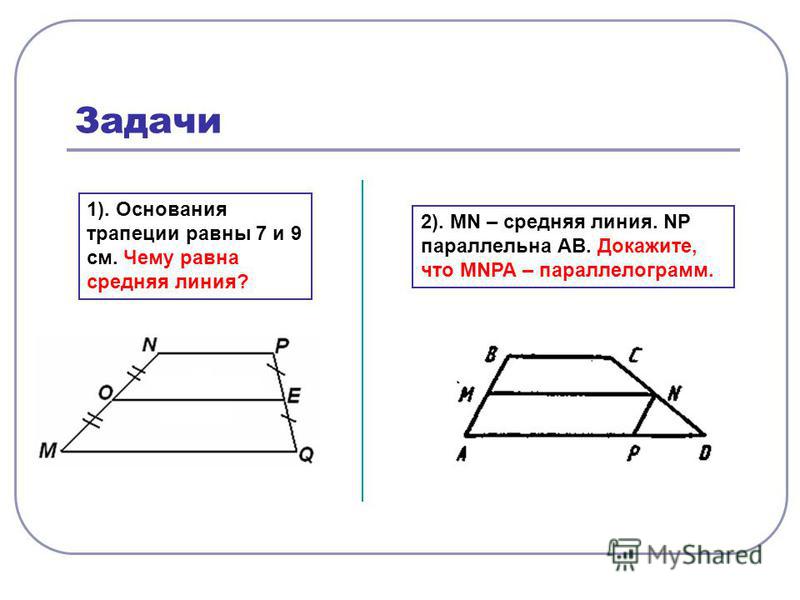
Школьный курс геометрии знакомит учащихся со свойствами углов и диагоналей, а также со средней линией равнобедренной трапеции. Но помимо этого упомянутая геометрическая фигура имеет и другие особенности. Но о них чуть позже…
Типы трапеций
Есть много типов этой фигуры. Однако чаще всего принято рассматривать две из них – равнобедренную и прямоугольную.
1. Прямоугольной трапецией называется фигура, у которой одна из боковых сторон перпендикулярна основаниям. Два его угла всегда равны девяноста градусам.
2. Равнобедренная трапеция – геометрическая фигура, стороны которой равны между собой. Это означает, что углы при основаниях также попарно равны.
Основные принципы методики изучения свойств трапеции
Основным принципом является использование так называемого задачного подхода. На самом деле нет необходимости вводить в теоретический курс геометрии новые свойства этой фигуры. Их можно обнаружить и сформулировать в процессе решения разных задач (лучше системных).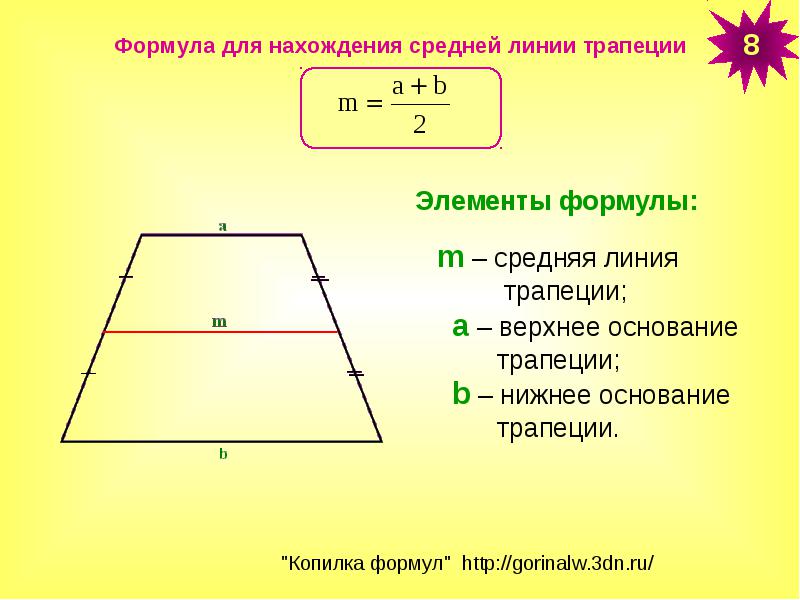
При этом очень важно, чтобы преподаватель знал, какие задачи необходимо ставить перед учащимися в тот или иной момент учебного процесса. При этом каждое свойство трапеции может быть представлено как ключевая задача в системе задач.
Второй принцип – так называемая спиральная организация изучения «замечательных» свойств трапеции. Это предполагает возврат в процессе обучения к отдельным признакам заданной геометрической фигуры. Это облегчает обучающимся их запоминание. Например, свойство четырех точек. Это можно доказать как изучением подобия, так и последующим использованием векторов. А равновеликость треугольников, примыкающих к боковым сторонам фигуры, можно доказать, применяя не только свойства равновеликих треугольников, проведенных к сторонам, лежащим на одной прямой, но и используя формулу S = 1/2 (аб*синα). Кроме того, можно работать на вписанной трапеции или прямоугольном треугольнике на описанной трапеции и т. д.
Использование «внеклассных» признаков геометрической фигуры в содержании школьного курса – задача технологии их обучения.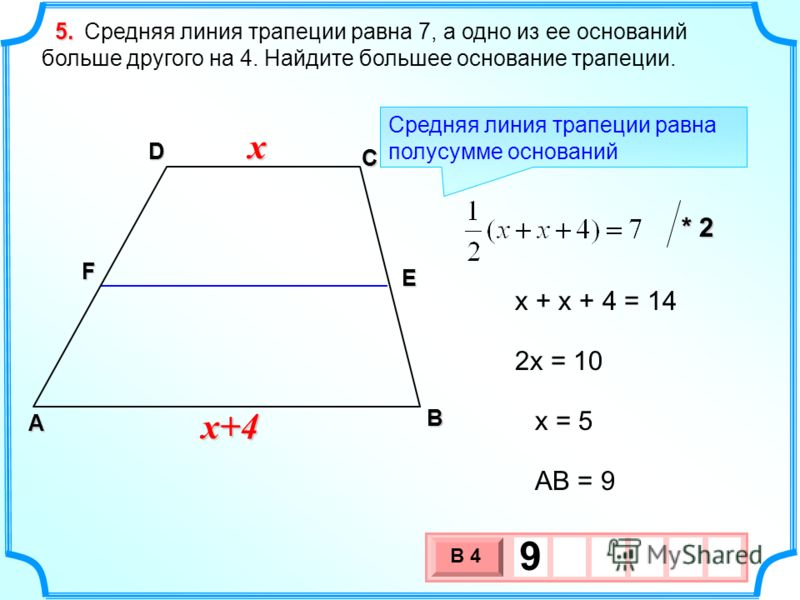
Постоянное обращение к изучаемым свойствам при прохождении других тем позволяет учащимся глубже понять трапецию и обеспечивает успешность решения поставленных задач. Итак, приступим к изучению этой замечательной фигуры.
Элементы и свойства равнобедренной трапеции
Как мы уже отмечали, эта геометрическая фигура имеет равные стороны. Его также называют правильной трапецией. И чем он так примечателен и почему получил такое название? К особенностям этой фигуры относится то, что равны не только стороны и углы при основаниях, но и диагонали. Кроме того, сумма углов равнобедренной трапеции равна 360 градусов. Но это не все! Из всех известных трапеций только вокруг равнобедренной можно описать окружность. Это связано с тем, что сумма противоположных углов этой фигуры равна 180 градусам, и только при этом условии вокруг четырехугольника можно описать окружность. Следующее свойство рассматриваемой геометрической фигуры состоит в том, что расстояние от вершины основания до проекции противоположной вершины на прямую, содержащую это основание, будет равно центральной линии.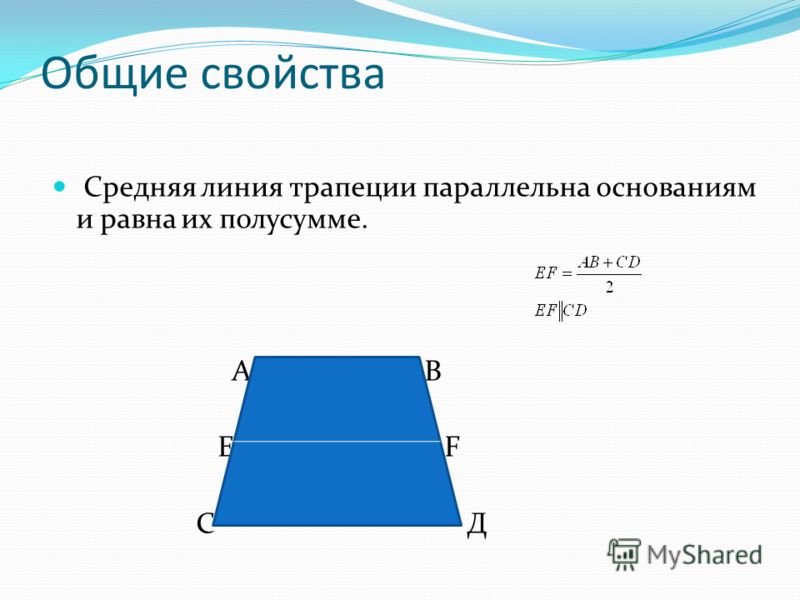
Теперь разберемся, как найти углы равнобедренной трапеции. Рассмотрим решение этой задачи при условии, что известны размеры сторон фигуры.
Раствор
Обычно четырехугольник принято обозначать буквами A, B, C, D, где BS и AD — основания. У равнобедренной трапеции стороны равны. Будем считать, что их размер равен X, а размеры оснований равны Y и Z (меньше и больше соответственно). Для проведения расчета необходимо из угла В провести высоту Н. В результате получится прямоугольный треугольник АВН, где АВ — гипотенуза, а ВН и АН — катеты. Вычисляем размер катета AH: из большего основания вычитаем меньшее, а результат делим на 2. Записываем в виде формулы: (Z-Y)/2=F. Теперь вычисляем острый угол треугольника, мы используем функцию cos. Получаем следующую запись: cos(β) = X/F. Теперь вычисляем угол: β = arcos(X/F). Далее, зная один угол, мы можем определить второй, для этого выполняем элементарное арифметическое действие: 180 — β. Все углы определены.
Есть и второе решение этой проблемы.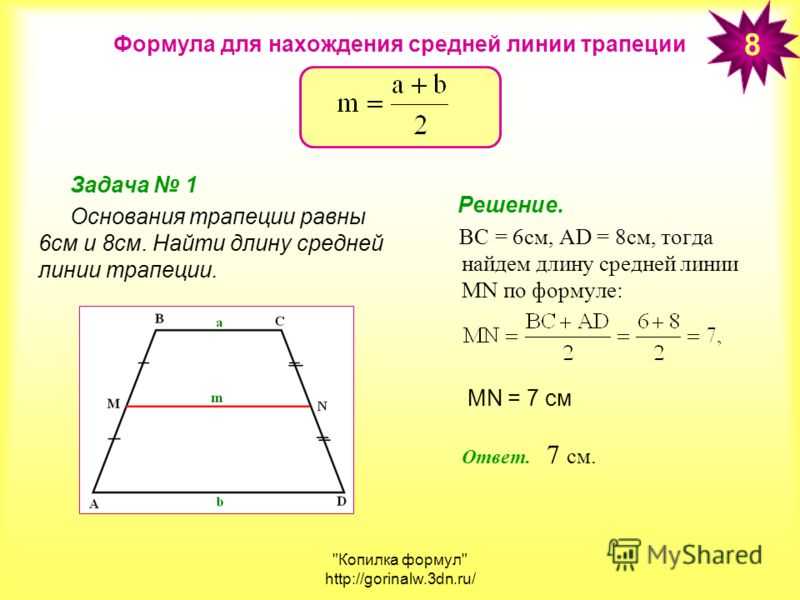
В начале опускаем высоту Н. от угла. Рассчитайте значение ножки BN. Мы знаем, что квадрат гипотенузы прямоугольного треугольника равен сумме квадратов катетов. Получаем: BN = √(X2-F2). Далее воспользуемся тригонометрической функцией tg. В итоге имеем: β = arctg (BN/F). Найден острый угол. Далее определяем так же, как и в первом способе.
Свойство диагоналей равнобедренной трапеции
Сначала запишем четыре правила. Если диагонали в равнобедренной трапеции перпендикулярны, то:
Высота фигуры будет равна сумме оснований, деленной на два;
Его высота и средняя линия равны;
Центром круга является точка их пересечения;
Если боковая сторона делится точкой касания на отрезки Н и М, то она равна произведениям квадратных корней этих отрезков;
Четырехугольник, образованный точками касания, вершиной трапеции и центром вписанной окружности, представляет собой квадрат, сторона которого равна радиусу;
Площадь фигуры равна произведению оснований и произведению полусуммы оснований на ее высоту.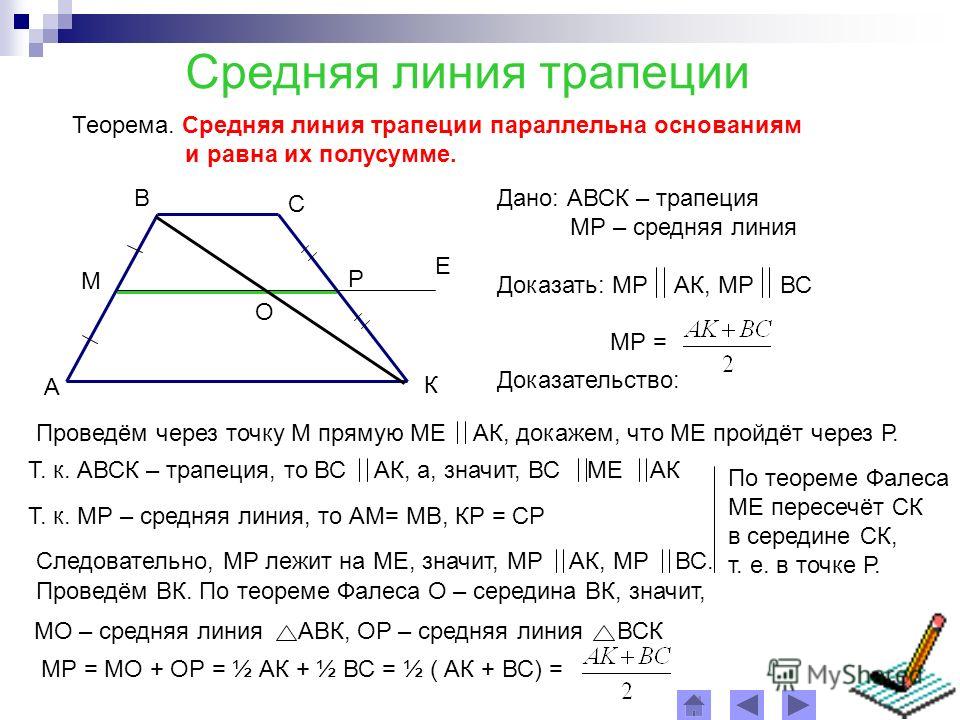
Аналогичная трапеция
Эта тема очень удобна для изучения свойств этой. Например, диагонали делят трапецию на четыре треугольника, причем прилежащие к основаниям подобны, а к боковым сторонам равны. Это утверждение можно назвать свойством треугольников, на которые трапеция делится своими диагоналями. Первая часть этого утверждения доказывается через признак подобия двух углов. Для доказательства второй части лучше использовать способ, описанный ниже.
Доказательство теоремы
Примем, что фигура АБСД (BP и BS — основания трапеции) делится диагоналями ВД и AS. Точка их пересечения — О. Получаем четыре треугольника: АОС — у нижнего основания, БОС — у верхнего основания, АВО и СОД у боковых сторон. Треугольники SOD и BFB имеют общую высоту, если их основаниями являются отрезки BO и OD. Получаем, что разность их площадей (Р) равна разнице между этими отрезками: ПБОС/ПСОД=БО/ОД=К. Следовательно, ПБОС=ПБОС/К. Аналогично, треугольники БФВ и АОВ имеют общую высоту.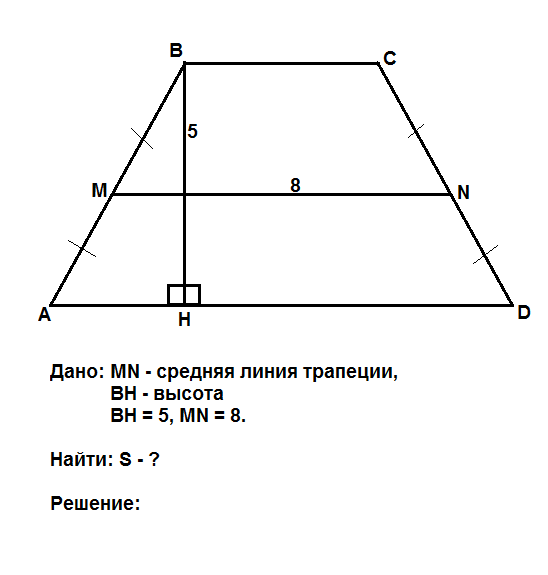
За их основания возьмем отрезки SB и OA. Получаем PBOS/PAOB=SO/OA=K и PAOB=PBOS/K. Отсюда следует, что PSOD=PAOB.
Для закрепления материала учащимся предлагается найти связь между площадями полученных треугольников, на которые трапеция делится своими диагоналями, решив следующую задачу. Известно, что площади треугольников биологической обратной связи и АОЗ равны; надо найти площадь трапеции. Поскольку PSOD = PAOB, это означает, что PABSD = PBOS + PAOD + 2 * PSOD. Из подобия треугольников BFB и AOD следует, что BO/OD = √(PBOS/PAOD). Следовательно, ПБОС/ПСОД=БО/ОД=√(ПБОС/ПАОД). Получаем PSOD=√(PBOS*PAOD). Тогда PABSD = PBOS + PAOD + 2 * √ (PBOS * PAOD) = (√ PSOS + √ PAOD) 2,
Подобие свойств
Продолжая развивать эту тему, можно доказать и другие интересные свойства трапеции. Итак, с помощью подобия можно доказать свойство отрезка, проходящего через точку, образованную пересечением диагоналей этой геометрической фигуры, параллельно основаниям. Для этого решим следующую задачу: необходимо найти длину отрезка RK, который проходит через точку O.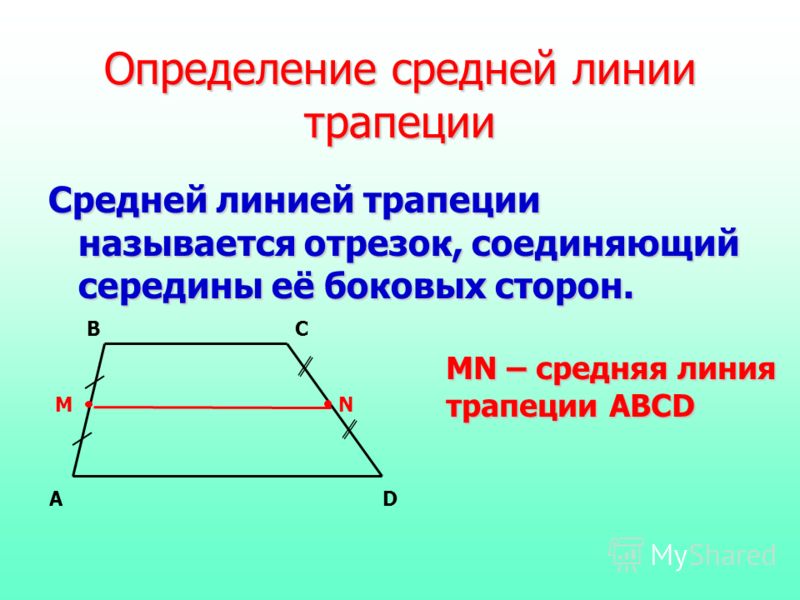
Из подобия треугольников AOD и BFB следует, что AO/OS = AD/BS . Из подобия треугольников АОР и АСБ следует, что АО/АС=РО/БС=АД/(БС+АД). Отсюда получаем, что РО = БС*АД/(БС+АД). Аналогично из подобия треугольников ДОК и ДБС следует, что ОК = БС * АД / (БС + АД). Отсюда получаем, что РО=ОК и РК=2*БС*АД/(БС+АД). Отрезок, проходящий через точку пересечения диагоналей, параллельных основаниям и соединяющий две стороны, делится точкой пересечения пополам. Его длина есть среднее гармоническое основания фигуры.
Рассмотрим следующее свойство трапеции, которое называется четырехточечным свойством. Точки пересечения диагоналей (О), пересечения продолжения боковых сторон (Е), а также середины оснований (Т и Г) всегда лежат на одной прямой. Это легко доказывается методом подобия. Получившиеся треугольники BES и AED подобны, и в каждом из них медианы ET и EZ делят угол при вершине E на равные части. Следовательно, точки E, T и Ж лежат на одной прямой. Точно так же точки Т, О и Ж расположены на одной прямой.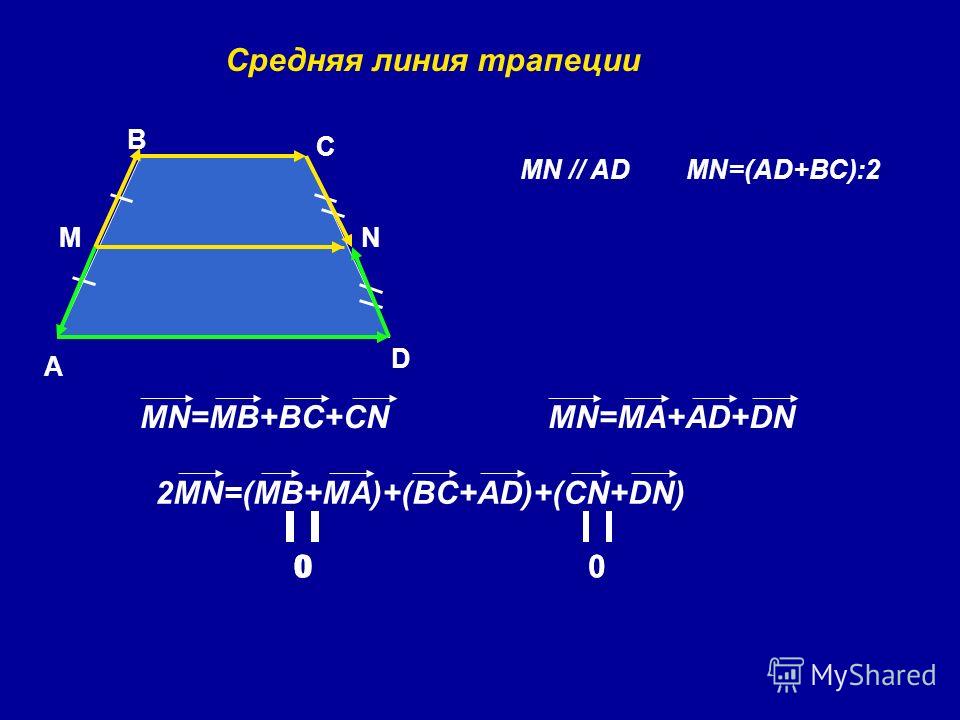
Все это следует из подобия треугольников BFB и AOD. Отсюда делаем вывод, что все четыре точки — Е, Т, О и F — будут лежать на одной прямой.
Используя такие трапеции, можно попросить учащихся найти длину отрезка (LF), который разбивает фигуру на две подобные. Этот отрезок должен быть параллелен основаниям. Так как полученные трапеции ALPD и LBSF подобны, то BS/LF = LF/BP. Отсюда следует, что ЛФ = √(БС*АД). Получаем, что отрезок, делящий трапецию на две подобные, имеет длину, равную среднему геометрическому длин оснований фигуры.
Рассмотрим следующее свойство сходства. В его основе лежит отрезок, который делит трапецию на две фигуры одинакового размера. Считаем, что трапеция ABSD разделена отрезком ЕН на две подобные. Высота сбрасывается с вершины B, которая делится отрезком EH на две части — B1 и B2. Получаем: ПАБСД/2=(БС+ЭХ)*Б1/2=(АД+ЭХ)*Б2/2 и ПАБСД=(БС+АД)*(Б1+Б2)/2. Далее составляем систему, первое уравнение которого (БС+ЭН)*В1=(АД+ЭН)*В2 и второе (БС+ЭН)*В1=(БС+АД)*(Б1+В2)/2.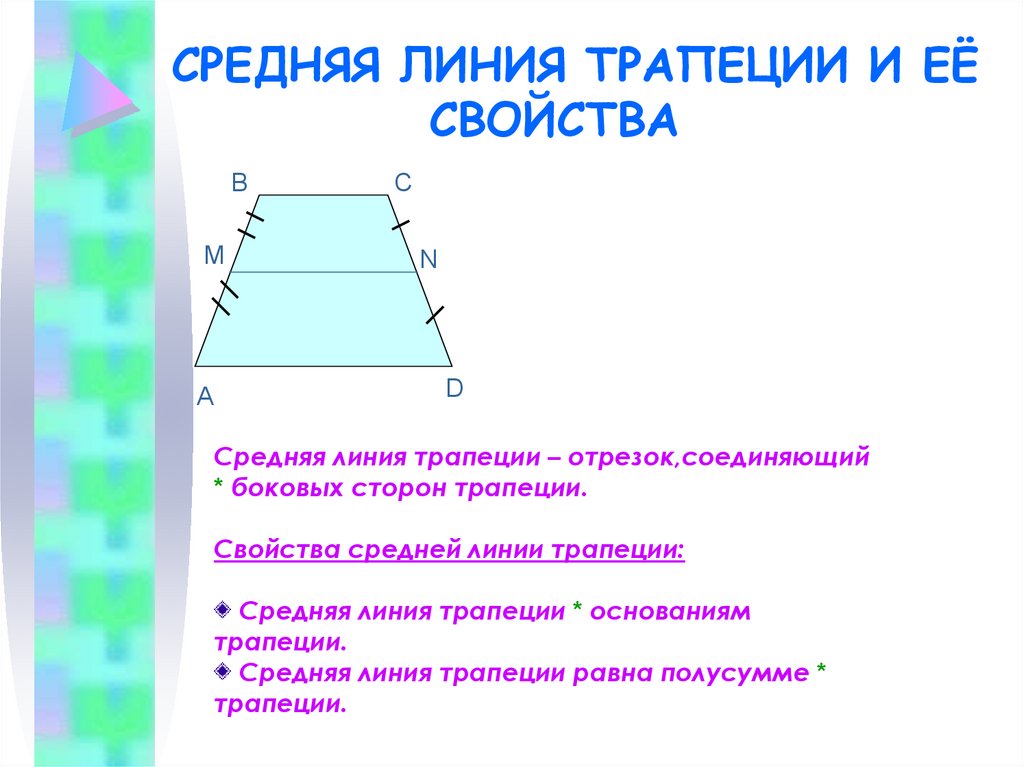
Отсюда следует, что В2 /Б1=(БС+ЭХ)/(АД+ЭХ) и БС+ЭХ=((БС+АД)/2)*(1+Б2/Б1). Получаем, что длина отрезка, делящего трапецию на две равные по размеру, равна среднему квадрату длин оснований: √ ((BS2 + AD2)/2).
Находки подобия
Итак, мы доказали, что:
1. Отрезок, соединяющий середины боковых сторон трапеции, параллелен ВР и ВР и равен среднему арифметическому между ВР и ВР (длина основание трапеции).
2. Прямая, проходящая через точку О пересечения диагоналей, параллельных АД и БС, будет равна среднему гармоническому чисел АД и БС (2*БС*АД/(БС+АД)).
3. Отрезок, делящий трапецию на подобные, имеет длину среднего геометрического оснований БС и АД.
4. Элемент, делящий фигуру на два равных размера, имеет длину средних квадратов чисел BP и BS.
Для закрепления материала и понимания связи между рассматриваемыми отрезками учащемуся необходимо построить их для конкретной трапеции. Он легко может отобразить среднюю линию и отрезок, проходящий через точку О — пересечение диагоналей фигуры — параллельно основаниям.
Но где будут находиться третий и четвертый? Этот ответ приведет студента к обнаружению желаемого соотношения между средними значениями.
Отрезок, соединяющий середины диагоналей трапеции
Рассмотрим следующее свойство этой фигуры. Предположим, что отрезок MH параллелен основаниям и делит диагонали пополам. Точки пересечения будем называть Ш и Ш. Этот отрезок будет равен половине разности оснований. Давайте посмотрим на это поближе. МШ — средняя линия треугольника АБС, она равна БС/2. МЧ — средняя линия треугольника АБД, она равна ВР/2. Тогда получаем, что ШШ = МШ-МШ, следовательно, ШШ = АД/2-БС/2=(АД+ВС)/2.
Центр тяжести
Давайте посмотрим, как определяется этот элемент для данной геометрической фигуры. Для этого необходимо вытянуть основания в противоположные стороны. Что это значит? К верхнему основанию необходимо добавить нижнее — в любую сторону, например, вправо. И удлинить нижний на длину верхнего влево. Далее соединяем их диагональю. Точка пересечения этого отрезка со средней линией фигуры является центром тяжести трапеции.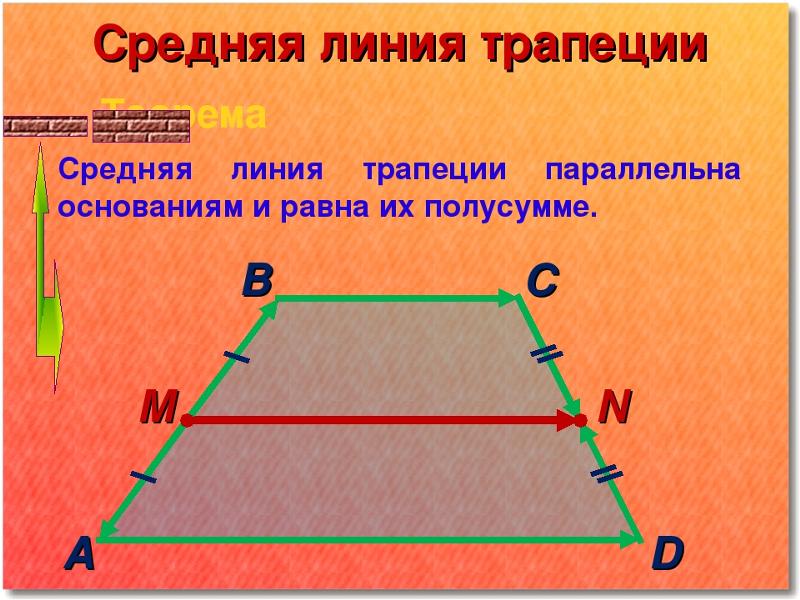
Вписанные и описанные трапеции
Перечислим признаки таких фигур:
1. Трапецию можно вписать в окружность, только если она равнобедренная.
2. Трапецию можно описать по окружности при условии, что сумма длин их оснований равна сумме длин боковых сторон.
Последствия вписанной окружности:
1. Высота описываемой трапеции всегда равна двум радиусам.
2. Боковая сторона описанной трапеции наблюдается из центра окружности под прямым углом.
Первое следствие очевидно, но для доказательства второго требуется установить, что угол СОД прямой, что, собственно, тоже не составит труда. Но знание этого свойства позволит использовать прямоугольный треугольник при решении задач.
Теперь конкретизируем эти следствия для равнобедренной трапеции, вписанной в окружность. Получаем, что высота есть среднее геометрическое основания фигуры: H = 2R = √(BS*АД). При отработке основного приема решения задач на трапеции (принцип удержания двух высот) учащийся должен решить следующую задачу.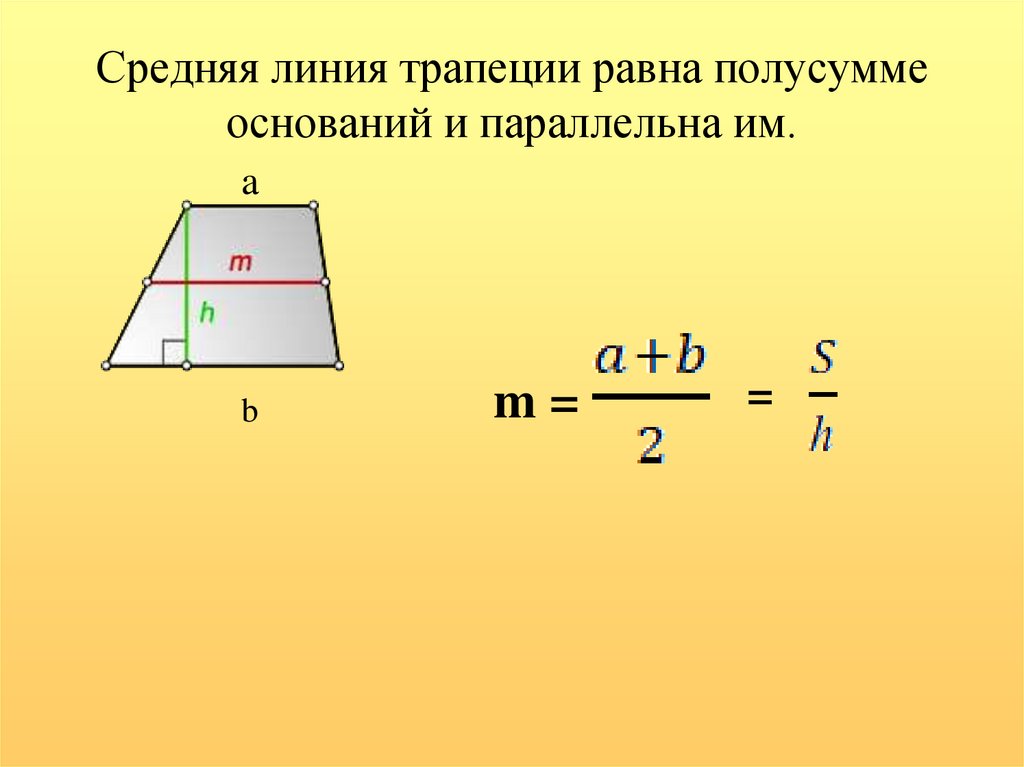
Будем считать, что ВТ — высота равнобедренной фигуры АБСД. Необходимо найти отрезки AT и TD. Используя формулу, описанную выше, сделать это не составит труда.
Теперь разберемся, как определить радиус окружности, используя площадь описываемой трапеции. Опускаем высоту от вершины Б к основанию АД. Так как окружность вписана в трапецию, то БС+АД=2АВ или АВ=(БС+АД)/2. Из треугольника АБН находим sinα=БН/АВ=2*БН/(БС+АД). ПАБСД=(БС+АД)*БН/2, БН=2Р. Получаем ПАБСД=(БС+АД)*R, отсюда следует, что R=ПАБСД/(БС+АД).
Все формулы средней линии трапеции
Теперь пришло время перейти к последнему элементу этой геометрической фигуры. Разберемся, чему равна средняя линия трапеции (М):
1. Через основания: М = (А+В)/2.
2. Через высоту, основание и углы:
М = А-Н* (ctgα + ctgβ)/2;
M = B + H * (ctgα + ctgβ) / 2.
3. Через высоту, диагонали и угол между ними. Например, D1 и D2 — диагонали трапеции; α, β — углы между ними:
М = D1 * D2 * sinα / 2H = D1 * D2 * sinβ / 2H.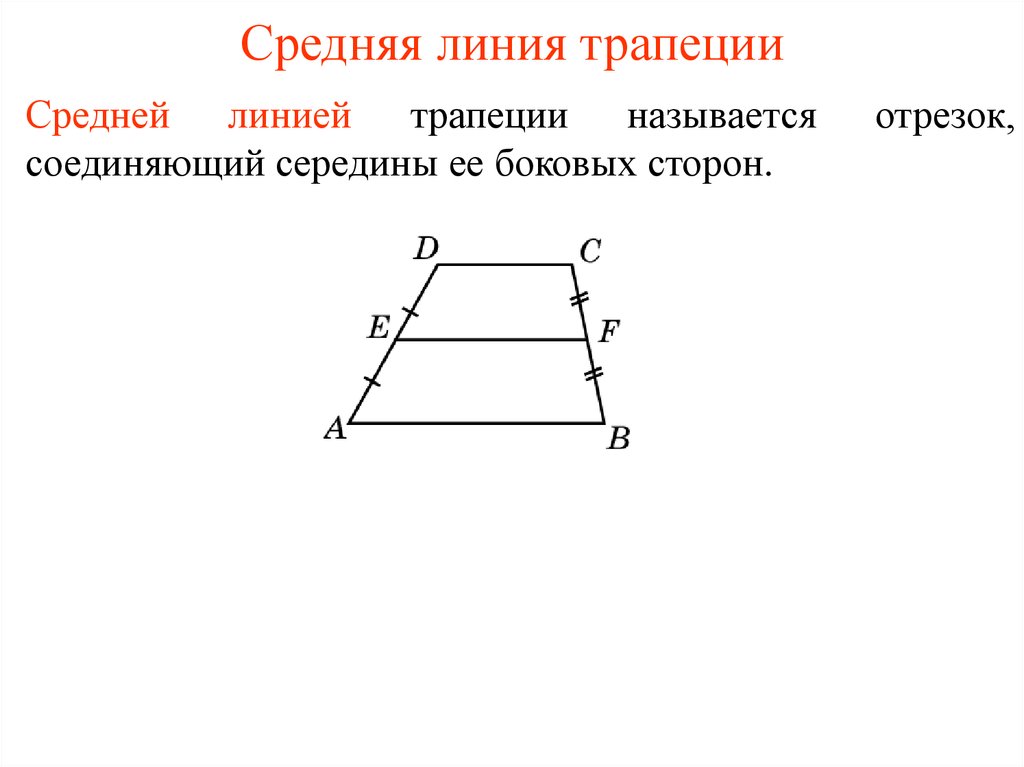
4. По площади и высоте: M = P / N.
Ваша конфиденциальность важна для нас. По этой причине мы разработали Политику конфиденциальности, в которой описывается, как мы используем и храним вашу информацию. Пожалуйста, ознакомьтесь с нашей политикой конфиденциальности и сообщите нам, если у вас есть какие-либо вопросы.
Сбор и использование личной информации
Личная информация относится к данным, которые могут быть использованы для идентификации конкретного лица или связи с ним.
Вас могут попросить предоставить личную информацию в любое время, когда вы свяжетесь с нами.
Ниже приведены некоторые примеры типов личной информации, которую мы можем собирать, и того, как мы можем использовать такую информацию.
Какую личную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваше имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу личную информацию:
- Личная информация, которую мы собираем, позволяет нам связываться с вами и сообщать об уникальных предложениях, рекламных акциях и других событиях и предстоящих событиях.
- Время от времени мы можем использовать вашу личную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать личную информацию для внутренних целей, таких как проведение аудитов, анализ данных и различные исследования, чтобы улучшить предоставляемые нами услуги и предоставить вам рекомендации относительно наших услуг.
- Если вы участвуете в розыгрыше призов, конкурсе или аналогичном рекламном мероприятии, мы можем использовать предоставленную вами информацию для управления этими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от вас информацию третьим лицам.
Исключения:
- В случае необходимости — в установленном законом порядке, в судебном порядке, в судебном порядке и/или на основании публичных запросов или запросов государственных органов на территории Российской Федерации — раскрыть Вашу персональную информацию . Мы также можем раскрыть информацию о вас, если решим, что такое раскрытие необходимо или уместно в целях безопасности, правоохранительных органов или по другим общественно важным причинам.
- В случае реорганизации, слияния или продажи мы можем передать собираемую нами личную информацию соответствующему третьему лицу — правопреемнику.
Защита личной информации
Мы принимаем меры предосторожности, в том числе административные, технические и физические, для защиты вашей личной информации от потери, кражи и злоупотребления, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Уважение к вашей конфиденциальности на уровне компании
Для того, чтобы убедиться, что ваша личная информация находится в безопасности, мы доводим до наших сотрудников правила конфиденциальности и безопасности, строго следим за выполнением мер конфиденциальности.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
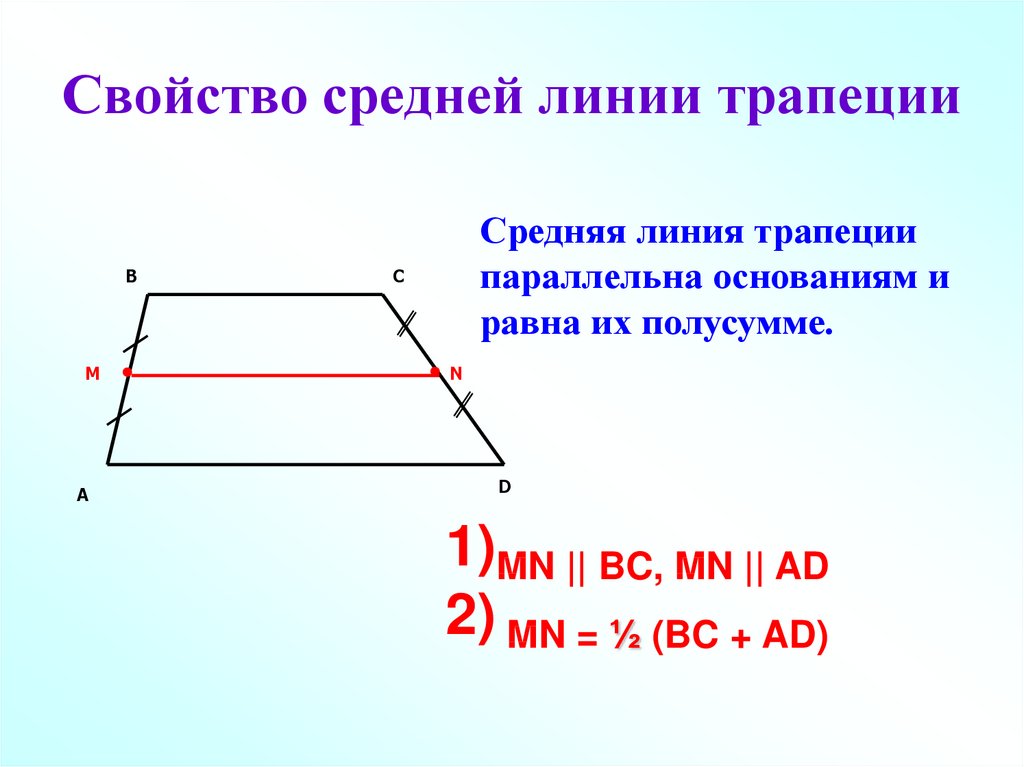
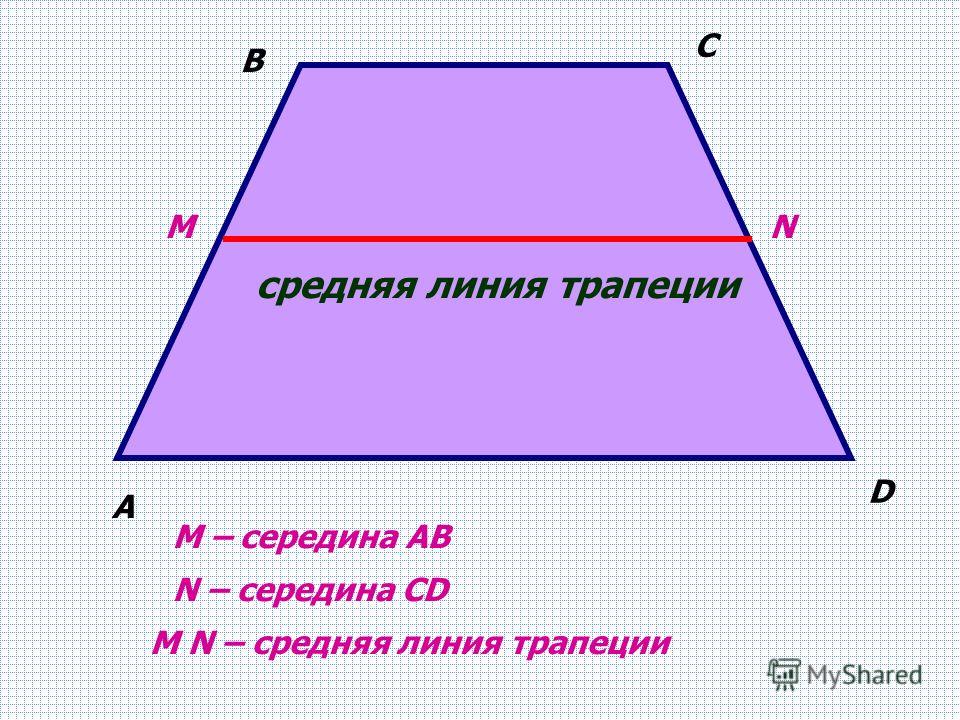
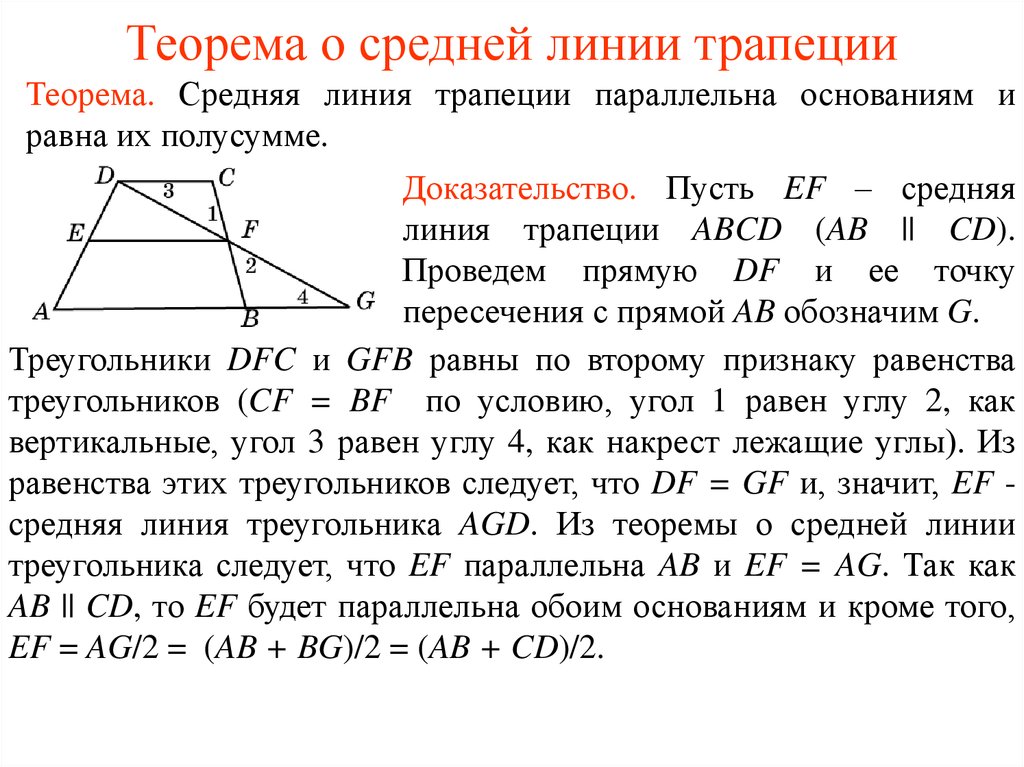Индекс.
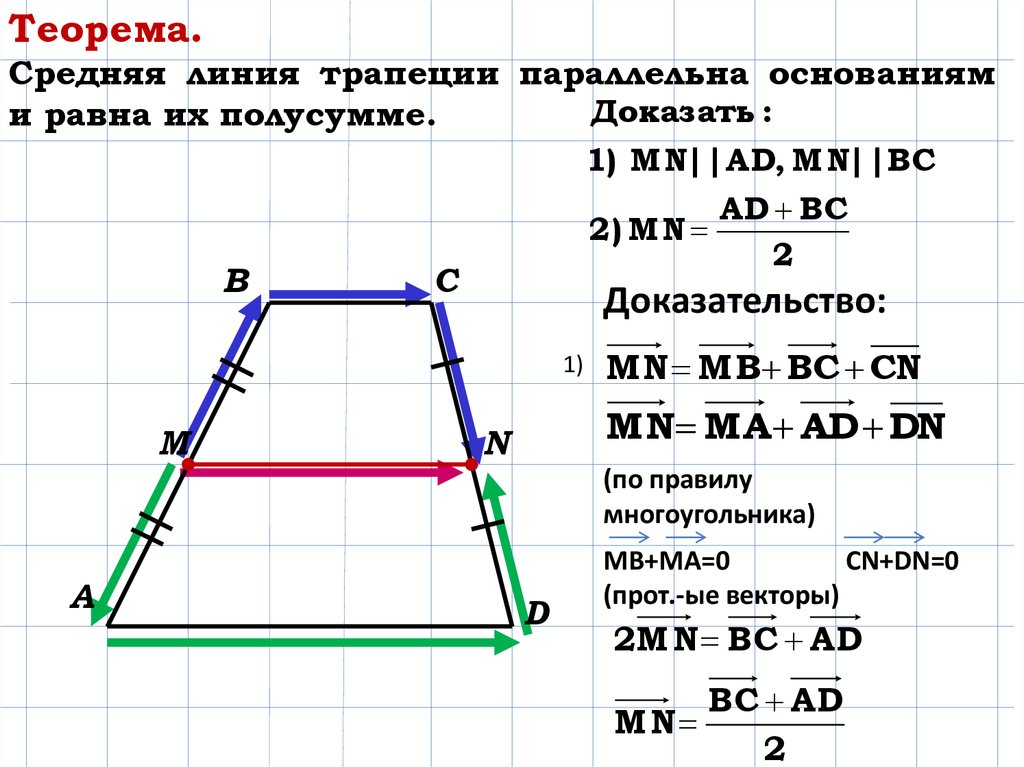Треугольник, середины, поперечное,
Перпендикулярные линии.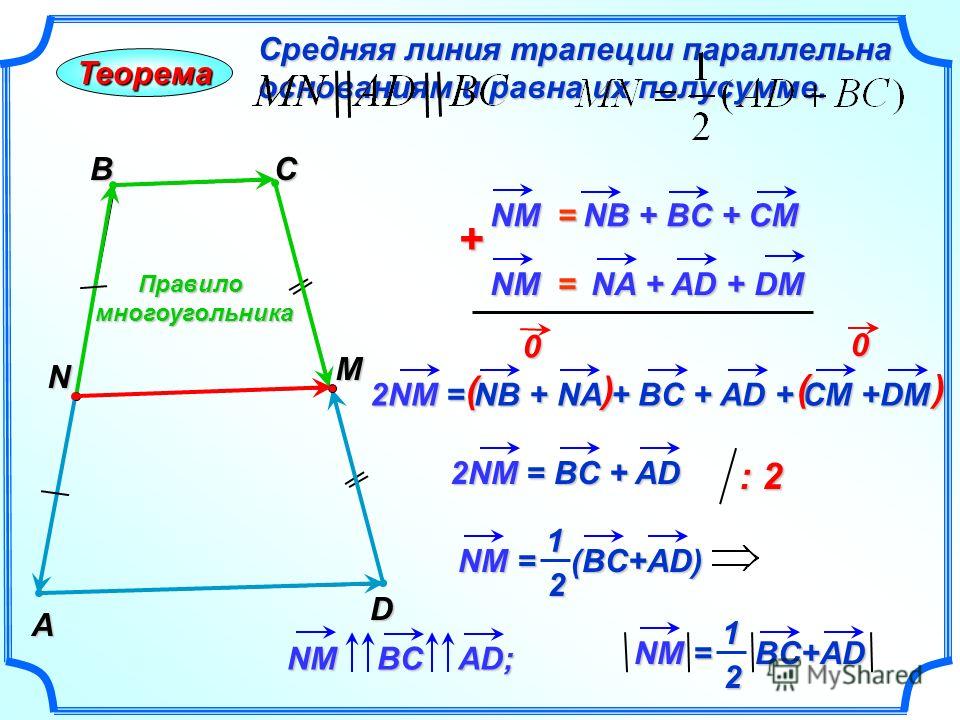
Треугольник, центроид, перпендикуляры. 
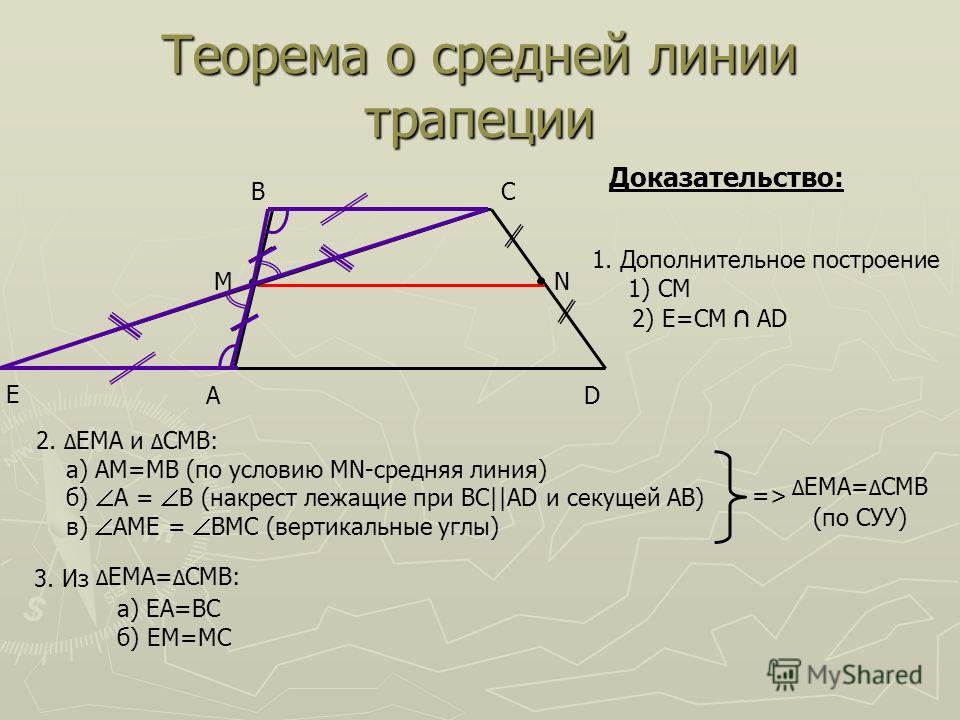Динамическая геометрия. 